Gaussian Mixture Estimation from Lower-Dimensional Data with Application to PET Imaging
Abstract
1. Introduction
2. Gaussian Estimation from PET Data
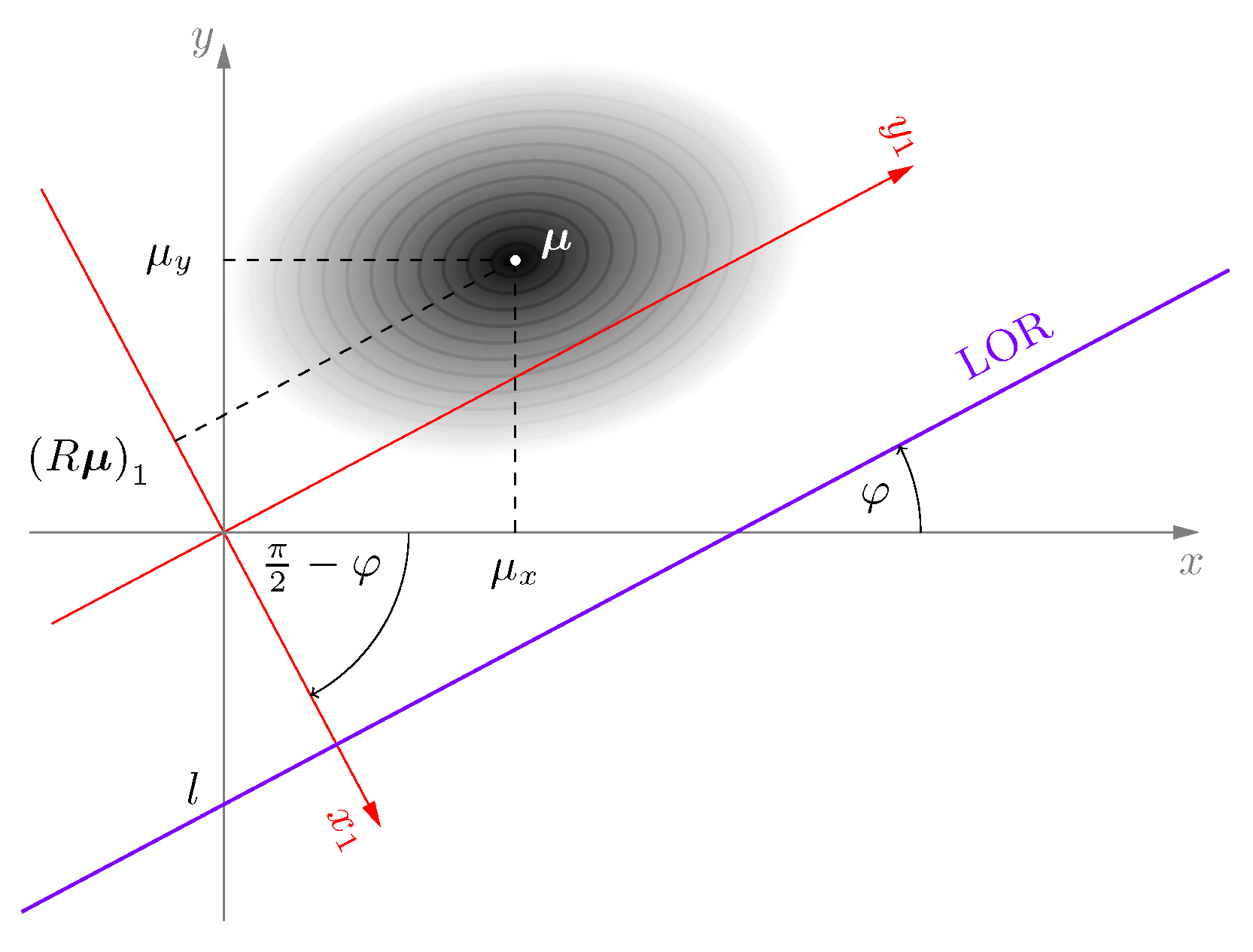
2.1. Estimation of
2.2. Estimation of
3. Gaussian Mixtures in PET Imaging
3.1. Gaussian Mixture Model
3.2. EM-like Algorithm
- E:
- Given a set of parameters , calculate the probability that each observation originated from the k-th component:These probabilities are sometimes also called responsibilities, or posterior probabilities.
- M:
- Given the set of probabilities , estimate the parameters of each component. This step is named after the maximum likelihood method that is used to estimate the parameters.
3.2.1. Initialization
- Each line is initially randomly assigned to exactly one component, while ensuring that each component has approximately the same number of lines.
- Mean vectors of each component are estimated as described in Section 2.
- Lines are reassigned to the component whose estimated mean vectors are nearest to them in terms of Euclidean distance. In this step, we still adhere to the so-called hard classification; i.e., each line is assigned to only one component.Steps 2 and 3 are repeated until the changes in mean vectors are sufficiently small.
3.2.2. E Step
- A Gaussian distribution retains properties when rotated.
- Marginal distributions of a Gaussian are again Gaussian.
3.2.3. M-like Step
- Find the nearest points to the (previous iterations’) center for each line.
- Calculate the weighted mean and covariance of with probabilities h as weights:
- Calculate from as in Section 2.
- Mixture weights are calculated, as in the original EM algorithm, as the proportion of all lines (events) assigned to each component: .
4. Experiments and Results
4.1. Single-Component Estimation
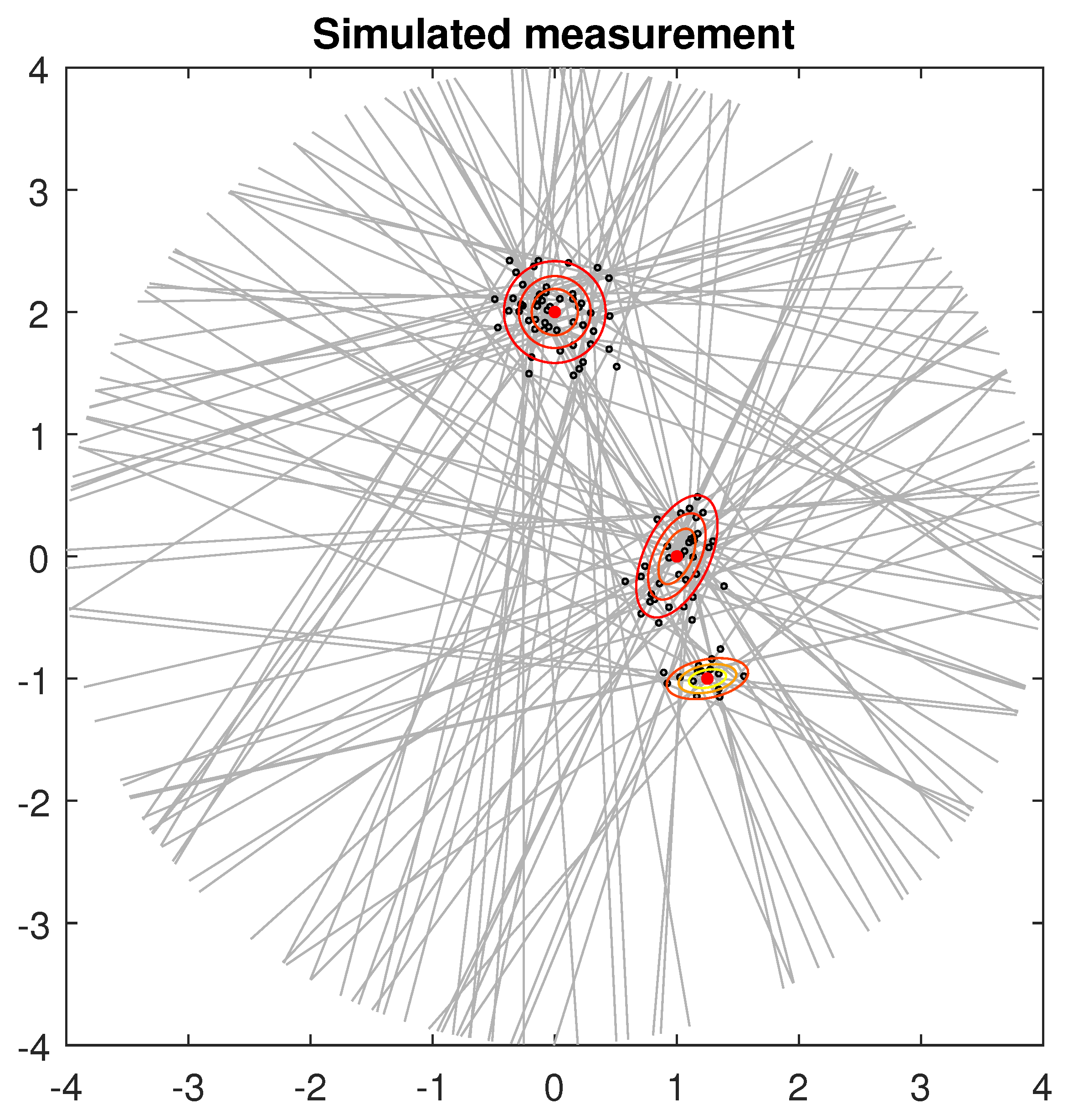
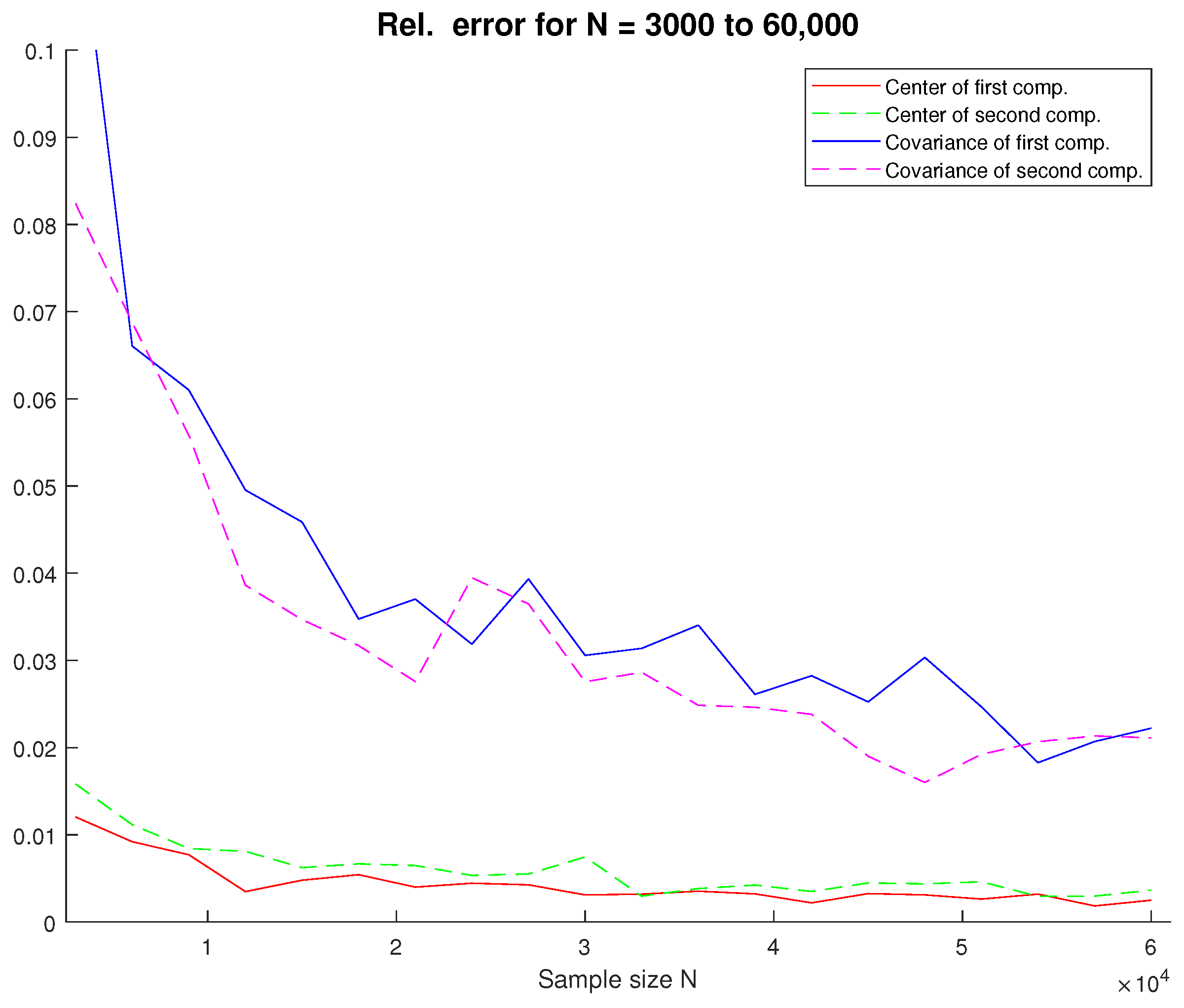
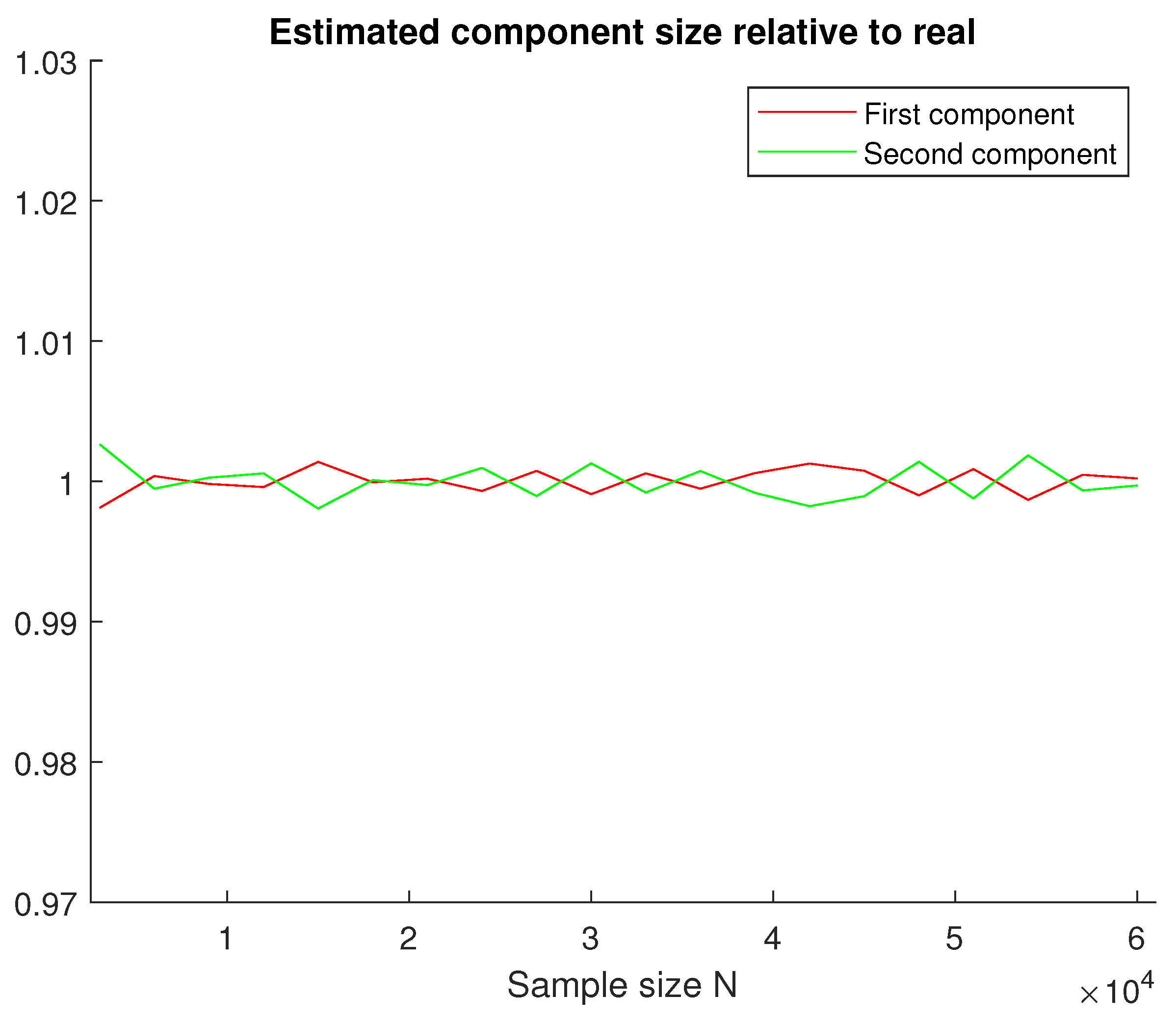
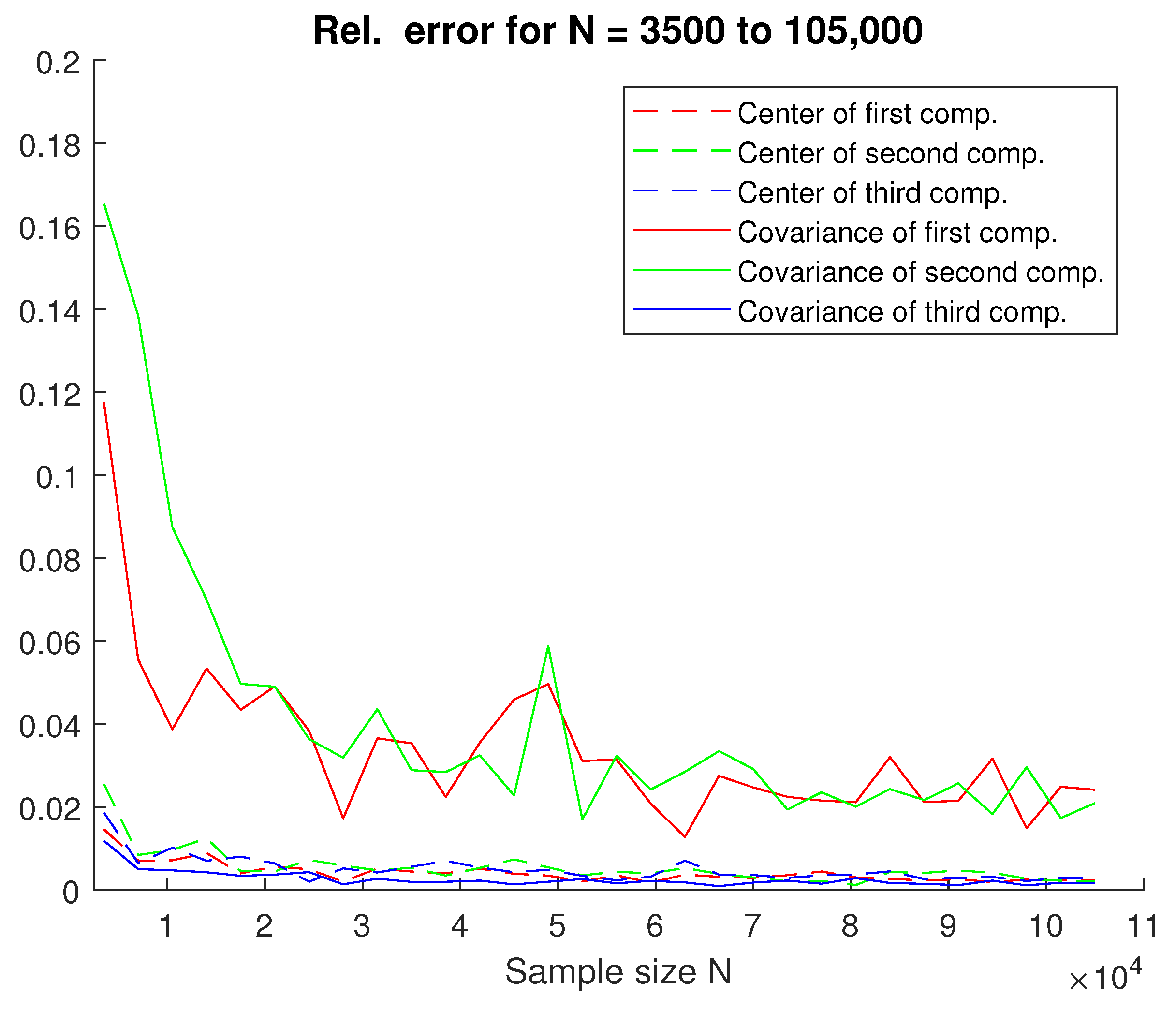
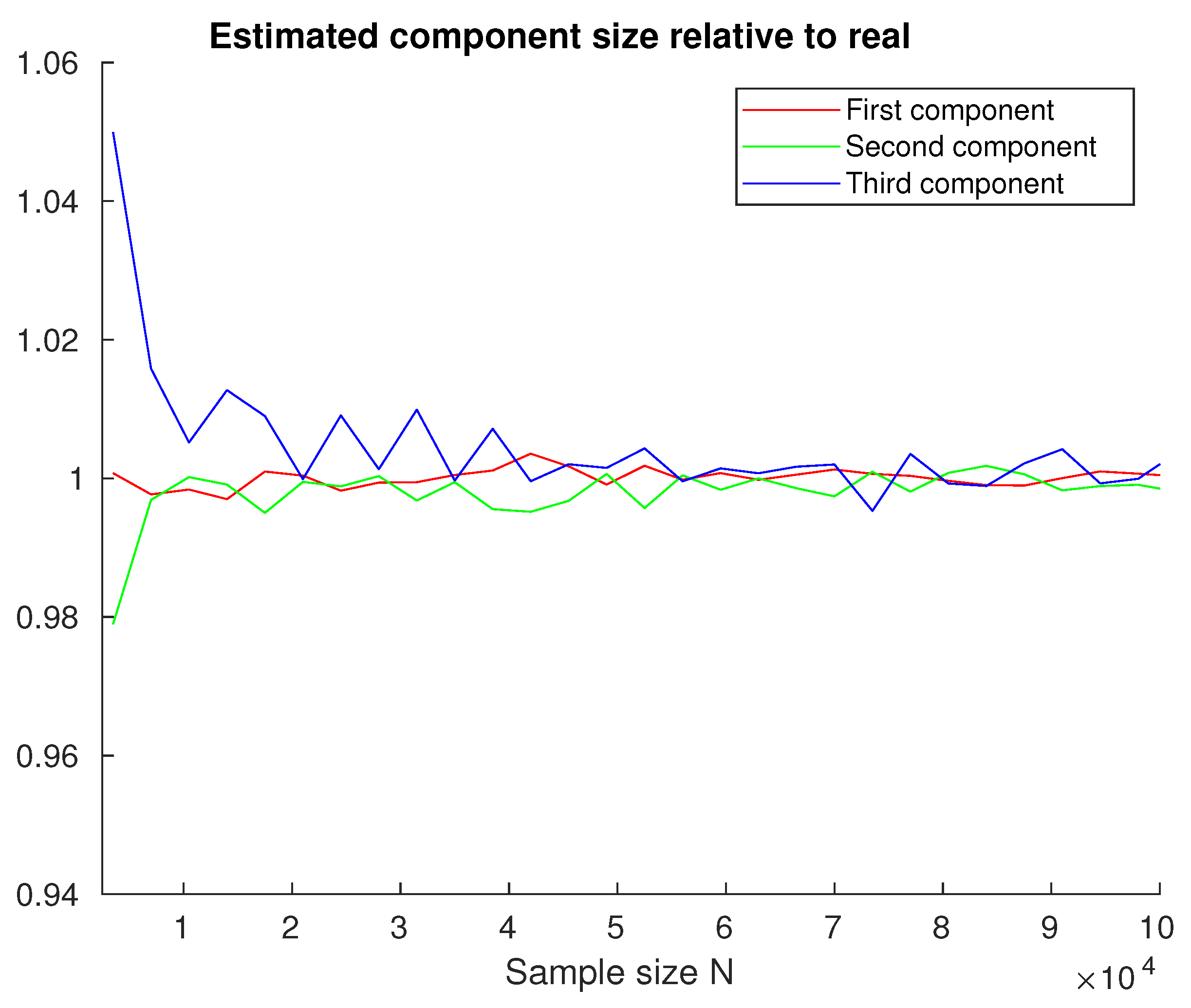
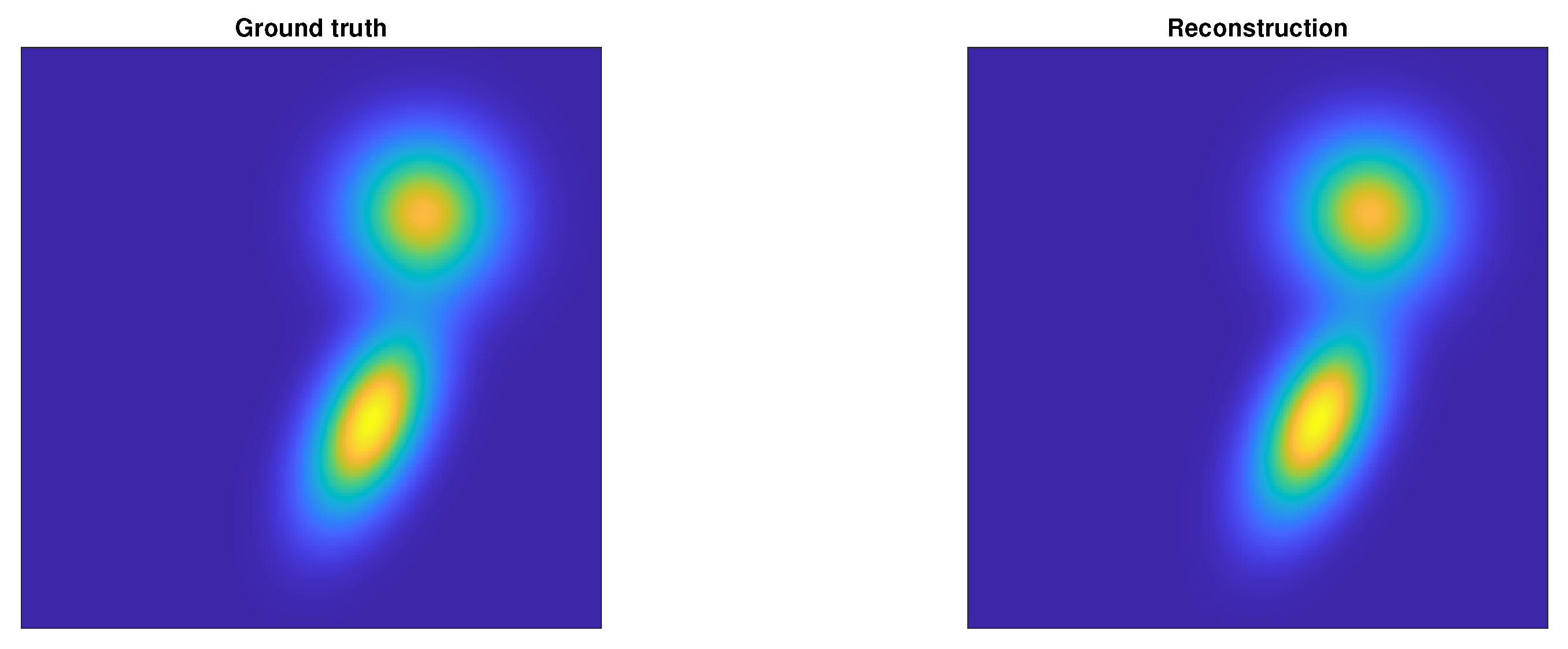
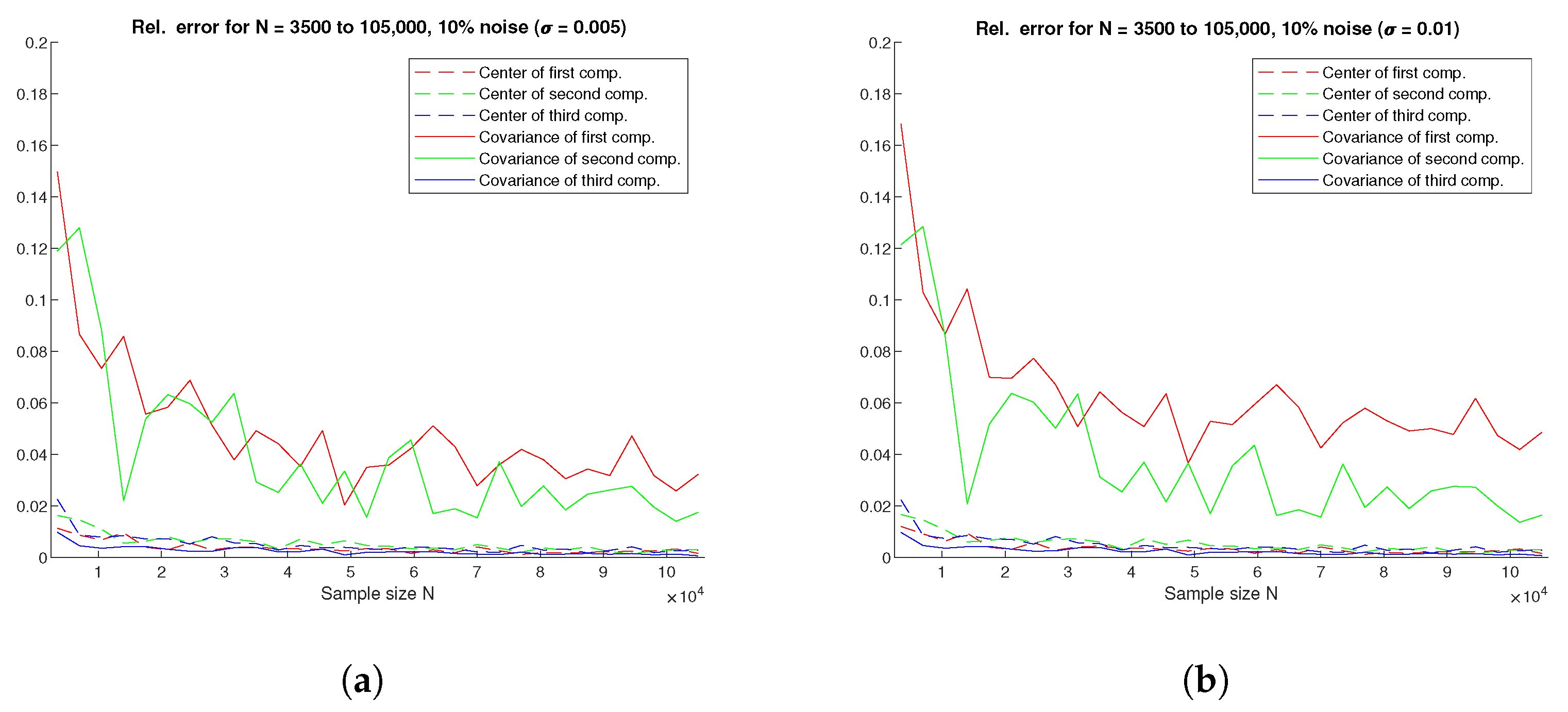
4.2. Gaussian Mixture Estimation
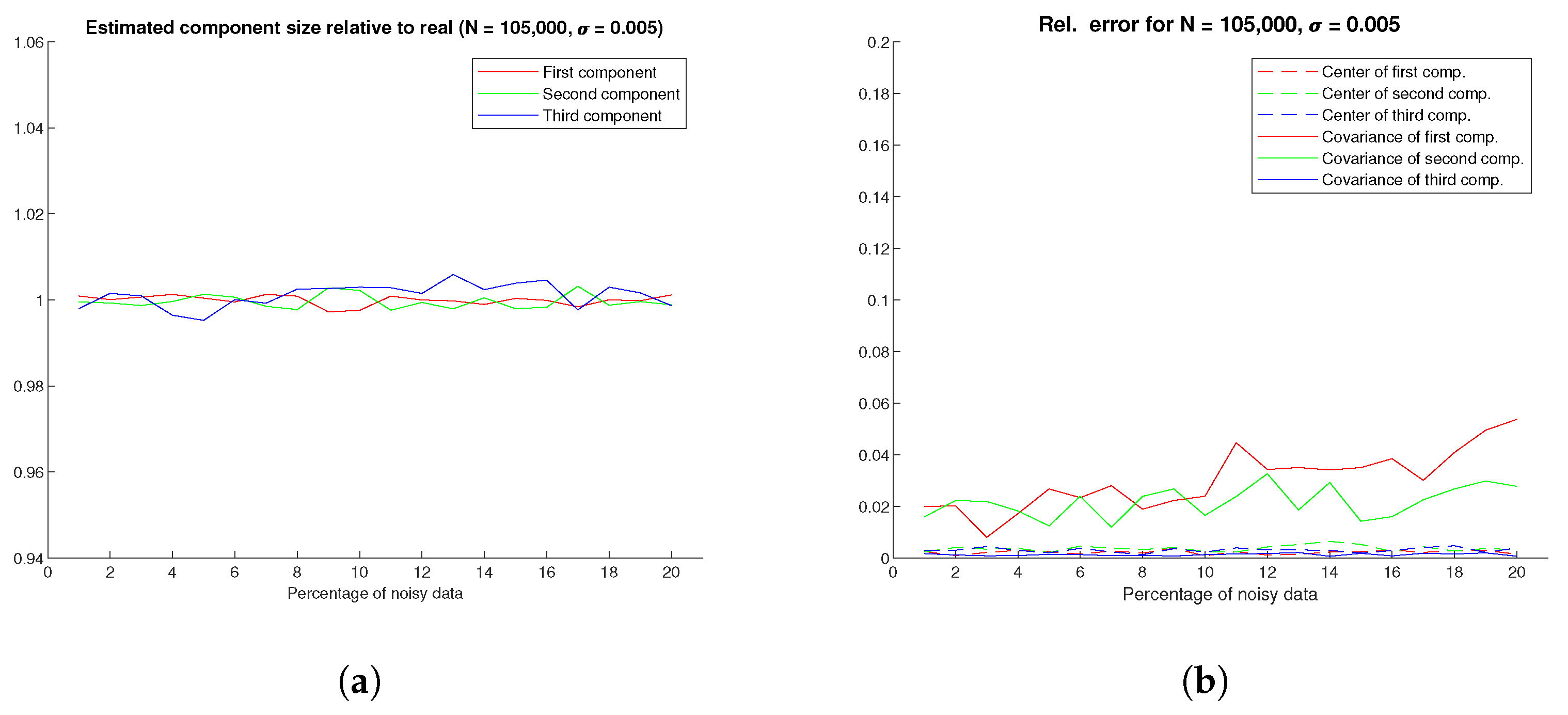
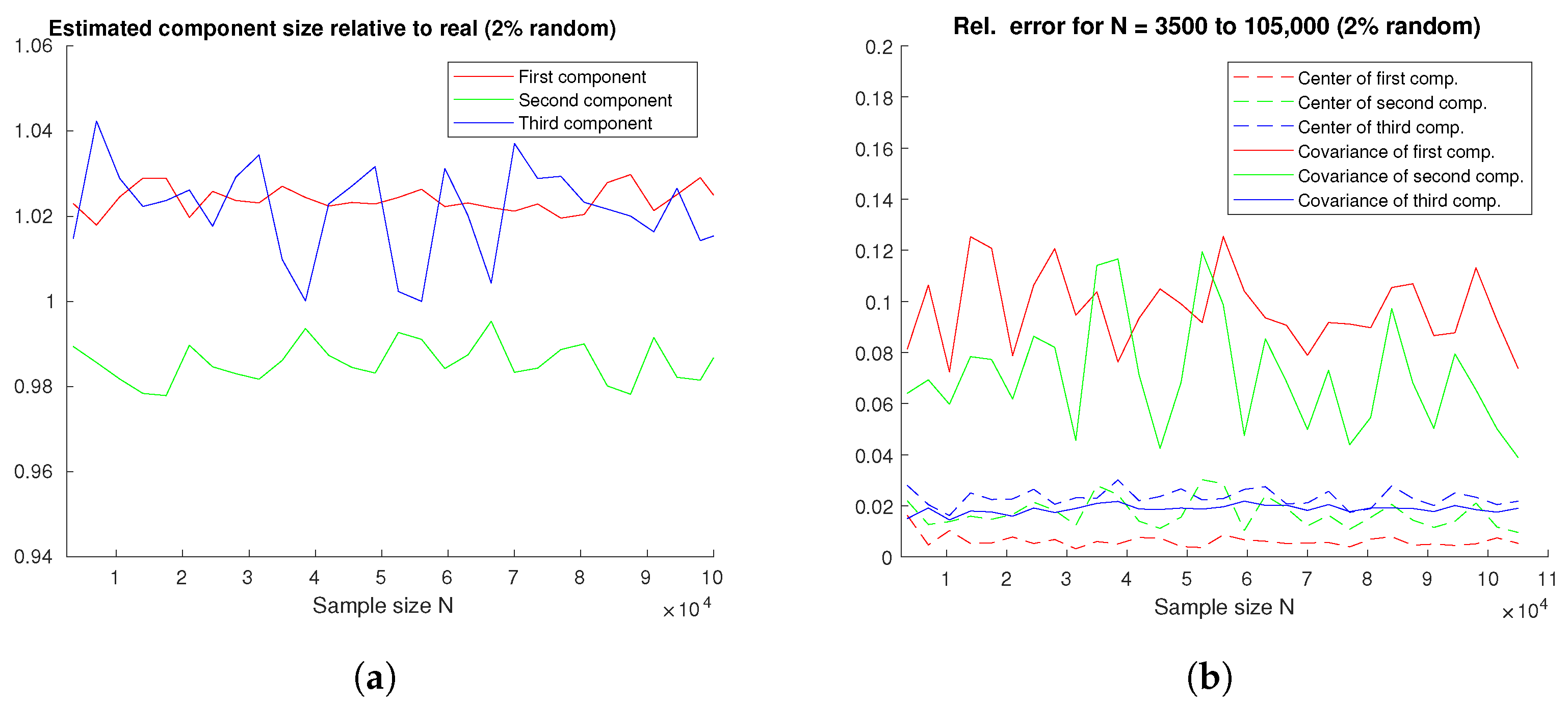
4.3. Noise Resistance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PET | positron emission tomography |
| LOR | line of response |
| GMM | Gaussian mixture model |
| EM | expectation maximization |
| VOR | volume of response |
Appendix A
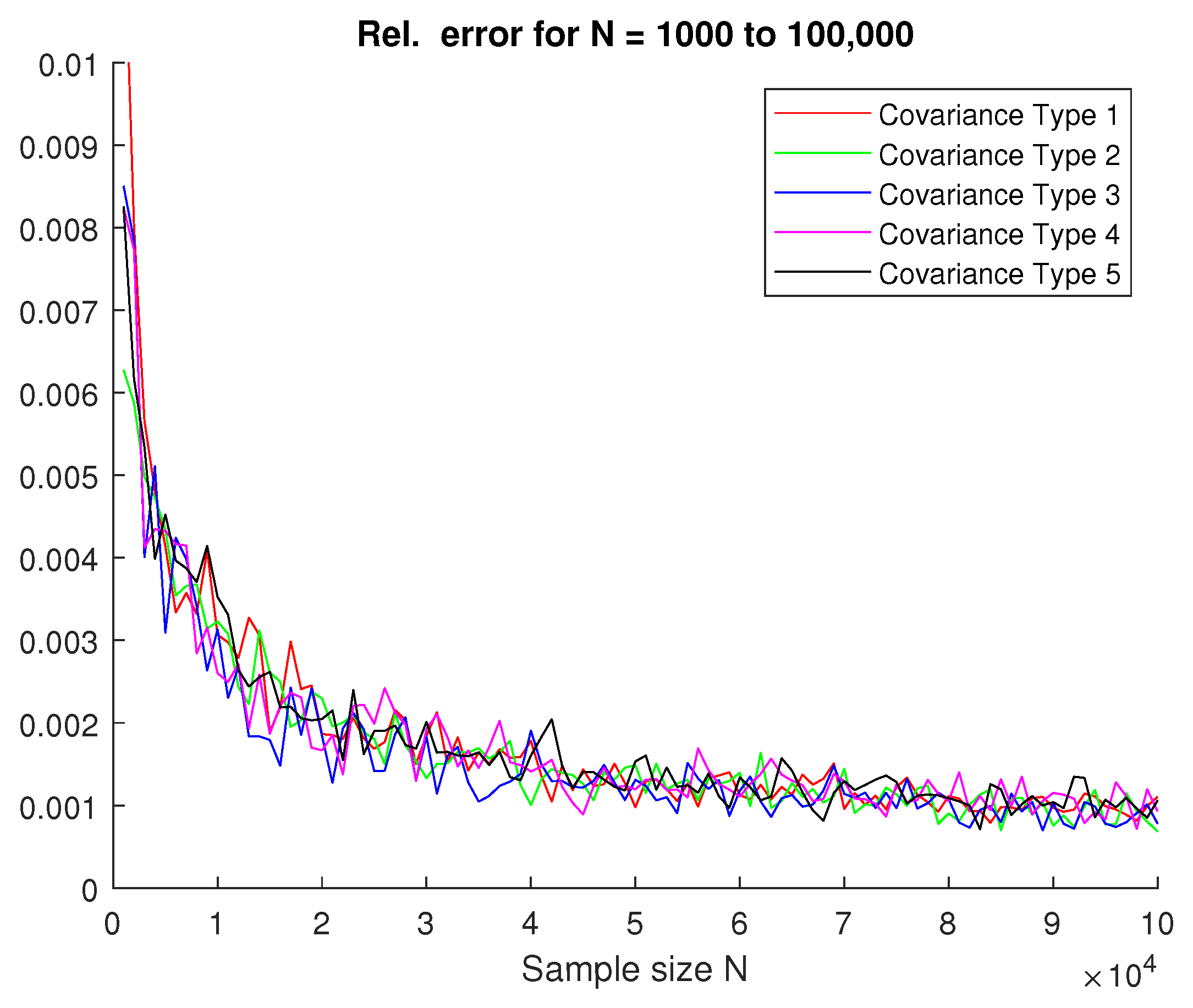
Appendix A.1. Different Covariances

Appendix A.2. Equal Component Sizes

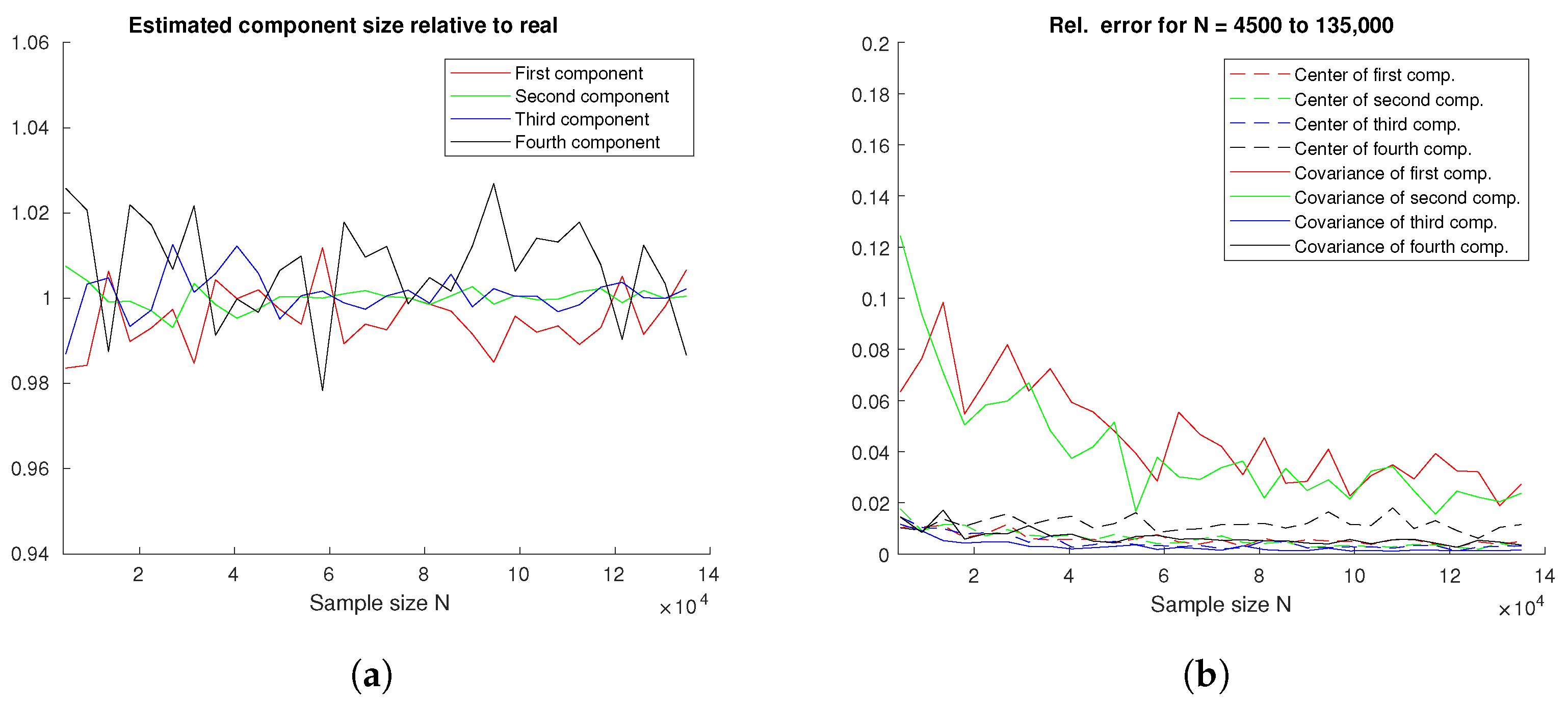
Appendix A.3. Four Components
References
- Bailey, D.L.; Maisey, M.N.; Townsend, D.W.; Valk, P.E. Positron Emission Tomography; Springer: London, UK, 2005; Volume 2. [Google Scholar]
- Tong, S.; Alessio, A.M.; Kinahan, P.E. Image reconstruction for PET/CT scanners: Past achievements and future challenges. Imaging Med. 2010, 2, 529–545. [Google Scholar] [CrossRef]
- Reader, A.J.; Zaidi, H. Advances in PET image reconstruction. PET Clin. 2007, 2, 173–190. [Google Scholar] [CrossRef]
- Kinahan, P.E.; Defrise, M.; Clackdoyle, R. Analytic image reconstruction methods. In Emission Tomography; Elsevier: Amsterdam, The Netherlands, 2004; pp. 421–442. [Google Scholar]
- Natterer, F. The Mathematics of Computerized Tomography; Siam: Philadelphia, PA, USA, 1986; Volume 32. [Google Scholar] [CrossRef]
- O’Sullivan, F.; Pawitan, Y. Multidimensional Density Estimation by Tomography. J. R. Stat. Soc. Ser. B Methodol. 1993, 55, 509–521. [Google Scholar] [CrossRef]
- Singh, S.; Kalra, M.K.; Hsieh, J.; Licato, P.E.; Do, S.; Pien, H.H.; Blake, M.A. Abdominal CT: Comparison of adaptive statistical iterative and filtered back projection reconstruction techniques. Radiology 2010, 257, 373–383. [Google Scholar] [CrossRef] [PubMed]
- Alessio, A.; Kinahan, P. PET image reconstruction. Nucl. Med. 2006, 1, 4095–4103. [Google Scholar] [CrossRef]
- Ahn, S.; Leahy, R.M. Analysis of resolution and noise properties of nonquadratically regularized image reconstruction methods for PET. IEEE Trans. Med. Imaging 2008, 27, 413–424. [Google Scholar] [PubMed]
- Zaidi, H.; Montandon, M.L.; Alavi, A. Advances in attenuation correction techniques in PET. PET Clin. 2007, 2, 191–217. [Google Scholar] [CrossRef] [PubMed]
- Chow, P.L.; Rannou, F.R.; Chatziioannou, A.F. Attenuation correction for small animal PET tomographs. Phys. Med. Biol. 2005, 50, 1837. [Google Scholar] [CrossRef] [PubMed]
- Mincke, J.; Courtyn, J.; Vanhove, C.; Vandenberghe, S.; Steppe, K. Guide to plant-pet imaging using 11CO2. Front. Plant Sci. 2021, 12, 602550. [Google Scholar] [CrossRef] [PubMed]
- Levitan, E.; Herman, G.T. A Maximum a Posteriori Probability Expectation Maximization Algorithm for Image Reconstruction in Emission Tomography. IEEE Trans. Med. Imaging 1987, 6, 185–192. [Google Scholar] [CrossRef]
- Lewitt, R.M.; Matej, S. Overview of methods for image reconstruction from projections in emission computed tomography. Proc. IEEE 2003, 91, 1588–1611. [Google Scholar] [CrossRef]
- Leahy, R.M.; Qi, J. Statistical approaches in quantitative positron emission tomography. Stat. Comput. 2000, 10, 147–165. [Google Scholar] [CrossRef]
- Meikle, S.R.; Hutton, B.F.; Bailey, D.L.; Hooper, P.K.; Fulham, M.J. Accelerated EM reconstruction in total-body PET: Potential for improving tumour detectability. Phys. Med. Biol. 1994, 39, 1689. [Google Scholar] [CrossRef] [PubMed]
- Zaidi, H.; Abdoli, M.; Fuentes, C.L.; El Naqa, I.M. Comparative methods for PET image segmentation in pharyngolaryngeal squamous cell carcinoma. Eur. J. Nucl. Med. Mol. Imaging 2012, 39, 881–891. [Google Scholar] [CrossRef] [PubMed]
- Hatt, M.; Le Rest, C.C.; Turzo, A.; Roux, C.; Visvikis, D. A fuzzy locally adaptive Bayesian segmentation approach for volume determination in PET. IEEE Trans. Med. Imaging 2009, 28, 881–893. [Google Scholar] [CrossRef] [PubMed]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. B 1977, 39, 1–38. [Google Scholar] [CrossRef]
- Shepp, L.A.; Vardi, Y. Maximum likelihood reconstruction for emission tomography. IEEE Trans. Med. Imaging 1982, 1, 113–122. [Google Scholar] [CrossRef] [PubMed]
- Hudson, H.M.; Larkin, R.S. Accelerated image reconstruction using ordered subsets of projection data. IEEE Trans. Med. Imaging 1994, 13, 601–609. [Google Scholar] [CrossRef]
- Qi, J.; Leahy, R.M. Iterative reconstruction techniques in emission computed tomography. Phys. Med. Biol. 2006, 51, R541. [Google Scholar] [CrossRef]
- Kim, K.; Wu, D.; Gong, K.; Dutta, J.; Kim, J.H.; Son, Y.D.; Kim, H.K.; El Fakhri, G.; Li, Q. Penalized PET Reconstruction Using Deep Learning Prior and Local Linear Fitting. IEEE Trans. Med. Imaging 2018, 37, 1478–1487. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, B.; Wang, L.; Zu, C.; Lalush, D.S.; Lin, W.; Wu, X.; Zhou, J.; Shen, D.; Zhou, L. 3D conditional generative adversarial networks for high-quality PET image estimation at low dose. Neuroimage 2018, 174, 550–562. [Google Scholar] [CrossRef]
- Häggström, I.; Schmidtlein, C.R.; Campanella, G.; Fuchs, T.J. DeepPET: A deep encoder—Decoder network for directly solving the PET image reconstruction inverse problem. Med. Image Anal. 2019, 54, 253–262. [Google Scholar] [CrossRef]
- Vlašić, T.; Matulić, T.; Seršić, D. Estimating Uncertainty in PET Image Reconstruction via Deep Posterior Sampling. In Proceedings of the Medical Imaging with Deep Learning, Nashville, TN, USA, 10–12 July 2023; pp. 1875–1894. [Google Scholar]
- Arabi, H.; AkhavanAllaf, A.; Sanaat, A.; Shiri, I.; Zaidi, H. The promise of artificial intelligence and deep learning in PET and SPECT imaging. Phys. Medica 2021, 83, 122–137. [Google Scholar] [CrossRef] [PubMed]
- Matsubara, K.; Ibaraki, M.; Nemoto, M.; Watabe, H.; Kimura, Y. A review on AI in PET imaging. Ann. Nucl. Med. 2022, 36, 133–143. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Ye, J.C.; De Man, B. Deep learning for tomographic image reconstruction. Nat. Mach. Intell. 2020, 2, 737–748. [Google Scholar] [CrossRef]
- Sadaghiani, M.S.; Rowe, S.P.; Sheikhbahaei, S. Applications of artificial intelligence in oncologic 18F-FDG PET/CT imaging: A systematic review. Ann. Transl. Med. 2021, 9, 823. [Google Scholar] [CrossRef] [PubMed]
- Reader, A.J.; Schramm, G. Artificial intelligence for PET image reconstruction. J. Nucl. Med. 2021, 62, 1330–1333. [Google Scholar] [CrossRef] [PubMed]
- Friedman, N.; Russell, S. Image Segmentation in Video Sequences: A Probabilistic Approach. In Proceedings of the Thirteenth Conference on Uncertainty in Artificial Intelligence, UAI’97, Providence, RI, USA, 1–3 August 1997; pp. 175–181. [Google Scholar]
- Nguyen, T.M.; Wu, Q.J. Fast and robust spatially constrained Gaussian mixture model for image segmentation. IEEE Trans. Circuits Syst. Video Technol. 2013, 23, 621–635. [Google Scholar] [CrossRef]
- Ralašić, I.; Tafro, A.; Seršić, D. Statistical Compressive Sensing for Efficient Signal Reconstruction and Classification. In Proceedings of the 2018 4th International Conference on Frontiers of Signal Processing (ICFSP), Poitiers, France, 24–27 September 2018; pp. 44–49. [Google Scholar] [CrossRef]
- Zhang, Y.; Brady, M.; Smith, S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans. Med. Imaging 2001, 20, 45–57. [Google Scholar] [CrossRef]
- Layer, T.; Blaickner, M.; Knäusl, B.; Georg, D.; Neuwirth, J.; Baum, R.P.; Schuchardt, C.; Wiessalla, S.; Matz, G. PET image segmentation using a Gaussian mixture model and Markov random fields. EJNMMI Phys. 2015, 2, 9. [Google Scholar] [CrossRef]
- Zhang, R.; Ye, D.H.; Pal, D.; Thibault, J.; Sauer, K.D.; Bouman, C.A. A Gaussian Mixture MRF for Model-Based Iterative Reconstruction With Applications to Low-Dose X-Ray CT. IEEE Trans. Comput. Imaging 2016, 2, 359–374. [Google Scholar] [CrossRef]
- Tafro, A.; Seršić, D.; Sović Kržić, A. 2D PET Image Reconstruction Using Robust L1 Estimation of the Gaussian Mixture Model. Informatica 2022, 33, 653–669. [Google Scholar] [CrossRef]
- Matulić, T.; Seršić, D. Accurate PET Reconstruction from Reduced Set of Measurements based on GMM. arXiv 2023, arXiv:2306.17028. [Google Scholar]
- Koščević, A.G.; Petrinović, D. Extra-low-dose 2D PET imaging. In Proceedings of the 2021 12th International Symposium on Image and Signal Processing and Analysis (ISPA), Zagreb, Croatia, 13–15 September 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 84–90. [Google Scholar]
- Reynolds, D. Gaussian Mixture Models. In Encyclopedia of Biometrics; Li, S.Z., Jain, A.K., Eds.; Springer: Boston, MA, USA, 2015; pp. 827–832. [Google Scholar] [CrossRef]
- Grafarend, E.W. Linear and Nonlinear Models: Fixed Effects, Random Effects, and Mixed Models; de Gruyter: Berlin, Germany, 2006. [Google Scholar]
- Matulić, T.; Seršić, D. Accurate 2D Reconstruction for PET Scanners based on the Analytical White Image Model. arXiv 2023, arXiv:2306.17652. [Google Scholar]
- Lo, Y.; Mendell, N.R.; Rubin, D.B. Testing the Number of Components in a Normal Mixture. Biometrika 2001, 88, 767–778. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tafro, A.; Seršić, D. Gaussian Mixture Estimation from Lower-Dimensional Data with Application to PET Imaging. Mathematics 2024, 12, 764. https://doi.org/10.3390/math12050764
Tafro A, Seršić D. Gaussian Mixture Estimation from Lower-Dimensional Data with Application to PET Imaging. Mathematics. 2024; 12(5):764. https://doi.org/10.3390/math12050764
Chicago/Turabian StyleTafro, Azra, and Damir Seršić. 2024. "Gaussian Mixture Estimation from Lower-Dimensional Data with Application to PET Imaging" Mathematics 12, no. 5: 764. https://doi.org/10.3390/math12050764
APA StyleTafro, A., & Seršić, D. (2024). Gaussian Mixture Estimation from Lower-Dimensional Data with Application to PET Imaging. Mathematics, 12(5), 764. https://doi.org/10.3390/math12050764





