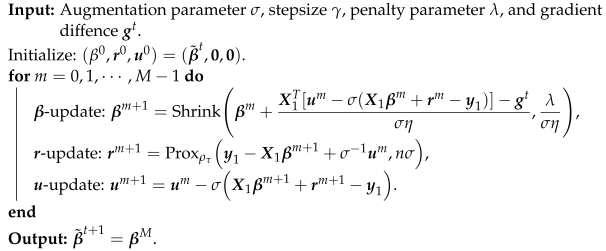Distributed Bootstrap Simultaneous Inference for High-Dimensional Quantile Regression

Abstract

Modern massive data with enormous sample size and tremendous dimensionality are usually impossible to process with a single machine. They are typically stored and processed in a distributed manner. In this paper, we propose a distributed bootstrap simultaneous inference for a high-dimensional quantile regression model using massive data. Meanwhile, a communication-efficient (CE) distributed learning algorithm is developed via the CE surrogate likelihood framework and ADMM procedure, which can handle the non-smoothness of the quantile regression loss and the Lasso penalty. We theoretically prove the convergence of the algorithm and establish a lower bound on the number of communication rounds ${\iota }_{min}$ that warrant statistical accuracy and efficiency. The distributed bootstrap validity and efficiency are corroborated by an extensive simulation study.

1. Introduction

With the rapid development of contemporary networks, science, and technology, large-scale and high-dimensional data have emerged. For a single computer or machine, due to the limitations of memory and computing power, the processing and storage of data have become a great challenge. Therefore, it is necessary to handle data scattered across various machines. Mcdonald et al. [1] considered a simple divide and conquer, that is, the  parameters of interest of the model are learned separately on the local samples of each machine, and then these estimated parameters are averaged on a master machine. The divide and conquer is communication-efficient for large-scale data, but its accuracy of learning is low. Van de Geer et al. [2] proposed an AVG-debias method, which improves the accuracy under a strong hypothesis but is time-consuming on computation because of the debiasing step. Therefore, it is necessary to develop communication-efficient distributed learning frameworks.

Afterwards, a novel communication-efficient distributed learning algorithm was proposed by [3,4]. Wang et al. [3] developed an Efficient Distributed Sparse Learning (EDSL) algorithm, which optimizes a shifted ${\ell }_1$ regularized M-estimation problem, and other machines to compute the gradient on local data for the high-dimensional model. Jordan et al. [4] adopted the same framework of distributed learning, which is called Communication-efficient Surrogate Likelihood (CSL), for solving distributed statistical inference problems in low-dimensional learning, high-dimensional regularized learning, and Bayesian inference. The two algorithms significantly improve the communication efficiency of distributed learning and have been widely used to analyze the big data in medical research, economic development, social security, and other fields. Under the CSL framework, Wang and Lian  [5] investigated a distributed quantile regression; Tong et al. [6] developed privacy-preserving and communication-efficient distributed learning, which accounts for the heterogeneity caused by a few clinical sites for a distributed electronic health records dataset; and Zhou et al. [7] developed two types of Byzantine-robust distributed learning with optimal statistical rates for strong convex losses and convex (non-smooth) penalties. It can be seen that the CSL framework plays an important role in distributed learning. In this paper, we will adopt the communication-efficient CSL for our distributed bootstrap simultaneous inference for high-dimensional data. When the data are complex with outliers or heteroscedasticity, the conventional mean regressions are unable to fully capture the information contained in the data. Quantile regression (QR) was proposed by [8], which not only captures the relationship between features and outcomes but also allows one to characterize the conditional distribution of the outcomes given these features. Compared with the mean regression model, quantile regression can handle heterogeneous data better, especially for these outcomes with heavy tail distribution or outliers. Quantile regression is widely used in many fields [9,10,11]. For quantile regression in high-dimensional sparse models, Belloni and Chernozhukov [12] considered ${\ell }_1$-penalized QR and post-penalized QR and showed that under general conditions, the two estimators are consistent at the near-oracle rate uniformly. However, they did not consider large-scale distributed circumstances. Under the distributed framework, quantile regression has also received great attention. For example, Yu et al. [13] proposed a parallel QPADM algorithm for a large-scale heterogeneous high-dimensional quantile regression model; Chen et al. [14] proposed a computationally efficient method, which only requires an initial QR estimator on a small batch of data, and proved that the algorithm with only a few rounds of aggregations achieves the same efficiency as the QR estimator obtained on all the data; Chen et al. [15] developed a distributed learning algorithm that is both computationally and communicationally efficient and showed that distributed learning achieves a near-oracle convergence rate without any restriction on the number of machines; Wang et al. [5] analyzed the high-dimensional sparse quantile regression under the CSL; and Hu et al. [16] considered an ADMM distributed quantile regression model for massive heterogeneous data under the CSL. However, the above works mainly focus on the distributed learning to parameters of quantile regression models in circumstances of massive or high-dimensional data and have not yet involved their distributed statistical inference. Volgushev et al.  [17] gave distributed statistical learning on quantile regression processes. So far, the statistical inferences for high-dimensional quantile models are still elusive, especially for distributed bootstrap simultaneous inference on high-dimensional quantile regression.

The bootstrap is a generic method for learning the sampling distribution of a statistic, typically by resampling one’s own data [18,19]. The bootstrap method can be used to evaluate the quality of estimators and can effectively solve the problem of statistical inference of high-dimensional parameters [20,21]. We refer to the fundamentals of the bootstrap method for high-dimensional data in [22]. Kleiner et al. [23] introduced the Bag of Little Bootstraps (BLB) for massive data via incorporating features of both the bootstrap and subsampling, which are suited to modern parallel and distributed computing architectures and maintain the statistical efficiency of the bootstrap. However, the BLB has restrictions on the number of machines in distributed learning. Recently, Yu et al. [24] proposed K-grad and n+K-1-grad distributed bootstrap algorithms for simultaneous inference for a linear model and a generalized linear model, which do not constrain the number of machines and provably achieve optimal statistical efficiency with minimal communication. Yu et al. [25] extended the K-grad and n+K-1-grad distributed bootstrap for simultaneous inference to high-dimensional data and adopted the CSL framework of [4], which not only relaxes the restrictions on the number of machines but also effectively reduces communication costs. In this paper, we will further extend the K-grad and n+K-1-grad distributed bootstrap for simultaneous inference in high-dimensional quantile regression models. This is challenging due to the non-smooth nature of the quantile regression loss function, which cannot directly use the existing methodology.

In this paper, we design a communication-efficient distributed bootstrap simultaneous inference algorithm for high-dimensional quantile regression and provide its theoretical analysis. The algorithm and its statistical theory are the focus of this article, which belongs to the topic of probability and statistics. Its specific sub-field is bootstrap statistical inference. It is a traditional issue in statistics, but it is novel in the context of big data. We consider these methods to fit our model best. First, we adopt a communication-efficient CSL framework for large-scale distributed data, which is a novel distributed learning algorithm proposed by [3,4]. Under the master-worker architectures, CSL makes full use of the total information of the data over the master machine while only merging the first-order gradients from all the workers. Especially, a quasi-newton optimization at the master is solved as the final estimator, instead of merely aggregating all the local estimators like one-shot methods [7]. It has been shown in [3,4] that CSL-based distributed learning can preserve sparsity structure and achieve optimal statistical estimation rates for convex problems in finite-step iterations. Second, we consider high-dimensional quantile regression for large-scale heterogeneous data, especially for these outcomes with heavy tail distribution or outliers. Thus, it brings more robust bootstrap inference. Third, we are motivated by communicate-efficient multiplier bootstrap methods K-grad/n+K-1-grad, which are originally proposed in [24,25] for mean regression, and propose our K-grad-Q/n+K-1-grad-Q Distributed Bootstrap Simultaneous Inference for high-dimensional quantile regression (Q-DistBoots-SI). Our proposed method relaxes the constraint on the number of machines and can provide more accurate and robust data for large-scale heterogeneous data. To the best of our knowledge, there is no more advanced distributed bootstrap simultaneous inference method available than our Q-DistBoots-SI for high-dimensional quantile regression.

Our main contributions are: (1) we develop a communication-efficient distributed bootstrap for simultaneous inference in high-dimensional quantile regression, under the CSL framework of distributed learning. Meanwhile, the ADMM is embedded for penalized quantile learning with distributed data, which is well suited for distributed convex optimization problems under minimum structural assumption [26] and can handle the non-smoothness of quantile loss and the Lasso penalty. (2) We theoretically prove the convergence of the algorithm and establish a lower bound on the number of communication rounds ${\tau }_{min}$ that warrants the statistical accuracy and efficiency. (3) The distributed bootstrap validity and efficiency are corroborated by an extensive simulation study.

The rest of this article is organized as follows. In Section 2, we present a communication-efficient distributed bootstrap inference algorithm. Some asymptotic properties of bootstrap validity for high-dimensional quantile learning are established in Section 3. The distributed bootstrap validity and efficiency are corroborated by an extensive simulation study in Section 4. Finally, Section 5 contains the conclusion and a discussion. The proof of the main results and additional experimental results is provided in Appendix A.

Notations

For every integer $k\ge 1$, ${\mathbb{R}}^k$ denotes a $k-$dimensional Euclidean space. The inter product of any two vectors is defined by ${\mathit{u}}^T\mathit{v}=\langle \mathit{u},\mathit{v}\rangle ={\sum }_{k=1}^p{u}_k{v}_k$ for $\mathit{u}={(u_1,\cdots ,u_p)}^T$ and $\mathit{v}={(v_1,\cdots ,v_p)}^T$. We denote the $l_q$-norm ($q\ge 1$) of any vector $\mathit{v}=(v_1,v_2,\cdots ,v_n)$ by ${\parallel \mathit{v}\parallel }_q=({\sum }_{i=1}^n|v_i{{|}^q)}^{(1/q)}$, and ${\parallel \mathit{v}\parallel }_{\infty }={max}_{1\le i\le n}\left|v_i\right|$. The induced q-norm and the max-norm of any matrix $\mathit{M}\in {\mathbb{R}}^{m\ast n}$ are denoted by ${\left|\right|\left|\mathit{M}\right|\left|\right|}_q={sup}_{\mathit{x}\in {\mathbb{R}}^n,{\parallel \mathit{x}\parallel }_q=1}{\parallel \mathit{M}\mathit{x}\parallel }_q$, and ${\left|\right|\left|\mathit{M}\right|\left|\right|}_{max}={max}_{1\le i\le m,1\le j\le n}\left|M_{i,j}\right|$, where the $M_{ij}$ is the i-th row and j-th column element of M. The ${\mathrm{\Lambda }}_{max}(·)$ denotes the largest eigenvalue of a real symmetric matrix. Let $f(·|\mathit{x})$ and $F(·|\mathit{x})$ be the conditional density and conditional cumulative distribution function of y given x, respectively. Denote $\mathit{S}=\{1\le k\le p:v_k\ne 0\}$ as the index set of nonzero coefficient and $\left|S\right|$ as the cardinality of S. ${\mathcal{M}}_k$ denotes the k worker machine. We write $a_n\asymp b_n$ for $a_n=O\left(b_n\right)$ and $b_n=O\left(a_n\right)$, $a_n\lesssim b_n$ for $a_n=O\left(b_n\right)$ and $a_n\gtrsim b_n$ for $b_n=O\left(a_n\right)$, and $a\ll b$ if $a=o\left(b\right)$.

2. Distributed Bootstrap Simultaneous Inference for High-Dimensional Quantile Learning

In this section, we introduce the distributed computing framework of the quantile regression model with high-dimensional data. In this framework, the bootstrap algorithm is used to establish the simultaneous statistical inference of high dimensional sparse parameters, and the ADMM algorithm is used to solve the non-convex optimization problem.

2.1. Problem Formulation of Distributed Quantile Learning

Quantile learning provides an effective way to depict the relationship between outcomes and features, especially for high-dimensional heterogeneity data. First, we define Y as the outcome and $\mathit{x}={(x_1,x_2,\cdots ,x_p)}^T$ as the features. Assume that the observed data are independent and identically distributed, and denote $Z={\left\{Z_i\right\}}_{i=1}^N$ with $Z_i=(y_i,{\mathit{x}}_i)$, where N is a total sample size. The conditional quantile of y given the features x and a level of quantile $\tau \in (0,1)$ is defined as a linear regression, as follows:

$$Q_{\tau }\left(y\right|\mathit{x})={\mathit{x}}^T{\mathit{\beta }}^{*}\left(\tau \right)=\sum _{j=1}^p{x}_j{\beta }_j^{*}\left(\tau \right),$$

(1)

where ${\mathit{\beta }}^{*}\left(\tau \right)={({\beta }_1^{*}\left(\tau \right),\cdots ,{\beta }_p^{*}\left(\tau \right))}^T\in {\mathbb{R}}^p$ is regression coefficients and $p>N$. We know that $Q_{\tau }\left(y\right|\mathit{x})$ is the $\tau -$th quantile function of the response variable y. Let $\epsilon =y-Q_{\tau }\left(y\right|\mathit{x})$, then $\epsilon$ satisfies $P(\epsilon \le 0|\mathit{x})=\tau$. To simplify notation, we omit the subscript $\tau$ from the parameter $\mathit{\beta }\left(\tau \right)$ subsequently. For high dimensional inference, we assume that the coefficients ${\mathit{\beta }}^{*}\left(\tau \right)$ are sparse in model (1), that is, most of its components are zero. Let $S=\{1\le k\le p:{\beta }_k^{*}\ne 0\}$ be the index set of nonzero coefficient, and $s=\left|S\right|\ll p$.

The interesting parameter ${\mathit{\beta }}^{*}$ is a minimizer of the following expected loss, i.e.,

$${\mathit{\beta }}^{*}={\mathrm{argmin}}_{\mathit{\beta }\in {\mathbb{R}}^p}{\mathcal{L}}^{*}\left(\mathit{\beta }\right),{\mathcal{L}}^{*}\left(\mathit{\beta }\right)=E\left[{\rho }_{\tau }(y-{\mathit{x}}^T\mathit{\beta })\right],$$

(2)

where the check function ${\rho }_{\tau }\left(u\right)=u(\tau -I\{u<0\})$ and $I(·)$ is an indicator function. We learn ${\mathit{\beta }}^{*}$ by minimizing the empirical loss based on the full observed data Z:

$${\widehat{\mathit{\beta }}}_Z={\mathrm{argmin}}_{\mathit{\beta }\in {\mathbb{R}}^p}{\mathcal{L}}_N\left(\mathit{\beta }\right)+\lambda {∥\mathit{\beta }∥}_1,{\mathcal{L}}_N\left(\mathit{\beta }\right)=\frac{1}{N}\sum _{i=1}^N{\rho }_{\tau }(y_i-{\mathit{x}}_i^T\beta ),$$

(3)

where $\lambda >0$ is a regularized parameter. However, it is not feasible because the data distributed across machines cannot be collected together. Even if these datasets can be gathered on a single machine, the number of data is too high for a single machine to process. Therefore, we consider statistical learning under distributed circumstances, in which the full data Z are distributed in K machines, and each machine has n data. Let $Z_k=\{Z_{ki},i=1,\cdots ,n\}$ denote the data on the kth machine, $k=1,\cdots ,K$, and $N=nK$. In addition, without a loss of generality, take the first machine as the host (central machine). Define the global and local loss functions as

$$\mathrm{Global}\mathrm{loss}:{\mathcal{L}}_N\left(\mathit{\beta }\right)=\frac{1}{K}\sum _{k=1}^K{\mathcal{L}}_k\left(\mathit{\beta }\right),$$

$$\mathrm{Local}\mathrm{loss}:{\mathcal{L}}_k\left(\mathit{\beta }\right)=\frac{1}{n}\sum _{i=1}^n{\rho }_{\tau }(y_{ki}-{\mathit{x}}_{ki}^T\mathit{\beta }),k\in \left[K\right].$$

In distributed learning, it is necessary to reduce communication costs, which can be considered in two aspects: what is transmitted between the master and worker, and what kind of distributed framework to use. In this paper, we adopt the CSL framework [3,4], in which each worker machine only transmits its local gradients to the 1st worker machine. The structure of the CSL algorithm leverages both global first-order information and local higher-order information. Thus, CSL has a minimax-optimal estimator with controlled communication cost. Correspondingly, we have the global and local gradients as

$$\mathrm{Global}\mathrm{gradients}:\nabla {\mathcal{L}}_N\left(\mathit{\beta }\right)=\frac{1}{K}\sum _{k=1}^K\nabla {\mathcal{L}}_k\left(\mathit{\beta }\right),$$

$$\mathrm{Local}\mathrm{gradients}:\nabla {\mathcal{L}}_k\left(\mathit{\beta }\right)=-\frac{1}{n}\sum _{i=1}^n{\mathit{x}}_{ki}{\psi }_{\tau }(y_{ki}-{\mathit{x}}_{ki}^T\mathit{\beta }),k\in \left[K\right],$$

where ${\psi }_{\tau }\left(u\right)=\tau -I(u<0)$. Based on the motivation of CSL for high-dimensional problems, the master machine minimizes the following ${\ell }_1$-regularized surrogate loss:

$$\widehat{\mathit{\beta }}={\mathrm{argmin}}_{\mathit{\beta }}{\mathcal{L}}_1\left(\mathit{\beta }\right)+\langle \nabla {\mathcal{L}}_N\left(\tilde{\mathit{\beta }}\right)-\nabla {\mathcal{L}}_1\left(\tilde{\mathit{\beta }}\right),\mathit{\beta }\rangle +\lambda {\parallel \mathit{\beta }\parallel }_1,$$

(4)

where the $\tilde{\mathit{\beta }}$ is a initial estimator, which can be obtained by the 1st machine via the optimization problem

$$\tilde{\mathit{\beta }}={\mathrm{argmin}}_{\mathit{\beta }}{\mathcal{L}}_1\left(\mathit{\beta }\right)+\lambda {∥\mathit{\beta }∥}_1.$$

In the distributed environment, the $\widehat{\mathit{\beta }}$ of  (4) is learned, starting from an initial estimator ${\mathit{\beta }}^0$. Let ${\mathit{\beta }}^0=\tilde{\mathit{\beta }}$ as well. Then, ${\mathit{\beta }}^0$ is broadcast to all other worker machines, which is used to compute the local gradients $\nabla {\mathcal{L}}_k\left(\mathit{\beta }\right)$ by each local worker machine and transmits the gradients back to the 1st machine. Thus, one round of communication is completed. At the $(t+1)$th round, the 1st machine solves (4) as an iterative program

$${\tilde{\mathit{\beta }}}^{t+1}={\mathrm{argmin}}_{\mathit{\beta }}{\mathcal{L}}_1\left(\mathit{\beta }\right)+〈{\displaystyle \frac{1}{K}}\sum _{k=1}^K\nabla {\mathcal{L}}_k\left({\tilde{\mathit{\beta }}}^t\right)-\nabla {\mathcal{L}}_1\left({\tilde{\beta }}^t\right),\mathit{\beta }〉+{\lambda }^{t+1}{\parallel \beta \parallel }_1,$$

(5)

which is broadcast to other worker machines, and they are used to compute the local gradients based on the local data as before. The regularized parameter ${\lambda }^t$ can be chosen as the way of [3], so that it decreases with the iteration number t. The iterative program (5) is the optimization problem of nonsmooth convex, which is solved via ADMM for computation efficiency. See Section 2.3 for details.

2.2. Distributed Bootstrap for Simultaneous Inference

First, we consider the case of nondistributed learning. Assume that ${\widehat{\mathit{\beta }}}_{Lasso}$ can be obtain via (3) based on the entire data Z. Then, for a large $\alpha \in (0,1)$, we construct the simultaneous confidence intervals by learning the quantile

$$c\left(\alpha \right):=inf\{t\in \mathbb{R}:P(\widehat{T}\le t)\ge \alpha \},$$

(6)

where

$$\widehat{T}:={\parallel \sqrt{N}({\widehat{\mathit{\beta }}}_N-{\mathit{\beta }}^{*})\parallel }_{\infty }.$$

(7)

The ${\widehat{\mathit{\beta }}}_N$ can be obtained through the debiased ${\ell }_1$-penalized quantile learning

$${\widehat{\mathit{\beta }}}_N={\widehat{\mathit{\beta }}}_Z+{\mathbf{\Sigma }}_N^{-1}\left\{{\displaystyle \frac{1}{N}}\sum _{k=1}^K\sum _{i=1}^n{\mathit{x}}_{ki}{\psi }_{\tau }(y_{ki}-{\mathit{x}}_{ki}^T{\widehat{\mathit{\beta }}}_Z)\right\},$$

(8)

where ${\mathbf{\Sigma }}_N=\frac{1}{N}{\sum }_{k=1}^K{\sum }_{i=1}^n{\mathit{x}}_{ki}{\mathit{x}}_{ki}^{T}f\left({\mathit{x}}_{ki}^T{\widehat{\mathit{\beta }}}_Z\right|{\mathit{x}}_{ki})$, and ${\widehat{\mathit{\beta }}}_Z$ is a global estimator defined in (3). In high dimensions such as $p>N$, ${\mathbf{\Sigma }}_N^{-1}$ cannot be defined because $\mathrm{rank}\left({\Sigma }_N\right)\le N<p$. So, we need to replace it with an estimator of its inverse, say ${\widehat{\mathbf{\Theta }}}_N$; then, the resulting debiased estimator is ${\ell }_1$-penalized quantile learning

$${\widehat{\widehat{\mathit{\beta }}}}_N={\widehat{\mathit{\beta }}}_Z+{\widehat{\mathbf{\Theta }}}_N\left\{{\displaystyle \frac{1}{N}}\sum _{k=1}^K\sum _{i=1}^n{\mathit{x}}_{ki}{\psi }_{\tau }(y_{ki}-{\mathit{x}}_{ki}^T{\widehat{\mathit{\beta }}}_Z)\right\}.$$

(9)

Note that the debiasing mechanism is similar to [2]. Then,

$$\widehat{\widehat{T}}:={∥\sqrt{N}({\widehat{\widehat{\mathit{\beta }}}}_N-{\mathit{\beta }}^{*})∥}_{\infty }.$$

(10)

However, the simultaneous inference based on $\widehat{\widehat{T}}$ and ${\widehat{\widehat{\mathit{\beta }}}}_N$ is unfeasible in the distributed framework, which is regarded as an “oracle” in this paper because it is impossible to obtain it based on full data Z. Therefore, we consider the simultaneous inference in distributed learning and keep statistical accuracy as the oracle $\widehat{\widehat{T}}$.

In the distributed environment, we need to replace ${\widehat{\mathit{\beta }}}_Z$ with the CSL distributed estimator $\widehat{\mathit{\beta }}$. In addition, ${\widehat{\mathbf{\Theta }}}_N$ generally is computed via the nodewise lasso [2], which cannot be translated to distributed learning because of communication inefficiency. To avoid large-scale communication, we compute the nodewise lasso only on the 1st machine based on its local data, which does not sacrifice statistical accuracy if $\widehat{\mathit{\beta }}$ or ${\tilde{\mathit{\beta }}}^T$ for a large enough T sufficiently closes to ${\mathit{\beta }}^{*}$. By the ideas of [24,25] for bootstrap inference, we need to estimate the asymptotic quantile $c\left(\alpha \right)$ of $\widehat{T}$ by bootstrapping ${∥{\widehat{\mathbf{\Theta }}}_1\sqrt{N}\nabla {\mathcal{L}}_N\left(\widehat{\mathit{\beta }}\right)∥}_{\infty }$ using K-grad or $n+K-1$-grad bootstrap.

In practice, the ${∥{\widehat{\mathbf{\Theta }}}_1\sqrt{N}\nabla {\mathcal{L}}_N\left(\widehat{\mathit{\beta }}\right)∥}_{\infty }$ still cannot be used to bootstrapping because the computation of ${\widehat{\mathbf{\Theta }}}_1$ is based on the value of ${\widehat{\mathbf{\Sigma }}}_1=\frac{1}{n}{\sum }_{i=1}^n{\mathit{x}}_{1i}{\mathit{x}}_{1i}^{T}f\left({\mathit{x}}_{1i}^T\widehat{\mathit{\beta }}\right|{\mathit{x}}_{1i})$, which depends on the unknown conditional density $f(·|·)$. We can estimate $f\left({\mathit{x}}_{1i}^T\widehat{\mathit{\beta }}\right|{\mathit{x}}_{1i})$ by the standard kernel density estimator $\varphi ((y_{1i}-{\mathit{x}}_{1i}^T\widehat{\mathit{\beta }})/h)/h$ with a small bandwidth $h>0$, where $\varphi$ is a kernel. For simplicity, we take $\varphi$ as the standard normal density; of course, other popular kernels also can be taken. Here, we do not estimate it in isolation because we are more interested in the estimator of ${\widehat{\mathbf{\Sigma }}}_1$. Therefore, we estimate ${\widehat{\mathbf{\Sigma }}}_1$ by

$${\tilde{\mathbf{\Sigma }}}_1={\displaystyle \frac{1}{nh}}\sum _{i=1}^n{\mathit{x}}_{1i}{\mathit{x}}_{1i}^T\varphi \left({\displaystyle \frac{y_{1i}-{\mathit{x}}_{1i}^T\widehat{\mathit{\beta }}}{h}}\right).$$

(11)

It is easy to show that under a mild assumption ${\tilde{\mathbf{\Sigma }}}_1$ is sufficiently close to ${\widehat{\mathbf{\Sigma }}}_1$ in the matrix norm ${∥·∥}_{\infty }$. By the nodewise lasso, we obtain ${\tilde{\mathbf{\Theta }}}_1$ from ${\tilde{\mathbf{\Sigma }}}_1$. The multiplier bootstrap [22] can be applied to simulate the distribution of $A=:{\tilde{\mathbf{\Theta }}}_1\sqrt{N}\nabla {\mathcal{L}}_N\left(\widehat{\mathit{\beta }}\right)$. Therefore, we approximate $c\left(\alpha \right)$ by the percentile of ${\left\{{\overline{W}}^{\left(b\right)}\right\}}_{b=1}^B$ via the K-grad algorithm, where

$${\overline{W}}^{\left(b\right)}=:\parallel \underset{=:\overline{A}}{\underbrace{-{\tilde{\mathbf{\Theta }}}_1\frac{1}{\sqrt{K}}\sum _{k=1}^K{ϵ}_k^{\left(b\right)}\sqrt{n}({\mathit{g}}_k-\overline{\mathit{g}})}}{\parallel }_{\infty },$$

(12)

where ${ϵ}_k^{\left(b\right)}{ }_{\sim }^{i.i.d.}N(0,1)$, ${\mathit{g}}_k=\nabla {\mathcal{L}}_k\left(\tilde{\mathit{\beta }}\right)$, and $\overline{\mathit{g}}=K^{-1}{\sum }_{k=1}^K{\mathit{g}}_k$. We call this method the K-grad-Q(uantile) distributed bootstrap. The K-grad algorithm cannot work well when K is small [24,25]. Further, the improved n+K-1-grad algorithm, such as the proposed method in [24,25], approximates $c\left(\alpha \right)$ by the percentile of ${\left\{{\tilde{W}}^{\left(b\right)}\right\}}_{b=1}^B$, where

$${\tilde{W}}^{\left(b\right)}:=\parallel \underset{=:\tilde{A}}{\underbrace{-{\tilde{\mathbf{\Theta }}}_1\frac{1}{\sqrt{n+K-1}}\left(\sum _{i=1}^n{ϵ}_{1i}^{\left(b\right)}({\mathit{g}}_{1i}-\overline{\mathit{g}})+\sum _{k=2}^K{ϵ}_k^{\left(b\right)}\sqrt{n}({\mathit{g}}_k-\overline{\mathit{g}})\right)}}{\parallel }_{\infty },$$

(13)

where ${ϵ}_{1i}^{\left(b\right)}{ }_{\sim }^{i.i.d.}N(0,1)$, ${ϵ}_k^{\left(b\right)}{ }_{\sim }^{i.i.d.}N(0,1)$, ${\mathit{g}}_{1i}=\nabla {\mathcal{L}}_1(\tilde{\mathit{\beta }};Z_{1i})=-{\mathit{x}}_{1i}{\psi }_{\tau }(y_{1i}-{\mathit{x}}_{1i}^T\tilde{\mathit{\beta }})$, ${\mathit{g}}_k=\nabla {\mathcal{L}}_k\left(\tilde{\mathit{\beta }}\right)$, and $\overline{\mathit{g}}=K^{-1}{\sum }_{k=1}^K{\mathit{g}}_k$. We call this method the n+K-1-grad-Q distributed bootstrap. In Algorithm 1, we refer to K-grad-Q and n+K-1-grad-Q as Q-DistBoots algorithm. The K-grad-Q and n+K-1-grad-Q distributed bootstrap are communication-efficient because ${\overline{W}}^{\left(b\right)}$ and ${\tilde{W}}^{\left(b\right)}$ only compute in the 1st machine without communicating with other worker machines, once all local gradients are collected by the 1st machine.

Since the quantile loss is non-smooth, the Newton–Raphson algorithm cannot be used to obtain $\widehat{\mathit{\beta }}$. We consider the proximal ADMM algorithm [27] for the Quantile regression program (5) in the CSL framework, which is also called the Q-ADMM-CSL algorithm. In addition, for computing ${\tilde{\mathbf{\Theta }}}_1$, we adopt the nodewise lasso technique [2], which is called the NodeLasso algorithm in this paper. Combined with our Q-ADMM-CSL, NodeLasso, and K-grad-Q and n+K-1-grad-Q algorithms under the CSL distributed framework, we propose Communication-Efficient K-grad-Q/n+K-1-grad-Q Distributed Bootstrap Simultaneous Inference for high-dimensional quantile regression (Q-DistBoots-SI), which is presented in Algorithm 1. Note that Q-DistBoots is provided in Algorithm 2, andQ-ADMM-CSL and NodeLasso algorithms are introduced in Algorithms 3 and 4 of Section 2.3.

In the Q-DistBoots-SI algorithm for high-dimensional quantile regression, we need running Q-DistBoots, which is the K-grad-Q/n+K-1-grad-Q distributed bootstrap learning algorithm. The key advantage of Q-DistBoots is that, once the 1st machine receives all local gradients ${\mathit{g}}_k$ from the worker machines, simultaneous inferences can be run on the 1st machine only. See Algorithm 2 for a detailed description of K-grad-Q/n+K-1-grad-Q.

Algorithm 1: Q-DistBoots-SI algorithm for high-dimensional quantile

Algorithm 2: Q-DistBoots algorithm about K-grad-Q/n+K-1-grad-Q distributed bootstrap for high-dimensional learning only on ${\mathcal{M}}_1$

2.3. Q-ADMM-CSL Algorithm and NodeLasso Optimization

In the section, we first develop a Q-ADMM-CSL algorithm for the high-dimensional large-scale data under the CSL distributed framework. It can tackle the non-smoothness of our loss function and has simply closed-form solutions. Then, we introduce the NodeLasso algorithm to approximate inverse Hessian matrix ${\mathbf{\Sigma }}_1$ in Algorithm 1.

2.3.1. Q-ADMM-CSL Algorithm for Penalized Quantile Regression in CSL

The alternating direction method of multipliers (ADMM) algorithm is a distributed algorithm and can be parallelized and implemented to learn large-scale problems. We refer to [26] for a comprehensive review of ADMM. Quantile regression typically adopts the simplex method and the interior point method, which work well for small- to moderate-size data. However, they are difficult to handle with the high-dimensional large-scale data because the penalization is normally necessary. Refs. [13,27] considered ADMM-based algorithms for penalized quantile regression with both convex and folded-concave penalties. Based on the penalized ADMMs [13,27], we propose the Q-ADMM-CSL algorithm to solve large-scale ${\ell }_1$-penalized quantile regression in the CSL distributed framework.

Recall that our optimization problem is to solve the following ${\ell }_1$-penalized quantile regression problem:

$$\widehat{\mathit{\beta }}={\mathrm{argmin}}_{\mathit{\beta }}{\mathcal{L}}_1\left(\mathit{\beta }\right)+\langle \nabla {\mathcal{L}}_N\left(\tilde{\mathit{\beta }}\right)-\nabla {\mathcal{L}}_1\left(\tilde{\mathit{\beta }}\right),\mathit{\beta }\rangle +\lambda {\parallel \mathit{\beta }\parallel }_1,$$

(14)

Let the $n\times p$ designed matrix ${\mathit{X}}_1={({\mathit{x}}_{11},\cdots ,{\mathit{x}}_{1n})}^T$, and the $n\times 1$ response vector ${\mathit{y}}_1={(y_{11},\cdots ,y_{1n})}^T$ on ${\mathcal{M}}_1$. Further, denote $Q_{\tau }\left(\mathit{r}\right)=\frac{1}{n}{\sum }_{i=1}^n{\rho }_{\tau }\left(r_i\right)$ with $\mathit{r}={(r_1,\cdots ,r_n)}^T={\mathit{y}}_1-{\mathit{X}}_1\mathit{\beta }$, and $\mathit{g}=\nabla {\mathcal{L}}_N\left(\tilde{\mathit{\beta }}\right)-\nabla {\mathcal{L}}_1\left(\tilde{\mathit{\beta }}\right)$. Then, the problem (14) can be recast into an equivalent problem

$$\underset{\mathit{\beta }\in {\mathbb{R}}^p,\mathit{r}\in {\mathbb{R}}^n}{min}{Q}_{\tau }\left(\mathit{r}\right)+{\mathit{g}}^T\mathit{\beta }+\lambda {\parallel \beta \parallel }_1,\mathrm{subject}\mathrm{to}{\mathit{X}}_1\mathit{\beta }+\mathit{r}={\mathit{y}}_1.$$

(15)

Following standard convex optimization, problem (15) has the following Lagrangian:

$${\mathcal{L}}_{\sigma }(\mathit{\beta },\mathit{r},\mathit{u})=Q_{\tau }\left(\mathit{r}\right)+{\mathit{g}}^T\mathit{\beta }+\lambda {\parallel \mathit{\beta }\parallel }_1-{\mathit{u}}^T(X_1\mathit{\beta }+\mathit{r}-{\mathit{y}}_1)+{\displaystyle \frac{\sigma }{2}}{∥X_1\mathit{\beta }+\mathit{r}-{\mathit{y}}_1∥}_2^2,$$

(16)

where $\sigma >0$ is a tunable augmentation parameter. That is, it solves the following updates at $m+1$,

$$\begin{array}{c}{\mathit{\beta }}^{m+1}={\mathrm{argmin}}_{\mathit{\beta }\in {\mathbb{R}}^p}{\mathit{g}}^T\mathit{\beta }+\lambda {\parallel \mathit{\beta }\parallel }_1-{\left({\mathit{u}}^m\right)}^T{\mathit{X}}_1\mathit{\beta }+\frac{\sigma }{2}{∥{\mathit{X}}_1\mathit{\beta }+{\mathit{r}}^m-{\mathit{y}}_1∥}_2^2,\hfill \\ {\mathit{r}}^{m+1}={\mathrm{argmin}}_{\mathit{r}\in {\mathbb{R}}^n}{Q}_{\tau }\left(\mathit{r}\right)-{\left({\mathit{u}}^m\right)}^T\mathit{r}+\frac{\sigma }{2}{∥{\mathit{X}}_1{\mathit{\beta }}^{m+1}+\mathit{r}-{\mathit{y}}_1∥}_2^2,\hfill \\ {\mathit{u}}^{m+1}={\mathit{u}}^m-\sigma \left({\mathit{X}}_1{\mathit{\beta }}^{m+1}+{\mathit{r}}^{m+1}-{\mathit{y}}_1\right).\hfill \end{array}$$

(17)

First, we introduce a proximal operator [27] as

$$\begin{array}{cc}\hfill {\mathrm{Prox}}_{{\rho }_{\tau }}(\xi ,\alpha )& ={\mathrm{argmin}}_{r\in \mathbb{R}}[{\rho }_{\tau }\left(r\right)+\frac{\alpha }{2}{(r-\xi )}^2]\hfill \\ \hfill & =max(\xi -{\alpha }^{-1}\tau ,0)-max(-\xi -{\alpha }^{-1}(1-\tau ),0)\hfill \\ \hfill & =\xi -max({\alpha }^{-1}(\tau -1),min(\xi ,{\alpha }^{-1}\tau )).\hfill \end{array}$$

(18)

For r-update in (17), we have

$$\begin{array}{ccc}\hfill {\mathit{r}}^{m+1}& =& {\mathrm{argmin}}_{\mathit{r}\in {\mathbb{R}}^n}{Q}_{\tau }\left(\mathit{r}\right)+\frac{\sigma }{2}{∥\mathit{r}-\left({\mathit{y}}_1-{\mathit{X}}_1{\mathit{\beta }}^{m+1}+{\sigma }^{-1}{\mathit{u}}^m\right)∥}_2^2\hfill \\ & =& {\mathrm{argmin}}_{\mathit{r}\in {\mathbb{R}}^n}{\rho }_{\tau }\left(\mathit{r}\right)+\frac{n\sigma }{2}{∥\mathit{r}-\left({\mathit{y}}_1-{\mathit{X}}_1{\mathit{\beta }}^{m+1}+{\sigma }^{-1}{\mathit{u}}^m\right)∥}_2^2,\hfill \end{array}$$

which has a closed form solutions

$$\begin{array}{ccc}\hfill {\mathit{r}}^{m+1}& =& {\mathrm{Prox}}_{{\rho }_{\tau }}\left({\mathit{y}}_1-{\mathit{X}}_1{\mathit{\beta }}^{m+1}+{\sigma }^{-1}{\mathit{u}}^m,n\sigma \right)\hfill \\ & =& {\left\{{\mathit{y}}_1-{\mathit{X}}_1{\mathit{\beta }}^{m+1}+{\sigma }^{-1}{\mathit{u}}^m-\tau {\left(n\sigma \right)}^{-1}{\mathbf{1}}_{\mathbf{n}}\right\}}_{+}\hfill \\ & & -{\left\{-{\mathit{y}}_1+{\mathit{X}}_1{\mathit{\beta }}^{m+1}-{\sigma }^{-1}{\mathit{u}}^m+(\tau -1){\left(n\sigma \right)}^{-1}{\mathbf{1}}_{\mathbf{n}}\right\}}_{+}.\hfill \end{array}$$

(19)

For $\mathit{\beta }$-update, it does not have a closed-form solution with the $\mathit{\beta }$-step in (17) in the standard ADMM. To this end, we add a proximal term to the objective function with respect to $\mathit{\beta }$ and then construct an augmented $\mathit{\beta }$-update as follows:

$${\mathit{\beta }}^{m+1}={\mathrm{argmin}}_{\mathit{\beta }\in {\mathbb{R}}^p}{\mathit{g}}^T\mathit{\beta }+\lambda {\parallel \mathit{\beta }\parallel }_1-{\left({\mathit{u}}^m\right)}^T{\mathit{X}}_1\mathit{\beta }+\frac{\sigma }{2}{∥{\mathit{X}}_1\mathit{\beta }+{\mathit{r}}^m-{\mathit{y}}_1∥}_2^2+\frac{1}{2}{∥\mathit{\beta }-{\mathit{\beta }}^m∥}_{\mathit{S}}^2,$$

where $\mathit{S}=\sigma (\eta {\mathit{I}}_p-{\mathit{X}}_1^T{\mathit{X}}_1)$ with $\eta \ge {\mathrm{\Lambda }}_{max}\left({\mathit{X}}_1^T{\mathit{X}}_1\right)$. Thus, the augmented $\mathit{\beta }$-update becomes a Lasso penalized least square problem

$$\begin{array}{ccc}\hfill {\mathit{\beta }}^{m+1}& =& {\mathrm{argmin}}_{\mathit{\beta }\in {\mathbb{R}}^p}\lambda {\parallel \mathit{\beta }\parallel }_1+{\displaystyle \frac{\sigma \eta }{2}}{∥\mathit{\beta }-{\displaystyle \frac{\sigma \eta {\mathit{\beta }}^m-\mathit{g}+{\mathit{X}}_1^T\left[{\mathit{u}}^m-\sigma \left({\mathit{X}}_1{\mathit{\beta }}^m+{\mathit{r}}^m-{\mathit{y}}_1\right)\right]}{\sigma \eta }}∥}_2^2\hfill \\ & =& \mathrm{Shrink}\left({\mathit{\beta }}^m+{\displaystyle \frac{{\mathit{X}}_1^T\left[{\mathit{u}}^m-\sigma \left({\mathit{X}}_1{\mathit{\beta }}^m+{\mathit{r}}^m-{\mathit{y}}_1\right)\right]-\mathit{g}}{\sigma \eta }},{\displaystyle \frac{\lambda }{\sigma \eta }}\right),\hfill \end{array}$$

(20)

where the soft shrinkage operator $\mathrm{Shrink}(\mathit{b},a)={\left(\mathrm{sgn}\left(b_j\right)max\left(\right|b_j|-a,0)\right)}_{1\le j\le p}$ for $\mathit{b}\in {\mathbb{R}}^p$ and $a\in \mathbb{R}$, and $\mathrm{sgn}(·)$ is the sign function.

Last, the r-update is

$${\mathit{u}}^{m+1}={\mathit{u}}^m-\sigma \left({\mathit{X}}_1{\mathit{\beta }}^{m+1}+{\mathit{r}}^{m+1}-{\mathit{y}}_1\right).$$

(21)

Thus, (19)–(21) constitute our Q-ADMM-CSL algorithm, which is presented in Algorithm 3.

2.3.2. NodeLasso Algorithm to Approximate Inverse Hessian Matrix

In the Q-DistBoots-SI algorithm, we apply a nodewise Lasso procedure [2,28] to approximate the inverse Hessian matrix ${\tilde{\mathbf{\Sigma }}}_1$, which is introduced in Algorithm 4. Let ${\mathbf{\xi }}_l=\left\{{\xi }_{l,l^{\prime }}:l^{\prime }=1,\cdots ,p,l^{\prime }\ne l\right\}$, and denote ${\mathit{M}}_{l,-l}$ to be the lth row of M without the diagonal element $(l,l)$ and ${\mathit{M}}_{-l,-l}$ to be the submatrix without the lth row and lth column.

Algorithm 3: Q-ADMM-CSL for the $(t+1)$th optimization of Q-DistBoots-SI algorithm on the 1st machine ${\mathcal{M}}_1$

Algorithm 4: NodeLasso procedure in Q-DistBoots-SI algorithm on the 1st machine ${\mathcal{M}}_1$

In the NodeLasso algorithm, we need to choose hyperparameters ${\left\{{\lambda }_l\right\}}_{l=1}^p$ and bandwidth h. As to ${\left\{{\lambda }_l\right\}}_{l=1}^p$, Ref. [2] suggested taking the same value for all ${\lambda }_l$ by Cross-Validation. Of course, the potentially good mode is to allow the different ${\lambda }_l$ across l. The bandwidth also can be chosen via Cross-Validation.

Here, we discuss the resources required for our algorithm to solve the distributed sparse quantile regression problems. The NodeLasso algorithm is a debiasing step, which requires solving $O\left(p\right)$ generalized lasso problems. In addition, our procedure requires solving one ${\ell }_1$ penalized objective (5) in each iteration. When $s^{2}logp\lesssim n\lesssim K{s}^{2}logp$, the computational complexity of Centralize learning is $O(K·{\mathrm{T}}_{\mathrm{lasso}})$, while ours is only $O(logK·{\mathrm{T}}_{\mathrm{lasso}})$, where ${\mathrm{T}}_{\mathrm{lasso}}$ is the runtime for solving a generalized lasso problem of size $n\times p$. For communication costs, Centralize learning requires $O(n·p)$ bits, while ours is only $O(K·p)$ bits. Usually, $n\gg K$. Therefore, our algorithm is effective in communication and computation. Regarding the discussion of computation and communication costs on CSL distributed learning framework, also see [3,4].

3. Theoretical Analysis

Recall that the quantile regression model has the conditional quantile $Q_{\tau }\left(y\right|\mathit{x})={\mathit{x}}^T{\mathit{\beta }}^{*}$ of Y given the feature x at quantile level $\tau$, that is,

$$y=Q_{\tau }\left(y\right|\mathit{x})+\epsilon$$

with $P(\epsilon \le 0|\mathit{x})=\tau$. In this section, we establish theoretical results for distributed bootstrap simultaneous inference on high-dimensional quantile regression. We use the following assumptions.

Assumption 1. 

x is sub-Gaussian, that is,

$$\underset{{\parallel \mathit{w}\parallel }_2\le 1}{sup}E[exp({\left({\mathit{w}}^T\mathit{x}\right)}^2/L^2)]=O\left(1\right),$$

for some absolute constant $L>0$.

Assumption 2. 

${\mathit{\beta }}^{*}$ is the unique minimizer of the objective function $E\left\{{\rho }_{\tau }(Y-{\mathit{x}}^T\mathit{\beta })\right\}$, and ${\mathit{\beta }}^{*}$ is an inner point in $\mathcal{B}$, where $\mathcal{B}\in {\mathbb{R}}^p$ is an compact subset.

Assumption 3. 

$F\left(y\right|\mathit{x})$ is absolutely continuous at y, its conditional density function $f\left(y\right|\mathit{x})$ is bounded and continuously differentiable at y for all x in the support of x, and $f^{\prime }\left(y\right|\mathit{x})$ is uniformly bounded by a constant. In addition, $f\left({\mathit{x}}^T{\mathit{\beta }}^{*}\right|\mathit{x}\left)\right)$ is uniformly bounded away from zero.

Assumption 4. 

${\mathit{\beta }}^{*}$ and ${\mathbf{\Theta }}_l$ are sparse for $l=1,\cdots ,p$, where $\mathbf{\Theta }={\left({\mathbf{\Sigma }}^{*}\right)}^{-1}$ with ${\mathbf{\Sigma }}^{*}=E\left(\mathit{x}{\mathit{x}}^{T}f\left({\mathit{x}}^T{\mathit{\beta }}^{*}\right|\mathit{x})\right)$. Especially, $S=\left\{l:{\beta }_l^{*}\ne 0\right\}$, $S_l=\left\{l^{\prime }\ne l:\mathrm{\Theta }\ne 0\right\}$, $s=\left|S\right|$, $s^{*}={max}_l\left|S_l\right|$, and $\overline{s}=s\vee s^{*}\ll p$.

Remark 1. 

Assumption 1 holds if the covariates are Gaussian. Under Assumption 1, $c_n:={max}_i{∥{\mathit{x}}_i∥}_{\infty }=O_p\left(\sqrt{lognp}\right)=O_p\left(\sqrt{logp}\right)$ when $n<p$ by Lemma 2.2.2 in [29]. Assumptions 2 and 3 are common in standard quantile regression [9]. Assumption 4 is a sparsity assumption typically adopted in penalized variable selection.

In order to state next assumptions, define a restricted set $\Delta :=\Delta (S,3)=\{\delta \in {\mathbb{R}}^p:\parallel {\delta }_{S^c}{\parallel }_1\le 3\parallel {\Delta }_S{\parallel }_1\}$, and $\overline{S}(\delta ,J)\subset \{1,\cdots ,p\}\setminus S$ is a support of J largest in absolute value components of $\delta$ outside S.

Assumption 5. 

Assume that

$${\kappa }_J^2:=\underset{\mathit{\delta }\in \Delta ,\mathit{\delta }\ne 0}{inf}\frac{{\mathit{\delta }}^{T}E\left[\mathit{x}{\mathit{x}}^T\right]\mathit{\delta }}{\parallel {\mathit{\delta }}_{S\cup \overline{S}(\delta ,J)}{\parallel }_2^2}>0$$

and

$$q:=\underset{\mathit{\delta }\in \Delta ,\mathit{\delta }\ne 0}{inf}\frac{\left(E\right|{\mathit{x}}_i^T\mathit{\delta }{{|}^2)}^{3/2}}{E|{\mathit{x}}_i^T{\mathit{\delta }|}^3}>0.$$

Remark 2. 

The assumptions of ${\kappa }_J^2$ and q come from [12]; they are called restricted eigenvalue conditions and restricted nonlinear impact coefficients, respectively. ${\kappa }_J^2>0$ holds when x are mean zero with diagonal elements of $E\left(\mathit{x}{\mathit{x}}^T\right)$ being 1’s by Lemma 1 in [12]. The restricted eigenvalue condition is analogous to the condition in [30]. The q controls the quality of minoration of the quantile regression objective function by a quadratic function over the restricted set, which holds under Design 1 in [12].

First, we give the convergence rates of distributed learning for high-dimensional quantile regression models under the CSL framework.

Theorem 1. 

Assume that Assumptions 1–5 hold, and ${\lambda }^{t+1}\ge 2{∥\nabla {\tilde{\mathcal{L}}}_1({\mathit{\beta }}^{*},{\tilde{\mathit{\beta }}}^t)∥}_{\infty }$. Then, with probability at least $1-p^{-C}$, we have

$${∥{\tilde{\mathit{\beta }}}^{t+1}-{\mathit{\beta }}^{*}∥}_1\le C\left({\lambda }^{t+1}s+\frac{s^2{c}_n^{2}logn}{n}\right),$$

$${∥{\tilde{\mathit{\beta }}}^{t+1}-{\mathit{\beta }}^{*}∥}_2\le C\left({\lambda }^{t+1}\sqrt{s}+\frac{s^{3/2}{c}_n^{2}logn}{n}\right),$$

where $c_n=\sqrt{logp}$.

Remark 3. 

Recall that Lemma A1,

$${∥\nabla {\tilde{\mathcal{L}}}_1({\mathit{\beta }}^{*},{\tilde{\mathit{\beta }}}^t)∥}_{\infty }\le C\left(\sqrt{{\displaystyle \frac{logp}{N}}}+{\displaystyle \frac{s{log}^{3/2}p}{n}}+{\delta }_t\left(\sqrt{{\displaystyle \frac{s{log}^{2}p}{n}}}+\sqrt{{\displaystyle \frac{{log}^{3}p}{n}}}\right)+{\delta }_t^2\sqrt{{log}^{3}p}\right),$$

where ${\delta }_t={∥{\tilde{\mathit{\beta }}}^t-{\mathit{\beta }}^{*}∥}_1$. We can take

$${\lambda }^{t+1}=C\left(\sqrt{{\displaystyle \frac{logp}{N}}}+{\displaystyle \frac{s{log}^{3/2}p}{n}}+{\delta }_t\left(\sqrt{{\displaystyle \frac{s{log}^{2}p}{n}}}+\sqrt{{\displaystyle \frac{{log}^{3}p}{n}}}\right)+{\delta }_t^2\sqrt{{log}^{3}p}\right).$$

(22)

Thus, Theorem 1 upper bounds the learning error ${∥{\tilde{\mathit{\beta }}}^{t+1}-{\mathit{\beta }}^{*}∥}_1$ as a function of ${∥{\tilde{\mathit{\beta }}}^t-{\mathit{\beta }}^{*}∥}_1$. So, applying it to the iterative program, we obtain the following learning error bound, which depends on the local ${\ell }_1$-regularized estimation error ${∥{\tilde{\mathit{\beta }}}^0-{\mathit{\beta }}^{*}∥}_1$.

Corollary 1. 

Suppose the conditions of Theorem 1 are satisfied; ${\lambda }^{t+1}$ takes as (22); and for all t, ${∥{\tilde{\mathit{\beta }}}^0-{\mathit{\beta }}^{*}∥}_1\le Cs\sqrt{{\displaystyle \frac{logp}{n}}}$. Then, with probability at least $1-p^{-C}$, we have

$${∥{\tilde{\mathit{\beta }}}^{t+1}-{\mathit{\beta }}^{*}∥}_1\lesssim {(1-b_n)}^{-1}(1-b_n^{t+1})\left(s\sqrt{{\displaystyle \frac{logp}{N}}}+{\displaystyle \frac{s^2{log}^{2}p}{n}}\right)+b_n^{t+1}{∥{\tilde{\mathit{\beta }}}^0-{\mathit{\beta }}^{*}∥}_1,$$

$${∥{\tilde{\mathit{\beta }}}^{t+1}-{\mathit{\beta }}^{*}∥}_2\lesssim {(1-b_n)}^{-1}(1-b_n^{t+1})\left(\sqrt{{\displaystyle \frac{slogp}{N}}}+{\displaystyle \frac{s^{3/2}{log}^{2}p}{n}}\right)+b_n^t{a}_n{∥{\tilde{\mathit{\beta }}}^0-{\mathit{\beta }}^{*}∥}_1,$$

where $b_n=s^2\sqrt{{\displaystyle \frac{{log}^{4}p}{n}}}$, and $a_n=s^{\frac{3}{2}}\sqrt{{\displaystyle \frac{{log}^{4}p}{n}}}$.

Remark 4. 

For initialization estimation, we refer to Theorem 2 in [12],

$$\parallel {\tilde{\beta }}^{\left(0\right)}-{\beta }^{*}{\parallel }_1=O_p\left\{s\sqrt{\frac{log(p\vee n)}{n}}\right\}.$$

We further explain the bound and see the scaling with respect to n, K, s, and p. When $n\gg s^4{log}^{4}p$, it is easy to see by taking

$${\lambda }^{t+1}=C\left\{\sqrt{{\displaystyle \frac{logp}{N}}}+{\displaystyle \frac{s^2{log}^{2.5}p}{n}}+\left(\sqrt{{\displaystyle \frac{logp}{n}}}\right){\left(s^2\sqrt{{\displaystyle \frac{{log}^{4}p}{n}}}\right)}^{t+1}\right\},$$

we have the following error bounds:

$${∥{\tilde{\mathit{\beta }}}^{t+1}-{\mathit{\beta }}^{*}∥}_1=O_p\left\{s\sqrt{{\displaystyle \frac{logp}{N}}}+\left(s\sqrt{\frac{logp}{n}}\right){\left(s^2\sqrt{{\displaystyle \frac{{log}^{4}p}{n}}}\right)}^{t+1}\right\},$$

$${∥{\tilde{\mathit{\beta }}}^{t+1}-{\mathit{\beta }}^{*}∥}_2=O_p\left\{\sqrt{{\displaystyle \frac{slogp}{N}}}+\left(\sqrt{\frac{slogp}{n}}\right){\left(s^2\sqrt{{\displaystyle \frac{{log}^{4}p}{n}}}\right)}^{t+1}\right\}.$$

Moreover, as long as t is large enough so that ${\left(s^2\sqrt{{\displaystyle \frac{{log}^{4}p}{n}}}\right)}^{t+1}\lesssim s\sqrt{{\displaystyle \frac{logp}{N}}}$, and $n\gg s^4{log}^{4}p$, then

$${∥{\tilde{\mathit{\beta }}}^{t+1}-{\mathit{\beta }}^{*}∥}_1=O_p\left(s\sqrt{{\displaystyle \frac{logp}{N}}}\right),$$

$${∥{\tilde{\mathit{\beta }}}^{t+1}-{\mathit{\beta }}^{*}∥}_2=O_p\left(\sqrt{{\displaystyle \frac{slogp}{N}}}\right),$$

which match the centralized lasso without any additional error term [30] as [3] has done in sparse linear regression distributed learning.

Based on the proposed Q-DistBoots-SI algorithm, we define

$$T={∥\sqrt{N}({\tilde{\mathit{\beta }}}^{\iota }-{\mathit{\beta }}^{*})∥}_{\infty }.$$

(23)

Theorem 2. 

(K-gard-Q) Assume that Assumptions 1–5 hold, let

$${\lambda }^t\asymp C\left\{\sqrt{{\displaystyle \frac{logp}{N}}}+{\displaystyle \frac{s^2{log}^{2.5}p}{n}}+\left(\sqrt{{\displaystyle \frac{logp}{n}}}\right){\left(s^2\sqrt{{\displaystyle \frac{{log}^{4}p}{n}}}\right)}^t\right\}$$

(24)

for $t\ge 0$, and ${\lambda }_l\asymp \sqrt{\frac{logp}{n}}$ for $l=1,\cdots ,p$. Then, if $n\gg \left(s^4{s}^{*}+{\left(s^{*}\right)}^3\right){log}^{6+2\kappa }p+s^4{log}^{4}p+s^6{\left(s^{*}\right)}^2{log}^{8+4\kappa }p$, $K\gg ({\left(s^{*}\right)}^2{s}^2+{\left(s^{*}\right)}^2){log}^{5+2\kappa }p$, and for $\iota \ge {\iota }_{min}$, where

$$\begin{array}{cc}\hfill {\iota }_{min}=1+O& ⌊max\left\{\frac{log\left(s^2\right)+log\left({\left(s^{*}\right)}^2\right)+log\left({log}^{5+2\kappa }p\right)}{logn-log\left(s^4\right)-log{log}^{4}p},\right.\hfill \\ & \left.\frac{log\left(s^3\right)+log\left(s^{*}\right)+logK+log\left({log}^{4+2\kappa }p\right)-log\left(n^{\frac{1}{2}}\right)}{logn-log\left(s^4\right)-log\left({log}^{4}p\right)}\right\}⌋,\hfill \end{array}$$

we have

$$\underset{\alpha \in (0,1)}{sup}|P\left(T\le c_{\overline{W}}\left(\alpha \right)\right)-\alpha |=o\left(1\right),$$

(25)

where $c_{\overline{W}}\left(\alpha \right):=inf\{w\in \mathbb{R}:P_{ϵ}(\overline{W}\le w)\ge \alpha \}$, in which ${\overline{W}}^{\left(b\right)}$ is the K-grad-Q bootstrap statistics with the same distribution as $\overline{W}$ in (12) and $P_{ϵ}$ denotes the probability with respect to the randomness from the multipliers. In addition,

$$\underset{\alpha \in (0,1)}{sup}\left|P\left(\widehat{T}\le c_{\overline{W}}\left(\alpha \right)\right)-\alpha \right|=o\left(1\right),$$

(26)

where $\widehat{T}$ is defined in (7).

Theorem 2 ensures the effectiveness of constructing simultaneous confidence intervals for quantile regression model parameters using the “K-grad-Q” bootstrap method in Algorithm 1. Moreover, it indicates that bootstrap quantiles can approximate the prior statistics, implying that our proposed bootstrap procedure possesses statistical validity similar to the prior estimation method.

Remark 5. 

If $n=p^{{\mathrm{{\rm Y}}}_n}$, $\overline{s}=s\vee s^{*}=p^{{\mathrm{{\rm Y}}}_{\overline{s}}}$, $K=p^{{\mathrm{{\rm Y}}}_K}$ for some constants ${\mathrm{{\rm Y}}}_n$, ${\mathrm{{\rm Y}}}_{\overline{s}}$, and ${\mathrm{{\rm Y}}}_K$, then a sufficient condition is ${\mathrm{{\rm Y}}}_n\gg 8{\mathrm{{\rm Y}}}_{\overline{s}}$, ${\mathrm{{\rm Y}}}_K\gg 4{\mathrm{{\rm Y}}}_{\overline{s}}$, and

$${\iota }_{min}=1+⌊max\left\{\frac{4{\mathrm{{\rm Y}}}_{\overline{s}}}{{\mathrm{{\rm Y}}}_n-4{\mathrm{{\rm Y}}}_{\overline{s}}},\frac{4{\mathrm{{\rm Y}}}_{\overline{s}}+{\mathrm{{\rm Y}}}_K-\frac{1}{2}{\mathrm{{\rm Y}}}_n}{{\mathrm{{\rm Y}}}_n-4{\mathrm{{\rm Y}}}_{\overline{s}}}\right\}⌋.$$

Notice that the representation of ${\iota }_{min}$ mentioned above is independent of the dimension p; the direct effect of p only enters through an iterative logarithmic term $log(logp)$, which is dominated by $log\overline{s}\asymp logp$.

Theorem 3. 

(n+K-1-grad-Q) Assume that Assumptions 1–5 hold; take ${\lambda }^t$ as (24) for $t\ge 0$ and ${\lambda }_l\asymp \sqrt{\frac{logp}{n}}$ for $l=1,\cdots ,p$. Then, if $n\gg \left(s^4{s}^{*}+{\left(s^{*}\right)}^3\right){log}^{6+2\kappa }p+s^4{log}^{4}p+s^6{\left(s^{*}\right)}^2{log}^{8+4\kappa }p$, $K\gg ({\left(s^{*}\right)}^2{s}^2+{\left(s^{*}\right)}^2){log}^{5+2\kappa }p$, and when $\iota \ge {\iota }_{min}$, where

$$\begin{array}{cc}\hfill {\iota }_{min}=1+O& ⌊max\left\{\frac{log\left(s^2\right)+log\left({\left(s^{*}\right)}^2\right)+log(n+{log}^{2}p)+log\left({log}^{5+2\kappa }p\right)-logn}{logn-log\left(s^4\right)-log\left({log}^{4}p\right)},\right.\hfill \\ & \left.\frac{log\left(s^3\right)+log\left(s^{*}\right)+logK+log\left({log}^{4+2\kappa }p\right)-log\left(n^{\frac{1}{2}}\right)}{logn-log\left(s^4\right)-log{log}^{4}p}\right\}⌋,\hfill \end{array}$$

we have

$$\underset{\alpha \in (0,1)}{sup}|P\left(T\le c_{\tilde{W}}\left(\alpha \right)\right)-\alpha |=o\left(1\right),$$

(27)

where $c_{\tilde{W}}\left(\alpha \right):=inf\{w\in \mathbb{R}:P_{ϵ}\left(\tilde{W}\le w\right)\ge \alpha \}$, in which $\tilde{W}$ is the n+K-1-grad-Q bootstrap statistics with the same distribution as ${\tilde{W}}^{\left(b\right)}$ in (13), and $P_{ϵ}$ denotes the probability with respect to the randomness from the multipliers. In addition, (27) also holds.

Theorem 3 establishes the statistical validity of the distributed bootstrap method when using “n+K-1-grad-Q”. To gain insight into the difference between “K-grad-Q” and “n+K-1-grad-Q”, we compare the difference between the covariance of the oracle score A and the conditional covariance of $\overline{A}$ and $\tilde{A}$ conditioning on the data, and we obtain

$${∥co{v}_{ϵ}\left(\overline{A}\right)-cov\left(A\right)∥}_{max}=O_p\left(s^{*}\sqrt{n}{r}_{\overline{\beta }}+s^{*}\sqrt{\frac{logp}{K}}+{\left(s^{*}\right)}^{\frac{3}{2}}\sqrt{\frac{logp}{n}}+s^{*}n{r}_{\overline{\beta }}^2\right),$$

and

$${∥co{v}_{ϵ}\left(\tilde{A}\right)-cov\left(A\right)∥}_{max}=O_p\left(s^{*}\sqrt{n}{r}_{\overline{\beta }}+s^{*}\sqrt{\frac{logp}{n+K}}+{\left(s^{*}\right)}^{\frac{3}{2}}\sqrt{\frac{logp}{n}}+s^{*}(n\wedge K){ }_{\overline{\beta }}^2\right).$$

Remark 6. 

If $n=p^{{\mathrm{{\rm Y}}}_n}$, $\overline{s}=s\vee s^{*}=p^{{\mathrm{{\rm Y}}}_{\overline{s}}}$, and $K=p^{{\mathrm{{\rm Y}}}_K}$ for some constants ${\mathrm{{\rm Y}}}_n$, ${\mathrm{{\rm Y}}}_{\overline{s}}$, and ${\mathrm{{\rm Y}}}_K$, then a sufficient condition is ${\mathrm{{\rm Y}}}_n\gg 8{\mathrm{{\rm Y}}}_{\overline{s}}$, ${\mathrm{{\rm Y}}}_n+{\mathrm{{\rm Y}}}_K\gg 4{\mathrm{{\rm Y}}}_{\overline{s}}$, and

$${\iota }_{min}=1+⌊max\left\{\frac{4{\mathrm{{\rm Y}}}_{\overline{s}}}{{\mathrm{{\rm Y}}}_n-4{\mathrm{{\rm Y}}}_{\overline{s}}},\frac{4{\mathrm{{\rm Y}}}_{\overline{s}}+{\mathrm{{\rm Y}}}_K-\frac{1}{2}{\mathrm{{\rm Y}}}_n}{{\mathrm{{\rm Y}}}_n-4{\mathrm{{\rm Y}}}_{\overline{s}}}\right\}⌋.$$

Notice that the representation of ${\iota }_{min}$ mentioned above is independent of the dimension p; the direct effect of p only enters through an iterative logarithmic term $log(logp)$, which is dominated by $log\overline{s}\asymp logp$.

Remark 7. 

The rates of ${\left\{{\lambda }^{\left(t\right)}\right\}}_{t=0}^{\iota }$ and ${\left\{{\lambda }_l\right\}}_{l=1}^p$ in Theorems 3.2 and 3.3 are motivated by Theorem 1 and [2]. Therefore, we fix ${\left\{{\lambda }^{\left(t\right)}\right\}}_{t=0}^{\iota }$ (e.g., 0.01 in the simulation study) and use the cross-validation method to choose ${\left\{{\lambda }_l\right\}}_{l=1}^p$.

Remark 8. 

The total communication cost in our algorithm is of the order ${\iota }_{min}Kp$ because in each iteration we communicate p-dimensional vectors between the master node and K-1 worker nodes, and ${\iota }_{min}$ only grows logarithmically with K when n and p are fixed. Our order matches those in the existing communication-efficient statistical inference literature, e.g., [3,4,25].

4. Simulation Experiments

In this section, we demonstrate the advantages of our proposed approach through numerical simulation. We consider the problem of parameter estimation for high-dimensional quantile regression models in a distributed environment. In Section 4.1, we compare our algorithm Q-ADMM-CSL with the oracle estimation (Q-Oracle) and simple divide and conquer (Q-Avg) for high-dimensional quantile regression, evaluating the computational effectiveness of our proposed algorithm. In Section 4.2, we construct confidence intervals and assess their validity. The data are generated from the following model:

$$y_{ki}={\mathit{x}}_{ki}^T{\mathit{\beta }}^{*}+{\epsilon }_{ki},k=1,\cdots ,K,i=1,\cdots ,n,$$

where ${\epsilon }_{ki}={\tilde{\epsilon }}_{ki}-F_{{\tilde{\epsilon }}_{ki}}^{-1}\left(\tau \right)$ by, respectively, taking ${\tilde{\epsilon }}_{ki}\sim N(0,0.25)$ and $t\left(2\right)$ to demonstrate the benefits of our method for large-scale high-dimensional data with heavy-tailed distribution.

In this section, we consider a high-dimensional quantile regression model with dimension of feature $p=1000$; fix the total sample size $N=3000$; and select the numbers of machines $K=5,10$, and 20, respectively. Therefore, the sample size on each machine is $n=N/K$, that is, $n=$ 600 for $K=5$, 300 for $K=10$ and 150 for $K=20$. Considering the scenario of parameter sparsity, we choose the real coefficient $\mathit{\beta }$ to be p-dimensional, in which s coefficients are non-zero, and the remaining $p-s$ parameters are 0. We consider the two cases: (1) sparsity with $s=4$, ${\beta }_5^{*}=1,{\beta }_8^{*}=1,{\beta }_{11}^{*}=1,{\beta }_{14}^{*}=1$, and the rest of the components are 0; (2) sparsity with $s=8$, ${\beta }_5^{*}=1,{\beta }_8^{*}=1,{\beta }_{11}^{*}=1,{\beta }_{14}^{*}=1,{\beta }_{16}^{*}=1,$${\beta }_{19}^{*}=1,$${\beta }_{21}^{*}=1,{\beta }_{25}^{*}=1$, and the rest are 0. We generate independent and identically distributed covariates ${\mathit{x}}_i$ from a multivariate normal distribution $\mathcal{N}(0,\mathrm{\Sigma })$, where the covariance matrix ${\mathrm{\Sigma }}_{l,l^{{ }^{\prime }}}=0.5^{|l-l^{{ }^{\prime }}|}$. Given a quantile level $\tau \in (0,1)$, we consider three levels: 0.25, 0.5, and 0.75.

4.1. Parameter Estimation

In this section, we study the effect of our proposed algorithm. We repeatedly generate 100 datasets of independent data, and we use the $l_2$- norm to evaluate the quality of parameter estimate. That is, $\parallel \tilde{\mathit{\beta }}-{\mathit{\beta }}^{*}{\parallel }_2$. Meanwhile, we compare the effect of $\tilde{\mathit{\beta }}$ obtained by our proposed algorithm, ${\mathit{\beta }}_{orcal\mathit{e}}$, obtained by all data estimation and ${\mathit{\beta }}_{av\mathit{g}}$, obtained by naively average data estimation.

For the choice of penalty parameter $\lambda$, in the oracle estimation, we refer to the method of selecting penalty parameter in [12]; in the construction of the average estimation, we choose $\lambda =0.1$; in our proposed distributed multi-round communication process, ${\lambda }^{\left(0\right)}=0.1$; and when $t>0$ we set ${\lambda }^{\left(t\right)}=0.01$. For the parameters $\sigma$ and $\eta$ in ADMM, we refer to the selection in [27] to choose $\sigma =0.01$ and $\eta =\mathrm{\Lambda }\left(\mathit{x}{\mathit{x}}^T\right)$.

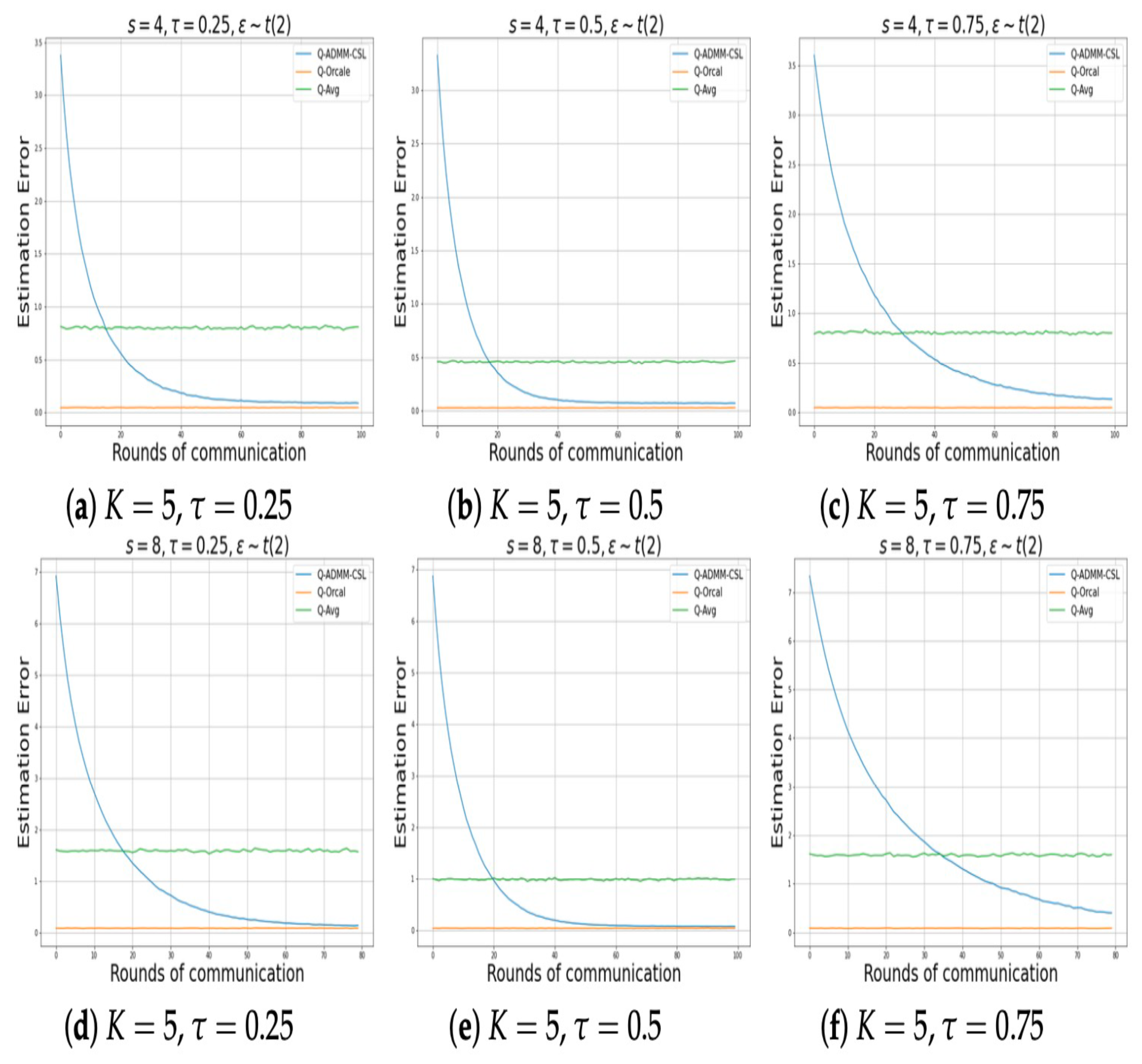
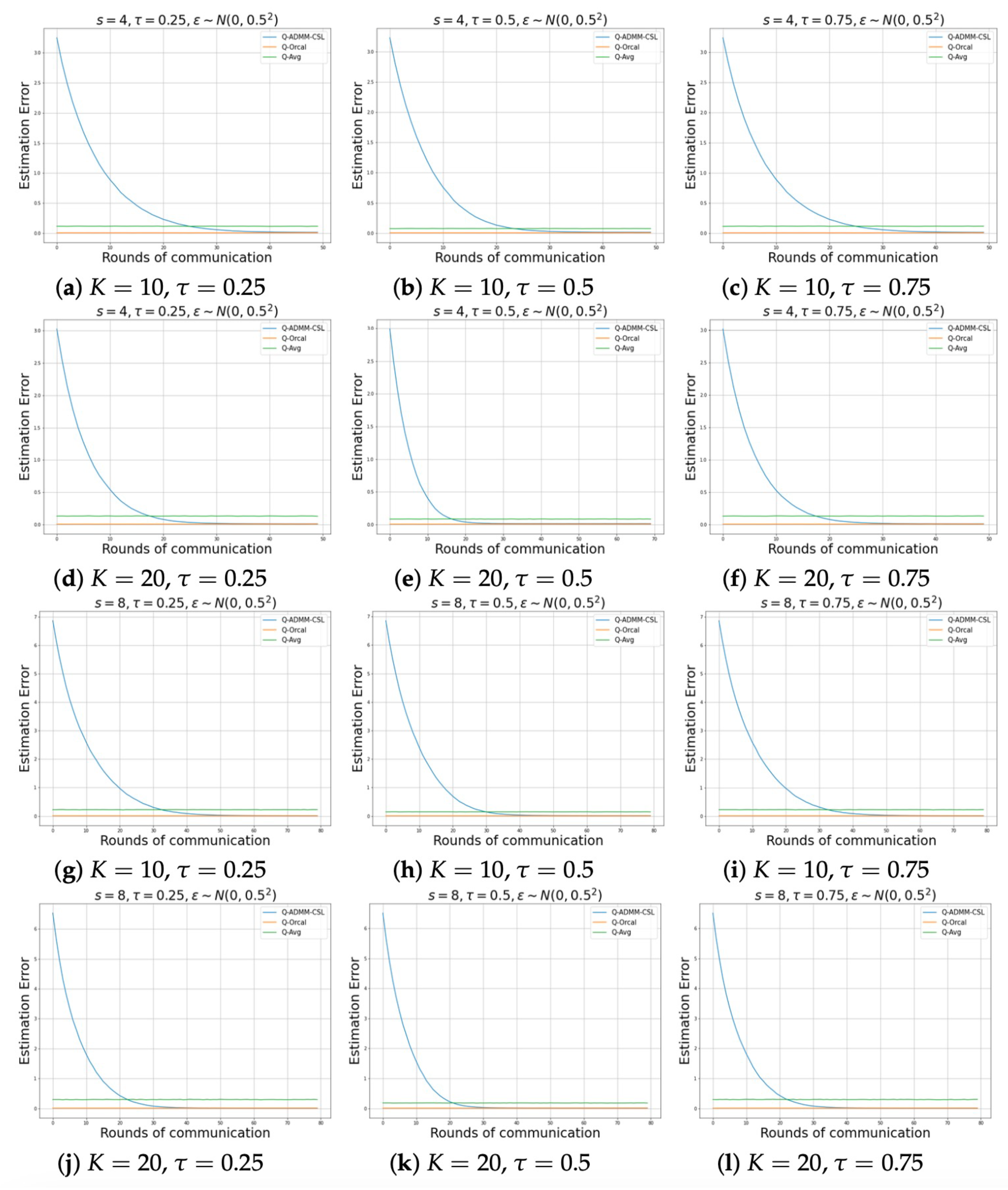
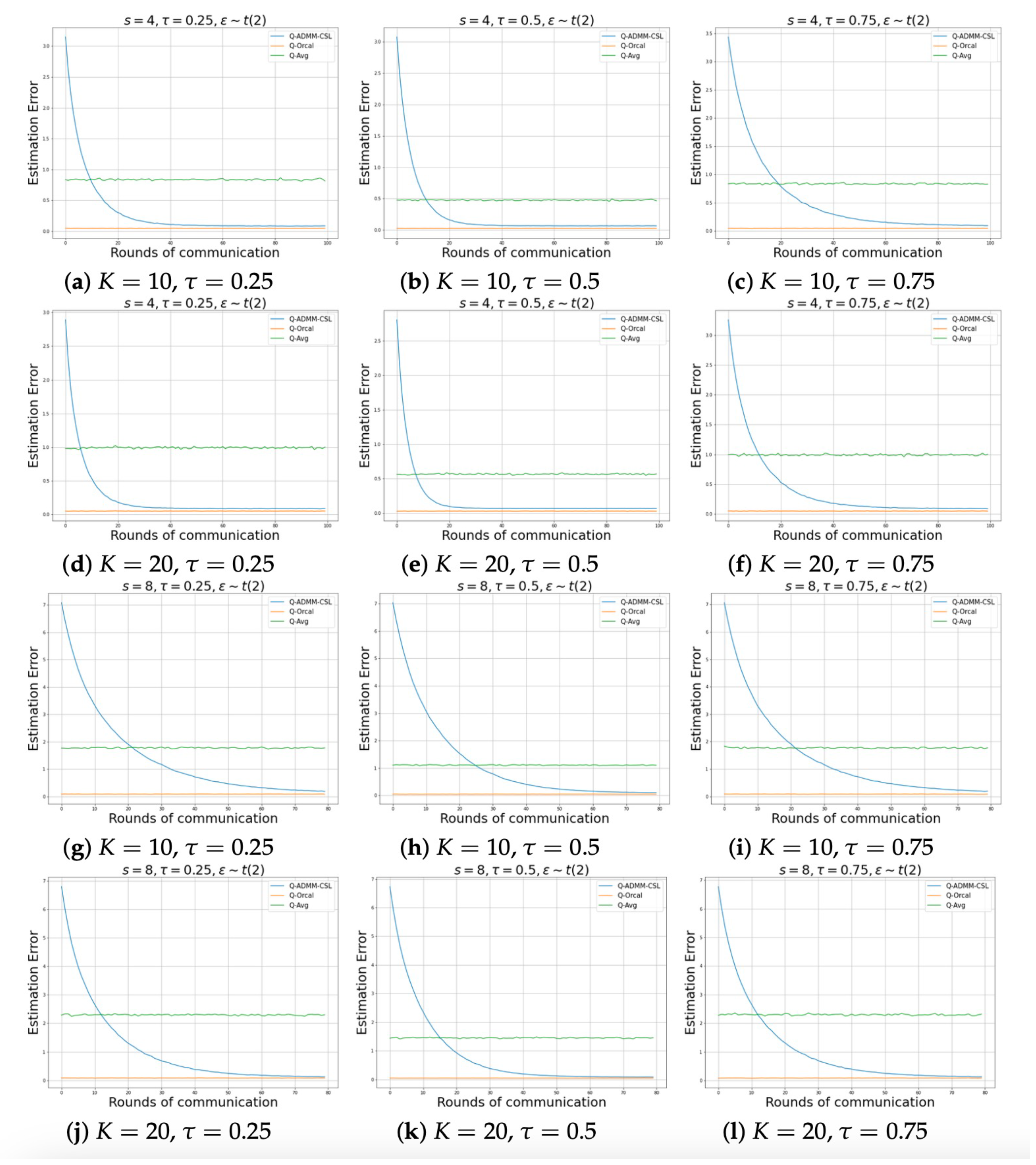
Figure 1 and Figure 2 show the relationship between the number of communication rounds and the estimation error of parameters, when the noise distributions are normal and $t\left(2\right)$, for the sparsity levels $s=4$ and $s=8$, respectively. We consider various scenarios involving different quantile levels and number of machines. It can be observed that after sufficient communication rounds, our parameter estimation method (Q-ADMM-CSL) can approximate the performance of the Oracle estimation (Q-Oracle), and the performance is significantly better than Q-Avg after a round of communication. In addition, our proposed method converges quickly, and matches the Oracle method after only about 30 rounds of communication.

4.2. Simultaneous Confidence Intervals

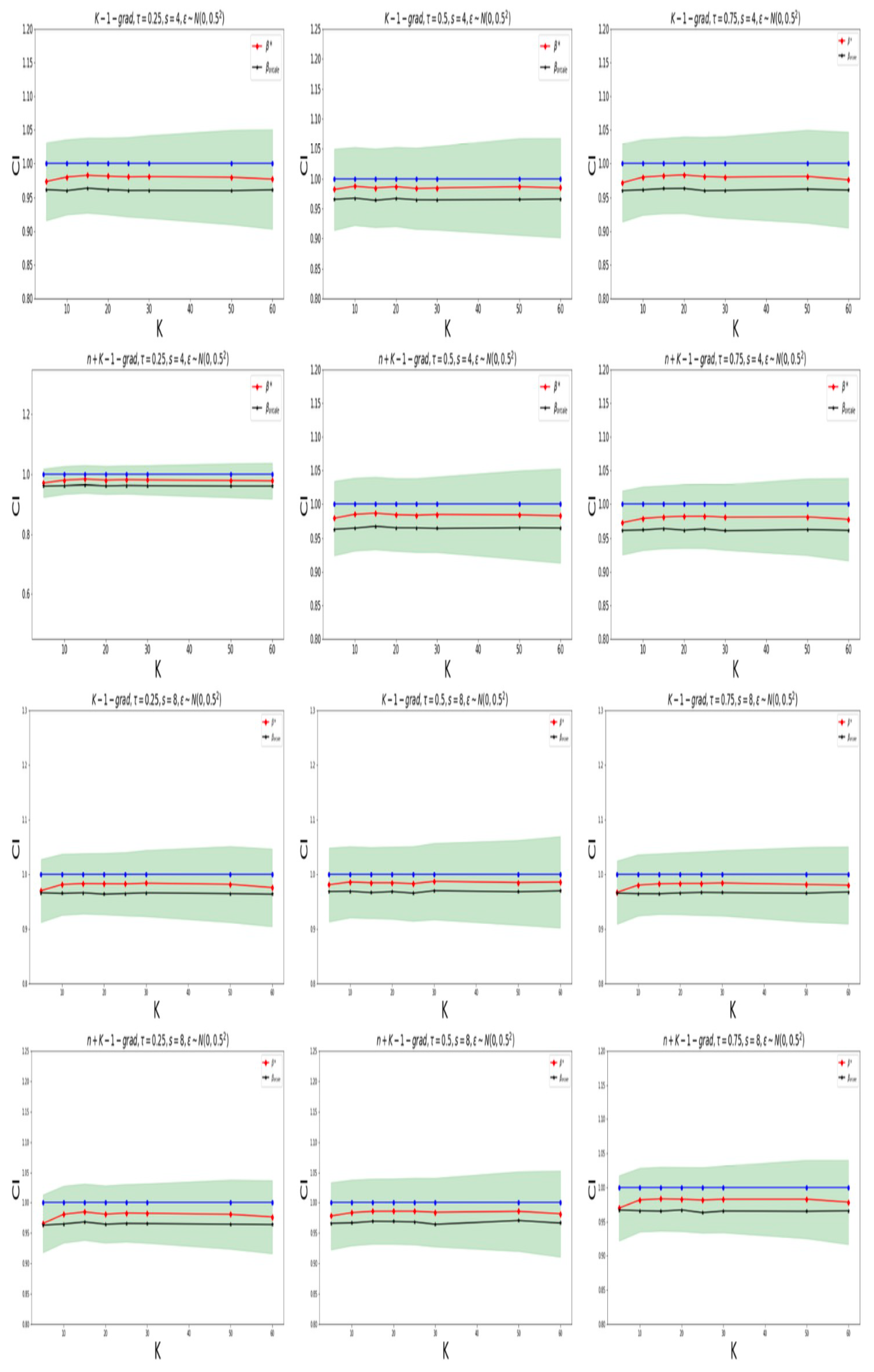
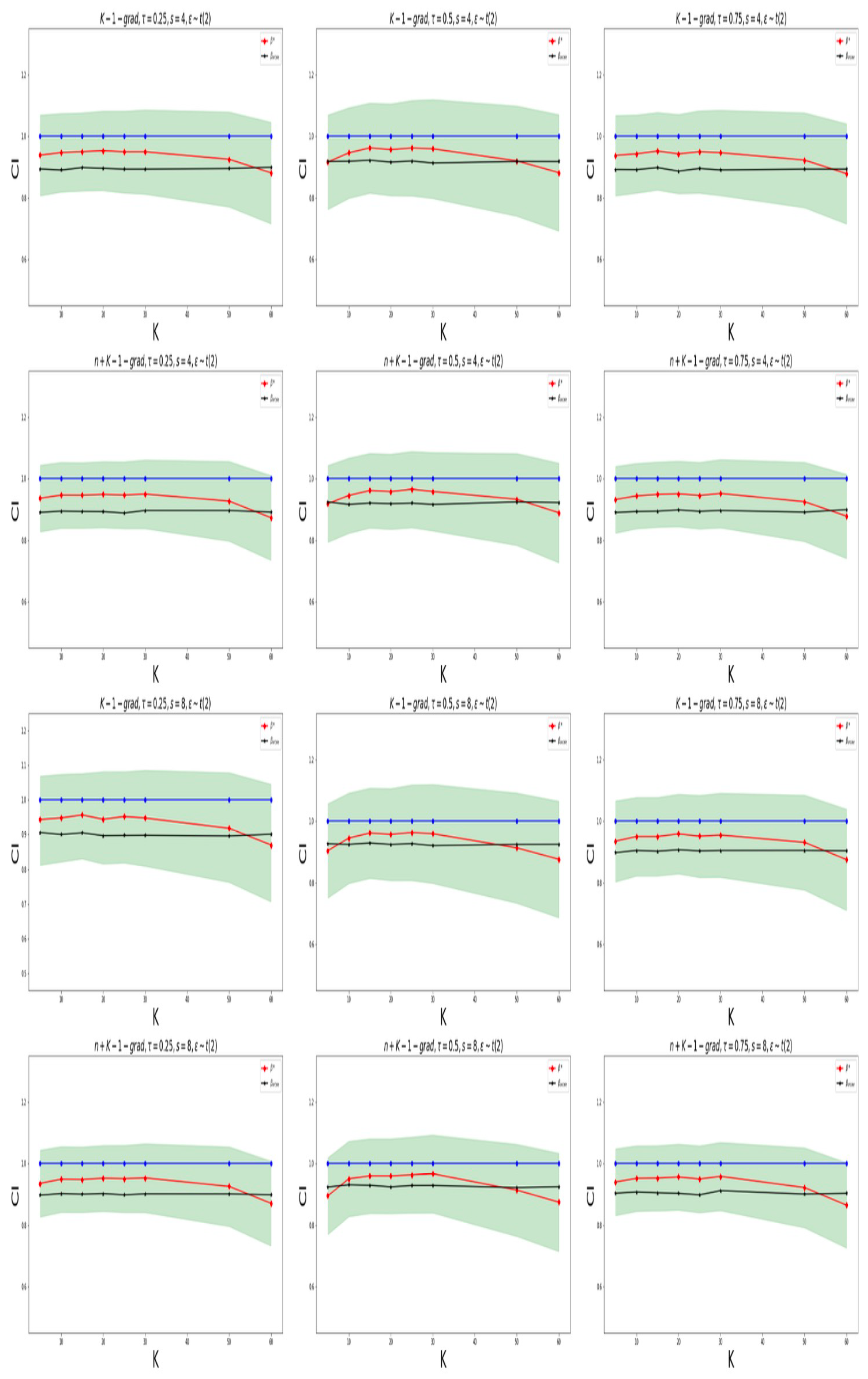
In this section, we demonstrate the statistical validity of confidence intervals constructed by our proposed method. For each choice of s and K, we run Algorithm 1 with “K-grad“ and “n+K-1-grad” on 100 independently generated datasets and compute the empirical coverage probabilities and the average widths based on the 100 running. At each running, we draw $B=500$ bootstrap samples and calculate B bootstrap statistics ($\overline{W}$ or $\tilde{W}$) simultaneously. We obtain the $90\%$ and $95\%$ empirical quantiles and further obtain the $90\%$ and $95\%$ simultaneous confidence intervals. For the selection of the adjustment parameter ${\lambda }_l$ in the nodewise algorithm, we refer to the method proposed in [25].

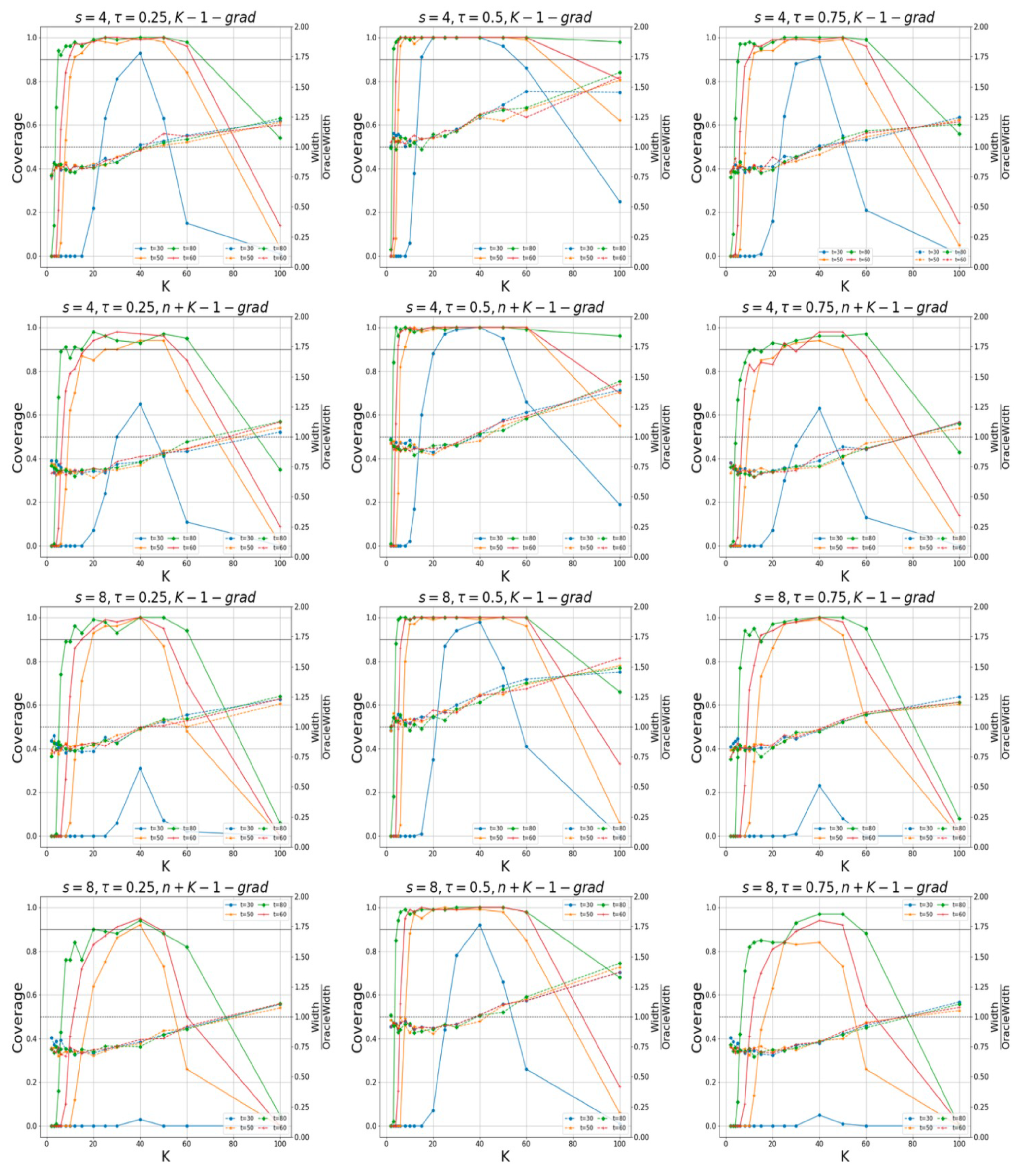
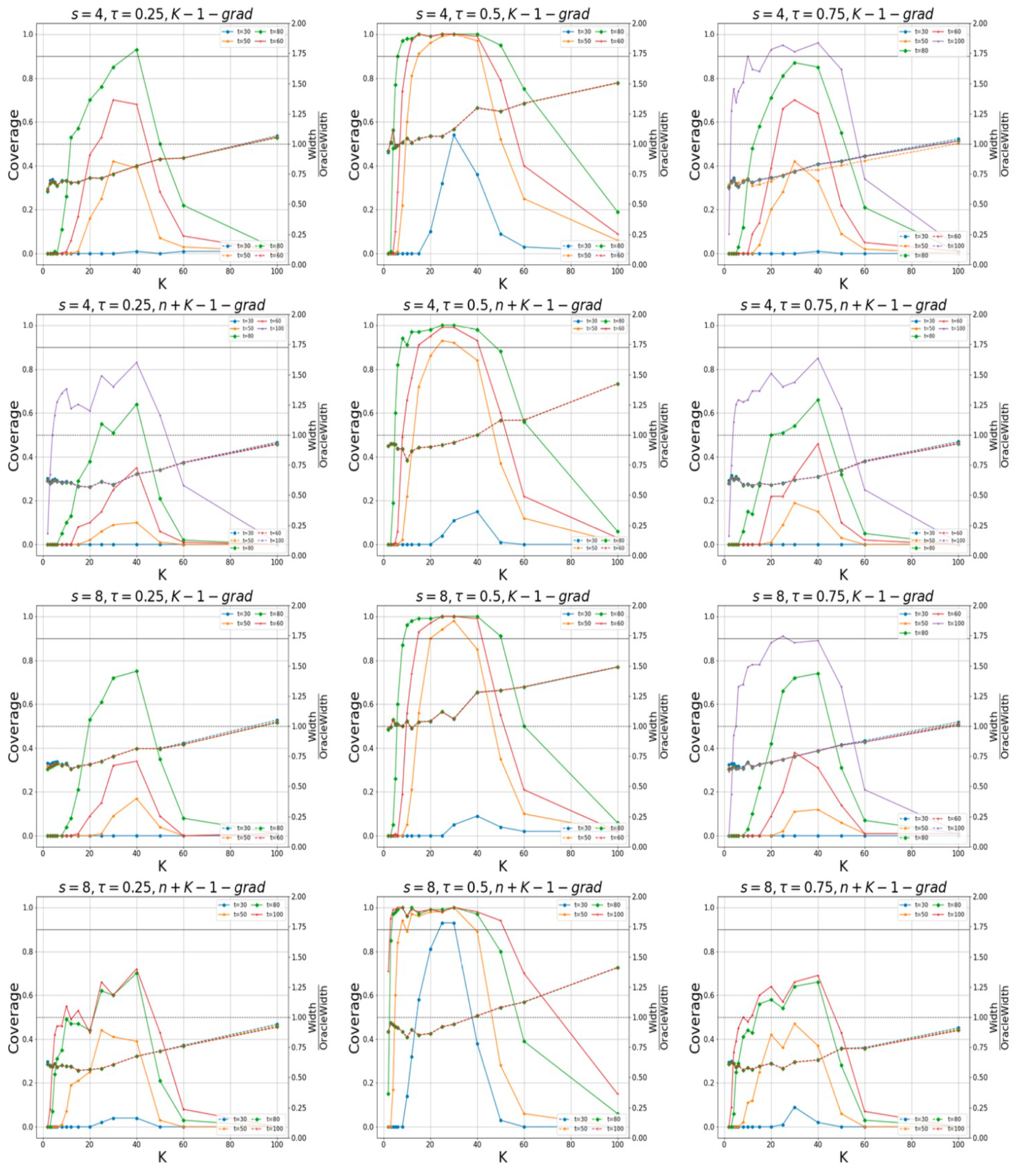
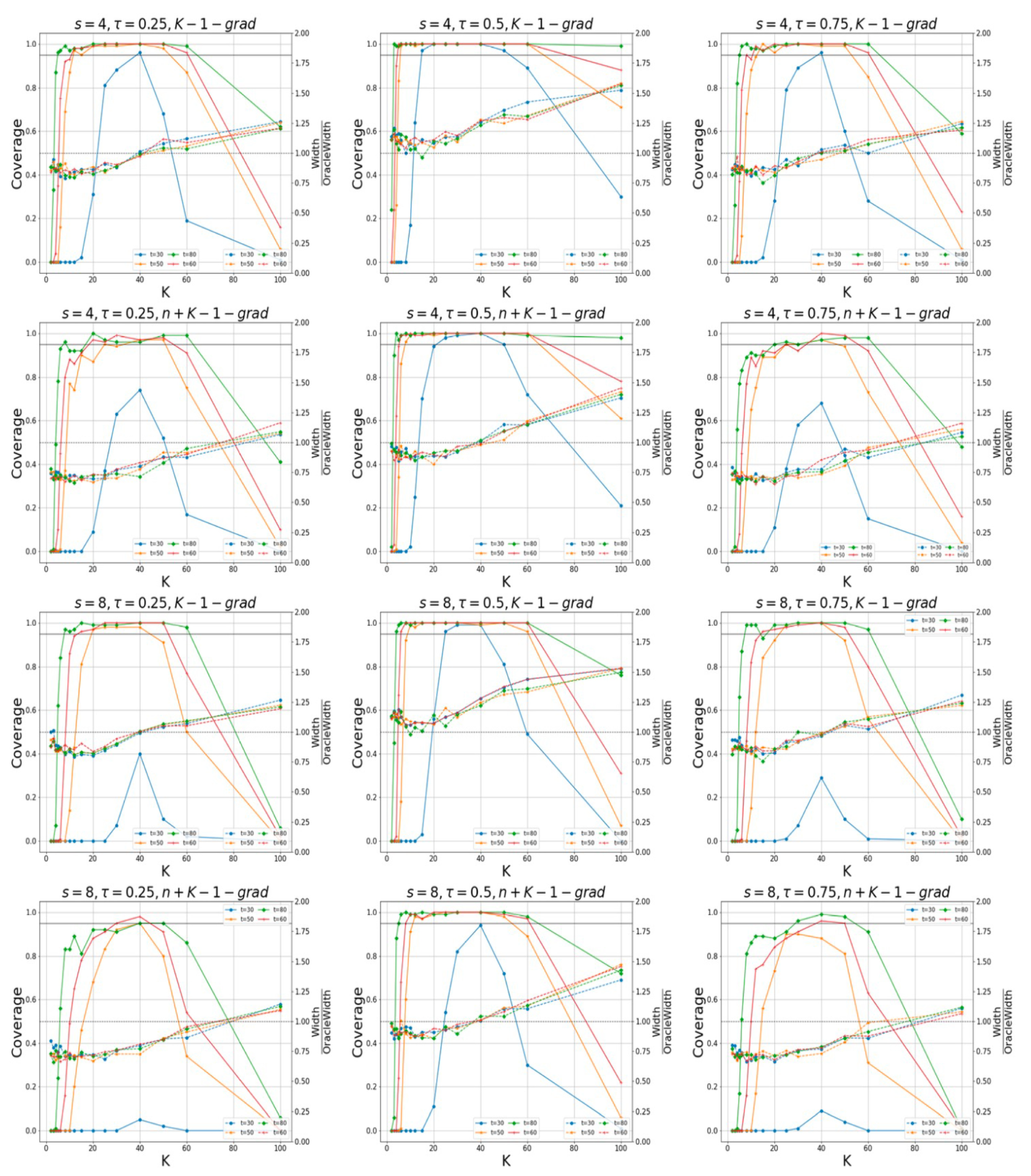
In Figure 3, for the case of $ϵ\sim N(0,0.5^2)$, and Figure 4, for the one of $ϵ\sim t\left(2\right)$, the coverage probabilities and the ratios of the average widths to the prior widths, calculated using the “K-grad-Q“ and “n+K-1-grad-Q” methods for different quantile levels, are displayed. The confidence levels are 95%. The sparsity levels are $s=4$ and $s=8$. To determine whether the true values of the non-zero elements in the parameter ${\beta }^{*}$ lie within the intervals constructed by our proposed method, we examine different values for the different number of machines, K. We observe that the confidence intervals constructed by our method are capable of effectively encompassing the true values of unknown parameters. 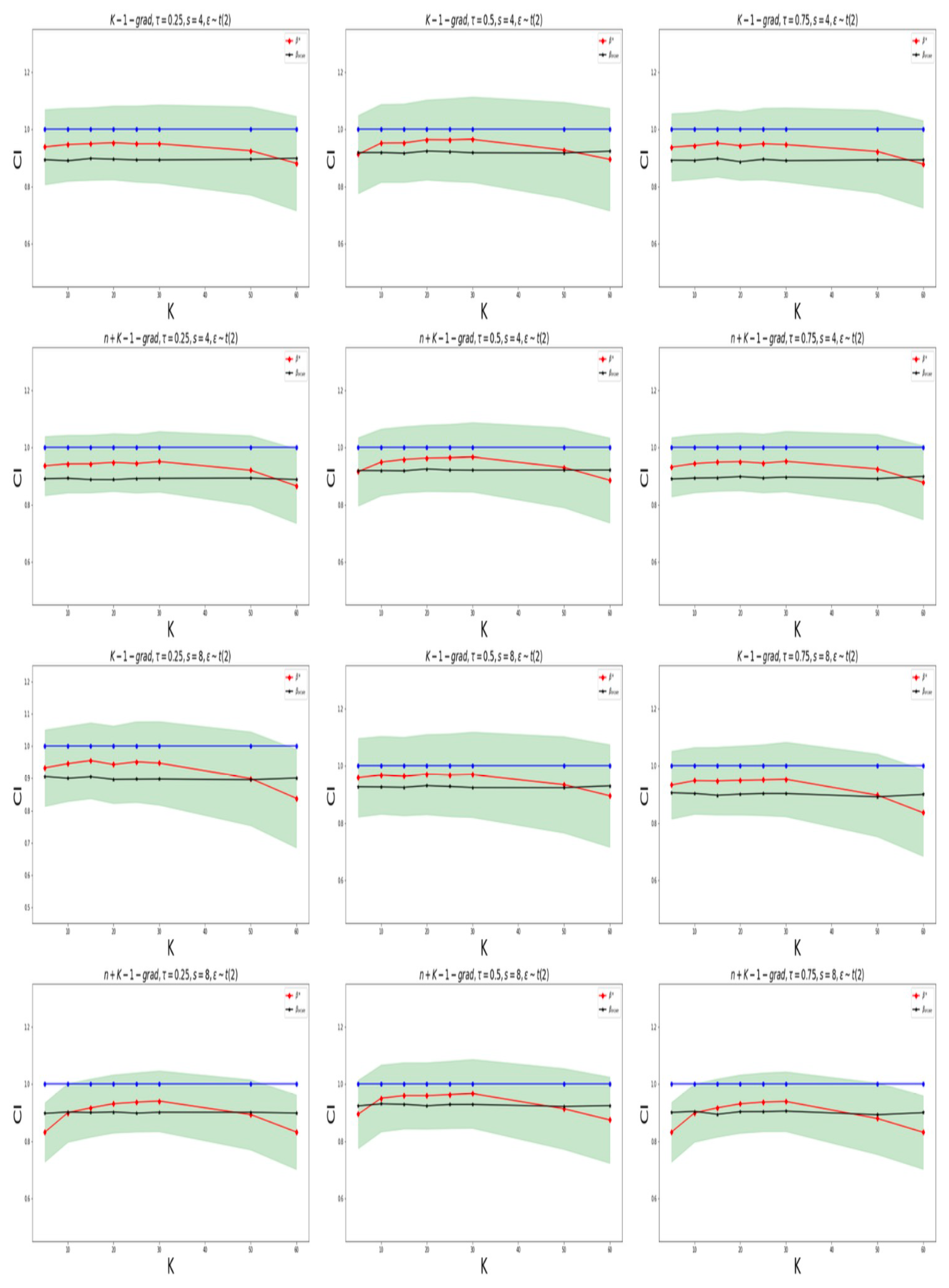In Figure 5 for $ϵ\sim N(0,0.5^2)$ and Figure 6 for $ϵ\sim t\left(2\right)$, we construct a 95% confidence interval for the fifth element of the true parameter (${\beta }_5^{*}=1$). The case for the confidence level of $90\%$ is listed in the Appendix A.

When the round of communication is low, the accuracy of parameter estimation is poor and the coverage probabilities of both methods are low. However, when the round of communication is sufficiently large, the estimation accuracy is relatively high, and the “k-1-grad-Q” method tends to coverage. In addition, the “n+k-1-grad-Q” method is relatively more accurate. The confidence intervals via our method can effectively cover the unknown true parameters. We also find that when the number of machines is too large (with small amounts of data on each machine), the estimation accuracy is low, which also leads to a low coverage probability; when K is too small, both algorithms perform poorly, which is consistent with the results in Remarks 7 and 8.

5. Conclusions and Discussions

Constructing confidence intervals for parameters in high-dimensional sparse quantile regression models is a challenging task. The bootstrap, as a standard inference tool, has been shown useful in handling the issue. However, previous works that extended the bootstrap technique to high-dimensional models focus on non-distributed mean regression [25] or distributed mean regression [24]. We extend their “k-1-grad” and “n+k-1-grad” bootstrap techniques to “k-1-grad-Q” and “n+k-1-grad-Q” distributed bootstrap simultaneous inference for high-dimensional quantile regression, which is applicable to large-scale heterogeneous data. Our proposed Q-DistBoots-SI algorithm is based on a communication-efficient distributed learning framework [3,4]. Therefore, the Q-DistBoots-SI is a novel communication-efficient distributed bootstrap inference, which relaxes the constraint on the number of machines and is more accurate and robust for the large-scale heterogeneous data. We theoretically prove the convergence of the algorithm and establish a lower bound on the number of communication rounds ${\iota }_{min}$ that warrants statistical accuracy and efficiency. This also enriches the statistical theory of distributed bootstrap inference and provides a theoretical basis for its widespread application. In addition, our proposed Q-DistBoots-SI algorithm can also be applied to large-scale distributed data in various fields. In fact, the bootstrap method has been applied to statistical inference for a long time. For example, Chattergee and Lahiri [31] studied the performance of the bootstrapping Lasso estimators on the prostate cancer data and stated that the covariates log(cancer volume), log(prostate weight), seminal vesicle invasion, and Gleason score have a nontrivial effect on log(prostate specific antigen); the rest of the variables (age, log(benign prostatic hyperplasia amount), log(capsular penetration), and percentage Gleason scores 4 or 5) were judged insignificant at level $1-\alpha =0.1$; Liu et al. [32] applied their proposed bootstrap lasso + partial ridge method to a data set containing 43,827 gene expression measurements from the Illumina RNA sequencing of 498 neuroblastoma samples and found some significant genes. Yu et al. [25] tested their distributed bootstrap for simultaneous inference on a semi-synthetic dataset based on the US Airline On-time Performance dataset and successfully selected the relevant variables associated with arrival delay. However, Refs. [25,31,32] mainly focused on bootstrap inference for mean regression. Therefore, they cannot select relevant predictive variables with the responses at the different quantile levels. In contrast, our method can be successfully applied to the US Airline On-time Performance dataset and gene expression dataset to infer predictors with significant effects on the response at each quantile level. This is very important because we may be more interested in the influencing factors of response variables at extreme quantile levels. For example, our approach can be applied to gene expression data to identify genes that have significant effects on predicting a cancer gene’s expression levels in a quantile regression model. Compared with mean regression methods, our method finds genes that should be biologically more reasonable and interpretable because of the characteristics of quantile regression. Future work is needed to investigate the applications of our distributed bootstrap simultaneous inference for quantile regression to large-scale distributed datasets in various fields. Although our Q-DistBoots-SI algorithm is communication-efficient, when the feature dimension of the data is extra-high, the gradient transmitted by each worker machine in the algorithm is still an ultra-high dimensional vector, which also has unbearable communication costs. Thus, we need to develop a more communication-efficient Q-DistBoots-SI algorithm via quantization and sparse techniques (such as Topk) for large-scale ultra-high-dimensional distributed data. In addition, our Q-DistBoots-SI algorithm cannot cope with Byzantine failure in distributed statistical learning. However, Byzantine failure has recently attracted significant attention [7] and is becoming more common in distributed learning frameworks because worker machines may exhibit abnormal behavior due to crashes, faulty hardware, and stalled computation or unpredictable communication channels. Byzantine-robust distributed bootstrap inference will also be a topic of our future research. Additionally, in the future, we can also extend our distributed bootstrap inference method into transfer learning and graph models for large-scale high-dimensional data.