1. Introduction
In any organization, whether private or public, performance evaluation unquestionably plays a pivotal role in human resource management. The increasing impact of globalization, fueled by worldwide competition, has raised new challenges for both researchers and practitioners in this field [
1,
2]. An organization’s ability to function effectively and realize its vision now hinges significantly on the quality of its performance evaluation practices. In the realm of employee performance assessment, there exist both qualitative and quantitative methods [
3]. It is imperative for organizations to establish a robust performance assessment system that can fairly and accurately evaluate staff performance. Such a system guides and channels employees’ skills and efforts toward achieving organizational goals. Without a robust evaluation system in place, managers may risk jeopardizing organizational competencies and making suboptimal decisions. Consequently, outstanding employees might not receive the constructive feedback they need, leading to dissatisfaction and potential departures, incurring high recruitment costs for the company [
4].
One strategy that organizations employ to take corrective actions backed by solid evidence is performance appraisal, which examines and assesses past performance records in the context of future expectations. This approach is not only used to inform employees about their workloads but also to motivate staff and shape their perceptions of the organization, both of which are crucial factors in achieving organizational objectives. Perception is the cognitive process through which individuals organize and analyze sensory input to make sense of their environment. Given that people’s perceptions are influenced by their unique ideas and experiences, it is inevitable that individuals will have diverse viewpoints and justifications [
5].
Understanding the staff’s capacity to accomplish tasks within a defined time frame is a fundamental element contributing to an organization’s success. Research indicates that organizations employing a performance appraisal process experience an average productivity improvement of 43% [
6]. Performance evaluations, as mentioned in a study, are a critical process through which organizations assess employees’ work and the goals they have set, utilizing these assessments to determine appropriate rewards [
7]. This process holds significant importance, as it underpins career growth, employee training, promotions, transfers, and compensation decisions [
8]. Moreover, it serves as a valuable tool for monitoring staff productivity and efficacy, making it imperative that it be conducted meticulously and impartially to continually enhance staff performance [
8].
Throughout the performance evaluation process, several fundamental assumptions come into play. Notably, it presupposes that employers possess the ability to differentiate among employees and recognize that each employee’s contribution to the organization varies due to their unique performance [
9]. Researchers such as the authors of [
10] argued that performance appraisal can be further improved by identifying employees’ strengths and limitations, providing constructive feedback and fostering effective communication between employees and managers. To implement such a procedure successfully, a pragmatic performance evaluation tool should account for various factors and constraints, including time and costs [
11].
Previous research underscores the pivotal role of performance reviews for staff members in terms of self-identification and goal setting, both in the short and long term, resulting in enhanced work output [
12,
13]. Furthermore, performance reviews hold great potential to boost organizational performance by outlining remuneration and evaluation systems, identifying growth opportunities and training requirements, and validating selection practices that may warrant corrective action or termination [
14]. Performance evaluation, similar to other decision-making challenges, is a multifaceted process. It involves generating accurate predictions for quantitative forecasting and making sound judgments on qualitative issues. To tackle this complexity, the application of a fuzzy linguistic model proves invaluable, bridging the gap between verbal expressions and numerical values [
15].
For an efficient and equitable execution of the performance review process, a systematic decision-making approach is imperative. Jafari et al. [
16] proposed a method for selecting performance appraisal methodologies and comparing various approaches to aid organizations in making informed choices, enabling them to assess their performance appraisal system’s essential components before implementation, thereby averting unnecessary costs. Staff performance reviews entail a multitude of perspectives in team decision-making processes, as observed by [
14]. To determine the relative importance of the evaluation group’s opinions and criteria, they introduce a fuzzy Delphi technique. Additionally, to enable decision-makers to express their evaluations using various linguistic scales, depending on their familiarity with the evaluated personnel, Andrés et al. [
6] introduced the multi-granular framework for linguistic assessment.
In the realm of linguistic variables, ref. [
17] introduced a unique 2-tuple linguistic expression framework capable of managing data in decision-making scenarios that incorporate both linguistic and numeric ratings. This framework expands the range of information that managers can effectively handle in heterogeneous contexts. Intuitive fuzzy sets, as employed by [
18], offerred a generalized approach to fuzzy entropy with a solid axiomatic foundation. These sets also shed light on the significance of the parameter
and provide a means for managers to handle heterogeneous information efficiently.
The development of complex decision models, including one of the key operations research techniques, MCDM has become widely utilized to assist assessors in analyzing and selecting the most suitable options [
19]. In response to MCDM challenges, various mathematical programming models have undergone significant improvement. However, MCDM has recently gained increased popularity in evaluating diverse approaches [
20]. Numerous criteria have been assessed, selected, and ranked using MCDM methodologies [
21]. The qualitative evaluation approach of MCDM places a strong emphasis on the subjective nature of criteria. It is essential to provide comprehensive details about the selected and recommended criteria [
22]. MCDM assists decision-makers in identifying the constituent variables that lead to the optimal operational strategy, particularly when faced with limited resources [
23]. Due to its effectiveness in addressing decision-related issues, this methodology has found application across a wide range of industries and continues to evolve.
Several well-known and prevalent MCDM techniques include Simple Additive Weighting (SAW) [
23], Elimination and Choice Expressing Reality (ELECTRE) [
24], the Preference Ranking Organization Method for Enrichment Evaluation (PROMETHEE) [
25], the Technique for Order of Preference by Similarity to an Ideal Solution (TOPSIS) [
26], linear programming techniques [
27], and the Analytic Hierarchy Process (AHP) [
28], among others. Among these, the widely recognized MCDM technique is TOPSIS, which was developed by [
26]. It is renowned for its advantages in dealing with both positive and negative ideal solutions and its user-friendly nature. Researchers have applied the traditional TOPSIS approach in various ambiguous scenarios. For specific applications, researchers have adapted MCDM techniques. For instance, ref. [
29] employed Fuzzy TOPSIS to select the top reverse logistics provider based on performance indicators. Kumari et al. [
30] introduced the Shapley-TOPSIS technique, based on intuitionistic fuzzy sets (IFSs), to identify the best solutions for a cloud service problem. Furthermore, ref. [
31] expanded the concept of IFSs in the TOPSIS model for assessing offshore wind (OFW) turbine infant failure.
The concept of divergence measures, which assess the discriminatory information, was originally introduced by [
32]. Over the years, various entropy metrics have been proposed, and extensive examinations of their applications, properties, and utility have been conducted [
33,
34]. In one study, the divergence measure in a fuzzy context was axiomatically defined, accompanied by computational methods for handling fuzzy sets [
35]. Essentially, the divergence measure serves to elucidate dissimilarity and introduces a set of intriguing axioms for approximating fuzzy set discrimination. Subsequently, ref. [
36] introduced the J-divergence metric for intuitionistic fuzzy sets (IFSs). This development underscored the importance of having reliable distance measures between IFSs, particularly in the context of inference problems. The proposed divergence measure proves to be effective in quantifying the actual separation and degree of similarity between IFSs.
In the realm of automated leukocyte recognition, ref. [
37] devised a method for computing fuzzy divergence. Furthermore, ref. [
38] went on to develop a modified fuzzy divergence measure, addressing the limitations of existing divergence measures while exploring their unique attributes. Joshi and Kumar [
39] introduced a divergence measure rooted in the well-known Shannon entropy concept, shedding light on some of its key characteristics. To tackle MCDM issues within a fuzzy environment, ref. [
40] proposed an approach based on a divergence measure for Fuzzy Systems (FSs). Subsequently, in their work in [
41], they introduced the fuzzy Technique for Order of Preference by Similarity to an Ideal Solution (TOPSIS) technique, incorporating a divergence measure to address decision-making challenges. However, it is worth noting that some of the preceding divergence measure techniques have limitations, as they are only applicable after the defuzzification process. This constraint prevents them from evaluating values within a fuzzy interval that may contain either 0 or 1.
The aim of this research is to introduce a generalized divergence measure, which can overcome the existing limitations, including potential anomalies in results, and provide a solution for assessing score values of alternatives. The research also addresses a real-world decision-making problem related to selecting the most suitable candidate for a staff performance review, illustrating the practical applicability of the proposed method. This study contributes significantly in three main ways. Firstly, it introduces a comprehensive and generalized divergence measure that effectively addresses the shortcomings of previous measures. This achievement is the result of an extensive review and analysis of existing measures. Secondly, the research improves the method proposed in [
42] by applying fuzzy
-cut to the MCDM problem of selecting the most appropriate candidate for staff performance reviews. This application enhances the widely utilized TOPSIS approach within the context of fuzzy sets, showcasing the versatility and adaptability of the methodology. Thirdly, the research applies the fuzzy MEREC technique adapted from [
43] to determine the weights of the criteria used in the evaluation process. The fuzzy MEREC is an effective objective weighting technique, as the existence of outliers only has a small effect on the results of the criteria weights.
3. Generalized Divergence Measure
In the fuzzy sets theory, it is essential to note that membership values must fall within the range of . For a function f to be well defined, it is imperative that the membership functions, denoted as and within f should not equate to zero. This, however, introduces a limitation to f because it cannot encompass the entire domain of membership functions and . The issue arises when either or equals zero, rendering the function f invalid. It is important to acknowledge that there exists the possibility of the values of or reaching zero, thus jeopardizing the overall function f.
Translating this into the context of staff performance evaluation, where alternatives are assessed and compared based on predetermined criteria, a similar principle applies. If an alternative fails to meet the requirements of a specific criterion, it receives a zero score for that criterion. To address this limitation effectively, a new variable denoted as
has been introduced into the function. This modification ensures that all membership values within the range of
can be accommodated in the given function.
The TOPSIS technique hinges on two key concepts: the positive ideal solution (PIS) and the negative ideal solution (NIS). To ensure the accurate and consistent derivation of these solutions, it is important that the distance function be symmetric. However, the current function remains non-symmetric, as evidenced by the lack of consistency in the distance values from both PIS and NIS, as demonstrated in the given numerical example.
Example 1. The function g as in Equation (9) is non-symmetric for some membership values. Let and be the performance scores of an alternative and the positive ideal alternative, respectively, where ; the distance value of the alternative from the PIS is determined as follows: Next, let be the performance score of the negative ideal alternative; the distance value of the alternative from the NIS is determined as follows: The example has clearly shown that . This leads to the firm conclusion that the function g lacks the property of symmetry.
Let us introduce a new function, denoted as
, which corresponds to the existing function
. Specifically, when
or
, function
h is defined as the reflection of function
g about the line
or
, where
. To achieve this reflection, we transform
to
and
to
as outlined below:
then
To ensure the calculation of consistent distance values from both the PIS and NIS as a symmetric function, it is important to combine the function
g with its corresponding reflected function,
h. Additionally, we modify the base of the logarithmic function to an exponent, allowing for better comparability with other divergence measures and enhancing the distinctiveness of function values for each point. This symmetric function is now introduced as the new generalized divergence measure and is defined as follows:
where
.
In the domain of divergence measures, it is customary to expect and establish various properties. In this research, the recently introduced divergence measure, , is bounded by the preexisting divergence measure, . Notably, all the properties characterizing are equally satisfied by , as explained in Theorem 1.
Theorem 1. The divergence measures and satisfy the inequality with and such thatwhere Proof. Firstly, the following inequality is proved such that
Case 1: For
and
, suppose that
By applying the ln function for both sides, it yields
Since
, by multiplying
for both sides, it yields
Case 2: For
and
, suppose that
By applying the ln function for both sides, it yields
Since
, by multiplying
for both sides, it yields
Secondly, the following inequality is proved such that
Case 3: For
and
, suppose that
By applying the ln function for both sides, it yields
Since
, by multiplying
for both sides, it yields
Case 4: For
and
, suppose that
By applying the ln function for both sides, it yields
Since
, by multiplying
for both sides, it yields
Thus, for any
and
, the following inequality is obtained such that:
Hence, it is proven that
□
The proposed divergence measure, also satisfies the fundamental properties of divergence measures such as nonnegativity and symmetricity as in Theorem 2.
Theorem 2. Let ; the following properties of the divergence measure described in Equation (11) are provided as: - 1.
,
- 2.
if ,
- 3.
.
Proof. (1) and (2):
Consider
and
then, assuming that
f has a first partial derivative with regard to
,
and also, the second partial derivative of
f with regard to
is provided by:
Due to the fact that
for
therefore
f is a concave upmapping of
making
a convex function. With constant
is decreasing in
and increasing in
. Therefore, when
,
and similarly for
,
Hence, for with constant reaches its highest point at , (or , ) and its minimum at .
Therefore, and if .
(3): Suppose
It is therefore shown that
□
The divergence measure , as stated in Theorem 3, exhibits some features that are related to the characteristics of the union and intersection of sets. The use of the properties provides the simplification and resolution of some instances of set union or intersection.
Theorem 3. For , the divergence measure described in Equation (11) satisfies the following properties: - 1.
,
- 2.
,
- 3.
,
- 4.
.
Proof. Let then
Union of P and ;
Intersection of P and .
Using the third property of Theorem 2,
. Hence,
(2) is also demonstrably true as (1).
Since as in Theorem 2, then .
(4) is also demonstrably true as (3). □
4. Formulation of -Cut Technique in Divergence Measure
A new fuzzy set divergence measure was recently developed by Rani et al. [
41] and is defined as:
where
and
.
The divergence measure is commonly employed to evaluate the discrimination of fuzzy sets. However, due to the fuzzy number being in interval form, its application is limited to the post-defuzzification procedure. To overcome this constraint and measure any feasible rating of alternatives, a new generalized divergence measure is proposed in this study. This innovation seeks to circumvent the limitations of current measures, eliminating the peculiarities observed in the results.
Md Saad et al. [
54] introduced the Hamming distance method by employing fuzzy
-cut for a triangular fuzzy number,
, in the evaluation process, as follows:
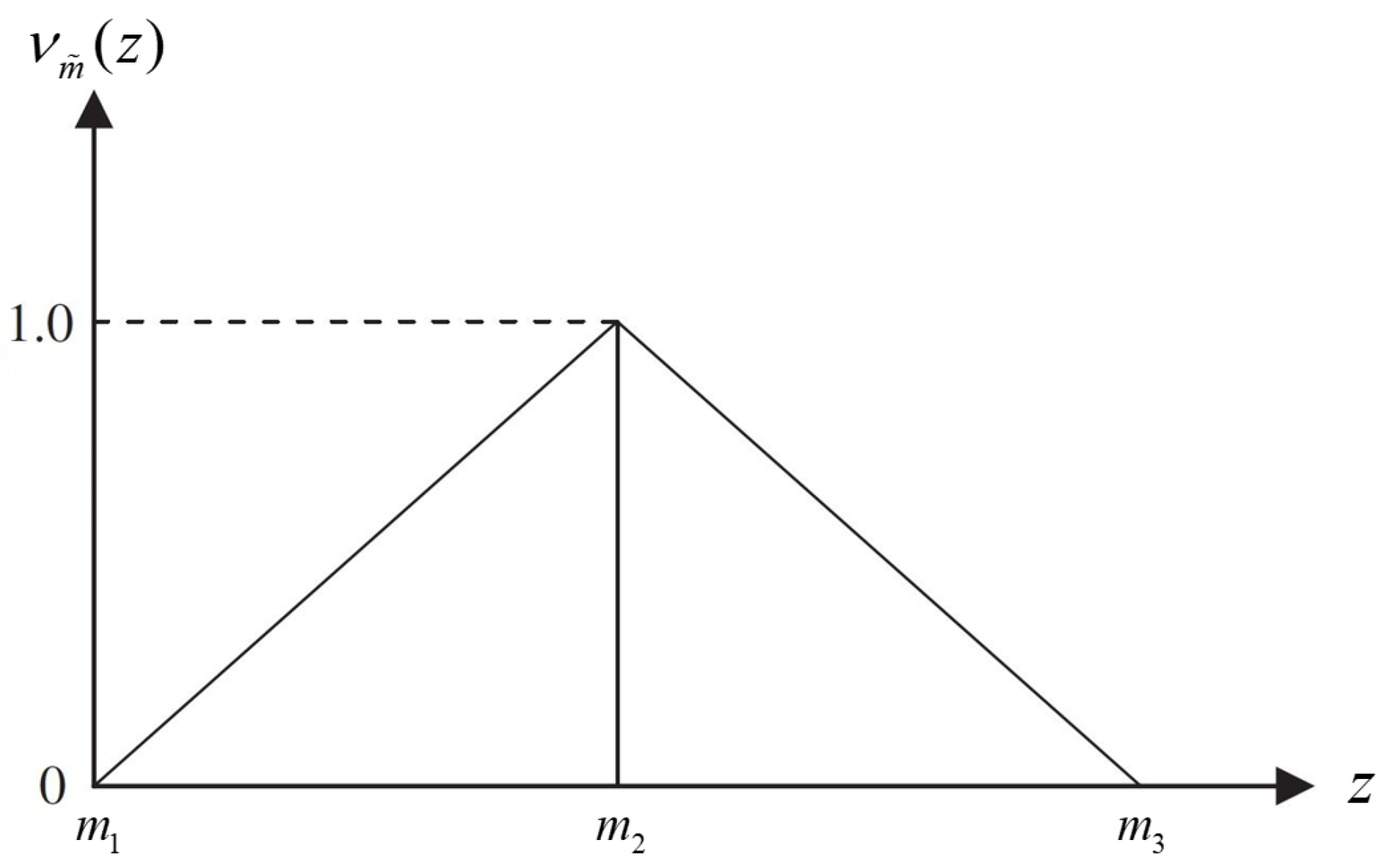
The fuzzy -cut is a fundamental concept in fuzzy logic that establishes a precise subset within a fuzzy set. Fuzzy logic allows for items to have varying degrees of membership in a set, unlike classical logic, which only considers elements as either fully in or out of a set. It is a way to generate a crisp set from a fuzzy set that involves setting a threshold value, usually represented as . The -cut of a fuzzy set A at a specific threshold , represented as , is the subset of A that includes all elements whose membership degrees are at least .
Later, Cavallaro et al. [
55] also presented the technique of
-cut for measuring objective weight by using the concept of Shannon’s entropy as:
and presented the distances between each alternative from
and
, which are determined using the following equations:
Building on this inspiration, the technique of
-cut from Equation (
14) is implemented in this study for the divergence measure
to assess the performance of alternatives based on main and sub-criteria weights, as follows:
and
where
and
5. Fuzzy Divergence Measure Based on TOPSIS Method
Assume the MCDM issue has m alternatives, , and the alternatives are appraised using n criteria, , and sub-criteria, , where p denotes the number of sub-criteria in the main criteria n. Let be the weight of the main criterion and be the weight of the sub-criterion, such that , , and . All criteria and alternatives are evaluated by several experts, based on linguistic terms. The proposed method includes several steps, as follows:
Step 1:
Develop a fuzzy decision matrix .
The experts provide the feasible assessments of alternative
regarding criterion
and sub-criterion
represented by the fuzzy numbers
acquired from linguistic variables in
Table 1 and demonstrated as:
for
.
The linguistic terms are employed based on the hierarchical degree of staff authority, and experts possess the ability to discern these terms without resorting to numerical scoring.
Step 2:
Aggregate the fuzzy evaluations of alternatives via the equation provided:
In this study, it is worth mentioning that the preference of each expert is assumed to be equal since they have an equal level of knowledge.
Step 3:
Normalize the fuzzy decision matrix.
Normalization aims to eliminate the difference between the attributes in magnitude and dimension, in which the normalized value is in the range of [0, 1]. Hence, the technical problems generated by distinct measurement categories can be eliminated. The preliminary data corresponding to each criterion is normalized by dividing it by the most dominant criterion value. The element of a normalized decision matrix
resulting from TFN
is given by:
Step 4:
Define the fuzzy positive-ideal solution (PIS) and negative-ideal solution (NIS) with regard to the decision matrix’s normalized values.
The PIS
and NIS
are as follows:
The positive ideal solution is typically determined by selecting the highest value for each criterion in the dataset for benefit criteria and the lowest value for each criterion for cost criteria. The negative ideal solution refers to the worst possible values for each criterion in the dataset. The construction process involves selecting the lowest value for each criterion in the dataset for benefit criteria and the highest value for each criterion for cost criteria. These serve as benchmarks against which the alternatives are assessed.
Step 5:
Construct the fuzzy interval for the decision matrices of normalized values, PIS and NIS.
By using -cut of triangular fuzzy number, the fuzzy interval of decision matrices for the normalized values, PIS and NIS are given as follows:
The interval decision matrix for the normalized values:
where
and
The interval decision matrix for the PIS and NIS, respectively:
where
and
The level of confidence in the expert’s fuzzy evaluation is measured by the value; the greater the number, the more confident the expert is. This means that the experts’ evaluations of the ideal alternative and alternatives are closer to the feasible value for the corresponding triangular fuzzy number , as represented by the related linguistic phrases. Their confidence level is a reflection of their understanding of the credentials and expertise of potential alternatives, as determined by the information provided. It is anticipated that the proposed solution for this issue will lessen the burden placed on the experts during the alternative selection process.
Step 6:
Compute the weights of the sub-criteria.
This step presents the criteria weights in an MCDM problem utilizing a modified technique of the fuzzy Method based on the Removal Effects of Criteria (MEREC) adapted from [
43]. To determine the weights of criteria, the fuzzy MEREC uses the removal effect of each criterion on the performance of the alternatives. The criteria with the greater impact on performance have received more weight. The fuzzy MEREC method for determining objective weights is described in detail as follows.
Step 6.1:
Defuzzify the fuzzy decision matrix.
The element of decision matrix is in TFN notation. When executing the algorithm, the fuzzy values must be appropriately defuzzified in order to generate crisp values. Defuzzification turns fuzzy values towards crisp values. Different defuzzification procedures result in distinct formulas or processes that provide diverse defuzzified values that could be used in the generation of varied ranking outcomes. Defuzzification techniques include the centroid method, center of mass, graded mean integration representation (GMIR), and mean of maxima. In this study, the GMIR technique is used to determine the crisp value, Crisp
, for TFN
, which is defined as follows:
Step 6.2:
Evaluate the overall performance of the alternatives.
The improved logarithm function is used to compute the performance of the alternatives as a whole. It is developed from a non-linear function introduced by Shannon and Weaver [
32] and has been revised by other scholars [
51,
52,
53]. The following equation is used in the computation:
Step 6.3:
Evaluate the performance of the alternatives by removing every criterion.
Based on the preceding, this step employs the logarithm function. As contrast to Step 6.2, the performance of the alternatives is assessed by eliminating every criteria separately. Given
m sets of performances and
p sub-criteria in
n main criteria, let
represent the overall performance of
i-th alternative with respect to the elimination of the
-th criterion. The following equation is used to compute this step:
Step 6.4:
Determine the cumulative amount of the absolute deviations.
In this step, we compute the removal effect of the
-th criterion based on the values given by Steps 6.2 and 6.3. Let
denote the effect of removing the
-th criterion. The formula that follows can be utilized for computing
values:
Step 6.5:
Determine the final weights of the criteria.
In this step, eliminating effects,
from Step 6.4, are used to establish the objective weight of each criterion. The symbol
represents the weight of the
-th criterion. The following equation can be used to calculate
:
Step 7:
Compute the separation measures
and
of interval values of fuzzy
from fuzzy intervals of PIS and NIS, respectively, using the given divergence measures as in Equations (
18)–(
21).
Step 8:
Compute the relative closeness coefficient, .
The closeness coefficient
for alternatives is calculated by using given equation:
The closeness coefficient quantifies the proximity of an alternative to the NIS in relation to the overall distance between the NIS and PIS. Alternatives with a higher closeness coefficient value indicate better performance in relation to the worst-case scenario, as they are viewed as being nearer to the PIS and further away from the NIS.
Step 9:
Rank the alternatives.
Sort the alternatives from top to bottom based on their performance, with the greatest value of being the best alternative.
6. Application of Staff Performance Appraisal
Through a process of comparative analysis, the outcomes of the fuzzy divergence measure are validated and demonstrated to be consistent with those of the Multi-Criteria Decision-Making (MCDM) methods currently in use. Microsoft software, specifically Visual C++ and Excel, were utilized for evaluating the suggested method and conducting the necessary statistical tests. To scrutinize and verify the efficacy of the proposed approach, data from [
42,
56] and a real case study involving staff performance reviews at educational institutes are referenced as Case Studies 1 and 2, respectively.
- (i)
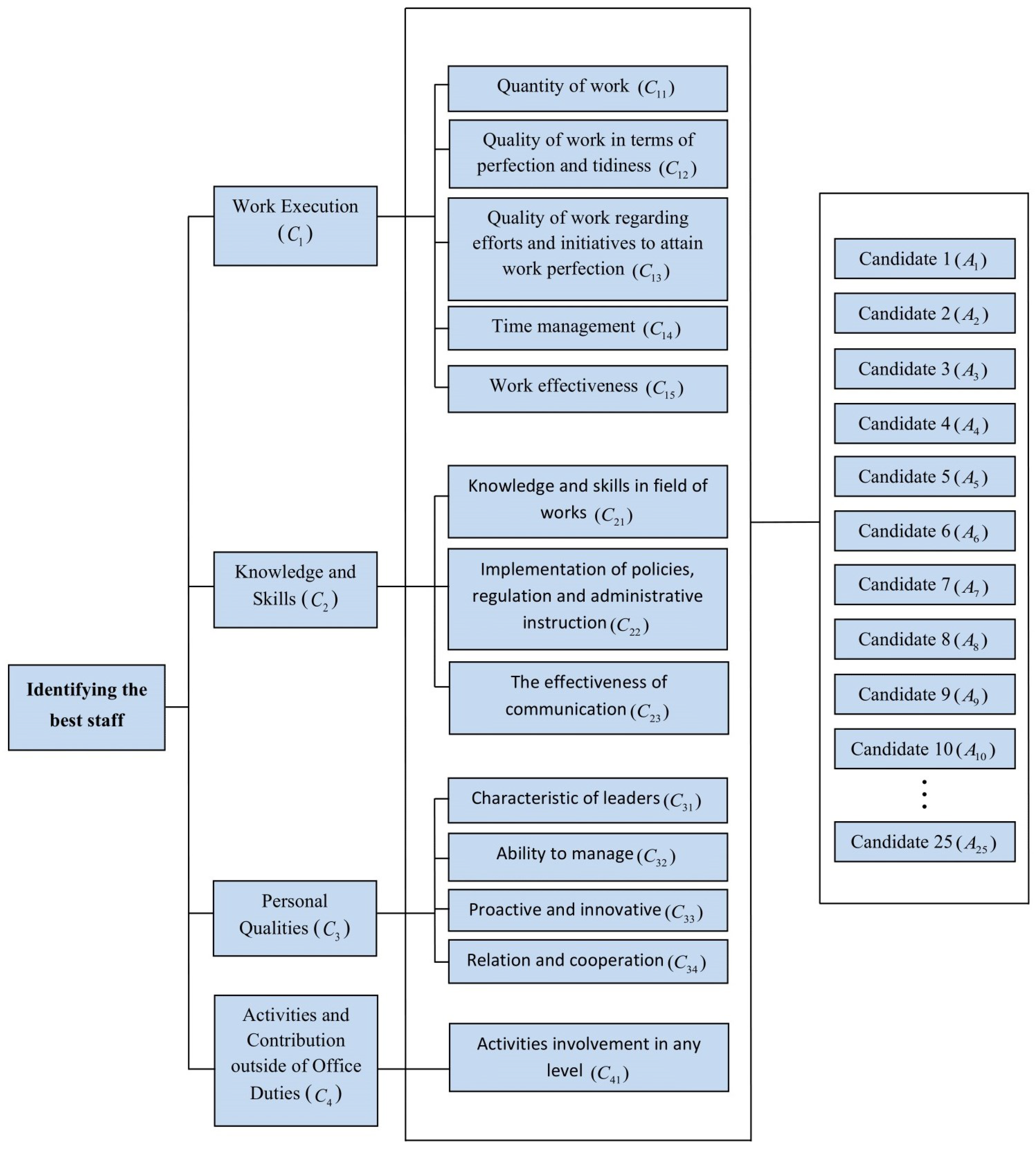
Case Study 1:
Let represent the university’s selected candidates, who are evaluated using four primary criteria and 13 sub-criteria
- (ii)
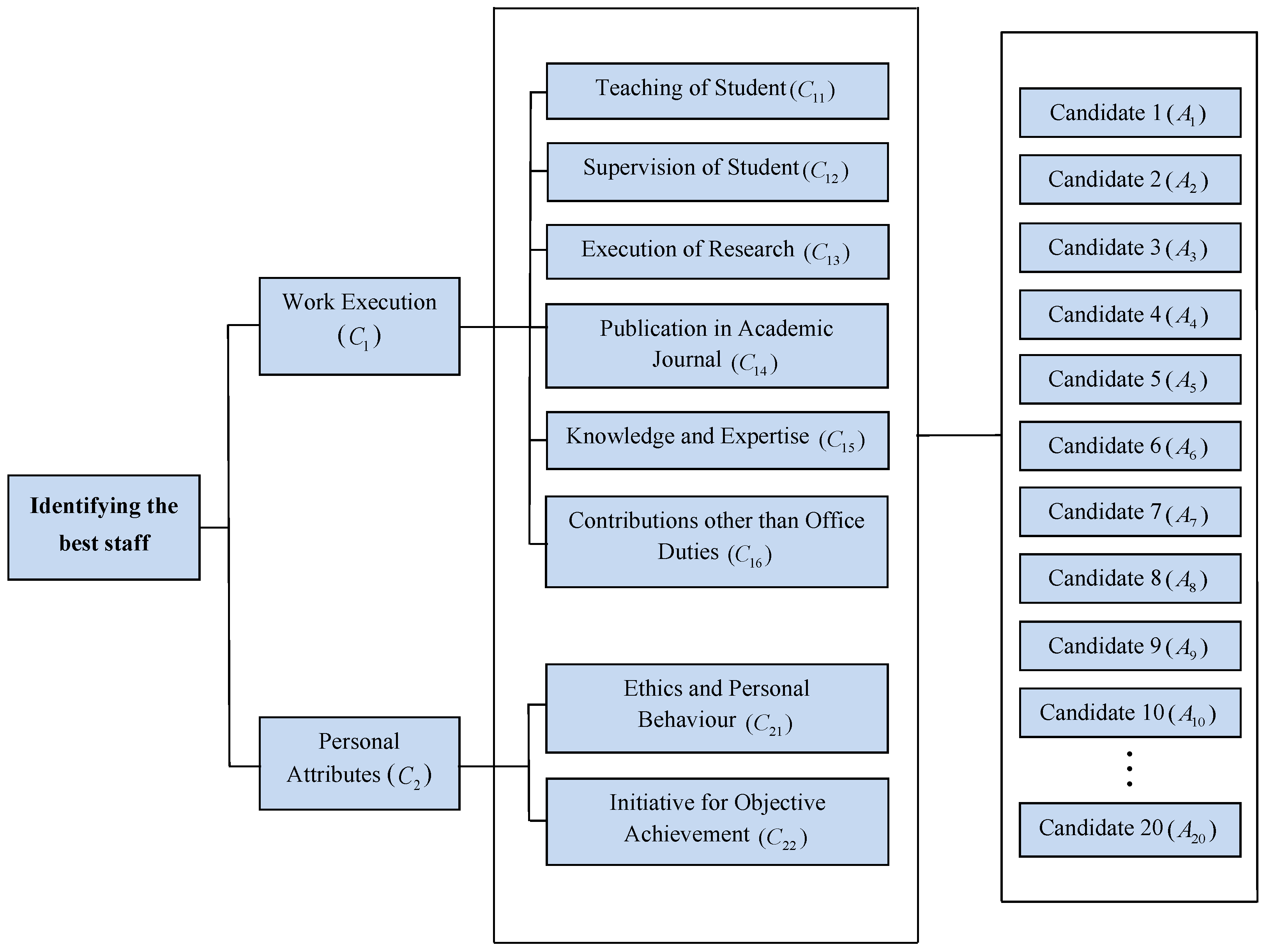
Case Study 2:
Let represent the university’s selected candidates, who are evaluated using four primary criteria and eight sub-criteria
For each case study, an expert group
was formed to evaluate the alternatives from a linguistic perspective.
Figure 2 and
Figure 3 illustrate the primary criteria, sub-criteria, and alternatives involved in these assessments, while
Appendix A provides the performance assessments of the alternatives from each expert. The proposed method was employed to measure and rank all candidates based on the defined criteria.
The results for the criteria weights, performance scores of staff, and their rankings within the institution are obtained through the application of the fuzzy divergence measure, as described in
Section 5.
Table 2 and
Table 3 present the findings of the primary criteria weights established by the university management, while
Table 4 and
Table 5 display the results of the sub-criteria weights generated using the fuzzy MEREC.
The rankings of alternatives corresponding to the closeness coefficient for
, and
are displayed in
Table 6 and
Table 7, and the rankings of the alternatives in descending order are shown in
Table 8 and
Table 9.
As observed in the tables for Case Study 1, the optimal alternative for , , and belongs to . Conversely, the least favorable alternative is consistently identified as for all values of . For Case Study 2, the optimal and least favorable alternatives for all values of are and , respectively. These results enable experts to discern the variations in rankings corresponding to their level of confidence during the evaluation of alternatives. The values of , and signify the confidence levels of the experts, representing very low, moderate, and very high confidence, respectively.
6.1. Comparison with Existing Methods
To observe the variations in ranking, the alternatives were additionally assessed and sorted using other divergence measure techniques and fuzzy TOPSIS. The results of this study are subsequently compared with those from other studies employing different methodologies, as outlined in
Table 10 and
Table 11 below.
The rankings of fuzzy divergence measures, fuzzy TOPSIS, and the proposed technique for staff performance rating exhibit a slightly different order. Despite these variations, all approaches converge to the same result, identifying the similar optimal alternatives for the departments.
The proposed divergence measure approach presents several advantages. To streamline the evaluation process for experts, language variables are initially used for alternative assessments, eliminating the need for numerical scaling. Subsequently, the fuzzy MEREC method is employed to assess criteria weights, representing one of the most effective approaches for determining objective weights. This eliminates the subjectivity associated with arbitrary decisions made by experts, who may occasionally make errors or assign grades dishonestly. Furthermore, when experts utilize the -cut approach to provide ratings, they can discern the range of rankings as their confidence levels shift. The degree of confidence is contingent on the experts’ awareness of the credentials and experience of alternatives based on the provided information. Lastly, the introduction of a generalized divergence measure is proposed. Some of the preceding divergence measures have the limitation that they can only be used after the defuzzification procedure has been concluded. If the defuzzification procedure is disregarded, divergence measures cannot evaluate the value in the fuzzy interval when the value is either 0 or 1. Unlike previous existing measures, the generalized divergence measure can evaluate any rating of an alternative and prevents results from becoming anomalous. This adds robustness to the methodology, ensuring its applicability across diverse rating scenarios.
As per
Table 12 and
Table 13, notable relationships are evident in the correlation coefficients across alternative rankings assessed using various Multi-Criteria Decision-Making (MCDM) techniques and the proposed approach. The changes in ranking for each alternative based on these techniques are minimal, as all correlation coefficient values exceed 0.93. For a comprehensive comparison, we chose to contrast the findings using a technique that adheres to the conventional TOPSIS concept, as discussed by Kabak et al. [
57], since the proposed approach aligns with TOPSIS principles. In the context of the TOPSIS concept, the alternative rankings of the proposed approach are deemed acceptable.
Subsequently, the outcomes of the proposed approach are compared to those of techniques employing divergence measure concepts. Here, we examine the CPU time, which represents the duration a CPU is utilized for the operational assessment process, as displayed in
Table 14 and
Table 15. Given that the proposed approach requires the least CPU time when compared to the other two techniques, it is reasonable to conclude that it is the superior approach.
6.2. Sensitivity Analysis
The present study used sensitivity analysis to examine the impact of varying criteria weights on ranks, with a particular focus on the influence of specific criterion weight modification. Since the weights assigned to criteria have a substantial impact on the outcomes of rankings, it is necessary to assess the changes made to the values of these weights. Initially, the weight of every single criterion is modified by increasing or lowering it by 5%, 10%, 20%, 50%, and 100%. To ensure that the criteria weights are set to a value of 1, it is necessary to proportionally decrease the weights of the other criteria when a specific criterion weight is increased. In other words, when a criterion changes
, the weights of the other criteria should be adjusted accordingly using the provided formula [
58]:
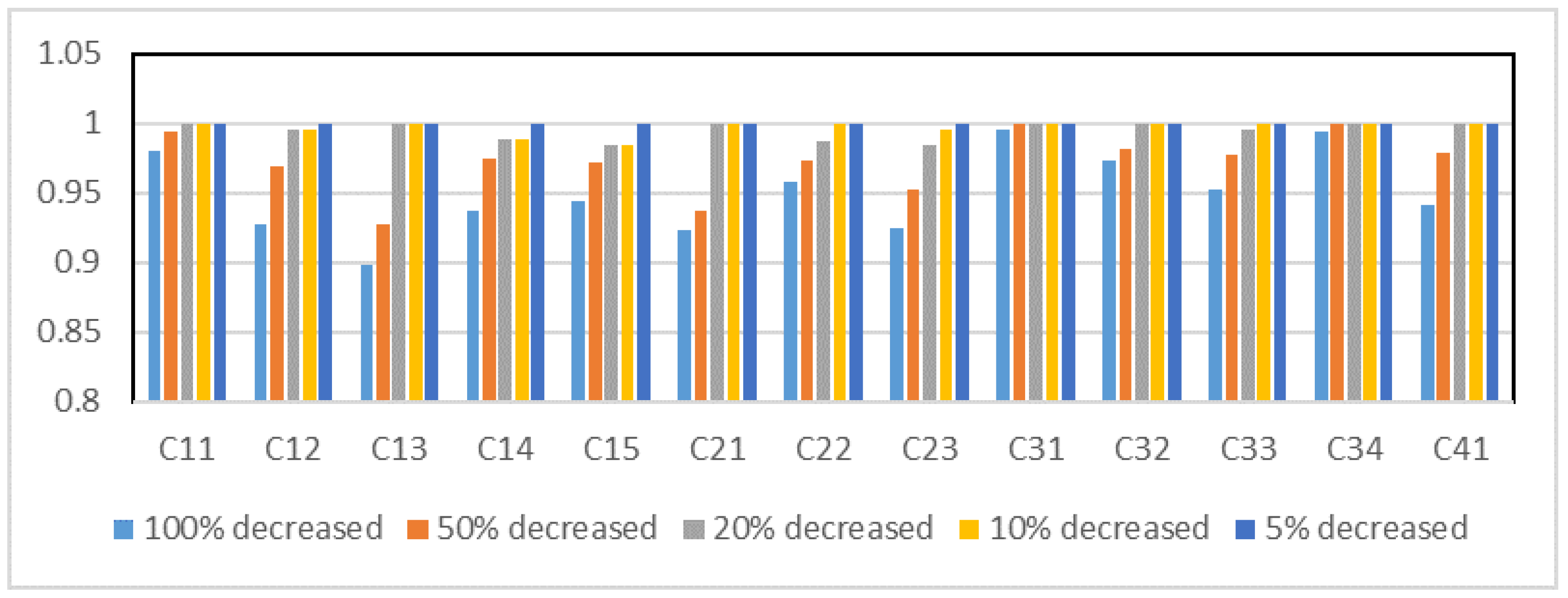
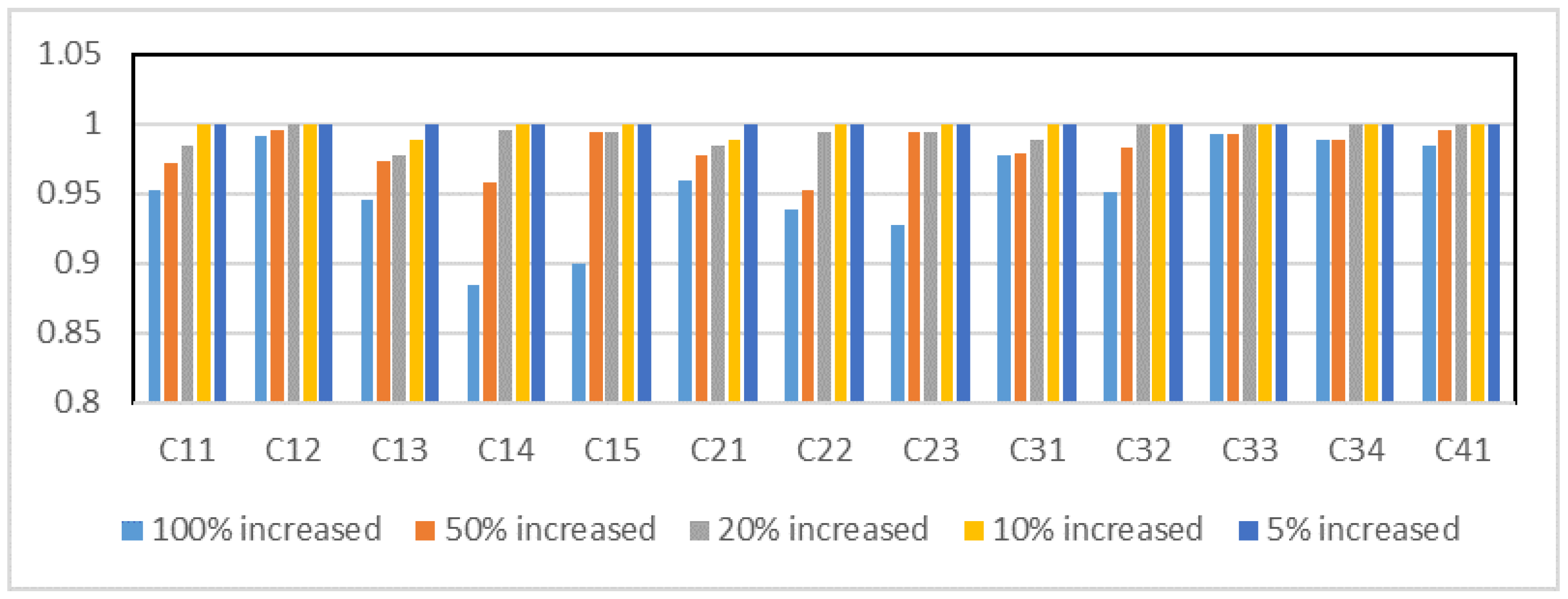
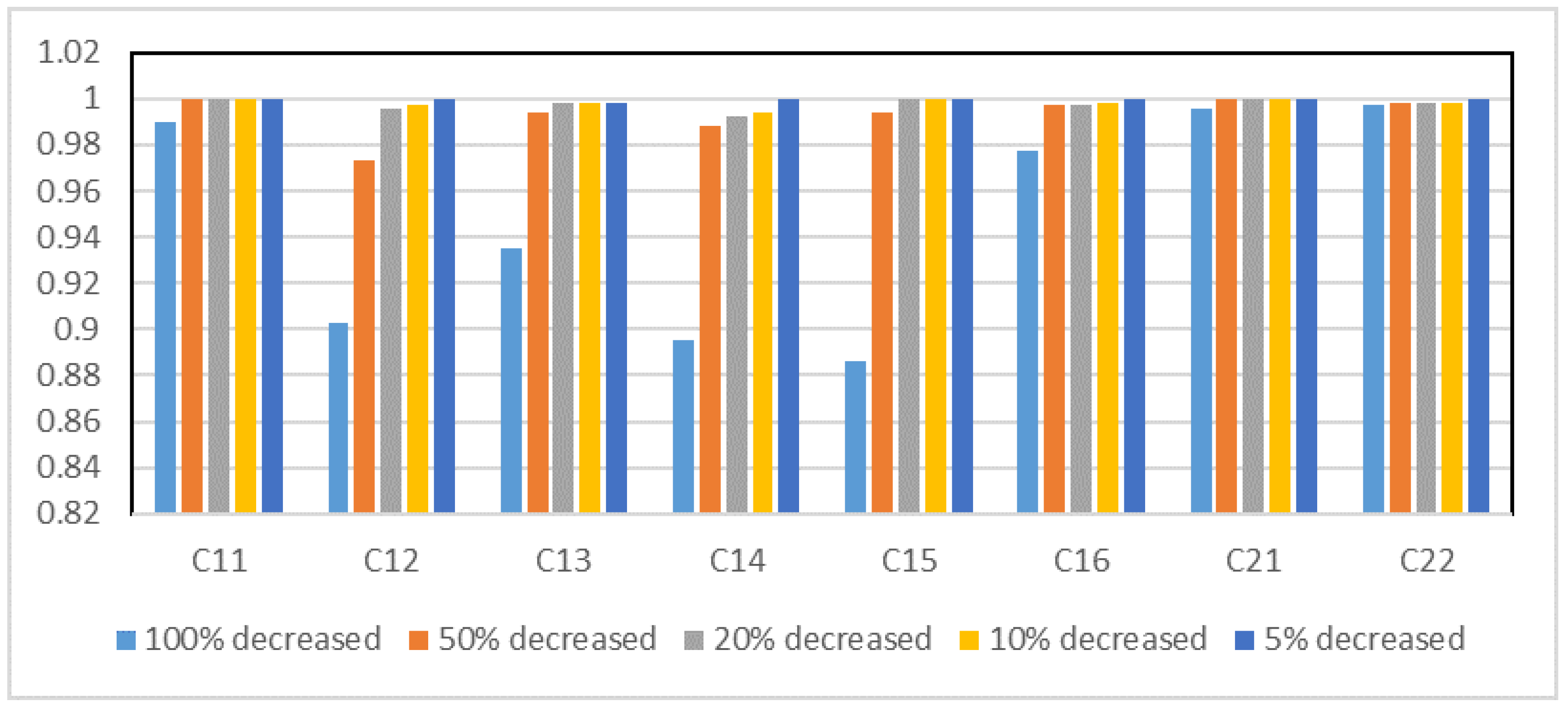
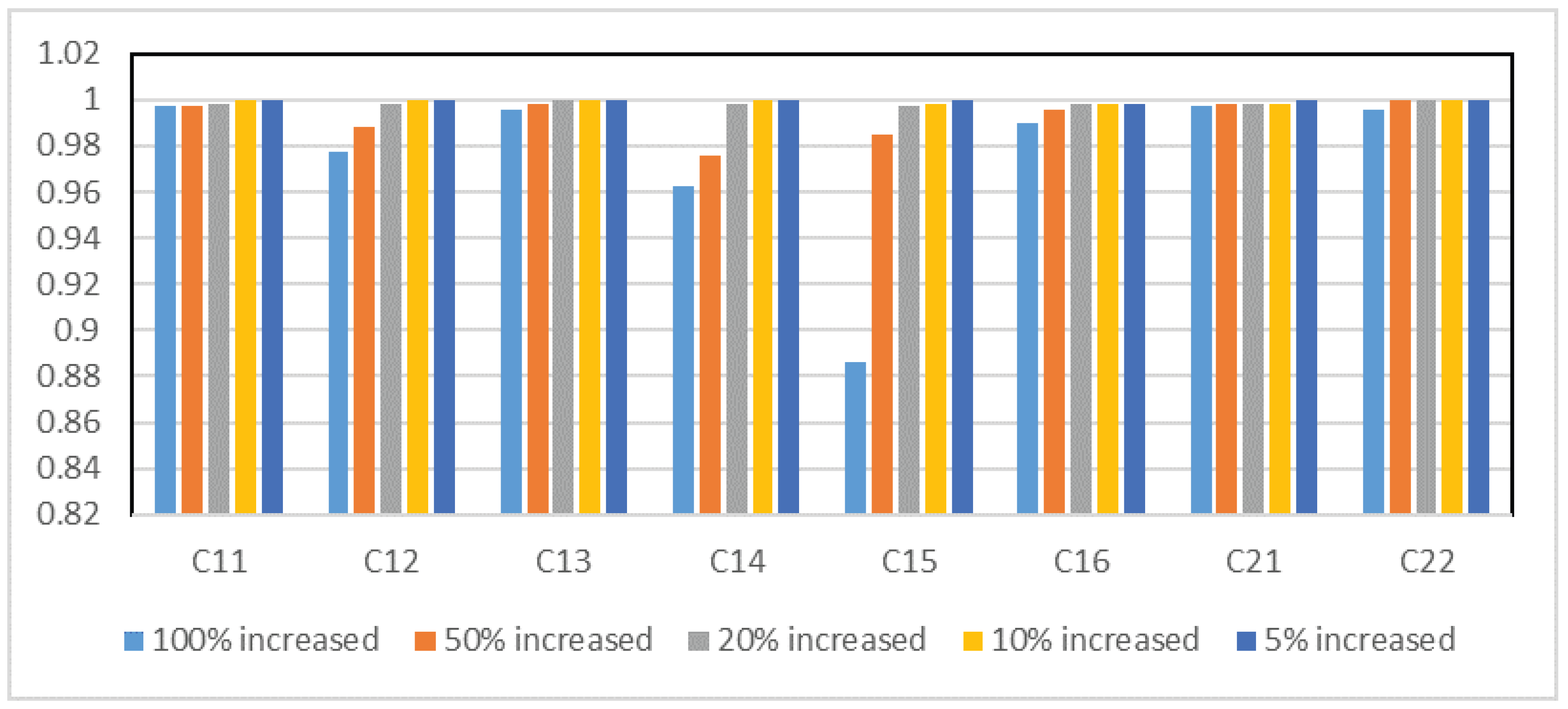
Figure 4,
Figure 5,
Figure 6 and
Figure 7 depict the correlation coefficient values between the initial ranking and the ranking obtained by decreasing and increasing the criteria weight for Case Studies 1 and 2, respectively. Based on the figures, the criterion that has the greatest impact on the ranking of alternatives for each case study is shown in
Table 16.
For Case Study 1, when the weight assigned to each criterion is reduced, it becomes clear that criterion exerts the most influence on the ranking of staff performance. While increasing the weight of each criterion, it turns out that criteria gives the most impact on the ranking of staff performance. Criterion and are defined as the quantity of work regarding efforts and initiatives to attain work perfection and time management, respectively. It reflects that the execution of work in terms of its quality represents an important responsibility that staff members must fulfill with exceptional proficiency. Implementing effective time management can help staff enhance productivity, decrease stress, and attain a healthier work–life balance.
For Case Study 2, changing the weight assigned to each criterion reveals that criteria and exert the greatest influence on the ranking of staff performance when reducing and increasing criterion weight, respectively. Criterion refers to the supervision of students, while criterion is related to the knowledge and expertise of the staff. The declaration stresses the importance of supervising students as staff members, emphasizing that neglecting this responsibility might have a detrimental impact on the achievement score of a staff member. Similarly, the influence of knowledge and expertise on the achievement score of a staff member should be considered.
7. Conclusions
The evaluation of an employee’s performance and an understanding of their potential for future development constitute integral aspects of performance assessment, crucial for the growth of any organization or institution. To execute performance appraisal, diverse decision-making strategies have been developed. This study introduced the generalized divergence measure, a modified technique enhancing current distance measures. It synergizes with the TOPSIS approach to address MCDM challenges. Given that evaluations often rely on qualitative measurements, fuzzy linguistic variables are employed to calculate alternative scores. In this paper, an illustrative example is presented to showcase the effectiveness of the proposed method. Despite the modification in the perspective of performance calculation, the study’s outcomes align consistently with current distance measures. At this level, the suggested approach exhibits a heightened capacity to address MCDM issues in fuzzy sets, particularly when alternatives are evaluated using fuzzy values. The incorporation of various fuzzy intervals in this research could further broaden the scope of this technique.
The results of the proposed approach are compared with fuzzy TOPSIS by Kabak et al. [
57] and fuzzy divergence measures by Joshi and Kumar [
39] and Rani et al. [
40] using a numerical example. Correlation coefficient values of the results indicate that the alternative rankings of the suggested approach are more likely to align with the pattern of present distance measures. Consequently, the proposed approach operates consistently with other techniques. The CPU test is employed to determine the most efficient method among those under consideration. The test reveals that the proposed approach’s alternative ranking generation consumes the least CPU time compared to other divergence measures. In essence, the proposed approach is deemed credible, reliable, and the most efficient methodology among all those compared for determining alternative rankings. Finally, this study provided sensitivity analysis for examining the impacts of criterion weights on the performance ranking of the alternatives.
While the evaluation procedure in this research was limited to a single MCDM application, the extension of the proposed technique with interval-valued intuitionistic fuzzy-divergence measures to real-world problems, such as establishing transportation systems, selecting financial goods, choosing suppliers, and addressing transportation options, warrants consideration.