Event-Triggered Relearning Modeling Method for Stochastic System with Non-Stationary Variable Operating Conditions
Abstract
1. Introduction
- 1
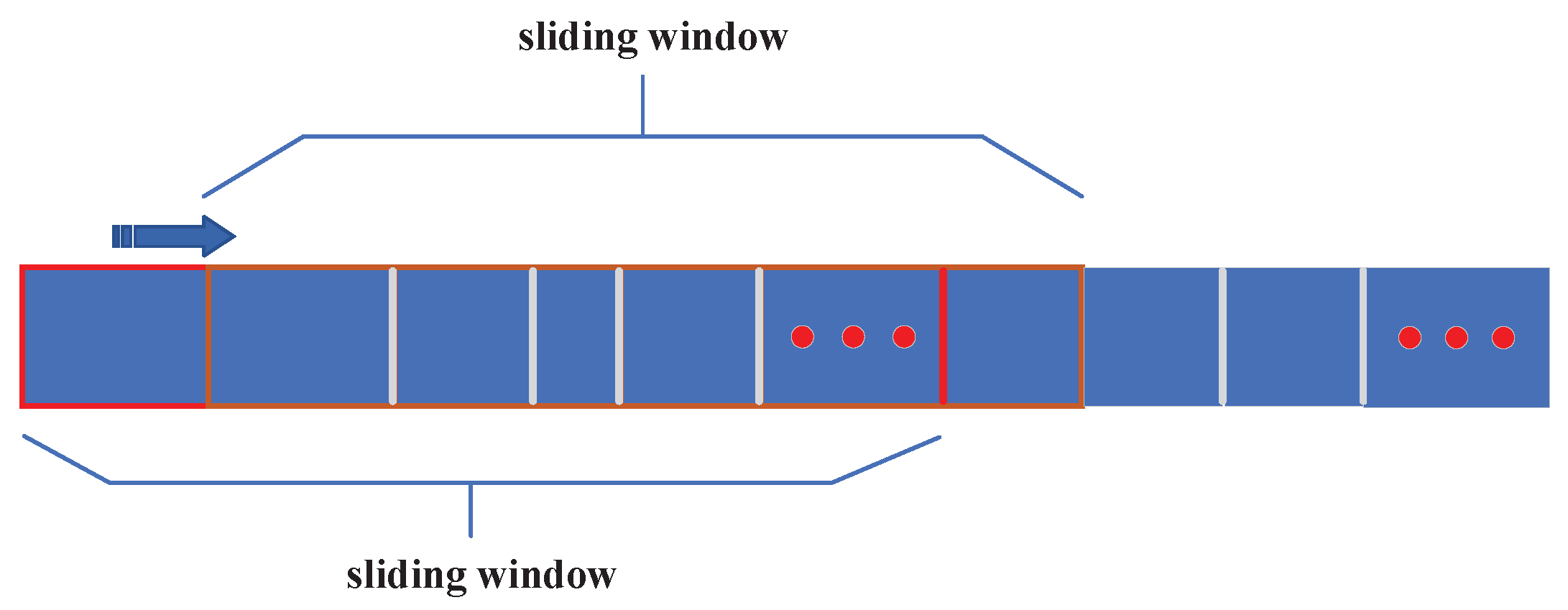
- By integrating the sliding window technique with entropy, our approach successfully detects and segments the boundary range of input data, thereby efficiently categorizing various working conditions.
- 2
- The prediction accuracy of the model decreases due to the change in working conditions. To address this, prediction errors are utilized to establish a group of event-triggered conditions, which guide the model’s retraining process across diverse working conditions.
- 3
- Distinct predictive models are developed corresponding to the segregated boundary ranges of input data. When the prediction data boundaries align with those of a pre-existing model’s input, the system seamlessly transitions to the appropriate model for prediction.
2. Problem Description
2.1. System Statement
2.2. Neural Networks Modeling Problem
- 1
- When the boundary range of the prediction data exceeds the boundary range of the training input data of the current model, how to detect the different boundaries of prediction data and redivide the input and output datasets.
- 2
- When the boundary range of the prediction data is detected, the data for the variable working conditions prediction accuracy of the established model will decrease, how to improve the prediction accuracy of the model.
- 3
- As time goes by, when the boundary range between the prediction data and training input data of established model will be consistent again, how to achieve the prediction of the data when the boundary range is the same.
3. Triggered Relearning Modeling Method
3.1. Modeling Strategy
- 1
- To address the issue of discrepancies of the boundary ranges between the prediction data and the training input data of the current model, a method that combines sliding window techniques with information entropy is employed. This approach is mainly applied to detect and define the boundaries of the prediction data, resulting in a reclassification of the input and output datasets accordingly.
- 2
- As we mentioned earlier, to address that issue of decline for the model’s prediction accuracy, a modeling strategy for event-triggered relearning is proposed. This strategy is implemented to construct an event-triggered condition group, setting reasonable thresholds. If the triggered conditions are met, the model will be retrained based on the datasets corresponding to the boundaries of the prediction input data.
- 3
- If the same boundary range of prediction data recurs, as the boundary range has already been identified, segmented, and an associated prediction model established, the process will simply involve switching directly to the relevant model based on the current data’s boundary range for subsequent predictions.
3.2. Dataset Boundary Detection Algorithm Based on Sliding Window and Information Entropy
3.3. Neural Networks for Triggered Relearning
| Algorithm 1: The triggered relearning algorithm. |
 |
4. Numerical Simulation
4.1. Acquisition of Experimental Data
4.2. Triggered Relearning for Neural Network
4.2.1. Model Development
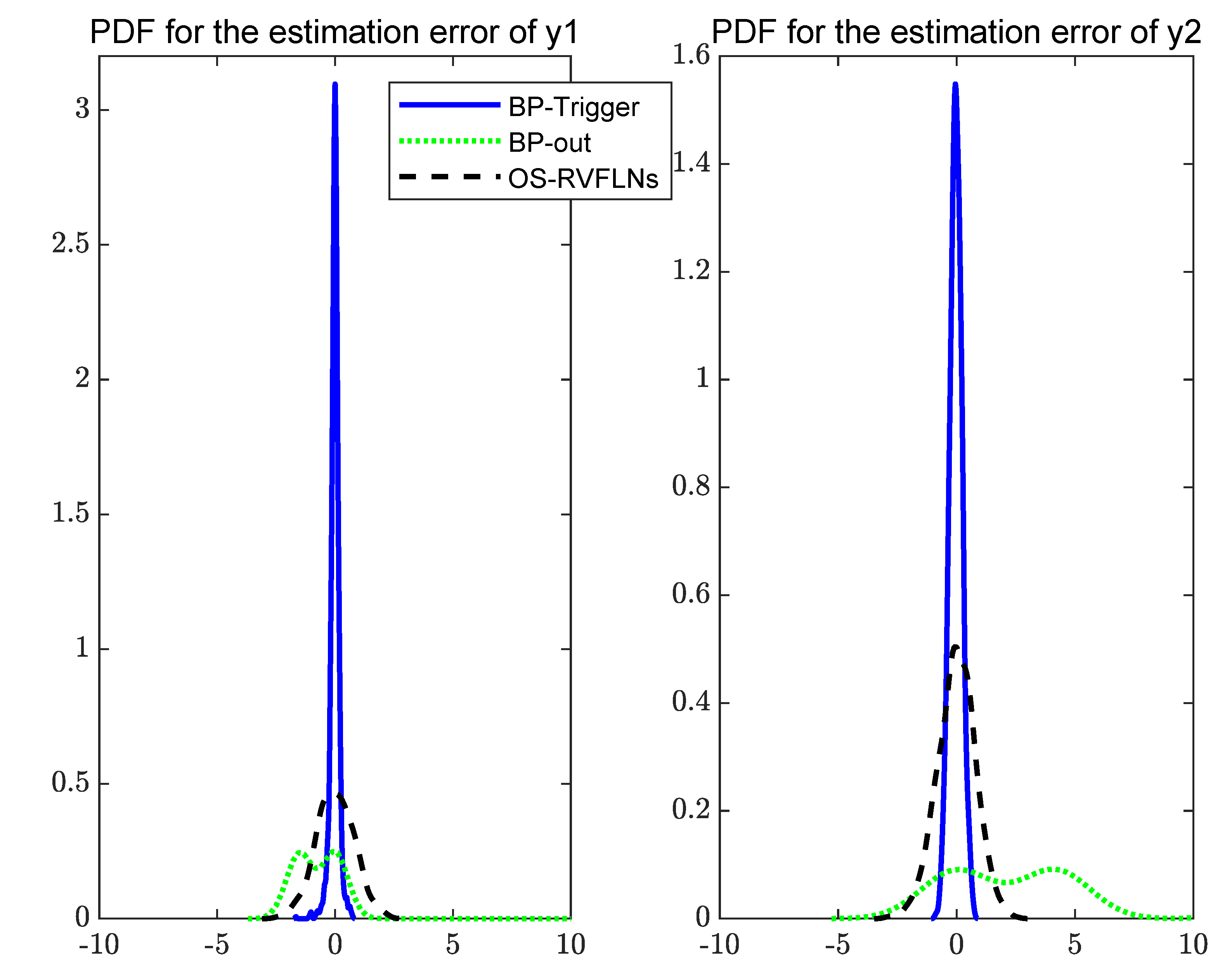
4.2.2. The Effect of Model Estimation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, Y.; Herzallah, R. Probabilistic message passing control for complex stochastic switching systems. J. Frankl. Inst. 2021, 358, 5451–5469. [Google Scholar] [CrossRef]
- Sykora, H.; Sadeghpour, M.; Ge, J. On the moment dynamics of stochastically delayed linear control systems. Int. J. Robust Nonlinear Control 2020, 30, 8074–8097. [Google Scholar] [CrossRef]
- Herzallah, R. A fully probabilistic design for stochastic systems with input delay. Int. J. Control 2021, 94, 2934–2944. [Google Scholar] [CrossRef]
- Gu, Z.; Lv, D.; Li, X.; Zhang, Y.; Dai, X. Fusion prediction of blast furnace temperature based on the combination of knowledge and data. China Meas. Test 2022, 48, 1–9. [Google Scholar]
- Zhuang, T.; Yang, C. Silicon content forecasting method for hot metal based on Elman-Adaboost strong predictor. Metall. Ind. Autom. 2017, 41, 1–6+17. [Google Scholar]
- Cui, G.; Chen, R.; Yu, K. The Study on Temperature Prediction of ELM Furnace Based on Multiscale Decomposition. Control Eng. 2020, 27, 1901–1906. [Google Scholar]
- Jiang, Z.; Dong, M.; Gui, W.; Yang, C. Two-dimensional Prediction for Silicon Content of Hot Metal of Blast Furnace Based on Bootstrap. Acta Autom. Sin. 2016, 42, 715–723. [Google Scholar]
- Zhou, P.; Zhang, L.; Li, W. Autoencoder and PCA Based RVFLNs Modeling for Multivariate Molten Iron Quality in Blast Furnace Ironmaking. Acta Autom. Sin. 2018, 44, 1799–1811. [Google Scholar]
- Su, X.; Zhang, S.; Yin, Y.; Hui, Y.; Xiao, W. Prediction of hot metal silicon content for blast furnace based on multi-layer online sequential extreme learning machine. In Proceedings of the 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 8025–8030. [Google Scholar]
- Zhou, P.; Yuan, M.; Wang, H.; Wang, Z.; Chai, T. Multivariable dynamic modeling for molten iron quality using online sequential random vector functional-link networks with self- feedback connections. Inf. Sci. 2015, 325, 237–255. [Google Scholar] [CrossRef]
- Jiang, Z.; Xu, C.; Gui, W.; Jiang, K. Prediction Method of Hot Metal Silicon Content in Blast Furnace Based on Optimal Smelting Condition Migration. Acta Autom. Sin. 2022, 48, 194–206. [Google Scholar]
- He, X.; Ji, J.; Liu, K.; Gao, Z.; Liu, Y. Soft sensing of silicon content via bagging local semi-supervised models. Sensors 2019, 19, 3814. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Chen, T.; Hao, F. A new event-triggered control scheme for stochastic systems. IEEE Trans. Autom. Control 2022, 68, 1463–1478. [Google Scholar] [CrossRef]
- Zhao, F.; Gao, W.; Jiang, Z.; Liu, T. Event-triggered adaptive optimal control with output feedback: An adaptive dynamic programming approach. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 5208–5221. [Google Scholar] [CrossRef] [PubMed]
- Shanmugam, S.; Vadivel, R.; Gunasekaran, N. Finite-Time Synchronization of Quantized Markovian-Jump Time-Varying Delayed Neural Networks via an Event-Triggered Control Scheme under Actuator Saturation. Mathematics 2023, 11, 2257. [Google Scholar] [CrossRef]
- Li, G.; Zeng, J.; Liu, J. Effluent Quality-Aware Event-Triggered Model Predictive Control for Wastewater Treatment Plants. Mathematics 2023, 11, 3912. [Google Scholar] [CrossRef]
- Liu, Y.; Zhu, Q. Event-triggered adaptive neural network control for stochastic nonlinear systems with state constraints and time-varying delays. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 1932–1944. [Google Scholar] [CrossRef]
- Yu, H.; Chen, T. Event-triggered neural-network adaptive control for strict-feedback nonlinear systems: Selections on valid compact sets. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 4750–4762. [Google Scholar] [CrossRef]
- Xing, L.; Wen, C. Dynamic event-triggered adaptive control for a class of uncertain nonlinear systems. Automatica 2017, 62, 2071–2076. [Google Scholar] [CrossRef]
- Herzallah, R.; Zhou, Y. A fully probabilistic control framework for stochastic systems with input and state delay. Sci. Rep. 2022, 12, 7812. [Google Scholar] [CrossRef]
- Wei, H. Stochastic Finite-Time Stability for Stochastic Nonlinear Systems with Stochastic Impulses. Control Theory Appl. 2022, 14, 817. [Google Scholar]
- Ma, K.; Kumar, P. Incentive Compatibility in Stochastic Dynamic Systems. IEEE Trans. Autom. Control 2020, 66, 651–666. [Google Scholar] [CrossRef]
- Wu, Y.; Feng, J. Development and application of artificial neural network. Wirel. Pers. Commun. 2018, 102, 1645–1656. [Google Scholar] [CrossRef]
- Abraham, T. (Physio) logical circuits: The intellectual origins of the McCulloch–Pitts neural networks. J. Hist. Behav. Sci. 2002, 38, 3–25. [Google Scholar] [CrossRef]
- Yin, L.; Li, L.; Jiang, Z. Prediction of silicon content in hot metal using neural network and rough set theory. J. Iron Steel Res. 2019, 31, 689–695. [Google Scholar]
- Liang, W.; Wang, G.; Ning, X.; Zhang, J.; Li, Y.; Jiang, C.; Zhang, N. Application of BP neural network to the prediction of coal ash melting characteristic temperature. Fuel 2020, 260, 116324. [Google Scholar] [CrossRef]
- Zhuo, Y.; Zhou, X.; Wang, Q.; Zou, Z.; Wang, S.; Liu, Y. Research on a Sliding Window Bats Code Method. In Proceedings of the 2020 17th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP), Chengdu, China, 18–20 December 2020; pp. 404–409. [Google Scholar]
- Xie, Y.; Yang, T.; Jia, D.; Zhang, C.; Li, Y. Minor fault detection based on PCA and moving window cumulative sum. Comput. Appl. Softw. 2023, 40, 60–66+96. [Google Scholar]
- Sabirov, D. Information entropy of mixing molecules and its application to molecular ensembles and chemical reactions. Comput. Theor. Chem. 2020, 1187, 112933. [Google Scholar] [CrossRef]
- Abdelmonem, M. Information entropies for the Morse potential using the J-matrix method. Results Phys. 2017, 7, 1178–1180. [Google Scholar] [CrossRef]
- Wang, Z. Research and Modeling Application of VSG Method Based on Monte Carlo and Kernel Density Estimation; Beijing University of Chemical Technology: Beijing, China, 2021. [Google Scholar]
- Pan, J.; Zou, Z.; Sun, S.; Su, Y.; Zhu, H. Research on output distribution modeling of photovoltaic modules based on kernel density estimation method and its application in anomaly identification. Sol. Energy 2022, 235, 1–11. [Google Scholar] [CrossRef]
- Houda, S.; Samira, K. A recursive parametric estimation algorithm of multivariable nonlinear systems described by Hammerstein mathematical models. Appl. Math. Model. 2015, 39, 4951–4962. [Google Scholar]
- Liu, Q. Recursive Identification for Hammerstein-Wiener Nonlinear Systems with Non-Uniform Sampling; Jiangnan University: Wuxi, China, 2022. [Google Scholar]
- Zheng, T.; Li, F.; Luo, Y.; Liu, R.; Gu, Y. Review of neural network-based methods for solving partial differential equations. Control Eng. China 2022, 29, 2034–2041. [Google Scholar]









| Model | FLOPs | MSE | MAE | ||
|---|---|---|---|---|---|
| Y1 | Y2 | Y1 | Y2 | ||
| BP | 148,180 | 81.23 | 74.93 | 5.71 | 6.26 |
| OS-RVFLNs | 3,413,100 | 0.18 | 0.12 | 0.26 | 0.27 |
| BP-trigger | 1,326,180 | 0.09 | 0.05 | 0.19 | 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhang, Y.; Zhou, Y.; Chen, J. Event-Triggered Relearning Modeling Method for Stochastic System with Non-Stationary Variable Operating Conditions. Mathematics 2024, 12, 667. https://doi.org/10.3390/math12050667
Liu J, Zhang Y, Zhou Y, Chen J. Event-Triggered Relearning Modeling Method for Stochastic System with Non-Stationary Variable Operating Conditions. Mathematics. 2024; 12(5):667. https://doi.org/10.3390/math12050667
Chicago/Turabian StyleLiu, Jiyan, Yong Zhang, Yuyang Zhou, and Jing Chen. 2024. "Event-Triggered Relearning Modeling Method for Stochastic System with Non-Stationary Variable Operating Conditions" Mathematics 12, no. 5: 667. https://doi.org/10.3390/math12050667
APA StyleLiu, J., Zhang, Y., Zhou, Y., & Chen, J. (2024). Event-Triggered Relearning Modeling Method for Stochastic System with Non-Stationary Variable Operating Conditions. Mathematics, 12(5), 667. https://doi.org/10.3390/math12050667






