Model Selection Path and Construction of Model Confidence Set under High-Dimensional Variables
Abstract
1. Introduction
2. Methods
2.1. AMac: Constructing MCS
| Algorithm 1 Constructing MCS using AMac |
|
2.2. MSP- {* }: Constructing MCS under High-Dimensional Variables in Linear Regression Model
| Algorithm 2 Alasso–lars (AL): the construction algorithm for MSP |
|
3. Theoretical Properties
3.1. Coverage Rate of MCS Constructed by AMac
3.2. The Effectiveness of Constructing MSP Using the Alasso–Lars Algorithm
4. Weight Selection
5. Simulation
5.1. Simulated Performance of AMac and Mac
5.2. Simulated Performances of AMac, Mac, AL-AMac, and AL-Mac
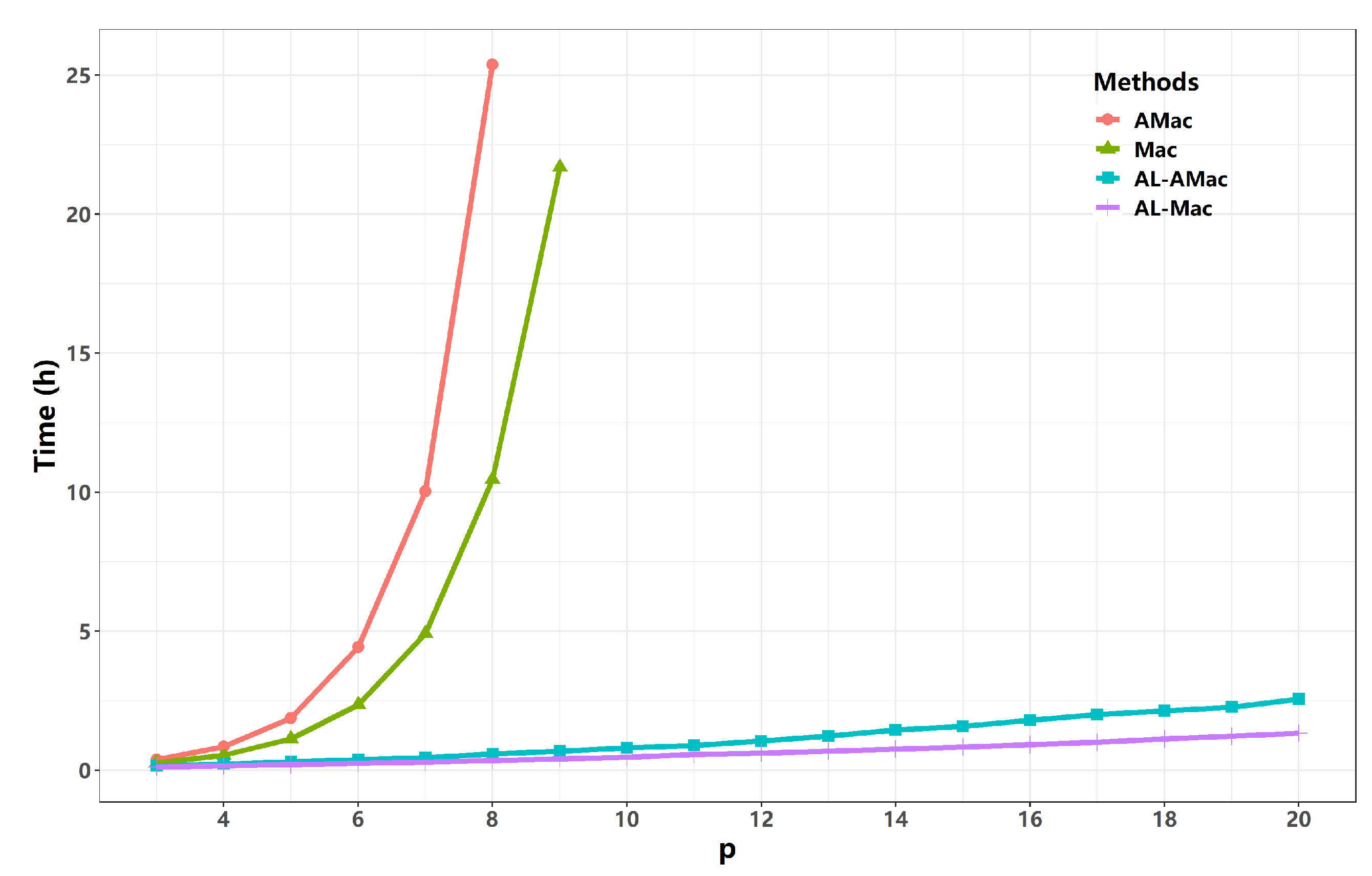
5.3. Numerical Performance of AL in High-Dimensional Scenarios
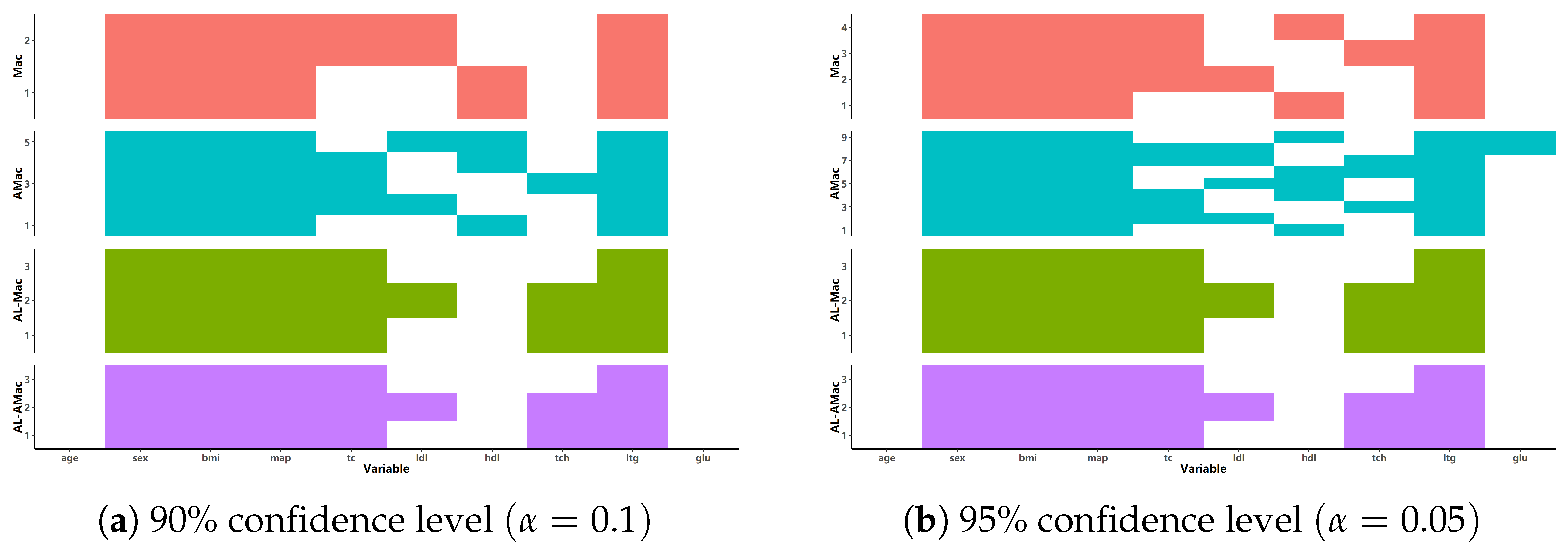
6. Real-Data Example
7. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MCS | model confidence set |
| MP | model path |
| Mac | make a cut |
| AMac | average make a cut |
| VSCS | variable select confidence sets |
| ECP | empirical coverage probability |
| AM | average model count |
| CV | coefficient of variation of the model count |
Appendix A
Appendix A.1
Appendix A.2
References
- Preacher, K.; Merkle, E. The problem of model selection uncertainty in structural equation modeling. Psychol. Methods 2012, 17, 1. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Tarokh, V.; Yang, Y. Model selection techniques: An overview. IEEE Signal Process. Mag. 2018, 35, 6–34. [Google Scholar] [CrossRef]
- Draper, D. Assessment and propagation of model uncertainty. J. R. Stat. Soc. Ser. B Stat. Methodol. 1995, 57, 45–70. [Google Scholar] [CrossRef]
- Chatfield, C. Model uncertainty, data mining and statistical inference. J. R. Stat. Soc. Ser. A Stat. Soc. 1995, 158, 419–444. [Google Scholar] [CrossRef]
- Lubke, G.; Campbell, I.; McArtor, D.; Miller, P.; Luningham, J.; van den Berg, S. Assessing model selection uncertainty using a bootstrap approach: An update. Struct. Equ. Model. Multidiscip. J. 2017, 158, 230–245. [Google Scholar] [CrossRef] [PubMed]
- Claeskens, G.; Hjort, N. Model Selection and Model Averaging; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Yang, Y. Adaptive regression by mixing. J. Am. Stat. Assoc. 2001, 96, 574–588. [Google Scholar] [CrossRef]
- Yang, Y. Regression with multiple candidate models: Selecting or mixing? Stat. Sin. 2003, 13, 783–809. [Google Scholar]
- Hoeting, J.; Madigan, D.; Raftery, A.; Volinsky, C. Bayesian model averaging: A tutorial (with comments by M. Clyde, David Draper and EI George, and a rejoinder by the authors). Stat. Sci. 1999, 14, 382–417. [Google Scholar] [CrossRef]
- Chipman, H.; George, E.; McCulloch, R.; Clyde, M.; Foster, D.; Stine, R. The practical implementation of Bayesian model selection. Lect. Notes Monogr. Ser. 2001, 38, 65–134. [Google Scholar]
- Chen, L.; Giannakouros, P.; Yang, Y. Model combining in factorial data analysis. J. Stat. Plan. Inference 2007, 137, 2920–2934. [Google Scholar] [CrossRef][Green Version]
- Hansen, P.; Lunde, A.; Nason, J. The model confidence set. Econometrica 2011, 79, 453–497. [Google Scholar] [CrossRef]
- Lubke, G.; Campbell, I. Inference based on the best-fitting model can contribute to the replication crisis: Assessing model selection uncertainty using a bootstrap approach. Struct. Equ. Model. Multidiscip. J. 2016, 23, 479–490. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, D.; Yang, Y. Confidence sets for model selection by F-testing. Stat. Sin. 2015, 1637–1658. [Google Scholar] [CrossRef]
- Zheng, C.; Ferrari, D.; Yang, Y. Model selection confidence sets by likelihood ratio testing. Stat. Sin. 2019, 29, 827–851. [Google Scholar] [CrossRef]
- Zheng, C.; Ferrari, D.; Zhang, M.; Baird, P. Ranking the importance of genetic factors by variable-selection confidence sets. J. R. Stat. Soc. Ser. C Appl. Stat. 2019, 68, 727–749. [Google Scholar] [CrossRef]
- Liu, X.; Li, Y.; Jiang, J. Simple measures of uncertainty for model selection. Test 2021, 30, 673–692. [Google Scholar] [CrossRef]
- Donoho, D. High-dimensional data analysis: The curses and blessings of dimensionality. AMS Math Chall. Lect. 2000, 1, 32. [Google Scholar]
- Li, Y.; Luo, Y.; Ferrari, D.; Hu, X.; Qin, Y. Model confidence bounds for variable selection. Biometrics 2019, 75, 392–403. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, J. Measures of Uncertainty for Shrinkage Model Selection. Stat. Sin. 2023. preprint. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least Angle Regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar] [CrossRef]
- Zou, H. The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 2006, 101, 1418–1429. [Google Scholar] [CrossRef]
- Yuan, Z.; Yang, Y. Combining linear regression models: When and how? J. Am. Stat. Assoc. 2005, 100, 1202–1214. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap methods: Another look at the jackknife. Ann. Statist. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. Ser. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Yuan, M.; Lin, Y. Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. B Stat. Methodol. 2006, 68, 49–67. [Google Scholar] [CrossRef]
- Rosset, S.; Zhu, J. Piecewise linear regularized solution paths. Ann. Stat. 2007, 1012–1030. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 461–464. [Google Scholar] [CrossRef]
- Breiman, L. Heuristics of instability and stabilization in model selection. Ann. Stat. 1996, 24, 2350–2383. [Google Scholar] [CrossRef]
- Jiang, J. Large Sample Techniques for Statistics; Springer: New York, NY, USA, 2010. [Google Scholar]
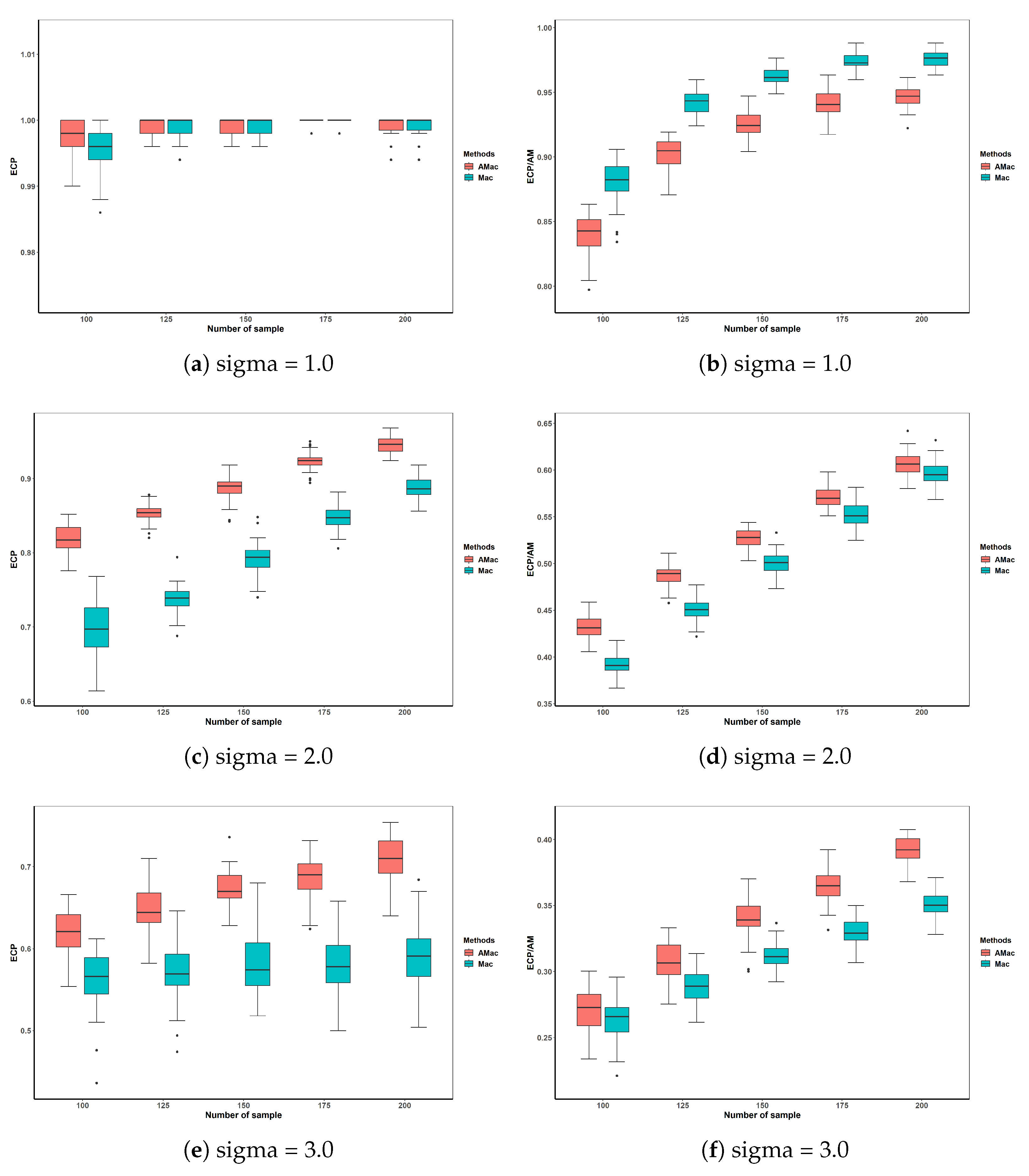
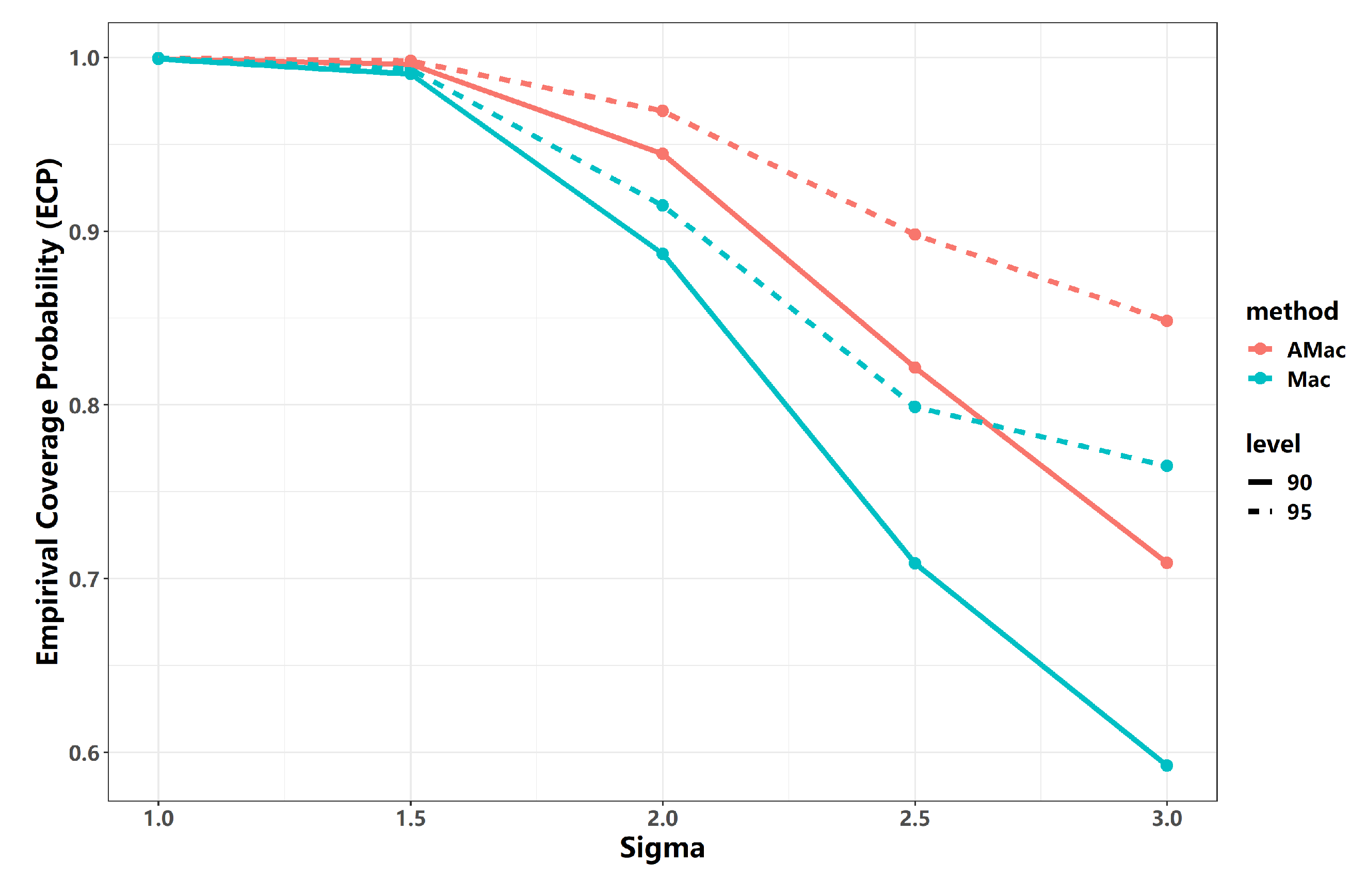

| Level (%) | n | Method | = 1.0 | = 2.0 | = 3.0 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ECP | AM | ECP/AM | ECP | AM | ECP/AM | ECP | AM | ECP/AM | ||||||
| 90 | 100 | AMac | 0.997 | 1.188 | 0.840 | 0.333 | 0.818 | 1.895 | 0.432 | 0.329 | 0.619 | 2.290 | 0.271 | 0.353 |
| Mac | 0.996 | 1.131 | 0.880 | 0.308 | 0.699 | 1.782 | 0.392 | 0.411 | 0.561 | 2.132 | 0.263 | 0.420 | ||
| 125 | AMac | 0.999 | 1.108 | 0.902 | 0.280 | 0.853 | 1.752 | 0.487 | 0.313 | 0.649 | 2.116 | 0.307 | 0.374 | |
| Mac | 0.999 | 1.059 | 0.943 | 0.224 | 0.738 | 1.640 | 0.450 | 0.388 | 0.571 | 1.976 | 0.289 | 0.450 | ||
| 150 | AMac | 0.999 | 1.080 | 0.925 | 0.251 | 0.887 | 1.682 | 0.527 | 0.316 | 0.674 | 1.986 | 0.340 | 0.374 | |
| Mac | 0.999 | 1.038 | 0.963 | 0.184 | 0.793 | 1.584 | 0.500 | 0.373 | 0.582 | 1.863 | 0.312 | 0.449 | ||
| 175 | AMac | 1.000 | 1.062 | 0.941 | 0.226 | 0.924 | 1.619 | 0.571 | 0.325 | 0.688 | 1.887 | 0.365 | 0.368 | |
| Mac | 1.000 | 1.027 | 0.974 | 0.156 | 0.847 | 1.534 | 0.552 | 0.367 | 0.581 | 1.762 | 0.330 | 0.443 | ||
| 200 | AMac | 0.999 | 1.056 | 0.947 | 0.217 | 0.944 | 1.557 | 0.607 | 0.339 | 0.709 | 1.809 | 0.392 | 0.356 | |
| Mac | 0.999 | 1.024 | 0.976 | 0.148 | 0.887 | 1.487 | 0.597 | 0.365 | 0.592 | 1.688 | 0.351 | 0.430 | ||
| 95 | 100 | AMac | 1.000 | 1.419 | 0.705 | 0.373 | 0.939 | 2.485 | 0.378 | 0.287 | 0.785 | 3.003 | 0.262 | 0.305 |
| Mac | 0.999 | 1.341 | 0.746 | 0.379 | 0.920 | 2.343 | 0.393 | 0.297 | 0.745 | 2.749 | 0.271 | 0.348 | ||
| 125 | AMac | 1.000 | 1.230 | 0.813 | 0.351 | 0.949 | 2.261 | 0.420 | 0.286 | 0.818 | 2.832 | 0.290 | 0.318 | |
| Mac | 1.000 | 1.149 | 0.870 | 0.319 | 0.914 | 2.150 | 0.426 | 0.302 | 0.782 | 2.623 | 0.299 | 0.354 | ||
| 150 | AMac | 1.000 | 1.144 | 0.874 | 0.310 | 0.956 | 2.121 | 0.451 | 0.307 | 0.841 | 2.608 | 0.323 | 0.331 | |
| Mac | 1.000 | 1.070 | 0.935 | 0.241 | 0.904 | 2.017 | 0.448 | 0.335 | 0.795 | 2.433 | 0.327 | 0.364 | ||
| 175 | AMac | 1.000 | 1.106 | 0.905 | 0.278 | 0.959 | 1.979 | 0.485 | 0.321 | 0.841 | 2.472 | 0.341 | 0.341 | |
| Mac | 1.000 | 1.036 | 0.965 | 0.179 | 0.902 | 1.889 | 0.478 | 0.352 | 0.776 | 2.302 | 0.338 | 0.380 | ||
| 200 | AMac | 1.000 | 1.084 | 0.923 | 0.255 | 0.969 | 1.871 | 0.518 | 0.337 | 0.848 | 2.337 | 0.363 | 0.345 | |
| Mac | 1.000 | 1.024 | 0.976 | 0.149 | 0.915 | 1.791 | 0.511 | 0.367 | 0.765 | 2.171 | 0.353 | 0.392 | ||
| n | Method | = 1.0 | = 2.0 | = 3.0 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ECP | AM | ECP/AM | ECP | AM | ECP/AM | ECP | AM | ECP/AM | ||||||||
| 100 | AMac | 0.984 | 2.368 | 0.416 | 0.305 | NA | 0.898 | 3.454 | 0.260 | 0.398 | NA | 0.646 | 4.228 | 0.153 | 0.406 | NA |
| Mac | 0.982 | 2.222 | 0.442 | 0.318 | NA | 0.868 | 3.148 | 0.276 | 0.486 | NA | 0.578 | 3.600 | 0.161 | 0.546 | NA | |
| AL-AMac | 0.978 | 1.412 | 0.693 | 0.369 | 1.000 | 0.756 | 1.852 | 0.408 | 0.295 | 0.856 | 0.344 | 1.614 | 0.213 | 0.366 | 0.500 | |
| AL-Mac | 0.976 | 1.224 | 0.797 | 0.356 | 1.000 | 0.644 | 1.650 | 0.390 | 0.372 | 0.856 | 0.206 | 1.330 | 0.155 | 0.396 | 0.500 | |
| 125 | AMac | 0.980 | 2.162 | 0.453 | 0.282 | NA | 0.912 | 2.892 | 0.315 | 0.359 | NA | 0.726 | 3.642 | 0.199 | 0.457 | NA |
| Mac | 0.976 | 2.088 | 0.467 | 0.311 | NA | 0.892 | 2.676 | 0.333 | 0.412 | NA | 0.678 | 3.298 | 0.206 | 0.594 | NA | |
| AL-AMac | 0.974 | 1.338 | 0.728 | 0.378 | 1.000 | 0.836 | 1.818 | 0.460 | 0.288 | 0.886 | 0.488 | 1.730 | 0.282 | 0.336 | 0.630 | |
| AL-Mac | 0.968 | 1.162 | 0.833 | 0.331 | 1.000 | 0.716 | 1.620 | 0.442 | 0.358 | 0.886 | 0.298 | 1.430 | 0.208 | 0.418 | 0.630 | |
| 150 | AMac | 0.984 | 1.876 | 0.525 | 0.361 | NA | 0.908 | 2.634 | 0.345 | 0.338 | NA | 0.756 | 3.298 | 0.229 | 0.424 | NA |
| Mac | 0.984 | 1.762 | 0.558 | 0.396 | NA | 0.900 | 2.516 | 0.358 | 0.374 | NA | 0.720 | 3.078 | 0.234 | 0.489 | NA | |
| AL-AMac | 0.980 | 1.282 | 0.764 | 0.358 | 1.000 | 0.838 | 1.710 | 0.490 | 0.300 | 0.898 | 0.564 | 1.728 | 0.326 | 0.316 | 0.686 | |
| AL-Mac | 0.978 | 1.112 | 0.879 | 0.290 | 1.000 | 0.760 | 1.578 | 0.482 | 0.345 | 0.898 | 0.430 | 1.502 | 0.286 | 0.376 | 0.686 | |
| 175 | AMac | 0.990 | 1.658 | 0.597 | 0.434 | NA | 0.952 | 2.542 | 0.375 | 0.386 | NA | 0.784 | 3.062 | 0.256 | 0.448 | NA |
| Mac | 0.990 | 1.522 | 0.650 | 0.464 | NA | 0.940 | 2.452 | 0.383 | 0.455 | NA | 0.750 | 2.848 | 0.263 | 0.520 | NA | |
| AL-AMac | 0.984 | 1.230 | 0.800 | 0.354 | 1.000 | 0.896 | 1.744 | 0.514 | 0.316 | 0.950 | 0.578 | 1.730 | 0.334 | 0.346 | 0.712 | |
| AL-Mac | 0.982 | 1.092 | 0.899 | 0.277 | 1.000 | 0.848 | 1.612 | 0.526 | 0.356 | 0.950 | 0.454 | 1.512 | 0.300 | 0.396 | 0.712 | |
| 200 | AMac | 0.984 | 1.438 | 0.684 | 0.457 | NA | 0.964 | 2.374 | 0.406 | 0.417 | NA | 0.790 | 2.798 | 0.282 | 0.435 | NA |
| Mac | 0.986 | 1.310 | 0.753 | 0.503 | NA | 0.932 | 2.280 | 0.409 | 0.484 | NA | 0.750 | 2.612 | 0.287 | 0.512 | NA | |
| AL-AMac | 0.978 | 1.202 | 0.814 | 0.338 | 1.000 | 0.904 | 1.678 | 0.539 | 0.332 | 0.962 | 0.620 | 1.694 | 0.366 | 0.332 | 0.768 | |
| AL-Mac | 0.978 | 1.094 | 0.894 | 0.279 | 1.000 | 0.856 | 1.574 | 0.544 | 0.362 | 0.962 | 0.492 | 1.502 | 0.328 | 0.383 | 0.768 | |
| Varia_num | n | Method | = 2.0 | ||||
|---|---|---|---|---|---|---|---|
| ECP | AM | ECP/AM | |||||
| (11, 3) | 100 | AL-AMac | 0.616 | 2.010 | 0.306 | 0.303 | 0.670 |
| AL-Mac | 0.556 | 1.734 | 0.321 | 0.393 | 0.670 | ||
| 200 | AL-AMac | 0.888 | 1.788 | 0.497 | 0.322 | 0.936 | |
| AL-Mac | 0.862 | 1.630 | 0.529 | 0.375 | 0.936 | ||
| 400 | AL-AMac | 0.980 | 1.300 | 0.754 | 0.363 | 0.996 | |
| AL-Mac | 0.980 | 1.194 | 0.821 | 0.344 | 0.996 | ||
| (21, 5) | 100 | AL-AMac | 0.496 | 2.432 | 0.204 | 0.291 | 0.584 |
| AL-Mac | 0.448 | 2.160 | 0.207 | 0.408 | 0.584 | ||
| 200 | AL-AMac | 0.776 | 2.038 | 0.381 | 0.317 | 0.860 | |
| AL-Mac | 0.742 | 1.820 | 0.408 | 0.401 | 0.860 | ||
| 400 | AL-AMac | 0.920 | 1.554 | 0.592 | 0.392 | 0.994 | |
| AL-Mac | 0.904 | 1.350 | 0.670 | 0.414 | 0.994 | ||
| (41, 9) | 100 | AL-AMac | 0.252 | 2.872 | 0.088 | 0.299 | 0.402 |
| AL-Mac | 0.224 | 2.608 | 0.086 | 0.422 | 0.402 | ||
| 200 | AL-AMac | 0.600 | 2.422 | 0.248 | 0.308 | 0.810 | |
| AL-Mac | 0.564 | 2.100 | 0.269 | 0.438 | 0.810 | ||
| 400 | AL-AMac | 0.826 | 1.908 | 0.433 | 0.360 | 0.984 | |
| AL-Mac | 0.802 | 1.600 | 0.501 | 0.458 | 0.984 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, F.; Jiang, J.; Luan, Y. Model Selection Path and Construction of Model Confidence Set under High-Dimensional Variables. Mathematics 2024, 12, 664. https://doi.org/10.3390/math12050664
Wen F, Jiang J, Luan Y. Model Selection Path and Construction of Model Confidence Set under High-Dimensional Variables. Mathematics. 2024; 12(5):664. https://doi.org/10.3390/math12050664
Chicago/Turabian StyleWen, Faguang, Jiming Jiang, and Yihui Luan. 2024. "Model Selection Path and Construction of Model Confidence Set under High-Dimensional Variables" Mathematics 12, no. 5: 664. https://doi.org/10.3390/math12050664
APA StyleWen, F., Jiang, J., & Luan, Y. (2024). Model Selection Path and Construction of Model Confidence Set under High-Dimensional Variables. Mathematics, 12(5), 664. https://doi.org/10.3390/math12050664






