Abstract
Since the emergence of blockchain, how to improve its transaction throughput and reduce transaction latency has always been an important issue. Hostuff has introduced a pipeline mechanism and combined it with a chain structure to improve the performance of blockchain networks. HCA has introduced a revoting mechanism on the basis of Hostuff, further reducing transaction latency, but it has also brought some problems. In HCA, if the leader is malicious, it would be possible to continuously call on the replica nodes to revote, which can lead to network congestion. This paper employs the global perfect coin technology to guarantee that every replica can obtain a globally consistent and the freshest candidate proposal during the Revote phase, thereby improving the robustness of the HCA protocol. The performance improvement of RHCA in attack scenarios has been verified through experiments.
MSC:
68M14
1. Introduction
Blockchain is a unique data structure in which each subsequent block stores the hash value of the previous block, and every block references its predecessor, with the reference in the genesis block being null. Due to the properties of hash functions, this data structure ensures that data stored within the blocks, such as transaction information, remains immutable. This enables the creation of a trustworthy and decentralized digital world.
However, since the emergence of blockchain, a low transaction throughput has been a persistent bottleneck limiting the application of blockchain technology. The throughput of Bitcoin [1], the first successful application of blockchain technology, is approximately 7 transactions per second (TPS), and Ethereum [2] achieves around 20 TPS. In contrast, the widely used centralized payment system VISA currently offers TPS rates of around 76,000 [3]. Additionally, transaction latency presents a significant challenge to blockchain applications. In the blockchain network, the confirmation of a transaction involves processes such as transaction broadcasting, block packaging, and the execution of consensus algorithms, resulting in generally prolonged transaction latency within blockchain systems. Consensus mechanisms are the core of blockchain technology, determining both its performance and security. Many research teams [4,5,6] have focused on improving blockchain system performance and efficiency by improving consensus mechanisms.
Numerous research teams have made groundbreaking contributions in the field of consensus mechanisms. In the permissionless blockchain domain, Bitcoin employs the Proof of Work (PoW) consensus mechanism [1], where miners gain the right to record transactions by solving a mathematical problem. However, this approach is plagued by issues such as computational waste and low transaction throughput. Subsequent Proof of Stake (PoS) [7] mechanisms have addressed computational waste but still face the “nothing at stake attack” issue [8]. In the realm of consortium blockchains, Practical Byzantine Fault Tolerance (PBFT) [9] relies on messages exchange to eliminate computational waste. Nonetheless, the voting process between nodes entails substantial communication overhead, leading to scalability challenges within the entire system. Hostuff [10] introduced a pipeline mechanism while simultaneously considering the blockchain structure, enhancing the performance of the blockchain network. Building upon Hostuff, HCA [11] introduced a revoting mechanism, further reducing transaction latency but also creating some issues.
The authors of HCA contend that conducting revoting for disputed proposals is more efficient than awaiting new votes. Therefore, they employed the revoting method in the design of HCA, reducing transaction latency and enhancing system responsiveness. However, with the introduction of revoting, if the leader acts maliciously, it can continuously send recall messages to replicas as long as the timer does not expire, as shown in Figure 1. This behavior, akin to a DDoS attack, can lead to network congestion, causing the blockchain to be unable to expand until the timer expires.
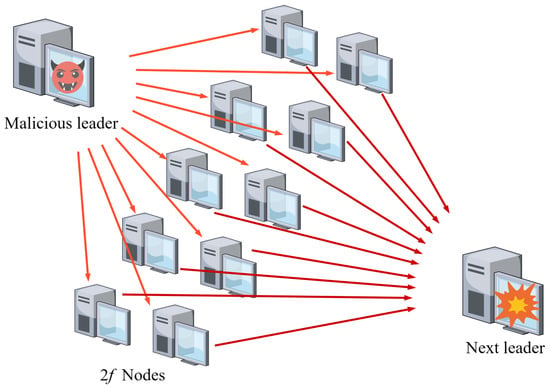
Figure 1.
Malicious leader can continuously send recall messages to replicas, and these replicas continuously vote on new proposals, which can lead to network congestion.
In this research, we leverage the global perfect coin technology [12,13,14,15] to share a globally consistent candidate proposal across multiple replicas. By employing this technology to share candidate proposals, our approach can reduce the impact of the aforementioned attacks. All in all, this paper focuses on enhancing the Revote phase within the context of HCA, aiming to bolster its robustness against malicious leader attacks. The main contributions of this paper are as follows:
- To the extent of our knowledge, our work pioneers the integration of the global perfect coin into the Revote phase, enabling each participating replica to access a globally consistent and up-to-date candidate proposal. The integration addresses a critical issue in HCA, where replicas heavily rely on the primary node during the Revote phase.
- We propose the RHCA protocol, which exhibits slightly lower performance than HCA in normal conditions but significantly outperforms HCA in scenarios involving attacks from malicious primary nodes.
- The paper provides theoretical proofs for the safety, liveness, and responsiveness of RHCA. Additionally, RHCA is implemented in Java, and experimental results confirm that it can effectively enhance the robustness of blockchain systems.
The rest of the paper proceeds as follows. The related works are presented in Section 2. Section 3 first recalls the basic content and data structure of HCA; then, it briefly introduces the concept and properties of the global perfect coin technology. In Section 4, the system model, threat model, goals, and message structures are defined. In Section 5, we propose the RHCA protocol and prove the safety, liveness, and responsiveness of RHCA. Then, Section 6 and Section 7 provide the theoretical and experimental analyses for the performance, respectively. Finally, the paper is concluded in Section 8.
2. Related Works
In distributed systems, scenarios such as node crashes leading to unresponsiveness or malicious nodes forging messages for malicious responses may occur. We refer to situations where nodes do not respond but do not maliciously forge messages as a “Crash Fault”, and situations where malicious nodes forge messages as a “Byzantine Fault”. Therefore, consensus algorithms suitable for these two scenarios are, respectively, termed Crash Fault Tolerance (CFT) and Byzantine Fault Tolerance (BFT) algorithms. This paper primarily focuses on BFT consensus algorithms.
Some algorithms are based on proof and use the longest chain principle to converge forks, such as PoW and PoS. PoW consensus leverages the characteristics of hash functions and designs a computationally challenging but easily verifiable mathematical problem. The node that first solves this problem gains the right to record transactions; while the computational intensity of PoW provides security, it also results in significant resource wastage. The Peercoin project pioneered the implementation of the Proof of Stake algorithm, introducing Coin Age as a form of stake to replace the computational competition of PoW with stake competition, while this conserves computational resources, it introduces issues such as the “nothing at stake attack” [8]. Delegated Proof of Stake (DPoS) [16], an improvement over PoS, can address the “nothing at stake attack” issue, but it falls short in terms of decentralization.
A study was based on a messages exchange, resulting in algorithms with deterministic finality [17]. The classical Byzantine Fault Tolerant algorithm (BFT) [18], proposed by Leslie Lamport et al., assumes a total number of n replicas, with f being the number of Byzantine replicas. BFT can ensure consensus among honest nodes in a Byzantine system only when . However, the voting between nodes involves substantial communication overhead, and the communication complexity of the system is . PBFT is an improvement over BFT. By employing a master–slave backup design, PBFT reduces the communication complexity of the entire system in normal states to . However, its introduced view-change process is relatively complex, and improvements can be made in terms of transaction latency and system throughput.
In recent years, the idea of a pipeline has inspired advancements, which refers to breaking down a task into several fixed stages so that each stage can be executed in parallel, thereby improving the efficiency and performance of the system. Some approaches utilize a pipeline strategy to simplify the voting phases, reducing transaction latency. The earliest integration of the pipeline concept was in the Paxos algorithm [19] proposed in 1990, but Paxos is only effective for Crash Fault Tolerance (CFT) problems. In 2019, Maofan Yin et al. [10] simplified the voting phases of HotStuff using a pipeline approach. In HotStuff, the prepare phase of view serves as both the pre-commit phase for view and the commit phase for view v. HotStuff not only simplifies the voting phases but also seamlessly incorporates view changes into the normal consensus process. Giridharan et al. [20] focused on the liveness degradation issue introduced by the pipeline, pointing out that in pipeline mode, block submissions span three or four leaders. If malicious leaders exist, it could lead to a reduction in system liveness. They proposed BeeGees [20], which can successfully submit blocks even in the presence of discontinuous honest leaders. TSBFT [21] synchronously optimizes the consensus layer and network layer of the protocol. It separates the transmission of block headers and block bodies, initiating the voting stages after the transmission of the block header. The first round of voting occurs simultaneously with the transmission of the block body, implementing a unique pipeline mode. In the context of a sharding blockchain, Liu et al. proposed FBFT [22], which combines the pipeline concept to enhance the efficiency of intra-shard consensus.
3. Preliminaries
3.1. The Basic Content of HCA
In the partial synchronous network assumption, HCA addresses the Byzantine Generals Problem in the context of a consortium blockchain. The original HCA consists of the normal state protocol and view-change protocol. In HCA, each participating blockchain node in the consensus is referred to as a replica, with a special replica known as the leader. When the view needs to be switched, the system selects a new leader through the view-change protocol. Under normal circumstances, each node in the system operates the normal state protocol. The primary node is responsible for proposing a new block, and it collects votes from replicas for this proposal. If the vote count reaches a threshold, a new block is proposed afterward to extend the blockchain. Additionally, to enhance system responsiveness, HCA introduces the Revote phase. When the primary node cannot obtain sufficient votes for the current proposal, it can issue recall messages to summon votes from replicas for the proposal. If the primary node fails to extend the blockchain before the timer expires, ensuring system liveness, each replica enters the view-change protocol and initiates a new primary node election after the timer expires.
The optimized HCA combines the normal state protocol and view-change protocol in a rolling manner. Each primary node can put forward at most one block in its view. After a replica node votes, its local view grows. Therefore, the votes of replica nodes for the current proposal are sent to the leader of the next view. Each proposal includes a proof of the legitimacy of its predecessor proposal (i.e., aggregate signature). Consequently, each vote for a new proposal simultaneously confirms the previous block. Once the block at height k is voted on, the block at height can be committed. HCA utilizes this approach to streamline block generation and confirmation, enhancing the efficiency of the consensus protocol. Theoretical analysis indicates that the communication complexity of the HCA mechanism is .
3.2. The Data Structure of HCA
HCA achieves consensus among nodes through a messages exchange, and messages emitted by each node are signed using their respective private keys. Digital signature technology [23] serves to prevent message forgery and tampering. In HCA, denotes a message signed by a replica node r. In the optimized HCA, three types of message structures are involved:
- Proposal message. In the HCA protocol, represents a block with height k. A proposal message essentially corresponds to a block that has not yet been confirmed. Consequently, only the primary node can send a proposal message. has the following format:where denotes the batch of transactions to be included in the block, represents the view at the time of proposing the block, denotes the hash value of the preceding block, and is derived from the aggregated votes on the preceding block.
- Vote message. Vote messages are emitted by replica nodes. Upon receiving a proposal message, each replica node verifies the legitimacy of the proposal, checking factors such as digital signatures and the correctness of the hash of the preceding block. Once the verification is successful, the replica node generates the hash value of , adds the view number for the next view, creates a vote message, signs it, and subsequently sends it to the primary node of the next view. A vote for has the following format:
- Recall message. A recall message is used in the Revote phase. When the proposal put forward by the leader L fails to garner sufficient votes, the leader L sends a Recall message, summoning some replicas to vote for the candidate proposal . The Recall message has the following format:where represents the current view number, and is the candidate proposal.
3.3. Global Perfect Coin
We employ a global perfect coin to enable each replica to obtain a globally consistent proposal, thereby avoiding the potential malicious behavior of the primary node in the Revote phase. Specifically, we design two functions: and . Replicas invoke these functions to interact with an instance of the coin. All honest replicas, after voting for proposal m, call once. validates the input, only accepting valid proposal m. Assuming that after the Vote phase, replicas separately vote for r different proposals. can be used to represent the set of proposals that have been voted on. The Coin sorts these candidate proposals based on their block heights, view numbers, and hash values. For any two candidate proposals, we consider the block with a higher height to be fresher. If their block heights are the same, we consider the block with a larger view number to be fresher. If their block heights and view numbers are also the same, we consider the one with the larger hash value to be fresher. In the Revote phase, after replica i receives a recall message from the primary node, calling returns a globally consistent and the freshest proposal . Replica i can then send a vote message for proposal .
Global perfect coin exhibits the following properties:
- Termination. can return a globally consistent proposal only after at least replicas have called .
- Unpredictability. As long as fewer than replicas call , the return value of will be indistinguishable from a random number.
- Agreement. Assuming replica i calls and gets proposal , and replica j calls and gets proposal , then .
- Freshness. The Coin sorts candidate proposals based on block height, view number, and hash value. will always return the freshest candidate proposal.
4. Overview
4.1. System Model
We assume the system is a distributed system composed of n replicas. We consider these replicas to satisfy the requirements of state machine replication (SMR) [24,25]: (i) all replicas have the same initial state; (ii) replicas with the same state, after executing a series of identical operations in the same order, will still have the same state. Based on the assumption of SMR, we only need to ensure that all honest replicas have the same order of proposals to guarantee the safety of the consensus algorithm. Each replica has a public/private key pair , and messages m emitted by replicas are signed using their private keys. denotes a message signed by a replica node r. Upon receiving a message, other replicas verify it using the sender’s public key. At the network level, we assume the network in the system is partially synchronous, meaning that after an unknown but finite global stabilization time (GST), messages between two honest replicas can be transmitted within a known communication delay .
4.2. Threat Model
Our consensus algorithm can tolerate up to Byzantine nodes. For simplicity, let us set . This configuration maximizes the proportion of potential malicious nodes and can simplify the description. Byzantine nodes are controlled by adversaries and can exhibit arbitrary behavior, such as stopping responses or performing malicious actions. Additionally, we assume that the computational power of these Byzantine nodes is limited. Therefore, they cannot break existing cryptographic techniques. For example, they cannot forge the digital signatures of honest nodes or infer the original information from hash values.
4.3. System Goal
All replicas in the system will execute the consensus algorithm to agree on the execution order of transactions. The consensus algorithm needs to satisfy the following three properties:
- Safety. All honest nodes have a consistent order of transaction execution.
- Liveness. Transactions submitted to the system will eventually be executed by all honest nodes.
- Responsiveness. Honest primary nodes can drive the system to the next view as soon as they receive votes for a new proposal.
The liveness of the system relies on the partial synchronous network assumption. However, even in an asynchronous network environment, the safety of the system is guaranteed.
4.4. Message Structure
The message types for communication between replica nodes include the following: Proposal message, Vote message, and Recall message. The structures of the Proposal and Vote messages are consistent with HCA, as detailed in Section 3.2. The Recall message used in this algorithm differs from HCA. The Recall message’s structure is . The Recall message is employed during the Revote phase. Here, represents the current view number. When the candidate proposal put forward by the leader fails to garner sufficient votes, the leader sends a Recall message, summoning some replicas to vote again. Upon receiving a Recall message, replicas use to obtain the proposal that needs to be voted on.
5. RHCA: Robust HCA via Consistent Revoting
The fundamental idea of RHCA is to coordinate various replicas, utilizing a peer-to-peer approach to the dual confirmation of proposals before committing. The protocol incorporates a pipeline technique, where the Vote phase of the proposal in view can simultaneously be regarded as the second confirmation of proposal in view v. Each proposal message in RHCA corresponds to a block containing the hash value of the preceding block and an aggregate signature. This aggregate signature results from the aggregation of votes on the previous block, signifying the confirmation of the preceding block by various replicas. As RHCA operates in a rolling manner, with a change of views and primary nodes in each round, it does not have a view-change phase akin to PBFT.
5.1. Rolling State Protocol
We denote n as the total number of replicas in the entire system and as the number of Byzantine nodes. The rolling state protocol continuously operates in rounds across all replicas. We use an integer to represent rounds, and in each round, a specific replica is chosen as the primary node. For simplicity, RHCA uses to determine the primary node for a given view.
- Propose. Under normal conditions, the primary node collects no fewer than votes for the preceding block and aggregates them into a single aggregate signature . Then, the primary node packs the transactions awaiting confirmation into and calculates the hash value of the preceding block . Finally, the leader assembles these data into a block , signs it, and broadcasts to all replicas via P2P.
- Vote. All replica nodes (including the primary node) maintain a timer that starts when entering a new view. If replica node r can receive a valid block before the timer times out, it will first verify this block and then send to the next primary node, indicating its confirmation of the block. Here, is the hash value of block . If the timer times out and r has not received a block, it will send its vote for the preceding block to the next primary node. Regardless, after replica r sends the vote message, it calls , invoking an instance of the coin and then enters the next view while resetting the timer.
- Revote. Let be the primary node for view . If collates votes from the previous view and finds that no proposal has received votes not less than , the protocol proceeds to the Revote phase. sends to some replica nodes, urging them to initiate the Revote phase. Upon receiving the Recall message, each replica node calls , obtaining a globally consistent and the freshest proposal . Subsequently, each replica can send a vote to .
- Commit. As each block contains an aggregate signature regarding the preceding block, the generation of a valid block signifies that some primary node has collected at least valid votes for block . This also implies that block has been confirmed twice by the majority of replica nodes. Therefore, upon receiving a valid block for the first time, the replica node can commit block .
5.2. Attack and Solution
The HCA protocol introduces the concept of revoting, and while it effectively enhances the speed of block generation, it also creates certain issues. Consider the following scenario with four replica nodes, namely, , where is the leader of the current view , and is the leader of view . As shown in Figure 2, if acts maliciously, in the HCA protocol, it can continuously send messages to other replicas, urging them to revote on multiple proposals from . This malicious revoting behavior can lead to network congestion and increase system latency. We believe that the reason why this attack is successful is that replica nodes trust the recall message sent by the leader too much, while neglecting the potential for malicious behavior by the primary node. Therefore, in RHCA, we modify the format of recall messages by not including candidate proposals within them. In RHCA, upon receiving a recall message, replica nodes invoke to obtain a globally consistent proposal . Honest replicas subsequently compare with the proposal they voted for in the previous round. If is deemed fresher, the replicas send votes for the proposal . Consequently, in RHCA, revoting can only be conducted entirely once in a view, thus addressing the issue of malicious primary nodes exploiting revoting for attacks.
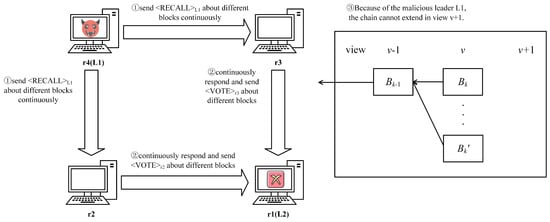
Figure 2.
Malicious leader continuously initiates revoting, resulting in the inability to expand the blockchain in this round.
5.3. Safety, Liveness, and Responsiveness of the RHCA Protocol
This subsection gradually proves the safety, liveness, and responsiveness of RHCA. As described in the threat model, in the following proofs, we set . In this configuration, the proportion of malicious nodes is maximized, and the description can be simplified.
Lemma 1.
If a valid block with height k is proposed in view v, then subsequent primary nodes no longer need to collect votes for blocks before height .
Proof.
Upon entering view v, we have at least replicas that have voted for block . Therefore, at least honest nodes have already verified block . According to the Revote phase, honest nodes that have voted for a block at height are not allowed to revote for blocks below height . Therefore, the other replicas (up to ) cannot gather at least votes for blocks with a height not greater than . □
Lemma 2.
The blockchain has only one main chain, and the length of any fork on the main chain is less than 2.
Proof.
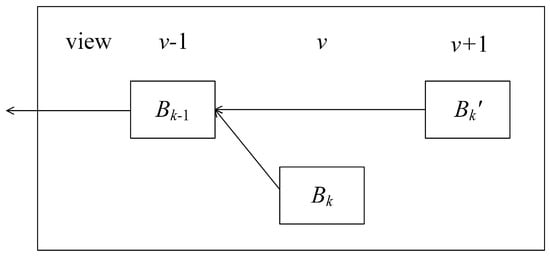
For a primary node in view v, within this view, either primary node does nothing or proposes a block. If it is the former, each replica waits for the proposed message from leader until the local timer times out. Eventually, each replica sends a vote message for the previous block (i.e., ) to the next view’s primary node . If it is the latter, primary node collects vote messages from each replica and proposes a new block. Assuming the height of this block is k, we use to represent the proposed block. For the primary node in view , by Lemma 1, can only collect votes for blocks with heights or k, i.e., and . If proposes a new block after , a fork will occur in the blockchain, as shown in Figure 3. and are at the same height, but the view number of is greater than that of .

Figure 3.
The leader of view directly collects votes for and extends the blockchain after the block , leading to a fork.
Subsequent primary nodes cannot collect enough votes for and . This will lead to revoting. Based on the Revote phase, honest nodes will call to get a globally consistent and the freshest proposal, namely, . Replicas then send their vote messages for proposal . Therefore, the block is discarded, and subsequent blocks can only be extended from the main chain. Thus, the length of any fork on the main chain will be less than 2. □
Theorem 1
(Safety). No two nodes will commit distinct blocks at the same height.
Proof.
A block is only committed after being confirmed twice. This implies that when a block is committed, there should be two blocks following it. Therefore, attempting to commit two distinct blocks at the same height would require the existence of a fork with a length of 3. However, according to Lemma 2, this is impossible. Thus, it can be ensured that replicas in the system commit the same block at the same height. □
Lemma 3.
After GST, there exists a period during which all honest replicas are in the same view. In this view, an honest leader can always broadcast a new block at a new height.
Proof.
Due to the use of both the revoting protocol and global perfect coin, the leader can synchronize the current voting status with the replica nodes. Replica nodes only change their votes to the freshest block. This ensures the existence of a single main chain in the blockchain. Even if the leader of the previous view behaves maliciously by proposing multiple blocks to create a fork, honest nodes will change their votes to the freshest block according to the Revote phase. Therefore, after GST, as long as the primary node is honest, it can always collect votes for the previous block and propose a new block at the current height. □
Theorem 2
(Liveness). All honest replicas continuously commit blocks that have been confirmed twice.
Proof.
The protocol operates continuously on each replica, selecting a new replica as the leader in a round-robin manner. In a new view, the leader proposes a new block to drive the protocol at a new height. When entering a new view, each replica starts a local timer. After voting for the proposed block or when the timer expires, each replica enters a new view and runs the protocol in the new view.
Building upon Lemma 3, an honest primary node can always broadcast a new block at a new height. Even if a malicious leader causes a fork, the revoting protocol ensures that the next leader extends the chain after the freshest block. Therefore, new blocks can continue to be generated at a higher height, and replicas can consistently commit new blocks. □
Theorem 3
(Responsiveness). After GST, when the network becomes synchronous, an honest leader can drive replicas to agree on a block within the real network delay time, without waiting for the timer to timeout.
Proof.
If the leader fails to collect sufficient votes for any block, it cannot propose a new block, and the system cannot extend. However, due to the introduction of revoting, the leader can summon replicas to revote and reach consensus before the timer times out, achieving an Optimistically Responsive outcome. □
6. Theoretical Analysis of the Performance
We compare the communication complexity of HCA and RHCA and analyze the performance improvement of RHCA in specific attack scenarios within this section.
The HCA protocol consists of two phases: Propose and Vote. Suppose there are n replicas running this protocol, in the Propose phase, the leader broadcasts the proposed block to all replicas, and the communication complexity of this phase is . In the Vote phase, each replica sends a vote message to the next leader, and the communication complexity of this phase is also . Therefore, under normal circumstances, the communication complexity of the HCA protocol is .
Considering the case of a malicious leader, assuming the malicious leader conducts j rounds of revoting before the timer expires, with a maximum of replicas participating in each round of revoting, the attack will add a communication overhead of . Therefore, under attack, the communication complexity of the HCA protocol becomes .
The RHCA protocol, like HCA, consists of two phases: Propose and Vote. Assuming there are n replicas in the entire system, in the Propose phase, the communication overhead caused by the leader’s broadcast is . In the Vote phase, each node sends vote messages to the leader of the next view and calls the coin instance once. The communication complexity of this phase is (where Q is the overhead of calling the coin; if implementing a global perfect coin using broadcasting, ). In normal circumstances, the communication complexity of the RHCA protocol is .
Considering the case of a malicious leader, assuming the malicious leader conducts j rounds of revoting before the timer expires, with a maximum of replicas participating in each round of revoting. The distinction from HCA lies in the fact that, in RHCA, each invocation of returns the same proposal. Therefore, replicas only invoke once and conduct revoting only once when receiving multiple recall messages in the same view in RHCA.
In the best-case scenario (also typical scenario), the leader of the next view can collect votes after two rounds of revoting. The malicious leader broadcasts two rounds of recall messages to replicas, resulting in a communication cost of . The replicas invoke the coin and vote, incurring a communication cost of . Therefore, the additional communication cost introduced by the attack is approximately . The overall communication complexity in the attack scenario is .
In the worst-case scenario, where the replicas participating in each round of revoting are the same, the next leader consistently fails to collect a sufficient number of votes. In this case, the attack increases the communication overhead by . Therefore, the communication complexity of the RHCA protocol in the attack scenario is .
In summary, under normal circumstances, RHCA’s communication complexity is slightly higher than HCA due to the added overhead of invoking the coin. However, in the scenario of malicious leaders, RHCA significantly reduces communication overhead compared to HCA. In extreme attack scenarios (large values of j), the communication cost of RHCA can be achieved independently of j. Even in the worst-case scenario, the communication cost is only half of that in HCA.
7. Experimental Analysis of the Performance
We implemented RHCA and HCA, and conducted a comparative analysis of their latency, throughput, scalability, and robustness. BFT-SMaRt is an open-source library written in Java that implements the PBFT consensus algorithm [26]. We forked the code of BFT-SMaRt from its GitHub repository and rewrote the consensus module based on the specific logic of RHCA and HCA, thereby realizing the RHCA and HCA protocols. Using identical parameters, we executed the RHCA and HCA protocols multiple times to illustrate the significant advantages of RHCA in terms of robustness.
7.1. Setup
We rented three compute service instances from Alibaba Cloud and Baidu Cloud for our experiments. These instances were equipped with the Ubuntu 18.04.6 operating system and the JRE 1.8 runtime environment, with specific parameters detailed in Table 1. We installed a virtual machine environment on each instance and ran a replica node within each virtual machine. The replicas exchanged messages in a peer-to-peer fashion, forming a blockchain network. Specifically, we designated one virtual machine to host a client that created multiple threads to concurrently send requests to the blockchain network.

Table 1.
The specifications of the instances.
The BFT-SMaRt library comprises two micro-benchmark programs: ThroughputLatencyServer and ThroughputLatencyClient. The former is designed to measure the time expenses of various phases of the consensus protocol, and we utilized it to calculate the consensus latency results. The latter is employed to gauge the average response time of requests, enabling us to assess the request throughput of the blockchain network.
7.2. Base Performance
We concurrently operated four replica nodes on different virtual machines, with the batch size set to 50. Under this configuration, RHCA and HCA support at most one Byzantine node in the network. We had the client continuously send requests while varying the payload size for multiple experiments. Figure 4a illustrates the consensus latency in milliseconds, while Figure 4b displays the request throughput in thousand operations per second. Additionally, to explore the impact of network latency on both consensus latency and request throughput, we used the traffic control tool in Linux to simulate network delay. Lines corresponding to different network delays are labeled as “d0”, “d5”, “d10”. For example, “RHCA-d0” represents data obtained for the RHCA algorithm without additional network delay.
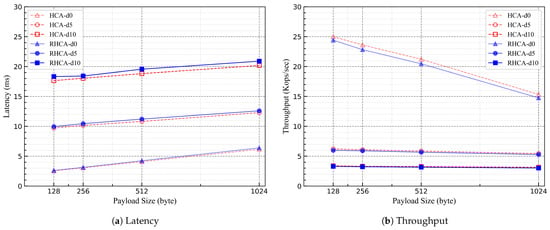
Figure 4.
Performance with various payload sizes while restricting the batch size to 50 under 4 replicas.
Figure 4 indicates that under normal conditions, the consensus latency of RHCA is slightly higher than that of HCA, and the throughput is slightly lower than HCA. This is primarily because RHCA introduces an additional step in the Vote phase to invoke the global perfect coin. In fact, this reflects a trade-off between performance and robustness in RHCA.
In addition, we also varied the batch size for multiple experiments and observed how the performance of RHCA and HCA changed. Figure 5a illustrates the consensus latency in milliseconds, while Figure 5b displays the request throughput in thousand operations per second. Figure 5 indicates that as the batch size increases, the consensus latency of both RHCA and HCA slightly increases, while the request throughput has a significant improvement relatively. For example, in the scenarios where the simulated network delay was 5 ms, the throughput of the RHCA protocol tripled when the batch size increased from 50 to 200, while the consensus latency only increased by approximately one-third. This suggests that in practical scenarios, as long as the consensus latency remains within an acceptable range, effectively enhancing the request throughput of the RHCA protocol can be achieved by appropriately increasing the batch size.
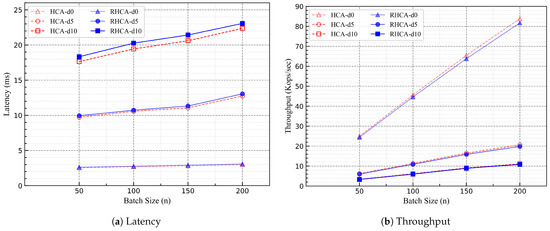
Figure 5.
Performance for various batch sizes while restricting the payload size to 128 bytes under 4 replicas.
7.3. Scalability
Next, we varied the number of replicas in the system to observe the changes in consensus latency and request throughput, examining the scalability of RHCA and HCA. We take the total number of nodes n as 4, 8, 16, 32, and 64, and the corresponding number f of tolerable Byzantine nodes as 1, 2, 5, 10, and 21. Under these configurations, we further adjusted the network latency and request payload size to observe the performance of the blockchain system.
In Figure 6, we used the traffic control tool to simulate network delays, setting network delays to 5 ms and 10 ms to run the blockchain network. The experimental results indicate that as the number of nodes increases, the performance trends of RHCA and HCA are similar. Both RHCA and HCA exhibit a slight increase in consensus latency, and the request throughput slightly decreases.
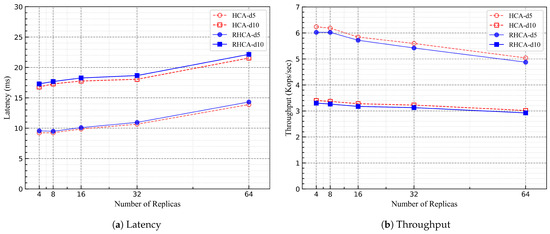
Figure 6.
Scalability under various numbers of replicas, restricting the batch size to 50 and setting payload size to 0.
In Figure 7, we set the network latency to 0 and set the size of the request payload to 128 bytes and 1024 bytes, respectively, for the experiment. The results indicate that as the number of nodes increases, the consensus latency of both RHCA and HCA gradually increases, while the request throughput gradually decreases. Additionally, with a payload size of 1024 bytes, the performance of RHCA and HCA deteriorates more rapidly as the number of nodes increases.
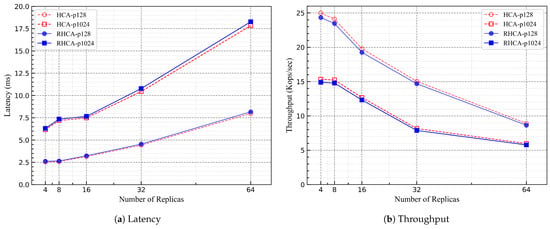
Figure 7.
Scalability under various numbers of replicas, restricting the batch size to 50 and setting network delay to 0.
In Figure 6 and Figure 7, the performance of RHCA is always slightly lower than that of HCA due to the need for consistent revoting, resulting in a slight decrease in RHCA’s performance. However, according to the experimental results, we observed that under normal conditions, the reduction in performance for RHCA compared to HCA is limited.
7.4. Robustness
To compare the robustness of RHCA and HCA, we set up an unconventional adversary. In both RHCA and HCA, the round-robin method is used to elect the primary node. When the adversary becomes the primary node, it continuously initiates several rounds of revoting. In each round of revoting, it calls on nodes to revote. As the votes never reach the threshold (i.e., ), this adversary can persist in revoting until the timer expires.
We conducted experiments with node counts of 4, 7, 10, and 13, each involving 1, 2, 3, and 4 unconventional adversaries, respectively. The experimental results, depicted in Figure 8, clearly illustrate that under attack conditions, the latency of HCA is significantly higher than that of RHCA, and its throughput is considerably lower than that of RHCA. Taking the example of four nodes with a network latency of 10 ms, we specifically illustrate the impact of the attack. In comparison to Figure 6, it is evident that under attack conditions, the latency of HCA increases approximately 20 times, while RHCA increases by only 70%. In terms of throughput, HCA’s throughput drops to 1/19th of the normal scenario, while RHCA maintains a throughput at around 60% of the normal scenario.
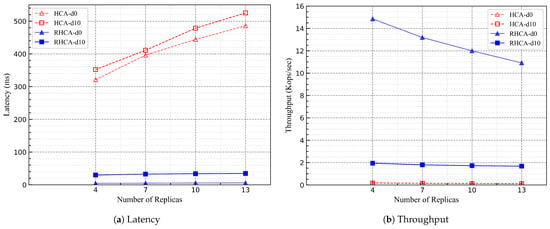
Figure 8.
Performance in attack scenarios.
In summary, while the use of consistent revoting may slightly impact the performance of the protocol under normal scenarios, it significantly ensures the system’s performance in attack scenarios, effectively enhancing the system’s robustness.
8. Conclusions
This paper introduces the RHCA protocol, which achieves consensus through a messages exchange. To expedite the voting process, we employ the pipeline technique. Each block in RHCA includes an aggregate signature, formed by aggregating votes on the preceding block. Consequently, the votes on the proposal for view can be simultaneously considered as the second confirmation of the proposal for view v. Additionally, we utilize the global perfect coin technology to implement consistent revoting. Through consistent revoting, each replica node participating in revoting can obtain a globally consistent and the freshest candidate proposal, facilitating rapid convergence of forks. Most importantly, consistent revoting can prevent special attacks from adversaries that may arise in HCA. We demonstrate the safety, liveness, and responsiveness of RHCA through a theoretical analysis. Additionally, an experimental analysis was conducted to evaluate the consensus latency, request throughput, and improvements in robustness. We confirmed that our algorithm slightly sacrifices performance in regular scenarios but significantly enhances robustness in special situations.
Author Contributions
Conceptualization, Z.Z.; Data curation, K.F.; Investigation, H.S.; Software, X.L. and H.S.; Supervision, X.L.; Visualization, X.C.; Writing—original draft, K.F. and X.C.; Writing—review and editing, Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by National Key Research and Development Program of China under grant No. 2021YFB2701202 and National Natural Science Foundation of China (NSFC) under grant No. 62172040.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Nakamoto, S. Bitcoin: A peer-to-peer electronic cash system. Decentralized Bus. Rev. 2008, 21260. [Google Scholar]
- Wood, G. Ethereum: A secure decentralised generalised transaction ledger. Ethereum Proj. Yellow Pap. 2014, 151, 1–32. [Google Scholar]
- Visa, a Technology Company. Available online: https://usa.visa.com/dam/VCOM/global/about-visa/documents/visanet-factsheet.pdf (accessed on 26 October 2023).
- Zhang, Z.; Liu, X.; Feng, K.; Wan, M.; Li, M.; Dong, J.; Zhu, L. Phantasm: Adaptive Scalable Mining Toward Stable BlockDAG. IEEE Trans. Serv. Comput. 2023. [Google Scholar] [CrossRef]
- Gai, K.; Hu, Z.; Zhu, L.; Wang, R.; Zhang, Z. Blockchain meets dag: A blockdag consensus mechanism. In Proceedings of the Algorithms and Architectures for Parallel Processing: 20th International Conference, ICA3PP 2020, New York, NY, USA, 2–4 October 2020; Proceedings, Part III 20. Springer: Berlin/Heidelberg, Germany, 2020; pp. 110–125. [Google Scholar]
- Li, W.; Feng, C.; Zhang, L.; Xu, H.; Cao, B.; Imran, M.A. A scalable multi-layer PBFT consensus for blockchain. IEEE Trans. Parallel Distrib. Syst. 2020, 32, 1146–1160. [Google Scholar] [CrossRef]
- King, S.; Nadal, S. Ppcoin: Peer-to-Peer Crypto-Currency with Proof-of-Stake. Self-Published Paper. 2012. Available online: https://bitcoin.peryaudo.org/vendor/peercoin-paper.pdf (accessed on 5 January 2024).
- Li, W.; Andreina, S.; Bohli, J.M.; Karame, G. Securing proof-of-stake blockchain protocols. In Proceedings of the Data Privacy Management, Cryptocurrencies and Blockchain Technology: ESORICS 2017 International Workshops, DPM 2017 and CBT 2017, Oslo, Norway, 14–15 September 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 297–315. [Google Scholar]
- Castro, M.; Liskov, B. Practical byzantine fault tolerance. In Proceedings of the OsDI, New Orleans, LA, USA, 22–25 February 1999; Volume 99, pp. 173–186. [Google Scholar]
- Yin, M.; Malkhi, D.; Reiter, M.K.; Gueta, G.G.; Abraham, I. HotStuff: BFT consensus in the lens of blockchain. arXiv 2018, arXiv:1803.05069. [Google Scholar]
- Zhang, Z.; Liu, X.; Li, M.; Yin, H.; Zhu, L.; Khoussainov, B.; Gai, K. HCA: Hashchain-based Consensus Acceleration via Re-voting. IEEE Trans. Dependable Secur. Comput. 2023. [Google Scholar] [CrossRef]
- Keidar, I.; Kokoris-Kogias, E.; Naor, O.; Spiegelman, A. All you need is dag. In Proceedings of the 2021 ACM Symposium on Principles of Distributed Computing, Virtual Event, 26–30 July 2021; pp. 165–175. [Google Scholar]
- Blum, E.; Katz, J.; Liu-Zhang, C.D.; Loss, J. Asynchronous byzantine agreement with subquadratic communication. In Proceedings of the Theory of Cryptography: 18th International Conference, TCC 2020, Durham, NC, USA, 16–19 November 2020; Proceedings, Part I 18. Springer: Berlin/Heidelberg, Germany, 2020; pp. 353–380. [Google Scholar]
- Lu, Y.; Lu, Z.; Tang, Q.; Wang, G. Dumbo-mvba: Optimal multi-valued validated asynchronous byzantine agreement, revisited. In Proceedings of the 39th Symposium on Principles of Distributed Computing, Salerno, Italy, 3–7 August 2020; pp. 129–138. [Google Scholar]
- Abraham, I.; Malkhi, D.; Spiegelman, A. Asymptotically optimal validated asynchronous byzantine agreement. In Proceedings of the 2019 ACM Symposium on Principles of Distributed Computing, Toronto, ON, Canada, 29 July–2 August 2019; pp. 337–346. [Google Scholar]
- Delegated Proof of Stake (DPOS). Available online: https://how.bitshares.works/en/master/technology/dpos.html (accessed on 10 October 2023).
- Hassanzadeh-Nazarabadi, Y.; Taheri-Boshrooyeh, S. A consensus protocol with deterministic finality. In Proceedings of the IEEE INFOCOM 2021-IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Vancouver, BC, Canada, 10–13 May 2021; pp. 1–2. [Google Scholar]
- Lamport, L.; Shostak, R.; Pease, M. The Byzantine generals problem. In Concurrency: The Works of Leslie Lamport; ACM: New York, NY, USA, 2019; pp. 203–226. [Google Scholar]
- Lamport, L. Paxos Made Simple. ACM SIGACT News (Distributed Computing Column) 32, 4 (Whole Number 121, December 2001). 2001, pp. 51–58. Available online: https://www.cs.columbia.edu/~du/ds/assets/papers/paxos-simple.pdf (accessed on 5 January 2024).
- Giridharan, N.; Suri-Payer, F.; Ding, M.; Howard, H.; Abraham, I.; Crooks, N. BeeGees: Stayin’alive in chained BFT. In Proceedings of the 2023 ACM Symposium on Principles of Distributed Computing, Orlando, FL, USA, 19–23 June 2023; pp. 233–243. [Google Scholar]
- Tian, J.; Tian, J.; Xu, H. TSBFT: A scalable and efficient leaderless byzantine consensus for consortium blockchain. Comput. Netw. 2023, 222, 109541. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; Li, D.; Yu, H.; Wu, Q. Fleetchain: A secure scalable and responsive blockchain achieving optimal sharding. In Proceedings of the International Conference on Algorithms and Architectures for Parallel Processing, New York, NY, USA, 2–4 October 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 409–425. [Google Scholar]
- Davies, D.W. Applying the RSA digital signature to electronic mail. Computer 1983, 16, 55–62. [Google Scholar] [CrossRef]
- Schneider, F.B. Implementing fault-tolerant services using the state machine approach: A tutorial. ACM Comput. Surv. (CSUR) 1990, 22, 299–319. [Google Scholar] [CrossRef]
- Lamport, L. Time, clocks, and the ordering of events in a distributed system. In Concurrency: The Works of Leslie Lamport; ACM: New York, NY, USA, 2019; pp. 179–196. [Google Scholar]
- Bessani, A.; Sousa, J.; Alchieri, E.E. State machine replication for the masses with BFT-SMART. In Proceedings of the 2014 44th Annual IEEE/IFIP International Conference on Dependable Systems and Networks, Atlanta, GA, USA, 23–26 June 2014; pp. 355–362. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).