Revisiting the Dynamics of Two-Body Problem in the Framework of the Continued Fraction Potential

Abstract

In this analytical study, a novel solving method for determining the precise coordinates of a mass point in orbit around a significantly more massive primary body, operating within the confines of the restricted two-body problem (R2BP), has been introduced. Such an approach entails the utilization of a continued fraction potential diverging from the conventional potential function used in Kepler’s formulation of the R2BP. Furthermore, a system of equations of motion has been successfully explored to identify an analytical means of representing the solution in polar coordinates. An analytical approach for obtaining the function t = t(r), incorporating an elliptic integral, is developed. Additionally, by establishing the inverse function r = r(t), further solutions can be extrapolated through quasi-periodic cycles. Consequently, the previously elusive restricted two-body problem (R2BP) with a continued fraction potential stands fully and analytically solved.

1. Introduction

In classical mechanics, the two-body problem entails describing the motion of two celestial bodies, treated as point masses from a theoretical standpoint. This problem stipulates that the sole influential force on the motion of these two bodies is the aggregate of the gravitational forces they exert on each other, while disregarding any additional forces stemming from the motion of other celestial objects [1]. A prevalent instance of such classical two-body motion is exemplified in the Kepler problem, which emerges in celestial mechanics to elucidate the trajectory of celestial bodies or their escape from gravitational influence, as observed in the motion of satellites, planets, or stars [2]. Although the two-body classical system provides a good description of the dynamical properties of motion and gives important insights and predictions on the future motion of a body, it is not enough in most cases to obtain precise results because, in reality, the sun acts as the major source of force in our solar system. Indeed, the sun serves as the predominant gravitational force within the solar system, yet it undergoes numerous accelerations, albeit often minor ones, due to the motion of planets or even other stars, as per Newton’s second and third laws. Moreover, there exists a mutually attractive force among the planets, resulting in their gravitational attraction towards one another. Hence, the total force influencing a planet’s motion is not solely attributable to the sun. Additionally, it is noteworthy that the elliptical trajectory expected for a given planet, were it the sole orbiter around an isolated sun, is perturbed by the gravitational influence of other planets.

Thus, Kepler’s laws exhibit inherent limitations, offering only approximations for actual motion [3,4]. The Kepler problem itself often fails to provide precise descriptions of the motion of two bodies in most scenarios, such as accurately determining their orbits, predicting future trajectories, or estimating the moment when one body escapes the gravitational sphere of influence of the other, along with its velocity and direction. Consequently, numerous researchers have endeavored to investigate this problem while considering various perturbing forces and proposing new models [5,6,7,8]. The perturbed two-body problem has been extensively studied to analyze the dynamic motion properties under the influence of diverse perturbation forces. For instance, certain perturbed models incorporate factors like radiation pressure and drag forces or explore the combined effects of both forces [9,10,11,12]. Furthermore, within the context of non-spherical bodies, analytical solutions for the perturbed two-body problem have been scrutinized and evaluated [13,14].

The perturbing forces affecting the two-body problem extend beyond factors like radiation pressure, the non-sphericity of celestial bodies, or resistance from surrounding mediums, such as drag force. The motion of additional celestial bodies can also introduce disturbances to the two-body motion. Furthermore, the motion in a three-body problem can often be approximated as a perturbed two-body problem [15]. Additionally, examining this problem while considering modifications to the Newtonian potential or incorporating quantum corrections or general relativity approximations yields perturbed models for the two-body problem [16,17,18,19]. These models generally offer a more realistic portrayal of motion and provide more accurate results. The two-body problem serves as the cornerstone of celestial mechanics studies, acting as a foundational element for enhancing our comprehension of n-body problems, including the three-body problem [20].

The two-body problem holds significant interest in both celestial mechanics and space dynamics, playing a crucial role in analyzing the motion of both natural and artificial celestial bodies. This significance motivates the current study of the perturbed two-body problem. Typically, celestial bodies are idealized as point masses in theoretical analyses, a simplification that diverges from reality. Thus, let us aim to address this discrepancy by investigating solutions for the restricted two-body problem under a modified potential, specifically derived from the continued fraction potential.

The paper follows a systematic structure: Section 1 outlines notable contributions relevant to the research theme. Section 2 provides a comprehensive description of the mathematical model, including equations governing the orbiting of the mass point. Section 3 briefly outlines the solving procedure for the system of equations introduced earlier. Section 4 meticulously examines graphical, analytical, and semi-analytical results. Lastly, the paper concludes with a concise in Section 5 and Section 6.

2. Model Description and Equations of Motion

Numerous issues within celestial mechanics and astrodynamics exhibit dynamic behaviors and motions that can be effectively studied and described using the framework of the two-body problem. Various models for the two-body problem exist, differing primarily in the perturbing forces they consider based on the specific nature of the study.

This study employs a particular type of modified Newtonian potential known as the continued fraction potential. This potential finds widespread applications in problems related to celestial mechanics [6] or quantum mechanics [16]. The continued fraction potential is viewed as a perturbed potential, extending Newton’s universal law of gravitation. In this formulation, the primary component of the potential corresponds to the Newtonian potential, while additional terms account for perturbed forces, such as those observed in the potential of oblate bodies [8]. The potential can be simplified to the following expression (1):

$$U=-\frac{mr}{r^2+\epsilon }$$

(1)

Here, m = Gm₁m₂ (m₁ is the mass of the primary body, m₂ is the mass of the secondary body), G is the universal gravitation constant, r denotes the separation distance, and ε signifies the parameter of the perturbed force originating from the continued fraction potential.

Now, let us impose that $m_1$ and $m_2$ be the masses of the two bodies that are moving around each other whereas r₁ and r₂ be the position vectors of the two bodies with respect to the origin of the inertial reference frame, while r = r₂ − r₁ is the relative position vector of the body m₂ with respect to the body m₁. Thus, with the help of Equation (1), the vectorial equation of motion of the second body around the first is given by (2)

$$\ddot{\mathit{r}}=-\mu \frac{r^2-\epsilon }{{\left(r^2+\epsilon \right)}^2}\widehat{\mathit{r}}.$$

(2)

Here, $\mu =G(m_1+m_2)$ and $\widehat{\mathit{r}}$ is a unit vector in the direction of the position vector r.

Let us begin by considering a non-rotating, inertial polar coordinate system. In this system, the origin O is positioned at the selected initial moment t₀, coinciding with the center of mass of the celestial body m₁. This body is either in dynamical equilibrium with outer space or moves uniformly in a straight line (without rotation) at a constant velocity. Let us then examine Equations (11A) and (11B), which describe the dynamics of the mass point m₂ in the aforementioned formulation from the work [8]. These equations are treated here as a Cauchy problem with given initial conditions and are represented in the forms (3) and (4) below:

$$\ddot{r}-r{\dot{\theta }}^2=-\mu \frac{r^2-\epsilon }{{\left(r^2+\epsilon \right)}^2},$$

(3)

$$\frac{d}{dt}\left(r^2\dot{\theta }\right)=0\Rightarrow r^2\dot{\theta }=h=\mathrm{const}.$$

(4)

Here, {r, θ} are the polar coordinates, ε = Gm₁m₂λ₁ is a parameter that represents the perturbed force of the continued fraction potential in the problem, and |λ₁| = const « 1.

3. Solving Procedure for the System of Equations (3) and (4)

Equation (3) can be written as follows:

$$r^3\ddot{r}-h^2=-\mu \frac{r^2-\epsilon }{{\left(r^2+\epsilon \right)}^2}{r}^3.$$

Let us assume that dr/dt= y(r) (→d²r/dt² = y dy/dr), we thus have

$$\frac{r^3}{2}\frac{d{y}^2}{dr}-h^2=-\mu \frac{r^2-\epsilon }{{\left(r^2+\epsilon \right)}^2}{r}^3.$$

Here, let us additionally explain that in transforming Equations (3) and (4) by virtue of a special change of variables, as above, we have taken into account that the independent variable (time, t) is not included in the left nor the right part of systems (3) and (4). Solving further for y, we obtain (C₁, C₂, C₃ are the constants, determined by the initial conditions)

$$y^2-y{(0)}^2=C_1-\frac{h^2}{r^2}+2\epsilon \mu {\displaystyle \underset{r_0}{\overset{r}{\int }}\frac{dr}{{(r^2+\epsilon )}^2}}-2\mu {\displaystyle \underset{r_0}{\overset{r}{\int }}\frac{r^{2}dr}{{(r^2+\epsilon )}^2}}.$$

(5)

Furthermore, expressions (6) and (7) in Equation (5) above are as follows:

$$A=-4\epsilon <0;{\displaystyle \underset{r_0}{\overset{r}{\int }}\frac{dr}{{(r^2+\epsilon )}^2}=C_2+\frac{r}{2\epsilon (r^2+\epsilon )}+\frac{1}{2\epsilon \sqrt{\epsilon }}}\arctan \left(\frac{r}{\sqrt{\epsilon }}\right).$$

(6)

$${\displaystyle \underset{r_0}{\overset{r}{\int }}\frac{r^{2}dr}{{(r^2+\epsilon )}^2}=C_3-\frac{r}{2(r^2+\epsilon )}+\frac{1}{2\sqrt{\epsilon }}}\arctan \left(\frac{r}{\sqrt{\epsilon }}\right).$$

(7)

Thus, one can obtain the following from (5) using (6) and (7) as below (where in (8) and (9), $y{(0)}^2={\left(\frac{dr}{dt}\right)}_0^2$ is a constant and determined by the initial conditions, C = C₁ + C₂ + C₃):

$$\begin{array}{ll}{y}^2-y{(0)}^2=& C-\frac{h^2}{r^2}+2\epsilon \mu \left[\frac{r}{2\epsilon (r^2+\epsilon )}+\frac{1}{2\epsilon \sqrt{\epsilon }}\arctan \left(\frac{r}{\sqrt{\epsilon }}\right)\right]\\ & -2\mu \left[-\frac{r}{2(r^2+\epsilon )}+\frac{1}{2\sqrt{\epsilon }}\arctan \left(\frac{r}{\sqrt{\epsilon }}\right)\right].\end{array}$$

$$\Rightarrow y^2-y{(0)}^2=C-\frac{h^2}{r^2}+2\mu \frac{r}{(r^2+\epsilon )}.$$

(8)

$$\Rightarrow {\displaystyle \underset{r_0}{\overset{r}{\int }}\frac{dr}{\sqrt{{\left(\frac{dr}{dt}\right)}_0^2+C-\frac{h^2}{r^2}+2\mu \frac{r}{(r^2+\epsilon )}}}=t.}$$

(9)

Let us note that since under the sign of the square root there is a polynomial of the fourth degree in the numerator and the third degree in the denominator, the left part of Equation (9) is given by an elliptic integral; then, by reinversing the dependence with respect to time t in Equation (9), one should obtain a further solution in terms of quasi-periodic cycles.

4. Analytical Results

In this analytical study, a novel solving method to determine the coordinates of a mass point, m₂, in orbit around a more massive primary body, m₁, (within the framework of the restricted two-body problem, R2BP) has been introduced. Such an approach involves the consideration of a continued fraction potential instead of the classical potential function in Kepler’s formulation of the R2BP. Simultaneously, a system of equations of motion has been successfully explored to identify an analytical means of representing the solution in polar coordinates, {r(t), φ(t)}. An analytical approach for obtaining the function t = t(r), incorporating an elliptic integral, was developed. By establishing the inverse function r = r(t), a further solution can be derived via quasi-period cycles. Consequently, the previously mentioned restricted two-body problem (R2BP) with a continued fraction potential is fully and analytically solved.

As can be seen from the derivation above, the equations of motion (3) and (4) have been fully solved. Namely, an analytical formula for the solution (9) describing the quasi-periodic dependence of the polar radius, r(t), on time, t, is obtained. Let us clarify that while transforming Equations (3) and (4) by virtue of a special change of variables, we have taken into account that the independent variable (time, t) is not included in the left nor the right part of systems (3) and (4). Therefore, this system yields an ordinary differential equation of the second order (5) by an elegant change of variables $\left\{y(r)=\frac{dr}{dt},\hspace{1em}\frac{d^{2}r}{d{t}^2}=y\left(\frac{dy}{dr}\right)\right\}$ in the first order differential equation. Then, having solved the equation with regard to the function y(r) in the form (8), let us then solve the ODE with regard to $\frac{dr}{\left(\sqrt{{\left(\frac{dr}{dt}\right)}_0^2+C-\frac{h^2}{r^2}\hspace{0.33em}\hspace{0.33em}+\hspace{0.33em}2\mu \frac{r}{(r^2+\hspace{0.33em}\epsilon )}}\right)}\hspace{0.33em}\hspace{0.33em}=\hspace{0.33em}dt$ in order to obtain the final result (9) (here, C and ${\left(\frac{dr}{dt}\right)}_0^2=const$ are a constants determined by the initial conditions).

The quadrature in (9) determines the dependence in the general form t = t(r), which contains the elliptic integral in the left part of (9) {under appropriate initial conditions; the upper limit of the integral is equal to r, and the lower limit is equal to r₀}, and the right part of the quadrature in (9) equals (t − t₀), where t₀ = 0. Let us re-inverse this expression into the dependence r = r(t), which can be obtained by numerical methods only (by an appropriate approximation technique or, e.g., by a series of Taylor expansions), and then afterwards, a solution can be obtained to be presented in terms of quasi-periodic cycles.

It should be especially outlined that in the case of the classical limit of the dynamical model of action of the gravitational field in (2) (when considering the case with a sufficiently small absolute meaning of h « 1), Equation (9) can be simplified by neglecting terms which have a third extent of smallness and less in the series of Taylor expansions (in expressions under the sign of a square root such as $\left(h^2\frac{\epsilon }{r^2}\right)$ or ${\left(\frac{\epsilon }{r^2}\right)}^2$, ε → 0) in the left part of the integrand of the entire integral expression in (9), as follows in (10):

$$\begin{array}{l}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\displaystyle \underset{r_0}{\overset{r}{\int }}\sqrt{\frac{(r^2+\hspace{0.33em}\epsilon )}{E_0(r^2+\hspace{0.33em}\epsilon )-h^2\left(1+\hspace{0.33em}\left(\frac{\epsilon }{r^2}\right)\right)\hspace{0.33em}\hspace{0.33em}+\hspace{0.33em}2\mu r}}dr}\hspace{0.33em}\hspace{0.33em}=\hspace{0.33em}t\hspace{0.33em}\hspace{1em}\Rightarrow \\ \left\{E_0=const={\left(\frac{dr}{dt}\right)}_0^2+C\right\}\hspace{1em}\Rightarrow \hspace{1em}\hspace{1em}\hspace{0.33em}{\displaystyle \underset{r_0}{\overset{r}{\int }}\left(\frac{\left(r+\left(\frac{\epsilon }{2r}\right)\right)}{\sqrt{E_0{r}^2\hspace{0.33em}+\hspace{0.33em}2\mu r\hspace{0.33em}+\hspace{0.33em}\left(\epsilon E_0\hspace{0.33em}-h^2\right)}}\right)dr}\hspace{0.33em}\hspace{0.33em}\cong \hspace{0.33em}t\end{array}$$

(10)

Having integrated the left part of (10) by parts, let us obtain Equation (11) below (A(r₀), B(r₀) are the constants, determined by the initial conditions)

$$\begin{array}{l}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}A(r)-A(r_0)+B(r)-B(r_0)\cong \hspace{0.33em}t\\ \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}A=\hspace{1em}\hspace{0.33em}{\displaystyle \underset{r_0}{\overset{r}{\int }}\left(\frac{r}{\sqrt{E_0{r}^2\hspace{0.33em}+\hspace{0.33em}2\mu r\hspace{0.33em}+\hspace{0.33em}\left(\epsilon E_0\hspace{0.33em}-h^2\right)}}\right)dr}\hspace{0.33em},\hspace{1em}\Rightarrow \hspace{0.33em}\hspace{1em}\left\{E_0>0\right\}\hspace{1em}\Rightarrow \\ \\ A\hspace{0.33em}=\hspace{0.33em}\hspace{0.33em}\left\{\begin{array}{c}\begin{array}{l}\hspace{0.33em}\hspace{0.33em}\frac{\sqrt{E_0{r}^2\hspace{0.33em}+\hspace{0.33em}2\mu r\hspace{0.33em}+\hspace{0.33em}\left(\epsilon E_0\hspace{0.33em}-h^2\right)}}{E_0}\hspace{0.33em}-\hspace{0.33em}\frac{\mu }{E_0}\frac{1}{\sqrt{E_0}}\ln \left|2E_{0}r+2\mu +2\sqrt{E_0}\left(\sqrt{E_0{r}^2\hspace{0.33em}+\hspace{0.33em}2\mu r\hspace{0.33em}+\hspace{0.33em}\left(\epsilon E_0\hspace{0.33em}-h^2\right)}\right)\right|\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{0.33em}\left\{{\mu }^2\ne E_0\left(\epsilon E_0\hspace{0.33em}-h^2\right)\right\}\end{array}\\ \\ \frac{\sqrt{E_0{r}^2\hspace{0.33em}+\hspace{0.33em}2\mu r\hspace{0.33em}+\hspace{0.33em}\left(\epsilon E_0\hspace{0.33em}-h^2\right)}}{E_0}\hspace{0.33em}\hspace{0.33em}-\hspace{0.33em}\frac{\mu }{E_0}\frac{1}{\sqrt{E_0}}\ln \left|2E_{0}r+2\mu \right|\hspace{0.33em}\hspace{1em}\hspace{1em}\hspace{1em}\left\{{\mu }^2=E_0\left(\epsilon E_0\hspace{0.33em}-h^2\right)\right\}\end{array}\right.\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}B={\displaystyle \underset{r_0}{\overset{r}{\int }}\left(\frac{\epsilon }{2r\sqrt{E_0{r}^2\hspace{0.33em}+\hspace{0.33em}2\mu r\hspace{0.33em}+\hspace{0.33em}\left(\epsilon E_0\hspace{0.33em}-h^2\right)}}\right)dr}\hspace{0.33em},\hspace{1em}\Rightarrow \hspace{1em}\left\{E_0>0,\hspace{1em}\left(\epsilon E_0\hspace{0.33em}-h^2\right)\ne 0\right\}\hspace{1em}\Rightarrow \\ B\hspace{0.33em}=\hspace{0.33em}\hspace{0.33em}\left\{\begin{array}{c}\begin{array}{l}\hspace{0.33em}-\frac{\epsilon }{\sqrt{\left(\epsilon E_0\hspace{0.33em}-h^2\right)}}\ln \left|\frac{2\mu r\hspace{0.33em}+\hspace{0.33em}2\left(\epsilon E_0\hspace{0.33em}-h^2\right)+2\sqrt{\left(\epsilon E_0\hspace{0.33em}-h^2\right)}\left(\sqrt{E_0{r}^2\hspace{0.33em}+\hspace{0.33em}2\mu r\hspace{0.33em}+\hspace{0.33em}\left(\epsilon E_0\hspace{0.33em}-h^2\right)}\right)}{r}\right|\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\left\{\left(\epsilon E_0\hspace{0.33em}-h^2\right)>0,\hspace{0.33em}\hspace{0.33em}{\mu }^2\ne E_0\left(\epsilon E_0\hspace{0.33em}-h^2\right)\right\}\end{array}\\ \\ -\frac{\epsilon }{\sqrt{\left(\epsilon E_0\hspace{0.33em}-h^2\right)}}\ln \left|\frac{2\mu r\hspace{0.33em}+\hspace{0.33em}2\left(\epsilon E_0\hspace{0.33em}-h^2\right)}{r}\right|\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left\{\left(\epsilon E_0\hspace{0.33em}-h^2\right)>0,\hspace{0.33em}\hspace{0.33em}{\mu }^2=E_0\left(\epsilon E_0\hspace{0.33em}-h^2\right)\right\}\\ \\ \hspace{1em}\frac{\epsilon }{\sqrt{-\hspace{0.33em}\left(\epsilon E_0\hspace{0.33em}-h^2\right)}}\arcsin \left(\frac{2\mu r\hspace{0.33em}+\hspace{0.33em}2\left(\epsilon E_0\hspace{0.33em}-h^2\right)}{r\sqrt{{\mu }^2-E_0\left(\epsilon E_0\hspace{0.33em}-h^2\right)}}\right)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\left\{\left(\epsilon E_0\hspace{0.33em}-h^2\right)<0,\hspace{0.33em}\hspace{0.33em}{\mu }^2>E_0\left(\epsilon E_0\hspace{0.33em}-h^2\right)\right\}\end{array}\right.\end{array}$$

(11)

When considering the case with a sufficiently small absolute meaning of h « 1, the last sub-case on the integral B(r) can be omitted for the reason that E₀ > 0. Thus, (11) can be simplified using the expressions in (12) as follows:

$$\begin{array}{l}A\hspace{0.33em}=\hspace{0.33em}\hspace{0.33em}\left\{\begin{array}{c}\begin{array}{l}\hspace{0.33em}\hspace{0.33em}\frac{\sqrt{E_0{r}^2\hspace{0.33em}+\hspace{0.33em}2\mu r\hspace{0.33em}+\hspace{0.33em}\epsilon E_0}}{E_0}\hspace{0.33em}-\hspace{0.33em}\frac{\mu }{E_0}\frac{1}{\sqrt{E_0}}\ln \left|2E_{0}r+2\mu +2\sqrt{E_0}\left(\sqrt{E_0{r}^2\hspace{0.33em}+\hspace{0.33em}2\mu r\hspace{0.33em}+\hspace{0.33em}\epsilon E_0}\right)\right|\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{1em}\hspace{0.33em}\left\{{\mu }^2\ne \epsilon {(E_0)}^2\right\}\end{array}\\ \\ \frac{\sqrt{E_0{r}^2\hspace{0.33em}+\hspace{0.33em}2\mu r\hspace{0.33em}+\hspace{0.33em}\epsilon E_0}}{E_0}\hspace{0.33em}\hspace{0.33em}-\hspace{0.33em}\frac{\mu }{E_0}\frac{1}{\sqrt{E_0}}\ln \left|2E_{0}r+2\mu \right|\hspace{0.33em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left\{{\mu }^2=\epsilon {(E_0)}^2\right\}\end{array}\right.\\ \\ B\hspace{0.33em}\hspace{0.33em}=\hspace{0.33em}\hspace{0.33em}\left\{\begin{array}{c}\hspace{0.33em}\hspace{0.33em}-\sqrt{\frac{\epsilon }{E_0}}\ln \left|\frac{2\mu r\hspace{0.33em}+\hspace{0.33em}2\epsilon E_0+2\sqrt{\epsilon E_0}\left(\sqrt{E_0{r}^2\hspace{0.33em}+\hspace{0.33em}2\mu r\hspace{0.33em}+\hspace{0.33em}\epsilon E_0}\right)}{r}\right|\hspace{1em}\hspace{0.33em}\left\{{\mu }^2\ne \epsilon {(E_0)}^2\right\}\\ \\ -\sqrt{\frac{\epsilon }{E_0}}\ln \left|\frac{2\mu r\hspace{0.33em}+\hspace{0.33em}2\epsilon E_0}{r}\right|\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left\{{\mu }^2=\epsilon {(E_0)}^2\right\}\end{array}\right.\hspace{0.33em}\end{array}$$

(12)

Let us choose special initial conditions (satisfying the equality $\epsilon {(E_0)}^2={\mu }^2$); then, Equation (11) can be presented accordingly, as below (13):

$$\begin{array}{l}\hspace{1em}\hspace{0.33em}\hspace{0.33em}\frac{\sqrt{E_0{r}^2\hspace{0.33em}+\hspace{0.33em}2\mu r\hspace{0.33em}+\hspace{0.33em}\epsilon E_0}}{E_0}\hspace{0.33em}\hspace{0.33em}-\hspace{0.33em}\frac{\mu }{E_0}\frac{1}{\sqrt{E_0}}\ln \left|2E_{0}r+2\mu \right|\hspace{0.33em}\hspace{0.33em}-\sqrt{\frac{\epsilon }{E_0}}\ln \left|\frac{2\mu r\hspace{0.33em}+\hspace{0.33em}2\epsilon E_0}{r}\right|\hspace{0.33em}\cong \hspace{0.33em}t+A(r_0)+B(r_0)\Rightarrow \\ \\ \hspace{0.33em}\left\{\epsilon {(E_0)}^2={\mu }^2\right\}\hspace{1em}\Rightarrow \hspace{1em}\frac{\sqrt{E_0{r}^2\hspace{0.33em}+\hspace{0.33em}2\sqrt{\epsilon }{E}_{0}r\hspace{0.33em}+\hspace{0.33em}\epsilon E_0}}{E_0}\hspace{0.33em}-\sqrt{\frac{\epsilon }{E_0}}\left(\ln \left|\left(4{E_0}^2\sqrt{\epsilon }\right)\frac{{(r+\sqrt{\epsilon })}^2}{r}\right|\right)\hspace{0.33em}\cong \hspace{0.33em}t+A(r_0)+B(r_0)\Rightarrow \\ \\ \hspace{0.33em}\frac{r}{\sqrt{\epsilon }}-\ln \left(1+\frac{r}{2\sqrt{\epsilon }}\right)\hspace{0.33em}\cong \hspace{0.33em}\left(\sqrt{\frac{E_0}{\epsilon }}\right)(t+A(r_0)+B(r_0))+\hspace{0.33em}\ln \left(8{E_0}^2\epsilon \right)-1\hspace{1em}\hspace{0.33em}\Rightarrow \hspace{0.33em}\hspace{1em}r\hspace{0.33em}\cong \hspace{0.33em}2\left(\sqrt{E_0}\right)(t+A(r_0)+B(r_0))+\hspace{0.33em}2\sqrt{\epsilon }\left[\ln \left(8{E_0}^2\epsilon \right)-1\right]\end{array}$$

(13)

By re-inversing the last of Equation (13) into the dependence r = r(t), we can then calculate in (14) an expression for θ(t) from (4), as below:

$$\begin{array}{l}\theta \hspace{0.33em}\hspace{0.33em}=\hspace{0.33em}h{\displaystyle \underset{o}{\overset{t}{\int }}\left(\frac{dt}{{(2\left(\sqrt{E_0}\right)(t+A(r_0)+B(r_0))+\hspace{0.33em}{R}_0)}^2}\right)}\hspace{0.33em}=\frac{1}{2\left(\sqrt{E_0}\right)R_0}\hspace{0.33em}-\hspace{0.33em}\frac{1}{2\left(\sqrt{E_0}\right)(2\left(\sqrt{E_0}\right)(t+A(r_0)+B(r_0))+\hspace{0.33em}{R}_0)}\\ \\ \hspace{1em}\hspace{0.33em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.33em}\hspace{1em}\hspace{0.33em}\left\{R_0=2\sqrt{\epsilon }\left[\ln \left(8{E_0}^2\epsilon \right)-1\right]\right\}\end{array}$$

(14)

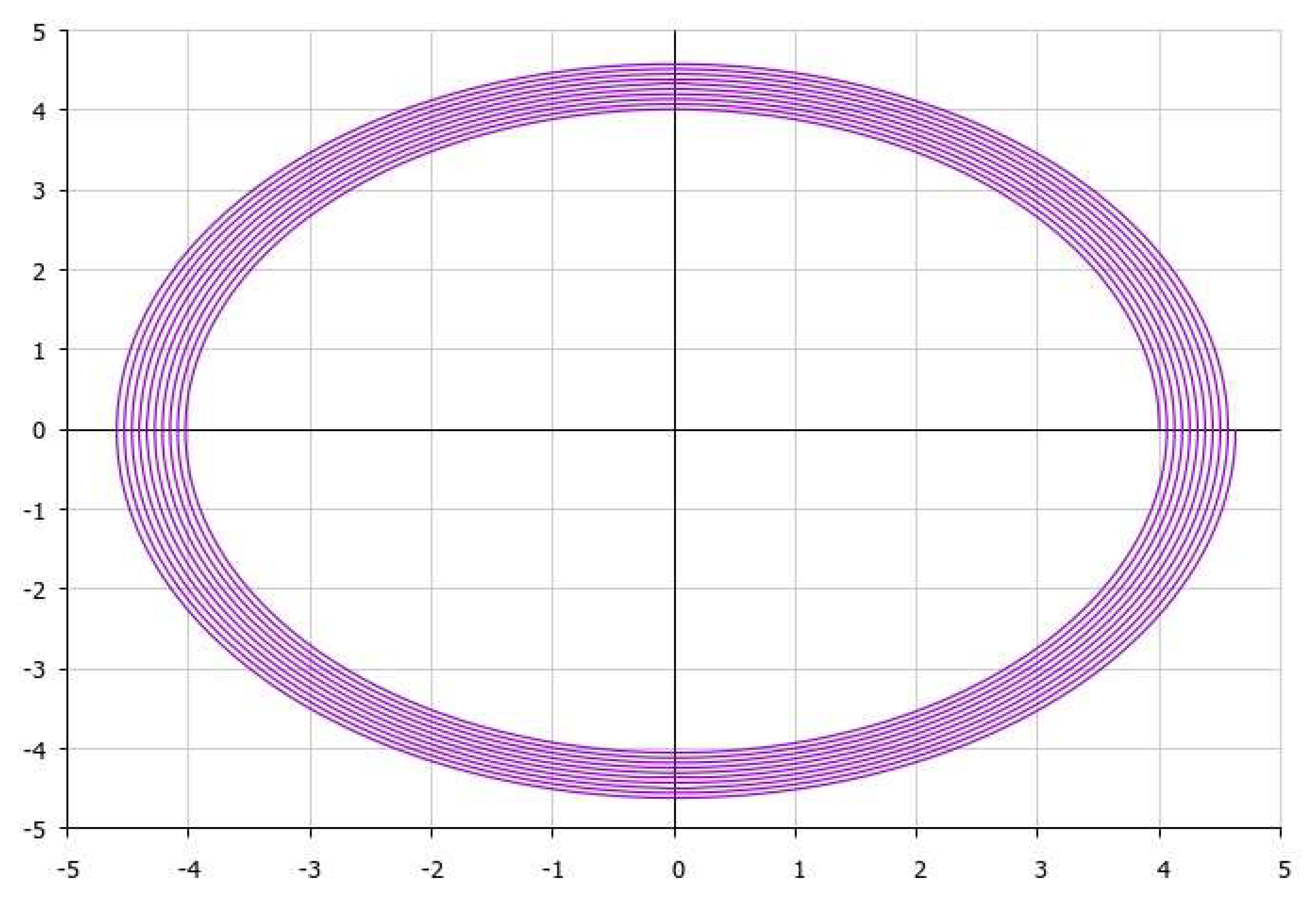
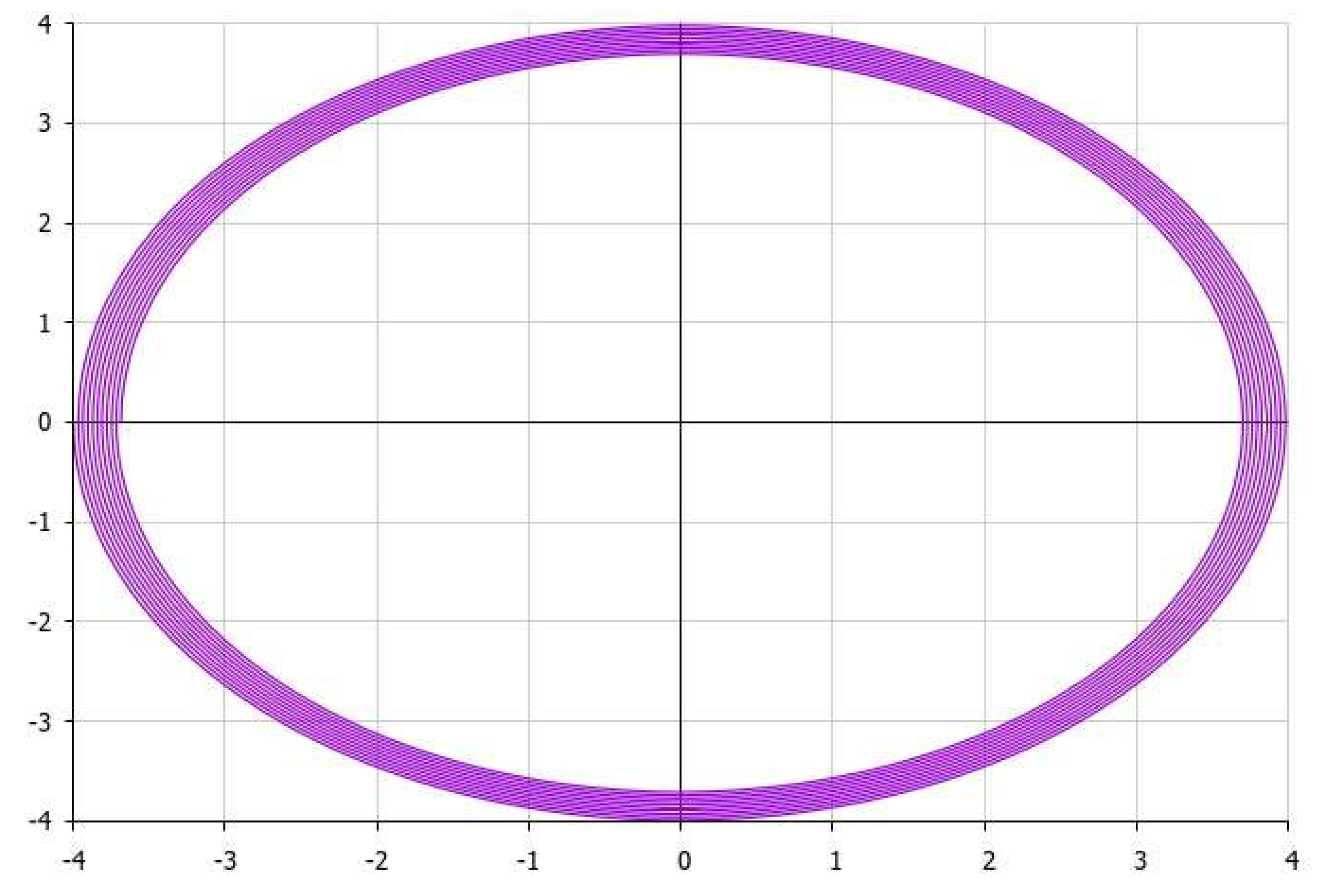
It is also worth schematically presenting the obtained solution as a graphical approximation of the last of formulae (13) via polar functions, as follows (Figure 1 and Figure 2):

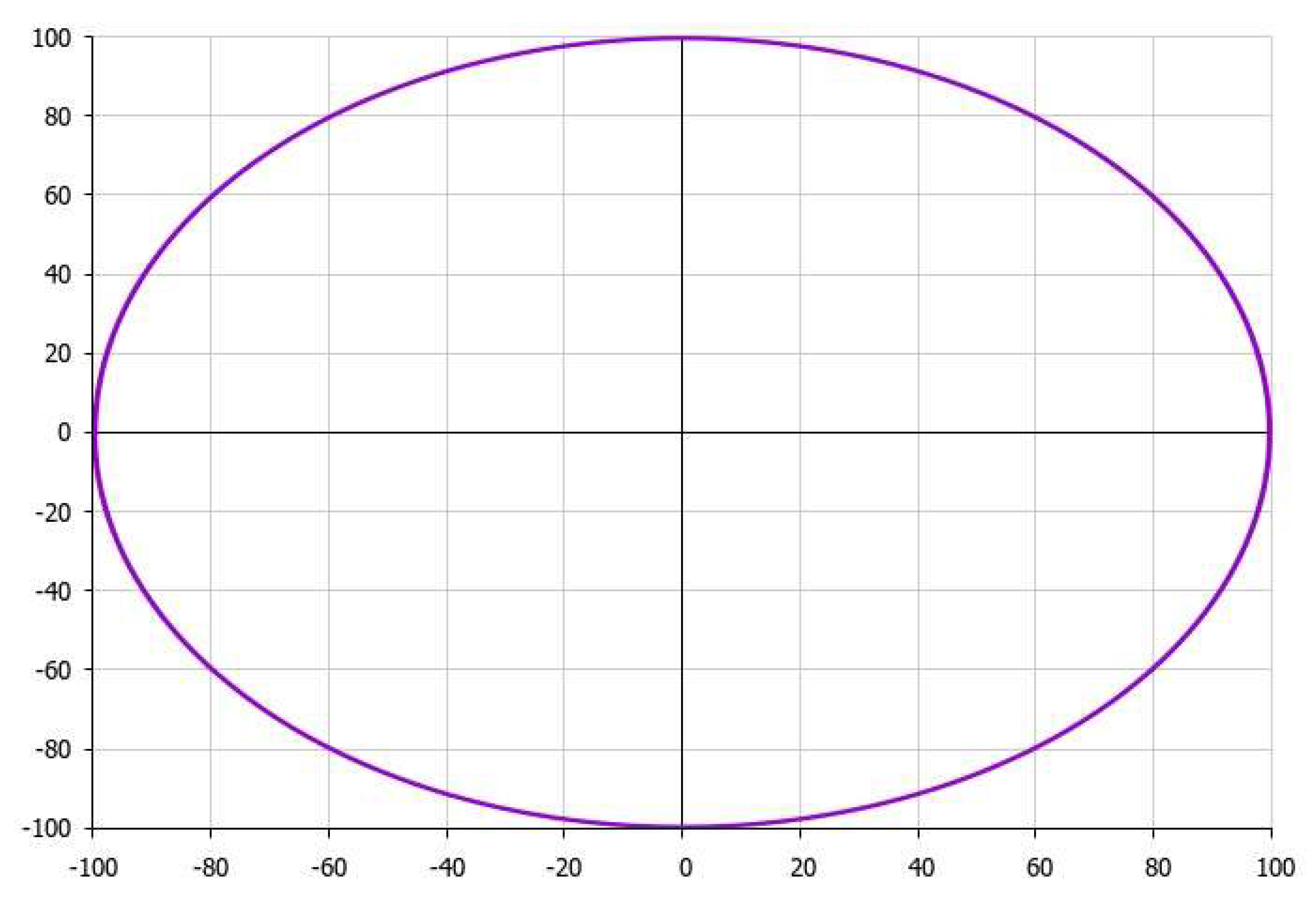
Obviously, with the aim of introducing a comparison between each of variants presented in Figure 1 and Figure 2, respectively, with the results obtained by simulation using the known classical equations, let us note that the latter generates classical ellipse as presented in Figure 3, without any perturbation of the orbit of the mass point (when we choose ε → 0 in (13)):

Furthermore, it is worth noting that the investigation of the real dynamics of a large companion of primary celestial body should be made with a detailed model based on real astronomical observations over a long period of time.

5. Discussion

While Newton/Kepler gravitation laws have been hallmarks of modern astronomy up to nowdays several recent results [5,6,7,8] have pointed out limitations to Kepler law of gravitation, considering various perturbing forces, proposing new models. It is our hypothesis here that a Kepler law can be approximated better by virtue of fractional equations. That is our hypothesis, and we discuss how a different initial point of view can generate better explanations of astronomical phenomena in our solar system.

Let us illuminate once again that the two-body classical system provides a good description of the dynamical properties of motion and gives important insights and predictions on the future motion of a body, but it is not enough in most cases to obtain precise results. This is because, in reality, the sun acts as the major source of force in the solar system. But it is not fixed and is subjected to many accelerations [21,22,23,24,25,26,27,28], even if they are small, due to the motion of the planets or even other stars according to Newton’s second and third laws or tidal phenomena. In addition, there is a mutual attractive force between the planets, and they attract each other. Therefore, the total force affecting a planet’s movement is not caused only by the sun. It is also worth noting that other planets perturb the elliptical motion that would occur for a specified planet if that planet were the only one orbiting an isolated sun. Therefore, Kepler’s laws have their own limitations and give only approximations for actual motion because the Kepler problem itself cannot provide an accurate description for the motion of two bodies in most cases (in the hope of obtaining accurate information about the properties of that motion, such as determining its orbit, predicting its paths in the future, or even estimating the moment of escape of one of the two bodies from the sphere of gravitational influence of the other), so the velocity and direction of motion cannot be estimated in a precise way. It is considered only in a theoretical sense to approximate the celestial bodies or treat them as point masses, which is nevertheless far from the realistic situation.

Thus, the aforeformulated problem under the modified potential, which is created from the continued fraction potential of a mass point orbiting a primary celestial body, has been studied in the current research, and an analytical solution has been found. Nevertheless, an essential limitation of the suggested approach is that it still approximates and treats the celestial bodies as point masses. This model does not take into account tidal phenomena [29] influencing the orbits of the celestial bodies, dancing in a gravitational waltz around each other (or other non-linear effects [30,31,32,33,34,35]). Let us also mention the works [36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55], where these refs. are within the framework of applying an analytical approach to the study of mathematical models in applications to various non-linear problems in electrodynamics, celestial mechanics, or the dynamics of rigid body rotation. Among these references, Refs. [36,37,38] present seminal books on celestial mechanics, where a lot of examples can be found regarding analytical aspects in the study of the perturbing forces in the two-body problem. The work [39] introduces in detail a description of the effectiveness of using Nekhoroshev stability to investigate non-linear aspects of the dynamics in the elliptic restricted three-body problem. Furthermore, Refs. [40,41,42,43,44,45] investigate the stability of the motion of a planetoid under various perturbing effects stemming from the primary properties in three- and four-body problems (such as primary bodies with variable masses [41], a body’s oblateness and orbital eccentricity [42], the mass distribution in the ring of satellites orbiting around Saturn [43], or nonlinear dynamical effects to search for the orbits of satellites around the moon of Jupiter [44], along with the effect of the oblateness of an artificial satellite orbiting around a planet in an ER3BP [45]). On the other hand, the research in [46,47,48,49,50,51,52,53] presents a detailed analysis taking into account the tidal phenomena [29] influencing the mutual orbits of celestial bodies orbiting each other in so far as a specific kind of two-body problem with tidal effects taking place on the surfaces both of the primary body (a planet or large asteroid) and a satellite orbiting around it in a perturbed elliptical motion. Thus, they are mostly devoted to the investigation of the dynamics of the natural satellites of planets (but not limited to them), with detailed models based on astronomical observations. The work [54] studies such celestial dynamics, taking into account a logarithmic correction to the Newtonian gravitational potential, whereas [55] contributes to the study of the perihelion precession of an appropriate celestial body with the concept of modified Newtonian gravity being introduced and thoroughly taken into account.

In this groundbreaking analytical study, we have delved into the fascinating realm of celestial mechanics. Specifically, a novel solving method has been introduced that promises to revolutionize the determination of the coordinates of a mass point in orbit around a more massive primary body. Within the framework of the restricted two-body problem (R2BP), such research brings forth an innovative approach that holds immense potential for further advancements in space exploration and scientific understanding. This innovative approach involves the consideration of a continued fraction potential instead of the classical potential function in Kepler’s formulation of the restricted two-body problem (R2BP). By incorporating a continued fraction potential, the main aim was to enhance the general understanding of celestial mechanics and improve the accuracy of predictions in space exploration. This alternative approach offers unique insights into the dynamics of celestial bodies and opens up new possibilities for studying complex gravitational interactions. Through rigorous research and meticulous analysis, this novel approach was revealed to yield more precise results compared to conventional methods. By embracing this paradigm shift, new avenues can be unlocked for exploring and gaining a deeper understanding of the outer universe. We firmly believe that by adopting this alternative perspective in Kepler’s formulation, such a novel understanding of celestial mechanics can be revolutionized and make significant contributions to space exploration.

6. Conclusions

The resolution of the restricted two-body problem (R2BP) with a continued fraction potential marks a thorough and comprehensive breakthrough, yielding remarkable results. This milestone in scientific exploration has paved the way for a deeper understanding and accurate prediction of intricate systems. Through a meticulous examination of this formulation, the researchers have acquired invaluable insights into the fundamental principles that govern the universe. The implications of this advancement span various disciplines, including astrophysics, quantum mechanics, and beyond. With this significant breakthrough, new perspectives emerge, beckoning exploration into uncharted territories in the continuous pursuit of unraveling the mysteries of the cosmos.

In the domain of mathematical analysis, a revolutionary formula has been derived, elucidating the interplay between the variables t and r. This formula, employing a pertinent elliptic integral, furnishes an analytical framework for grasping their intricate relationship. Through the establishment of the inverse relation r = r(t), this remarkable solution unveils novel avenues for comprehending quasi-periodic cycles. The resultant formula offers profound insights into the intricate dynamics governing these variables, empowering mathematicians and researchers to delve deeper into their patterns and behaviors. With its meticulous formulation, this analytical tool facilitates a comprehensive understanding of how changes in one variable correspond to variations in the other. Moreover, by establishing an inverse connection between r and t, this formula facilitates the exploration of quasi-periodic cycles—phenomena marked by repetitive patterns that lack strict periodicity. This breakthrough sets the stage for investigating intricate systems characterized by cyclical behaviors exhibiting subtle temporal variations.

Armed with this potent formula, a plethora of hidden insights can be unveiled, unlocking mysteries across diverse domains, including physics, engineering, and beyond. The capability to scrutinize quasi-periodic cycles with precision and accuracy holds immense value in comprehending a myriad of phenomena within the intricate outer world.

7. Remarks (with Highlights)

• The novel approach is applied to obtain the stable orbit of a planetoid in a modified ER2BP.
• A continued fraction potential is considered here instead of Kepler’s formulation.
• The perturbation effect on the Kepler gravitational potential is tackled in this scheme.
• The modified ER2BP with a continued fraction potential has been fully solved.
• The orbiter demonstrates stable dynamics, as shown by the numerical findings presented in graphical plots.