Two-Stage Estimation of Partially Linear Varying Coefficient Quantile Regression Model with Missing Data

Abstract

In this paper, the statistical inference of the partially linear varying coefficient quantile regression model is studied under random missing responses. A two-stage estimation procedure is developed to estimate the parametric and nonparametric components involved in the model. Furthermore, the asymptotic properties of the estimators obtained are established under some mild regularity conditions. In addition, the empirical log-likelihood ratio statistic based on imputation is proposed, and it is proven that this statistic obeys the standard Chi-square distribution; thus, the empirical likelihood confidence interval of the parameter component of the model is constructed. Finally, simulation results show that the proposed estimation method is feasible and effective.

1. Introduction

The partially linear varying coefficient model, originally proposed by Zhang et al. [1], is a very flexible model that includes several sub-models, such as parametric, nonparametric, and semiparametric models. It not only has the advantages of the general linear model and robust nonparametric model but can also dynamically express the relationship between covariates and responses. At the same time, it maintains the explanatory power of parameters and the flexibility of nonparametric models (see [2,3]). Therefore, the model has been widely studied by many scholars. As we know, this model is usually estimated using the least-square (LS) estimation method. Although the LS method is the best method for normal distribution data sets, it may produce large deviations when there are abnormal values or errors in the data sets that obey heavy-tailed distributions. In order to remedy the defects of the LS method, Koenker and Bassett [4] proposed the quantile regression method, which can be used to explore the potential relationship between the response variables and covariates. Further, in order to avoid being influenced by the specific value of the quantile and improve estimation efficiency, the composite quantile regression (CQR) method was proposed by Zou and Yuan [5] based on quantile regression. So far, the CQR method has been applied to solve many problems. For example, new estimation and variable selection procedures for the semiparametric partially linear varying coefficient model were proposed by Kai et al. [6], showing that compared with the least-squares-based method, the CQR method is much more efficient for many non-normal errors. Jiang et al. [7] proposed a functional single-index composite quantile regression method and estimated the unknown slope function and link function using B-spline basis functions. Song et al. [8] proposed a penalized composite quantile regression estimator based on SCAD and the Laplacian error penalty (LEP), which can realize variable selection and estimation at the same time.

Despite significant advances in CQR theory and its applications, the CQR method has attracted more attention when missing values are contained in data samples, which arises in various fields, including economics, engineering, biology, and epidemiology. Due to various man-made or other unknown factors, it is easy to produce a large number of missing data. Considering this problem, several methods have been proposed to deal with missing data, such as the imputation method [9,10,11], complete-case (CC) analysis method [12], likelihood-based method [13], and inverse probability weighted method (IPW) [14,15,16]. Thus, some scholars have applied the CQR method in the case of missing data. Based on inverse probability weighted and B-spline approximations, Jin et al. [17] proposed a weighted B-spline composite quantile regression method to estimate nonparametric functions and regression coefficients for the partially linear varying coefficient model with missing covariates.

Further, the empirical likelihood method, introduced by Owen in [18,19], is a non-parametric statistical inference method for complete samples, which has similar sampling characteristics to the bootstrap method. It has many outstanding advantages, including domain preservation, the shape of the confidence region determined by the data, Bartlett correction, and without constructing axis statistics compared with classical or modern statistical methods. As a result, this method has attracted the attention of many statisticians and thus has been applied to analyze linear, nonparametric, and semiparametric regression models. For example, Zhao and Xue [20] used this method to give the adjusted empirical likelihood ratio function of the parameter part and proved that it asymptotically obeyed the standard Chi-square distribution. Wang and Zhu [21] developed two methods of longitudinal data inference based on this method under the framework of quantile regression. Yan et al. [22] proposed an empirical likelihood method based on imputation combined with quantile regression to construct confidence intervals of parametric and nonparametric components. In this paper, we combine the imputation method and the empirical likelihood inference to propose a composite quantile regression estimation for the partially linear varying coefficient model when the responses are missing at random.

The rest of this paper is organized as follows. In Section 2, a two-stage estimation procedure is developed to estimate the parametric and nonparametric components. Based on this, methods for constructing imputation empirical likelihood-based confidence intervals for the parametric components are presented, and some asymptotic properties of the proposed estimator are studied. In Section 3, some simulation studies and a real data application are used to evaluate the performance of the proposed method. In addition, the proofs of the main results are given in Section 4.

2. Two-Stage Estimation Method

In what follows, we use the two-stage estimation procedure [23] to estimate the parametric and nonparametric components involved in the following partially linear varying coefficient model:

$$Y=X^T\alpha \left(U\right)+Z^T\beta +\epsilon ,$$

(1)

where Y is the response, U is a one-dimensional variable, and $X^T$ and $Z^T$ are the corresponding covariates. Suppose that $\alpha (·)=({\alpha }_1(·),{\alpha }_2(·),\cdots ,{\alpha }_p(·))$ is the unknown vector whose components are smooth coefficient functions, $\beta =({\beta }_1,{\beta }_2,\cdots ,{\beta }_q)$ is a $q\times 1$ vector, $\epsilon$ is the model error, and $\epsilon$ and $(U,X^T,Z^T)$ are independent of each other. If $Y_i,X_i,U_i,Z_i$ are random samples, we have

$$Y_i=X_i^T\alpha \left(U_i\right)+Z_i^T\beta +{\epsilon }_i,i=1,2,\cdots ,n.$$

(2)

An indicator variable ${\delta }_i$ is introduced in this paper such that

$${\delta }_i=\left\{\begin{array}{c}0,\mathrm{if}{Y}_i\mathrm{is}\mathrm{observed},\\ 1,\mathrm{if}{Y}_i\mathrm{is}\mathrm{missing}.\end{array}\right.$$

(3)

Further, $Y_i$ follows the following missing mechanism:

$$P({\delta }_i=1\mid Y_i,X_i,U_i,Z_i)=P({\delta }_i=1\mid X_i,U_i,Z_i).$$

Assuming $\beta$ is known, the model in (2) can be regarded as the general varying coefficient model. Next, we use the local linear composite quantile estimation method to estimate the varying coefficient function $\alpha (·)$. Specifically, for u in a neighborhood of $U_i$, the unknown coefficient function ${\alpha }_j\left(U_i\right)$ can be locally linearly approximated as

$${\alpha }_j\left(U_i\right)\approx {\alpha }_j\left(u\right)+{\alpha }_j^{\prime }\left(u\right)(U_i-u)\equiv a_j+b_j(U_i-u),j=1,\cdots ,p.$$

(4)

Let $c_k$ be the ${\tau }_k$ quantile of ${\epsilon }_i$, then $0<{\tau }_1<\cdots <{\tau }_k<1$. For a given non-negative integer K, let ${\tau }_k=\frac{k}{1+K}$, and let ${\rho }_{\tau }\left(v\right)=v(\tau -I(v<0))$ be a quantile loss function for $\tau \in (0,1)$, so $c_k$ is uniquely deterministic for any $0<{\tau }_k<1$. Then, the initial estimation ${\tilde{c}}_1,\cdots ,{\tilde{c}}_K,\tilde{a},\tilde{b},\tilde{\beta }$ of $c_1,\cdots ,c_K,a,b,\beta$ under complete data can be obtained by minimizing the following formula

$$\sum _{k=1}^K\sum _{i=1}^n{\delta }_i{\rho }_{{\tau }_k}\left\{Y_i-c_k-Z_i^T\beta -X_i^T[a+b(U_i-u)]\right\}{K}_h(U_i-u),$$

(5)

where $a={(a_1,\cdots ,a_p)}^T$, $b={(b_1,\cdots ,b_p)}^T$, $K_h(·)=h^{-1}K(·/h)$, and $K(·)$ is the kernel function. Then, we have $\tilde{a}=\tilde{\alpha }(U_i;\beta ),\tilde{b}={\tilde{\alpha }}^{\prime }(U_i;\beta )$. Further, by substituting $\tilde{a}$ into Formula (2), we can obtain

$${\tilde{Y}}_i=Z_i^T\beta +{\epsilon }_i,$$

(6)

where ${\tilde{Y}}_i=Y_i-X_i^T\tilde{\alpha }(U_i;\beta )$. Now, the model in (6) can be regarded as a general linear model. Then, the estimation for $\beta$ can be obtained by minimizing the following formula using the composite quantile regression estimation method

$$\widehat{\beta }=\mathrm{argmin}\sum _{k=1}^K\sum _{i=1}^n{\delta }_i{\rho }_{{\tau }_k}({\tilde{Y}}_i-c_k-Z_i^T\beta ).$$

(7)

The estimated efficiency of $\alpha \left(u\right)$ can be further improved by substituting $\widehat{\beta }$ into (5). Then, we have $\widehat{a}=\widehat{\alpha }(u;\widehat{\beta })$ and $\widehat{b}={\widehat{\alpha }}^{\prime }(u;\widehat{\beta })$.

2.1. Imputation-Based Empirical Likelihood Inference for $\beta$

Now, the confidence interval for $\beta$ is constructed for the imputation-based empirical likelihood inference method. When a large amount of data are missing, an empirical likelihood inference method based on imputation is proposed [24] to improve the accuracy of the confidence interval. Let $\widehat{\beta }$ and $Z_i^T\widehat{\beta }$ denote the estimation for $\beta$ and ${\tilde{Y}}_i$, respectively. In addition, the auxiliary random vectors based on imputation are defined as

$${\tilde{\eta }}_i\left(\beta \right)=\sum _{k=1}^K{Z}_i\left\{{\tau }_k-I({\delta }_i{\tilde{Y}}_i+(1-{\delta }_i)Z_i^T\widehat{\beta }-Z_i^T\beta \le {\tilde{c}}_k)\right\},$$

(8)

where $I(·)$ is an indicator function. The empirical log-likelihood ratio for $\beta$ is defined as

$$\tilde{R}\left(\beta \right)=-2\max \left\{\sum _{i=1}^n\log \left(n{p}_i\right)|p_i\ge 0,\sum _{i=1}^n{p}_i=1,\sum _{i=1}^n{p}_i{\tilde{\eta }}_i\left(\beta \right)=0\right\}.$$

(9)

If zero is inside the convex hull of the point $({\tilde{\eta }}_1\left(\beta \right),{\tilde{\eta }}_2\left(\beta \right),\dots ,{\tilde{\eta }}_n\left(\beta \right))$, there exists a unique optimal point for the optimization problem (9). It follows from the Lagrange multiplier method that $\tilde{R}\left(\beta \right)$ can be rewritten as

$$\tilde{R}\left(\beta \right)=2\sum _{i=1}^n\log \{1+{\lambda }^T{\tilde{\eta }}_i\left(\beta \right)\},$$

(10)

where $\lambda$ is a Lagrange multiplier that satisfies

$$\sum _{i=1}^n\frac{{\tilde{\eta }}_i\left(\beta \right)}{1+{\lambda }^T{\tilde{\eta }}_i\left(\beta \right)}=0.$$

(11)

2.2. Asymptotic Properties of Estimators

For convenience, the following notation is given. Note that $f(·)$ and $F(·)$ represent the density function and distribution function of the model error $\epsilon$, respectively. $f_U\left(u\right)$ represents the marginal density of the covariate u. Note that ${\tau }_{k{k}^{\prime }}=min({\tau }_k,{\tau }_{k^{\prime }})-{\tau }_k{\tau }_{k^{\prime }}$. To prove the asymptotic properties, we assume that the following regularity conditions hold:

C1: The random variable U has a bounded support $\mathrm{\Omega }$, and its density function $f_U\left(u\right)$ satisfies the Lipschitz condition and is continuous.

C2: $\{{\alpha }_j(·),j=1,\cdots ,p\}$ has a continuous second derivative.

C3: The density function of the model error $\epsilon$ satisfies f(·) > 0, and its derivative is continuously bounded.

C4: The random variable X has bounded support.

C5: The kernel function $K(·)$ is a symmetric probability density function with bounded support and satisfies the Lipschitz condition. Let

$${\mu }_j=\int u^{j}K\left(u\right)du<\infty ,v_j=\int u^j{K}^2\left(u\right)du<\infty ,j=0,1,2,\cdots .$$

C6: For a given $u\in \mathrm{\Omega }$, $D_1\left(u\right),\sum$ and ${\sum }_1$ are positive definite matrices.

C7: The covariates $X_i,i=1,\cdots ,n$ are $i.i.d.$ centred random vectors and satisfy

$${max}_{1\le i\le n}\Vert X_i\Vert /n^{1/2}⟶0$$

as $n⟶\infty$.

C8. Suppose that $\pi (x,u,z)=E\left({\delta }_i\right|X_i=x,U_i=u,Z_i=z)$ and $\pi \left(u\right)=E\left({\delta }_i\right|U_i=u)$. Furthermore, we let $\pi (x,u,z)>0$ for all $x,u$, and z.

Theorem 1.

Assume that conditions C1-C8 hold. Then,

$$\sqrt{n}(\widehat{\beta }-\beta )\stackrel{L}{⟶}N\left(0,c^{-2}{\sum }^{-1}\sum _{k=1}^K\sum _{k^{\prime }=1}^K{\tau }_{k{k}^{\prime }}\Delta {\sum }^{-1}\right)$$

if β is the true value of the parameter, where $\stackrel{L}{⟶}$ denotes convergence in distribution, $\sum =\pi (U,X,Z)E\left(Z{Z}^T\right)$, $\Delta =E\left(\pi (U,X,Z)\right)E\left\{[\delta Z-\omega (U,X,Z)]{[\delta Z-\omega (U,X,Z)]}^T\right\}$, $\omega (U,X,Z)$$=E\left[Z(0^T,X^T,0)\right|U=u]D^{-1}\left(u\right){(I_K,{\mathbf{1}}^{T}X,{\mathbf{1}}^{T}Z)}^T$, and

$$D\left(u\right)=E\left[\left(\begin{array}{ccc}I& \mathbf{1}{X}^T& \mathbf{1}{Z}^T\\ X{\mathbf{1}}^T& X{X}^T& X{Z}^T\\ Z{\mathbf{1}}^T& Z{X}^T& Z{Z}^T\end{array}\right)|\begin{array}{c}\\ U=u\\ \end{array}\right],$$

where $I=diag(1,\cdots ,1),\mathbf{1}={(1,\cdots ,1)}^T.$

Theorem 2.

Assume that conditions C1-C8 hold, as $n⟶\infty$. Then,

$$\sqrt{nh}(\widehat{a}-\alpha \left(u\right)-\frac{1}{2}{h}^2{\mu }_2{\alpha }^{″}\left(u\right))\stackrel{L}{⟶}N\left(0,\sum _{k=1}^K\sum _{k^{\prime }=1}^K{\tau }_{k{k}^{\prime }}E\left(\pi \left(u\right)\right)v_0{f}_U^{-1}\left(u\right){\sum }_1^{-1}\right),$$

where $\stackrel{L}{⟶}$ denotes convergence in distribution, and ${\mu }_2=\int u^{2}K\left(u\right)du$, $v_0=\int K^2\left(u\right)du$, and ${\sum }_1=Var\left(X\right|U=u)$.

Theorem 3.

Assume that conditions C1-C8 hold. Then,

$$R\left(\beta \right)\stackrel{L}{⟶}{\chi }_q^2$$

if β is the true value of the parameter, where $\stackrel{L}{⟶}$ denotes convergence in distribution, and ${\chi }_q^2$ is the Chi-square distribution with q degrees of freedom.

Then, the confidence region for $\beta$ will be constructed based on the results. For a given $\alpha$ with $0<\alpha <1$, let $c_{\alpha }$ satisfy $P({\chi }_q^2\le c_{\alpha })=1-\alpha$. Then, the approximate $1-\alpha$ confidence region for $\beta$ can be defined as

$$C_{\alpha }\left(\beta \right)=\left\{\beta \right|R\left(\beta \right)\le {\chi }_q^2(1-\alpha )\}.$$

3. Numerical Results

3.1. Simulation Studies

A numerical simulation experiment was carried out to study the performance of the proposed method under finite samples. We considered the following partially linear varying coefficient model and the data were also generated using this model

$$Y_i=Z_i\beta +X_i\left(\sin \left(2\pi U_i\right)\right)+{\epsilon }_i,$$

where $\beta =3$, $X_i\sim N(0,1)$, $U_i\sim U(0,1)$, $Z_i\sim N(0,1)$, ${\epsilon }_i\sim N(0,0.01)$, and the response $Y_i$ is generated according to the model. Throughout the simulation study, we used the Epanechnikov kernel function, where $K\left(u\right)=0.75(1-u^2)$. Further, we used the cross-validation method to select the optimal bandwidth $h_{CV}$

$$CV\left(h\right)=\sum _{i=1}^n{\delta }_i{\rho }_{\tau }(Y_i-X_i^T{\widehat{\alpha }}^{\left[i\right]}\left(U_i\right)-Z_i^T{\widehat{\beta }}^{\left[i\right]}),$$

where ${\rho }_{\tau }\left(v\right)=v(\tau -I(v<0))$ is the quantile loss function, and ${\widehat{\alpha }}^{\left[i\right]}\left(U_i\right)$ and ${\widehat{\beta }}^{\left[i\right]}$ are the estimators of $\alpha \left(u\right)$ and $\beta$ after deleting the ith subject. Next, we considered the following three cases of missing probabilities: $\pi (x,u,z)=P(\delta =1\mid X_i=x,Z_i=z,U_i=u)$: (1) ${\pi }_1(x,z,u)={\{2.5+\exp (y-0.6x-0.3z-0.2u-3)\}}^{-1}$; (2) ${\pi }_2(x,z,u)={\{1+\exp (y-0.4x-0.2z-0.1u-3)\}}^{-1}$; (3) ${\pi }_3(x,z,u)={\{1+2\exp (y-0.5x-0.2z-0.1u-3)\}}^{-1}$.

Thus, the missing probabilities corresponding to the scenarios were approximately 0.1, 0.25, and 0.4, respectively. In this simulation, the quantile vector was taken as $\tau ={(0.1,\cdots ,0.9)}^T$ with $K=9$, and the sample sizes were set to $n=100,n=300$, and $n=1000$, respectively. For each case, we conducted 1000 simulation runs. The estimation errors, standard deviations, and mean squared errors of the estimator with the three missing probabilities are summarized in Table 1. For the nonparametric component, we provide an estimation curve for the component of the coefficient $\alpha \left(u\right)$ with a missing probability of 0.25 and $n=300$.

Table 1. The bias, SD, and MSE for $\beta$ with three missing probabilities.

$\mathit{\pi }$	n	Bias	SD	MSE
${\pi }_1$	$n=100$	−0.0127	0.0956	0.0093
	$n=300$	−0.0004	0.0474	0.0022
	$n=1000$	−0.0002	0.0247	0.0010
${\pi }_2$	$n=100$	−0.0102	0.2559	0.0655
	$n=300$	−0.0044	0.1187	0.0142
	$n=1000$	−0.0027	0.0827	0.0101
${\pi }_3$	$n=100$	0.0212	0.1893	0.0363
	$n=300$	0.0030	0.0764	0.0058
	$n=1000$	0.0019	0.0402	0.0039

The following conclusions can be drawn from Table 1:

(1) For a given missing probability, with the increase in the sample size, the standard deviation and mean square error of the given estimator decrease.

(2) For a given sample size, with the increase in the missing probability, the deviation and mean square error of the given estimator increase.

In addition, by comparing the real curve with the estimated curve, as shown in Figure 1, we can see that the method proposed in this paper is effective.

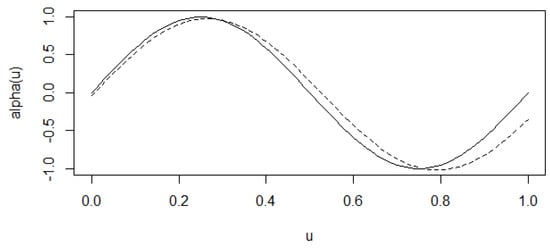
Figure 1. Estimation curve (dashed line) and true curve (solid line) of $\alpha \left(u\right)$.

Next, we used the empirical likelihood method to construct the confidence interval for $\beta$. In order to evaluate the performance of the proposed statistical inference method, two methods were compared in the following simulation study: the imputation-based empirical likelihood method (IEL) proposed in this paper and the complete data-based empirical likelihood method (CEL). Under three different missing probabilities, the upper and lower 95% confidence limits for $\beta$ and the corresponding coverage probabilities were computed. The sample sizes were set to $n=100,n=300$, and $n=1000$, respectively. The upper and lower confidence limits, the average length of the confidence intervals, and the coverage probabilities are summarized in Table 2.

Table 2. Confidence intervals and coverage probabilities for $\beta$ under two different methods.

		IEL				CEL
$\mathit{n}$	$\mathit{\pi }$	LOW	UP	LEN	CP	LOW	UP	LEN	CP
$n=100$	${\pi }_1$	2.8469	3.1435	0.2966	0.946	2.7012	3.3273	0.6261	0.931
	${\pi }_2$	2.8495	3.1526	0.3031	0.940	2.6794	3.3398	0.6604	0.928
	${\pi }_3$	2.8430	3.1498	0.3068	0.932	2.6558	3.3424	0.6866	0.920
$n=300$	${\pi }_1$	2.9137	3.0791	0.1654	0.952	2.8765	3.1177	0.2412	0.942
	${\pi }_2$	2.9166	3.0833	0.1666	0.948	2.8496	3.2121	0.3625	0.940
	${\pi }_3$	2.9119	3.0785	0.1665	0.940	2.8270	3.2215	0.3945	0.937
$n=1000$	${\pi }_1$	2.9731	3.0515	0.0784	0.957	2.9626	3.0617	0.0991	0.952
	${\pi }_2$	2.9705	3.0689	0.0984	0.956	2.9186	3.1044	0.1858	0.950
	${\pi }_3$	2.9698	3.0949	0.1251	0.954	2.9067	3.1328	0.2261	0.949

As can be seen in Table 2, as the sample size increased under the same missing probability, the confidence interval lengths of the two methods decreased and the coverage probabilities increased. However, the IEL method yielded smaller confidence intervals and higher coverage probabilities compared to the CEL method, so the IEL method is better than the CEL method. Similarly, as the missing probability increased under the same sample size, the confidence interval lengths of the two methods increased and the coverage probability decreased. However, the IEL method yielded smaller confidence intervals and higher coverage probabilities compared to the CEL method, so the IEL method is superior to the CEL method.

3.2. Application to a Real Data Example

In this section, we apply our proposed method to NCCTG lung cancer data, which are available in the R software (latest v. 4.2.3). In this data set, there are 228 patients with lung cancer, and the survival days for 63 of these patients have been deleted for various reasons, with a missing rate of about 27.63%. There are 10 variables in this data set, but we paid more attention to the following variables: time (survival time), ph.karno (Karnofsky performance score, assessed by doctors), meal.cal (calories consumed from three meals), and age (age of lung cancer patients). Here, we used the model in (1) to fit the lung cancer data, where Y represents the survival time, U represents age, Z represents meal.cal, and X represents ph.karno. For comparison, we considered composite levels K of 5 and 9 in the CQR method, denoted as CQR5 and CQR9, respectively.

Next, we compare the results obtained using the CQR5 and CQR9 methods for estimating $\beta$ and give an estimation curve for the component of the coefficient $\alpha (·)$ using the CQR9 method. Then, we present the estimator and its corresponding 95% confidence interval for $\beta$ based on the proposed IEL method. The results for the CQR method and the confidence interval for $\beta$ are summarized in Table 3. The estimation curve for the component of the varying coefficient $\alpha (·)$ is shown in Figure 2. From Table 3, we can see that the confidence interval length of the CQR9 method is smaller than that of the CQR5 method, which indicates that the CQR9 method synthesizes more information about the quantile, which is consistent with the theory. In addition, it can be seen in Figure 2 that the varying coefficient function fluctuates with age.

Table 3. The results and confidence intervals for $\beta$ under the CQR5 method and CQR9 method.

Method	Estimator	Confidence Intervals
$CQR5$	0.6164	(0.1436, 0.8375)
$CQR9$	0.4297	(0.2547, 0.7155)

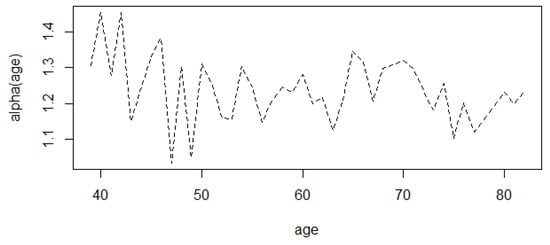
Figure 2. Estimation curve of $\alpha (·)$.

4. Proofs of Theorems

Lemma 1.

Let $(X_1,Y_1),\cdots ,(X_n,Y_n)$ be the $i.i.d$ random vectors, where $Y_i,i=1,\cdots ,n$ are one-dimensional random variables. At the same time, ${E\left|Y\right|}^s<\infty$ and $\underset{x}{sup}\int {\left|y\right|}^{s}f(x,y)dy<\infty$ hold, where $f(x,y)$ represents the joint density function of (X, Y). Let $K(·)$ be a bounded positive function with bounded support, satisfying the Lipschitz condition. Then, we have

$$\underset{x\in D}{sup}\mid \frac{1}{n}\sum _{i=1}^n[K_h(X_i-x)Y_i-E\left(K_h(X_i-x)Y_i\right)]\mid =O_p\left[{\left(\frac{log(1/h)}{nh}\right)}^{1/2}\right],$$

where $n^{2\epsilon -1}h⟶\infty$ for $\epsilon <1-s^{-1}$.

For the proof of Lemma 1, the reader is referred to Fan and Huang [3].

Lemma 2.

Suppose that $A_n\left(s\right)$ is convex and can be represented as $\frac{1}{2}{s}^{T}Vs+U_n^{T}s+C_n+r_n\left(s\right)$, where V is a symmetric and positive definite matrix, $U_n$ is stochastically bounded, $C_n$ is arbitrary, and $r_n\left(s\right)$ converges to 0 in probability for any s. Let the minimized solution of $A_n$ be ${\alpha }_n$, the minimized solution of $\frac{1}{2}{s}^{T}Vs+U_n^{T}s+C_n$ be ${\beta }_n=-V^{-1}{U}_n$, and the difference between them be of order $o_p\left(1\right)$. Further, if $U_n\stackrel{L}{⟶}U$, then ${\alpha }_n\stackrel{L}{⟶}-V^{-1}U$, where $\stackrel{L}{⟶}$ denotes convergence in distribution.

Lemma 2 is taken from the basic propositions in Hjort and Pollard [25].

Lemma 3.

Suppose that conditions C1-C8 hold. Then, we have

$$\sqrt{nh}{({\tilde{c}}_1-c_1,\cdots ,{\tilde{c}}_K-c_K,{(\tilde{a}-\alpha \left(u\right))}^T,{(\tilde{\beta }-\beta )}^T)}^T=-\pi {\left(u\right)}^{-1}{f}_U{\left(u\right)}^{-1}{D}_1^{-1}\left(u\right)W_n\left(u\right)+o_p\left(1\right),$$

where

$$D_1\left(u\right)=E\left[\left(\begin{array}{ccc}C& c{X}^T& c{Z}^T\\ X{c}^T& cX{X}^T& cX{Z}^T\\ Z{c}^T& cZ{X}^T& cZ{Z}^T\end{array}\right)|\begin{array}{c}\\ U=u\\ \end{array}\right],$$

$$\pi \left(u\right)=E\left(\delta \right|U=u),C=diag(f\left(c_1\right),\cdots ,f\left(c_k\right)),c={(f\left(c_1\right),\cdots ,f\left(c_k\right))}^T,$$

$$W_n\left(u\right)=\frac{1}{\sqrt{nh}}\sum _{k=1}^K\sum _{i=1}^n{\delta }_i{K}_i\left(u\right){\eta }_{i,k}^{*}\left(u\right){(e_k^T,X_i^T,Z_i^T)}^T,$$

$${\eta }_{i,k}^{*}\left(u\right)=I({\epsilon }_i\le c_k-r_i\left(u\right))-{\tau }_k,$$

$$r_i\left(u\right)=X_i^T[\alpha \left(U_i\right)-\alpha \left(u\right)-{\alpha }^{\prime }\left(u\right)(U_i-u)].$$

Proof. 

Note that $\theta =\sqrt{nh}({\tilde{c}}_1-c_1,\cdots ,{\tilde{c}}_K-c_K,{(\tilde{a}-\alpha \left(u\right))}^T,{(\tilde{\beta }-\beta )}^T,{(\tilde{b}-{\alpha }^{\prime }{\left(u\right)}^T)}^T$. Then, the estimate of $\theta$ can be obtained by minimizing the following loss function:

$$\sum _{k=1}^K\sum _{i=1}^n{\rho }_{{\tau }_k}\{Y_i-c_k-Z_i^T\beta -X_i[a+b(U_i-u)]\}{\delta }_i{K}_i(U_i-u).$$

(12)

(12) is equivalent to minimizing the following formula:

$$L_n\left(\theta \right)=\sum _{k=1}^K\sum _{i=1}^n{\delta }_i\left\{{\rho }_{{\tau }_k}({\epsilon }_i-c_k+r_i\left(u\right)-d_{i,k})-{\rho }_{{\tau }_k}({\epsilon }_i-c_k+r_i\left(u\right))\right\},$$

where $K_i\left(u\right)=K_h(U_i-u)$, $d_{i,k}={\tilde{X}}_{i,k}{\left(u\right)}^T\theta /\sqrt{nh}$, ${\tilde{X}}_{i,k}\left(u\right)={[e_k^T,X_i^T,Z_i^T,X_i^T(U_i-u)/h]}^T$. $e_k$ is the K-dimensional unit vector; its kth component is 1, and the remaining component is 0. According to the identity proposed by Knight [26],

$${\rho }_{\tau }(u-v)-{\rho }_{\tau }\left(u\right)=-v(\tau -I(u<0))+{\int }_0^v(I(u\le s)-I(u\le 0))ds,$$

(13)

and it is easy to obtain

$$\begin{array}{ccc}{L}_n\left(\theta \right)\hfill & =\hfill & {\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{K}_i\left(u\right)d_{i,k}[I({\epsilon }_i\le c_k-r_i\left(u\right))-{\tau }_k]\hfill \\ & \hfill & +{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{K}_i\left(u\right){\int }_0^{d_{i,k}}[I({\epsilon }_i\le c_k-r_i\left(u\right)+s)-I({\epsilon }_i\le c_k-r_i\left(u\right))]ds\hfill \\ & =\hfill & W_n^{*}{\left(u\right)}^T\theta +{\displaystyle \sum _{k=1}^K}{M}_{n,k}\left(\theta \right),\hfill \end{array}$$

where

$$W_n^{*}\left(u\right)=\frac{1}{\sqrt{nh}}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{K}_i\left(u\right){\eta }_{i,k}^{*}\left(u\right){\tilde{X}}_{i,k}\left(u\right),$$

$$M_{n,k}\left(\theta \right)={\displaystyle \sum _{i=1}^n}{\delta }_i{K}_i\left(u\right){\int }_0^{d_{i,k}}[I({\epsilon }_i\le c_k-r_i\left(u\right)+s)-I({\epsilon }_i\le c_k-r_i\left(u\right))]ds.$$

According to Lemma 1, we can obtain

$$M_{n,k}\left(\theta \right)=E\left[M_{n,k}\left(\theta \right)\right]+O_p({log}^{\frac{1}{2}}(1/h)/\sqrt{nh}).$$

Moreover,

$$\begin{array}{ccc}E\left[M_{n,k}\left(\theta \right)\right]\hfill & =\hfill & {\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}\pi \left(u\right)K_i\left(u\right){\int }_0^{d_{i,k}}[F(c_k-r_i\left(u\right)+s)-F(c_k-r_i\left(u\right))]ds\hfill \\ & =\hfill & {\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}\pi \left(u\right)K_i\left(u\right){\int }_0^{d_{i,k}}\left\{sf(c_k-r_i\left(u\right))[1+o\left(1\right)]\right\}ds\hfill \\ & =\hfill & \frac{1}{2}{\theta }^T\left(\frac{1}{nh}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}\pi \left(u\right)K_i\left(u\right)f(c_k-r_i\left(u\right)){\tilde{X}}_{i,k}\left(u\right){\tilde{X}}_{i,k}{\left(u\right)}^T\right)\theta +O_p({log}^{\frac{1}{2}}(1/h)/\sqrt{nh})\hfill \\ & =\hfill & \frac{1}{2}{\theta }^T{S}_n\left(u\right)\theta +O_p({log}^{\frac{1}{2}}(1/h)/\sqrt{nh}),\hfill \end{array}$$

where $S_n\left(u\right)=\frac{1}{nh}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}\pi \left(u\right)K_i\left(u\right)f(c_k-r_i\left(u\right)){\tilde{X}}_{i,k}\left(u\right){\tilde{X}}_{i,k}{\left(u\right)}^T$. Thus, it is easy to obtain

$$\begin{array}{ccc}{L}_n\left(\theta \right)\hfill & =\hfill & W_n^{*}{\left(u\right)}^T\theta +{\displaystyle \sum _{k=1}^K}E\left[M_{n,k}\left(\theta \right)\right]+O_p({log}^{\frac{1}{2}}(1/h)/\sqrt{nh})\hfill \\ & =\hfill & W_n^{*}{\left(u\right)}^T\theta +{\displaystyle \sum _{k=1}^K}E\left\{E\left[M_{n,k}\left(\theta \right)\right|U,X,Z]\right\}+O_p({log}^{\frac{1}{2}}(1/h)/\sqrt{nh})\hfill \\ & =\hfill & W_n^{*}{\left(u\right)}^T\theta +\frac{1}{2}{\theta }^{T}E\left[S_n\left(u\right)\right]\theta +O_p({log}^{\frac{1}{2}}(1/h)/\sqrt{nh}).\hfill \end{array}$$

Since $E\left[S_n\left(u\right)\right]=\pi \left(u\right)f_U\left(u\right)S\left(u\right)+O\left(h^2\right)$ is established, where $S\left(u\right)=diag(D_1\left(u\right),{\mu }_{2}E$$\left[{(X^T,X^T)}^T(X^T,X^T)\right|U=u\left]\right)$. Then,

$$L_n\left(\theta \right)=W_n^{*}{\left(u\right)}^T\theta +\frac{\pi \left(u\right)}{2}{f}_U\left(u\right){\theta }^{T}S\left(u\right)\theta +O_p({log}^{\frac{1}{2}}(1/h)/\sqrt{nh}).$$

From Lemma 2, a minimum resolution $\tilde{\theta }$ of $L_n\left(\theta \right)$ can be written as

$$\tilde{\theta }=-\pi {\left(u\right)}^{-1}{f}_U{\left(u\right)}^{-1}{S}^{-1}\left(u\right)W_n^{*}\left(u\right)+o_p\left(1\right).$$

Because $S\left(u\right)$ is a pseudo-diagonal matrix, Lemma 3 can be proven. □

Lemma 4.

Assume that conditions C1-C8 hold. Then,

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\tilde{\eta }}_i\left(\beta \right)\stackrel{L}{⟶}N(0,\mathrm{\Lambda })$$

(14)

if β is the true value of the parameter, where $\stackrel{L}{⟶}$ denotes convergence in distribution, $\mathrm{\Lambda }={\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{k^{\prime }=1}^K}(\min ({\tau }_k,{\tau }_{k^{\prime }})-{\tau }_k{\tau }_{k^{\prime }})E\left({\delta }^{2}Z{Z}^T\right)$.

Proof. 

It is easy to show that

$$\begin{array}{ccc}\frac{1}{\sqrt{n}}{\displaystyle \sum _{i=1}^n}{\tilde{\eta }}_i\left(\beta \right)\hfill & =\hfill & \frac{1}{\sqrt{n}}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{k=1}^K}{Z}_i\{{\tau }_k-I({\delta }_i{\tilde{Y}}_i+(1-{\delta }_i)Z_i^T\widehat{\beta }-Z_i^T\beta \le {\tilde{c}}_k)\}\hfill \\ \hfill & =\hfill & \frac{1}{\sqrt{n}}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{k=1}^K}{\delta }_i{Z}_i[{\tau }_k-I({\epsilon }_i\le {\tilde{c}}_k)]\hfill \\ \hfill & \hfill & +\frac{1}{\sqrt{n}}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{k=1}^K}(1-{\delta }_i)Z_i[{\tau }_k-I(Z_i^T\widehat{\beta }-Z_i^T\beta \le {\tilde{c}}_k)]\hfill \\ \hfill & =\hfill & \frac{1}{\sqrt{n}}{\displaystyle \sum _{i=1}^n}{A}_{i1}+\frac{1}{\sqrt{n}}{\displaystyle \sum _{i=1}^n}{A}_{i2}.\hfill \end{array}$$

(15)

Note that

$$E\left\{A_{i1}\right\}=E\left\{{\displaystyle \sum _{k=1}^K}{\delta }_i{Z}_i[{\tau }_k-I({\epsilon }_i\le {\tilde{c}}_k)]\right\},$$

then, we have the following calculation:

$$\begin{array}{ccc}Var\left\{A_{i1}\right\}\hfill & =\hfill & Var\left\{{\displaystyle \sum _{k=1}^K}{\delta }_i{Z}_i[{\tau }_k-I({\epsilon }_i\le {\tilde{c}}_k)]\right\}\hfill \\ & =\hfill & E\left\{\left[{\displaystyle \sum _{k=1}^K}{\delta }_i{Z}_i({\tau }_k-I({\epsilon }_i\le {\tilde{c}}_k))\right]{\left[{\displaystyle \sum _{k=1}^K}{\delta }_i{Z}_i({\tau }_k-I({\epsilon }_i\le {\tilde{c}}_k))\right]}^T\right\}\hfill \\ & =\hfill & E\left\{{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{k^{\prime }=1}^K}{\delta }_i^2({\tau }_k-I({\epsilon }_i\le {\tilde{c}}_k))({\tau }_{k^{\prime }}-I({\epsilon }_i\le {\tilde{c}}_{k^{\prime }}))Z_i{Z}_i^T\right\}.\hfill \end{array}$$

Then, we can obtain

$$\begin{array}{ccc}& \hfill & E\left\{({\tau }_k-I({\epsilon }_i\le {\tilde{c}}_k))({\tau }_{k^{\prime }}-I({\epsilon }_i\le {\tilde{c}}_{k^{\prime }}))\right\}\hfill \\ & =\hfill & E\{{\tau }_k{\tau }_{k^{\prime }}-{\tau }_{k}I({\epsilon }_i\le {\tilde{c}}_{k^{\prime }})-I({\epsilon }_i\le {\tilde{c}}_k){\tau }_{k^{\prime }}+I({\epsilon }_i\le {\tilde{c}}_k)I({\epsilon }_i\le {\tilde{c}}_{k^{\prime }})\}\hfill \\ & =\hfill & min\left({\tau }_k{\tau }_{k^{\prime }}\right)-{\tau }_k{\tau }_{k^{\prime }}.\hfill \end{array}$$

Thus, we have

$$Var\left\{A_{i1}\right\}={\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{k^{\prime }=1}^K}(min\left({\tau }_k{\tau }_{k^{\prime }}\right)-{\tau }_k{\tau }_{k^{\prime }})E\left({\delta }_i^2{Z}_i{Z}_i^T\right).$$

Moreover, using the central limit theorem, we can obtain

$$\frac{1}{\sqrt{n}}{\displaystyle \sum _{i=1}^n}{A}_{i1}\stackrel{L}{⟶}N(0,\mathrm{\Lambda }).$$

(16)

Next, we prove $\frac{1}{\sqrt{n}}{\displaystyle \sum _{i=1}^n}{A}_{i2}=o_p\left(1\right)$. It is easy to show that

$$\begin{array}{ccc}{A}_{i2}\hfill & =\hfill & {\displaystyle \sum _{k=1}^K}(1-{\delta }_i)Z_i[{\tau }_k-I(Z_i^T\widehat{\beta }-Z_i^T\beta \le {\tilde{c}}_k)]\hfill \\ & =\hfill & {\displaystyle \sum _{k=1}^K}(1-{\delta }_i)f\left({\tilde{c}}_k\right)Z_i{Z}_i^T(\widehat{\beta }-\beta )+O_p(\parallel \widehat{\beta }-\beta {\parallel }^2).\hfill \end{array}$$

Let $A_{i2,j}$ be the jth component of $A_{i2}$. Then, using Lemma 2 from Zhao and Xue [20], we can obtain

$$\begin{array}{ccc}|\frac{1}{\sqrt{n}}{A}_{i2,j}|\hfill & =\hfill & \mid \frac{1}{\sqrt{n}}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{k=1}^K}(1-{\delta }_i)f\left({\tilde{c}}_k\right)Z_i{Z}_i^T(\widehat{\beta }-\beta )\mid +o_p\left(1\right)\hfill \\ & \le \hfill & \frac{1}{\sqrt{n}}\underset{1\le i\le n}{max}|{\displaystyle \sum _{k=1}^K}(1-{\delta }_i)f\left({\tilde{c}}_k\right)Z_i^T(\widehat{\beta }-\beta )|\underset{1\le s\le n}{max}{\displaystyle \sum _{i=1}^s}\left|Z_{ij}\right|\hfill \\ & =\hfill & o_p\left(1\right).\hfill \end{array}$$

Thus, we have

$$\frac{1}{\sqrt{n}}{\displaystyle \sum _{i=1}^n}{A}_{i2}=o_p\left(1\right).$$

(17)

Then, by invoking (15)–(17), we complete the proof of Lemma 4. □

Lemma 5.

Assume that conditions C1–C8 hold. Then,

$$\frac{1}{n}\sum _{i=1}^n{\tilde{\eta }}_i\left(\beta \right){\tilde{\eta }}_i^T\left(\beta \right)\stackrel{P}{⟶}\mathrm{\Lambda }$$

(18)

if β is the true value of the parameter, where $\stackrel{P}{⟶}$ denotes convergence in probability, $\mathrm{\Lambda }={\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{k^{\prime }=1}^K}(min({\tau }_k,{\tau }_{k^{\prime }})-{\tau }_k{\tau }_{k^{\prime }})E\left({\delta }^{2}Z{Z}^T\right)$.

Proof. 

We also use the notations in the proof of Lemma 4. Then, we obtain

$$\begin{array}{ccc}\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\tilde{\eta }}_i\left(\beta \right){\tilde{\eta }}_i^T\left(\beta \right)\hfill & =\hfill & \frac{1}{n}{\displaystyle \sum _{i=1}^n}{A}_{i1}{A}_{i1}^T+\frac{1}{n}{\displaystyle \sum _{i=1}^n}{A}_{i1}{A}_{i2}^T+\frac{1}{n}{\displaystyle \sum _{i=1}^n}{A}_{i2}{A}_{i1}^T+\frac{1}{n}{\displaystyle \sum _{i=1}^n}{A}_{i2}{A}_{i2}^T\hfill \\ & =\hfill & B_1+B_2+B_3+B_4.\hfill \end{array}$$

Using the law of large numbers, we can derive that $B_1\stackrel{P}{⟶}\mathrm{\Lambda }$. Let $B_{2,rs}$ be the $(r,s)$ component of $B_2$ and $A_{ij,r}$ be the rth component of $A_{ij},j=1,2$. Further, using the Cauchy–Schwarz inequality, we can obtain

$$|B_{2,rs}|\le {\left(\frac{1}{n}{\displaystyle \sum _{i=1}^n}{A}_{i1,r}^2\right)}^{\frac{1}{2}}{\left(\frac{1}{n}{\displaystyle \sum _{i=1}^n}{A}_{i2,s}^2\right)}^{\frac{1}{2}}.$$

From the proof of Lemma 4, we can obtain $\frac{1}{n}{\displaystyle \sum _{i=1}^n}{A}_{i1,r}^2=O_p\left(1\right)$ and $\frac{1}{n}{\displaystyle \sum _{i=1}^n}{A}_{i2,s}^2=O_p\left(1\right)$. Hence, $B_2\stackrel{P}{⟶}0$. $B_3\stackrel{P}{⟶}0$ and $B_4\stackrel{P}{⟶}0$ are also easy to improve using a similar argument. Hence, Lemma 5 can be proven. □

Proof of Theorem 1.

Note that ${\beta }^{*}=\sqrt{n}(\widehat{\beta }-\beta )$, ${\eta }_{i,k}=I({\epsilon }_i\le c_k)-{\tau }_k$, ${\tilde{r}}_{i,k}=X_i^T(\tilde{a}-\alpha \left(U_i\right))$. Then, the estimate of ${\beta }^{*}$ can be obtained by minimizing the following loss function:

$$\mathrm{argmin}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{\rho }_{{\tau }_k}(Y_i-c_k-X_i^T\tilde{a}-Z_i^T\beta ).$$

(19)

(19) is equivalent to minimizing the following formula,

$$L_n\left({\beta }^{*}\right)={\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i\{{\rho }_{{\tau }_k}({\epsilon }_i-c_k-{\tilde{r}}_{i,k}-Z_i^T{\beta }^{*}/\sqrt{n})-{\rho }_{{\tau }_k}({\epsilon }_i-c_k-{\tilde{r}}_{i,k})\}.$$

(20)

According to the identity proposed by Knight,

$${\rho }_{\tau }(u-v)-{\rho }_{\tau }\left(u\right)=-v(\tau -I(u<0))+{\int }_0^v(I(u\le s)-I(u\le 0))ds,$$

(21)

(20) can be expressed equivalently as

$$\begin{array}{ccc}{L}_n\left({\beta }^{*}\right)\hfill & =\hfill & {\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i\frac{Z_i^T{\beta }^{*}}{\sqrt{n}}(I({\epsilon }_i<c_k)-{\tau }_k)\hfill \\ & \hfill & +{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{\int }_{{\tilde{r}}_{i,k}}^{{\tilde{r}}_{i,k}+Z_i^T{\beta }^{*}/\sqrt{n}}[I({\epsilon }_i-c_k\le s)-I({\epsilon }_i-c_k\le 0)]ds\hfill \\ & =\hfill & {\left(\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{\eta }_{i,k}{Z}_i\right)}^T{\beta }^{*}+M_n\left({\beta }^{*}\right),\hfill \end{array}$$

where $M_n\left({\beta }^{*}\right)={\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{\int }_{{\tilde{r}}_{i,k}}^{{\tilde{r}}_{i,k}+Z_i^T{\beta }^{*}/\sqrt{n}}[I({\epsilon }_i-c_k\le s)-I({\epsilon }_i-c_k\le 0)]ds$.

Next, we calculate the expectation of $M_n\left({\beta }^{*}\right)$. The calculation is as follows:

$$\begin{array}{ccc}E\left[M_n\left({\beta }^{*}\right)\right|U_i,X_i,Z_i]\hfill & =\hfill & {\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}\pi (U_i,X_i,Z_i){\int }_{{\tilde{r}}_{i,k}}^{{\tilde{r}}_{i,k}+Z_i^T{\beta }^{*}/\sqrt{n}}[F(c_k+s)-F\left(c_k\right)]ds\hfill \\ & =\hfill & {\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}\pi (U_i,X_i,Z_i){\int }_{{\tilde{r}}_{i,k}}^{{\tilde{r}}_{i,k}+Z_i^T{\beta }^{*}/\sqrt{n}}\left[sf\left(c_k\right)(1+o\left(1\right))\right]ds\hfill \\ & =\hfill & \frac{1}{2}{{\beta }^{*}}^T\left(\frac{1}{n}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}\pi (U_i,X_i,Z_i)f\left(c_k\right)Z_i{Z}_i^T\right){\beta }^{*}+{\left(\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}\pi (U_i,X_i,Z_i)f\left(c_k\right){\tilde{r}}_{i,k}{Z}_i\right)}^T{\beta }^{*}\hfill \\ & \hfill & +o_p\left(1\right).\hfill \end{array}$$

Note that $R_n\left({\beta }^{*}\right)=M_n\left({\beta }^{*}\right)-E\left[M_n\left({\beta }^{*}\right)\right|U_i,X_i,Z_i]$, then $R_n\left({\beta }^{*}\right)=o_p\left(1\right)$. Thus,

$$\begin{array}{ccc}{L}_n\left({\beta }^{*}\right)\hfill & =\hfill & {\left(\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{\eta }_{i,k}{Z}_i\right)}^T{\beta }^{*}+E\left[M_n\left({\beta }^{*}\right)\right|U_i,X_i,Z_i]+R_n\left({\beta }^{*}\right)\hfill \\ & =\hfill & \frac{1}{2}{{\beta }^{*}}^T{\sum }_n{\beta }^{*}+{\left(\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{\eta }_{i,k}{Z}_i\right)}^T{\beta }^{*}+{\left(\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}\pi (U_i,X_i,Z_i)f\left(c_k\right){\tilde{r}}_{i,k}{Z}_i\right)}^T{\beta }^{*}+o_p\left(1\right).\hfill \end{array}$$

where ${\sum }_n=\frac{1}{n}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}\pi (U_i,X_i,Z_i)f\left(c_k\right)Z_i{Z}_i^T=E\left({\sum }_n\right)+o_p\left(1\right)=c\pi (U_i,X_i,Z_i)E\left(Z_i{Z}_i^T\right)+o_p\left(1\right)=c\sum +o_p\left(1\right)$. Further, we obtain

$$\begin{array}{ccc}{L}_n\left({\beta }^{*}\right)\hfill & =\hfill & \frac{c}{2}{{\beta }^{*}}^T\sum {\beta }^{*}+{\left(\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{\eta }_{i,k}{Z}_i\right)}^T{\beta }^{*}+{\left(\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}\pi (U_i,X_i,Z_i)f\left(c_k\right){\tilde{r}}_{i,k}{Z}_i\right)}^T{\beta }^{*}+o_p\left(1\right)\hfill \\ \hfill & =\hfill & L_1{\beta }^{*}+L_2{\beta }^{*}+L_3{\beta }^{*}+o_p\left(1\right).\hfill \end{array}$$

(22)

Then, $L_3$ in (22) can be represented as

$$\begin{array}{ccc}& \hfill & \frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}\pi (U_i,X_i,Z_i)f\left(c_k\right){\tilde{r}}_{i,k}{Z}_i\hfill \\ & =\hfill & -\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}\frac{f\left(c_k\right)}{f_U\left(U_i\right)}{Z}_i{\left(\begin{array}{c}0\\ X_i\\ 0\end{array}\right)}^T{D}_1^{-1}\left(U_i\right)\left(\frac{1}{nh}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{\eta }_{i,k}^{*}\left(U_i\right)\left(\begin{array}{c}{e}_k\\ X_i\\ Z_i\end{array}\right)K_i\left(U_i\right)\right)\hfill \\ & \hfill & +O_p(h^{\frac{3}{2}}+\sqrt{log(1/h)}/\sqrt{n{h}^2})\hfill \\ & =\hfill & -\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{\eta }_{i,k}\omega (U_i,X_i,Z_i)+o_p\left(1\right),\hfill \end{array}$$

where $\omega (U_i,X_i,Z_i)=\pi (U_i,X_i,Z_i)E\left[Z_i(0^T,X_i^T,0)\right|U=U_i]D^{-1}\left(U_i\right){(I_K,{\mathbf{1}}^T{X}_i,{\mathbf{1}}^T{Z}_i)}^T$. Below, we give the calculation

$$\begin{array}{ccc}{L}_n\left({\beta }^{*}\right)\hfill & =\hfill & \frac{c}{2}{{\beta }^{*}}^T\sum {\beta }^{*}+{\left(\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{\eta }_{i,k}{Z}_i\right)}^T{\beta }^{*}-{\left(\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{\eta }_{i,k}\omega (U_i,X_i,Z_i)\right)}^T{\beta }^{*}+o_p\left(1\right)\hfill \\ & =\hfill & \frac{c}{2}{{\beta }^{*}}^T\sum {\beta }^{*}+{\left[\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{\eta }_{i,k}({\delta }_i{Z}_i-\omega (U_i,X_i,Z_i))\right]}^T{\beta }^{*}+o_p\left(1\right)\hfill \\ & =\hfill & \frac{c}{2}{{\beta }^{*}}^T\sum {\beta }^{*}+{C_n^{*}}^T{\beta }^{*}+o_p\left(1\right),\hfill \end{array}$$

where $C_n^{*}={\left[\frac{1}{\sqrt{n}}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{\eta }_{i,k}({\delta }_i{Z}_i-\omega (U_i,X_i,Z_i))\right]}^T$. According to Lemma 2, the minimum solution ${\widehat{\beta }}^{*}$ of $L_n\left({\beta }^{*}\right)$ can be expressed as

$${\widehat{\beta }}^{*}=-\frac{1}{c}{\sum }^{-1}{C}_n^{*}+o_p\left(1\right).$$

By using the Cramér–Wold theorem and the central limit theorem, it is easy to obtain

$$Var\left(C_n^{*}\right)⟶{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{k^{\prime }=1}^K}{\tau }_{k{k}^{\prime }}E\left(\pi (U,X,Z)\right)E\left\{[\delta Z-\omega (U,X,Z)]{[\delta Z-\omega (U,X,Z)]}^T\right\}.$$

Further, by the Lindeberg–Feller central limit theorem, we can obtain

$$\sqrt{n}(\widehat{\beta }-\beta )\stackrel{D}{⟶}N(0,c^{-2}{\sum }^{-1}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{k^{\prime }=1}^K}{\tau }_{k{k}^{\prime }}\Delta {\sum }^{-1}).$$

□

Proof of Theorem 2.

From Lemma 3, we can obtain

$$\sqrt{nh}({\tilde{c}}_1-c_1,\cdots ,{\tilde{c}}_K-c_K,{(\widehat{a}-\alpha \left(u\right))}^T)=-\pi {\left(u\right)}^{-1}{f}_U^{-1}\left(u\right)D_2^{-1}\left(u\right)W_{n1}\left(u\right)+o_p\left(1\right),$$

where $D_2\left(u\right)=E\left[\left(\begin{array}{cc}C& c{X}^T\\ X{c}^T& cX{X}^T\end{array}\right)|\begin{array}{c}\\ \end{array}U=u\right]$, $W_{n1}\left(u\right)=\frac{1}{\sqrt{nh}}{\sum }_{k=1}^K{\sum }_{i=1}^n{\delta }_i{K}_i\left(u\right){\eta }_{i,k}^{*}\left(u\right)$${(e_k^T,X_i^T)}^T$. It is easy to obtain

$${\left(D_2^{-1}\left(u\right)\right)}_{22}={(D_{22}\left(u\right)-D_{21}\left(u\right)D_{11}^{-1}\left(u\right)D_{12}\left(u\right))}^{-1}={\left[{\displaystyle \sum _{k=1}^K}f\left(c_k\right)\right]}^{-1}{\sum }_1^{-1},$$

$${\left(D_2^{-1}\left(u\right)\right)}_{21}=-{\left(D_2^{-1}\left(u\right)\right)}_{22}{D}_{21}\left(u\right)D_{11}^{-1}\left(u\right)=-1_K^T{\left\{{\left[{\displaystyle \sum _{k=1}^K}f\left(c_k\right)\right]}^{-1}{\sum }_1^{-1}E\left[X\right|U=u]\right\}}^T.$$

Then, we have

$$\begin{array}{ccc}\sqrt{nh}(\widehat{a}-\alpha \left(u\right))\hfill & =\hfill & -\frac{1}{\pi \left(u\right)f_U\left(u\right)}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{K}_i\left(u\right){\eta }_{i,k}^{*}\left(u\right)(-{\left[{\displaystyle \sum _{k=1}^K}f\left(c_k\right)\right]}^{-1}{\sum }_1^{-1}E\left[X\right|U=u]\hfill \\ & \hfill & +{\left[{\displaystyle \sum _{k=1}^K}f\left(c_k\right)\right]}^{-1}{\sum }_1^{-1}{X}_i)+o_p\left(1\right)\hfill \\ & =\hfill & -\frac{{\sum }_1^{-1}}{\pi \left(u\right)f_U\left(u\right){\displaystyle \sum _{k=1}^K}f\left(c_k\right)}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{\delta }_i{K}_i\left(u\right){\eta }_{i,k}^{*}\left(u\right)(X_i-E\left(X\right|U=u))+o_p\left(1\right).\hfill \end{array}$$

Further,

$$\begin{array}{ccc}E\left[\sqrt{nh}(\widehat{a}-\alpha \left(u\right))\right]\hfill & =\hfill & -\frac{{\sum }_1^{-1}}{\pi \left(u\right)f_U\left(u\right){\displaystyle \sum _{k=1}^K}f\left(c_k\right)}{\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{i=1}^n}{K}_i\left(u\right)\pi \left(u\right)[F(c_k-r_i\left(u\right))-F\left(c_k\right)][X_i-E\left(X\right|U=u)]\hfill \\ & =\hfill & \frac{{\sum }_1^{-1}}{f_U\left(u\right)}{\displaystyle \sum _{i=1}^n}{K}_i\left(u\right)[X_i-E\left(X\right|U=u)]r_i\left(u\right)(1+o_p\left(1\right))\hfill \\ & =\hfill & \frac{1}{2f_U\left(u\right)}{\displaystyle \sum _{i=1}^n}{K}_i\left(u\right){\alpha }^{″}\left(u\right){(U_i-u)}^2(1+o_p\left(1\right))\hfill \\ & =\hfill & \frac{1}{2}{\alpha }^{″}\left(u\right){\mu }_2{h}^2+o_p\left(1\right).\hfill \end{array}$$

Thus, we can obtain

$$Cov\left(\widehat{a}\right|U=u)=({\displaystyle \sum _{k=1}^K}{\displaystyle \sum _{k^{\prime }=1}^K}min({\tau }_k,{\tau }_{k^{\prime }})-{\tau }_k{\tau }_{k^{\prime }})\frac{E\left(\pi \left(u\right)\right)v_0}{f_U\left(u\right)}{\sum }_1^{-1}.$$

Consequently, we complete the proof of Theorem 2. □

Proof of Theorem 3.

Based on the definition of ${\tilde{\eta }}_i\left(\beta \right)$ and using the same proof as in Owen, we obtain

$$\underset{1\le i\le n}{max}\Vert {\tilde{\eta }}_i\left(\beta \right)\Vert =o_p\left(n^{\frac{1}{2}}\right),$$

(23)

and

$$\Vert \lambda \Vert =O_p\left(n^{\frac{-1}{2}}\right).$$

(24)

Invoking (23) and (24) and using theories similar to those of Xue and Zhu [27], we can obtain

$$R\left(\beta \right)={\left\{\frac{1}{\sqrt{n}}\sum _{i=1}^n{\tilde{\eta }}_i\left(\beta \right)\right\}}^T{\widehat{\mathrm{\Lambda }}}^{-1}\left\{\frac{1}{\sqrt{n}}\sum _{i=1}^n{\tilde{\eta }}_i\left(\beta \right)\right\}+o_p\left(1\right),$$

(25)

where $\widehat{\mathrm{\Lambda }}=n^{-1}{\displaystyle \sum _{i=1}^n}{\tilde{\eta }}_i\left(\beta \right){\tilde{\eta }}_i^T\left(\beta \right)$. Combining Lemma 4 and Lemma 5, we complete the proof of this theorem. □

5. Conclusions

In this paper, we discussed the statistical inference for the partially linear varying coefficient composite quantile regression model with missing data. By introducing a two-stage estimation process, we effectively solved the challenge introduced by random missing responses and proved the asymptotic property of the obtained estimator under mild and regular conditions. It is worth noting that this paper contributes a new empirical log-likelihood ratio statistic based on imputation and determines that it follows the standard Chi-square distribution. The feasibility and performance of the proposed method were verified with a comprehensive evaluation through a simulation study and applications using real data.

However, for more complex problems with missing data, there is still a lot of work to be done. For example, some new imputation methods should be proposed to solve these problems. On the other hand, in future work, we will use bootstrap methods to conduct simulation studies for varying coefficient functions in terms of coverage probability and average length [28].