A Study on Determining the Optimal Feedback Rate in Distributed Block Diagonalization with Limited Feedback for Dense Cellular Networks
Abstract
1. Introduction
- To attain a more precise estimation, we conduct an analysis of the derivative of the net spectral efficiency. This derivative comprises two functions demonstrating distinct growth rates with an increase in feedback bits. Unlike in previous studies, both functions are rigorously approximated through mathematical analysis.
- Consequently, our proposed estimate surpasses the accuracy of estimates found in prior research, delivering precise approximations that are independent of and ultimately aim to maximize the net spectral efficiency.
- Simulation results affirm that the proposed estimate consistently provides an accurate approximation of the optimal feedback rate. This is particularly notable in scenarios where assumes relatively smaller values, showcasing significantly improved precision compared to previous findings.
2. System Model and Preliminaries
2.1. Network Model
2.2. Finite-Rate Feedback Model
2.3. Block Diagonalization
2.4. Performance Measure
2.5. Distance Measure
2.6. Quantization-Cell Upper Bound Model
2.7. Previous Findings: Growth Rate of the Optimal Number of Feedback Bits
3. Accurate Estimate for the Optimal Feedback Rate
Determination of the Optimal Feedback Rate
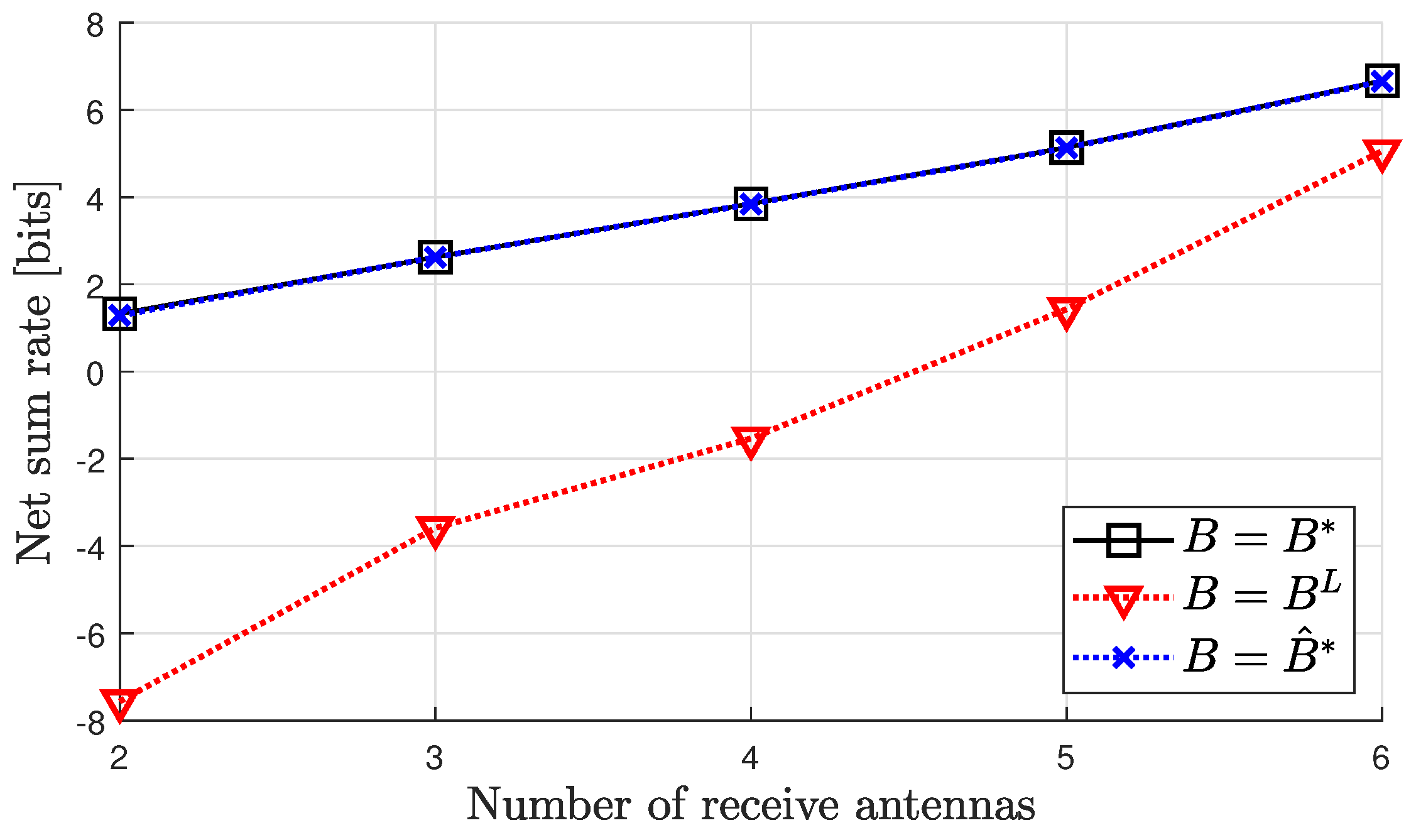
4. Simulation Results and Discussions
- As previously denoted, represents the optimal number of feedback bits in terms of maximizing .
- signifies the proposed estimate derived by numerically approximating the rightmost zero crossing point of , as outlined in Section Determination of the Optimal Feedback Rate.
- stands for the lower bound of obtained in [12].
- Initialization: Specify the values of the system parameters , , K, B, , and . Fix the network’s radius to a sufficiently large value. For our results, we used a radius of 5 km for the entire network, and the values of and are fixed as and .
- BS Locations: At each frame, determine the locations of BSs based on a Poisson point process. The number of BSs in the current frame follows a Poisson distribution with the corresponding density. Then, the BSs are uniformly distributed within a 2D circle.
- User and channel setup: Assuming the target user is located at the origin, identify the BS closest to the origin as . Calculate the distances between the BSs and the target user. Generate small-scale fading channel matrices for , where components are i.i.d. circularly symmetric Gaussian with a variance of one. denotes the channel matrix between and user , with user 1 as the target user. Note that, for simplicity, is denoted by throughout this paper.
- Quantization and precoding: Each user obtains by quantizing in a distributed manner based on the QUB criterion described in Section 2.6. Construct precoding matrices using quantized channels, collected from users, based on the BD criterion.
- Inter-cell interference: Calculate matrices and following a similar approach used for obtaining and .
- Monte Carlo simulation: Repeat steps (1)–(6) to obtain the ergodic average of the net spectral efficiency .
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Notations
Appendix B. Proof of Lemma 1
References
- Jindal, N. MIMO broadcast channels with finite-rate feedback. IEEE Trans. Inf. Theory 2006, 52, 5045–5060. [Google Scholar] [CrossRef]
- Yoo, T.; Jindal, N.; Goldsmith, A. Multi-antenna downlink channels with limited feedback and user selection. IEEE J. Sel. Areas Commun. 2007, 25, 1478–1491. [Google Scholar] [CrossRef]
- Renzo, M.D.; Guan, P. A mathematical framework to the computation of the error probability of downlink MIMO cellular networks by using stochastic geometry. IEEE Trans. Commun. 2014, 62, 2860–2879. [Google Scholar] [CrossRef]
- Renzo, M.D.; Lu, W. Stochastic geometry modeling and performance evaluation of MIMO cellular networks using the equivalent-in-distribution (EiD)-based approach. IEEE Trans. Commun. 2015, 63, 977–996. [Google Scholar] [CrossRef]
- Li, C.; Zhang, J.; Andrews, J.G.; Letaief, K.B. Success probability and area spectral efficiency in multiuser MIMO HetNets. IEEE Trans. Commun. 2016, 64, 1544–1556. [Google Scholar] [CrossRef]
- Lu, X.; Niyato, D.; Privault, N.; Jiang, H.; Wang, P. Managing Physical Layer Security in Wireless Cellular Networks: A Cyber Insurance Approach. IEEE J. Sel. Areas Commun. 2018, 36, 1648–1661. [Google Scholar] [CrossRef]
- Gao, Y.; Yang, S.; Wu, S.; Wang, M.; Song, X. Coverage probability analysis for mmWave communication network with ABSF-based interference management by stochastic geometry. IEEE Access. 2019, 7, 133572–133582. [Google Scholar] [CrossRef]
- Jia, X.; Ji, P.; Chen, Y. Modeling and analysis of multi-tier clustered millimeter-wave cellular networks with user classification for large-scale hotspot area. IEEE Access 2019, 7, 140278–140299. [Google Scholar] [CrossRef]
- Park, J.; Lee, N.; Andrews, J.G.; Heath, R.W., Jr. On the Optimal Feedback Rate in Interference-Limited Multi-Antenna Cellular System. IEEE Trans. Wireless Commun. 2016, 15, 5748–5762. [Google Scholar] [CrossRef]
- Min, M. Bounds on the Optimal Feedback Rate for Multi-Antenna Systems in Interference-Limited Cellular Networks. IEEE Trans. Wirel. Commun. 2018, 17, 4845–4860. [Google Scholar] [CrossRef]
- Sun, L.; Tian, X. Physical layer security in multi-antenna cellular systems: Joint optimization of feedback rate and power allocation. IEEE Trans. Wirel. Commun. 2022, 21, 7165–7180. [Google Scholar] [CrossRef]
- Lee, S.; Min, M. Analysis of the Optimal Feedback Rate for Limited Feedback-Based Block Diagonalization in Cellular MU-MIMO Systems. IEEE Wirel. Commun. Lett. 2023; Early Access. [Google Scholar] [CrossRef]
- Baccelli, F.; Blaszczyszyn, B. Stochastic Geometry and Wireless Networks: Volume I Theory; NOW Publishers: Norwell, MA, USA, 2009; Volume 3. [Google Scholar]
- Ravindran, N.; Jindal, N. Limited feedback-based block diagonalization for the MIMO broadcast channel. IEEE J. Sel. Areas Commun. 2008, 26, 1473–1482. [Google Scholar] [CrossRef]
- Andrews, J.G.; Baccelli, F.; Ganti, R.K. A tractable approach to coverage and rate in cellular networks. IEEE Trans. Commun. 2011, 59, 3122–3134. [Google Scholar] [CrossRef]
- Kang, Y.-S.; Min, M. Unified Derivation of Optimal Feedback Rate in Downlink Cellular Systems With Multi-Antenna Base Stations. IEEE Access. 2019, 7, 161871–161886. [Google Scholar] [CrossRef]
- Khatri, C.G. Classical statistical analysis based on a certain multivariate complex gaussian distribution. Ann. Math. Stat. 1965, 36, 98–114. [Google Scholar] [CrossRef]
- Gupta, A.; Nagar, D. Matrix Variate Distributions; Chapman & Hall/CRC: Boca Raton, FL, USA, 2000. [Google Scholar]
- Magnus, J.; Neudecker, H. Matrix Differential Calculus with Applications in Statistic and Econometrics; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, T.; Min, M. A Study on Determining the Optimal Feedback Rate in Distributed Block Diagonalization with Limited Feedback for Dense Cellular Networks. Mathematics 2024, 12, 460. https://doi.org/10.3390/math12030460
Kim T, Min M. A Study on Determining the Optimal Feedback Rate in Distributed Block Diagonalization with Limited Feedback for Dense Cellular Networks. Mathematics. 2024; 12(3):460. https://doi.org/10.3390/math12030460
Chicago/Turabian StyleKim, Taehwi, and Moonsik Min. 2024. "A Study on Determining the Optimal Feedback Rate in Distributed Block Diagonalization with Limited Feedback for Dense Cellular Networks" Mathematics 12, no. 3: 460. https://doi.org/10.3390/math12030460
APA StyleKim, T., & Min, M. (2024). A Study on Determining the Optimal Feedback Rate in Distributed Block Diagonalization with Limited Feedback for Dense Cellular Networks. Mathematics, 12(3), 460. https://doi.org/10.3390/math12030460




