Fuzzy Rough Set Models Based on Fuzzy Similarity Relation and Information Granularity in Multi-Source Mixed Information Systems

Abstract

As a pivotal research method in the field of granular computing (GrC), fuzzy rough sets (FRSs) have garnered significant attention due to their successful overcoming of the limitations of traditional rough sets in handling continuous data. This paper is dedicated to exploring the application potential of FRS models within the framework of multi-source complex information systems, which undoubtedly holds profound research significance. Firstly, a novel multi-source mixed information system (MsMIS), encompassing five distinct data types, is introduced, thereby enriching the dimensions of data processing. Subsequently, a similarity function, designed based on the unique attributes of the data, is utilized to accurately quantify the similarity relations among objects. Building on this foundation, fuzzy T-norm operators are employed to integrate the similarity matrices derived from different data types into a cohesive whole. This integration not only lays a solid foundation for subsequent model construction but also highlights the value of multi-source information fusion in the analysis of the MsMIS. The integrated results are subsequently utilized to develop FRS models. Through rigorous examination from the perspective of information granularity, the rationality of the FRS model is proven, and its mathematical properties are explored. This paper contributes to the theoretical advancement of FRS models in GrC and offers promising prospects for their practical implementation.

1. Introduction

The fuzzy rough set (FRS) [1] is an extension of the Pawlak rough set (PRS), designed to address uncertainty and fuzziness. The RST, proposed by Zdzisław Pawlak in 1982, is utilized for data analysis and decision-making problems under incomplete knowledge [2]. It relies on upper and lower approximations, enabling effective handling of classification and attribute reduction.

Granular computing (GrC) is a computational model and methodology that uses “granules” as the fundamental units for processing information. Breaking down information into smaller, more meaningful “granules” simplifies the analysis and resolution of complex problems. Granules can encompass collections of datasets, objects, knowledge, and other forms of information. The central concept of GrC is to enable simplification and efficient processing by exploiting information granularity [3]. FRSs and PRSs are important approaches to granular computing. In PRSs, lower and upper approximations are defined as unions of some sets, which demonstrate a distinct granular structure among those sets. However, in the existing theory of FRSs, the definitions of lower and upper approximations are based on fuzzy membership functions, rather than being constructed as unions of some fuzzy sets. For instance, Jensen and Shen introduced the concept of attribute reduction using special fuzzy rough sets; however, the reduction structure in fuzzy rough sets is not as clearly defined as it is in classical rough sets [4]. This distinction between fuzzy and classical rough sets has inspired us to develop a theory of granular fuzzy sets, which we apply to capture the granular structure of fuzzy rough sets. In fuzzy set theory, a fuzzy point is defined as a fuzzy set containing only one element with a non-zero membership value [5], and any non-empty fuzzy set can be seen as the union of several fuzzy points. This implies that fuzzy points in fuzzy set theory serve a similar function to crisp points in classical set theory [6]. This insight has motivated us to construct information granules around fuzzy points. In particular, within a specialized type of information system, such as a multi-source mixed information system (MsMIS), there has been limited research exploring the underlying granular structure using the approach of GrC. In this paper, a multi-source mixed information system can be called a hybrid information system or a mixed information system. The purpose of adding the prefix ‘multi-source’ is to highlight the consideration of a hybrid/mixed information system composed of data collected from different sensors or information sources, viewed from a specific application perspective. The research work on hybrid/mixed information systems mainly focuses on applications and rarely focuses on the theoretical aspects of granular structure. For example, Zeng et al. introduced a new hybrid distance in a hybrid information system, and a novel fuzzy rough set was constructed by combining the hybrid distance and the Gaussian kernel. This fuzzy rough set model mainly solves the problem of feature selection in incremental situations [7]. Li et al. presented a novel three-way decision approach in a hybrid information system with images and applied it to medical diagnosis [8]. Yuan et al. introduced a fuzzy rough set method to deal with the problem of outlier detection in mixed attribute data [9].

The MsMIS can be found everywhere in real life, such as electronic medical record systems, health record systems, and some common databases. These systems contain rich multi-source information, and researching this type of data will help to mine useful information in big data. In this paper, each data type of an MsMIS is considered and the fuzzy rough set needs to calculate the similarity between them according to its characteristics, so as to construct a fuzzy similarity relation.The fusion of all fuzzy similarity relations is also a great challenge. In [10], the authors demonstrate that multi-kernel learning can be used to transform complex data into a unified framework.

Therefore, it would be advisable to employ a multi-kernel approach to integrate the information derived from various fuzzy similarity relations. Kernel functions are utilized to measure similarity, subsequently combined through a specific fusion approach. A collection of kernel functions is devised to assess the similarity among samples characterized by diverse attribute types. An equivalence relation is established using a match kernel [11]; a string kernel is applied to determine the similarity of two strings in genetic analysis [12]; and a histogram intersection kernel is employed for image matching [13]. Recently, numerous studies have been conducted on multi-kernel learning [14], attribute reduction [10,15,16], and classification tasks [17,18]. However, the application of fuzzy similarity relations to construct fuzzy information granularity aims to reveal several mathematical properties within the framework of a MsMIS, particularly highlighting its significant exploratory value when integrated with FRS theory [19].

The work presented in this paper makes several meaningful contributions to the domain of fuzzy granulation, as outlined below.

(1) The concept of an MsMIS is defined, which adeptly combines multi-kernel learning techniques with similarity measures among samples to establish basic information granules within the framework of granular computing.

(2) By drawing on the principles of multi-source information fusion, this paper achieves effective integration of different information granules.

(3) This work validates the rationale and effectiveness of the proposed information granules within the MsMIS framework, developing a novel FRS model based on this validation.

(4) This model not only enriches the theoretical system of fuzzy sets and granular computing but also provides robust tools and support for subsequent researchers to conduct more in-depth explorations in attribute reduction.

In summary, the presented work opens new perspectives and pathways for future research, carrying significant theoretical and practical implications.

The rest of this paper is organized as follows. Section 2 provides some fundamental concepts about Pawlak rough sets and fuzzy rough sets. In Section 3, the concept of multi-source mixed information systems is defined and explained with an example. Section 4 provides definitions and proofs related to fuzzy information granularity in the context of FRSs, and the concepts of the classical attribute reduction method based on FRS are given. Finally, Section 5 concludes this paper.

2. Preliminaries

In this section, we first introduce some concepts of Pawlak rough sets and fuzzy rough sets.

Definition 1 

([2]). Given an information system $(U,A,V,f)$, $U=\{x_1,x_2,\cdots ,x_n\}$ is a non-empty finite set of object, A is a non-empty finite set of attribute, $V={\bigcup }_{a_i\in A}{V}_{a_i}$ is a union of attribute domain, and $f:U\times A\to V$ is an information function, $\forall x\in U$ and $a_i\in A$, $f(x,a_i)\in V_{a_i}$. For the sake of simplicity, $f(x,a_i)$ can be expressed as $a_i\left(x\right)$.

In general, the domain U is divided into a set of equivalence classes by an equivalence relation $\mathcal{R}$, denoted as ${\left[x\right]}_{\mathcal{R}}$. For each $x_i,y_i,x_k\in U$, equivalence relation $\mathcal{R}$ satisfies 1) reflexivity ($\mathcal{R}(x_i,x_i)=1$), 2) symmetry ($\mathcal{R}(x_i,x_j)=\mathcal{R}(x_j,x_i)$), and 3) transitivity ($\mathcal{R}(x_i,x_j)=\mathcal{R}(x_j,x_k)\Rightarrow \mathcal{R}(x_i,x_j)=\mathcal{R}(x_i,x_k)$). Given $X\subseteq U$, the lower and upper approximations can be denoted as

$$\begin{array}{c}\hfill \underline{\mathcal{R}}\left(X\right)=\{x\in U|{\left[x\right]}_{\mathcal{R}}\subseteq X\};\overline{\mathcal{R}}\left(X\right)=\{x\in U|{\left[x\right]}_{\mathcal{R}}\cap X\ne \varnothing \},\end{array}$$

(1)

where ${\left[x\right]}_{\mathcal{R}}=\{x_i\in U|x_i\mathcal{R}{x}_j\}$ refers to the equivalence class containing X.

Definition 2 

([20]). Given the universe $U=\{x_1,x_2,\cdots ,x_n\}$, let $\mathcal{A}$ be a map of U to [0,1], then $\mathcal{A}$ is known as the membership function on $\mathcal{A}$. The fuzzy set can be defined as $\mathcal{A}={\displaystyle \frac{\mathcal{A}\left(x_1\right)}{x_1}}+{\displaystyle \frac{\mathcal{A}\left(x_2\right)}{x_2}}+\cdots +{\displaystyle \frac{\mathcal{A}\left(x_n\right)}{x_n}}$.

Let $\mathcal{F}\left(U\right)$ be all fuzzy sets on U, given $\mathcal{A},\mathcal{B}\in \mathcal{F}\left(U\right)$, the following operations of fuzzy sets are defined as

$\left(1\right)$ $\mathcal{A}=\mathcal{B}\iff \mathcal{A}\left(x\right)=\mathcal{B}\left(x\right)$,

$\left(2\right)$ $\mathcal{A}\subseteq \mathcal{B}\iff \mathcal{A}\left(x\right)\le \mathcal{B}\left(x\right)$,

$\left(3\right)$ $(\mathcal{A}\cup \mathcal{B})\left(x\right)=max\left\{\mathcal{A}\right(x),\mathcal{B}(x\left)\right\}=\mathcal{A}\left(x\right)\vee \mathcal{B}\left(x\right)$,

$\left(4\right)$ $(\mathcal{A}\cap \mathcal{B})\left(x\right)=min\left\{\mathcal{A}\right(x),\mathcal{B}(x\left)\right\}=\mathcal{A}\left(x\right)\wedge \mathcal{B}\left(x\right)$,

$\left(5\right)$ ${\mathcal{A}}^c\left(x\right)=1-\mathcal{A}\left(x\right)$.

Definition 3 

([21]). Let the binary operator $\mathcal{T}$ be a triangular function on the interval $[0,1]$, called $\mathcal{T}$-norm, if for any $x_i,x_j,x_k,x_z\in [0,1]$, it satisfies (1) commutativity ($\mathcal{T}(x_i,x_j)=\mathcal{T}(x_j,x_i)$); (2) associativity ($\mathcal{T}(\mathcal{T}(x_i,x_j),x_k)=\mathcal{T}(x_i,\mathcal{T}(x_j,x_k))$); and (3) monotonicity ($x_i\le x_j,x_k\le x_z\Rightarrow \mathcal{T}(x_i,x_k)\le \mathcal{T}(x_j,x_z)$) and boundary condition ($\mathcal{T}(x_i,1)=x_i$, $\mathcal{T}(1,x_i)=x_i$).

If the mapping $S:[0,1]\times [0,1]\to [0,1]$ fulfills the four conditions outlined in Definition 3, then for any $x_i\in [0,1]$, the value $S(x_i,0)$ signifies that S is termed a triangular-conorm, abbreviated as a t-conorm. If N is a monotone decreasing mapping from $[0,1]$ to $[0,1]$ with $N\left(0\right)=1$ and $N\left(1\right)=0$, then N is called a complement operator. $N_s\left(x_i\right)=1-x_i$ is the standard complement operator. $c{o}_{N}X\left(x_i\right)=N\left(X\left(x_i\right)\right)$ for any $X\in \mathcal{F}\left(U\right)$, $c{o}_{N}X\left(x_i\right)$ is known as fuzzy complement of X determined by a negator N. If for any $x_i\in U$, $N\left(X\left(x_i\right)\right)=x_i$, then

$$\begin{array}{c}\hfill S(x_i,x_j)=N\left(T(N\left(x_i\right),N\left(x_j\right))\right),T(x_i,x_j)=N\left(S(N\left(x_i\right),N\left(x_j\right))\right),\end{array}$$

(2)

where T and S are dual w.r.t. N.

Let $A,B,C\in \mathcal{F}\left(U\right)$, we have (1) If for any $x\in U$, $C\left(x\right)=S\left(A\right(x),B(x\left)\right)$, then C is the S-norm union of A and B, denoted as $C=A{\cup }_{S}B;$ and (2) If for any $x\in U$, $C\left(x\right)=T\left(A\right(x),B(x\left)\right)$, then C is the T-norm intersection of A and B, denoted as $C=A{\cap }_{T}B.$ In addition, let $\mathit{J}$ be a non-empty index set, for any $j\in \mathit{J}$, $x,x_j\in [0,1]$, we call T a left-continuous t-norm if and only if $T({\vee }_{j\in \mathit{J}}{x}_j,x)={\vee }_{j\in \mathit{J}}T(x_j,x)$. Similarly, S is called right-continuous t-norm if and only if $S({\wedge }_{i\in \mathit{J}}{x}_j,x)={\wedge }_{i\in \mathit{J}}S(x_j,x)$.

Given a T-norm, for any $x_i,x_j\in [0,1]$, then,

$$\begin{array}{c}\hfill \theta (x_i,x_j)=sup\{x_k\in [0,1]:T(x_i,x_k)\le x_j\},\sigma (x_i,x_j)=inf\{z\in [0,1]:T(x_i,x_z)\ge x_j\},\end{array}$$

(3)

where θ is an R-implicator induced by a T-norm, and σ is a T-coimplicator induced by a T-norm and negation, it is noteworthy that the fuzzy intersection operation denoted as “min" and the fuzzy union operation denoted as “max" constitute a special pair of T-norm and T-conorm operators. These operators are widely utilized and further extended in various contexts. Hu et al. [22] comprehensively summarized several common T-norm and T-conorm operators, which we will not reiterate here.

For nominal variables, the relationship between objects is established by analyzing whether the values of the objects in the variables are equal, forming a division of the domain. However, if the variables are numerical or fuzzy, then a clear equivalence relation is not enough to accurately describe the relationship between objects. The equivalence relation is the most basic concept in the Pawlak rough set. Similarly, for fuzzy rough sets, the concept of the fuzzy equivalence relation is fundamental. Given a non-empty finite set U, the fuzzy relation $\mathcal{R}$ is called the fuzzy equivalence relation on U. For any $x_i,x_j,x_k\in U$, it satisfies three conditions, namely, (1) reflexivity $\mathcal{R}(x_i,x_i)=1$; (2) symmetry $(\mathcal{R}(x_i,x_j)=\mathcal{R}(x_j,x_i))$; and (3) transitivity $\mathcal{R}(x_i,x_j)\ge min\{\mathcal{R}(x_i,x_k),\mathcal{R}(x_k,x_j)\}$. $\mathcal{R}$ is the fuzzy equivalence relation on U [21]. More generally, we call $\mathcal{R}$ the fuzzy T-equivalence relation, if for any $x_i,x_j,x_k\in U$, $\mathcal{R}$ satisfies reflexivity, symmetry, and T-transitivity ($T(\mathcal{R}(x_i,x_j),\mathcal{R}(x_j,x_k))\le \mathcal{R}(x_i,x_k)$).

Definition 4 

([1]). Let $\mathcal{R}$ be an equivalence relation on U. $\forall x_i\in U$, ${\left[x_i\right]}_{\mathcal{R}}={\displaystyle \frac{r_{i1}}{x_1}}+{\displaystyle \frac{r_{i2}}{x_2}}+\cdots +{\displaystyle \frac{r_{in}}{x_n}}$ denotes a fuzzy equivalence class. If $X\in \mathcal{F}\left(U\right)$, the lower and upper approximations of X are a pair of fuzzy sets on U whose membership functions are, respectively,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\underline{\mathcal{R}}}_{S}X\left(x\right)=\underset{y\in U}{inf}S(N\left(\mathcal{R}(x,y)\right),X\left(y\right))\hfill \\ {\overline{\mathcal{R}}}_{T}X\left(x\right)=\underset{y\in U}{sup}T(\mathcal{R}(x,y),X\left(y\right))\hfill \end{array}\right.\end{array}$$

(4)

where $({\underline{\mathcal{R}}}_{S}X,{\overline{\mathcal{R}}}_{T}X)$ are called the $(S,T)$-fuzzy rough sets of X.

3. Multi-Source Mixed Information Systems

Definition 5. 

A multi-source mixed information system (MsMIS) can be expressed as $(U,A\cup \{d\},V,f)$, where U is the object set, and $A=A^c\cup A^n\cup A^{im}\cup A^{sv}\cup A^{iv}$, where $A^c$ is the categorical attribute, $A^n$ is the numerical attribute, $A^{im}$ is the image attribute, $A^{sv}$ is the set-valued attribute, and $A^{iv}$ is the interval-valued attribute. d means the decision attribute set (sometimes written as $D=\{d_1,d_2,\cdots ,d_l\}$). For the sake of simplicity, $A=\{a_1,a_2,\cdots ,a_m\}$ is used to represent the attribute set, where m represents the number of attributes.

Example 1. 

Table 1. An MsMIS.

U	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{a}}_3$	${\mathit{a}}_4$	${\mathit{a}}_5$	d
$x_1$	-	50	{M, P}	[1,3]		1
$x_2$	+	36	{M, U, P}	[1,2]		0
$x_3$	+	28	{M, U}	[2,3]		0
$x_4$	+	16	{U}	[0,2]		1

illustrates an MsMIS, wherein $X=\{x_1,x_2,x_3,x_4\}$ represents the collection of four patients and $A=\{a_1,a_2,a_3,a_4,a_5\}$ signifies the set comprising five different attributes. In this table, $a_1$ is the categorical attribute ("-" and "+" represent negative and positive, respectively), $a_2$ is the numerical attribute, $a_3$ is the set-valued attribute, $a_4$ is the interval-valued attribute, and $a_5$ is the image attribute, and d denotes the set of decision attributes.

3.1. Similarity Relations

In an MsMIS, mixed attributes can encompass a diverse range of data types, including Boolean values, categorical information, real-valued data, set-valued data, interval-valued data, text content, image files, video clips, audio recordings, and sensor signals [23]. In this article, we consider the similarity between two attributes, and their related definitions [11,24,25,26,27] are as follows.

Definition 6. 

Let $MsMIS=(U,A\cup \{d\},V,f)$ be an MsMIS. $\forall x_i,x_j\in U$, the similarity of categorical data is denoted as

$$\begin{array}{c}\hfill {\mathcal{S}}_c(x_i,x_j)=\left\{\begin{array}{cc}0& if{x}_i\ne x_j;\\ 1& if{x}_i=x_j.\end{array}\right.\end{array}$$

(5)

From Definition 6, the similarity function ${\mathcal{R}}_c(x_i,x_j)$ can be applied to extract the equivalence relation from categorical data.

Definition 7. 

Let $MsMIS=(U,A\cup \{d\},V,f)$ be an MsMIS. $\forall x_i,x_j\in U$, the similarity of numerical data is denoted by

$$\begin{array}{c}\hfill {\mathcal{S}}_n(x_i,x_j)=exp(-{\displaystyle \frac{\left|\right|x_i-x_j{\left|\right|}^2}{{\delta }^2}}).\end{array}$$

(6)

The similarity function ${\mathcal{S}}_n(x_i,x_j)$ is called a Gaussian kernel, which can be used to extract information from numerical data.

Definition 8. 

Let $MsMIS=(U,A\cup \{d\},V,f)$ be an MsMIS. The similarity of image data is denoted as

$$\begin{array}{c}\hfill {\mathcal{S}}_{im}(x_i,x_j)=\sum _{k=1}^{P}min(x_i^k,x_j^k).\end{array}$$

(7)

The similarity function ${\mathcal{S}}_{im}(x_i,x_j)$ is a histogram intersection kernel, which is used to compute the similarity between histograms of image data. $x_i^k$ and $x_j^k$ express the number of pixels that have colors in the k-th fixed list of P color ranges, where ${\sum }_{k=1}^P{x}_i^k=1$ and ${\sum }_{k=1}^P{x}_j^k=1$. In image data, a color histogram indicates the distribution of colors.

Definition 9. 

Let $MsMIS=(U,A\cup \{d\},V,f)$ be an MsMIS. The similarity of set-valued data is denoted by

$$\begin{array}{c}\hfill {\mathcal{S}}_{sv}(x_i,x_j)={\displaystyle \frac{a\left(x_i\right)\cap a\left(x_j\right)}{a\left(x_i\right)\cup a\left(x_j\right)}},\end{array}$$

(8)

where $a\left(x_i\right)$ is the attribute set on a. The similarity function ${\mathcal{S}}_{sv}(x_i,x_j)$ can measure the similarity between set-valued data.

Definition 10. 

Let $MsMIS=(U,A\cup \{d\},V,f)$ be an MsMIS. The similarity of interval-valued data is denoted as

$$\begin{array}{c}\hfill {\mathcal{S}}_{iv}(x_{ij},x_{lj})=exp\left\{-{\displaystyle \frac{1}{2}}\left|\right|x_{ij}-x_{lj}{\left|\right|}^2\right\}(i,l=1,2,\cdots ,k),\end{array}$$

(9)

where $\left|\right|x_{ij}-x_{lj}{\left|\right|}^2={(a_{ij}-a_{lj})}^2+{(b_{ij}-b_{lj})}^2$ and the interval-valued data $x_{ij}=(a_{ij},b_{ij})$ with $a_{ij}\le b_{ij}$. The similarity function ${\mathcal{S}}_{iv}(x_i,x_j)$ can normalize each interval-valued variable.

3.2. Kernel Functions Fusion Based on Similarity

In rough sets, the relation between two attributes can be calculated by an intersection operation, while in fuzzy rough sets, T-norm operations are used [10]. In this paper, the min operation is applied to the fusion of multiple similarities in terms of T-norm.

Definition 11. 

Let $MsMIS=(U,A\cup \{d\},V,f)$ be an MsMIS. The matrix of the m-th similarity function ${\mathcal{S}}_m$ can be denoted by

$$\begin{array}{c}\hfill M{\left({\mathcal{S}}_m(x_i,x_j)\right)}_{n\times n}=\left[\begin{array}{cccc}{\mathcal{S}}_m\left(x_1,x_1\right)& {\mathcal{S}}_m\left(x_1,x_2\right)& \cdots & {\mathcal{S}}_m\left(x_1,x_n\right)\\ {\mathcal{S}}_m\left(x_2,x_1\right)& {\mathcal{S}}_m\left(x_2,x_2\right)& \cdots & {\mathcal{S}}_m\left(x_2,x_n\right)\\ ⋮& ⋮& \ddots & ⋮\\ {\mathcal{S}}_m\left(x_n,x_1\right)& {\mathcal{S}}_m\left(x_n,x_2\right)& \cdots & {\mathcal{S}}_m\left(x_n,x_n\right)\end{array}\right],\end{array}$$

(10)

where ${\mathcal{S}}_m$ refers to a similarity function, which is calculated for attributes $a_i,i=1,2,\cdots ,m$.

Definition 12. 

Let $MsMIS=(U,A\cup \{d\},V,f)$ be an MsMIS. If two similarity functions ${\mathcal{S}}_i$ and ${\mathcal{S}}_j$ are used to calculate the attributes $a_i$ and $a_j$, respectively, then, for $\forall x,y\in U$, new operators based on fuzzy T-norm operators are denoted as follows:

(1) Standard min operator

$$\begin{array}{c}\hfill {\mathit{K}}_{T_m}(x,y)=min\left({\mathcal{S}}_i(x,y),{\mathcal{S}}_j(x,y)\right).\end{array}$$

(11)

(2) Algebraic product

$$\begin{array}{c}\hfill {\mathit{K}}_{T_P}(x,y)={\mathcal{S}}_i(x,y)\times {\mathcal{S}}_j(x,y).\end{array}$$

(12)

(3) Lukasiewicz T-norm

$$\begin{array}{c}\hfill {\mathit{K}}_{T_l}(x,y)=max\left({\mathcal{S}}_i(x,y)+{\mathcal{S}}_j(x,y)-1,0\right).\end{array}$$

(13)

(4) $T_{cos}$-norm

$$\begin{array}{c}\hfill {\mathit{K}}_{T_{cos}}(x,y)=max\left({\mathcal{S}}_i(x,y)\ast {\mathcal{S}}_j(x,y)-\sqrt{1-{\mathcal{S}}_i{(x,y)}^2}\sqrt{1-{\mathcal{S}}_j{(x,y)}^2},0\right)\end{array}$$

(14)

Proposition 1. 

Given two similarity functions ${\mathcal{S}}_i,{\mathcal{S}}_j\in [0,1]$ for any two conitional attributes $a_i$ and $a_j$, then

$$\begin{array}{c}\hfill {\mathit{K}}_{•}\subseteq {\mathcal{S}}_{i}and{\mathit{K}}_{•}\subseteq {\mathcal{S}}_j,\end{array}$$

(15)

where $•=T_m,T_P,T_l,T_{cos}$, and ${\mathcal{S}}_i(x,x)=1,{\mathcal{S}}_j(x,x)=1$.

Proof of Proposition 1. 

Proposition 1 is easy to prove. For example, let $•=T_m$. Suppose that $A=\{a_i,a_j\}$ and ${\mathbf{K}}_{T_m}^A=min\{{\mathcal{S}}_i,{\mathcal{S}}_j\}$. We have ${\mathcal{S}}_i(x,y)\ge {\mathbf{K}}_{T_m}(x,y)$ and ${\mathcal{S}}_j(x,y)\ge {\mathbf{K}}_{T_m}^A(x,y)$. Therefore, ${\mathbf{K}}_{T_m}\subseteq {\mathcal{S}}_i$ and ${\mathbf{K}}_{T_m}\subseteq {\mathcal{S}}_j$. In the same way, we can prove ${\mathbf{K}}_{T_P}\subseteq {\mathcal{S}}_i$ and ${\mathbf{K}}_{T_P}\subseteq {\mathcal{S}}_j$, ${\mathbf{K}}_{T_l}\subseteq {\mathcal{S}}_i$ and ${\mathbf{K}}_{T_l}\subseteq {\mathcal{S}}_j$, ${\mathbf{K}}_{T_{cos}}\subseteq {\mathcal{S}}_i$ and ${\mathbf{K}}_{T_{cos}}\subseteq {\mathcal{S}}_j$. □

Example 2. 

Figure 1 indicates the process of multi-source mixed data fusion. Four objects are described using the five attributes $a_1$, $a_2$, $a_3$, $a_4$, and $a_5$. Thus, the similarity of categorical data ${\mathcal{S}}_c$, the similarity of numerical data ${\mathcal{S}}_n$, the similarity of set-valued ${\mathcal{S}}_{sv}$, the similarity of interval-valued data ${\mathcal{S}}_{iv}$, and the similarity of image data ${\mathcal{S}}_{im}$ are considered to calculate the fuzzy relation between objects. We use the objects $x_2$ and $x_4$ as an example, i.e.,

(1) For categorical data: ${\mathcal{S}}_c(x_2,x_4)=1$;

(2) For numerical data: ${\mathcal{S}}_n(x_2,x_4)=exp(-{\displaystyle \frac{\left|\right|0.5-{0.2\left|\right|}^2}{0.5^2}})=0.70$;

(3) For set-valued data: ${\mathcal{S}}_{sv}(x_2,x_4)={\displaystyle \frac{\{M,U,P\}\cap \left\{U\right\}}{\{M,U,P\}\cup \left\{U\right\}}}={\displaystyle \frac{1}{3}}=0.33;$

(4) For interval-valued data: ${\mathcal{S}}_{iv}(x_2,x_4)=exp\{-{\displaystyle \frac{1}{2}}({(1-0)}^2+{(2-2)}^2)\}=0.61$;

(5) For image data: ${\mathcal{S}}_{im}(x_2,x_4)=min(0.6,0.5)+min(0.1,0.1)+min(0.2,0.2)+min(0.1,0.2)=0.9$. Then, these five attributes are combined by ${\mathit{K}}_{T_m}$:

$${\mathit{K}}_{T_m}(x_1,x_2)=min(1,0.70,0.33,0.61,0.9)=0.33.$$

Therefore,

$$M{\left({\mathit{K}}_{T_m}(x_i,x_j)\right)}_{4\times 4}={\left[\begin{array}{cccc}1\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0.37\hfill & 0.33\hfill \\ 0\hfill & 0.37\hfill & 1\hfill & 0.14\hfill \\ 0\hfill & 0.33\hfill & 0.14\hfill & 1\hfill \end{array}\right]}_{4\times 4};$$

Similarly, $M{\left({\mathit{K}}_{T_P}(x_i,x_j)\right)}_{4\times 4}={\left[\begin{array}{cccc}1\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0.19\hfill & 0.08\hfill \\ 0\hfill & 0.19\hfill & 1\hfill & 0.02\hfill \\ 0\hfill & 0.08\hfill & 0.02\hfill & 1\hfill \end{array}\right]}_{4\times 4};$

$M{\left({\mathit{K}}_{T_l}(x_i,x_j)\right)}_{4\times 4}={\left[\begin{array}{cccc}1\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 1\hfill \end{array}\right]}_{4\times 4};$

$M{\left({\mathit{K}}_{T_{cos}}(x_i,x_j)\right)}_{4\times 4}={\left[\begin{array}{cccc}1\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 1\hfill \end{array}\right]}_{4\times 4}.$

$M{\left({\mathbf{K}}_{T_m}(x_i,x_j)\right)}_{4\times 4},M{\left({\mathbf{K}}_{T_P}(x_i,x_j)\right)}_{4\times 4},M{\left({\mathbf{K}}_{T_l}(x_i,x_j)\right)}_{4\times 4}$ and $M{\left({\mathbf{K}}_{T_{cos}}(x_i,x_j)\right)}_{4\times 4}$ are the fuzzy T-equivalence relation matrix in terms of fuzzy T-norm operators ${\mathbf{K}}_{T_m}(x,y)$, ${\mathbf{K}}_{T_P}(x,y)$, ${\mathbf{K}}_{T_l}(x,y)$, and ${\mathbf{K}}_{T_{cos}}(x,y)$, respectively. In addition, this example can easily verify Proposition 1.

From Figure 1, it is evident that by calculating the similarity function for each data type, feature information is extracted. This extracted information can then be fused using the operator $\mathbf{K}Tm$. This computational process can be viewed as multi-source information fusion, where information from different sensors or sources is integrated and processed in a similar manner.

3.3. Two Types of FRSs Based on Similarity Function

Let $MsMIS=(U,A\cup \{d\},V,f)$ be an MsMIS. Given $P\subseteq A$, $P=\{a_i,a_j\}$, if two similarity functions ${\mathcal{S}}_i$ and ${\mathcal{S}}_j$ are derived with $a_i$ and $a_j$, respectively, then, we can fuse similarity functions (${\mathbf{K}}_T^P=f_T({\mathcal{S}}_i,{\mathcal{S}}_j)$) based on T-norm to obtain fuzzy relation, which can be called the fuzzy T-equivalence relation. Based on the work in [10,22], we can derive two types of FRSs as shown below.

Definition 13. 

Let $MsMIS=(U,A\cup \{d\},V,f)$ be an MsMIS. Given $P\subseteq A$, the fuzzy S-lower and T-upper approximations of X are defined by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underline{{\mathit{K}}_{T,S}^P}\left(X\right)\left(x\right)=\underset{y\in U}{inf}S(N\left({\mathit{K}}_T^P(x,y)\right),X\left(y\right)),\hfill \\ \overline{{\mathit{K}}_{T,T}^P}\left(X\right)\left(x\right)=\underset{y\in U}{sup}T\left({\mathit{K}}_T^P(x,y)\right),X\left(y\right)),\hfill \end{array}\right.\end{array}$$

(16)

where ${\mathit{K}}_T^P=f_T({\mathcal{S}}_i,{\mathcal{S}}_j)$ and ($\underline{{\mathit{K}}_{T,S}^P}X,\overline{{\mathit{K}}_{T,T}^P}X$) are known as the $(S,T)$-fuzzy rough sets.

Definition 14. 

Let $MsMIS=(U,A\cup \{d\},V,f)$ be an MsMIS. Given $P\subseteq A$, the fuzzy θ-lower and σ-upper approximations of X are defined by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underline{{\mathit{K}}_{T,\theta }^P}\left(X\right)\left(x\right)=\underset{y\in U}{inf}\theta ({\mathit{K}}_T^P(x,y),X\left(y\right)),\hfill \\ \overline{{\mathit{K}}_{T,\sigma }^P}\left(X\right)\left(x\right)=\underset{y\in U}{sup}\sigma (N\left({\mathit{K}}_T^P(x,y)\right),X\left(y\right)),\hfill \end{array}\right.\end{array}$$

(17)

where ${\mathit{K}}_T^P=f_T({\mathcal{S}}_i,{\mathcal{S}}_j)$, and ($\underline{{\mathit{K}}_{T,\theta }^P}X,\overline{{\mathit{K}}_{T,\sigma }^P}X$) are known as the $(\theta ,\sigma )$-fuzzy rough sets.

4. FRSs Based on Fuzzy Information Granularity

According to Equations (2) and (3), T, S, and N are discussed based on logical operators. In this section, we will study them from the perspective of fuzzy information granularity.

Definition 15 

([6]). For any $x\in U$, given $\vartheta \in [0,1]$, a fuzzy set is denoted as $x_{\vartheta }$, and it follows that:

$$\begin{array}{c}\hfill x_{\vartheta }\left(y\right)=\left\{\begin{array}{c}\vartheta ,y=x,\hfill \\ 0,y\ne x.\hfill \end{array}\right.\end{array}$$

(18)

Definition 16 

([6]). Let $MsMIS=(U,A\cup \{d\},V,f)$ be an MsMIS. Given $P\subseteq A$, if ${\mathit{K}}_T^P$ is a fuzzy T-equivalence relation on U, for $X\in \mathcal{F}\left(U\right)$ and $\vartheta \in [0,1]$, then several fuzzy information granularities can be defined as

$$\begin{array}{c}\hfill {\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^T\left(y\right)=T({\mathit{K}}_T^P(x,y),\vartheta ),{\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^S\left(y\right)=S(N\left({\mathit{K}}_T^P(x,y)\right),N\left(\vartheta \right)).\end{array}$$

(19)

$$\begin{array}{c}\hfill {\left[x_X\right]}_{{\mathit{K}}_T^P}^T\left(y\right)=T({\mathit{K}}_T^P(x,y),X\left(x\right)),{\left[x_X\right]}_{{\mathit{K}}_T^P}^S\left(y\right)=S(N\left({\mathit{K}}_T^P(x,y)\right),N\left(X\left(x\right)\right)).\end{array}$$

(20)

4.1. The Rationality of Fuzzy Information Granularities Is in an MsMIS

Definition 17. 

Assume that $MsMIS=(U,A\cup \{d\},V,f)$ is an MsMIS. Given $P\subseteq A$, let ${\mathcal{A}}_{{\mathit{K}}_T^P}^T=\{{\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^T:x\in U,\vartheta \in [0,1]\}$ and ${\mathcal{A}}_{{\mathit{K}}_T^P}^S=\{{\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^S:x\in U,\vartheta \in [0,1]\}$. Then, we have:

$\left(1\right)$ $\forall x\in U,{\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^T\left(y\right)=T({\left[x\right]}_{{\mathit{K}}_T^P}^T\left(y\right),\vartheta )$, ${\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^S\left(y\right)=S({\left[x\right]}_{{\mathit{K}}_S^P}^T\left(y\right),N\left(\vartheta \right))$.

$\left(2\right)$ $\forall x\in U,$ if ${\vartheta }^{\prime }<\vartheta$, then ${\left[x_{{\vartheta }^{\prime }}\right]}_{{\mathit{K}}_T^P}^T\subseteq {\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^{MP}}^T$ and ${\left[x_{{\vartheta }^{\prime }}\right]}_{{\mathit{K}}_T^P}^S\supseteq {\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^S$.

$\left(3\right)$ $\forall x\in U,$ ${\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^T={\cup }_{{\vartheta }^{\prime }<\vartheta }{\left[x_{{\vartheta }^{\prime }}\right]}_{{\mathit{K}}_T^P}^T$, ${\left[x_{\vartheta }\right]}_{{\mathit{K}}_S^P}^T={\cap }_{{\vartheta }^{\prime }<\vartheta }{\left[x_{{\vartheta }^{\prime }}\right]}_{{\mathit{K}}_T^P}^S$.

$\left(4\right)$ $c{o}_N\left({\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^T\right)={\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^{MP}}^S$, $c{o}_N\left({\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^S\right)={\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^{MP}}^T$.

(Proof of Definition 17). 

$\left(1\right)$ Let ${\mathbf{K}}_T^P(x,y)={\left[x\right]}_{{\mathbf{K}}_T^P}^T\left(y\right)$, $N\left({\mathbf{K}}_S^P(x,y)\right)={\left[x\right]}_{{\mathbf{K}}_T^P}^S\left(y\right)$. Hence, the proof is obtained.

$\left(2\right)$ Since ${\vartheta }^{\prime }<\vartheta$, it is easy prove that ${\left[x_{{\vartheta }^{\prime }}\right]}_{{\mathbf{K}}_T^P}^T\subseteq {\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T$ holds. As T and S are dual w.r.t. N, then, ${\left[x_{{\vartheta }^{\prime }}\right]}_{{\mathbf{K}}_T^P}^S\supseteq {\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^S$ also holds.

$\left(3\right)$ Obviously.

$\left(4\right)$ See $\left(1\right)$ and $\left(2\right)$. □

According to Definition 17, it exhibits the relationships between ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T$ and ${\left[x\right]}_{{\mathbf{K}}_T^P}^T$, and ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^S$ and ${\left[x\right]}_{{\mathbf{K}}_T^P}^S$, respectively. This means ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T$ and ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^S$ can be defined through ${\left[x\right]}_{{\mathbf{K}}_T^P}^T$ and ${\left[x\right]}_{{\mathbf{K}}_T^P}^S$, respectively. Therefore, it can be used as an axiom to characterize elements of ${\mathcal{A}}_{{\mathbf{K}}_T^P}^T$ and ${\mathcal{A}}_{{\mathbf{K}}_S^P}^S$.

Proposition 2. 

Assume that $MsMIS=(U,A\cup \{d\},V,f)$ is an MsMIS. Given $P\subseteq A$, if ${\mathit{K}}_T^P$ is a fuzzy T-equivalence relation on U, for any $x\in U$ and $\vartheta \in [0,1]$, then, the following conditions are equivalent.

$\left(1\right)$ ${\mathit{K}}_T^P$ is reflexive;

$\left(2\right)$ ${\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^{MP}}^T\left(x\right)=\vartheta$;

$\left(3\right)$ ${\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^{MP}}^S\left(x\right)=N\left(\vartheta \right)$.

Proof of Proposition 2. 

It is obvious that $\left(1\right)\Rightarrow \left(2\right)$ and $\left(1\right)\Rightarrow \left(3\right)$.

“$\left(2\right)\Rightarrow \left(1\right)$”: ${\mathbf{K}}_T^P(x,x)<1$, pick ${\mathbf{K}}_T^P(x,x)<\vartheta$, then ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^{MP}}^T\left(x\right)\le {\mathbf{K}}_T^P(x,x)<\vartheta$, it is a contradiction, so ${\mathbf{K}}_T^P(x,x)=1$.

“$\left(3\right)\Rightarrow \left(1\right)$”: if ${\mathbf{K}}_T^P(x,x)<1$, then $N({\mathbf{K}}_T^P(x,x)>0$. If ${\mathbf{K}}_T^P(x,x)<\vartheta$, then $N({\mathbf{K}}_T^P(x,x)>N\left(\vartheta \right)$. Hence, ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^S\left(y\right)=S(N\left({\mathbf{K}}_T^P(x,y)\right),N\left(\vartheta \right))>N({\mathbf{K}}_T^P(x,x)>N\left(\vartheta \right)$ is a contradiction. Therefore, ${\mathbf{K}}_T^P(x,x)=1.$ □

From Proposition 2, if ${\mathbf{K}}_T^P$ is reflexive, we have $x_{\vartheta }\subseteq {\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T$ and $x_{N\left(\vartheta \right)}\subseteq {\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^S$. As a result, ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T$ and ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^S$ can be referred to as fuzzy information granularities with $x_{\vartheta }$ and $x_{N\left(\vartheta \right)}$ as their centers, respectively.

Proposition 3. 

Assume that $MsMIS=(U,A\cup \{d\},V,f)$ is an MsMIS. Given $P\subseteq A$, if ${\mathit{K}}_T^P$ is a fuzzy T-equivalence relation on U, for any $x\in U$, then, the following conditions are equivalent.

$\left(1\right)$ ${\mathit{K}}_T^P$ is symmetric;

$\left(2\right)$ ${\left[x\right]}_{{\mathit{K}}_T^P}^T\left(y\right)={\left[y\right]}_{{\mathit{K}}_T^P}^T\left(x\right)$;

$\left(3\right)$ ${\left[x\right]}_{{\mathit{K}}_T^P}^S\left(y\right)={\left[y\right]}_{{\mathit{K}}_T^P}^S\left(x\right)$.

Proof of Proposition 3. 

Since ${\left[x\right]}_{{\mathbf{K}}_T^P}^T\left(y\right)={\mathbf{K}}_T^P(x,y)$ and ${\left[x\right]}_{{\mathbf{K}}_T^P}^S\left(y\right)=N\left({\mathbf{K}}_T^P(x,y)\right)$, $\left(1\right)$ and $\left(2\right)$ can be easily proved. □

Proposition 4. 

Assume that $MsMIS=(U,A\cup \{d\},V,f)$ is an MsMIS. Given $P\subseteq A$, if ${\mathit{K}}_T^P$ is a fuzzy T-equivalence relation on U, for any $x\in U$, then, the following conditions are equivalent.

$\left(1\right)$ ${\mathit{K}}_T^P$ is T-transitive;

$\left(2\right)$ ${\left[x\right]}_{{\mathit{K}}_T^P}^T\left(y\right)\ge {sup}_{z\in U}T({\left[x\right]}_{{\mathit{K}}_T^P}^T\left(z\right),{\left[z\right]}_{{\mathit{K}}_T^P}^T\left(y\right))$;

$\left(3\right)$ ${\left[x\right]}_{{\mathit{K}}_T^P}^S\left(y\right)\le {inf}_{z\in U}S({\left[x\right]}_{{\mathit{K}}_S^P}^T\left(z\right),{\left[z\right]}_{{\mathit{K}}_T^P}^S\left(y\right))$.

Proof of Proposition 4. 

“$\left(1\right)\Rightarrow \left(2\right)$”: $\forall x,y,z\in U,{\left[x\right]}_{{\mathbf{K}}_T^P}^T\left(y\right)={\mathbf{K}}_T^P(x,y)\ge T({\mathbf{K}}_T^P(x,z),{\mathbf{K}}_T^P(z,y))=T({\left[x\right]}_{{\mathbf{K}}_T^P}^T\left(z\right),{\left[z\right]}_{{\mathbf{K}}_T^P}^T\left(y\right))$. Hence, ${\left[x\right]}_{{\mathbf{K}}_T^P}^T\left(y\right)\ge {sup}_{z\in U}T({\left[x\right]}_{{\mathbf{K}}_T^P}^T\left(z\right),{\left[z\right]}_{{\mathbf{K}}_T^P}^T\left(y\right))$.

“$\left(2\right)\Rightarrow \left(1\right)$”: It is easily proved by the T-transitive.

“$\left(1\right)\Rightarrow \left(3\right)$”: $\forall x,y,z\in U,{\left[x\right]}_{{\mathbf{K}}_T^P}^S\left(y\right)=N\left({\mathbf{K}}_T^P\right)\le N\left(T({\mathbf{K}}_T^P(x,z),{\mathbf{K}}_T^P(z,y))\right)=S(N\left({\mathbf{K}}_T^P(x,z)\right),N\left({\mathbf{K}}_T^P(z,y)\right))=S({\left[x\right]}_{{\mathbf{K}}_T^P}^S\left(z\right),{\left[z\right]}_{{\mathbf{K}}_T^P}^S\left(y\right))$. Hence, we have the conclusion: ${\left[x\right]}_{{\mathbf{K}}_T^P}^S\left(y\right)\le {inf}_{z\in U}S({\left[x\right]}_{{\mathbf{K}}_S^P}^T\left(z\right),{\left[z\right]}_{{\mathbf{K}}_T^P}^S\left(y\right))$.

“$\left(3\right)\Rightarrow \left(1\right)$”: it can be easily proved according to T-transitivity and duality. □

Theorem 1. 

Assume that $MsMIS=(U,A\cup \{d\},V,f)$ is an MsMIS. Given $P\subseteq A$, if ${\mathit{K}}_T^P$ is a fuzzy T-equivalence relation on U, for any $x,y,z\in U$ and $\vartheta \in [0,1]$, then,

$\left(1\right)$ ${\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^T=\vartheta$, ${\left[x\right]}_{{\mathit{K}}_T^P}^T\left(y\right)={\left[y\right]}_{{\mathit{K}}_T^P}^T\left(x\right)$, ${\left[x\right]}_{{\mathit{K}}_T^P}^T\left(y\right)={sup}_{z\in U}T({\left[x\right]}_{{\mathit{K}}_T^P}^T\left(z\right),{\left[z\right]}_{{\mathit{K}}_T^P}^T\left(y\right))$.

$\left(2\right)$ ${\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^S=N\left(\vartheta \right)$, ${\left[x\right]}_{{\mathit{K}}_T^P}^S\left(y\right)={\left[y\right]}_{{\mathit{K}}_T^P}^S\left(x\right)$, ${\left[x\right]}_{{\mathit{K}}_T^P}^T\left(y\right)={inf}_{z\in U}S({\left[x\right]}_{{\mathit{K}}_T^P}^S\left(z\right),{\left[z\right]}_{{\mathit{K}}_T^P}^S\left(y\right))$.

Proof of Theorem 1. 

As ${\mathbf{K}}_T^P$ is reflexive, it can be easily proved. □

Proposition 5. 

Assume that $MsMIS=(U,A\cup \{d\},V,f)$ is an MsMIS. Given $P\subseteq A$, if ${\mathit{K}}_T^P$ is a fuzzy T-equivalence relation on U, then, we have:

$\left(1\right)$ If $\vartheta ={\vartheta }^{\prime }$, $T({\mathit{K}}_T^P(x,y),\vartheta )=\vartheta$ and $S(N\left({\mathit{K}}_T^P(x,y)\right),N\left(\vartheta \right))=N\left(\vartheta \right)$, then ${\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^T={\left[y_{{\vartheta }^{\prime }}\right]}_{{\mathit{K}}_T^P}^T$ and ${\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^S={\left[y_{{\vartheta }^{\prime }}\right]}_{{\mathit{K}}_T^P}^S$.

$\left(2\right)$ ${\left[x\right]}_{{\mathit{K}}_T^P}^T$ and ${\left[x\right]}_{{\mathit{K}}_T^P}^S$ are the maximal element in ${\mathcal{A}}_{{\mathit{K}}_T^P}^T$ and the minimal element in ${\mathcal{A}}_{{\mathit{K}}_T^P}^S$, respectively.

$\left(3\right)$ ${\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^T=\cap \{{\left[y_{\nu }\right]}_{{\mathit{K}}_T^P}^T:x_{\vartheta }\subseteq {\left[y_{\nu }\right]}_{{\mathit{K}}_T^P}^T\}$, ${\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^S=\cup \{{\left[y_{\nu }\right]}_{{\mathit{K}}_T^{MP}}^S:{\left[y_{\nu }\right]}_{{\mathit{K}}_T^P}^S\left(x\right)\le N\left(\vartheta \right)\}$.

$\left(4\right)$ ${\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^T={\cup }_{z\in U}{\left[z_{\nu }\right]}_{{\mathit{K}}_T^P}^T$ where $\nu ={\left[z_{\vartheta }\right]}_{{\mathit{K}}_T^P}^T\left(x\right)$; ${\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^S={\cap }_{z\in U}{\left[z_{\iota }\right]}_{{\mathit{K}}_T^P}^S$ where $\iota ={\left[z_{\vartheta }\right]}_{{\mathit{K}}_T^P}^S\left(x\right)$.

$\left(5\right)$ $y_{\xi }\subseteq {\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^T$⇒${\left[y_{\xi }\right]}_{{\mathit{K}}_T^P}^T\subseteq {\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^T$; $y_{\xi }\neg \subset {\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^S$⇒${\left[y_{\xi }\right]}_{{\mathit{K}}_T^P}^S\supseteq {\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^S$.

Proof of Proposition 5. 

$\left(1\right)$ If ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T={\left[y_{{\vartheta }^{\prime }}\right]}_{{\mathbf{K}}_T^P}^T,$ then $\vartheta ={\vartheta }^{\prime }$. According to Theorem 1(1), $T({\mathbf{K}}_T^P(x,y),\vartheta )={\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T\left(y\right)=\vartheta ={\left[x_{{\vartheta }^{\prime }}\right]}_{{\mathbf{K}}_T^P}^T\left(y\right)={\vartheta }^{\prime }$ holds. On the contrary, if $\vartheta ={\vartheta }^{\prime }$ and $T({\mathbf{K}}_T^P(x,y),\vartheta )=\vartheta$. $\forall z\in U,{\left[z_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T\left(z\right)=T({\mathbf{K}}_T^P(x,z),\vartheta )\le T(T({\mathbf{K}}_T^P(x,z),{\mathbf{K}}_T^P(y,z)),\vartheta )=T(T({\mathbf{K}}_T^P(x,z),\vartheta ),{\mathbf{K}}_T^P(y,z))=T({\mathbf{K}}_T^P(y,z),\vartheta )={\left[y_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T\left(z\right)$. Hence, ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T\subseteq {\left[y_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T$. Similarly, ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T\supseteq {\left[y_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T$. In the same way, we can prove that ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^S={\left[y_{{\vartheta }^{\prime }}\right]}_{{\mathbf{K}}_T^P}^S$.

$\left(2\right)$ Suppose ${\left[x\right]}_{{\mathbf{K}}_T^P}^T\subseteq {\left[y\right]}_{{\mathbf{K}}_T^P}^T$, we have ${\mathbf{K}}_T^P(x,y)=1$, it implies ${\left[x\right]}_{{\mathbf{K}}_T^P}^T={\left[y\right]}_{{\mathbf{K}}_T^P}^T$. Suppose ${\left[x\right]}_{{\mathbf{K}}_T^P}^S\supseteq {\left[y\right]}_{{\mathbf{K}}_T^P}^S$, then $N\left({\mathbf{K}}_T^P(x,y)\right)=0$, this implies ${\left[x\right]}_{{\mathbf{K}}_T^P}^S={\left[y\right]}_{{\mathbf{K}}_T^P}^S$.

$\left(3\right)$ Suppose $x_{\vartheta }\subseteq {\left[y_{\nu }\right]}_{{\mathbf{K}}_T^P}^T$, we have $\vartheta \le T({\mathbf{K}}_T^P(x,y),\nu )$. $\forall z\in U,{\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T\left(z\right)=T({\mathbf{K}}_T^P(x,y),\vartheta )$ $\le T({\mathbf{K}}_T^P(x,z),T({\mathbf{K}}_T^P(x,y),\nu ))=T(T({\mathbf{K}}_T^P(x,z),{\mathbf{K}}_T^P(x,y)),\nu )\le T({\mathbf{K}}_T^P(y,z),\nu )={\left[y_{\nu }\right]}_{{\mathbf{K}}_T^P}^T\left(z\right)$. Hence, ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T\subseteq {\left[y_{\nu }\right]}_{{\mathbf{K}}_T^P}^T$, which implies ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T=\cap \{{\left[y_{\nu }\right]}_{{\mathbf{K}}_T^P}^T:x_{\vartheta }\subseteq {\left[y_{\nu }\right]}_{{\mathbf{K}}_T^P}^T\}$. Suppose ${\left[y_{\nu }\right]}_{{\mathbf{K}}_T^P}^S\le N\left(\vartheta \right)$, we have $S(N\left({\mathbf{K}}_T^P(x,y)\right),N\left(\nu \right))\le N\left(\vartheta \right)$. Hence, ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^S\left(z\right)=S(N\left({\mathbf{K}}_T^P(x,z)\right),N\left(\vartheta \right))\ge S(N\left({\mathbf{K}}_T^P(x,z)\right),S\left(N({\mathbf{K}}_T^P(x,y),N\left(\nu \right))\right)\ge S(S(N\left({\mathbf{K}}_T^P(y,z)\right),N\left(\nu \right))={\left[y_{\nu }\right]}_{{\mathbf{K}}_T^P}^S\left(z\right)$. This implies ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^S=\cup \{{\left[y_{\nu }\right]}_{{\mathbf{K}}_T^P}^S:{\left[y_{\nu }\right]}_{{\mathbf{K}}_T^P}^S\left(x\right)\le N\left(\vartheta \right)\}$.

$\left(4\right)$ According to T-transitivity of ${\mathbf{K}}_T^P$, then ${\mathbf{K}}_T^P(x,y)\ge T({\mathbf{K}}_T^P(x,y),{\mathbf{K}}_T^P(y,z))$. This implies $T({\mathbf{K}}_T^P(x,y),\vartheta )\ge {sup}_{z\in U}T(T({\mathbf{K}}_T^P(x,y),{\mathbf{K}}_T^P(x,z)),\vartheta )={sup}_{z\in U}T({\mathbf{K}}_T^P(z,y),T({\mathbf{K}}_T^P(x,z),\vartheta ))$. Hence, ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T={\cup }_{z\in U}{\left[z_{\nu }\right]}_{{\mathbf{K}}_T^P}^T$, $\nu ={\left[z_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T\left(x\right)$. Similarly, we can prove that ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^S={\cap }_{z\in U}{\left[z_{\iota }\right]}_{{\mathbf{K}}_T^P}^S$ where $\iota ={\left[z_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^S\left(x\right)$.

$\left(5\right)$: It is straightforward.

□

4.2. The Lower and Upper Approximations of Fuzzy Sets Are Constructed Using Information Granularities

In this subsection, we combine fuzzy information granularity from the perspective of granular computing. Initially, fuzzy information granularities are employed to form the lower and upper approximations of fuzzy sets. These approximations represent a seamless extension of the precise approximations found in traditional rough sets and align perfectly with those in FRSs.

Definition 18. 

Assume that $MsMIS=(U,A\cup \{d\},V,f)$ is an MsMIS. Given $P\subseteq A$, if ${\mathit{K}}_T^P$ is a fuzzy T-equivalence relation on U, for any $X\in \mathcal{F}\left(U\right)$ and $\vartheta \in [0,1]$, then,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underline{G{\mathit{K}}_{T,T}^P}\left(X\right)=\bigcup \{{\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^T:x\in U,\vartheta \in [0,1],{\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^T\subseteq X\},\hfill \\ \overline{G{\mathit{K}}_{T,S}^P}\left(X\right)=\bigcap \{{\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^S:x\in U,\vartheta \in [0,1],X\subseteq {\left[x_{\vartheta }\right]}_{{\mathit{K}}_T^P}^S\},\hfill \end{array}\right.\end{array}$$

(21)

where $\underline{G{\mathit{K}}_{T,T}^P}$ is referred to as the T-lower approximation of X and $\overline{G{\mathit{K}}_{T,S}^P}$ is referred to as the S-upper approximation of X. We can call ($\underline{G{\mathit{K}}_{T,T}^P}\left(X\right),\overline{G{\mathit{K}}_{T,S}^P}\left(X\right)$) granular $(T,S)$-fuzzy rough sets.

Theorem 2. 

Assume that $MsMIS=(U,A\cup \{d\},V,f)$ is an MsMIS. Given $P\subseteq A$, if ${\mathit{K}}_T^P$ is a fuzzy T-equivalence relation on U, for any $X\in \mathcal{F}\left(U\right),$ then

(1) $\underline{G{\mathit{K}}_{T,T}^P}\left(X\right)\left(x\right)=\underline{{\mathit{K}}_{T,\theta }^P}\left(X\right)\left(x\right)$;

(2) $\overline{G{\mathit{K}}_{T,S}^P}\left(X\right)\left(x\right)=\overline{{\mathit{K}}_{T,\sigma }^P}\left(X\right)\left(x\right)$.

Proof of Theorem 2. 

$\left(1\right)$ We first need to prove $\underline{G{\mathbf{K}}_{T,T}^P}\left(X\right)\left(x\right)={inf}_{y\in U}\theta ({\mathbf{K}}_T^P(x,y),X\left(y\right))$. According to Definitions 16 and 18, $\forall x\in U$, let $\vartheta =\underline{G{\mathbf{K}}_{T,T}^P}\left(X\right)\left(x\right),$ then, ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T\left(y\right)=T({\mathbf{K}}_T^P(x,y),\vartheta )=T({\mathbf{K}}_T^P(x,y),sup\{{\left[z_{\nu }\right]}_{{\mathbf{K}}_T^P}^T\left(x\right):{\left[z_{\nu }\right]}_{{\mathbf{K}}_T^P}^T\subseteq X\})=sup\{T({\mathbf{K}}_T^P(x,y),T({\mathbf{K}}_T^P(z,x),\nu )\}$. Because T-transitivity of ${\mathbf{K}}_T^P$, so $sup\{T({\mathbf{K}}_T^P(x,y),T({\mathbf{K}}_T^P(z,x),\nu )\}\le sup\left\{T({\mathbf{K}}_T^P(z,y),\nu )\right\}$. Hence, $sup\{T({\mathbf{K}}_T^P(x,y),T({\mathbf{K}}_T^P(z,x),\nu ):{\left[z_{\nu }\right]}_{{\mathbf{K}}_T^P}^T\subseteq X\}\le sup\{T({\mathbf{K}}_T^P(z,y),\nu ):{\left[z_{\nu }\right]}_{{\mathbf{K}}_T^P}^T\subseteq X\}=\underline{G{\mathbf{K}}_{T,T}^P}\left(X\right)\left(y\right)$. Therefore, we have ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T\subseteq \underline{G{\mathbf{K}}_{T,T}^P}\left(X\right).$

$\forall {\vartheta }^{\prime }>\vartheta$, then ${\left[x_{{\vartheta }^{\prime }}\right]}_{{\mathbf{K}}_T^P}^T⊈X$. Otherwise $\underline{G{\mathbf{K}}_{T,T}^P}\left(X\right)\left(x\right)={\vartheta }^{\prime }$, it is a contradiction. This implies ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T$ is the maximal in $\{{\left[x_{\omega }\right]}_{{\mathbf{K}}_T^P}^T:\omega \in [0,1]\}\subseteq X$. Conversely, $\forall y\in U$, if for any ${\left[x_{\omega }\right]}_{{\mathbf{K}}_T^P}^T$ such that ${\left[x_{\omega }\right]}_{{\mathbf{K}}_T^P}^T\left(y\right)\le X\left(y\right)$, we have ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T\subseteq \cup {\left[x_{\omega }\right]}_{{\mathbf{K}}_T^P}^T$ and ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T\subseteq {\cap }_{y\in U}(\cup {\left[x_{\omega }\right]}_{{\mathbf{K}}_T^P}^T)$. Since ${\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T$ is the maximal in $\{{\left[x_{\omega }\right]}_{{\mathbf{K}}_T^P}^T:\omega \in [0,1]\}\subseteq X$, then, $\vartheta ={\left[x_{\vartheta }\right]}_{{\mathbf{K}}_T^P}^T\left(x\right)={inf}_{y\in U}sup\{\omega :T({\mathbf{K}}_T^P(x,y),\omega )\le X\left(y\right)\}={inf}_{y\in U}\theta ({\mathbf{K}}_T^P(x,y),X\left(y\right))=\underline{G{\mathbf{K}}_{T,T}^P}\left(X\right)\left(x\right)$. Therefore, $\underline{G{\mathbf{K}}_{T,T}^P}\left(X\right)\left(x\right)=\underline{{\mathbf{K}}_{T,\theta }^P}\left(X\right)\left(x\right)$.

$\left(2\right)$ $\overline{G{\mathbf{K}}_{T,S}^P}\left(X\right)=c{o}_N\left(\underline{G{\mathbf{K}}_{T,T}^P}\left(c{o}_{N}X\right)\right)=c{o}_N\left(\underline{{\mathbf{K}}_{T,\theta }^P}\left(c{o}_{N}X\right)\right)=\overline{{\mathbf{K}}_{T,\sigma }^P}\left(X\right)$. □

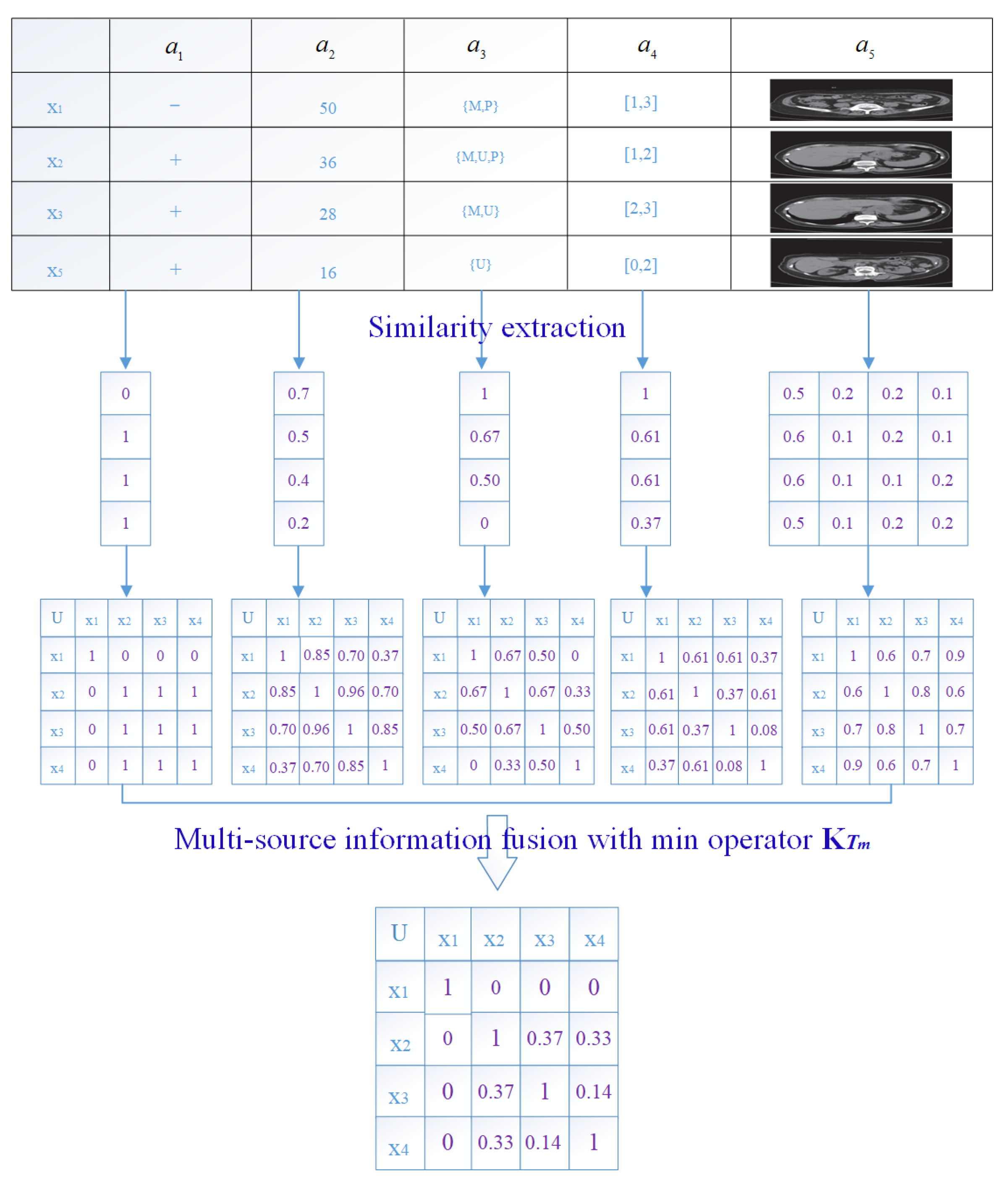
Example 3. 

By Example 2, a fuzzy T-equivalence relation ${\mathit{K}}_{Tm}^P$ in terms of min operator $T_m$, is denoted by

$${\mathit{K}}_{T_m}^P\left(x_i,x_j\right)=\left(\begin{array}{cccc}1\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0.37\hfill & 0.33\hfill \\ 0\hfill & 0.37\hfill & 1\hfill & 0.14\hfill \\ 0\hfill & 0.33\hfill & 0.14\hfill & 1\hfill \end{array}\right).$$

Then, for any $X\in \mathcal{F}\left(U\right)$, let $T(x,y)=max\{0,x+y-1\};$ $S(x,y)=min\{1,x+y\}.$ By Definition 15, then, $\overline{{\mathit{K}}_{T,\sigma }^P}\left(X\right)\left(x\right)={sup}_{y\in U}max\{0,{\mathit{K}}_T^P(x,y)+X\left(y\right)-1\}$, $\underline{{\mathit{K}}_{T,\theta }^P}\left(X\right)\left(x\right)={inf}_{y\in U}min\{1,1-{\mathit{K}}_T^P(x,y)+X\left(y\right)\}$. Assume that $X={\displaystyle \frac{0.1}{x_1}}+{\displaystyle \frac{0.2}{x_2}}+{\displaystyle \frac{0.7}{x_3}}+{\displaystyle \frac{0.9}{x_4}}$. We have:

$$\overline{{\mathit{K}}_{T,\sigma }^P}\left(X\right)={\displaystyle \frac{0.1}{x_1}}+{\displaystyle \frac{0.23}{x_2}}+{\displaystyle \frac{0.7}{x_3}}+{\displaystyle \frac{0.9}{x_4}};$$

$$\underline{{\mathit{K}}_{T,\theta }^P}\left(X\right)={\displaystyle \frac{0.1}{x_1}}+{\displaystyle \frac{0.2}{x_2}}+{\displaystyle \frac{0.7}{x_3}}+{\displaystyle \frac{0.87}{x_4}}.$$

$\forall x\in U$ and $\vartheta \in [0,1]$. ${\left[x_{\vartheta }\right]}_{{\mathit{K}}_{Tm}^P}^T\left(y\right)=max\{0,{\mathit{K}}_{Tm}^P(x,y)+\vartheta -1\}$, for each $\underline{{\mathit{K}}_{T,\theta }^P}\left(X\right)\left(x_i\right)={\vartheta }_i$, then:

${\left[{\left(x_1\right)}_{0.1}\right]}_{{\mathit{K}}_{Tm}^P}^T={\displaystyle \frac{0.1}{x_1}}+{\displaystyle \frac{0}{x_2}}+{\displaystyle \frac{0}{x_3}}+{\displaystyle \frac{0}{x_4}}$; ${\left[{\left(x_1\right)}_{0.2}\right]}_{{\mathit{K}}_{Tm}^P}^T={\displaystyle \frac{0}{x_1}}+{\displaystyle \frac{0.2}{x_2}}+{\displaystyle \frac{0}{x_3}}+{\displaystyle \frac{0}{x_4}}$;

${\left[{\left(x_1\right)}_{0.7}\right]}_{{\mathit{K}}_{Tm}^P}^T={\displaystyle \frac{0}{x_1}}+{\displaystyle \frac{0.07}{x_2}}+{\displaystyle \frac{0.7}{x_3}}+{\displaystyle \frac{0}{x_4}}$; ${\left[{\left(x_1\right)}_{0.87}\right]}_{{\mathit{K}}_{Tm}^P}^T={\displaystyle \frac{0}{x_1}}+{\displaystyle \frac{0.2}{x_2}}+{\displaystyle \frac{0.01}{x_3}}+{\displaystyle \frac{0.87}{x_4}}$.

From Example 3, $\underline{{\mathbf{K}}_{T,\theta }^P}\left(X\right)\left(x\right)$ consists of the union of these four fuzzy granularities (${\left[{\left(x_1\right)}_{0.1}\right]}_{{\mathbf{K}}_{Tm}^P}^T$, ${\left[{\left(x_2\right)}_{0.2}\right]}_{{\mathbf{K}}_{Tm}^P}^T$, ${\left[{\left(x_3\right)}_{0.7}\right]}_{{\mathbf{K}}_{Tm}^P}^T$, and ${\left[{\left(x_4\right)}_{0.87}\right]}_{{\mathbf{K}}_{Tm}^P}^T$), i.e.,

$$\underline{G{\mathbf{K}}_{T,T}^P}\left(X\right)={\left[{\left(x_1\right)}_{0.1}\right]}_{{\mathbf{K}}_{Tm}^P}^T\cup {\left[{\left(x_2\right)}_{0.2}\right]}_{{\mathbf{K}}_{Tm}^P}^T\cup {\left[{\left(x_3\right)}_{0.7}\right]}_{{\mathbf{K}}_{Tm}^P}^T\cup {\left[{\left(x_4\right)}_{0.87}\right]}_{{\mathbf{K}}_{Tm}^P}^T=\underline{{\mathbf{K}}_{T,\theta }^P}\left(X\right).$$

Definition 19. 

Assume that $MsMIS=(U,A\cup \{d\},V,f)$ is an MsMIS. Given $P\subseteq A$, if ${\mathit{K}}_T^P$ is a fuzzy T-equivalence relation on U, for any $X\in \mathcal{F}\left(U\right)$ and $\vartheta \in [0,1]$, then,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\underline{G{\mathit{K}}_{T,\theta }^P}\left(X\right)=\bigcup \{{\left[x_{N\left(X\right(x\left)\right)}\right]}_{{\mathit{K}}_T^P}^S:x\in U\},\hfill \\ \overline{G{\mathit{K}}_{T,\sigma }^P}\left(X\right)=\bigcap \{{\left[x_{X\left(x\right)}\right]}_{{\mathit{K}}_T^P}^T:x\in U\},\hfill \end{array}\right.\end{array}$$

(22)

where $\underline{G{\mathit{K}}_{T,\theta }^P}$ is referred to as the θ-lower approximation of X and $\overline{G{\mathit{K}}_{T,\sigma }^P}$ is referred to as the σ-upper approximation of X. We can call the ($\underline{G{\mathit{K}}_{T,\theta }^P}\left(X\right),\overline{G{\mathit{K}}_{T,\sigma }^P}\left(X\right)$) granular $(\theta ,\sigma )$-fuzzy rough sets.

Theorem 3. 

Assume that $MsMIS=(U,A\cup \{d\},V,f)$ is an MsMIS. Given $P\subseteq A$, if ${\mathit{K}}_T^P$ is a fuzzy T-equivalence relation on U, for any $X\in \mathcal{F}\left(U\right),$ then

(1) $\underline{G{\mathit{K}}_{T,\theta }^P}\left(X\right)\left(x\right)=\underline{{\mathit{K}}_{T,S}^P}\left(X\right)\left(x\right)$;

(2) $\overline{G{\mathit{K}}_{T,\sigma }^P}\left(X\right)\left(x\right)=\overline{{\mathit{K}}_{T,T}^P}\left(X\right)\left(x\right)$.

Proof of Theorem 3. 

(1) For $\forall x\in U,$ $\underline{G{\mathbf{K}}_{T,\theta }^P}\left(X\right)\left(x\right)={inf}_{x\in U}{\left[x_{N\left(X\right(x\left)\right)}\right]}_{{\mathbf{K}}_T^P}^S\left(x\right)={inf}_{x\in U}S(N\left({\mathbf{K}}_T^P(x,y)\right),X\left(y\right))$.

(2) For $\forall x\in U,$ $\overline{G{\mathbf{K}}_{T,\sigma }^P}\left(X\right)\left(x\right)=(\cup \{{\left[x_{X\left(x\right)}\right]}_{{\mathbf{K}}_T^P}^T:x\in U\})\left(x\right)={sup}_{x\in U}{\left[x_{X\left(x\right)}\right]}_{{\mathbf{K}}_T^P}^T\left(x\right)={sup}_{x\in U}T({\mathbf{K}}_T^P(x,y),X\left(y\right)).$

□

4.3. Continuation of the Classic Attribute Reduction in the FRS Model

Definition 20. 

Let $MsMIS=(U,A\cup \{d\},V,f)$ be an MsMIS. Given $P\subseteq A$, $\forall x,y\in U$, and ${\mathit{K}}_T^P$ is the fuzzy T-equivalence relation in P calculated by ${\mathit{K}}_T^P(x,y)$, for any $\vartheta \in [0,1]$, the fuzzy positive regions of D w.r.t. P is defined by

$$\begin{array}{c}\hfill PO{S}_{T,\vartheta }^P\left(D\right)=\bigcup _{i=1}^l\underline{G{\mathit{K}}_{T,\vartheta }^P}{d}_i,\end{array}$$

(23)

where $D=\{d_1,d_2,\cdots ,d_l\}$.

Definition 21. 

Let $MsMIS=(U,A\cup \{d\},V,f)$ be an MsMIS. Given $P\subseteq A$, and ${\mathit{K}}_T^P$ is the fuzzy T-equivalence relation in P calculated by ${\mathit{K}}_T^P(x,y)$, for any $\vartheta \in [0,1]$, the quality of approximating classification can be denoted as

$$\begin{array}{c}\hfill {\gamma }_{T,\vartheta }^P\left(D\right)={\displaystyle \frac{|PO{S}_{T,\vartheta }^P\left(D\right)|}{\left|U\right|}},\end{array}$$

(24)

where $D=\{d_1,d_2,\cdots ,d_l\}$ and $|{\displaystyle \frac{|PO{S}_{T,\vartheta }^P\left(D\right)|}{\left|U\right|}}|={\sum }_{i=1}^l{\sum }_{x\in d_i}\underline{G{\mathit{K}}_{T,\vartheta }^P}{d}_i\left(x\right)$.

The fuzzy approximation quality is a fuzzy extension of the Pawlak rough set approximation quality. Since the lower approximation reflects the degree to which a sample necessarily belongs to its decision in the fuzzy approximation space, the fuzzy approximation quality as an indicator reflects the average degree to which a sample necessarily belongs to its decision in the feature fuzzy approximation space. The larger the value of this indicator, the more certain the classification in the fuzzy approximation space, and the stronger the ability to approximate multi-decisions. The greater the dependency of the decision on the attribute subset. Therefore, the approximation quality is also referred to as the degree of dependence of the decision on the condition.

Theorem 4. 

Let $MsMIS=(U,A\cup \{d\},V,f)$ be an MsMIS. Given $P,Q\subseteq A$, $P=\{a_1,a_2,\cdots ,a_p\},Q=\{a_1,a_2,\cdots ,a_q\},p\le q$. ${\mathit{K}}_T^P$ and ${\mathit{K}}_T^Q$ are the fuzzy T-equivalence relation calculated by kernel fusion function ${\mathit{K}}_{T_m}(x,y)$ in feature spaces P and Q, respectively, for any $\vartheta \in [0,1]$, we have

(1) ${\mathit{K}}_{T,\vartheta }^P\supseteq {\mathit{K}}_{T,\vartheta }^Q$;

(2) $\underline{{\mathit{K}}_{T,\vartheta }^P}{d}_i\subseteq \underline{{\mathit{K}}_{T,\vartheta }^Q}{d}_i$;

(3) $\overline{{\mathit{K}}_{T,\vartheta }^P}{d}_i\supseteq \overline{{\mathit{K}}_{T,\vartheta }^Q}{d}_i$;

(4) $PO{S}_T^P\left(D\right)\subseteq PO{S}_{T,\vartheta }^Q\left(D\right)$;

(5) ${\gamma }_{T,\vartheta }^P\left(D\right)\le {\gamma }_{T,\vartheta }^Q\left(D\right)$.

Proof of Theorem 4 

$\left(1\right)$ Obviously.

$\left(2\right)$ Let $P=a_1\cup a_2\cup \cdots \cup a_p$ and $Q=a_1\cup a_2\cup \cdots \cup a_q$. Since $P\subseteq Q$, then $p\le q$. We have ${\mathbf{K}}_{T_m}^P=min\{{\mathbf{K}}_1,{\mathbf{K}}_2,\cdots ,{\mathbf{K}}_P\}=a$, and ${\mathbf{K}}_{T_m}^Q=min\{a,{\mathbf{K}}_{P+1},{\mathbf{K}}_{P+2},\cdots ,{\mathbf{K}}_Q\}$. Hence, ${\mathbf{K}}_{T_m}^P\ge {\mathbf{K}}_{T_m}^Q$. Using the same method, we can prove the other T-norms. Hence, for any $\vartheta \in [0,1]$, we can easy obtain $\underline{{\mathbf{K}}_{T,\vartheta }^P}{d}_i\subseteq \underline{{\mathbf{K}}_{T,\vartheta }^Q}{d}_i$ and $\overline{{\mathbf{K}}_{T,\vartheta }^P}{d}_i\supseteq \overline{{\mathbf{K}}_{T,\vartheta }^Q}{d}_i$.

$\left(3\right)$ See $\left(2\right)$.

$\left(4\right)$ According to Definition 20 and $\left(2\right)$, the proof is derived from the monotonicity of the lower approximation.

$\left(5\right)$ According to Definition 21 and $\left(4\right)$, it is easy to obtain the proof.

Theorem 4 shows that with an increase in attributes, the approximation quality monotonically increases. This indicates that the addition of new attributes will inevitably introduce new classification information, causing the granulation structure of the approximation space to become finer. Consequently, the approximation ability is enhanced, and the approximation of the classification decision may become more accurate. □

Definition 22. 

Let $MsMIS=(U,A\cup \{d\},V,f)$ be an MsMIS, and $D=\{d_1,d_2,\cdots ,d_l\}$. For any $\vartheta \in [0,1]$, and $a\in P\subseteq A$, if ${\gamma }_{T,\vartheta }^P\left(D\right)={\gamma }_{T,\vartheta }^{P-\left\{a\right\}}\left(D\right)$, then a is redundant in P w.r.t. D; otherwise, a is indispensable.

Definition 23. 

Let $MsMIS=(U,A\cup \{d\},V,f)$ be an MsMIS, and $D=\{d_1,d_2,\cdots ,d_l\}$. For any $\vartheta \in [0,1]$, and $a\in P\subseteq A$, P is a relative reduct to D if it satisfies:

(1) ${\gamma }_{T,\vartheta }^P\left(D\right)={\gamma }_{T,\vartheta }^{P-\left\{a\right\}}\left(D\right)$;

(2) $\forall a\in P$, a is indispensable in P to decision attribute D.

Definitions 22 and 23 are classical attribute reduction methods. The advantage of this approach is that it obtains the attribute indistinguishability relation through an approximation quality. It is a continuation of the classical rough set theory applied to attribute reduction, and similarly applies within the FRS models.

5. Conclusions

In this paper, the multi-source mixed information system (MsMIS) is defined as a complex data representation that integrates diverse data types. For each data type, a similarity function is designed based on its inherent characteristics, which functions similarly to a kernel function in computing the similarity between two samples. Under the framework of granular computing, we further utilize fuzzy similarity relations to construct information granules, thereby building a fuzzy rough set model tailored for the MsMIS. We have demonstrated that the basic information granularity can be used to represent this complex mathematical property. The proposed fuzzy rough set model holds significant implications for both theoretical research and practical applications.

In future work, we aim to explore the application of the proposed FRS models to two key areas, attribute reduction and outlier detection. By leveraging FRS models, we intend to streamline datasets by identifying and eliminating redundant or irrelevant attributes, thus improving computational efficiency and model interpretability. Additionally, we will apply the models to outlier detection, helping to identify data points that deviate significantly from the norm, which could enhance the accuracy and robustness of predictive models. This approach will be evaluated to verify the superior performance of the FRS models in these tasks.