Abstract
An enhanced whale optimization algorithm (WOA) through the implementation of a generalized type-2 fuzzy logic system (GT2FLS) is outlined. The initial idea is to improve the efficacy of the original WOA using a GT2FLS to find the optimal values of the and parameters of the WOA, for the case of optimizing mathematical functions. In the WOA algorithm, is a variable that affects the new position of the whale in the search space, in this case, affecting the exploration, and is a variable that has an effect on finding the local optima, which is an important factor for the exploration. The efficiency of a fuzzy WOA with a GT2FLS (FWOA-GT2FLS) is highlighted by presenting the excellent results of the case study of the benchmark function optimization. A relevant analysis and comparison with a bio-inspired algorithm based on artificial bees is also presented. Statistical tests and comparisons with other bio-inspired algorithms and the initial WOA, with type-1 FLS (FWOA-T1FLS) and interval type-2 FLS (FWOA-IT2FLS), are presented. For each of the methodologies, the metric for evaluation is the average of the minimum squared errors.
MSC:
03B52; 94D05; 90C70
1. Introduction
In recent years, the increasing complexity of the problems has required greater analysis in achieving the solutions, which is why techniques that allow for greater precision in the evaluation have been developed, and one of them is the GT2FLS. The contribution of this paper is the implementation of the GT2FLS, as a hybridization technique that allows for a better WOA performance. Recently, there have been some relevant studies in which GT2 fuzzy sets have been shown to generate excellent results, like in [1], where a GT2 fuzzy reasoning approach is utilized to control a mobile robot trajectory in a dynamic environment under sensory uncertainty, with good results by Santal et al.; in [2], in which fuzzy sets (FSs) in the dynamic parameter adaptation of an algorithm based on virtual bees applied to fuzzy controller are analyzed by Amador-Angulo et al.; in [3], where a new generalization of fuzzy soft sets is presented by Al-shami et al.; in [4], where a comparative study with different fuzzy sets including GT2FSs for medical diagnosis is presented by Ontiveros et al.; in [5], where a comparison of several FSs applied in control problems is outlined by Castillo et al.; in [6], where a new fractional-order GT2FS prediction control system and its applications in medicine are studied by Mohammadzadeh et al.; in [7], where an approach to the development of GT2 fuzzy classifiers applied in medical problems is presented by Ontiveros-Robles et al.; in [8], where a GT2FS applied to a fuzzy controller is presented by Sanchez et al.; and in [9], where an improved GT2FS type reduction and its applications in GT2 fuzzy controllers are proposed by Jianzhong et al. This is just a sample of the existing works in this area.
The problem statement is finding an enhancement of the popular algorithm based on the intelligent behavior of virtual whales. Several authors have shown a particular interest in analyzing the performance of this algorithm and in improving its original version, and some techniques have been proposed. For example, some relevant research: in [10], research and applications of WOA are presented by Wang et al.; in [11], recent advances in WOA versions and applications are presented by Alyasseri et al.; in [12], an improved WOA in an engineering problem is presented by Dai et al.; in [13], a WOA comprehensive meta-analysis on hybridization to solve complex optimization problems is presented by Majumdar et al.; in [14], an application of an enhanced WOA is presented by Zhao et al.; in [15], an enhanced WOA for the identification of solar cell models is presented by Yang et al.; in [16], an improved WOA inspired by the Fibonacci search principle for optimization is presented by Sahoo et al.; in [17], the applications of WOA in optimal power flow problems are presented by Ghasemi et al.; and in [18], a review of the applications in water engineering is presented by Dadrasajirlou et al. The goal of combining these algorithms is achieving the optimal settings of the parameters that indicate a good performance in the execution of the analysis of the essential elements, such as finding the exact solution, high precision of the results, a fast convergence rate, and fast stabilization.
Based on the previous review, a study on the effect of two parameters ( and ) of the WOA is presented with respect to exploration and exploitation, which allows us to propose a novel FWOA-GT2FLS variant and this is the main contribution.
The organization of the paper is detailed as follows: several relevant related works are presented in Section 2; a description of the initial WOA and the proposal are outlined in Section 3; the mathematical functions are outlined in Section 4; the experimentations are shown in Section 5; in Section 6, the results are analyzed; and in Section 7, the conclusions are presented.
2. Related Work
In the past decade, fuzzy sets have proven to be an efficient tool in the hybridization of bio-inspired algorithms, with the aim of enhancing the original algorithms. The metaheuristics have offered better stabilization and reduced errors when the fuzzy methodology is utilized in controlling the parameters. For example, in [19], Chandrasekaran et al. present an energy-efficient cluster head using a modified fuzzy WOA and hybridization with the algorithm based on the performance of the chicken; in [20], Xu et al. propose a fuzzy logic-based WOA for trust-aware routing applied in the field of medicine; in [21], Alhafedh et al. study an optimizing goshawk algorithm with the fuzzy logic and WOA strategies; in [22], Amador-Angulo et al. demonstrate the efficiency of the WOA with fuzzy logic; in [23], Castillo et al. propose a hybridization of the differential evolution algorithm and fuzzy logic in the parameter adaptation and application in function optimization; in [24], Ou et al. demonstrate the effectiveness of the cuckoo search algorithm and the Gauss–Cauchy algorithm to solve engineering problems; in [25], Cuevas et al. study the improvement in the marine predator algorithm with fuzzy sets applied to optimize a fuzzy controller; in [26], Ntakolia et al. propose a fuzzy genetic algorithm enhancement for multi-objective unmanned aircraft planning; and in [27], the development of an adaptive fuzzy-neural controller for temperature control in a brick tunnel kiln is presented.
To demonstrate the improvement provided in various algorithms, several researchers have used mathematical optimization functions, known as “sets of mathematical optimization function (SMOFs)”. To mention some relevant works: Sharma et al. implemented the SMOF to evaluate metaheuristics optimization algorithms in [28]; Wang et al. used this case study to evaluate the performance of a black-winged kite algorithm in [29]; Benmamoun et al. studied the SMOF to assess the efficiency in the wombat optimization algorithm in [30]; Solanki et al. used this problem in a quadratic approximation salp swarm algorithm in [31]; Kaabneh et al. implemented a dollmaker optimization algorithm to evaluate the performance of SMOF in [32]; and Mohamed et al. evaluated the performance of metaheuristics using this case study in [33].
The WOA is an algorithm that in the past decade has caused great interest because it has been applied and improved by several authors. It has been used in various areas of computer science for engineering problems. For this reason, in this paper, the main contribution is to be able to verify that the use of the GT2FLS, when performing the hybridization with the WOA, helps in finding the appropriate values of and , which are the essential parameters in the efficient operation of the algorithm. This was verified by achieving better results when optimizing the mathematical functions with the new proposed FWOA-GT2FLS.
3. Whale Optimization Algorithm
In 2016, Mirjalili and Lewis were the first to propose the idea of using whales in nature as an inspiration for the creation of the WOA, which is based on three main ideas: the whale brain has cells that are similar to humans, the whales are recognized for their intelligence, and each whale presents a social behavior that could be successfully used when living alone or in a group [34].
3.1. The Original WOA
The most important technique that is used by a virtual whale is the function of locating food and is based on three mechanisms: encircling the prey, spiral bubble-net feeding (exploitation stage), and the search for prey (exploration stage) to achieve the goal [34]. When the execution stage starts, the best whale has to find the best solution, which is updated depending on the current location.
The sequence of steps of the WOA is detailed in Table 1, which is from the original proposal of the whale optimization algorithm (WOA) in [34].

Table 1.
WOA pseudo-code.
3.1.1. Surround the Prey
This mechanism is based on the humpback whale’s behavior. In this algorithm, a whale can locate its prey by rotating around it. Equations (1) and (2) model this [34]:
where indicates the total executions; the actual position is denoted by ; , is the current position; and is the coefficients of and . Therefore, Equations (3) and (4) indicate the expression to find and [34].
In this phase, changes from 2 to 0, and the range of values of the and parameters is [0,1]. The focus of this paper is to study the impact of these two parameters.
3.1.2. Bubble-Net Attacking
In this stage, there are two motions—shrink and surround—which are enabled by decreasing in Equation (3). is a random value in [−d, d], where decreases from 2 to 0. Set d = 1, that is, is a random value in [−1,1]. This stage is calculated using Equation (5).
where ; is the helix constant; and a random number in [−1,1] is indicated by .
3.1.3. Search for Prey (Exploration Phase)
In the last phase, is utilized to find the prey. A random value of is established higher than 1. Equation (6) indicates this mechanism [34]:
where expresses a random position in the current population. In each iteration, a whale selects a way to update its location depending on . In this phase, when , a whale is selected, and when , the best solution in the population for the whale is assigned.
3.2. Fuzzy WOA
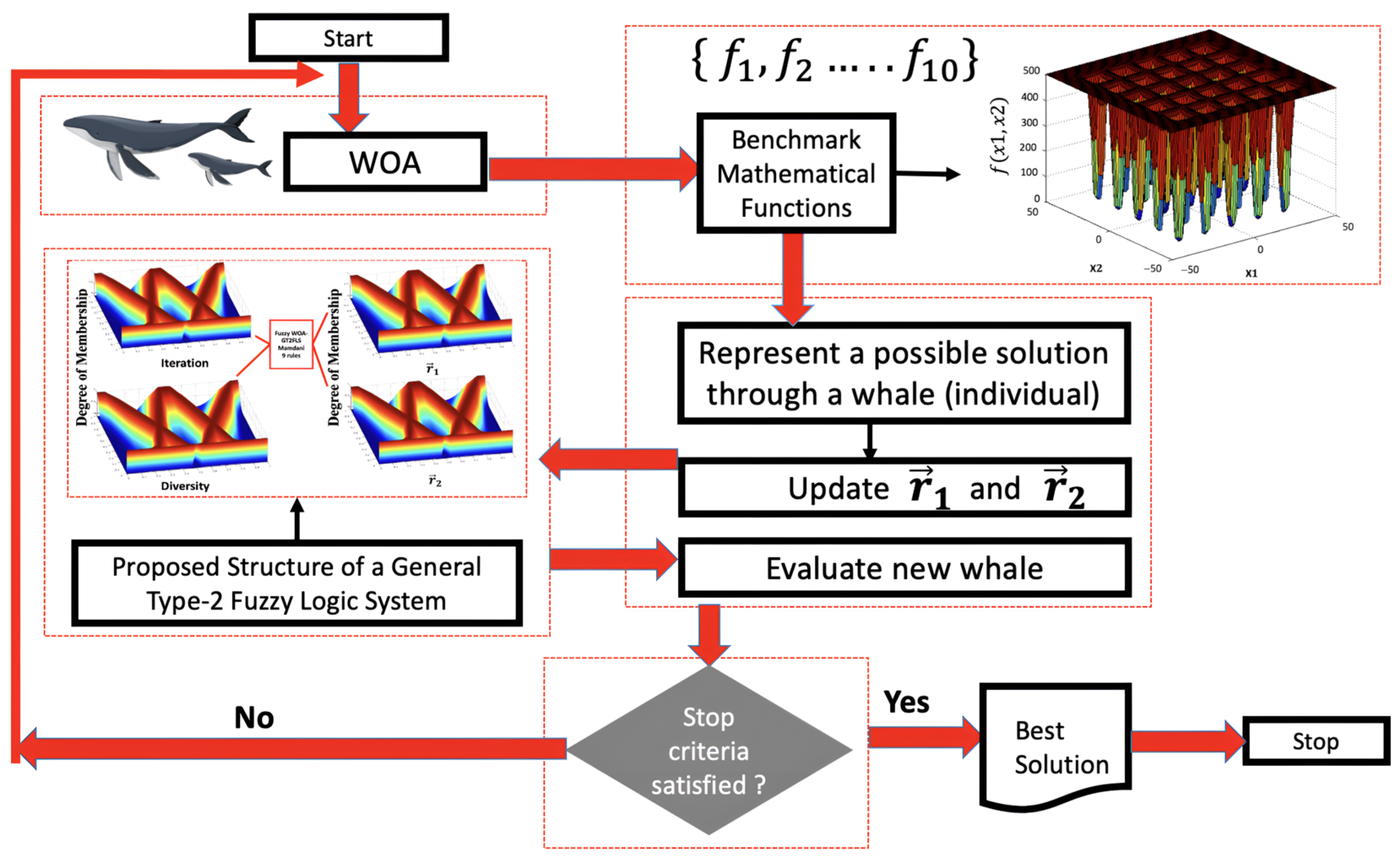
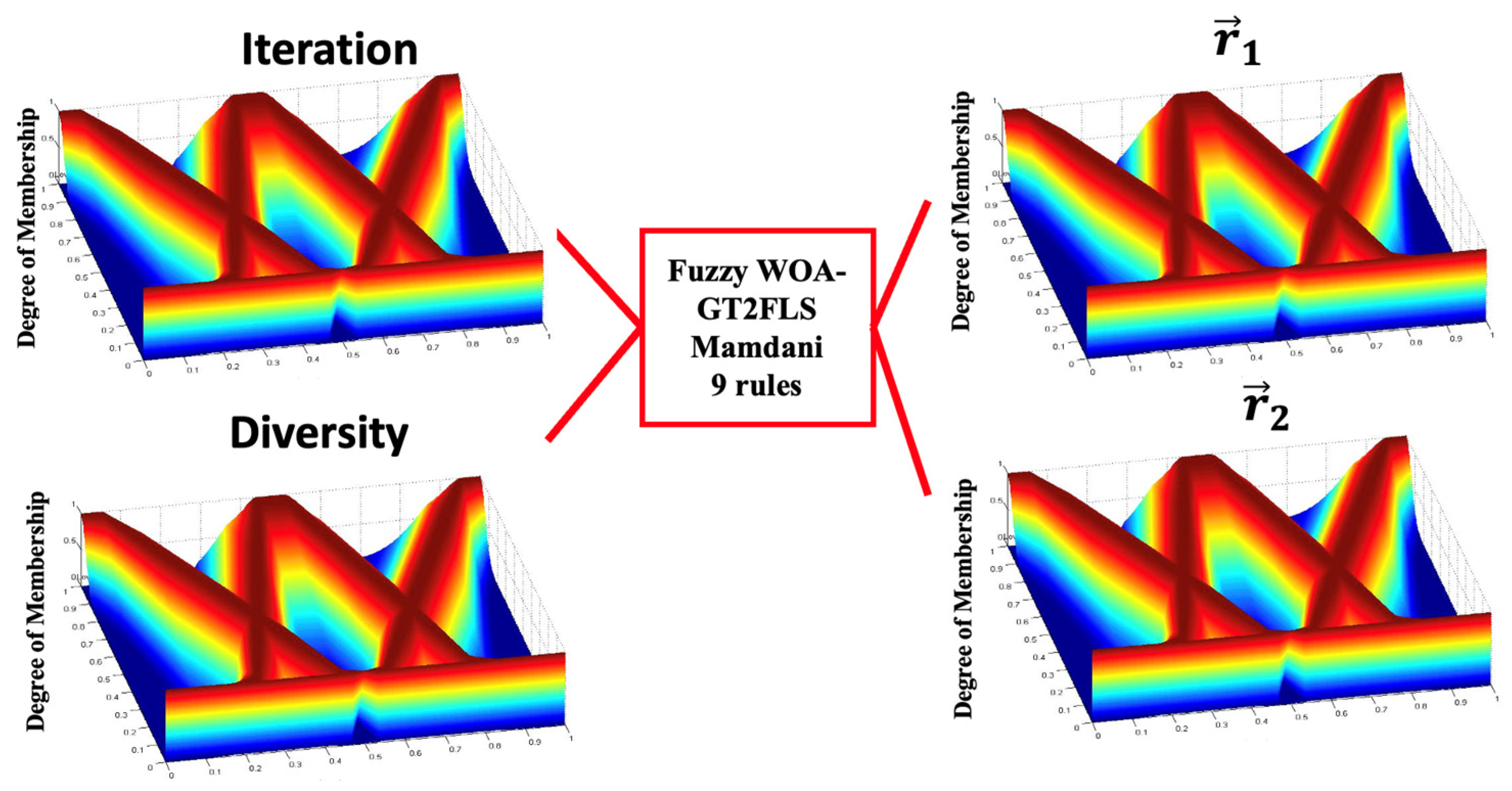
The main idea for the proposed fuzzy GT2FLS is illustrated in Figure 1.
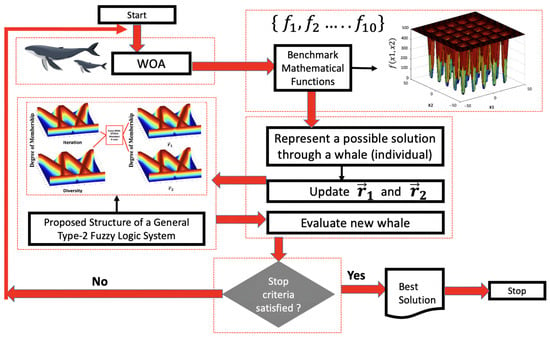
Figure 1.
Visualization of the idea for the fuzzy WOA–GT2FLS.
The structure and composition of a GT2FLS are presented in the following subsection, with a detailed explanation of each process.
3.2.1. Definitions
The first idea of fuzzy logic was proposed by Zadeh [35,36,37], and later, an extension of the fuzzy sets was created by Mendel [38,39], and the generalized fuzzy sets were proposed by Mendel in 2009 [40]. The mathematical representation is expressed in Equation (7), which shows the main operation with the GT2FLS, which is similar to the T1FLS and the IT2FLS.
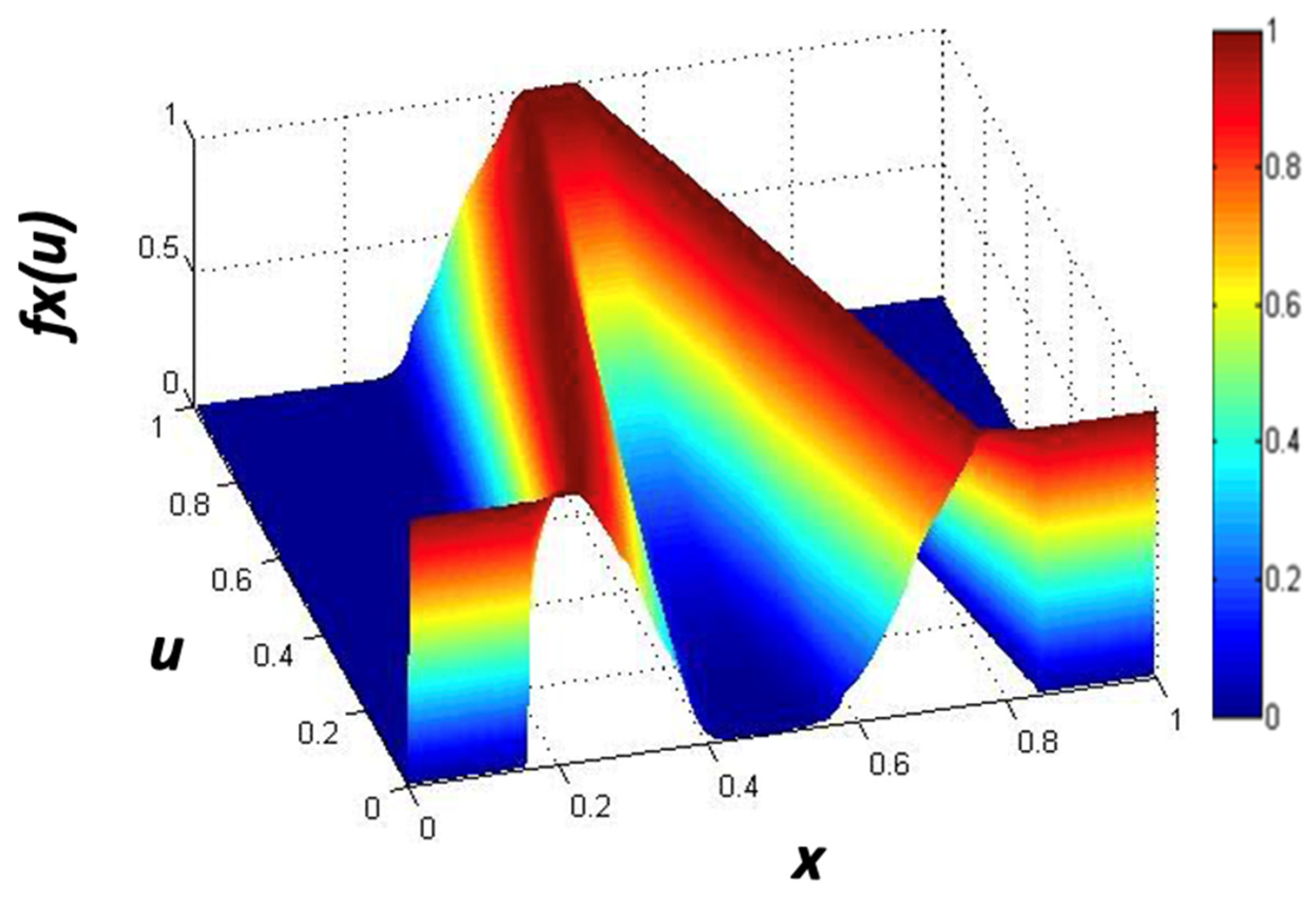
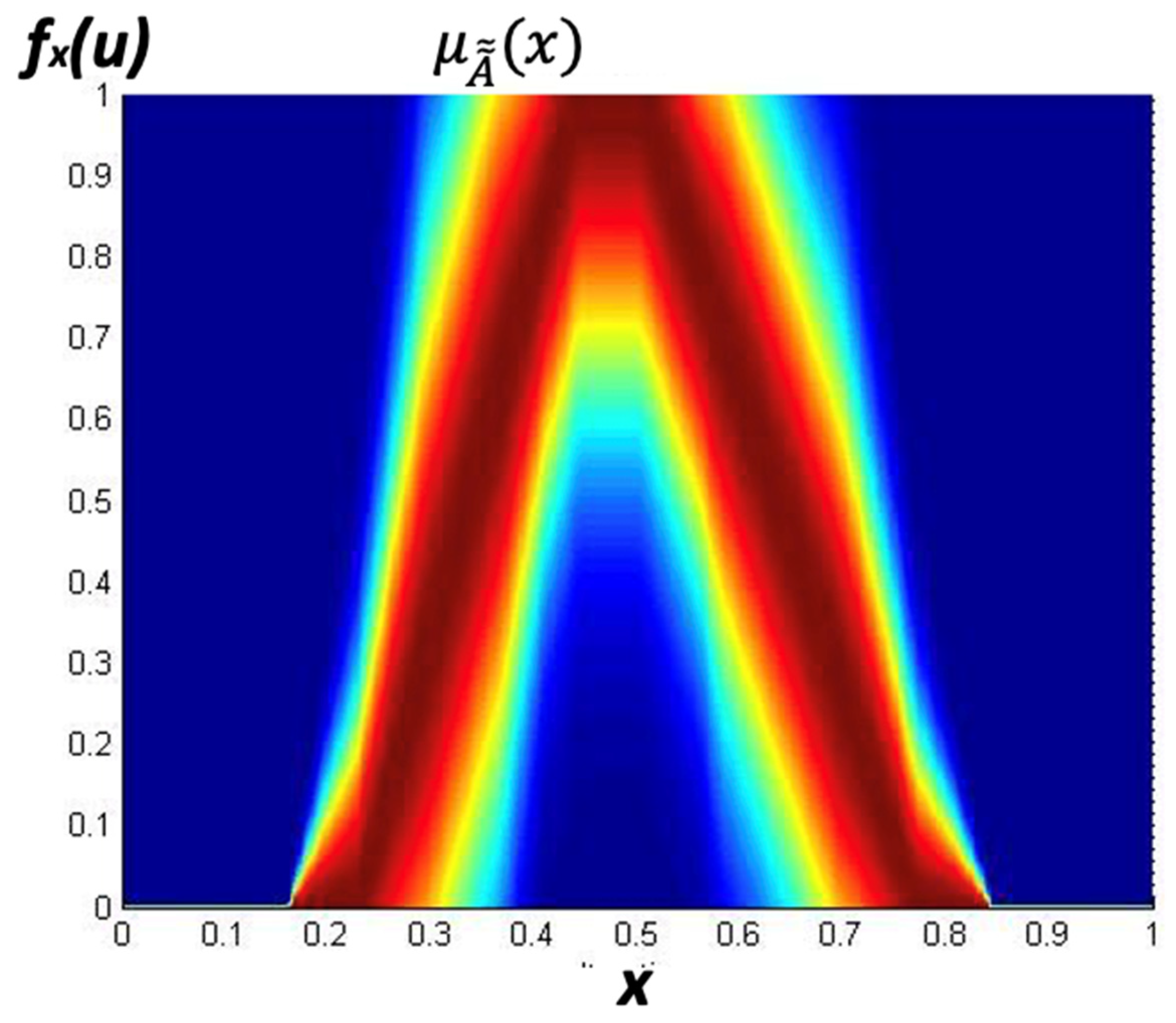
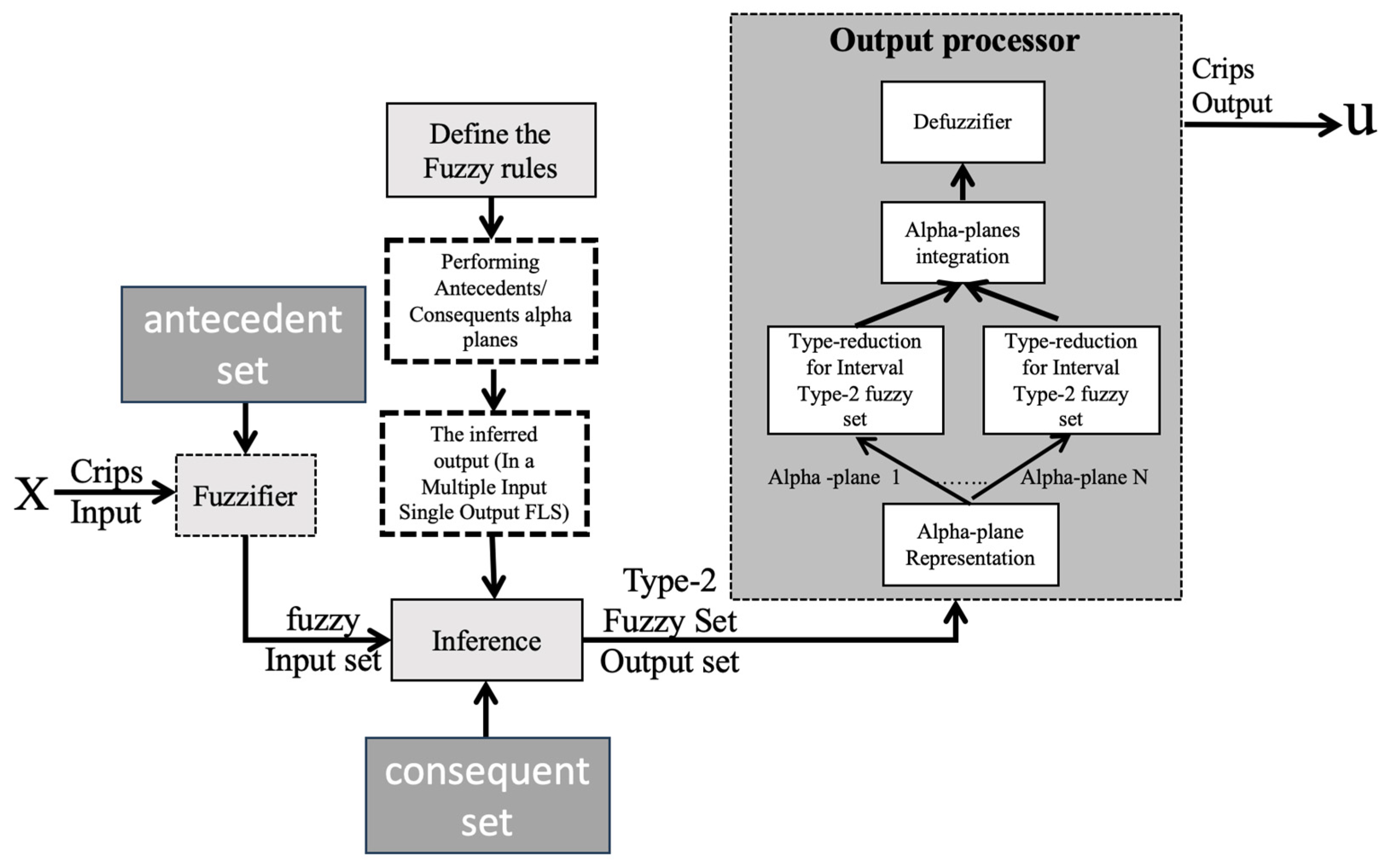
where , x is the partition of the primary MF, and u is the partition of the secondary MF. In Figure 2, we illustrate a generalized type-2 membership function (GT2MF). In Figure 3, the footprint of uncertainty (FOU) is shown. It can be noted that the difference in notation with respect to the T1FLS and the IT2FLS, which utilize the notation but the GT2FS utilizes , in the vertical axis. Figure 4 shows the representation of a GT2FLS including the calculations needed to find the result.
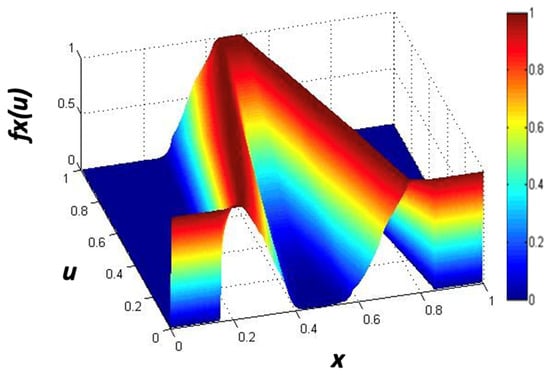
Figure 2.
Visual representation of a GT2MF.
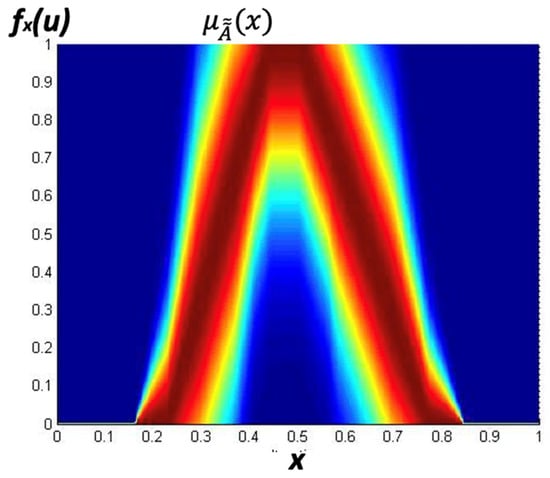
Figure 3.
FOU of a GT2MF.
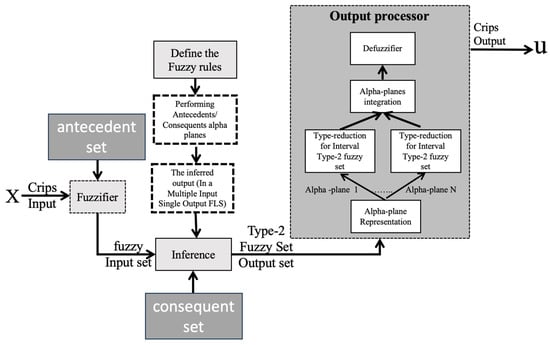
Figure 4.
General structure of a GT2FLS.
3.2.2. Fuzzification
In this paper, a type-2 singleton fuzzifier is implemented in the fuzzification process because it is fast to be computed. A singleton fuzzification maps the crisp input into a fuzzy set. Hence, the fuzzifier maps the crisp input into a type-2 fuzzy singleton, whose MF is for and for all and for all where P is the number of inputs [40].
An important point for choosing a singleton in the fuzzifier is because we compare our GT2FLS with respect to the dynamic adjustment of two parameters of a bee colony optimization, described in [2], which also uses a singleton in the fuzzifier, and the objective is that the comparison is as fair as possible. Both GT2FLSs with a singleton fuzzifier are using fewer calculations compared with a non-singleton.
Another important decision when choosing this fuzzifier in the process of inference is because the result of this process obtains a value that is utilized for each input variable that the GT2FLS finds, in this case, this is the value of the iteration and the diversity parameters, which is between the range of 0–1 (See Figure 6).
3.2.3. Inference
The rule structure of the GT2FLS is the standard Mamdani rule structure utilized in the T1FLS, but now, the antecedent and consequent sets are type-2. So, the kth rule in the GT2FLS is postulated by:
The inference of a GT2FLS is reduced to two operations, meet and join, of Equations (9) and (10), respectively.
3.2.4. α-Planes
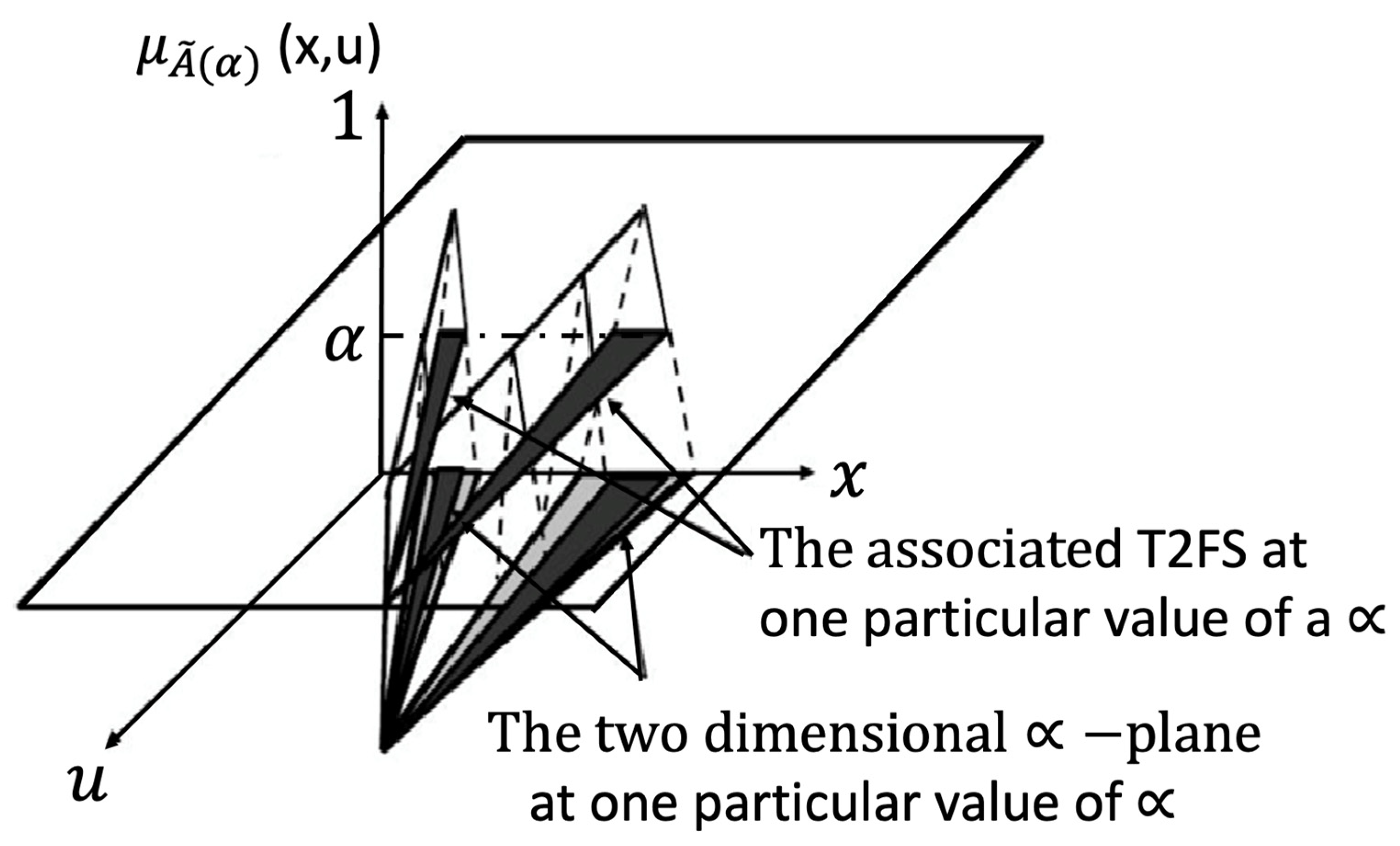
The α-plane for is symbolized by Ãα, which is the union of all the primary MFs of Ã, where the secondary memberships are higher than or equal to α [41]. The mathematical representation is postulated by Equation (11). In Figure 5, the α-planes are illustrated [42].
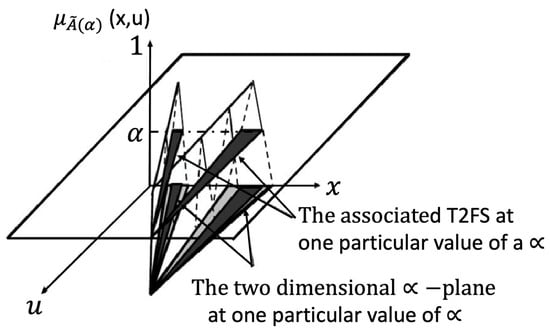
Figure 5.
Example of an -plane.
3.2.5. Type Reduction
The Karnik and Mendel algorithm is used for this task [38,39,40] and Equations (12) and (13) express this reduction.
Equations (14) and (15) are used in the integration of the -planes [41,42].
3.2.6. Defuzzification
The last process is the defuzzification, which is performed by employing the average of and to estimate the output [39] and is expressed by Equation (16).
3.3. Proposed GT2FLS
The structure to find the values of the and in the FWOA-GT2FLS is depicted in Figure 6 with two inputs and two outputs, and triangular MFs.
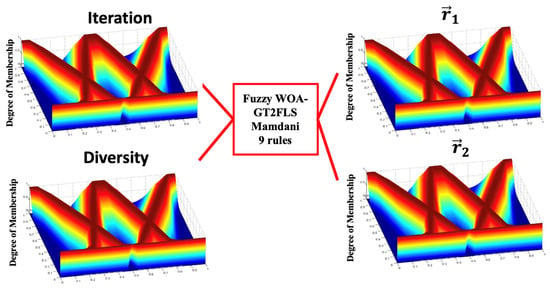
Figure 6.
Proposed structure of the GT2FLS.
3.3.1. Expression of the ScaleTriScaleGaussIT2MF
ScaleTriScaleGaussIT2MF(x,{{[a1, b1, c1]},,}) is the presentation of a triangular IT2MF denoted by = ScaleTriScaleGaussIT2MF, defined by the triangular FOU () that has as the upper parameters for the UMF, and (LowerScale) and (LowerLag) for the LMF, which define the .
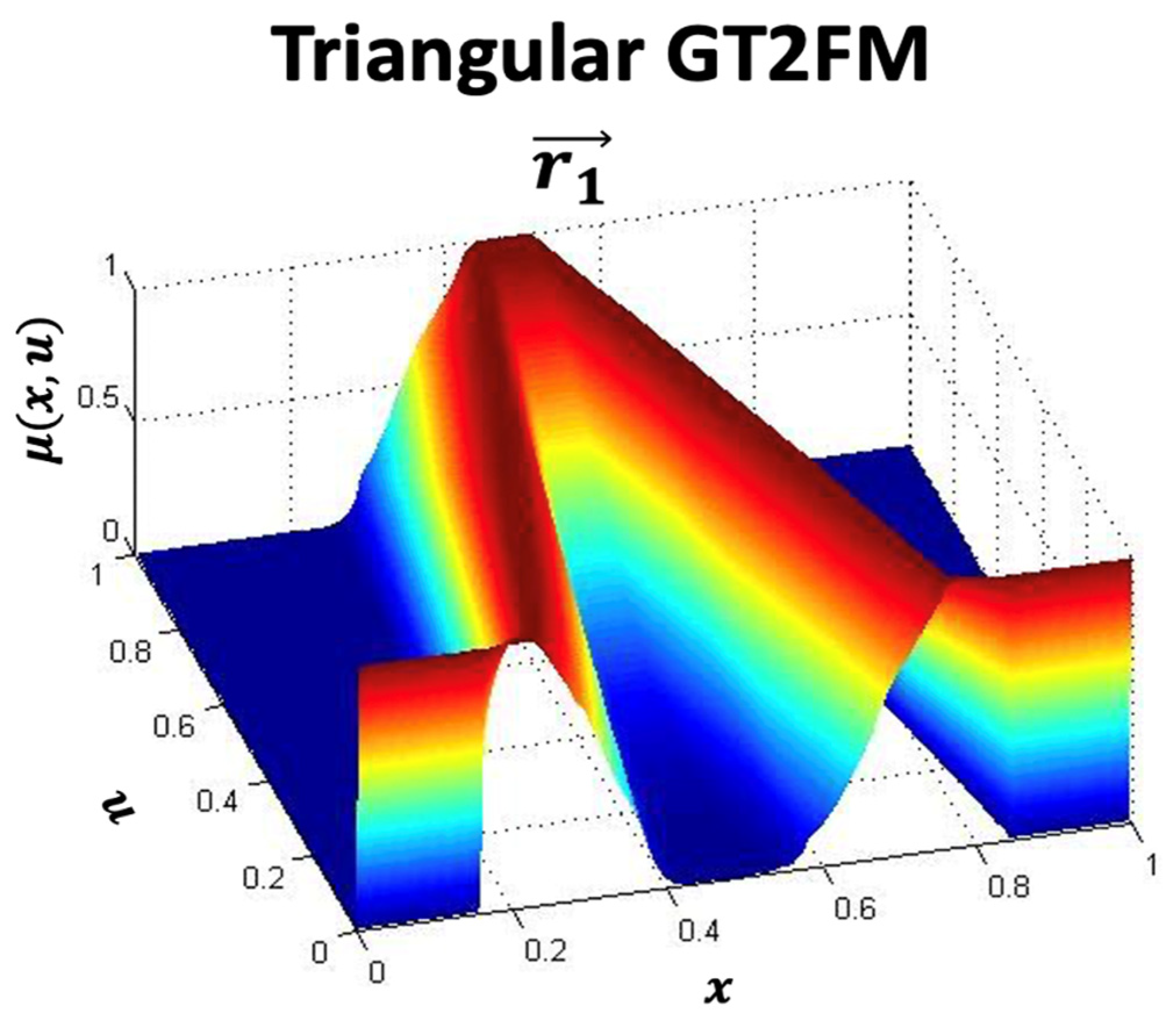
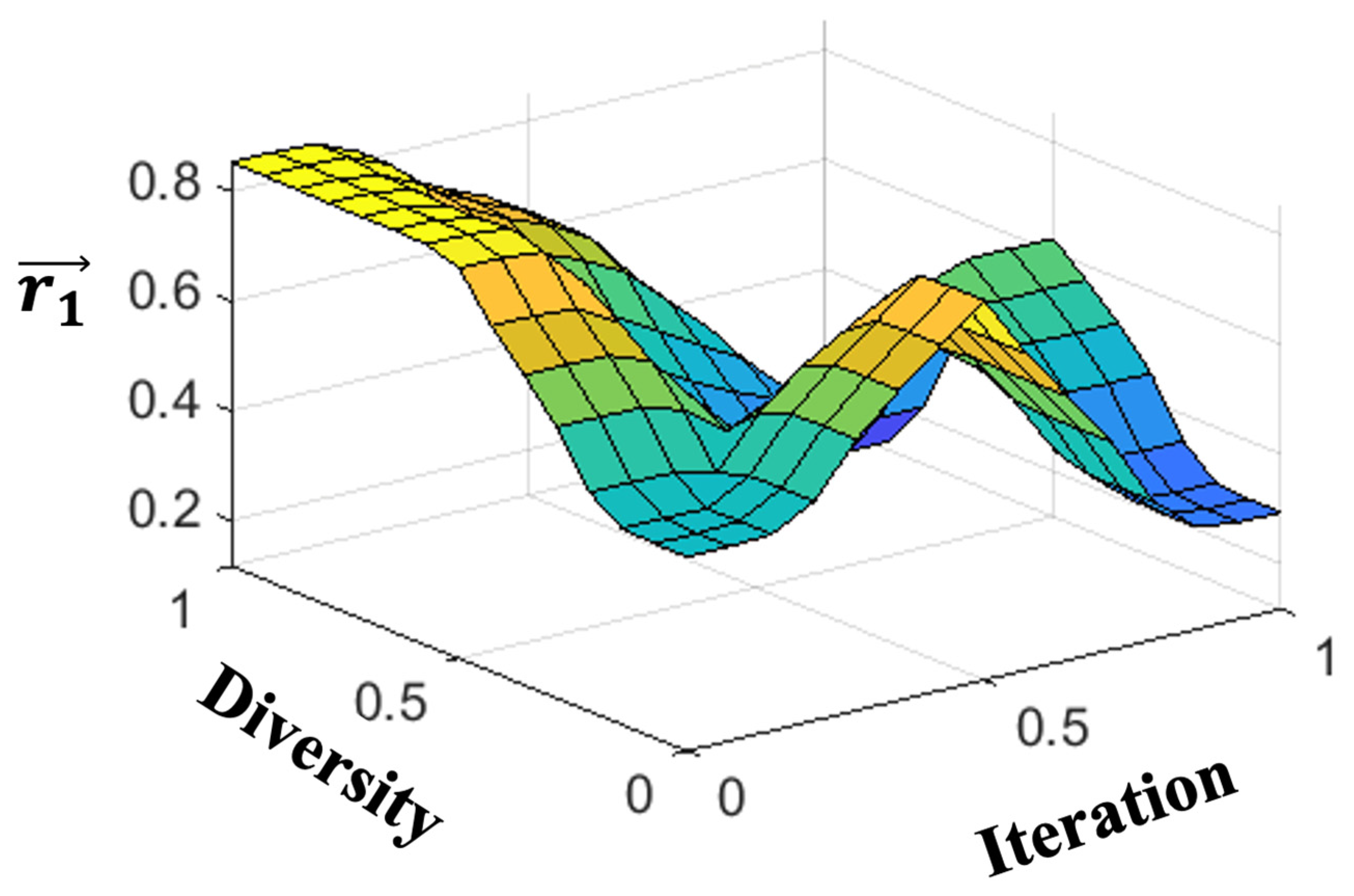
The visual representation of the MFs, the surface, and its description are denoted in Figure 7 and Figure 8 and Equation (17), respectively:
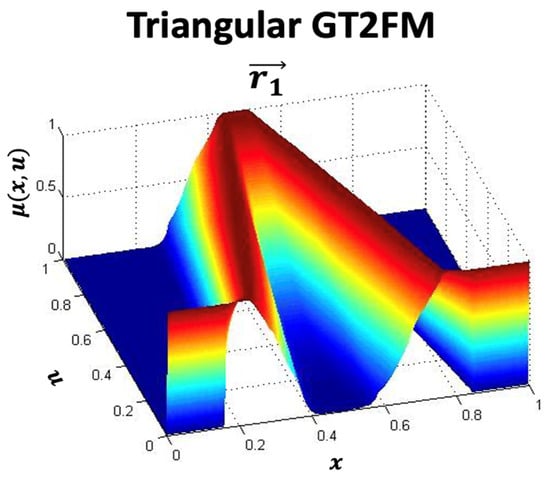
Figure 7.
Graphical illustration of the ScaleTriScaleGaussT2MF.
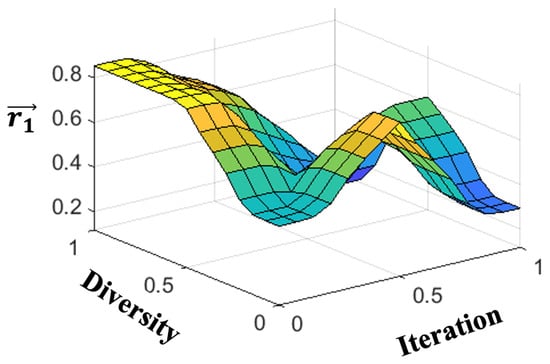
Figure 8.
Representation of the surface of the output for .
The DOU LMF, is defined by and , the parameters of the UMF, , and the vector . The idea is formulated by Equation (18):
The Function is multiplied by to formulate the LMF of the DOU, , given by: . Thus, and are the upper and lower limits of the DOU. The range is and the is the radius of the FOU. Equations (19) and (20) summarize this:
where is a small value.
The apex or nucleus of in the IT2MF is defined by Equation (21):
where and . Therefore, the vertical cuts with the T1MFs are Gaussian, . This idea is expressed by Equation (22):
where is the MF of T1FS with the vertical cuts of the secondary IT2MFs.
3.3.2. Strategies to Determine the and Parameters of the FWOA
In the analysis of the results, we find that the parameter is an essential element in the process of exploring, for example, when is closer to 1, this indicates that the population has explored, in this case with the final iterations, and when is closer to 1, this indicates that a better solution is near to the best solution, and indicates the end of the exploitation process in the WOA. At the start, the iteration is “low”, and when all the iterations have been executed or are close to 100%, the iteration is “high”. The expression is given by Equation (23) [43,44]:
The diversity is the second input to analyze in the GT2FLS, and is postulated by Equation (24), which measures the dispersion of the whales, i.e., when the whales are closer there is less diversity and when whales are far apart the diversity is higher. The fuzzy rules verifying this mechanism are shown in Figure 9 [43,44]
where t represents the current iteration, the value for all the population is indicated by , a whale is expressed by i, the number of possible solutions is (for example, the number of dimensions), j is the next solution, indicates the solution j of the whale i, and finally, is the solution j of the best whale.

Figure 9.
Fuzzy rules of the GT2FLS.
4. Set of Benchmark Functions
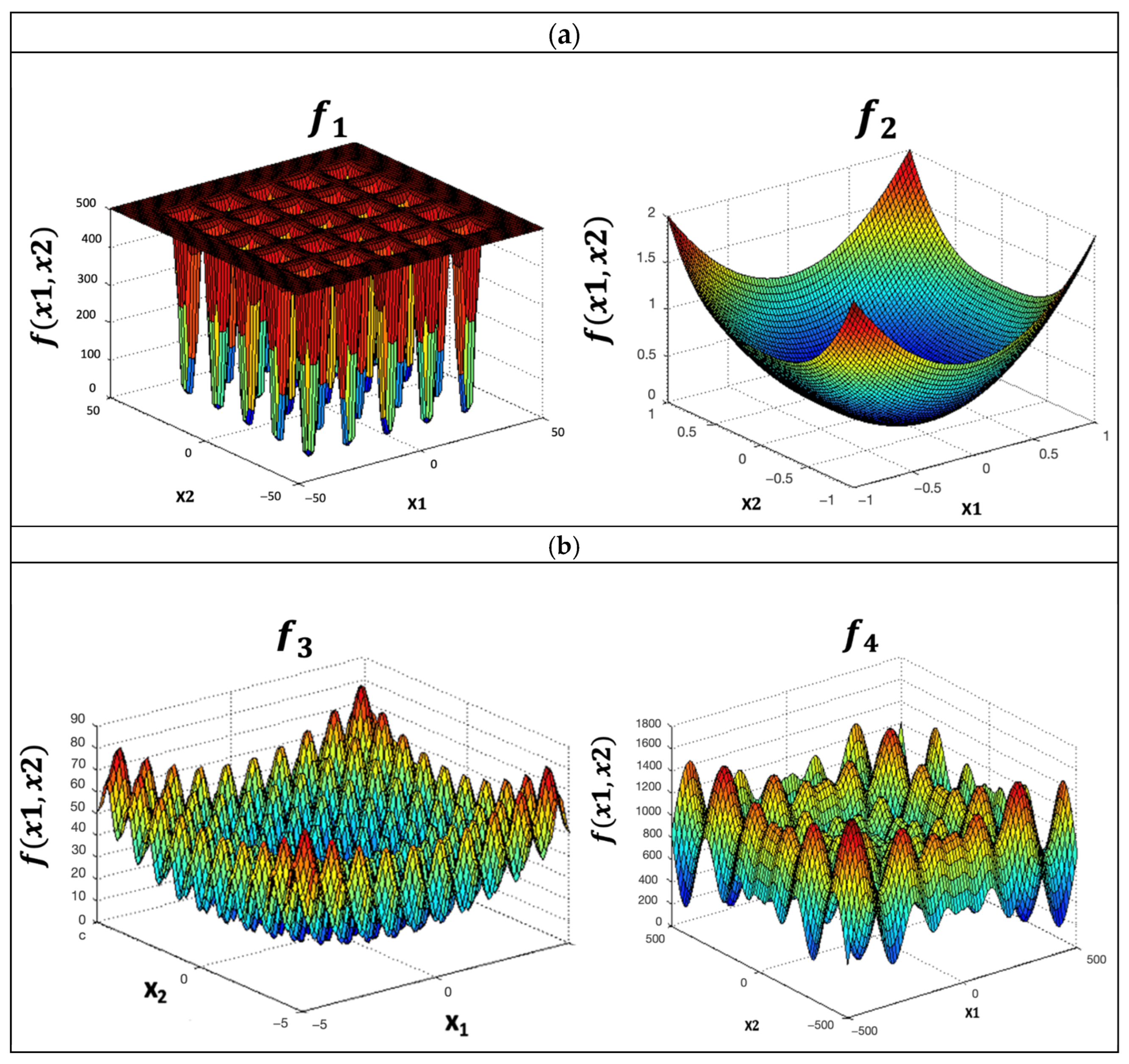
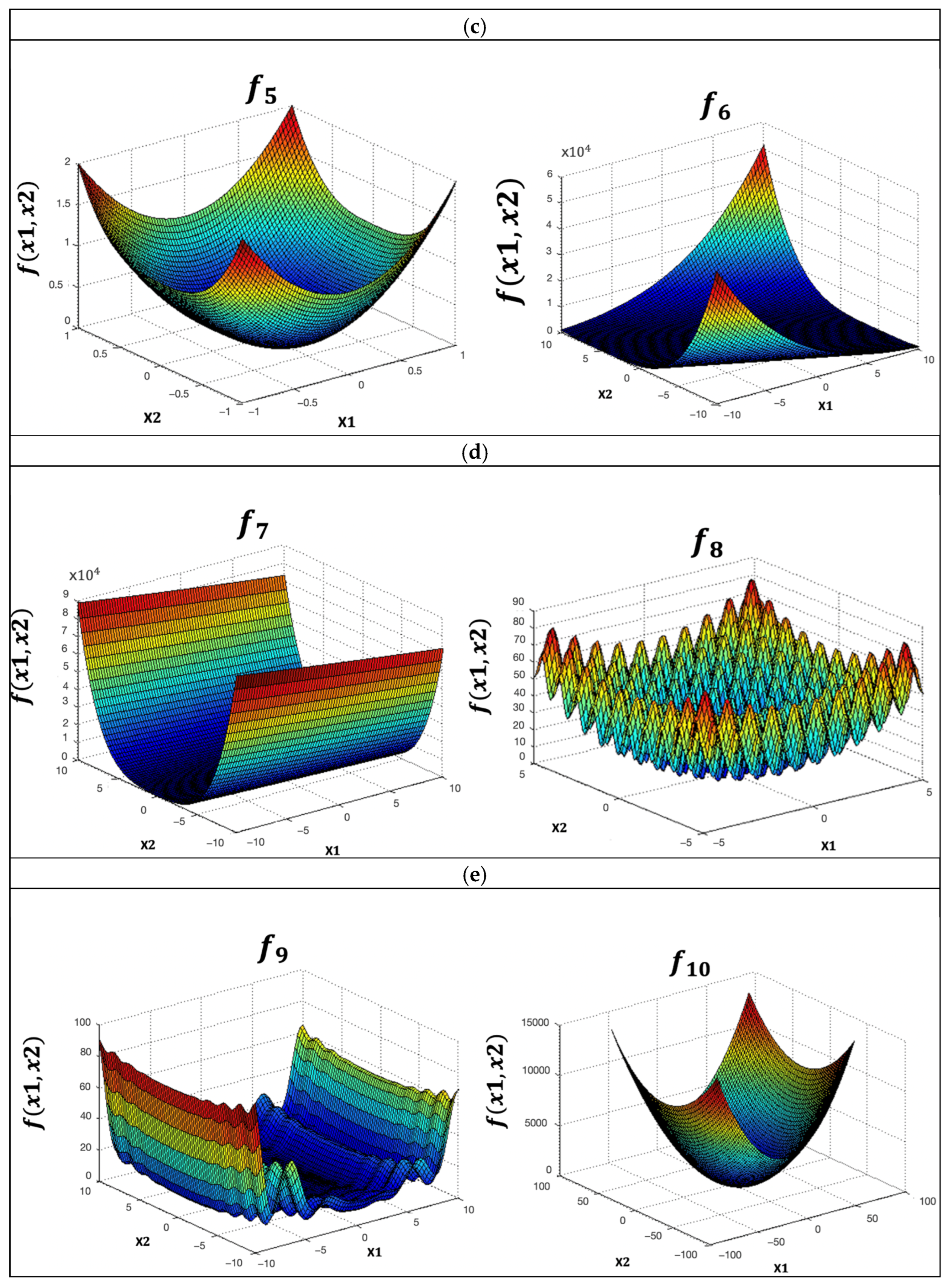
Ten benchmark functions are utilized with the goal of FWOA-GT2FLS validation: Sphere, Giewangk, Rastrigin, Schewefel, Sum of Different Power, Zakharov, Dixon and Price, Levy, Sum Squares, and Rotated Hyper-Ellipsoid. Each function was evaluated with 10, 20, 30, 50, 100, and 500 dimensions. The functions are presented in Table 2, and the corresponding plots are illustrated in Figure 10.

Table 2.
Benchmark functions.
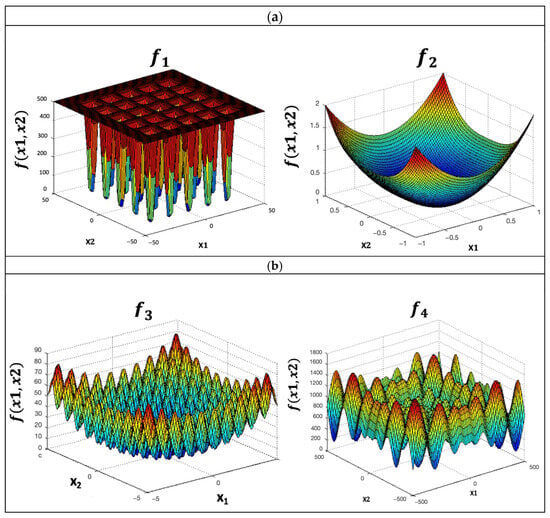
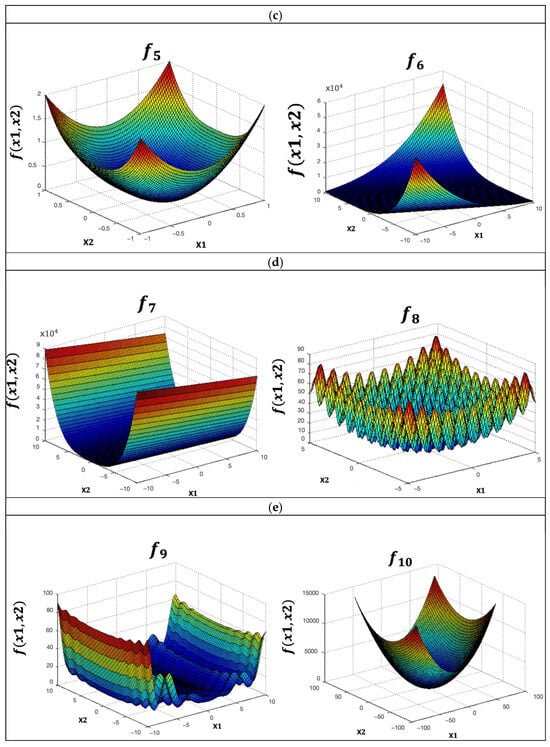
Figure 10.
Plots of the functions: (a) Sphere, Griewangk; (b) Rastringin, Shewefel; (c) Sum of Different Power, Zakharov; (d) Dixon and Price, Levy; (e) Sum Squares and Rotated Hyper-Ellipsoid.
5. Results
The objective of this experimentation is to study the FWOA behavior with the GT2FLS in finding the values of the and parameters. The setting of the relevant parameters is based according to [22,44], with the goal of comparing the results with the proposed FWOA-GT2FLS (Table 3).

Table 3.
Parameter settings for the experimental results in each methodology.
Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9 depict the comparisons with the WOA (fixed and random parameters), utilizing 10 dimensions in Table 4, Table 5 for 20, Table 6 for 30, Table 7 for 50, Table 8 for 100, and Table 9 for 500 dimensions, respectively (averages are summarized in Table 10).

Table 4.
Results of varying and for 10 dimensions.

Table 5.
Results of varying and for 20 dimensions.

Table 6.
Results of varying and for 30 dimensions.

Table 7.
Results of varying and for 50 dimensions.

Table 8.
Results of varying and for 100 dimensions.

Table 9.
Results of varying and for 500 dimensions.

Table 10.
Statistical tests.
Table 4 illustrates that the better results for the FWOA-GT2FLS are with the F3, F5, F6, and F7 functions. In Table 5, the proposed method is better when compared with the others for F2, F6, and F7. When the dimensions increase to 30, better results are achieved for F5, F4, F5, and F7 (See Table 6). With 50 dimensions, better results are achieved for F2, F4, F5, and F7 (see Table 7). The averages with minimum errors presented in Table 6 are for F1, F2, F3, F7, and F8 (see Table 8), and finally, when the dimensions are increased to 500, the functions with minimal errors are F2, F3, and F7 (See Table 9).
6. Analysis of Results
Statistical tests and comparisons with other fuzzy sets and with fuzzy bee colony optimization (FBCO) [43] are outlined in this section. The Z-test has a significance of 5%, Ha = µ1 µ2, H0 = µ1 µ2, Alpha of 5%, and −1.645 is the critical value. The hypotheses are: Ho: the FWOA-GT2FLS is greater than or equal to the WOA with random values; and Ha: the results for the FWOA-GT2FLS are smaller than for the WOA. A sample of 30 values was selected based on the results in Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9. Equation (25) describes the mathematical expression to calculate the Z-value:
The null hypothesis is rejected with evidence called “Significant” when the Z-value is smaller than −1.645; therefore, the alternative hypothesis is accepted. The values used in this statistical test are for the average of 10 dimensions shown in Table 10.
Table 10 indicates that the proposal has significant evidence to reject the null hypothesis with F6 and F7.
To demonstrate the efficiency of the FWOA-GT2FLS, a comparison with the results for 50 dimensions with the FBCO-IT2FLS [43] is summarized in Table 11 (best means best values).

Table 11.
Comparison of the results with the FBCO, the WOA, and the proposal.
The proposed fuzzy WOA in the hybridization with the GT2FLS presents lower errors with functions F2 and F7. The original WOA presents errors very close with respect to the FWOA-GT2FLS. Another measure considered is the standard deviation (). Table 12 shows the comparison with the FBCO-IT2FLS [43], the FWOA-IT2FLS [44], the original WOA, and the proposed FWOA-GT2FLS.

Table 12.
Comparison with the results of the FBCO-IT2FLS, the WOA, and the proposal.
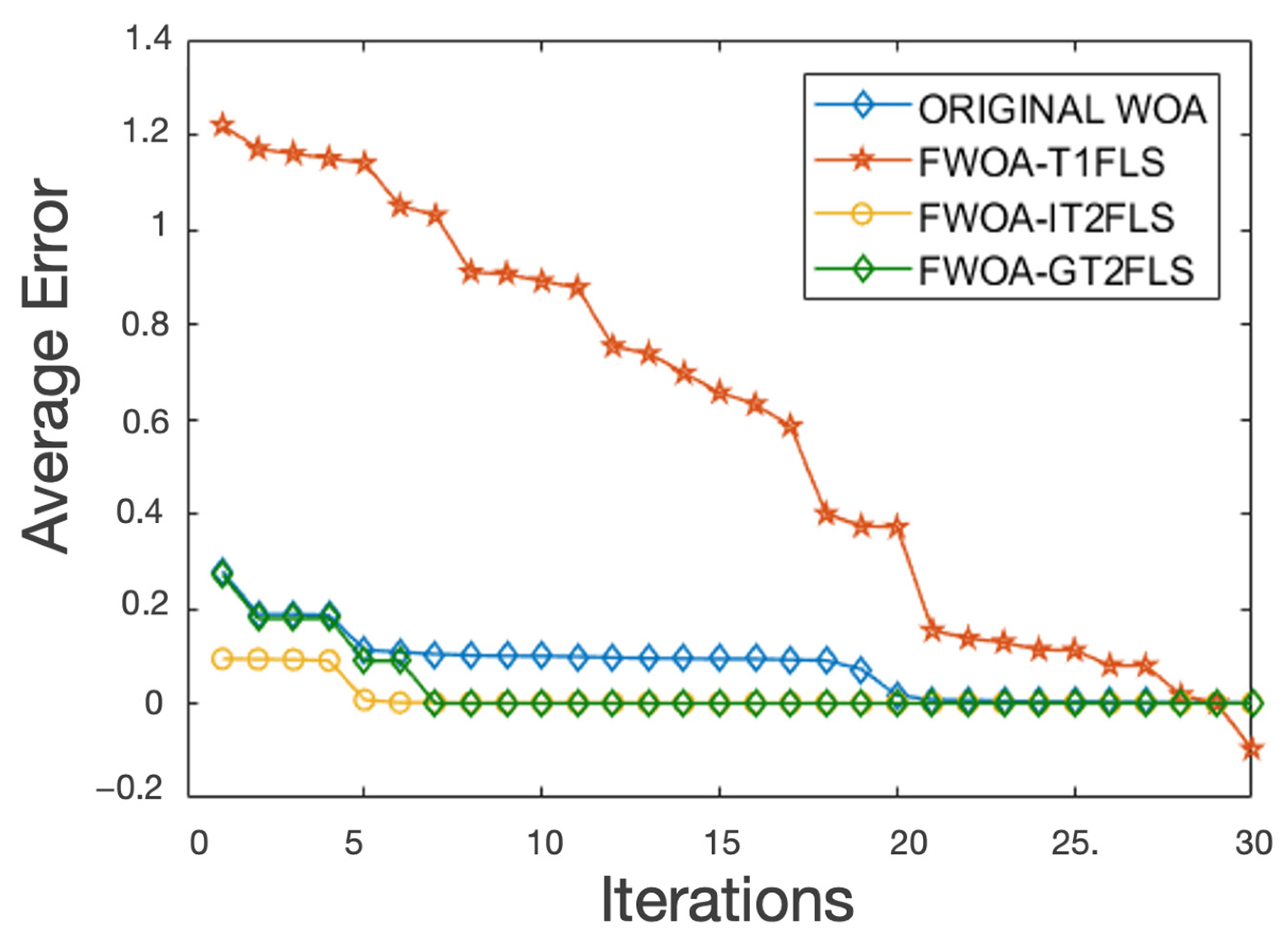
The computational complexity of the GT2FLS is high due to the fact that more calculations are required, but we have found that the proposed FWOA-GT2FLS method requires less iterations to find a good solution. Figure 11 depicts a visual comparison with the results of each method for the mathematical function with excellent results found, which is the Levy (F8) function with 500 dimensions.
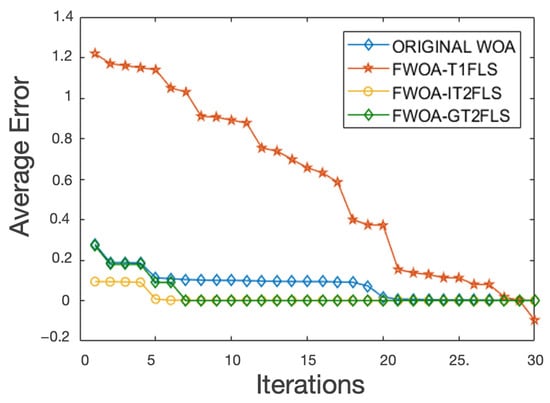
Figure 11.
Behavior of the Levy function with 500 dimensions.
Figure 11 illustrates a fast convergence with the proposed method using the GT2FLS in the dynamic adjustment of the and parameters when compared with the original WOA and the other FSs (see green line). The experiments carried out illustrate that by increasing the number of the iterations, the FWOA-GT2FLS algorithm maintains similar results without the need to increase the iterations. This is because the proposed method quickly finds the minimum desired values of the mathematical functions. For example, Figure 11 shows the results of the Levy mathematical function with 500 dimensions; the green line indicates that the FWOA-GT2FLS in iteration number 6 finds the minimum value and this behavior is similar in all the other mathematical functions. The reason is because the values of the and parameters found with the proposed algorithm are the indicated combination to reach the minimum value in the proposed problem.
7. Conclusions
A proposal to analyze the uncertainty in the case study using the methodology of the GT2FLSs to find the and values of the WOA algorithm is outlined. These parameters are part of the exploration () and exploitation () of the WOA, and a fuzzy WOA algorithm was designed that allows us to find excellent results when compared with the original WOA algorithm. When the number of dimensions is increased, the effectiveness of the proposal can be appreciated (see Table 7, Table 8 and Table 9 and Figure 11).
Statistically, it is observed that the results of the proposal are very close to the original algorithm, hence this proposal is considered a good approximation to continue exploring the performance of the WOA algorithm.
The main limitation found in this article is the processing time of the GT2FLS, because the calculation is performed in each iteration at the time of evaluating the iteration and the diversity of the virtual whales; therefore, when finding the values of and , the GT2FLS is executed to later find the minimum value of the function. This calculation is executed in each iteration of the algorithm. However, if we take advantage of the fact that the proposed method can reach a minimum value in less iterations, then we can overcome this limitation.
As future work, a relevant extension of this paper would be the implementation of an interval type-3 FLS to find the optimal values of the and parameters when the dimensions are increased to 1000 or 5000 values. It would be interesting to observe if the proposed method obtains the minimum values for the mathematical functions. Another important work is to explore other case studies, for example the stabilization of an inverted pendulum or trajectories in an autonomous mobile robot with fuzzy controllers, to further test the proposed FWOA-GT2FLS. Finally, we could extend the parameter adaptation to type-3 fuzzy logic based on [45,46,47,48,49,50], which could potentially enhance the results.
Author Contributions
Conceptualization, creation of main idea, writing—review, formal analysis, and editing, L.A.-A.; methodology, validation, editing, and supervision, O.C.; formal analysis, P.M.; editing, supervision, and funding, Z.W.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry and Energy, Republic of Korea (RS-2024-00441420; RS-2024-00442817).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We thank the program of the Division of Graduate Studies and Research of Tijuana Institute of Technology for the support in our research and for creating an excellent team working in collaboration with all the co-authors on this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sanyal, S.; Konar, D.; Bhattacharjee, A.; Chatterjee, S. General Type-2 Fuzzy Reasoning for Path-Planning of a Mobile Robot in a Dynamic Environment under Sensory Uncertainty. In Proceedings of the 2024 IEEE 3rd International Conference on Control, Instrumentation, Energy & Communication (CIEC), Kolkata, India, 25–27 January 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 73–78. [Google Scholar]
- Amador-Angulo, L.; Mendoza, O.; Castro, J.R.; Rodríguez-Díaz, A.; Melin, P.; Castillo, O. Fuzzy Sets in Dynamic Adaptation of Parameters of a Bee Colony Optimization for Controlling the Trajectory of an Autonomous Mobile Robot. Sensors 2016, 16, 1458. [Google Scholar] [CrossRef] [PubMed]
- Al-shami, T.M.; Alcantud, J.C.R.; Mhemdi, A. New generalization of fuzzy soft sets:(a, b)-Fuzzy soft sets. Aims Math. 2023, 8, 2995–3025. [Google Scholar] [CrossRef]
- Ontiveros, E.; Melin, P.; Castillo, O. Comparative study of interval Type-2 and general Type-2 fuzzy systems in medical diagnosis. Inf. Sci. 2020, 525, 37–53. [Google Scholar] [CrossRef]
- Castillo, O.; Amador-Angulo, L.; Castro, J.R.; Garcia-Valdez, M. A comparative study of type-1 fuzzy logic systems, interval type-2 fuzzy logic systems and generalized type-2 fuzzy logic systems in control problems. Inf. Sci. 2016, 354, 257–274. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Kumbasar, T. A new fractional-order general type-2 fuzzy predictive control system and its application for glucose level regulation. Appl. Soft Comput. 2020, 91, 106241. [Google Scholar] [CrossRef]
- Ontiveros-Robles, E.; Melin, P. Toward a development of general type-2 fuzzy classifiers applied in diagnosis problems through embedded type-1 fuzzy classifiers. Soft Comput. 2019, 24, 83–99. [Google Scholar] [CrossRef]
- Sanchez, M.A.; Castillo, O.; Castro, J.R. Generalized Type-2 Fuzzy Systems for controlling a mobile robot and a performance comparison with Interval Type-2 and Type-1 Fuzzy Systems. Expert Syst. Appl. 2015, 42, 5904–5914. [Google Scholar] [CrossRef]
- Jianzhong, S.; Shaohua, L.; Yong, Y.; Rong, L. An improved general type-2 fuzzy sets type reduction and its application in general type-2 fuzzy controller design. Soft Comput. 2019, 23, 13513–13530. [Google Scholar] [CrossRef]
- Wang, Y.C. Research and application of whale optimization algorithm. Comput. Eng. Sci. 2024, 46, 881. [Google Scholar]
- Alyasseri, Z.A.A.; Ali, N.S.; Al-Betar, M.A.; Makhadmeh, S.N.; Jamil, N.; Awadallah, M.A.; Mirjalili, S. Recent advances of whale optimization algorithm, its versions and applications. In Handbook of Whale Optimization Algorithm; Academic Press: Cambridge, MA, USA, 2024; pp. 9–31. [Google Scholar]
- Dai, L.; Wang, H. An Improved WOA (Whale Optimization Algorithm)-Based CNN-BIGRU-CBAM Model and Its Application to Short-Term Power Load Forecasting. Energies 2024, 17, 2559. [Google Scholar] [CrossRef]
- Majumdar, P.; Mitra, S.; Mirjalili, S.; Bhattacharya, D. Whale optimization algorithm-comprehensive meta analysis on hybridization, latest improvements, variants and applications for complex optimization problems. In Handbook of Whale Optimization Algorithm; Academic Press: Cambridge, MA, USA, 2024; pp. 81–90. [Google Scholar]
- Zhao, L.; Liu, J.; Li, Y. Application of Improved WOA in Hammerstein Parameter Resolution Problems under Advanced Mathematical Theory. J. Appl. Math. 2024, 2024, 5619098. [Google Scholar] [CrossRef]
- Yang, S.; Xiong, G.; Fu, X.; Mirjalili, S.; Mohamed, A.W. Enhanced Whale optimization algorithms for parameter identification of solar photovoltaic cell models: A comparative study. Sci. Rep. 2024, 14, 16765. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, S.K.; Reang, S.; Saha, A.K.; Chakraborty, S. F-WOA: An improved whale optimization algorithm based on Fibonacci search principle for global optimization. In Handbook of Whale Optimization Algorithm; Academic Press: Cambridge, MA, USA, 2024; pp. 217–233. [Google Scholar]
- Ghasemi, M.; Zare, M.; Mohammadi, S.K.; Mirjalili, S. Applications of whale migration algorithm in optimal power flow problems of power systems. In Handbook of Whale Optimization Algorithm; Academic Press: Cambridge, MA, USA, 2024; pp. 347–364. [Google Scholar]
- Dadrasajirlou, Y.; Karami, H. A survey of different Whale Optimization Algorithm applications in water engineering and management. In Handbook of Whale Optimization Algorithm; Academic Press: Cambridge, MA, USA, 2024; pp. 613–624. [Google Scholar]
- Chandrasekaran, S.K.; Rajasekaran, V.A. Energy-efficient cluster head using modified fuzzy logic with WOA and path selection using enhanced CSO in IoT-enabled smart agriculture systems. J. Supercomput. 2024, 80, 11149–11190. [Google Scholar] [CrossRef]
- Xu, H.; Liu, W.D.; Li, L.; Yao, D.J.; Ma, L. FSRW: Fuzzy logic-based whale optimization algorithm for trust-aware routing in IoT-based healthcare. Sci. Rep. 2024, 14, 16640. [Google Scholar] [CrossRef]
- Alhafedh, M.A.A.; Mitras, B.A. Optimizing Northern Goshawk Algorithm with Fuzzy Logic and Whale Algorithm Strategies. Math. Model. Eng. Probl. 2024, 11, 1265. [Google Scholar] [CrossRef]
- Amador-Angulo, L.; Castillo, O. Fuzzy Dynamic Adaptation of a Whale Algorithm for the Optimization of Benchmark Functions. In New Horizons for Fuzzy Logic, Neural Networks and Metaheuristics; Springer Nature: Cham, Switzerland, 2024; pp. 251–265. [Google Scholar]
- Castillo, O.; Ochoa, P.; Soria, J. Differential evolution with fuzzy logic for dynamic adaptation of parameters in mathematical function optimization. In Imprecision and Uncertainty in Information Representation and Processing: New Tools Based on Intuitionistic Fuzzy Sets and Generalized Nets; Springer: Cham, Switzerland, 2016; pp. 361–374. [Google Scholar]
- Ou, X.; Wu, M.; Pu, Y.; Tu, B.; Zhang, G.; Xu, Z. Cuckoo search algorithm with fuzzy logic and Gauss–Cauchy for minimizing localization error of WSN. Appl. Soft Comput. 2022, 125, 109211. [Google Scholar] [CrossRef]
- Cuevas, F.; Castillo, O.; Cortes-Antonio, P. A New Fuzzy Approach to Dynamic Adaptation of the Marine Predator Algorithm Parameters in the Optimization of Fuzzy Controllers for Autonomous Mobile Robots. In New Perspectives on Hybrid Intelligent System Design Based on Fuzzy Logic, Neural Networks and Metaheuristics; Springer International Publishing: Cham, Switzerland, 2022; pp. 179–204. [Google Scholar]
- Ntakolia, C.; Platanitis, K.S.; Kladis, G.P.; Skliros, C.; Zagorianos, A.D. A genetic algorithm enhanced with fuzzy-logic for multi-objective unmanned aircraft vehicle path planning missions. In Proceedings of the 2022 International Conference on Unmanned Aircraft Systems (ICUAS), Dubrovnik, Croatia, 21–24 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 114–123. [Google Scholar]
- Du Phan, V.; Nguyen, X.H.; Dinh, V.N.; Dang, T.S.; Le, V.C.; Ho, S.P.; Ta, H.C.; Duong, D.T.; Mai, T.A. Development of an Adaptive Fuzzy-Neural Controller for Temperature Control in a Brick Tunnel Kiln. Electronics 2024, 13, 342. [Google Scholar] [CrossRef]
- Sharma, P.; Raju, S. Metaheuristic optimization algorithms: A comprehensive overview and classification of benchmark test functions. Soft Comput. 2023, 28, 3123–3186. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.C.; Hu, X.X.; Qiu, L.; Zang, H.F. Black-winged kite algorithm: A nature-inspired meta-heuristic for solving benchmark functions and engineering problems. Artif. Intell. Rev. 2024, 57, 98. [Google Scholar] [CrossRef]
- Benmamoun, Z.; Khlie, K.; Dehghani, M.; Gherabi, Y. WOA: Wombat Optimization Algorithm for Solving Supply Chain Optimization Problems. Mathematics 2024, 12, 1059. [Google Scholar] [CrossRef]
- Solanki, P.; Deep, K. Quadratic approximation salp swarm algorithm for function optimization. OPSEARCH 2023, 61, 282–314. [Google Scholar] [CrossRef]
- Kaabneh, K.; AbuFalahah, I.; Eguchi, K.; Gochhait, S.; Leonova, I.; Montazeri, Z.; Dehghani, M. Dollmaker Optimization Algorithm: A Novel Human-Inspired Optimizer for Solving Optimization Problems. Int. J. Intell. Eng. Syst. 2024, 17, 816–828. [Google Scholar]
- Mohamed, A.W.; Sallam, K.M.; Agrawal, P.; Hadi, A.A.; Mohamed, A.K. Evaluating the performance of meta-heuristic algorithms on CEC 2021 benchmark problems. Neural Comput. Appl. 2023, 35, 1493–1517. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy logic. In Granular, Fuzzy, and Soft Computing; Springer: New York, NY, USA, 2023; pp. 19–49. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. In Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems: Selected Papers by Lotfi A. Zadeh; World Scientific: Singapore, 1996; pp. 394–432. [Google Scholar]
- Zadeh, L.A.; Klir, G.J.; Yuan, B. Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems, Selected Papers; World Scientific: Singapore, 1996; Volume 6. [Google Scholar]
- Karnik, N.N.; Mendel, J.; Liang, Q. Type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 1999, 7, 643–658. [Google Scholar] [CrossRef]
- Karnik, N.N.; Mendel, J.M. Operations on type-2 fuzzy sets. Fuzzy Sets. Syst. 2001, 122, 327–348. [Google Scholar] [CrossRef]
- Mendel, J.M. General type-2 fuzzy systems. In Explainable Uncertain Rule-Based Fuzzy Systems; Springer International Publishing: Cham, Switzerland, 2024; pp. 519–568. [Google Scholar]
- Mendel, J.M.; Liu, F.; Zhai, D. σ-plane representation for type-2 fuzzy sets: Theory and applications. IEEE Trans. Fuzzy Syst. 2009, 17, 1189–1207. [Google Scholar] [CrossRef]
- Hamrawi, H.; Coupland, S.; John, R. Type-2 fuzzy alpha-cuts. IEEE Trans. Fuzzy Syst. 2016, 25, 682–692. [Google Scholar] [CrossRef]
- Castillo, O.; Amador-Angulo, L. A generalized type-2 fuzzy logic approach for dynamic parameter adaptation in bee colony optimization applied to fuzzy controller design. Inf. Sci. 2018, 460, 476–496. [Google Scholar] [CrossRef]
- Amador-Angulo, L.; Castillo, O. An Interval Type-2 Fuzzy Logic Approach for Dynamic Parameter Adaptation in a Whale Optimization Algorithm Applied to Mathematical Functions. Axioms 2023, 13, 33. [Google Scholar] [CrossRef]
- Nabipour, N.; Qasem, S.N.; Jermsittiparsert, K. Type-3 fuzzy voltage management in PV/Hydrogen fuel cell/battery hybrid systems. Int. J. Hydrogen Energy 2020, 45, 32478–32492. [Google Scholar] [CrossRef]
- Taghieh, A.; Aly, A.A.; Felemban, B.F.; Althobaiti, A.; Mohammadzadeh, A.; Bartoszewicz, A. A Hybrid Predictive Type-3 Fuzzy Control for Time-Delay Multi-Agent Systems. Electronics 2022, 11, 63. [Google Scholar] [CrossRef]
- Vafaie, R.H.; Mohammadzadeh, A.; Piran, J. A new type-3 fuzzy predictive controller for MEMS gyroscopes. Nonlinear Dyn. 2021, 106, 381–403. [Google Scholar] [CrossRef]
- Tian, M.-W.; Yan, S.-R.; Mohammadzadeh, A.; Tavoosi, J.; Mobayen, S.; Safdar, R.; Assawinchaichote, W.; Vu, M.T.; Zhilenkov, A. Stability of Interval Type-3 Fuzzy Controllers for Autonomous Vehicles. Mathematics 2021, 9, 2742. [Google Scholar] [CrossRef]
- Qasem, S.N.; Ahmadian, A.; Mohammadzadeh, A.; Rathinasamy, S.; Pahlevanzadeh, B. A type-3 logic fuzzy system: Optimized by a correntropy based Kalman filter with adaptive fuzzy kernel size. Inf. Sci. 2021, 572, 424–443. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Sabzalian, M.H.; Zhang, W. An Interval Type-3 Fuzzy System and a New Online Fractional-Order Learning Algorithm: Theory and Practice. IEEE Trans. Fuzzy Syst. 2019, 28, 1940–1950. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).