Summed Series Involving 1F2 Hypergeometric Functions
Abstract
1. Introduction
2. Summed Series Involving Hypergeometric Functions from Chebyshev Polynomial Expansions of Bessel Functions
3. Summed Series Involving Hypergeometric Functions from Gegenbauer Polynomial Expansions of Bessel Functions
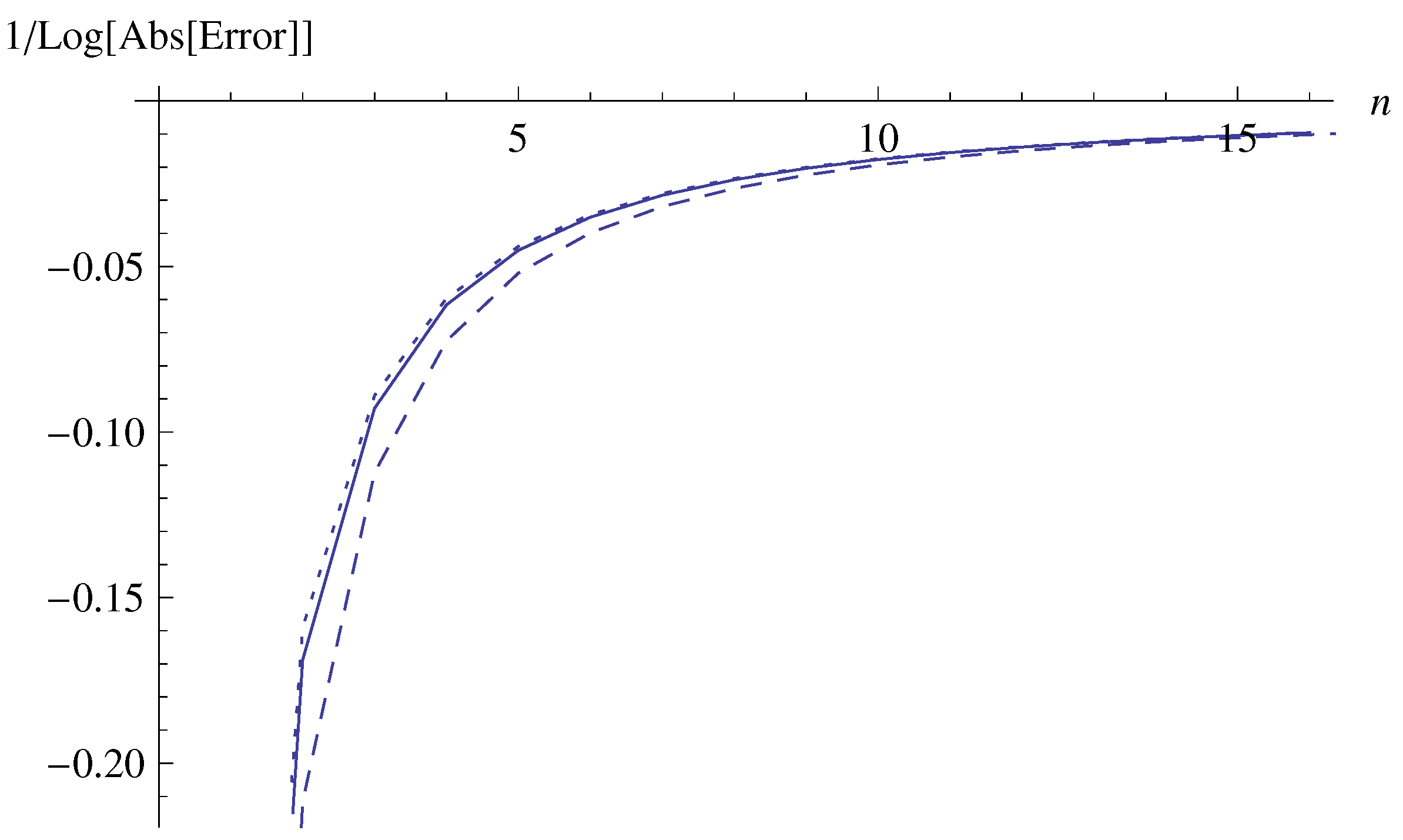
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Legendre Series for J0 (kx)
Appendix A.2. Chebyshev Series for J0 (kx) and J1 (kx)
Appendix A.3. Gegenbauer Series for J0 (kx) and J1 (kx)
References
- Bjorken, J.D.; Drell, S. Relativistic Quantum Fields; McGraw-Hill: New York, NY, USA, 1965; p. 286. [Google Scholar]
- Dickhoff, W.H.; Barbieri, C. Self-consistent Green’s function method for nuclei and nuclear matter. Prog. Part. Nucl. Phys. 2004, 52, 377–496. [Google Scholar] [CrossRef]
- Duine, R.A.; Stoof, H.T.C. Microscopic many-body theory of atomic Bose gases near a Feshbach. J. Opt. Quantum Semiclass. Opt. 2003, 5, S212. [Google Scholar] [CrossRef][Green Version]
- Dalgarno, A.; Lewis, J.T. The exact calculation of long-range forces between atoms by perturbation theory. Proc. R. Soc. Lond. Ser. A 1955, 233, 70. [Google Scholar] [CrossRef]
- Alvarez, G.; Silverstone, H.J. A new method to sum divergent power series: Educated match. J. Phys. Commun. 2017, 1, 025005. [Google Scholar] [CrossRef]
- Mera, H.; Pedersen, T.G.; Nikolić, B. Nonperturbative Quantum Physics from Low-Order Perturbation Theory. Phys. Rev. Lett. 2015, 115, 143001. [Google Scholar] [CrossRef] [PubMed]
- Mera, H.; Pedersen, T.G.; Nikolić, B.K. Hypergeometric resummation of self-consistent sunset diagrams for steady-state electron-boson quantum many-body systems out of equilibrium. Phys. Rev. B 2016, 94, 165429. [Google Scholar] [CrossRef]
- Pedersen, T.G.; Mera, H.; Nikolić, B.K. Stark effect in low-dimensional hydrogen. Phys. Rev. A 2016, 93, 013409. [Google Scholar] [CrossRef]
- Chaundy, T.W. An Extension of Hypergeometric Eunctions (I). Q. J. Math. Oxf. Ser. 1942, 13, 159–171. [Google Scholar] [CrossRef]
- Burchnall, J.L.; Chaundy, T.W. The Hypergeometric Identities of Cayley, Orr, And Bailey. Proc. Lond. Math. Soc. 1948, 50, 56–74. [Google Scholar] [CrossRef]
- Henrici, P. On Certain Series Expansions Involving Whittaker Functions and Jacobi Polynomials. Pac. J. Math. 1955, 5, 725–744. [Google Scholar] [CrossRef][Green Version]
- Gasper, G.; Rahman, M. Product Formulas of Watson, Bailey and Bateman Types and Positivity of the Poisson Kernel for Q-Racah Polynomials. SIAM J. Math. Anal. 1984, 15, 768–798. [Google Scholar] [CrossRef]
- Jain, V.K.; Verma, A. A q-analogue of Watson’s product formula and its applications. Indian J. Pure Appl. Math. 1997, 28, 237–255. [Google Scholar]
- Slater, L.J. Expansions of Generalized Whittaker Functions. Math. Proc. Camb. Philos. Soc. 1954, 50, 628–631. [Google Scholar] [CrossRef]
- Shah, M. On generalizations of some results and their applications. Collect. Math. 1973, 24, 249–265. [Google Scholar]
- Verma, A.; Jain, V.K. Some Transformations of Basic Hypergeometric Functions, Part I. SIAM J. Math. Anal. 1981, 12, 943–956. [Google Scholar] [CrossRef]
- Luke, Y.L. The Special Functions and Their Approximations; Academic Press: New York, NY, USA, 1969; Volume 2, p. 45, No. 9.4.1.4. [Google Scholar]
- Bühring, W. Transformation Formulas for Terminating Saalschützian Hypergeometric Series of Unit Argument. J. Appl. Math. Stoch. Anal. 1995, 8, 189–194. [Google Scholar] [CrossRef]
- Miller, A.R. A class of generalized hypergeometric summations. J. Comput. Appl. Math. 1997, 87, 79–85. [Google Scholar] [CrossRef]
- Lópeza, J.L.; Pagolaa, P.; Sinusía, E.P. New series expansions of the 3F2 function. J. Math. Anal. Appl. 2015, 421, 982–995. [Google Scholar] [CrossRef]
- Awad, M.; Koepf, W.; Mohammed, A.O.; Rakha, M.A.; Rathie, A.K. A Study of Extensions of Classical Summation Theorems for the Series 3F2 and 4F3 with Applications. Results Math. 2021, 76, 65. [Google Scholar] [CrossRef]
- Mathai, A.M.; Saxena, R.K.; Haubold, H.J. The H-Function Theory and Applications; Springer: New York, NY, USA, 2010; p. 205. [Google Scholar] [CrossRef]
- Luke, Y.L. The Special Functions and Their Approximations; Academic Press: New York, NY, USA, 1969; Volume 1, pp. 230–231, No. 6.5.1-4. [Google Scholar]
- Ragab, F.M. Expansions of Kampé de Fériet’s Double Hypergeometric Function of Higher Order; Contract No.: Da-11-022-Ord-2059, MRC Technical Summary Report #589 September 1965; Mathematics Research Center, United States Army the University of Wisconsin: Madison, WI, USA, 1965; pp. 5–10. [Google Scholar]
- Miller, A.R. On the Mellin transform of products of Bessel and generalized hypergeometric functions. J. Comput. Appl. Math. 1995, 8, 271–286. [Google Scholar] [CrossRef]
- Cuchta, T. The Chebyshev Difference Equation. Mathematics 2020, 8, 74. [Google Scholar] [CrossRef]
- Straton, J.C. The Fourier–Legendre Series of Bessel Functions of the First Kind and the Summed Series Involving 1F2 Hypergeometric Functions that Arise from them. Axioms 2024, 13, 134. [Google Scholar] [CrossRef]
- Keating, C.M. Using Strong Laser Fields to Produce Antihydrogen Ions, appendix D. Ph.D. Dissertation, Portland State University, Portland, OR, USA, 2018. Available online: https://pdxscholar.library.pdx.edu/open_access_etds/4519/ (accessed on 6 February 2024).
- Available online: http://functions.wolfram.com/07.26.26.0001.01 (accessed on 6 February 2024).
- Wimp, J. Polynomial Expansions of Bessel Functions and Some Associated Functions. Math. Comp. 1962, 16, 446–458. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 5th ed.; Academic: New York, NY, USA, 1994. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series; Gorden and Breach: New York, NY, USA, 1986; Volume 3. [Google Scholar]
- Available online: http://functions.wolfram.com/07.23.03.0191.01 (accessed on 6 February 2024).
- Clenshaw, C.W. Mathematical Tables. In Chebyshev Series for Mathematical Functions; Department of Scientific and Industrial Research, Her Majesty’s Stationery Office: London, UK, 1962; Volume 5. [Google Scholar]
- Khajah, H.; Ortiz, E. Ultra-high precision computations. Comput. Math. Appl. 1994, 27, 41–57. [Google Scholar] [CrossRef]
- Vujevic, S.; Modrić, T. A Highly Accurate Algorithm For Computation of Complex-Valued Bessel, Neumann and Hankel Functions of Integer Order. Facta Univ. Ser. Electron. Energetics 2024, 37, 517–529. [Google Scholar] [CrossRef]
- Georgieva, I.; Hofreither, C. Computation of polynomial and rational approximations in complex domains by the τ-method. Numer. Algorithms 2024. [CrossRef]
- Yuste, S.B.; Abad, E. On a novel iterative method to compute polynomial approximations to Bessel functions of the first kind and its connection to the solution of fractional diffusion/diffusion-wave problems. J. Phys. A Math. Theor. 2011, 44, 075203. [Google Scholar] [CrossRef]
- Karatsuba, E.A. Calculation of Bessel Functions via the Summation of Series. Numer. Anal. Appl. 2019, 12, 372–387. [Google Scholar] [CrossRef]
- Kislenkov, V.V. Grid-oriented computation: Modified Bessel functions Jv(z) and Kv(z). Program. Comput. Softw. 2003, 29, 88–93. [Google Scholar] [CrossRef]
- Takekawa, T. Fast parallel calculation of modified Bessel function of the second kind and its derivatives. SoftwareX 2022, 17, 100923. [Google Scholar] [CrossRef]
- Rao, N.; Ayman-Mursaleen, M.; Aslan, R. A note on a general sequence of λ-Szász Kantorovich type operators. Comput. Appl. Math. 2024, 43, 428. [Google Scholar] [CrossRef]
- Bohner, M.; Cuchta, T. The Bessel Difference Equation. Proc. Am. Math. Soc. 2017, 145, 1567–1580. [Google Scholar] [CrossRef]
- Tumakov, D.N. The Faster Methods for Computing Bessel Functions of the First Kind of an Integer Order with Application to Graphic Processors. Lobachevskii J. Math. 2019, 40, 1725–1738. [Google Scholar] [CrossRef]
- Bezubik, A.; Dàbrowska, A.; Strasburger, A. A new derivation of the plane wave expansion into spherical harmonics and related Fourier transforms. J. Nonlinear Math. Phys. 2004, 11 (Suppl. S1), 167–173. [Google Scholar] [CrossRef]
- Elgindy, K.T.; Smith-Miles, K.A. Optimal Gegenbauer quadrature over arbitrary integration nodes. J. Comput. Appl. Math. 2013, 242, 82–106. [Google Scholar] [CrossRef]
- Keiner, J. Computing With Expansions In Gegenbauer Polynomials. SIAM J. Sci. Comput. 2009, 31, 2151–2171. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Straton, J.C. Summed Series Involving 1F2 Hypergeometric Functions. Mathematics 2024, 12, 4016. https://doi.org/10.3390/math12244016
Straton JC. Summed Series Involving 1F2 Hypergeometric Functions. Mathematics. 2024; 12(24):4016. https://doi.org/10.3390/math12244016
Chicago/Turabian StyleStraton, Jack C. 2024. "Summed Series Involving 1F2 Hypergeometric Functions" Mathematics 12, no. 24: 4016. https://doi.org/10.3390/math12244016
APA StyleStraton, J. C. (2024). Summed Series Involving 1F2 Hypergeometric Functions. Mathematics, 12(24), 4016. https://doi.org/10.3390/math12244016





