Sustainable Design Factors and Solutions Analysis and Assessment for the Graphic Design Industry: A Hybrid Fuzzy AHP–Fuzzy MARCOS Approach
Abstract
1. Introduction
1.1. Motivation
1.2. Research Objectives
- To construct an evaluation structure for graphic design sustainability.
- To analyze and calculate the weight of dimensions and indicators using the FAHP.
- To evaluate and rank all solutions using the FMARCOS.
- To provide related sustainable decision-making suggestions to practitioners in the graphic design industry.
2. Literature Review
2.1. Research Gaps
2.2. The Development of the Graphic Design Industry
2.3. Fuzzy Analytic Hierarchy Process (FAHP)
2.4. Fuzzy Measurement of Alternatives and Ranking According to Compromise Solution (FMARCOS)
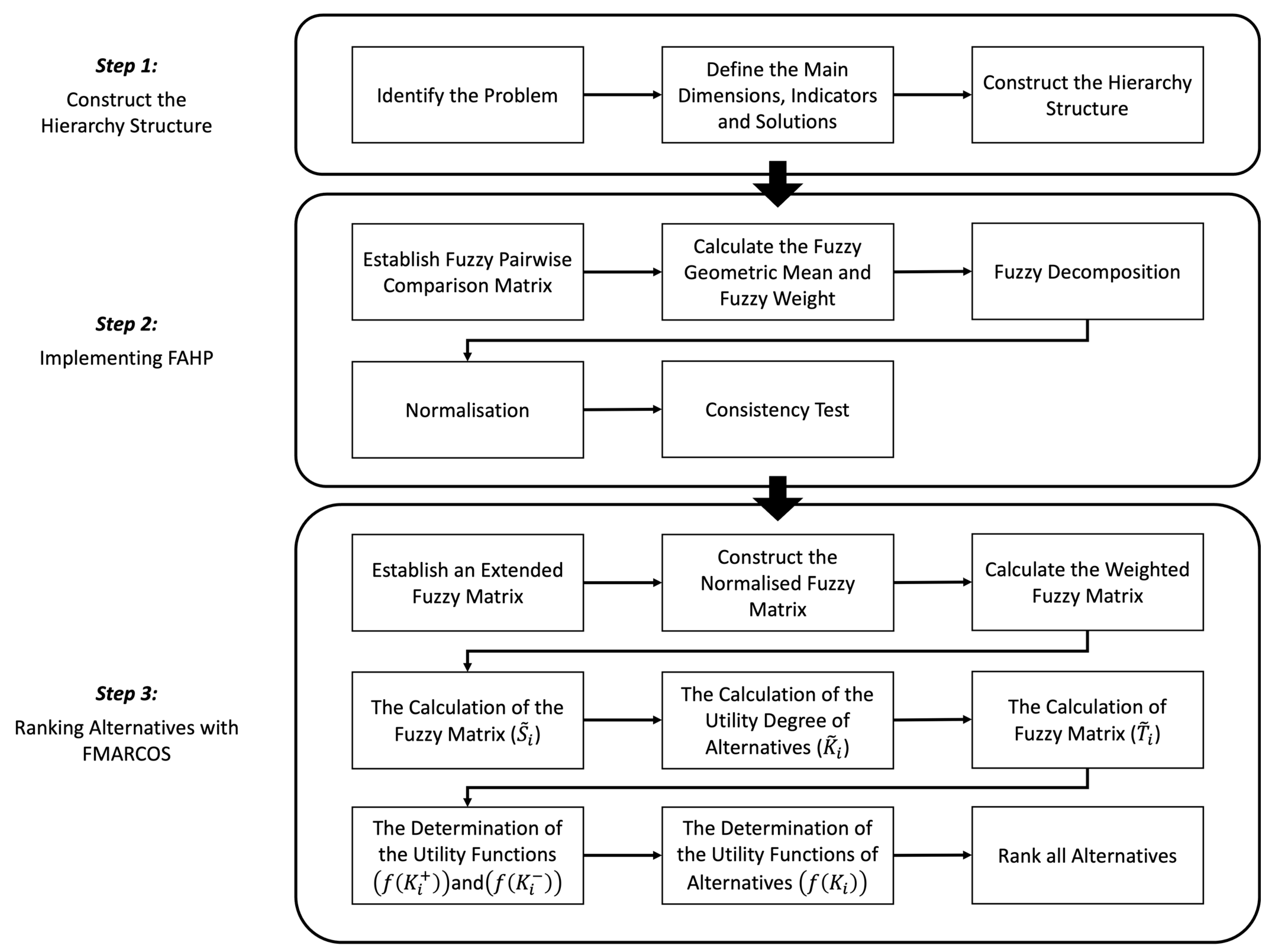
3. Materials and Methods
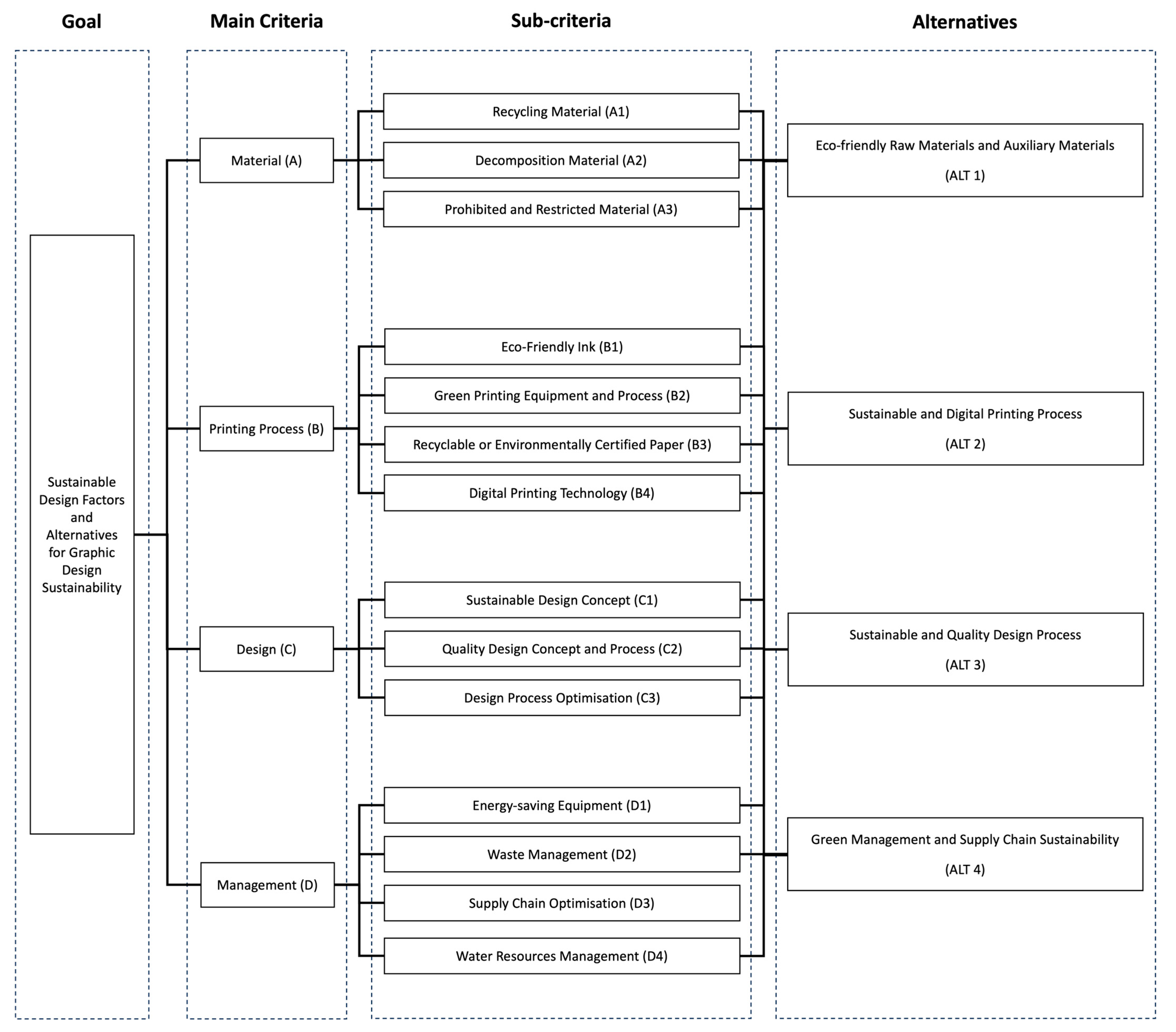
3.1. The Construction of the Hierarchy Structure
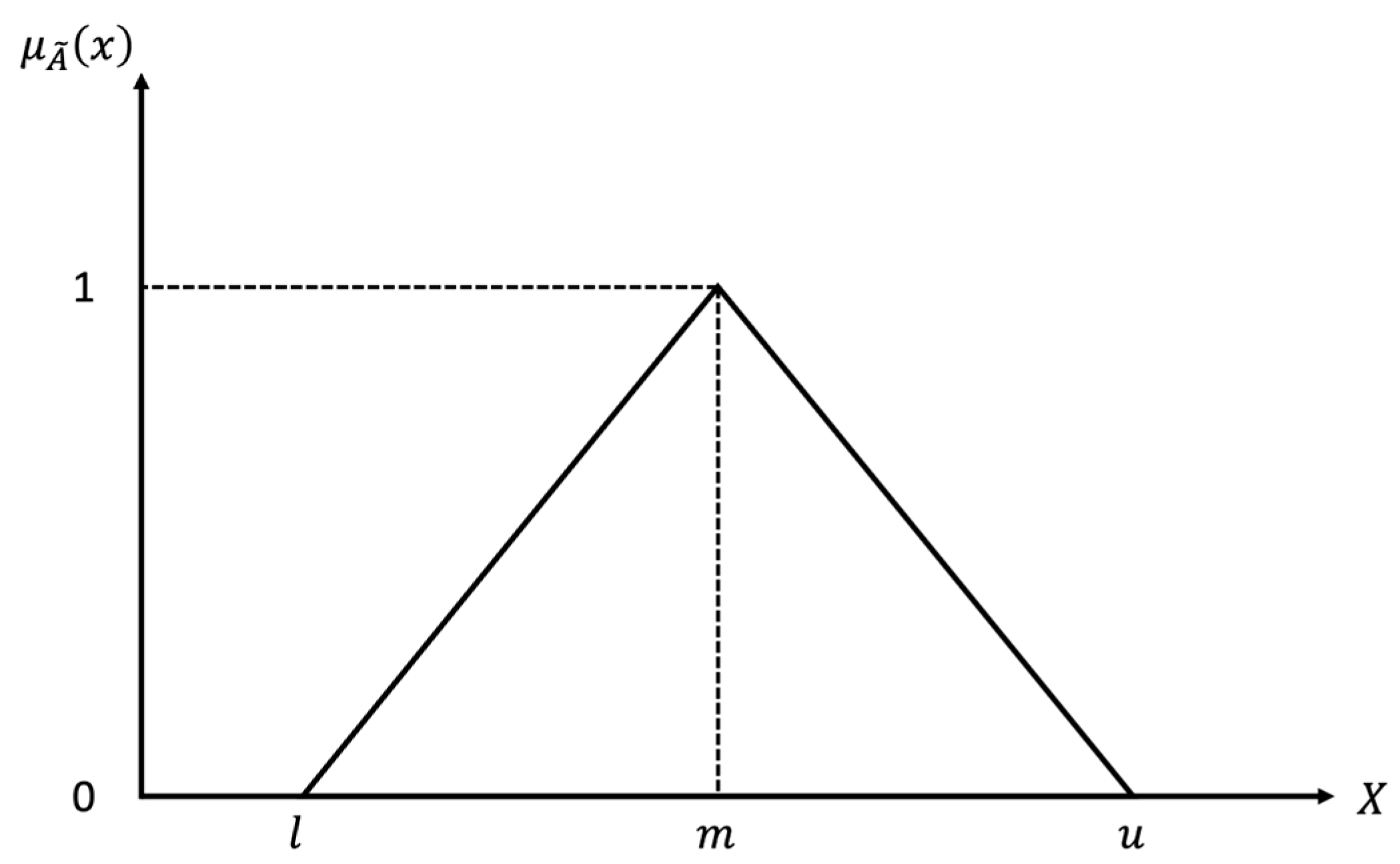
3.2. Fuzzy Theory and Triangular Fuzzy Numbers
3.3. Fuzzy Analytic Hierarchy Process (FAHP)
3.4. Fuzzy Measurement of Alternatives and Ranking According to Compromise Solution (FMARCOS)
4. Results
4.1. Numerical Analysis
4.1.1. Fuzzy Analytic Hierarchy Process (FAHP)
4.1.2. Fuzzy Measurement of Alternatives and Ranking According to Compromise Solution (FMARCOS)
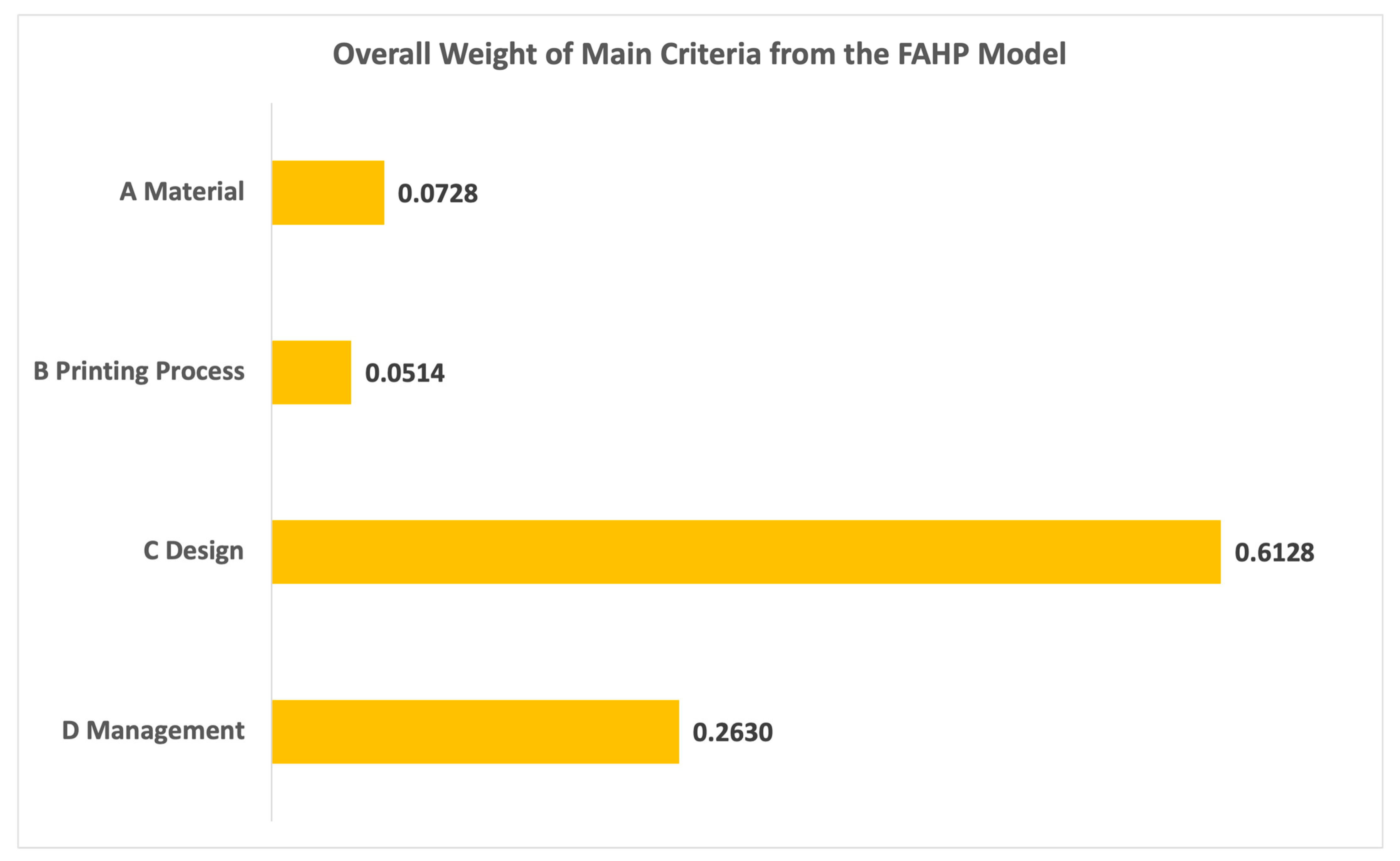
4.2. Research Results
4.2.1. Fuzzy Analytic Hierarchy Process (FAHP)
4.2.2. Fuzzy Measurement of Alternatives and Ranking According to Compromise Solution (FMARCOS)
5. Validation and Discussion
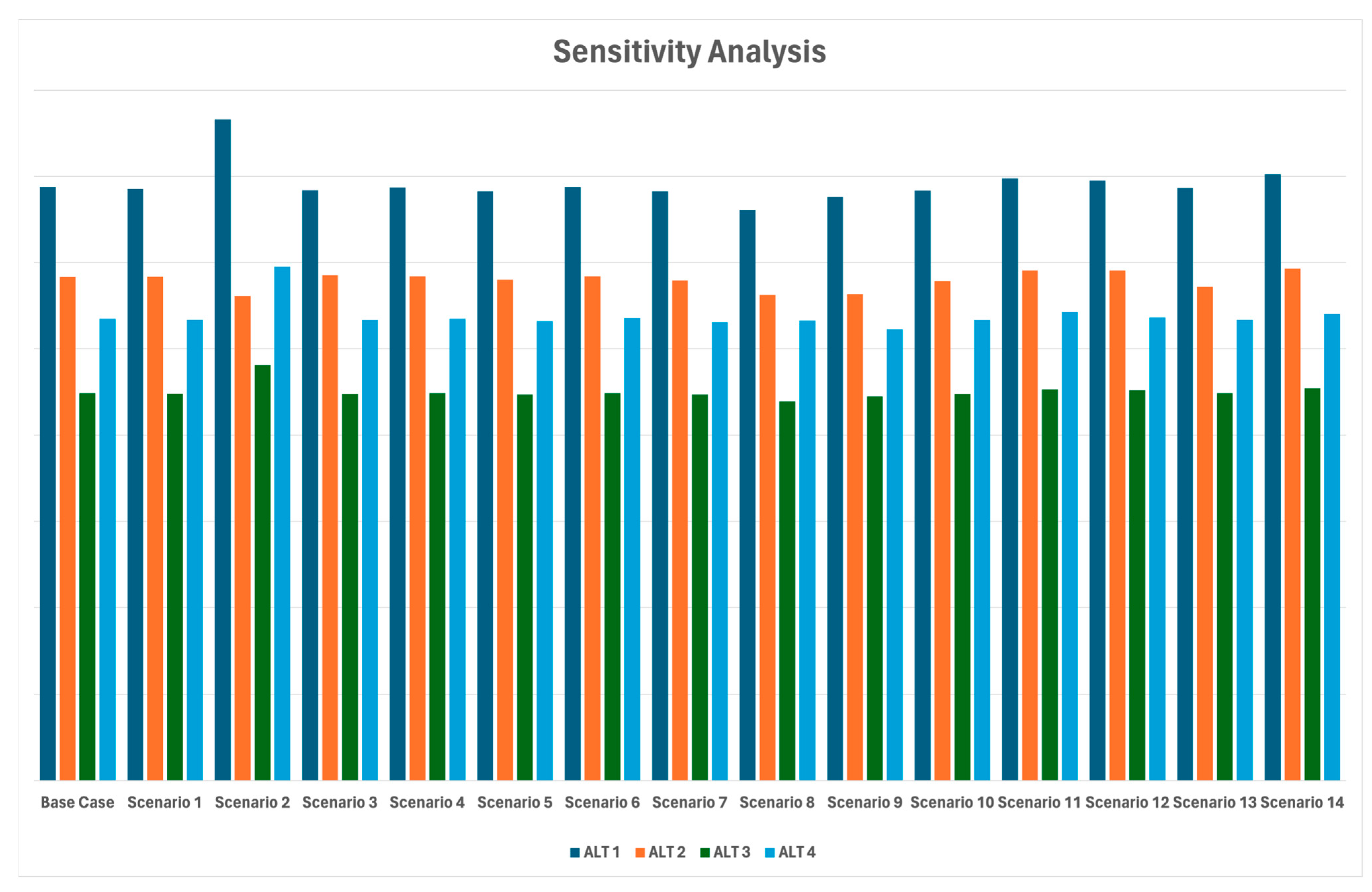
5.1. Sensitivity Analysis of Criteria Weight
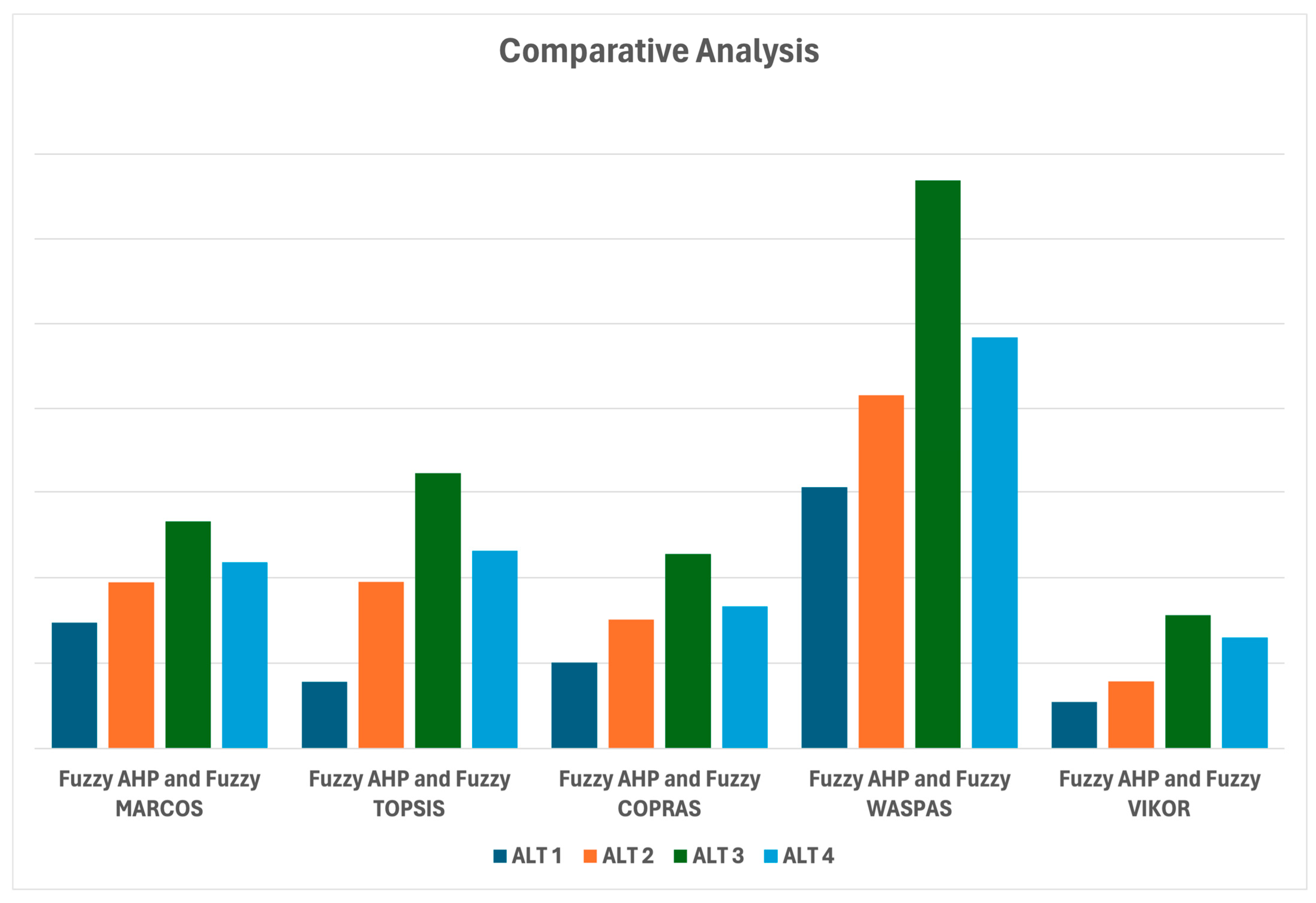
5.2. Comparative Analysis of Other Fuzzy MCDM Methods
5.3. Implications for Research
5.4. Implications for Management
5.5. Research Limitations
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Carson, R. Silent Spring; Houghton Mifflin Harcourt: Boston, MA, USA, 1962. [Google Scholar]
- Olgyay, V. Design with Climate; Princeton University Press: Princeton, NJ, USA, 1963. [Google Scholar]
- Papanek, V. Design for the Real World: Human Ecology and Social Change; Thames and Hudson: London, UK, 1971. [Google Scholar]
- McDonough, W.; Braungart, M. Cradle to Cradle: Remaking the Way We Make Things, 1st ed.; North Point Press: New York, NY, USA, 2002; ISBN 978-0-86547-587-8. [Google Scholar]
- Tu, J.-C. A Study of Sustainability Assessment Model for Recycling Materials from the Life Cycle Design. In Proceedings of the 1998 IEEE International Symposium on Electronics and the Environment. ISEE—1998 (Cat. No.98CH36145), Oak Brook, IL, USA, 6 May 1998; pp. 316–321. [Google Scholar]
- Tu, J.-C. Product Sustainable Design: Green Design in Theory and Practice; Asia-Pacific: Taipei, Taiwan, 2002; ISBN 978-986-7809-03-2. [Google Scholar]
- Clark, G.; Kosoris, J.; Hong, L.N.; Crul, M. Design for Sustainability: Current Trends in Sustainable Product Design and Development. Sustainability 2009, 1, 409–424. [Google Scholar] [CrossRef]
- Morelli, N. Active, Local, Connected: Strategic and Methodological Insights in Three Cases. Des. Issues 2011, 27, 90–110. [Google Scholar] [CrossRef]
- Müller, M. Design-Driven Innovation for Sustainability: A New Method for Developing a Sustainable Value Proposition. Int. J. Innov. Sci. 2012, 4, 11–24. [Google Scholar] [CrossRef]
- United Nations. Transforming Our World: The 2030 Agenda for Sustainable Development. Resolution Adopted by the General Assembly on 25 September 2015; United Nations: New York, NY, USA, 2015. [Google Scholar]
- United Nations. 17 Goals to Transform Our World. 2015. Available online: https://www.un.org/sustainabledevelopment/ (accessed on 18 May 2022).
- Kellert, S.; Calabrese, E. The Practice of Biophilic Design. 2015. Available online: www.biophilic-design.com (accessed on 17 February 2023).
- Goubran, S.; Cucuzzella, C. Integrating the Sustainable Development Goals in Building Projects. J. Sustain. Res. 2019, 1, 1–43. [Google Scholar] [CrossRef]
- Fan, K.-K.; Feng, T.-T. Sustainable Development Strategy of Chinese Animation Industry. Sustainability 2021, 13, 7235. [Google Scholar] [CrossRef]
- Li, Y. Design Visual Elements and Brand-Based Equity: Mediating Role of Green Concept. Front. Psychol. 2022, 13, 888164. [Google Scholar] [CrossRef] [PubMed]
- Murdoch-Kitt, K.M.; Emans, D.; Martin, K.N. Sustainability at the Forefront: Educating Students through Complex Challenges in Visual Communication and Design. Interdiscip. Environ. Rev. 2015, 16, 285–311. [Google Scholar] [CrossRef]
- Ji, S.; Lin, P.-S. Aesthetics of Sustainability: Research on the Design Strategies for Emotionally Durable Visual Communication Design. Sustainability 2022, 14, 4649. [Google Scholar] [CrossRef]
- Lin, C.-L.; Hsu, C.-Y.; Ting, C.-H. Research on the Key Influencing Goals for Visual Design Sustainability: A Dual Perspective. Sustainability 2024, 16, 1885. [Google Scholar] [CrossRef]
- Chang, W.-S.; Yin, M.-C. A Study on the Construction of Science Education Website Evaluation Indicators from the Perspective of Learning Strategy. Contemp. Educ. Res. Q. 2014, 22, 47–91. [Google Scholar]
- Gupta, S.; Gupta, S. What Drives Customers Crazy for Green Vehicles? A Fuzzy AHP Approach. Environ. Dev. Sustain. 2024, 26, 23283–23302. [Google Scholar] [CrossRef]
- Aminuddin, A.S.A.; Khalif, K.M.N.K.; Jamil, F.C.; Jaini, N.I. Fuzzy Analytic Hierarchy Process Using Intuitive Vectorial Centroid for Eco-Friendly Car Selection. J. Phys. Conf. Ser. 2019, 1366, 012076. [Google Scholar] [CrossRef]
- Wang, C.-N.; Thi-Be-Oanh-Cao; Dang, T.-T.; Nguyen, N.-A.-T. Third-Party Logistics Provider Selection in the Industry 4.0 Era by Using a Fuzzy AHP and Fuzzy MARCOS Methodology. IEEE Access 2024, 12, 67291–67313. [Google Scholar] [CrossRef]
- Bakır, M.; Atalık, Ö. Application of Fuzzy AHP and Fuzzy MARCOS Approach for the Evaluation of E-Service Quality in the Airline Industry. Decis. Mak. Appl. Manag. Eng. 2021, 4, 127–152. [Google Scholar] [CrossRef]
- Wang, J.-J.; Jing, Y.-Y.; Zhang, C.-F.; Zhao, J.-H. Review on Multi-Criteria Decision Analysis Aid in Sustainable Energy Decision-Making. Renew. Sustain. Energy Rev. 2009, 13, 2263–2278. [Google Scholar] [CrossRef]
- Odu, G.O. Weighting Methods for Multi-Criteria Decision Making Technique. J. Appl. Sci. Environ. Manag. 2019, 23, 1449–1457. [Google Scholar] [CrossRef]
- Deng, H.; Yeh, C.-H.; Willis, R.J. Inter-Company Comparison Using Modified TOPSIS with Objective Weights. Comput. Oper. Res. 2000, 27, 963–973. [Google Scholar] [CrossRef]
- Kumar, A.; Dhiman, P. Reliability Range Through Upgraded Operation with Trapezoidal Fuzzy Number. Fuzzy Inf. Eng. 2020, 12, 452–463. [Google Scholar] [CrossRef]
- Dhiman, P.; Kumar, A. A Situational Based Reliability Indices Estimation of ULT Freezer Using Preventive Maintenance under Fuzzy Environment. Int. J. Math. Eng. Manag. Sci. 2023, 8, 477–503. [Google Scholar] [CrossRef]
- Kumar, A.; Dhiman, P. Performance Analysis of “Injection Moulding Machine” under Fuzzy Environment through Contemporary Arithmetic Operations on Right Triangular Generalized Fuzzy Numbers (RTrGFN). J. Intell. Fuzzy Syst. 2023, 45, 4427–4445. [Google Scholar] [CrossRef]
- Dwiggins, W. New Kind of Printing Calls for New Design; Firefly Press: Wales, UK, 1922. [Google Scholar]
- Meggs, P.; Purvis, A. Meggs’ History of Graphic Design; Wiley: Chichester, UK, 1983. [Google Scholar]
- Eskilson, S. Graphic Design: A New History; Yale University Press: New Haven, CO, USA, 2007. [Google Scholar]
- Barnard, M. Graphic Design as Communication; Routledge: London, UK, 2013; ISBN 978-1-315-01538-5. [Google Scholar]
- Albadi, N.; Zollinger, S.W. Dominant Learning Styles of Interior Design Students in Generation Z. J. Inter. Des. 2021, 46, 49–65. [Google Scholar] [CrossRef]
- Martins, N.; Raposo, D. (Eds.) Communication Design and Branding: A Multidisciplinary Approach; Springer Series in Design and Innovation; Springer Nature: Cham, Switzerland, 2023; Volume 32, ISBN 978-3-031-35384-0. [Google Scholar]
- Szenasy, S.S. Ethics and Sustainability: Graphic Designers’ Role. In Proceedings of the Power of Design: AIGA National Design Conference, Vancouver, BC, Canada, 23–25 October 2003. [Google Scholar]
- Barth, C. Sustainable Graphic Design for the Print Industry. Ph.D. Thesis, California Polytechnic State University, San Luis Obispo, CA, USA, 2008. [Google Scholar]
- Jedlicka, W. Sustainable Graphic Design: Tools, Systems and Strategies for Innovative Print Design; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Fine, P.C. Sustainable Graphic Design: Principles and Practices; Bloomsbury Publishing: London, UK, 2016. [Google Scholar]
- Huang, H.-L. Examining the Design Policies and Taiwan’s Visual Design Industry from the Design Ladder Perspective. Ph.D. Thesis, National Cheng Kung University, Tainan, Taiwan, 2021. [Google Scholar]
- Bonsu, G.; Chisin, A.; Cronjé, J. Challenges to Sustainability in the Graphic Design Practices of a Developing Nation. Des. Cult. 2019, 12, 57–81. [Google Scholar] [CrossRef]
- Kadas, S. An Effort to Integrate Social and Environmental Awareness into Graphic Design Education. In Care, Climate, and Debt; Wilson, B.C., Ed.; Palgrave Macmillan: London, UK, 2022. [Google Scholar]
- Alahira, J.; Ninduwezuor-Ehiobu, N.; Olu-lawal, K.A.; Ani, E.C.; Ejibe, I. Eco-innovative graphic design practices: Leveraging fine arts to enhance sustainability in industrial design. Eng. Sci. Technol. J. 2024, 5, 783–793. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resources Allocation; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Tseng, H.-E.; Li, R.-K. Analytic Hierarchical Process for Design Alternative Selection. J. Des. 1998, 3, 43–54. [Google Scholar]
- Shahin, A.; Mahbod, M.A. Prioritization of Key Performance Indicators: An Integration of Analytical Hierarchy Process and Goal Setting. Int. J. Product. Perform. Manag. 2007, 56, 226–240. [Google Scholar] [CrossRef]
- Tu, J.-C.; Chang, Y.-C. Strategy of Sustainable Product Development by Applying Analytic Hierarchy Process (AHP). Kaohsiung Norm. Univ. J. 2006, 21, 139–153. [Google Scholar]
- Chang, D.-Y. Applications of the Extent Analysis Method on Fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Hsu, Y.; Lee, C.; Kreng, V.B. The Application of Fuzzy Delphi Method and Fuzzy AHP in Lubricant Regenerative Technology Selection. Expert Syst. Appl. 2010, 37, 419–425. [Google Scholar] [CrossRef]
- Kaganski, S.; Majak, J.; Karjust, K. Fuzzy AHP as a Tool for Prioritization of Key Performance Indicators. Procedia CIRP 2018, 72, 1227–1232. [Google Scholar] [CrossRef]
- Kwong, C.K.; Bai, H. A Fuzzy AHP Approach to the Determination of Importance Weights of Customer Requirements in Quality Function Deployment. J. Intell. Manuf. 2002, 13, 367–377. [Google Scholar] [CrossRef]
- Lam, K.C.; Lam, M.C.K.; Wang, D. MBNQA–Oriented Self-Assessment Quality Management System for Contractors: Fuzzy AHP Approach. Constr. Manag. Econ. 2008, 26, 447–461. [Google Scholar] [CrossRef]
- Rehman, A.U.; Mian, S.H.; Umer, U.; Usmani, Y.S. Strategic Outcome Using Fuzzy-AHP-Based Decision Approach for Sustainable Manufacturing. Sustainability 2019, 11, 6040. [Google Scholar] [CrossRef]
- Larimian, T.; Zarabadi, Z.S.S.; Sadeghi, A. Developing a Fuzzy AHP Model to Evaluate Environmental Sustainability from the Perspective of Secured by Design Scheme—A Case Study. Sustain. Cities Soc. 2013, 7, 25–36. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nguyen, V.T.; Thai, H.T.N.; Duong, D.H. Multi-Criteria Decision Making (MCDM) Approaches for Solar Power Plant Location Selection in Viet Nam. Energies 2018, 11, 1504. [Google Scholar] [CrossRef]
- Mostafa, M.; Hatami, N.; Espahbodi, K.; Asadi, F. Fuzzy Analytic Hierarchy Process (FAHP) Applied to Evaluating the Forest Management Approaches. J. For. Sci. 2022, 68, 263–276. [Google Scholar] [CrossRef]
- Alyamani, R.; Long, S. The Application of Fuzzy Analytic Hierarchy Process in Sustainable Project Selection. Sustainability 2020, 12, 8314. [Google Scholar] [CrossRef]
- Pan, N.F. Fuzzy AHP Approach for Selecting the Suitable Bridge Construction Method. Autom. Constr. 2008, 17, 958–965. [Google Scholar] [CrossRef]
- Ashour, M.; Mahdiyar, A.; Haron, S.H.; Hanafi, M.H. Barriers to the Practice of Sustainable Interior Architecture and Design for Interior Renovations: A Parsimonious-Cybernetic Fuzzy AHP Approach. J. Clean. Prod. 2022, 366, 132958. [Google Scholar] [CrossRef]
- Stević, Ž.; Pamučar, D.; Puška, A.; Chatterjee, P. Sustainable Supplier Selection in Healthcare Industries Using a New MCDM Method: Measurement of Alternatives and Ranking According to COmpromise Solution (MARCOS). Comput. Ind. Eng. 2020, 140, 106231. [Google Scholar] [CrossRef]
- El-Araby, A. The Utilization of MARCOS Method for Different Engineering Applications: A Comparative Study. Int. J. Res. Ind. Eng. 2023, 12, 155–164. [Google Scholar] [CrossRef]
- Badi, I.; Jibril, M.; Abubakar, M.; Bakir, M. Measuring Sustainability Performance Indicators Using FUCOM-MARCOS Methods. Oper. Res. Eng. Sci. Theory Appl. 2022, 5, 99–116. [Google Scholar] [CrossRef]
- Pamucar, D.; Ecer, F.; Deveci, M. Assessment of Alternative Fuel Vehicles for Sustainable Road Transportation of United States Using Integrated Fuzzy FUCOM and Neutrosophic Fuzzy MARCOS Methodology. Sci. Total Environ. 2021, 788, 147763. [Google Scholar] [CrossRef]
- Krishankumar, R.; Mishra, A.R.; Rani, P.; Ecer, F.; Ravichandran, K.S. Assessment of Zero-Carbon Measures for Sustainable Transportation in Smart Cities: A CRITIC-MARCOS Framework Based on Q-Rung Fuzzy Preferences. IEEE Internet Things J. 2023, 10, 18651–18662. [Google Scholar] [CrossRef]
- Birkocak, D.T.; Acar, E.; Bakadur, A.Ç.; Ütebay, B.; Özdağoğlu, A. An Application of the MARCOS Method Within the Framework of Sustainability to Determine the Optimum Recycled Fibre-Containing Fabric. Fibers Polym. 2023, 24, 2595–2608. [Google Scholar] [CrossRef]
- Morente-Molinera, J.A.; Kou, G.; Pérez, I.J.; Samuylov, K.; Selamat, A.; Herrera-Viedma, E. A Group Decision Making Support System for the Web: How to Work in Environments with a High Number of Participants and Alternatives. Appl. Soft Comput. 2018, 68, 191–201. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Stević, Ž.; Tanackov, I.; Prentkovskis, O. A Novel Multicriteria Approach—Rough Step-Wise Weight Assessment Ratio Analysis Method (R-SWARA) and Its Application in Logistics. Stud. Inform. Control 2018, 27, 97–106. [Google Scholar] [CrossRef]
- Tripathy, P.; Khambete, A.K.; Chauhan, K.A. An Innovative Approach to Assess Sustainability of Urban Mobility—Using Fuzzy MCDM Method. In Proceedings of the Innovative Research in Transportation Infrastructure; Deb, D., Balas, V.E., Dey, R., Shah, J., Eds.; Springer: Singapore, 2019; pp. 55–63. [Google Scholar]
- Stanković, M.; Stević, Ž.; Das, D.K.; Subotić, M.; Pamučar, D. A New Fuzzy MARCOS Method for Road Traffic Risk Analysis. Mathematics 2020, 8, 457. [Google Scholar] [CrossRef]
- Puška, A.; Stević, Ž.; Stojanović, I. Selection of Sustainable Suppliers Using the Fuzzy MARCOS Method. Curr. Chin. Sci. 2021, 1, 218–229. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, W.; Wang, Z.; Deveci, M.; Roy, S.K.; Kadry, S. Selection of Sustainable Food Suppliers Using the Pythagorean Fuzzy CRITIC-MARCOS Method. Inf. Sci. 2024, 664, 120326. [Google Scholar] [CrossRef]
- Tuş, A.; Adalı, E.A. Green Supplier Selection Based on the Combination of Fuzzy SWARA (SWARA-F) and Fuzzy MARCOS (MARCOS-F) Methods. Gazi Univ. J. Sci. 2022, 35, 1535–1554. [Google Scholar] [CrossRef]
- Çakır, E.; Taş, M.A.; Ulukan, Z. Neutrosophic Fuzzy MARCOS Approach for Sustainable Hybrid Electric Vehicle Assessment. In Proceedings of the 2021 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Melbourne, Australia, 17–20 October 2021; pp. 3423–3428. [Google Scholar]
- Wang, C.-N.; Chung, Y.-C.; Wibowo, F.D.; Dang, T.-T.; Nguyen, N.-A.-T. Sustainable Last-Mile Delivery Solution Evaluation in the Context of a Developing Country: A Novel OPA–Fuzzy MARCOS Approach. Sustainability 2023, 15, 12866. [Google Scholar] [CrossRef]
- Tsai, W.C.; Kung, P.T.; Wang, R.H.; Chang, Y.H.; Lee, S.Y. Applying the SERVQUAL Questionnaire to Establish Quality Indicators for Chinese Medicine. Taiwan J. Public Health 2008, 27, 309–319. [Google Scholar]
- Zadeh, L. Fuzzy Sets. Inf. Control 1965, 9, 338–353. [Google Scholar] [CrossRef]
- Sun, C.-C. A Performance Evaluation Model by Integrating Fuzzy AHP and Fuzzy TOPSIS Methods. Expert Syst. Appl. 2010, 37, 7745–7754. [Google Scholar] [CrossRef]
- Tseng, G.-H.; Huang, J.-J. Multiple Attribute Decision Making: Methods and Applications; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Gumus, A.T. Evaluation of Hazardous Waste Transportation Firms by Using a Two Step Fuzzy-AHP and TOPSIS Methodology. Expert Syst. Appl. 2009, 36, 4067–4074. [Google Scholar] [CrossRef]
- Wang, C.-N.; Chou, C.-C.; Dang, T.-T.; Nguyen, H.-P.; Nguyen, N.-A.-T. Integrating Triple Bottom Line in Sustainable Chemical Supplier Selection: A Compromise Decision-Making-Based Spherical Fuzzy Approach. Processes 2022, 10, 889. [Google Scholar] [CrossRef]
- Lin, C.-L.; Chen, J.-J.; Ma, Y.-Y. Ranking of Service Quality Solution for Blended Design Teaching Using Fuzzy ANP and TOPSIS in the Post-COVID-19 Era. Mathematics 2023, 11, 1255. [Google Scholar] [CrossRef]
- Chou, S.-W.; Chang, Y.-C. The Implementation Factors That Influence the ERP (Enterprise Resource Planning) Benefits. Decis. Support Syst. 2008, 46, 149–157. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy and Analytic Network Processes for the Measurement of Intangible Criteria and for Decision-Making. Mult. Criteria Decis. Anal. State Art Surv. 2016, 363–419. [Google Scholar]
- Alinezhad, A.; Amini, A. Sensitivity Analysis of TOPSIS Technique: The Results of Change in the Weight of One Attribute on the Final Ranking of Alternatives. J. Optim. Ind. Eng. 2011, 7, 23–28. [Google Scholar]
- Agarwal, S.; Kant, R.; Shankar, R. Evaluating Solutions to Overcome Humanitarian Supply Chain Management Barriers: A Hybrid Fuzzy SWARA—Fuzzy WASPAS Approach. Int. J. Disaster Risk Reduct. 2020, 51, 101838. [Google Scholar] [CrossRef]
- Yazdani, M.; Alidoosti, A.; Zavadskas, E.K. Risk Analysis of Critical Infrastructures Using Fuzzy Copras. Econ. Res.-Ekon. Istraživanja 2011, 24, 27–40. [Google Scholar] [CrossRef]
- Wang, C.-N.; Nguyen, V.T.; Duong, D.H.; Thai, H.T.N. A Hybrid Fuzzy Analysis Network Process (FANP) and the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) Approaches for Solid Waste to Energy Plant Location Selection in Vietnam. Appl. Sci. 2018, 8, 1100. [Google Scholar] [CrossRef]
- Zare, A.; Feylizadeh, M.; Mahmoudi, A.; Liu, S. Suitable Computerized Maintenance Management System Selection Using Grey Group TOPSIS and Fuzzy Group VIKOR: A Case Study. Decis. Sci. Lett. 2018, 7, 341–358. [Google Scholar] [CrossRef]
| Linguistic Variables | Fuzzy Numbers | Triangular Fuzzy Scale | Reversed Triangular Fuzzy Scale | ||||
|---|---|---|---|---|---|---|---|
| Equally Preferred | 1 | 1 | 1 | 1 | 1 | 1 | |
| Intermediate | 1 | 2 | 3 | 1/3 | 1/2 | 1 | |
| Moderately Preferred | 2 | 3 | 4 | 1/4 | 1/3 | 1/2 | |
| Intermediate | 3 | 4 | 5 | 1/5 | 1/4 | 1/3 | |
| Strongly Preferred | 4 | 5 | 6 | 1/6 | 1/5 | 1/4 | |
| Intermediate | 5 | 6 | 7 | 1/7 | 1/6 | 1/5 | |
| Very Strongly Preferred | 6 | 7 | 8 | 1/8 | 1/7 | 1/6 | |
| Intermediate | 7 | 8 | 9 | 1/9 | 1/8 | 1/7 | |
| Extremely Preferred | 9 | 9 | 9 | 1/9 | 1/9 | 1/9 | |
| Linguistic Scale | Symbol | TFN |
|---|---|---|
| Extremely Poor | EP | |
| Very Poor | VP | |
| Poor | P | |
| Medium–Poor | MP | |
| Medium | M | |
| Medium–Good | MG | |
| Good | G | |
| Very Good | VG | |
| Extremely Good | EG |
| Dimensions | Material (A) | Printing Process (B) | Design (C) | Management (D) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| l | m | U | l | m | u | l | m | u | l | m | u | |
| Material (A) | 1 | 1 | 1 | 1/3 | 1/2 | 1 | 6 | 7 | 8 | 5 | 6 | 7 |
| Printing Process (B) | 1 | 2 | 3 | 1 | 1 | 1 | 7 | 8 | 9 | 4 | 5 | 6 |
| Design (C) | 1/8 | 1/7 | 1/6 | 1/9 | 1/8 | 1/7 | 1 | 1 | 1 | 1/5 | 1/4 | 1/3 |
| Management (D) | 1/7 | 1/6 | 1/5 | 1/6 | 1/5 | 1/4 | 3 | 4 | 5 | 1 | 1 | 1 |
| Dimensions | Computation Process | Results | ||
|---|---|---|---|---|
| Material (A) | 1.778 | 2.141 | 2.736 | |
| Printing Process (B) | 2.300 | 2.991 | 3.568 | |
| Design (C) | 0.230 | 0.258 | 0.298 | |
| Management (D) | 0.517 | 0.604 | 0.707 | |
| Total | 4.825 | 5.994 | 7.309 | |
| Dimensions | Computation Process | Results | ||
|---|---|---|---|---|
| Material (A) | 0.243 | 0.357 | 0.567 | |
| Printing Process (B) | 0.315 | 0.499 | 0.739 | |
| Design (C) | 0.031 | 0.043 | 0.062 | |
| Management (D) | 0.071 | 0.101 | 0.147 | |
| Dimensions | Computation Process | Results |
|---|---|---|
| Material (A) | 0.389 | |
| Printing Process (B) | 0.518 | |
| Design (C) | 0.045 | |
| Management (D) | 0.106 | |
| Total | 1.058 |
| Dimensions | Computation Process | Results |
|---|---|---|
| Environment (A) | 0.368 | |
| Society (B) | 0.489 | |
| Production (C) | 0.043 | |
| Management (D) | 0.100 | |
| Total | 1.000 |
| Dimensions | Material | Printing Process | Design | Management | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| l | m | u | l | m | u | l | m | u | l | m | u | ||
| Material | 1 | 1 | 1 | 1/3 | 1/2 | 1 | 6 | 7 | 8 | 5 | 6 | 7 | 0.368 |
| Printing Process | 1 | 2 | 3 | 1 | 1 | 1 | 7 | 8 | 9 | 4 | 5 | 6 | 0.489 |
| Design | 1/8 | 1/7 | 1/6 | 1/9 | 1/8 | 1/7 | 1 | 1 | 1 | 1/5 | 1/4 | 1/3 | 0.043 |
| Management | 1/7 | 1/6 | 1/5 | 1/6 | 1/5 | 1/4 | 3 | 4 | 5 | 1 | 1 | 1 | 0.100 |
| Total | 1 | ||||||||||||
| Dimensions | A1 | A2 | A3 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| l | m | u | l | m | u | l | m | u | ||
| A1 | 1 | 1 | 1 | 1/3 | 1/2 | 1 | 3 | 4 | 5 | 0.355 |
| A2 | 1 | 2 | 3 | 1 | 1 | 1 | 4 | 5 | 6 | 0.549 |
| A3 | 1/5 | 1/4 | 1/3 | 1/6 | 1/5 | 1/4 | 1 | 1 | 1 | 0.097 |
| Total | 1 | |||||||||
| Dimensions | B1 | B2 | B3 | B4 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| l | m | u | l | m | u | l | m | u | l | m | u | ||
| B1 | 1 | 1 | 1 | 4 | 5 | 6 | 2 | 3 | 4 | 1 | 2 | 3 | 0.470 |
| B2 | 1/6 | 1/5 | 1/4 | 1 | 1 | 1 | 1/4 | 1/3 | 1/2 | 1/3 | 1/2 | 1 | 0.093 |
| B3 | 1/4 | 1/3 | 1/2 | 2 | 3 | 4 | 1 | 1 | 1 | 1 | 2 | 3 | 0.246 |
| B4 | 1/3 | 1/2 | 1 | 1 | 2 | 3 | 1/3 | 1/2 | 1 | 1 | 1 | 1 | 0.191 |
| Total | 1 | ||||||||||||
| Dimensions | C1 | C2 | C3 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| l | m | u | l | m | u | l | m | u | ||
| C1 | 1 | 1 | 1 | 1/4 | 1/3 | 1/2 | 1/7 | 1/6 | 1/5 | 0.094 |
| C2 | 2 | 3 | 4 | 1 | 1 | 1 | 1/5 | 1/4 | 1/3 | 0.220 |
| C3 | 5 | 6 | 7 | 3 | 4 | 5 | 1 | 1 | 1 | 0.686 |
| Total | 1 | |||||||||
| Dimensions | D1 | D2 | D3 | D4 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| l | m | u | l | m | u | l | m | u | l | m | u | ||
| D1 | 1 | 1 | 1 | 1/3 | 1/2 | 1 | 3 | 4 | 5 | 1/3 | 1/2 | 1 | 0.240 |
| D2 | 1 | 2 | 3 | 1 | 1 | 1 | 2 | 3 | 4 | 1 | 1 | 1 | 0.334 |
| D3 | 1/5 | 1/4 | 1/3 | 1/4 | 1/3 | 1/2 | 1 | 1 | 1 | 1/4 | 1/3 | 1/2 | 0.093 |
| D4 | 1 | 2 | 3 | 1 | 1 | 1 | 2 | 3 | 4 | 1 | 1 | 1 | 0.334 |
| Total | 1 | ||||||||||||
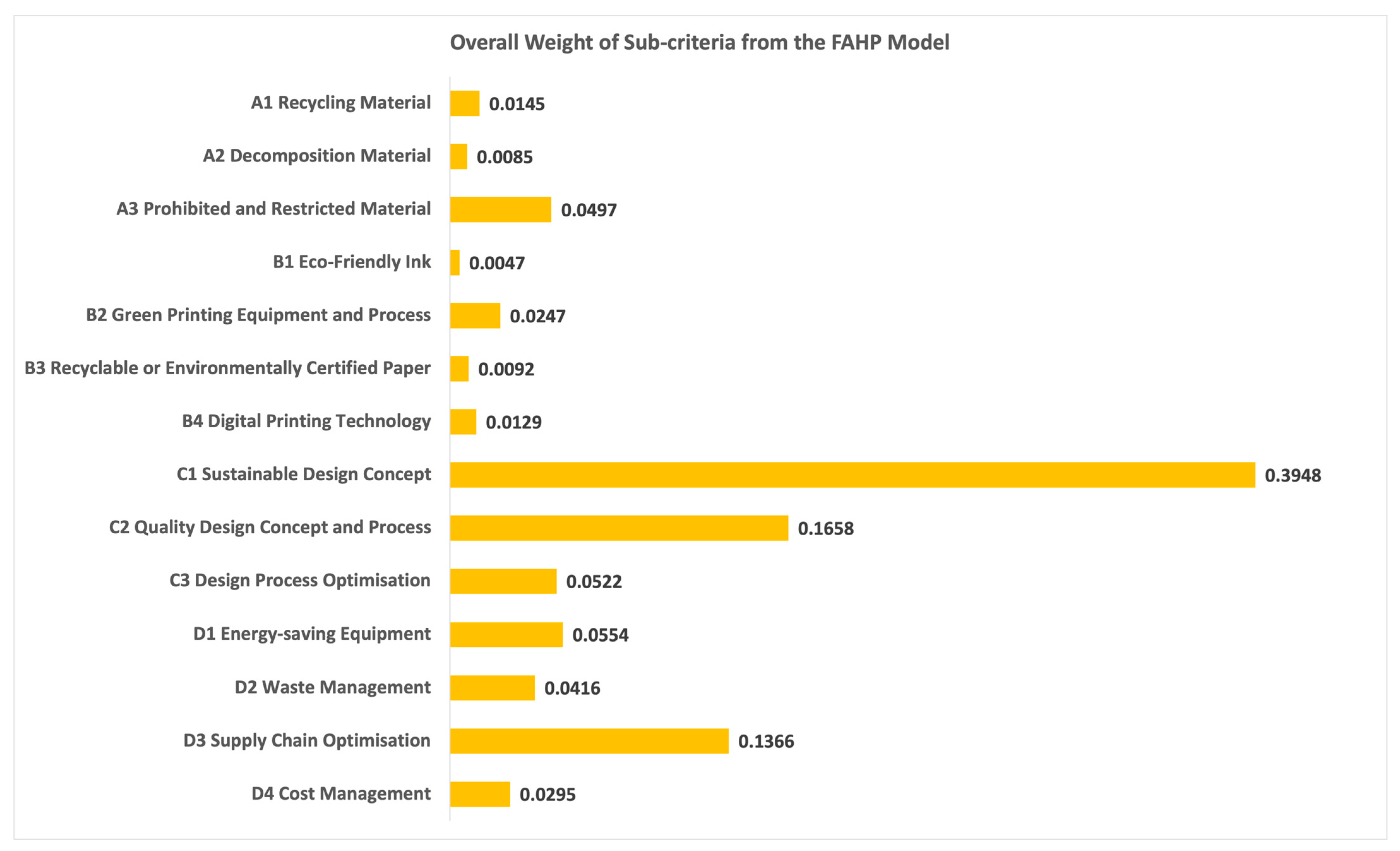
| Indicators | Description | Fuzzy Weight () | ||
|---|---|---|---|---|
| A1 | Recycling Material | 0.210 | 0.333 | 0.588 |
| A2 | Decomposition Material | 0.333 | 0.570 | 0.901 |
| A3 | Prohibited and Restricted Material | 0.068 | 0.097 | 0.150 |
| B1 | Eco-Friendly Ink | 0.263 | 0.488 | 0.846 |
| B2 | Green Printing Equipment and Process | 0.054 | 0.089 | 0.173 |
| B3 | Recyclable or Environmentally Certified Paper | 0.132 | 0.248 | 0.455 |
| B4 | Digital Printing Technology | 0.090 | 0.175 | 0.382 |
| C1 | Sustainable Design Concept | 0.068 | 0.091 | 0.131 |
| C2 | Quality Design Concept and Process | 0.152 | 0.218 | 0.312 |
| C3 | Design Process Optimization | 0.510 | 0.691 | 0.926 |
| D1 | Energy-saving Equipment | 0.132 | 0.220 | 0.431 |
| D2 | Waste Management | 0.207 | 0.345 | 0.536 |
| D3 | Supply Chain Optimization | 0.058 | 0.090 | 0.155 |
| D4 | Cost Management | 0.207 | 0.345 | 0.536 |
| Sub-Criteria | ALT 1 | ALT 2 | ALT 3 | ALT 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| l | m | u | l | m | U | l | m | u | l | m | u | |
| A1 | 5 | 7 | 7 | 1 | 3 | 3 | 1 | 1 | 3 | 3 | 3 | 5 |
| A2 | 5 | 5 | 7 | 3 | 5 | 5 | 1 | 3 | 3 | 1 | 3 | 3 |
| A3 | 7 | 9 | 9 | 3 | 3 | 5 | 1 | 3 | 3 | 3 | 5 | 5 |
| B1 | 7 | 9 | 9 | 1 | 3 | 3 | 1 | 3 | 3 | 3 | 3 | 5 |
| B2 | 7 | 7 | 9 | 3 | 5 | 5 | 1 | 1 | 3 | 3 | 3 | 5 |
| B3 | 7 | 7 | 9 | 3 | 3 | 5 | 1 | 3 | 3 | 1 | 3 | 3 |
| B4 | 5 | 7 | 7 | 3 | 5 | 5 | 1 | 1 | 1 | 3 | 5 | 5 |
| C1 | 5 | 5 | 7 | 3 | 3 | 5 | 1 | 1 | 3 | 1 | 3 | 3 |
| C2 | 5 | 5 | 7 | 3 | 5 | 5 | 1 | 1 | 3 | 3 | 3 | 5 |
| C3 | 7 | 9 | 9 | 5 | 7 | 7 | 1 | 3 | 3 | 3 | 5 | 5 |
| D1 | 7 | 7 | 9 | 5 | 5 | 7 | 3 | 3 | 5 | 3 | 5 | 5 |
| D2 | 7 | 7 | 9 | 3 | 5 | 5 | 3 | 3 | 5 | 5 | 7 | 7 |
| D3 | 7 | 7 | 9 | 5 | 7 | 7 | 1 | 3 | 3 | 3 | 5 | 5 |
| D4 | 3 | 5 | 5 | 3 | 5 | 5 | 3 | 3 | 5 | 5 | 5 | 7 |
| Sub-Criteria | ALT 1 | ALT 2 | ALT 3 | ALT 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| l | m | u | l | m | u | l | m | u | l | m | u | |
| A1 | 0.556 | 0.778 | 0.778 | 0.143 | 0.429 | 0.429 | 0.200 | 0.200 | 0.600 | 0.429 | 0.429 | 0.714 |
| A2 | 0.556 | 0.556 | 0.778 | 0.429 | 0.714 | 0.714 | 0.200 | 0.600 | 0.600 | 0.143 | 0.429 | 0.429 |
| A3 | 0.778 | 1.000 | 1.000 | 0.429 | 0.429 | 0.714 | 0.200 | 0.600 | 0.600 | 0.429 | 0.714 | 0.714 |
| B1 | 0.778 | 1.000 | 1.000 | 0.143 | 0.429 | 0.429 | 0.200 | 0.600 | 0.600 | 0.429 | 0.429 | 0.714 |
| B2 | 0.778 | 0.778 | 1.000 | 0.429 | 0.714 | 0.714 | 0.200 | 0.200 | 0.600 | 0.429 | 0.429 | 0.714 |
| B3 | 0.778 | 0.778 | 1.000 | 0.429 | 0.429 | 0.714 | 0.200 | 0.600 | 0.600 | 0.143 | 0.429 | 0.429 |
| B4 | 0.556 | 0.778 | 0.778 | 0.429 | 0.714 | 0.714 | 0.200 | 0.200 | 0.200 | 0.429 | 0.714 | 0.714 |
| C1 | 0.556 | 0.556 | 0.778 | 0.429 | 0.429 | 0.714 | 0.200 | 0.200 | 0.600 | 0.143 | 0.429 | 0.429 |
| C2 | 0.556 | 0.556 | 0.778 | 0.429 | 0.714 | 0.714 | 0.200 | 0.200 | 0.600 | 0.429 | 0.429 | 0.714 |
| C3 | 0.778 | 1.000 | 1.000 | 0.714 | 1.000 | 1.000 | 0.200 | 0.600 | 0.600 | 0.429 | 0.714 | 0.714 |
| D1 | 0.778 | 0.778 | 1.000 | 0.714 | 0.714 | 1.000 | 0.600 | 0.600 | 1.000 | 0.429 | 0.714 | 0.714 |
| D2 | 0.778 | 0.778 | 1.000 | 0.429 | 0.714 | 0.714 | 0.600 | 0.600 | 1.000 | 0.714 | 1.000 | 1.000 |
| D3 | 0.778 | 0.778 | 1.000 | 0.714 | 1.000 | 1.000 | 0.200 | 0.600 | 0.600 | 0.429 | 0.714 | 0.714 |
| D4 | 0.333 | 0.556 | 0.556 | 0.429 | 0.714 | 0.714 | 0.600 | 0.600 | 1.000 | 0.714 | 0.714 | 1.000 |
| Sub-Criteria | ALT 1 | ALT 2 | ALT 3 | ALT 4 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| l | m | u | l | m | u | l | m | u | L | m | u | |
| A1 | 0.117 | 0.259 | 0.457 | 0.030 | 0.143 | 0.252 | 0.042 | 0.067 | 0.353 | 0.090 | 0.143 | 0.420 |
| A2 | 0.185 | 0.316 | 0.701 | 0.143 | 0.407 | 0.643 | 0.067 | 0.342 | 0.541 | 0.048 | 0.244 | 0.386 |
| A3 | 0.053 | 0.097 | 0.150 | 0.029 | 0.042 | 0.107 | 0.014 | 0.058 | 0.090 | 0.029 | 0.070 | 0.107 |
| B1 | 0.205 | 0.488 | 0.846 | 0.038 | 0.209 | 0.363 | 0.053 | 0.293 | 0.508 | 0.113 | 0.209 | 0.604 |
| B2 | 0.042 | 0.069 | 0.173 | 0.023 | 0.064 | 0.123 | 0.011 | 0.018 | 0.104 | 0.023 | 0.038 | 0.123 |
| B3 | 0.102 | 0.193 | 0.455 | 0.056 | 0.106 | 0.325 | 0.026 | 0.149 | 0.273 | 0.019 | 0.106 | 0.195 |
| B4 | 0.050 | 0.136 | 0.297 | 0.039 | 0.125 | 0.273 | 0.018 | 0.035 | 0.076 | 0.039 | 0.125 | 0.273 |
| C1 | 0.038 | 0.051 | 0.102 | 0.029 | 0.039 | 0.094 | 0.014 | 0.018 | 0.079 | 0.010 | 0.039 | 0.056 |
| C2 | 0.085 | 0.121 | 0.242 | 0.065 | 0.155 | 0.223 | 0.030 | 0.044 | 0.187 | 0.065 | 0.093 | 0.223 |
| C3 | 0.397 | 0.691 | 0.926 | 0.364 | 0.691 | 0.926 | 0.102 | 0.415 | 0.556 | 0.219 | 0.494 | 0.661 |
| D1 | 0.103 | 0.171 | 0.431 | 0.094 | 0.157 | 0.431 | 0.079 | 0.132 | 0.431 | 0.057 | 0.157 | 0.308 |
| D2 | 0.161 | 0.268 | 0.536 | 0.089 | 0.246 | 0.383 | 0.124 | 0.207 | 0.536 | 0.148 | 0.345 | 0.536 |
| D3 | 0.045 | 0.070 | 0.155 | 0.042 | 0.090 | 0.155 | 0.012 | 0.054 | 0.093 | 0.025 | 0.064 | 0.111 |
| D4 | 0.069 | 0.192 | 0.298 | 0.089 | 0.246 | 0.383 | 0.124 | 0.207 | 0.536 | 0.148 | 0.246 | 0.536 |
| Alternatives | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| l | m | u | L | m | u | l | m | u | l | m | u | |
| ALT1 | 1.581 | 2.931 | 5.470 | 0.413 | 1.601 | 9.260 | 0.289 | 1.000 | 3.460 | 0.702 | 2.601 | 12.720 |
| ALT2 | 1.040 | 2.475 | 4.297 | 0.272 | 1.352 | 7.273 | 0.190 | 0.844 | 2.718 | 0.462 | 2.196 | 9.992 |
| ALT3 | 0.591 | 1.831 | 3.824 | 0.154 | 1.000 | 6.474 | 0.108 | 0.624 | 2.419 | 0.262 | 1.624 | 8.893 |
| ALT4 | 0.882 | 2.128 | 4.003 | 0.231 | 1.162 | 6.776 | 0.161 | 0.726 | 2.532 | 0.392 | 1.888 | 9.308 |
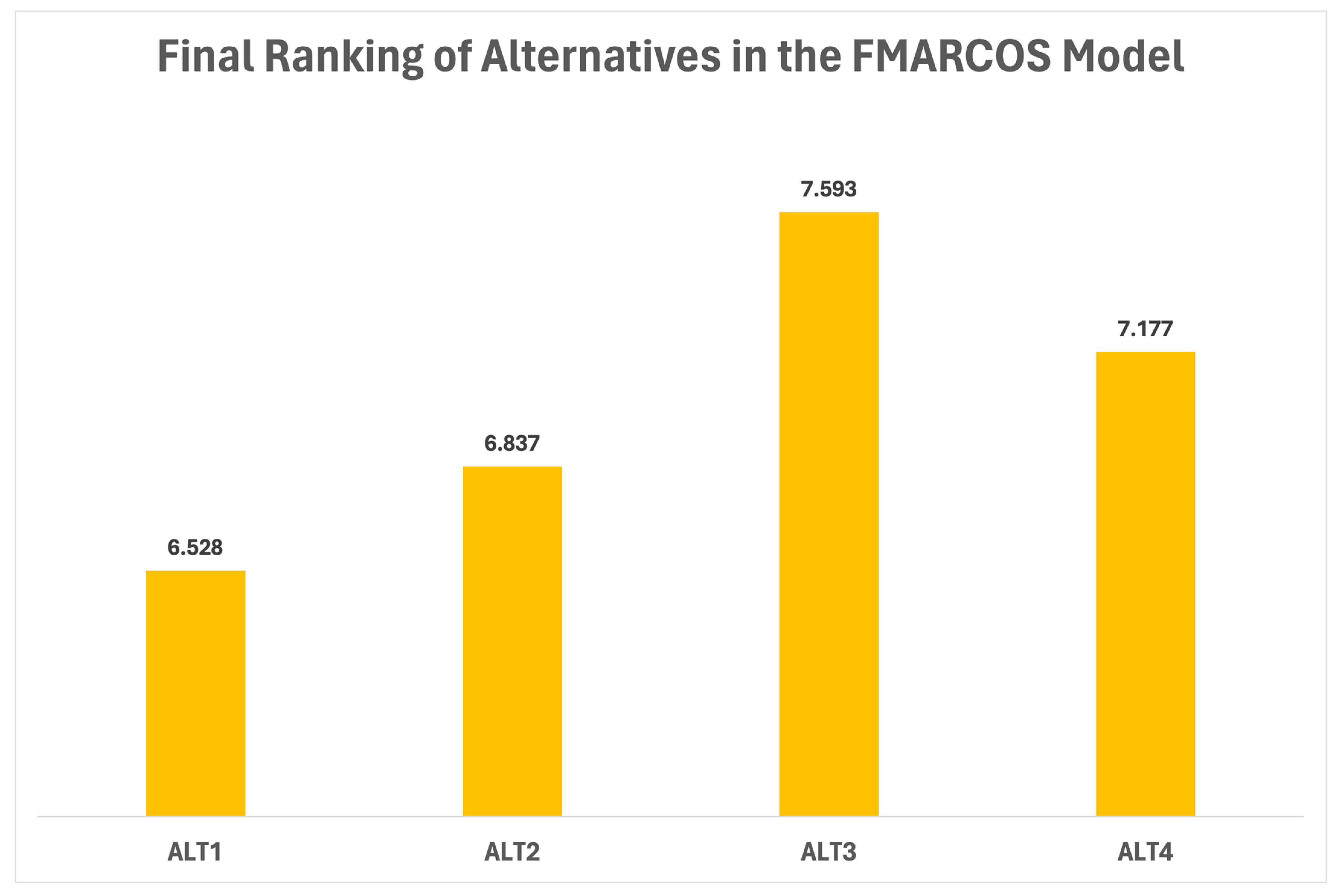
| Alternatives | Utility Degrees | ||||||
|---|---|---|---|---|---|---|---|
| ALT 1 | 2.680 | 1.292 | 0.675 | 0.325 | 6.528 | ||
| ALT 2 | 2.159 | 1.048 | 0.544 | 0.264 | 6.837 | ||
| ALT 3 | 1.771 | 0.838 | 0.446 | 0.211 | 7.593 | ||
| ALT 4 | 1.943 | 0.933 | 0.489 | 0.235 | 7.177 | ||
| Sub-Criteria | Scenarios | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| A1 | 0.0145 | 0.0000 | 0.0151 | 0.0181 | 0.0149 | 0.0163 | 0.0152 | 0.0155 | 0.0427 | 0.0264 | 0.0183 | 0.0185 | 0.0175 | 0.0243 | 0.0166 |
| A2 | 0.0085 | 0.0095 | 0.0000 | 0.0121 | 0.0088 | 0.0103 | 0.0092 | 0.0094 | 0.0367 | 0.0203 | 0.0122 | 0.0125 | 0.0115 | 0.0183 | 0.0106 |
| A3 | 0.0497 | 0.0508 | 0.0503 | 0.0000 | 0.0500 | 0.0515 | 0.0504 | 0.0506 | 0.0779 | 0.0616 | 0.0534 | 0.0537 | 0.0527 | 0.0595 | 0.0518 |
| B1 | 0.0047 | 0.0057 | 0.0053 | 0.0082 | 0.0000 | 0.0064 | 0.0053 | 0.0056 | 0.0328 | 0.0165 | 0.0084 | 0.0086 | 0.0076 | 0.0144 | 0.0068 |
| B2 | 0.0247 | 0.0257 | 0.0253 | 0.0282 | 0.0250 | 0.0000 | 0.0253 | 0.0256 | 0.0529 | 0.0365 | 0.0284 | 0.0286 | 0.0276 | 0.0344 | 0.0268 |
| B3 | 0.0092 | 0.0103 | 0.0098 | 0.0128 | 0.0095 | 0.0110 | 0.0000 | 0.0101 | 0.0374 | 0.0211 | 0.0129 | 0.0132 | 0.0122 | 0.0190 | 0.0113 |
| B4 | 0.0129 | 0.0139 | 0.0135 | 0.0164 | 0.0132 | 0.0147 | 0.0136 | 0.0000 | 0.0411 | 0.0247 | 0.0166 | 0.0168 | 0.0159 | 0.0226 | 0.0150 |
| C1 | 0.3948 | 0.3958 | 0.3954 | 0.3983 | 0.3951 | 0.3965 | 0.3954 | 0.3957 | 0.0000 | 0.4066 | 0.3985 | 0.3987 | 0.3977 | 0.4045 | 0.3969 |
| C2 | 0.1658 | 0.1668 | 0.1664 | 0.1693 | 0.1661 | 0.1676 | 0.1664 | 0.1667 | 0.1940 | 0.0000 | 0.1695 | 0.1697 | 0.1688 | 0.1755 | 0.1679 |
| C3 | 0.0522 | 0.0533 | 0.0528 | 0.0558 | 0.0526 | 0.0540 | 0.0529 | 0.0531 | 0.0804 | 0.0641 | 0.0000 | 0.0562 | 0.0552 | 0.0620 | 0.0543 |
| D1 | 0.0554 | 0.0564 | 0.0560 | 0.0589 | 0.0557 | 0.0571 | 0.0560 | 0.0563 | 0.0836 | 0.0672 | 0.0591 | 0.0000 | 0.0584 | 0.0651 | 0.0575 |
| D2 | 0.0416 | 0.0426 | 0.0422 | 0.0451 | 0.0419 | 0.0433 | 0.0422 | 0.0425 | 0.0697 | 0.0534 | 0.0453 | 0.0455 | 0.0000 | 0.0513 | 0.0437 |
| D3 | 0.1366 | 0.1376 | 0.1372 | 0.1401 | 0.1369 | 0.1383 | 0.1372 | 0.1375 | 0.1648 | 0.1484 | 0.1403 | 0.1405 | 0.1395 | 0.0000 | 0.1387 |
| D4 | 0.0295 | 0.0306 | 0.0301 | 0.0331 | 0.0299 | 0.0313 | 0.0302 | 0.0304 | 0.0577 | 0.0414 | 0.0333 | 0.0335 | 0.0325 | 0.0393 | 0.0000 |
| Alternatives | Scenarios | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
| ALT 1 | 6.8738 | 6.8576 | 7.6631 | 6.8400 | 6.8706 | 6.8259 | 6.8734 | 6.8279 | 6.6109 | 6.7619 | 6.8383 | 6.9798 | 6.9528 | 6.8676 | 7.0282 |
| ALT 2 | 5.8371 | 5.8397 | 5.6123 | 5.8543 | 5.8408 | 5.8012 | 5.8432 | 5.7959 | 5.6244 | 5.6354 | 5.7850 | 5.9102 | 5.9128 | 5.7199 | 5.9321 |
| ALT 3 | 4.4886 | 4.4823 | 4.8121 | 4.4761 | 4.4874 | 4.4701 | 4.4886 | 4.4707 | 4.3930 | 4.4475 | 4.4755 | 4.5319 | 4.5208 | 4.4887 | 4.5427 |
| ALT 4 | 5.3486 | 5.3372 | 5.9545 | 5.3342 | 5.3493 | 5.3226 | 5.3572 | 5.3076 | 5.3257 | 5.2270 | 5.3335 | 5.4295 | 5.3664 | 5.3385 | 5.4069 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-L. Sustainable Design Factors and Solutions Analysis and Assessment for the Graphic Design Industry: A Hybrid Fuzzy AHP–Fuzzy MARCOS Approach. Mathematics 2024, 12, 4014. https://doi.org/10.3390/math12244014
Lin C-L. Sustainable Design Factors and Solutions Analysis and Assessment for the Graphic Design Industry: A Hybrid Fuzzy AHP–Fuzzy MARCOS Approach. Mathematics. 2024; 12(24):4014. https://doi.org/10.3390/math12244014
Chicago/Turabian StyleLin, Chia-Liang. 2024. "Sustainable Design Factors and Solutions Analysis and Assessment for the Graphic Design Industry: A Hybrid Fuzzy AHP–Fuzzy MARCOS Approach" Mathematics 12, no. 24: 4014. https://doi.org/10.3390/math12244014
APA StyleLin, C.-L. (2024). Sustainable Design Factors and Solutions Analysis and Assessment for the Graphic Design Industry: A Hybrid Fuzzy AHP–Fuzzy MARCOS Approach. Mathematics, 12(24), 4014. https://doi.org/10.3390/math12244014









