Bioconvective Flow Characteristics of NEPCM–Water Nanofluid over an Inclined Cylinder in Porous Medium: An Extended Darcy Model Approach

Abstract

Bioconvection phenomena play a pivotal role in diverse applications, including the synthesis of biological polymers and advancements in renewable energy technologies. This study develops a comprehensive mathematical model to examine the effects of key parameters, such as the Lewis number (Lb), Peclet number (Pe), volume fraction ($\phi$), and angle of inclination $\left(\alpha \right)$, on the flow and heat transfer characteristics of a nanofluid over an inclined cylinder embedded in a non-Darcy porous medium. The investigated nanofluid comprises nano-encapsulated phase-change materials (NEPCMs) dispersed in water, offering enhanced thermal performance. The governing non-linear partial differential equations are transformed into dimensionless ordinary differential equations using similarity transformations and solved numerically via the Network Simulation Method (NSM) and an implicit Runge–Kutta method implemented through the bvp4c routine in MATLAB R2021a. Validation against the existing literature confirms the accuracy and reliability of the numerical approach, with strong convergence observed. Quantitative analysis reveals that an increase in the Peclet number reduces the shear stress at the cylinder wall by up to 18% while simultaneously enhancing heat transfer by approximately 12%. Similarly, the angle of inclination ($\alpha$) significantly boosts heat transmission rates. Additionally, higher Peclet and Lewis numbers, along with greater nanoparticle volume fractions, amplify the density gradient of microorganisms, intensifying the bioconvection process by nearly 15%. These findings underscore the critical interplay between bioconvection and transport phenomena, providing a framework for optimizing bioconvection-driven heat and mass transfer systems. The insights from this investigation hold substantial implications for industrial processes and renewable energy technologies, paving the way for improved efficiency in applications such as thermal energy storage and advanced cooling systems.

1. Introduction

Nanofluids are special types of engineered fluids in which a small number of nanosized particles are suspended in some working fluid to enhance the overall thermal conductivity of the fluid. Enhancing the thermal efficiency of fluids has been a subject of significant exploration from an energy-saving point of view to designing cooling devices. According to [1], using nanofluidic coolants in electronics saves energy and lowers pollution, resulting in reduced production costs. The authors of [2] studied the motion of nanofluid through an elongated cylinder while taking radiation and natural convection into account. The authors of [3] investigated the influence of composite nanostructures in nanofluids and used a statistical technique to evaluate the properties of copper- and graphene-type nanoparticles. The impact of thermal radiation due to heat transport, mechanism of slip flow, and wall suction on non-steady nanofluid with Lorentz force toward the wall in a stretched surface was investigated in [4]. Notably, researchers in [5,6,7,8] have scrutinized the boundary layer flow in nanofluid across stretched sheets (linear/non-linear) under various physical circumstances. The application of the Coriolis force on the dynamics of a Carreau–Yasuda spinning nanofluid subjected to the Darcy–Forchheimer model was investigated by [9]. The two-phase flow of Casson fluid with dust particles under the influence of Lorentz force has been studied in [10]. Although nanoparticles accelerate the heat transfer of a base fluid, they also have the drawback of reduced heat capacity, which is not good for many applications [11]. Temperature gradients along cooling fluids increase when fluids have low heat capacities. NEPCMs are special types of nanoparticles comprising a core and a shell, which are composed of phase-change materials. Due to the applications of phase-change materials, improvement in these materials has raised interest among many researchers. The authors of [12] explored the advantages of using PCM energy storage and concluded that the application of NEPCMs in cold storage could save energy, while [13] focused on the key factors of nanoparticles such as size, shape, and core–shell ratio of nanoparticles to study the heat transfer of PCMs. Finally, hydrodynamics and heat transfer in micro/nanochannels filled with porous media for different porosities and Knudsen numbers were studied in [14].

Bioconvection is a significant mode of convection in which the microorganisms move collectively in response to a natural or imposed stimulus. Enhancement in the mass transfer and improved stability of nanofluid, along with microscale mixing, are some of the advantages of suspending motile microorganisms in nanofluids [15]. There is a broad range of uses for bioconvection, including medicine administration in humans, biological systems, biotechnology, and the creation of effective cooling devices. Microorganisms induce convection in which the cells and oxygen are transported from higher to lower concentration regions. The phenomenon of bioconvection in nanofluids is primarily addressed by [16,17]. The combined effect of Brownian motion and the thermophoretic force on the motion of oscillatory nanofluid by employing Buongiorno’s model was explored in [18], while the authors of [19] considered the incompressible flow of nanofluid between two parallel surfaces and found that the buoyancy force elevates the velocity of nanofluids. The aforementioned studies have primarily focused on recognizing nanofluid bioconvection; however, the effects of Darcy–Forchheimer, Lorentz force, and endothermic and exothermic reactions on the bioconvective flow of nanofluid may provide some understanding of the intricate behavior of self-propelled microorganisms in nanofluid in the application of an external magnetic field for industrial and medicinal applications [20,21,22,23,24].

By examining the above studies, it was found that very little attention has been given to the bioconvective flow of nanofluid flowing over an inclined stretching cylinder. So, the prime objective of this investigation is to study the impact of bioconvection on heat and momentum diffusivity with a non-Darcy background. The effect of the non-dimensional parameters arising in the dimensionless ODEs of the bioconvection equation on the physical variables is investigated and discussed. The novelty of this investigation is to study the impact of the Soret and Dufour effects on the flow of NEPCM–water nanofluid under the influence of a magnetic field. The stability and convergence of the numerical scheme are studied, and the simulation results are compared with the results of existing studies.

Throughout the analysis, an attempt is made to discuss the following points:

• What are the factors that cause variations in the flow pattern of nanofluid?
• Does bioconvection help in controlling the fluid temperature and cooling of the surface?
• Does nanofluidic properties influence the shear force and rate of heat diffusion from the surface?
• How are NEPCM nanoparticles different from other nanoparticles?

As no analytical solution has yet been presented to the scientific community for the mathematical model posed, to verify and validate the network method, and also to perform a comparison between the efficiency of this method and common numerical methods, we also solved this problem using the implicit Runge–Kutta method via the bvp4c MATLAB routine. In general, the electrical analogy of the network method implies a formal equivalence between a system of DDEs and an electrical network, so that once the strongly coupled electrical circuits are completed, the numerical solution is obtained using circuit software. There are different alternatives for this last choice, but in this work, we selected the free software LT Spice version 24 [25], for its ease of use and its powerful numerical codes.

2. Mathematical Formulation

A two-dimensional time-independent flow of a Newtonian fluid containing motile microbes over an extending cylinder immersed in a porous matrix was taken into consideration. The radius of the cylinder was assumed to be a, and the cylindrical coordinates $(\mathit{x},\mathit{r})$ were considered in axial and radial directions, respectively. The cylinder was linearly stretched in the x direction with a velocity of ${\mathit{u}}_{\mathit{w}}=bx$. The external Lorentz force was applied in the radial direction. The prescribed heat flux, concentration flux, and microorganism flux were assumed at the surface of the cylinder, while ${\mathit{T}}_{\infty },{\mathit{C}}_{\infty },$ and ${\mathit{N}}_{\infty }$ were defined as the ambient temperature, concentration, and microorganism, respectively. The physical configuration of the current flow problem is given in Figure 1.

The basic assumptions made throughout the analysis are as follows:

• Porous material was considered to be a non-Darcy medium with Forchheimer;
• Fluid was laminar, viscous, incompressible, and electrically conductive;
• The induced magnetic field was neglected;
• The fluid was assumed to be Newtonian, and the flow was laminar two-dimensional, where the cylinder was assumed to be infinitely long;
• The porous medium was assumed to be homogeneous and isotropic, with a constant permeability;
• The influence of pressure gradient was neglected.

With the above considerations and assumptions, a set of governing equations was established as follows [26]:

$${\displaystyle \frac{\partial }{\partial x}}\left(ru\right)+{\displaystyle \frac{\partial }{\partial r}}\left(rv\right)=0,$$

(1)

$$\begin{gathered} u{\displaystyle \frac{\partial u}{\partial x}}+v{\displaystyle \frac{\partial u}{\partial r}}={\nu }_{nf}\left[{\displaystyle \frac{{\partial }^{2}u}{\partial r^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial u}{\partial r}}\right]-{\displaystyle \frac{{\sigma }_{nf}{B}_0^2}{ {\rho }_{nf}}}u-{\displaystyle \frac{{\nu }_{nf}}{k}}u-{\displaystyle \frac{C_b}{\sqrt{k}}}{u}^2+ \\ {\displaystyle \frac{1}{{\rho }_{nf}}}\left[\begin{array}{c}g\left(T-T_{\infty }\right)\rho {\beta }_{nf}\left(1-C_{\infty }\right)cos\alpha +\\ g\left(C_{\infty }-C\right)\left({\rho }_p-\rho \right)cos\alpha -\left({\rho }_m-{\rho }_p\right)\left(N_{\infty }-N\right)g{\gamma }^{*}cos\alpha \end{array}\right], \end{gathered}$$

(2)

$$\left(u{\displaystyle \frac{\partial T}{\partial x}}+v{\displaystyle \frac{\partial T }{\partial r}}\right)={\displaystyle \frac{{\kappa }_{nf}}{{\left(\rho C_p\right)}_{nf}}}\left[{\displaystyle \frac{{\partial }^{2}T}{\partial r^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial T}{\partial r}}\right]+\tau \left[D_B{\displaystyle \frac{\partial T}{\partial r}}{\displaystyle \frac{\partial C}{\partial r}}+{\displaystyle \frac{D_T}{T_{\infty }}}{\left({\displaystyle \frac{\partial T}{\partial r}}\right)}^2\right]+{\displaystyle \frac{{\sigma }_{nf}{B}_0^2}{{\left(\rho C_p\right)}_{nf}}}{u}^2,$$

(3)

$$\left(u{\displaystyle \frac{\partial C}{\partial x}}+v{\displaystyle \frac{\partial C }{\partial r}}\right)=D_B\left[{\displaystyle \frac{{\partial }^{2}C}{\partial r^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial C}{\partial r}}\right]+{\displaystyle \frac{D_T}{T_{\infty }}}\left[{\displaystyle \frac{{\partial }^{2}T}{\partial r^2}}+{\displaystyle \frac{1}{r}}{{\displaystyle \frac{\partial T}{\partial r}}}^2\right],$$

(4)

$$\left(u{\displaystyle \frac{\partial N}{\partial x}}+v{\displaystyle \frac{\partial N }{\partial r}}\right)=D_N\left[{\displaystyle \frac{{\partial }^{2}N}{\partial r^2}}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial N}{\partial r}}\right]+{\displaystyle \frac{\lambda W_c}{(C_w-C_{\infty })}}\left[{\displaystyle \frac{\partial C}{\partial r}}{\displaystyle \frac{\partial N}{\partial r}}+N{\displaystyle \frac{{\partial }^{2}C}{\partial r^2}}\right].$$

(5)

The associated constraints were as follows [26]:

$$\left\{\begin{array}{c}\left\{\begin{array}{c}u=u_w, v=0, T=T_w,\\ C=C_w, N=N_w\end{array}\right\} at r=a,\\ \left\{u=0, v=0, T_{\infty }, C_{\infty }, N_{\infty }\right\} at r\to \infty \end{array}\right\}.$$

(6)

The following transformations [26] were used to convert the above equations to a non-dimensional form:

$$\left\{\begin{array}{c}u=bx{f}^{\prime }\left(\eta \right), v=-{\displaystyle \frac{a}{r}} {\sqrt{b\nu }}_{bf}f\left(\eta \right),\eta ={\displaystyle \frac{\left(r^2-a^2\right)}{2a}}\sqrt{{\displaystyle \frac{b}{{\nu }_{bf}}}},\\ \theta ={\displaystyle \frac{T-T_{\infty }}{T_w-T_{\infty }}}, \varphi ={\displaystyle \frac{C-C_{\infty }}{C_w-C_{\infty }}}, \chi ={\displaystyle \frac{N-N_{\infty }}{N_w-N_{\infty }}}\end{array}\right\}$$

(7)

Employing Equation (7), Equations (2)–(6) become

$$\begin{gathered} {\displaystyle \frac{{\nu }_{nf}}{{\nu }_{bf}}}\left\{\left(1+2ϵ\eta \right)f^{‴}+2ϵf^{″}\right\}-{\displaystyle \frac{{\sigma }_{nf}}{{\sigma }_{bf}}}{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}} M^2{f}^{\prime }-{f^{\prime }}^2-{\displaystyle \frac{{\nu }_{nf}}{{\nu }_{bf}}}K{f}^{\prime }-Fr{f^{\prime }}^2+f{f}^{″}+ \\ MCcos\alpha \left({\displaystyle \frac{{\beta }_{nf}}{{\beta }_f}}\theta -{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}}Nr\varphi +{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}}NC\chi \right)=0, \end{gathered}$$

(8)

$$\begin{gathered} {\displaystyle \frac{{\kappa }_{nf}}{{\kappa }_{bf}}}{\displaystyle \frac{{\left(\rho C_p\right)}_{bf}}{{\left(\rho C_p\right)}_{nf}}}{\displaystyle \frac{1}{Pr}}\left(\left(1+2ϵ\eta \right){\theta }^{″}+2ϵ{\theta }^{\prime }\right)+Nb\left(1+2ϵ\eta \right){\theta }^{\prime }{\varphi }^{\prime }+Nt\left(1+2ϵ\eta \right){{\theta }^{\prime }}^2+ \\ f{\theta }^{\prime }+{\displaystyle \frac{{\sigma }_{nf}}{{\sigma }_{bf}}}{\displaystyle \frac{{\left(\rho C_p\right)}_{bf}}{{\left(\rho C_p\right)}_{nf}}}{M}^{2}Ec{f^{\prime }}^2=0, \end{gathered}$$

(9)

$$\left(1+2ϵ\eta \right){\varphi }^{″}+2ϵ{\varphi }^{\prime }+Scf{\varphi }^{\prime }+{\displaystyle \frac{Nt}{Nb}}\left(\left(1+2ϵ\eta \right){\theta }^{″}+2ϵ{\theta }^{\prime }\right)=0,$$

(10)

$$\left(1+2ϵ\eta \right){\chi }^{″}+LbPrf{\chi }^{\prime }+2ϵ{\chi }^{\prime }-Pe\left[\begin{array}{c}\left(1+2ϵ\eta \right){\chi }^{\prime }{\varphi }^{\prime }+\\ \left(\Delta N+\chi \right)\left(\left(1+2ϵ\eta \right){\varphi }^{″}+ϵ{\varphi }^{\prime }\right)\end{array}\right]=0$$

(11)

When subjected to non-dimensional constraints, we have

$$\left\{\begin{array}{c}f\left(0\right)=0, f^{\prime }\left(0\right)=1, \theta \left(0\right)=1, \\ \varphi \left(0\right)=1, \chi \left(0\right)=1\\ f^{\prime }\left(\infty \right)=0, \theta \left(\infty \right)=0, \varphi \left(\infty \right)=0.\end{array}\right\},$$

(12)

where prime denotes derivative with respect to η, and the non-dimensional parameters involved are defined as follows:

$$\left\{\begin{array}{c}ϵ=\sqrt{{\displaystyle \frac{{\nu }_{bf}}{b{a}^2}}}, M^2={\displaystyle \frac{{\sigma }_{bf}{B}_0^2}{{\rho }_{bf}b}}, Fr={\displaystyle \frac{C_{b}x}{\sqrt{k}}}, K={\displaystyle \frac{{\nu }_{bf}}{kb}},\\ Pr={\displaystyle \frac{{\nu }_{bf}}{\alpha }}, Nb={\displaystyle \frac{\tau D_B\left(C_w-C_{\infty }\right)}{{\nu }_{bf}}}, Nt={\displaystyle \frac{\tau D_T\left(T_w-T_{\infty }\right)}{{\nu }_{bf}{T}_{\infty }}},\\ Sc={\displaystyle \frac{{\nu }_{bf}}{D_B}}, Lb={\displaystyle \frac{\alpha }{D_N}}, Pe={\displaystyle \frac{\lambda W_c}{D_N}}, \Delta N={\displaystyle \frac{N_{\infty }}{\left(N_w-N_{\infty }\right)}},\end{array}\right\}.$$

(13)

where ϵ is the curvature parameter, M is the magnetic parameter, Fr is the Forchheimer number, K is the permeability constant, Nb is the Brownian motion number, Pr is the Prandtl number, Sc is the Schmidt number, Lb is the bioconvection Lewis number, Pe is the bioconvection Peclet number, ΔN is the density ratio, and Nt is the thermophoresis number.

The dimensional form of the drag coefficient, the heat transfer rate, the rate of mass transfer, and the change in the density number of motile microorganisms are as follows:

$$C_{fx}={\displaystyle \frac{{\left.{\mu }_{nf}\frac{\partial u}{\partial r}\right|}_{r=R}}{\rho u_w^2}}, N{u}_x={\displaystyle \frac{x{q}_w}{k_{nf}\left(T_w-T_{\infty }\right)}}, S{h}_x={\displaystyle \frac{x{j}_w}{D_B}}\left(C_w-C_{\infty }\right), N{n}_x={\displaystyle \frac{x{q}_n}{D_N\Delta N}} .$$

(14)

with,

$$w={\left.{-\kappa }_{nf}{\displaystyle \frac{\partial T}{\partial r}}\right|}_{r=R}, j_w={\left.-D_B{\displaystyle \frac{\partial C}{\partial r}}\right|}_{r=R}, q_n={-D_N{\displaystyle \frac{\partial N}{\partial r}}⌋}_{r=a },$$

(15)

Employing (7), (14) becomes

$$\left\{\begin{array}{c}R{e}_x^{{\displaystyle \frac{1}{2}}}C{f}_x=-{\displaystyle \frac{{\mu }_{nf}}{{\mu }_{bf}}}{f}^{″}\left(0\right), R{e}_x^{-{\displaystyle \frac{1}{2}}}S{h}_x=-{\varphi }^{\prime }\left(0\right), \\ R{e}_x^{-{\displaystyle \frac{1}{2}}}N{u}_x=-{\displaystyle \frac{{\kappa }_{nf}}{{\kappa }_{bf}}}{\theta }^{\prime }\left(0\right), R{e}_x^{-{\displaystyle \frac{1}{2}}}N{n}_x=-{\chi }^{\prime }\left(0\right)\end{array}\right\}$$

(16)

3. Thermophysical Properties of the Nanofluid

The thermophysical characteristics of nanofluid are assessed with some thermophysical models. The density of NEPCM–water nanofluid can be estimated by the following correlation [27]:

$${\rho }_{nf}=\left(1+\phi \right){\rho }_{bf}+\phi {\rho }_{NEPCM}$$

(17)

where the subscript f indicates the base fluid, and φ is the mass concentration. The NEPCM nanoparticles consist of a shell and a core PCM [27,28]. Therefore, the density of NEPCM should be evaluated in terms of the density of the shell and the core. Following [27,29], the density of NEPCM nanoparticles is evaluated using the following formula:

$${\rho }_{NEPCM}={\displaystyle \frac{\left(1+t\right){\rho }_c{\rho }_s}{{\rho }_s+{t\rho }_c }}$$

(18)

where the density of the core and shell are ρ_c and ρ_s, respectively, and t is the weight ratio of the core–shell. The density of the core PCM is the mean density of solid and liquid phases.

The assumption of thermal equilibrium between the NEPCM and the water supports deriving the effective heat capacity. The effective heat capacity is given as follows:

$${\left(\rho C_p\right)}_{NEPCM}=\left\{\left(1+\phi \right)+\lambda \phi +{\displaystyle \frac{1}{\delta Ste}}\phi F\right\}{\left(\rho C_p\right)}_{bf}$$

(19)

where F is the non-dimensional fusion function defined as follows:

$$F={\displaystyle \frac{\pi }{2}}\sin \left({\displaystyle \frac{\pi }{\delta }}\left(\theta -{\theta }_f+{\displaystyle \frac{\delta }{2}}\right)\right)\times \left\{\begin{array}{c}0, \theta <{\theta }_f-{\displaystyle \frac{\delta }{2}}\\ 1, { \theta }_f-{\displaystyle \frac{\delta }{2}}<\theta <{\theta }_f+{\displaystyle \frac{\delta }{2}}\\ 0, {\theta }_f+{\displaystyle \frac{\delta }{2}}<\theta \end{array}\right.$$

(20)

where ${\theta }_f={\displaystyle \frac{T_f-T_{\mathrm{\infty }}}{T_w-T_{\mathrm{\infty }}}}$ is the fusion temperature.

The effective dynamic viscosity and thermal conductivity of NEPCM–water nanofluid is given by the following equations:

$${\mu }_{nf}=\left(1+Nv\phi \right){\mu }_{bf}$$

(21)

$${\kappa }_{nf}=\left(1+Nc\phi \right){\kappa }_{bf}$$

(22)

The thermophysical properties of base fluid and NEPCM nanoparticles are given in

Table 1. Thermophysical properties of $NEPCM$ nanoparticles and water at $303 \mathrm{K}$.

Substance	$\mathsf{\rho }\left(\frac{\mathbf{k}\mathbf{g}}{{\mathbf{m}}^3}\right)$	${\mathbf{C}}_{\mathbf{p}}\left(\frac{\mathbf{J}}{\mathbf{k}\mathbf{g} \mathbf{K}}\right)$	$\mathsf{\kappa }\left(\frac{\mathbf{W}}{\mathbf{m}\mathbf{K}}\right)$	$\mathsf{\mu }·{10}^{-6}\left(\frac{\mathbf{k}\mathbf{g}}{\mathbf{m}\mathbf{s}}\right)$
Water	995.6	4180	0.615	796
Nonadecane (core)	721	2037	0.190	---
Polyurethane (shell)	786	1317	0.025	---

.

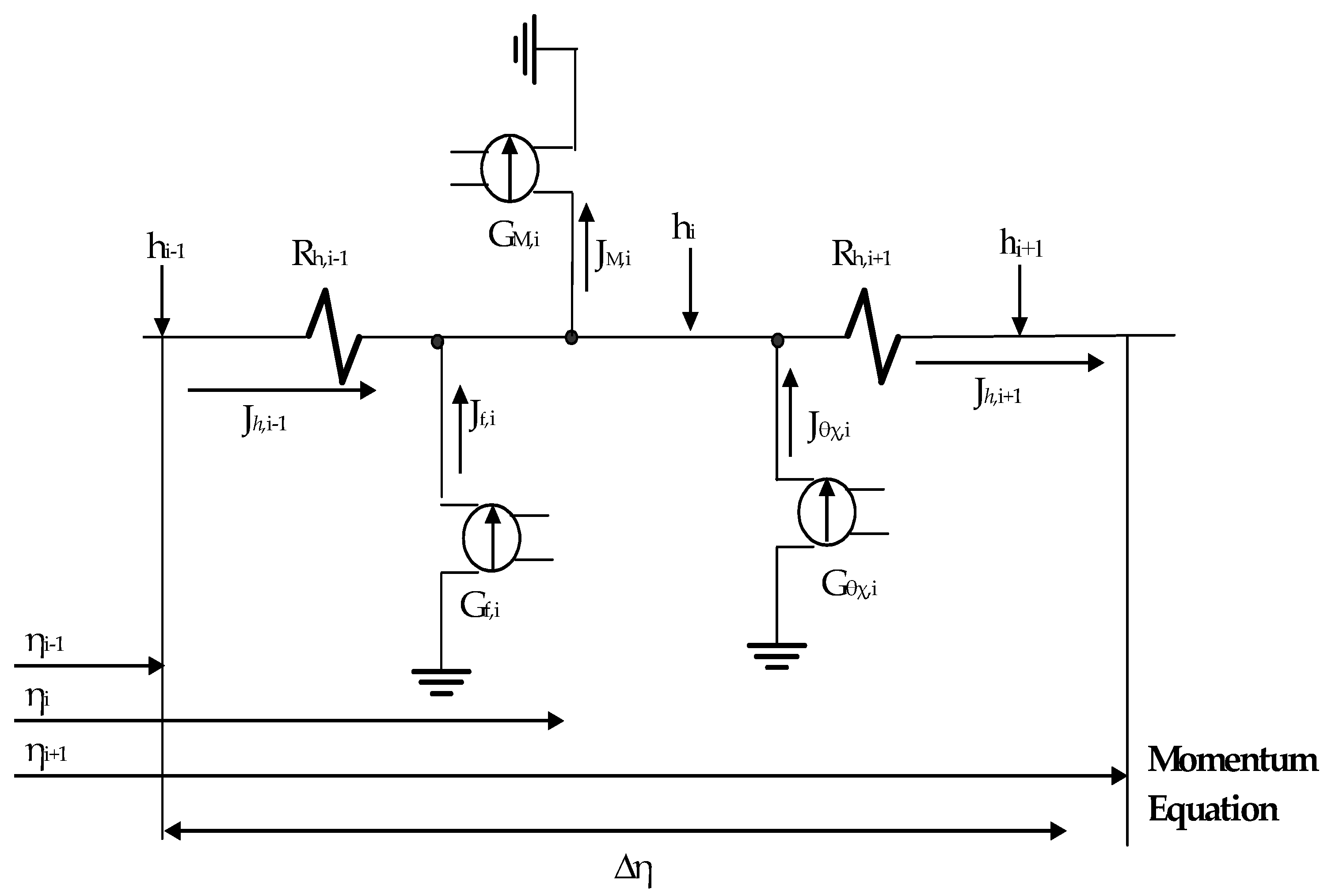
4. Numerical Solution

The governing non-linear coupled ODEs (8)–(11) with the boundary conditions (12) were tackled by means of the network simulation method (NSM) and using an implicit Runge–Kutta method via bvp4c MATLAB routine. The schemes require the conversion of the ODEs of a higher order into a system differential equation of the first order. The grid size for the solution of the current flow problem was taken to be 10⁻³ with relative tolerance of 10⁻⁶.

NSM: The discretization of the boundary–layer equations is based on the finite difference formulation, and only the discretization of the spatial coordinates is necessary, with the time remaining as a real continuous variable. Based on these equations, an electrical network circuit whose equations are formally equivalent to the discretized ones is designed. It is necessary to employ the electric analogy, according to which the variable voltage is equivalent to the velocities, temperature, concentration, and density of motile microorganisms, while the variable electric current (J) is equivalent to the spatial partial derivatives of these variables. The whole network must be converted into a suitable program that is solved using a computer code (electric circuits simulator), where the theorems of conservation and uniqueness of the flow and potential electrical variables (Kirchhoff laws) are satisfied.

Runge–Kutta Method via bvp4c (MATLAB): The bvp4c routine in MATLAB is a numerical solver specifically designed for solving boundary value problems (BVPs). It employs a collocation method with a built-in Runge–Kutta solver, which is implicit and adaptive, making it highly stable and accurate for stiff systems or problems with intricate boundary conditions. This method directly solves the discretized ordinary differential equations (ODEs) using adaptive mesh refinement, ensuring accuracy and efficiency.

Justification: Using NSM alongside the Runge–Kutta method via bvp4c provides a multifaceted computational approach to solving the boundary value problem. The NSM offers an efficient and intuitive means to model and discretize complex systems like the bioconvective flow in a porous medium, while the bvp4c solver ensures the mathematical consistency and numerical accuracy needed for precise boundary-value solutions. Together, they address the potential weaknesses of each method individually, ensuring reliable, validated, and high-quality solutions for complex fluid dynamics problems.

To solve the system defined by (8)–(11), we employed the network simulation method (NSM). This method has been used successfully in other works [30,31]. The concept of electrical analogy was applied to the spatially discretized equations and, subsequently, Kirchhoff’s second law, which indicates that the sum of currents in a node is equal to zero.

To achieve second-order in all equations, Equation (8) is written as follows:

$$\begin{gathered} {\displaystyle \frac{{\nu }_{nf}}{{\nu }_{bf}}}\left\{\left(1+2ϵ\eta \right)h^{″}+2ϵh^{\prime }\right\}-{\displaystyle \frac{{\sigma }_{nf}}{{\sigma }_{bf}}}{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}} M^{2}h-h^2-{\displaystyle \frac{{\nu }_{nf}}{{\nu }_{bf}}}Kh-Fr{h}^2+f h^{\prime }+ \\ MCcos\alpha \left({\displaystyle \frac{{\beta }_{nf}}{{\beta }_f}}\theta -{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}}Nr\varphi +{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}}NC\chi \right)=0, \end{gathered}$$

(23)

where df/dy = h. The transformed boundary conditions (12) now become

$$\left\{\begin{array}{c}f\left(0\right)=0, h\left(0\right)=1, \theta \left(0\right)=1, \\ \varphi \left(0\right)=1, \chi \left(0\right)=1\\ h\left(\mathrm{\infty }\right)=0, \theta \left(\mathrm{\infty }\right)=0, \varphi \left(\mathrm{\infty }\right)=0.\end{array}\right\},$$

(24)

Initially, the elementary cells of each discretized Equations (8)–(11) were developed, with a total of four cells. Next, the boundary conditions applicable to each elementary cell were modeled using discrete elements. The following currents were defined:

$$J_h={\displaystyle \frac{\partial h}{\partial r}}, J_{\theta }={\displaystyle \frac{\partial \theta }{\partial r}}, J_{\varphi }={\displaystyle \frac{\partial \varphi }{\partial \eta }}, J_{\chi }={\displaystyle \frac{\partial \chi }{\partial r}},$$

(25)

With these definitions of the currents, Equations (23) and (9)–(11) can be established as follows:

$$\begin{gathered} {\displaystyle \frac{{\nu }_{nf}}{{\nu }_{bf}}}\left\{\left(1+2ϵ\eta \right) J_h^{\prime }+2ϵ J_h\right\}-{\displaystyle \frac{{\sigma }_{nf}}{{\sigma }_{bf}}}{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}} M^{2}h-h^2-{\displaystyle \frac{{\nu }_{nf}}{{\nu }_{bf}}}Kh-Fr{h}^2+f J_h+ \\ MCcos\alpha \left({\displaystyle \frac{{\beta }_{nf}}{{\beta }_f}}\theta -{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}}Nr\varphi +{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}}NC\chi \right)=0, \end{gathered}$$

(26)

$$\begin{gathered} {\displaystyle \frac{{\kappa }_{nf}}{{\kappa }_{bf}}}{\displaystyle \frac{{\left(\rho C_p\right)}_{bf}}{{\left(\rho C_p\right)}_{nf}}}{\displaystyle \frac{1}{Pr}}\left(\left(1+2ϵ\eta \right){ J_{\theta }}^{\prime }+2ϵJ_{\theta }\right)+Nb\left(1+2ϵ\eta \right)J_{\theta }{J}_{\varphi }+ \\ Nt\left(1+2ϵ\eta \right){J_{\theta }}^2+f{J}_{\theta }+{\displaystyle \frac{{\sigma }_{nf}}{{\sigma }_{bf}}}{\displaystyle \frac{{\left(\rho C_p\right)}_{bf}}{{\left(\rho C_p\right)}_{nf}}}{M}^{2}Ec{h}^2=0, \end{gathered}$$

(27)

$$\left(1+2ϵ\eta \right){ J_{\varphi }}^{\prime }+2ϵJ_{\varphi }+Scf{J}_{\varphi }+{\displaystyle \frac{Nt}{Nb}}\left(\left(1+2ϵ\eta \right){J_{\theta }}^{\prime }+2ϵ J_{\theta }\right)=0,$$

(28)

$$\left(1+2ϵ\eta \right){J_{\chi }}^{\prime }+LbPrf{J}_{\chi }+2ϵJ_{\chi }-Pe\left[\begin{array}{c}\left(1+2ϵ\eta \right)J_{\chi } J_{\varphi }+\\ \left(\Delta N+\chi \right)\left(\left(1+2ϵ\eta \right){ J_{\varphi }}^{\prime }+ϵJ_{\varphi }\right)\end{array}\right]=0.$$

(29)

These partial differential equations can be transformed into a system of connected differential equations, by means of the spatial discretization, where Δη is the size of the elementary cell. We can take it a step further if we develop the derivatives of the currents:

$$\begin{gathered} {\displaystyle \frac{J_{h,i-1}-J_{h,i+1}}{\Delta \eta }} {\displaystyle \frac{{\nu }_{nf}}{{\nu }_{bf}}} \left(1+2ϵ\eta \right)+2ϵ J_{h,i}-{\displaystyle \frac{{\sigma }_{nf}}{{\sigma }_{bf}}}{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}} M^2{h}_i-h_i^2-{\displaystyle \frac{{\nu }_{nf}}{{\nu }_{bf}}}K{h}_i-Fr{h}_i^2+f_i J_{h,i}+ \\ MCcos\alpha \left({\displaystyle \frac{{\beta }_{nf}}{{\beta }_f}}{\theta }_i-{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}}Nr{\varphi }_i+{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}}NC{\chi }_i\right)=0, \end{gathered}$$

(30)

$$\begin{gathered} {\displaystyle \frac{{\kappa }_{nf}}{{\kappa }_{bf}}}{\displaystyle \frac{{\left(\rho C_p\right)}_{bf}}{{\left(\rho C_p\right)}_{nf}}}{\displaystyle \frac{1}{Pr}} \left({\displaystyle \frac{J_{\theta ,i-1}-J_{\theta ,i+1}}{\Delta \eta }}\left(1+2ϵ\eta \right)+2ϵJ_{\theta ,i}\right)+Nb\left(1+2ϵ\eta \right)J_{\theta ,i}{J}_{\varphi ,i}+ \\ Nt\left(1+2ϵ\eta \right){J_{\theta ,i}}^2+f_i{ J}_{\theta ,i}+{\displaystyle \frac{{\sigma }_{nf}}{{\sigma }_{bf}}}{\displaystyle \frac{{\left(\rho C_p\right)}_{bf}}{{\left(\rho C_p\right)}_{nf}}}{M}^{2}Ec h_i^2=0, \end{gathered}$$

(31)

$${\displaystyle \frac{J_{\varphi ,i-1}-J_{\varphi ,i+1}}{\Delta \eta }}\left(1+2ϵ\eta \right)+2ϵJ_{\varphi ,i}+Sc{f}_i{J}_{\varphi ,i}+{\displaystyle \frac{Nt}{Nb}}\left(\left(1+2ϵ\eta \right){\displaystyle \frac{J_{\theta ,i-1}-J_{\theta ,i+1}}{\Delta \eta }}+2ϵ J_{\theta ,i}\right)=0,$$

(32)

$$\begin{gathered} {\displaystyle \frac{J_{\chi ,i-1}-J_{\chi ,i+1}}{\Delta \eta }}\left(1+2ϵ\eta \right)+LbPr{f}_i{J}_{\chi ,i}+2ϵJ_{\chi ,i}-Pe [\left(1+2ϵ\eta \right)J_{\chi ,i}{J}_{\varphi ,i}+ \\ \left(\Delta N+{\chi }_i\right)\left(\left(1+2ϵ\eta \right){\displaystyle \frac{J_{\varphi ,i-1}-J_{\varphi ,i+1}}{\Delta \eta }}+ϵJ_{\varphi ,i}\right)]=0 \end{gathered}$$

(33)

A first-order central difference approximation was used for the first derivate for J_h, J_θ, J_ϕ, and J_χ, while a second-order central difference approximation was used for the second derivate. Thus, focusing on the momentum equation (the rest of the equations would be treated in the same manner), we have

J_h,i ≈ (h_i+1 − h_i−1)/2Δη

(34)

∂J_h/∂r ≈ (J_h,i−1 − J_h,i+1)/Δη = (h_i−1 + h_i+1 − 2 h_i)/Δη²

(35)

Substituting both expressions,

$$\begin{gathered} {\displaystyle \frac{(h_{i-1}+h_{i+1}-2 h_i)}{{\Delta \eta }^2}} {\displaystyle \frac{{\nu }_{nf}}{{\nu }_{bf}}} \left(1+2ϵ\eta \right)+2ϵ{\displaystyle \frac{h_{i+1}-h_{i-1}}{2\Delta \mathsf{\eta }}}-{\displaystyle \frac{{\sigma }_{nf}}{{\sigma }_{bf}}}{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}} M^2{h}_i-h_i^2-{\displaystyle \frac{{\nu }_{nf}}{{\nu }_{bf}}}K{h}_i-Fr{h}_i^2+f_i (h_{i+1}-h_{i-1})/2\Delta \mathsf{\eta }+ \\ MCcos\alpha \left({\displaystyle \frac{{\beta }_{nf}}{{\beta }_f}}{\theta }_i-{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}}Nr{\varphi }_i+{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}}NC{\chi }_i\right)=0, \end{gathered}$$

(36)

In the previous equation, all members were considered a current, and by applying Kirchhoff’s second law, the network model was obtained (Figure 2).

J_h,i−1 − J_h,i+1 + J_f,i + J_θχ,i − J_M,i = 0

(37)

It is known that electrical resistance is a source of constant current, so when the terms involved in a current are constants, that current can be modeled using electrical resistance. This was the case for J_h,i−1 and J_h,i+1, where R_h,i−1 = R_h,i+1 = ${\Delta \eta }^2$ ${\nu }_{bf}/\left(1+2ϵ\eta \right)$ ${\nu }_{nf}.$ The other currents were modeled with a voltage-control current generator:

$${\mathrm{J}}_{\mathrm{M},\mathrm{i}}=\{{\displaystyle \frac{{\sigma }_{nf}}{{\sigma }_{bf}}}{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}} M^2{h}_i+h_i^2+{\displaystyle \frac{{\nu }_{nf}}{{\nu }_{bf}}}K{h}_i+Fr{h}_i^2\}$$

(38)

$${\mathrm{J}}_{\mathsf{\theta }\mathsf{\chi },\mathrm{i}}=MCcos\alpha \left({\displaystyle \frac{{\beta }_{nf}}{{\beta }_f}}{\theta }_i-{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}}Nr{\varphi }_i+{\displaystyle \frac{{\rho }_f}{{\rho }_{nf}}}NC{\chi }_i\right)$$

(39)

$${\mathrm{J}}_{\mathrm{f},\mathrm{i}}=J_{h,i}(2ϵ+f_i)$$

(40)

To implement the boundary conditions at $\eta =0$ and $\eta \to \infty$, constant voltage sources were employed for the velocity, temperature, concentration, and density of motile microorganisms.

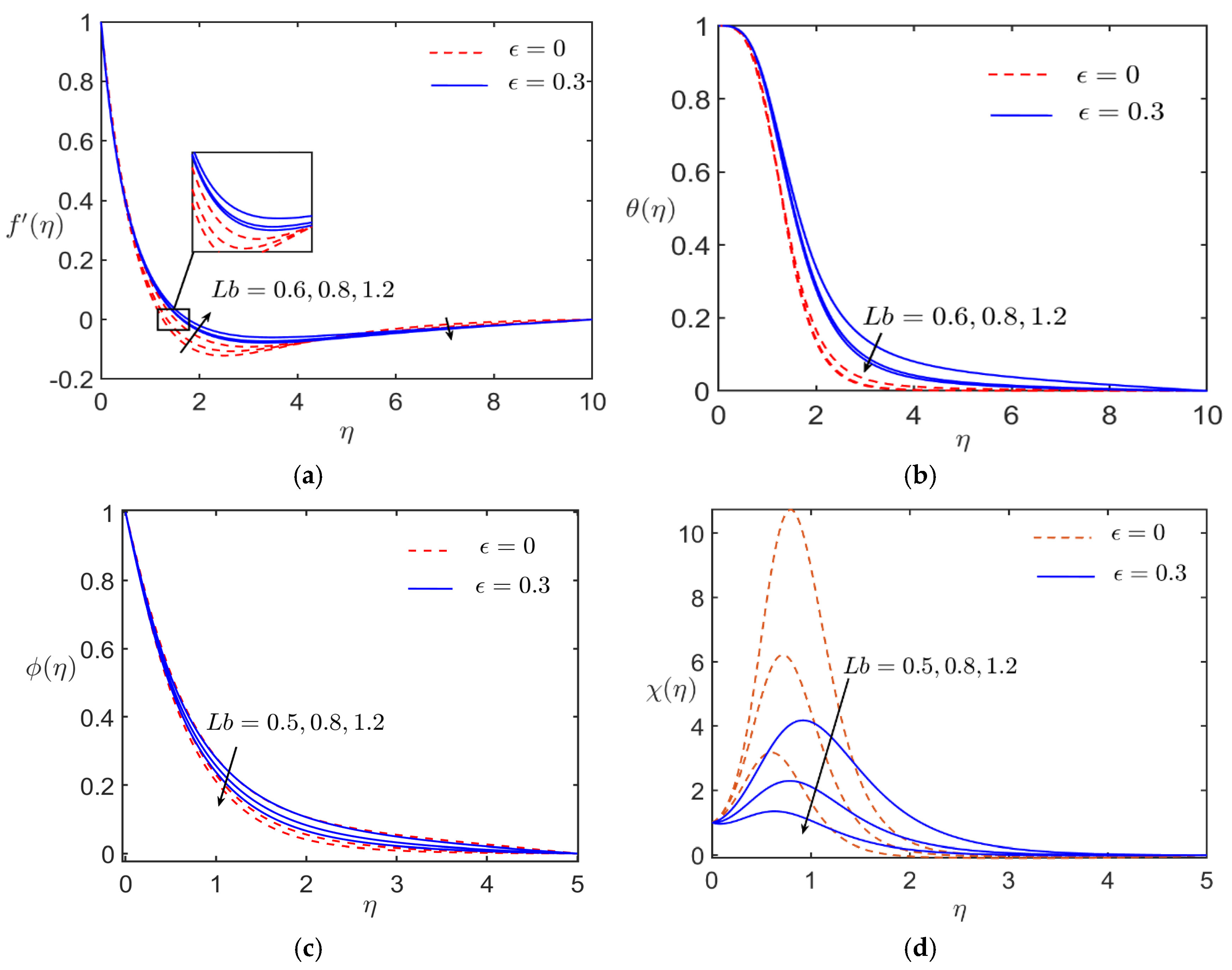
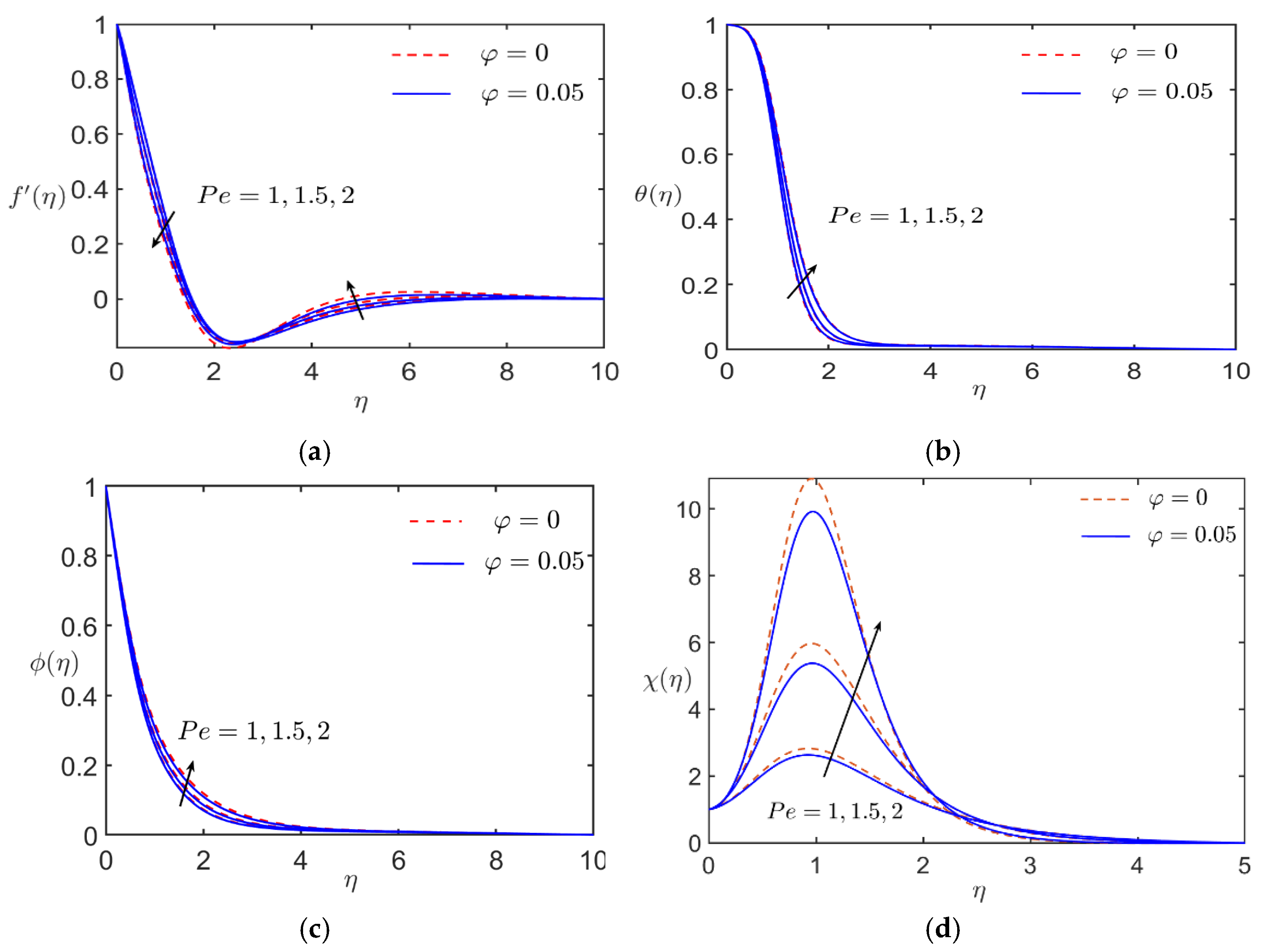
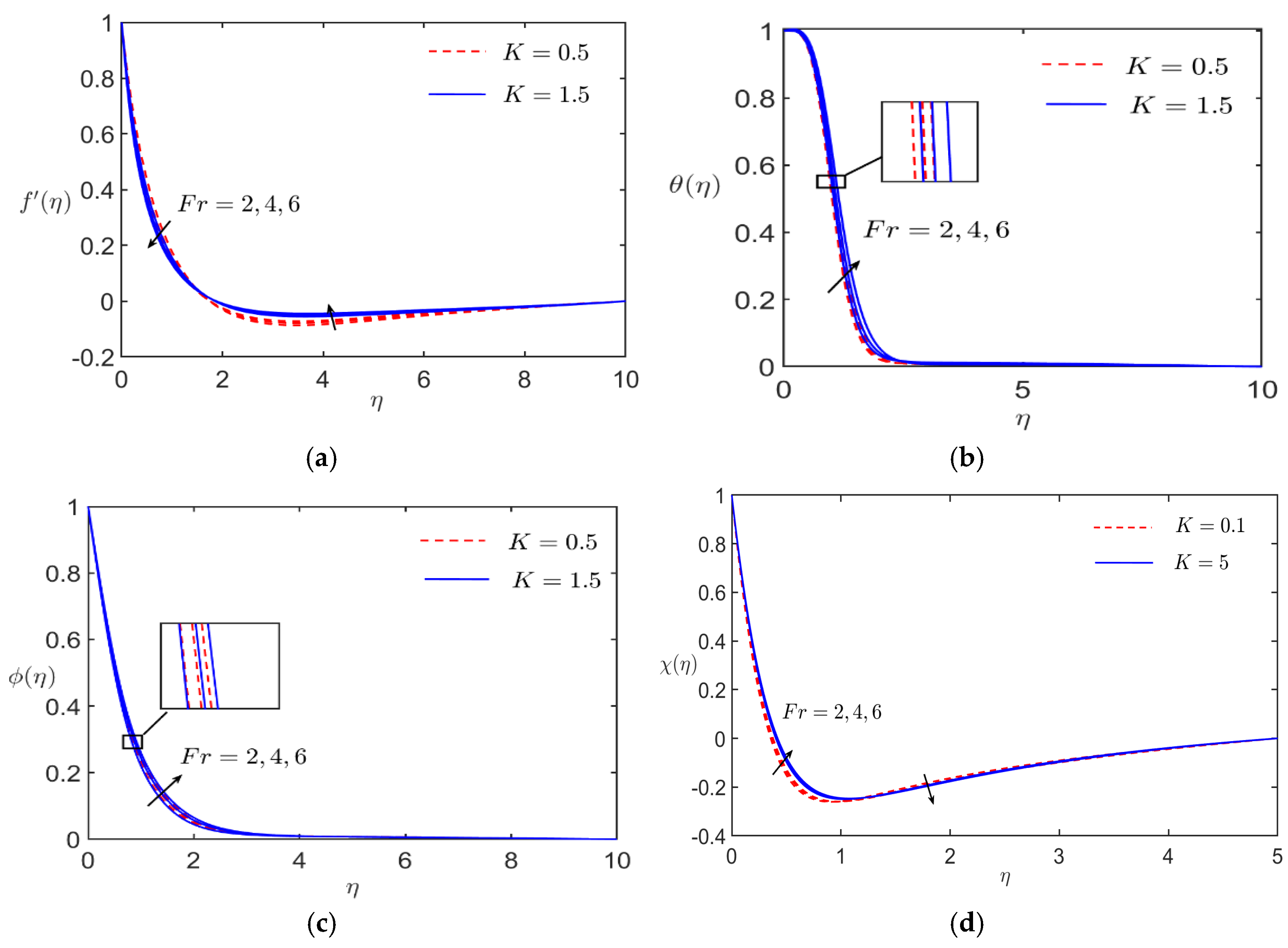
5. Discussion

In this study, the MHD flow of NEPCM–water nanofluid containing motile microbes past a stretching cylinder implanted in a porous matrix was considered. Buongiorno’s model was adopted to study the Soret and Dufour effect. This section deals with the examination of the influence of different parameters over the velocity, temperature, concentration, and microorganism fields.

Table 2. Validation of numerical values of $-f^{″}\left(0\right)$ with [32,33] when, $M=0, 0.2, 0.5, 0.8,\mathrm{a}\mathrm{n}\mathrm{d} 1.0$.

M	Present, NSM −f″(0)	Present, Runge–Kutta −f″(0)	[32] −f″(0)	[33] −f″(0)
0	0.9984	0.9988	1.00000	1.00000
0.2	1.0146	1.0139	1.01981	1.01980
0.5	1.0901	1.0868	1.11803	1.11803
0.8	1.2709	1.2847	1.28062	1.28062
1.0	1.4101	1.4036	1.41421	1.41421

substantiates the outlined results in this investigation by comparing it with the findings of [32,33], and good agreement was observed. The stability of the adopted scheme was verified by means of a grid point stability test for $\Delta \eta =0.001$ and $\Delta \eta =0.0001$, as shown in

Table 3. Grid point stability test (Runge–Kutta method) for $\Delta \mathsf{\eta }=0.001$ and $\Delta \mathsf{\eta }=0.0001$.

	Δη = 0.001				Δη = 0.0001
η	f″(η)	θ(η)	ϕ(η)	χ(η)	f″(η)	θ(η)	ϕ(η)	χ(η)
0	1	1	1	1	1	1	1	1
1	0.1726	0.4870	0.9209	0.5116	0.1727	0.4871	0.9210	0.5117
2	−0.0378	0.4870	0.9209	0.2230	−0.0378	0.2251	0.7313	0.2230
3	−0.0724	0.2251	0.7312	0.0745	−0.0724	0.1117	0.4618	0.0746
4	−0.0492	0.1116	0.4617	0.01881	−0.04992	0.0462	0.2140	0.0181
5	0	0	0	0	0	0	0	0

. Here, the core and shell of the NPCEM nanoparticles were constructed using nonadecane and polyurethane, respectively. For the simulation process, the default values of the non-dimensional parameters were set as $Pr=7$, ${\theta }_f=0.2$, $t=0.7$, $\lambda =0.4$, $Ste=0.3$, $Nc=3$, and $Nv=3$, and in other circumstances, the values were stated.

Figure 3 describes the velocity, temperature, concentration, and microorganism profile for different values of Lb and ε. The profiles were plotted against the similarity variable η. In Figure 3a, a solved case is presented using both methods, to check the accuracy of the solutions and validate them both; a full coincidence is observed in both cases. In this figure, we can distinguish two zones (cross flow) based on the value of the η parameter (similarity variable). Thus, for η < 1.8 (with ε = 0), an increase in Lb (bioconvection Lewis number) causes a decrease in velocity, with this effect becoming more pronounced as the curvature radius decreases. For values of η < 1.8 (with ε = 0), this trend is reversed, with velocity increasing with the increase in Lb. We can also observe that an increase in the curvature radius shifts the inflection point to higher η values; thus, for ε = 0.3, this point is approximately at η ≈ 2.6, indicating that, for η > 2.6, the velocity profile is approximately constant.

Figure 3b shows the effect of $Lb$ and $\epsilon$ on the temperature profile. We observe that increasing $Lb$ increases the temperature, with higher temperature values reached as the curvature parameter ($\epsilon$) increases. Additionally, it is observed that the differences in the temperature profile are more pronounced as the curvature parameter decreases. Figure 3c describes the concentration profile for different values of the bioconvective Lewis number $Lb$ and curvature parameter ε. From the figure, we can see that an increase in $Lb$ results in a decrease in the concentration profile. Physically, Lewis number ($Lb$) represents the relative contribution of thermal diffusion rate to species diffusion rate in the boundary layer regime. Thus, higher values of $Lb$ imply less species diffusion as a result of the reduced ability of microorganisms to disperse throughout the fluid, leading to a more localized accumulation of microorganisms and a sharper decline in the concentration profile. The increase in the curvature parameter ε leads to an increase in the concentration profile.

The effects of $Lb$ and $\epsilon$ on the density of motile microorganisms are shown in Figure 3d. We observe that the boundary layer decreases as $Lb$ increases, resulting in a decrease in the density of motile microorganisms. It is observed that the density of motile microorganisms increases until reaching a maximum and then decreases to its value outside the boundary layer. The decrease in the curvature parameter ε leads to an increase in the density of motile microorganisms, and for these cases, the differences in the profiles of the density of motile microorganisms can be appreciated more clearly.

Figure 4 shows the effects of the Peclet number and the mass concentration $\phi$ on the velocity, temperature, concentration, and microorganism fields. The profiles were plotted against the similarity variable $\eta$. In Figure 4a, we observe a cross-flow in the velocity profiles $f^{\prime }\left(\eta \right)$ at $\eta \approx 2$. There is a greater variation in velocity in the region $\eta <2$, indicating that an increase in the Peclet number leads to higher velocity profiles in this zone. However, for $\eta >2$, the opposite occurs: as the Peclet number increases, the velocity decreases. The effect of the mass fraction $\phi$ is very weak in the $\eta <2$ region, with the velocity decreasing slightly (especially at high $Pe$) with the increase in $\phi$. In the $\eta >2$ zone, this trend is reversed, with the velocity profile increasing as the mass fraction φ increases. Additionally, there is a greater influence of $\phi$ in this zone (especially for high $Pe$ values). From Figure 4b, we can observe that as the Peclet number increases, the thermal field decreases, leading to a decrease in the thickness of the temperature boundary layer. We can also see that an increase in the mass concentration φ causes an increase in the thickness of the temperature boundary layer, consequently increasing the temperature.

The concentration profiles grow with an increase in the Peclet number (Pe), as seen in Figure 4c. This emerges because a system with a greater Peclet number has more advection (convective transport) than diffusion. As a consequence, the fluid flow is able to carry the nanoparticles more efficiently, which improves concentration accumulation in certain areas. The upward shift of the concentration profiles with increasing Pe reflects this phenomenon. Conversely, a reduction in the nanoparticle volume fraction ($\phi$) also causes the concentration profile to rise. The percentage of nanoparticles in the fluid is indicated by the volume fraction $\phi$. As $\phi$ falls, there is less interaction between the nanoparticles, which lowers flow resistance and improves convective transport. The concentration profiles rise as a result of the nanoparticles becoming more distributed throughout the fluid.

Figure 5 illustrates the impact of $K$ (permeability parameter) and $Fr$ (Forchheimer number) on the velocity, temperature, concentration, and microorganism fields. Increased values of $K$ and $Fr$ enhance the flow resistance due to the porous medium. Physically, higher values of $K$ reduce the permeability of the porous medium, thereby impeding the fluid flow and causing a decline in velocity, as depicted in Figure 4a. This reduction in velocity leads to an increase in the nanofluid temperature, as the convective heat transfer diminishes. Similarly, a higher Forchheimer number $\left(Fr\right)$ signifies stronger non-linear inertial effects within the porous medium, which further resist fluid motion and reduce the overall fluid velocity. The decline in velocity due to Forchheimer drag directly influences the temperature of the nanofluid, causing it to rise. This behavior is evident in Figure 4b, where the temperature profile increases as a result of the enhanced resistance from the Forchheimer drag force.

The concentration profile also increases with higher values of $K$ and $Fr$. This is because the increased resistance to fluid flow, caused by the reduced permeability from higher values of $K$ and the non-linear inertial effects from larger values of $Fr$, leads to a more localized accumulation of nanoparticles and microorganisms. The resulting decrease in velocity enhances the retention time of particles in the medium, which promotes higher concentrations. As a result, both the velocity decline and reduced transport efficiency contribute to an increase in the concentration profile as well as the microorganism fields for higher values of $K$ and $Fr$, as depicted in Figure 5c,d.

• Comments on Table 4 and Table 5

In this section, the influence of the parameters Pe, φ, $Lb, ϵ$, and $\alpha$ on the shear stress, the rate of heat transmission from the surface of the cylinder, the rate of mass transfer, and changes in the density of microorganism is presented (Table 4). $R{e}_x^{-{\displaystyle \frac{1}{2}}}N{u}_x$ is a non-dimensional number known as the Nusselt number, which characterizes the significance of convective heat transmission over conductive heat transmission at the boundaries. It is reported that the enhanced values of $Pe$ and $\phi$ escalate the Nusselt number. The improved values of the Nusselt number indicate that the rate of heat transmission by convection is more efficient. However, the values of $R{e}_x^{-{\displaystyle \frac{1}{2}}}N{u}_x<1$ signify the supremacy of conduction over convection. The addition of $NEPCM$ nanoparticles in the water boosts the heat transfer by $10\%$ and the increment in the solid volume fraction of $NEPCM$ nanoparticles from 0.03 to 0.05 enhances the Nusselt number by $17.04\%$. This enhancement of the Nusselt number is due to the improved thermal conductivity of the fluid. The augmented values of $Lb, ϵ$ and $\alpha$ cause a decline in $R{e}_x^{-{\displaystyle \frac{1}{2}}}N{u}_x$. The reason behind this trend can be the flow pattern or the increased skin friction coefficient. The Nusselt number for $ϵ=0$ (flat plate) is greater than $1$, which marks the dominance of convection over conduction in the system. The conductive heat transfer from the surface dominates the convective heat transfer for $ϵ>0$. It is also seen that the Nusselt number corresponding to $\alpha =0$ (vertical cylinder) is greater than the inclined $\alpha =45$ and horizontal cylinder $\alpha =90$.

Table 4. Impact of some critical parameters on $R{e}_x^{{\displaystyle \frac{1}{2}}}C{f}_x,R{e}_x^{-{\displaystyle \frac{1}{2}}}N{u}_x,R{e}_x^{-{\displaystyle \frac{1}{2}}}S{h}_x$, and $R{e}_x^{-{\displaystyle \frac{1}{2}}}N{n}_x$.

Pe	φ	Lb	ε	$\mathit{\alpha }$	$\mathbf{R}{\mathbf{e}}_{\mathbf{x}}^{\frac{1}{2}}\mathbf{C}{\mathbf{f}}_{\mathbf{x}}$	$\mathbf{R}{\mathbf{e}}_{\mathbf{x}}^{-\frac{1}{2}}\mathbf{N}{\mathbf{u}}_{\mathbf{x}}$	$\mathbf{R}{\mathbf{e}}_{\mathbf{x}}^{-\frac{1}{2}}\mathbf{S}{\mathbf{h}}_{\mathbf{x}}$	$\mathbf{R}{\mathbf{e}}_{\mathbf{x}}^{-\frac{1}{2}}\mathbf{N}{\mathbf{n}}_{\mathbf{x}}$
1.0	0.05	0.4	0.3	45	1.7752	0.5694	0.2611	0.857
1.5					1.7711	0.5721	0.2571	0.9692
2.0					1.767	0.5747	0.2534	1.0818
	0.0				1.5529	0.4865	0.2742	0.8684
	0.03				1.6861	0.5364	0.2657	0.8608
	0.05				1.7752	0.5694	0.2611	0.857
		0.5			1.7792	0.5654	0.2668	1.1493
		0.8			1.7964	0.5526	0.2853	1.6213
		1.2			1.8153	0.5418	0.3009	2.4097
			0.0		1.6263	1.1589	−1.2229	−1.1057
			0.2		1.7232	0.7016	−0.1123	0.3843
			0.4		1.8192	0.4781	0.5624	1.4808
				0.0	1.7145	0.5836	0.2407	0.9488
				60	1.8118	0.5632	0.2699	0.9857
				90	1.9130	0.5385	0.3055	1.0336

Table 4. Impact of some critical parameters on $R{e}_x^{{\displaystyle \frac{1}{2}}}C{f}_x,R{e}_x^{-{\displaystyle \frac{1}{2}}}N{u}_x,R{e}_x^{-{\displaystyle \frac{1}{2}}}S{h}_x$, and $R{e}_x^{-{\displaystyle \frac{1}{2}}}N{n}_x$.

Pe	φ	Lb	ε	$\mathit{\alpha }$	$\mathbf{R}{\mathbf{e}}_{\mathbf{x}}^{\frac{1}{2}}\mathbf{C}{\mathbf{f}}_{\mathbf{x}}$	$\mathbf{R}{\mathbf{e}}_{\mathbf{x}}^{-\frac{1}{2}}\mathbf{N}{\mathbf{u}}_{\mathbf{x}}$	$\mathbf{R}{\mathbf{e}}_{\mathbf{x}}^{-\frac{1}{2}}\mathbf{S}{\mathbf{h}}_{\mathbf{x}}$	$\mathbf{R}{\mathbf{e}}_{\mathbf{x}}^{-\frac{1}{2}}\mathbf{N}{\mathbf{n}}_{\mathbf{x}}$
1.0	0.05	0.4	0.3	45	1.7752	0.5694	0.2611	0.857
1.5					1.7711	0.5721	0.2571	0.9692
2.0					1.767	0.5747	0.2534	1.0818
	0.0				1.5529	0.4865	0.2742	0.8684
	0.03				1.6861	0.5364	0.2657	0.8608
	0.05				1.7752	0.5694	0.2611	0.857
		0.5			1.7792	0.5654	0.2668	1.1493
		0.8			1.7964	0.5526	0.2853	1.6213
		1.2			1.8153	0.5418	0.3009	2.4097
			0.0		1.6263	1.1589	−1.2229	−1.1057
			0.2		1.7232	0.7016	−0.1123	0.3843
			0.4		1.8192	0.4781	0.5624	1.4808
				0.0	1.7145	0.5836	0.2407	0.9488
				60	1.8118	0.5632	0.2699	0.9857
				90	1.9130	0.5385	0.3055	1.0336

The rate of nanoparticle diffusion from the surface of the cylinder can be interpreted with a non-dimensional quantity known as the Sherwood number $\left(R{e}_x^{-{\displaystyle \frac{1}{2}}}S{h}_x\right)$. Reduced values of $\left(R{e}_x^{-{\displaystyle \frac{1}{2}}}S{h}_x\right)$ indicate less transfer of nanoparticles from the surface of the cylinder. The contrary result for the effect of $Pe$ over $\left(R{e}_x^{-{\displaystyle \frac{1}{2}}}S{h}_x\right)$ should be noted. The Sherwood number values were found to decrease for higher values of $Pe$, despite the fact that reduced skin friction for increased values of $Pe$ should increase the $R{e}_x^{-{\displaystyle \frac{1}{2}}}S{h}_x$; however, for $Nr=1.5$, the $Pe$ number accelerates the rate of rate of change in nanoparticle concentrations from the cylinder’s surface. The inclusion of $NEPCM$ nanoparticles in the water enhances the density of the water and thus decreases the mass transfer from the surface of the cylinder. Higher values of the Sherwood number have been reported for increased values of Lb. The increase in the Sherwood number indicates that the rate of nanoparticle diffusion from the surface of the cylinder increases as Lb is increased. Negative values of $R{e}_x^{-{\displaystyle \frac{1}{2}}}S{h}_x$ corresponding to $ϵ=0$ and $ϵ=0.2$ represent nanoparticle diffusion from the surrounding to the surface of the cylinder, i.e., the nanoparticle diffuses from the surrounding fluid to the surface of the flat plate. However, for $ϵ=0.4$ (cylinder), the rate of mass transfer becomes positive and indicates that nanoparticles diffuse from the surface of the cylinder. Higher values of $\left(R{e}_x^{-{\displaystyle \frac{1}{2}}}S{h}_x\right)$ represent a better rate of nanoparticle diffusion from the surface of the cylinder. It is noteworthy that the horizontal cylinder provides a better rate of nanoparticle diffusion as compared to the vertical cylinder.

The effect of all the non-dimensional parameters on microorganism diffusion resembles the rate of nanoparticle diffusion from the surface of the cylinder to the fluid medium. The augmented values of $Pe$ and $Lb$ suggest stronger bioconvection, while the increased values of volume fraction reduce the diffusion rate of microorganisms from the surface of the cylinder. The diffusion of microorganisms is higher for the horizontal cylinder as compared to the vertical cylinder. The negative value of $R{e}_x^{-{\displaystyle \frac{1}{2}}}N{n}_x$ for $ϵ=0$ indicates the reverse flux of microorganisms from the fluid medium to the surface of the stretching cylinder. The increased values of $R{e}_x^{-{\displaystyle \frac{1}{2}}}N{n}_x$ indicate better diffusion of microorganisms from the surface of the cylinder to the fluid medium and enhanced bioconvection. This enhances the density of microorganisms in the fluid medium, which ultimately improves the convection process.

Table 5. Impact of some critical parameters on $R{e}_x^{{\displaystyle \frac{1}{2}}}C{f}_x,R{e}_x^{-{\displaystyle \frac{1}{2}}}N{u}_x,R{e}_x^{-{\displaystyle \frac{1}{2}}}S{h}_x$ and $R{e}_x^{-{\displaystyle \frac{1}{2}}}N{n}_x$ for $M=0.1$.

${\mathit{\Theta }}_{\mathit{f}}$	Ste	Nv	Nc	Ns	$\mathbf{R}{\mathbf{e}}_{\mathbf{x}}^{\frac{1}{2}}\mathbf{C}{\mathbf{f}}_{\mathbf{x}}$	$\mathbf{R}{\mathbf{e}}_{\mathbf{x}}^{-\frac{1}{2}}\mathbf{N}{\mathbf{u}}_{\mathbf{x}}$	$\mathbf{R}{\mathbf{e}}_{\mathbf{x}}^{-\frac{1}{2}}\mathbf{S}{\mathbf{h}}_{\mathbf{x}}$	$\mathbf{R}{\mathbf{e}}_{\mathbf{x}}^{-\frac{1}{2}}\mathbf{N}{\mathbf{n}}_{\mathbf{x}}$
0.05	0.3	6.0	3.0	2.0	1.7539	1.233	0.3156	1.0607
0.5					1.7535	1.2315	0.3162	1.0624
0.9					1.7532	1.2229	0.3183	1.0667
	0.4				1.7538	1.2316	0.316	1.0616
	0.5				1.7537	1.2306	0.3163	1.0622
	0.6				1.7536	1.23	0.3165	1.0626
		0.3			1.5736	1.214	0.3191	1.0569
		3.0			1.7539	1.2331	0.3156	1.0608
		6.0			1.9531	1.2495	0.3128	1.0652
			0.3		1.7639	1.0521	0.2859	1.0036
			3.0		1.7589	1.1412	0.3008	1.0319
			6.0		1.7539	1.2331	0.3156	1.0608
				0.3	1.7537	1.2338	0.3155	1.0605
				3.0	1.7540	1.2326	0.3157	1.061
				6.0	1.7543	1.2312	0.3161	1.0615

Table 5. Impact of some critical parameters on $R{e}_x^{{\displaystyle \frac{1}{2}}}C{f}_x,R{e}_x^{-{\displaystyle \frac{1}{2}}}N{u}_x,R{e}_x^{-{\displaystyle \frac{1}{2}}}S{h}_x$ and $R{e}_x^{-{\displaystyle \frac{1}{2}}}N{n}_x$ for $M=0.1$.

${\mathit{\Theta }}_{\mathit{f}}$	Ste	Nv	Nc	Ns	$\mathbf{R}{\mathbf{e}}_{\mathbf{x}}^{\frac{1}{2}}\mathbf{C}{\mathbf{f}}_{\mathbf{x}}$	$\mathbf{R}{\mathbf{e}}_{\mathbf{x}}^{-\frac{1}{2}}\mathbf{N}{\mathbf{u}}_{\mathbf{x}}$	$\mathbf{R}{\mathbf{e}}_{\mathbf{x}}^{-\frac{1}{2}}\mathbf{S}{\mathbf{h}}_{\mathbf{x}}$	$\mathbf{R}{\mathbf{e}}_{\mathbf{x}}^{-\frac{1}{2}}\mathbf{N}{\mathbf{n}}_{\mathbf{x}}$
0.05	0.3	6.0	3.0	2.0	1.7539	1.233	0.3156	1.0607
0.5					1.7535	1.2315	0.3162	1.0624
0.9					1.7532	1.2229	0.3183	1.0667
	0.4				1.7538	1.2316	0.316	1.0616
	0.5				1.7537	1.2306	0.3163	1.0622
	0.6				1.7536	1.23	0.3165	1.0626
		0.3			1.5736	1.214	0.3191	1.0569
		3.0			1.7539	1.2331	0.3156	1.0608
		6.0			1.9531	1.2495	0.3128	1.0652
			0.3		1.7639	1.0521	0.2859	1.0036
			3.0		1.7589	1.1412	0.3008	1.0319
			6.0		1.7539	1.2331	0.3156	1.0608
				0.3	1.7537	1.2338	0.3155	1.0605
				3.0	1.7540	1.2326	0.3157	1.061
				6.0	1.7543	1.2312	0.3161	1.0615

In this section, the influence of non-dimensional parameters due to the NEPCM nanoparticles over the shear stress, the rate of heat transmission from the surface of the cylinder, the rate of mass transfer, and changes in the density of microorganisms is presented in Table 5. The lower values of ${\theta }_f$ indicate more resistance to the surface of the cylinder as the fluid passes over it; as a result, $R{e}_x^{{\displaystyle \frac{1}{2}}}C{f}_x$ is higher for lower values of ${\theta }_f$. The melting process of the NEPCM core occurs when the ambient temperature gets close to ${\theta }_f$. At ${\theta }_f=1$, the heated surface and the small portion of the region surrounding the surface undergo a phase transition. Lower values of ${\theta }_f$ indicate larger melting zones, and more particles experience phase change. It is reported that the augmented values of ${\theta }_f$ in the range $0.01–0.1$ enhance the Nusselt number; beyond this range of ${\theta }_f$, the Nusselt number descends for the elevated values of ${\theta }_f$. So, fusion temperature must be regulated to enhance the cooling process. The mass diffusion rate and the diffusion rate of microorganisms elevate toward the higher values of ${\theta }_f$; this may be due to the change in temperature of the nanofluid and flow pattern. The Stefan number corresponds to the reciprocal of the latent heat of the $PCM$, and thus, the rate of heat exchange increases as the Stefan number decreases. In other words, the rate of exchanged heat increases when the sole contribution of the latent heat of the nanoparticles is taken into consideration. It is reported that $R{e}_x^{{\displaystyle \frac{1}{2}}}C{f}_x$ and $R{e}_x^{-{\displaystyle \frac{1}{2}}}N{u}_x$ decrease for the improved values of $Ste$. The augmented values of $Ste$ result in a decrease in the latent heat of the core of the particle and thus $R{e}_x^{-{\displaystyle \frac{1}{2}}}N{u}_x$. This result resembles the result published by [34]. The improved values of $Ste$ lead to an increase in the rate of mass diffusion and motile microorganisms from the surface of the cylinder. The thermal conductivity parameter $Nc$ results in an increase in the rate of heat transmission from the surface and the shear stress at the surface, while $Nv$ causes a decrease in both skin friction and Nusselt number. The mass diffusion rate and the rate of motile microorganism diffusion decrease for the augmented values of $Nc$, which is due to the flow pattern and the heat diffusion phenomenon.

• Highlights of the physical significance of the findings

This analysis highlights the significant role of bioconvection in enhancing cooling mechanisms and mass transfer. By examining the effects of key non-dimensional parameters, such as the Peclet number, the bioconvection Lewis number, and nanoparticle volume fraction, on the velocity and temperature fields, this study reveals how bioconvection influences fluid momentum and nanofluid temperature. These findings provide valuable insights for optimizing heat and mass transfer processes in applications involving nanofluids, phase-change materials, and porous media. The results pave the way for advancements in renewable energy technologies, efficient cooling systems, and thermal energy storage, promoting more sustainable industrial and environmental solutions.

A key feature of this investigation is the inclusion of nanoparticles with phase-changing properties, known as NEPCMs. These nanoparticles transition between solid and liquid phases at specific temperatures, enabling them to absorb, store, and release significant amounts of heat as needed. This unique thermal regulation capability makes NEPCMs highly suitable for enhancing applications such as solar energy systems, where they can significantly improve the efficiency of solar panels by optimizing heat management.

6. Conclusions

A novel analysis based on electrical analogy was performed regarding the bioconvective flow of NEPCM–water nanofluid over an inclined cylinder in a porous medium with an extended Darcy model. The fluid characteristics, momentum, temperature, nanoparticle volume fraction, and microorganism conservation boundary layer equations were transformed into non-dimensional equations and then solved numerically using two numerical methods: the network simulation method and the implicit finite difference method. The present study’s numerical results were compared with available data, and excellent agreement was found. Bioconvection phenomena appear in different applications, ranging from the synthesis of biological polymers to renewable energy technologies. The present research provides very valuable information on the optimization of mass and heat transfer processes driven by bioconvection, with important implications for various industrial and renewable energy applications, such as the design of microbial fuel cells and bioconvection nanotechnological devices. The analysis revealed several critical findings:

• The fusion temperature ${\theta }_f$ plays a significant role in optimizing the heat transfer efficiency; in this investigation, the optimal range of the fusion temperature was $0.01–0.1$. In this range, the rate of heat transfer from the surface of the cylinder was maximum, and beyond this range, the rate of heat transfer declined.
• Increasing the Peclet number ($Pe$) and the inclination angle ($\theta$) significantly enhanced the Nusselt number, indicating improved heat transfer rates. Specifically, $Pe$ led to a heat transfer enhancement of up to 12%, demonstrating its role in optimizing thermal regulation.
• The wall shear stress decreased with higher $Pe$, highlighting its impact on reducing frictional resistance, which can contribute to the design of energy-efficient systems.
• The interplay of $Lb$, $Pe$, and nanoparticle volume fraction ($\varphi$) intensified the density gradient of microorganisms by nearly 15%, amplifying bioconvection and facilitating enhanced mixing in the fluid system.
• The non-Darcy porous medium increased resistance to flow but contributed to stabilizing the thermal boundary layer, improving heat transfer efficiency around the cylinder.
• In a horizontal configuration, the microorganism concentration gradients and the associated bioconvective flow patterns were more evenly distributed around the surface, leading to enhanced diffusion. Such behavior can be beneficial in applications like microbial fuel cells and bioreactors, where maximizing microorganism activity and distribution can enhance efficiency and performance.
• A lower $Ste$ indicates the dominance of latent heat effects, which enhances heat absorption or release during the phase-change process. This leads to a more pronounced thermal gradient near the surface, thereby increasing the Nusselt number, which measures the rate of convective heat transfer.

Future research should focus on experimental validation and extending the model to account for dynamic phase-change behavior and transient effects.