Bioconvective Flow Characteristics of NEPCM–Water Nanofluid over an Inclined Cylinder in Porous Medium: An Extended Darcy Model Approach
Abstract
1. Introduction
- What are the factors that cause variations in the flow pattern of nanofluid?
- Does bioconvection help in controlling the fluid temperature and cooling of the surface?
- Does nanofluidic properties influence the shear force and rate of heat diffusion from the surface?
- How are NEPCM nanoparticles different from other nanoparticles?
2. Mathematical Formulation
- Porous material was considered to be a non-Darcy medium with Forchheimer;
- Fluid was laminar, viscous, incompressible, and electrically conductive;
- The induced magnetic field was neglected;
- The fluid was assumed to be Newtonian, and the flow was laminar two-dimensional, where the cylinder was assumed to be infinitely long;
- The porous medium was assumed to be homogeneous and isotropic, with a constant permeability;
- The influence of pressure gradient was neglected.
3. Thermophysical Properties of the Nanofluid
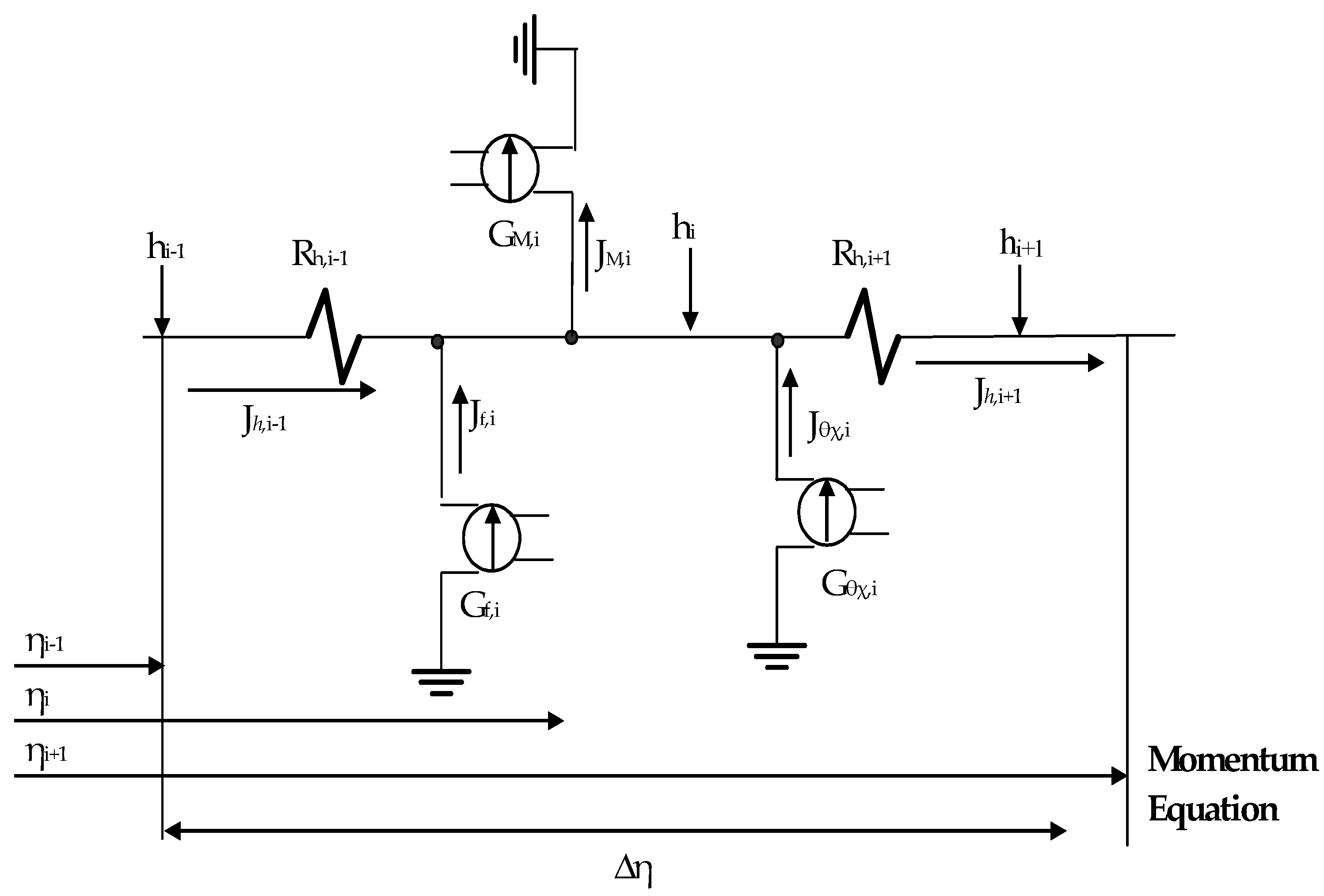
4. Numerical Solution
5. Discussion
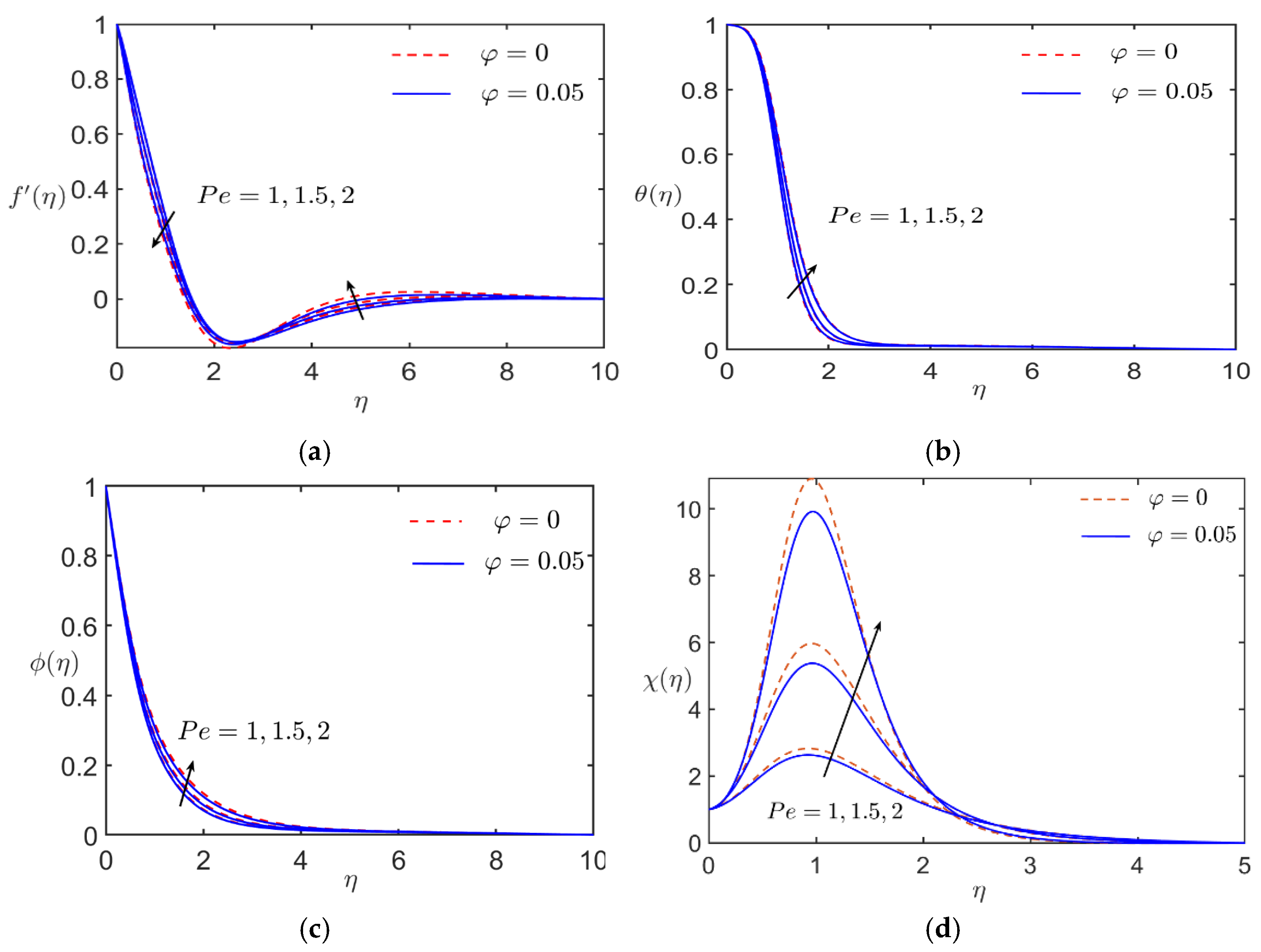
| Pe | φ | Lb | ε | |||||
|---|---|---|---|---|---|---|---|---|
| 1.0 | 0.05 | 0.4 | 0.3 | 45 | 1.7752 | 0.5694 | 0.2611 | 0.857 |
| 1.5 | 1.7711 | 0.5721 | 0.2571 | 0.9692 | ||||
| 2.0 | 1.767 | 0.5747 | 0.2534 | 1.0818 | ||||
| 0.0 | 1.5529 | 0.4865 | 0.2742 | 0.8684 | ||||
| 0.03 | 1.6861 | 0.5364 | 0.2657 | 0.8608 | ||||
| 0.05 | 1.7752 | 0.5694 | 0.2611 | 0.857 | ||||
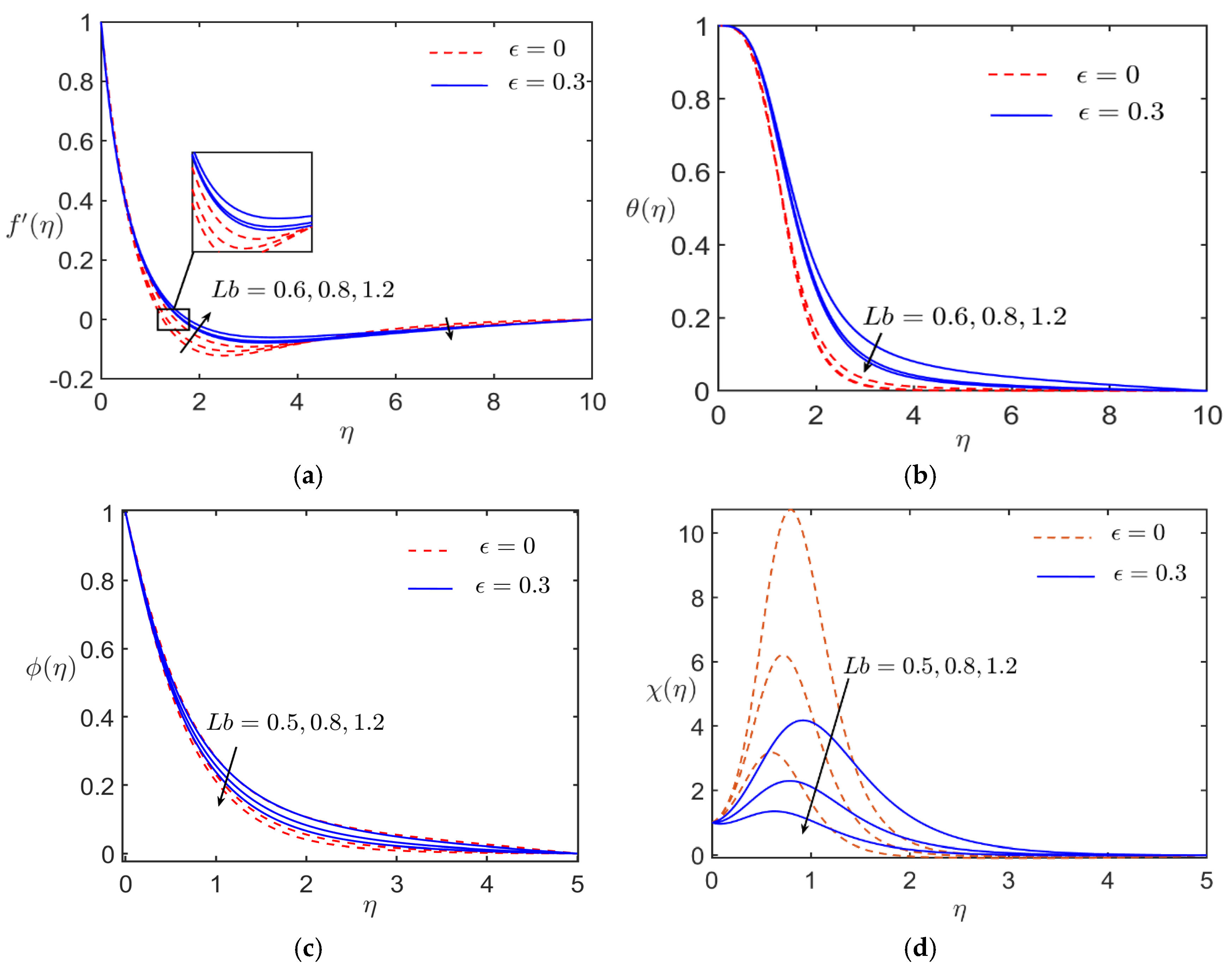
| 0.5 | 1.7792 | 0.5654 | 0.2668 | 1.1493 | ||||
| 0.8 | 1.7964 | 0.5526 | 0.2853 | 1.6213 | ||||
| 1.2 | 1.8153 | 0.5418 | 0.3009 | 2.4097 | ||||
| 0.0 | 1.6263 | 1.1589 | −1.2229 | −1.1057 | ||||
| 0.2 | 1.7232 | 0.7016 | −0.1123 | 0.3843 | ||||
| 0.4 | 1.8192 | 0.4781 | 0.5624 | 1.4808 | ||||
| 0.0 | 1.7145 | 0.5836 | 0.2407 | 0.9488 | ||||
| 60 | 1.8118 | 0.5632 | 0.2699 | 0.9857 | ||||
| 90 | 1.9130 | 0.5385 | 0.3055 | 1.0336 |
| Ste | Nv | Nc | Ns | |||||
|---|---|---|---|---|---|---|---|---|
| 0.05 | 0.3 | 6.0 | 3.0 | 2.0 | 1.7539 | 1.233 | 0.3156 | 1.0607 |
| 0.5 | 1.7535 | 1.2315 | 0.3162 | 1.0624 | ||||
| 0.9 | 1.7532 | 1.2229 | 0.3183 | 1.0667 | ||||
| 0.4 | 1.7538 | 1.2316 | 0.316 | 1.0616 | ||||
| 0.5 | 1.7537 | 1.2306 | 0.3163 | 1.0622 | ||||
| 0.6 | 1.7536 | 1.23 | 0.3165 | 1.0626 | ||||
| 0.3 | 1.5736 | 1.214 | 0.3191 | 1.0569 | ||||
| 3.0 | 1.7539 | 1.2331 | 0.3156 | 1.0608 | ||||
| 6.0 | 1.9531 | 1.2495 | 0.3128 | 1.0652 | ||||
| 0.3 | 1.7639 | 1.0521 | 0.2859 | 1.0036 | ||||
| 3.0 | 1.7589 | 1.1412 | 0.3008 | 1.0319 | ||||
| 6.0 | 1.7539 | 1.2331 | 0.3156 | 1.0608 | ||||
| 0.3 | 1.7537 | 1.2338 | 0.3155 | 1.0605 | ||||
| 3.0 | 1.7540 | 1.2326 | 0.3157 | 1.061 | ||||
| 6.0 | 1.7543 | 1.2312 | 0.3161 | 1.0615 |
- Highlights of the physical significance of the findings
6. Conclusions
- The fusion temperature plays a significant role in optimizing the heat transfer efficiency; in this investigation, the optimal range of the fusion temperature was . In this range, the rate of heat transfer from the surface of the cylinder was maximum, and beyond this range, the rate of heat transfer declined.
- Increasing the Peclet number () and the inclination angle () significantly enhanced the Nusselt number, indicating improved heat transfer rates. Specifically, led to a heat transfer enhancement of up to 12%, demonstrating its role in optimizing thermal regulation.
- The wall shear stress decreased with higher , highlighting its impact on reducing frictional resistance, which can contribute to the design of energy-efficient systems.
- The interplay of , , and nanoparticle volume fraction () intensified the density gradient of microorganisms by nearly 15%, amplifying bioconvection and facilitating enhanced mixing in the fluid system.
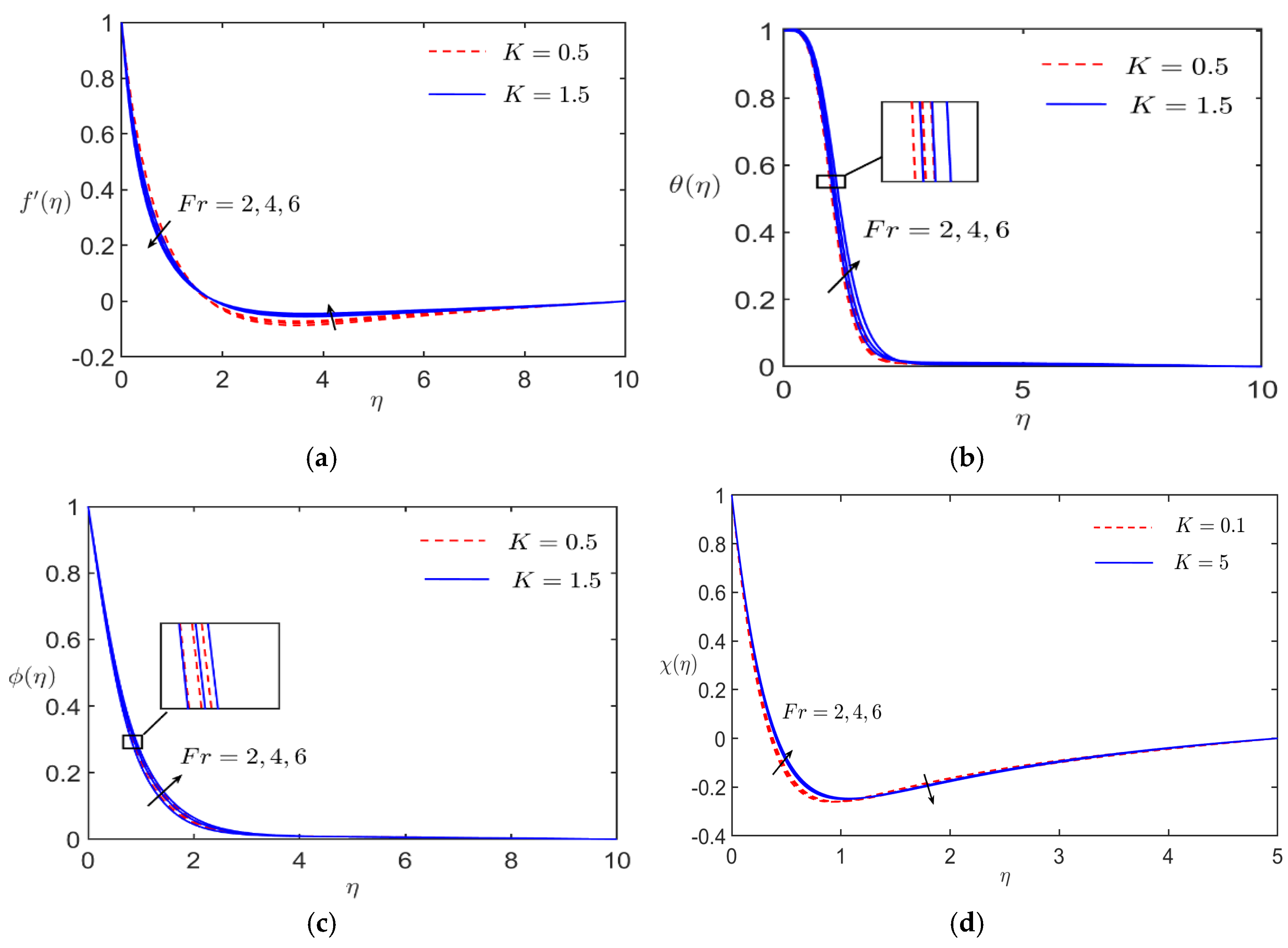
- The non-Darcy porous medium increased resistance to flow but contributed to stabilizing the thermal boundary layer, improving heat transfer efficiency around the cylinder.
- In a horizontal configuration, the microorganism concentration gradients and the associated bioconvective flow patterns were more evenly distributed around the surface, leading to enhanced diffusion. Such behavior can be beneficial in applications like microbial fuel cells and bioreactors, where maximizing microorganism activity and distribution can enhance efficiency and performance.
- A lower indicates the dominance of latent heat effects, which enhances heat absorption or release during the phase-change process. This leads to a more pronounced thermal gradient near the surface, thereby increasing the Nusselt number, which measures the rate of convective heat transfer.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | Symbols | ||
| Fluid velocity components along and axis | Buoyancy parameter | ||
| Coordinates | Peclet number | ||
| Magnetic field strength | Prandtl number | ||
| Nanoparticle concentration | Schmidt number | ||
| Drag coefficient | Sherwood number | ||
| Ambient concentration | Ste | Stefan number | |
| Concentration at the surface | Temperature | ||
| Concentration at the surface | t | weight ratio of the core–shell | |
| Skin friction | Ambient temperature | ||
| Coefficient of Brownian diffusion | Wall temperature | ||
| Diffusivity of microorganism | Maximum cell swimming speed | ||
| Coefficient of thermophoretic diffusion | Fluid density | ||
| Non-dimensional stream function | Mass density of nanoparticles | ||
| Dimensionless velocity | Curvature parameter | ||
| Forchheimer number | Dynamic viscosity | ||
| Non-dimensional fusion function | Kinematic viscosity | ||
| Acceleration due to gravity | Dimensionless temperature | ||
| J | Variable electric current | Dimensionless concentration | |
| Permeability | Dimensionless density of motile microorganisms | ||
| Permeability constant | Similarity variable | ||
| Bioconvection Lewis number | Expansion coefficient | ||
| Magnetic parameter | Electrical conductivity | ||
| Density of the motile microorganism | Chemo-taxis constant | ||
| Ambient motile microorganism | Inclination angle | ||
| Density of the motile microorganism at the surface | Heat capacity ratio | ||
| Brownian motion number | Mass concentration | ||
| Thermophoresis number | Density ratio | ||
| Brownian parameter | Abbreviations | ||
| Nusselt number | Nanofluid | ||
| Density number of motile microorganisms | Base fluid | ||
| Thermophoresis parameter | Nano-encapsulated phase-change material |
References
- Wong, K.V.; Leon, O.D. Applications of nanofluids: Current and future. Adv. Mech. Eng. 2010, 2, 519659. [Google Scholar] [CrossRef]
- Pandey, A.K.; Kumar, M. Natural convection and thermal radiation influence on nanofluid flow over a stretching cylinder in a porous medium with viscous dissipation. Alex. Eng. J. 2017, 56, 55–62. [Google Scholar] [CrossRef]
- Bhattacharyya, A.; Sharma, R.; Hussain, S.M.; Chamkha, A.J.; Mamatha, E. A numerical and statistical approach to capture the flow characteristics of Maxwell hybrid nanofluid containing copper and graphene nanoparticles. Chin. J. Phys. 2022, 77, 1278–1290. [Google Scholar] [CrossRef]
- Sreedevi, P.; Sudarsana, P.R.; Chamkha, A.J. Heat and mass transfer analysis of unsteady hybrid nanofluid flow over a stretching sheet with thermal radiation. SN Appl. Sci. 2020, 2, 1222. [Google Scholar] [CrossRef]
- Cui, J.; Razzaq, R.; Farooq, U.; Khan, W.A.; Farooq, F.B.; Muhammad, T. Impact of non-similar modelling for forced convection analysis of nano-fluid flow over stretching sheet with chemical reaction and heat generation. Alex. Eng. J. 2022, 61, 4253–4261. [Google Scholar] [CrossRef]
- Gowda, R.P.; Kumar, R.N.; Prasannakumara, B.C.; Nagaraja, B.; Gireesha, B.J. Exploring magnetic dipole contribution on ferromagnetic nanofluid flow over a stretching sheet: An application of Stefan blowing. J. Mol. Liq. 2021, 335, 116215. [Google Scholar] [CrossRef]
- Rawat, S.K.; Upreti, H.; Kumar, M. Numerical study of activation energy and thermal radiation effects on Oldroyd-B nanofluid flow using the Cattaneo–Christov double diffusion model over a convectively heated stretching sheet. Heat Transf. 2021, 50, 5304–5331. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, W.A.; Abbas, S.Z.; Nadeem, S.; Ahmad, S. Impact of induced magnetic field on second-grade nanofluid flow past a convectively heated stretching sheet. Appl. Nanosci. 2020, 10, 3001–3009. [Google Scholar] [CrossRef]
- Ahmad, B.; Ahmad, M.O.; Ali, L.; Ali, B.; Hussein, A.K.; Shah, N.A.; Chung, J.D. Significance of the Coriolis force on the dynamics of Carreau–Yasuda rotating nanofluid subject to Darcy–forchheimer and gyrotactic microorganisms. Mathematics 2022, 10, 2855. [Google Scholar] [CrossRef]
- Rehman, S.U.; Fatima, N.; Ali, B.; Imran, M.; Ali, L.; Shah, N.A.; Chung, J.D. The Casson dusty nanofluid: Significance of Darcy–Forchheimer law, magnetic field, and non-Fourier heat flux model subject to stretch surface. Mathematics 2022, 10, 2877. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K. A critical synthesis of thermophysical characteristics of nanofluids. Int. J. Heat Mass Transf. 2011, 54, 4410–4428. [Google Scholar] [CrossRef]
- Sarkar, S.; Mestry, S.; Mhaske, S. Developments in phase change material (PCM) doped energy efficient polyurethane (PU) foam for perishable food cold-storage applications: A review. J. Energy Storage 2022, 50, 104620. [Google Scholar] [CrossRef]
- Sidik, N.A.C.; Kean, T.H.; Chow, H.K.; Rajaandra, A.; Rahman, S.; Kaur, J. Performance enhancement of cold thermal energy storage system using nanofluid phase change materials: A review. Int. Commun. Heat Mass Transf. 2018, 94, 85–95. [Google Scholar] [CrossRef]
- Meghdadi Isfahani, A.H. Parametric study of rarefaction effects on micro- and nanoscale thermal flows in porous structures. J. Heat Trans. 2017, 139, 092601. [Google Scholar] [CrossRef]
- Kuznetsov, A.V. The onset of nanofluid bioconvection in a suspension containing both nanoparticles and gyrotactic microorganisms. Int. Commun. Heat Mass Transf. 2010, 37, 1421–1425. [Google Scholar] [CrossRef]
- Geng, P.; Kuznetsov, A.V. Effect of small solid particles on the development of bioconvection plumes. Int. Commun. Heat Mass Transf. 2004, 31, 629–638. [Google Scholar] [CrossRef]
- Rana, B.M.J.; Arifuzzaman, S.M.; Islam, S.; Reza-E-Rabbi, S.; Al-Mamun, A.; Mazumder, M.; Chandra Roy, K.; Khan, M.S. Swimming of microbes in blood flow of nano-bioconvective Williamson fluid. Thermal Sci. Eng. Prog. 2021, 25, 101018. [Google Scholar] [CrossRef]
- Kuznetsov, A.V. Non-oscillatory and oscillatory nanofluid bio-thermal convection in a horizontal layer of finite depth. Eur. J. Mech. B/Fluids 2011, 30, 156–165. [Google Scholar] [CrossRef]
- Xu, Y.J.; Bilal, M.; Al-Mdallal, Q.; Khan, M.A.; Muhammad, T. Gyrotactic micro-organism flow of Maxwell nanofluid between two parallel plates. Sci. Rep. 2021, 11, 15142. [Google Scholar] [CrossRef]
- Khan, M.I.; Waqas, H.; Khan, S.U.; Imran, M.; Chu, Y.M.; Abbasi, A.; Kadry, S. Slip flow of micropolar nanofluid over a porous rotating disk with motile microorganisms, nonlinear thermal radiation and activation energy. Int. Commun. Heat Mass Transf. 2021, 122, 105161. [Google Scholar] [CrossRef]
- Ramzan, M.; Gul, H.; Kadry, S.; Chu, Y.M. Role of bioconvection in a three dimensional tangent hyperbolic partially ionized magnetized nanofluid flow with Cattaneo-Christov heat flux and activation energy. Int. Commun. Heat Mass Transf. 2021, 20, 104994. [Google Scholar] [CrossRef]
- Ashraf, M.; Abbas, A.; Zia, S.; Chu, Y.M.; Khan, I.; Nisar, K.S. Computational analysis of the effect of nano particle material motion on mixed convection flow in the presence of heat generation and absorption. CMC-Comput. Mater. Contin. 2020, 65, 1809–1823. [Google Scholar] [CrossRef]
- Abbas, A.; Khandelwal, R.; Ahmad, H.; Ilyas, A.; Ali, K.; Ghachem, R.; Hassen, W.; Kolsi, L. Magnetohydrodynamic bioconvective flow of Williamson nanofluid over a moving inclined plate embedded in a porous medium. Mathematics 2023, 11, 1043. [Google Scholar] [CrossRef]
- Ali, L.; Apsari, R.; Abbas, A.; Tak, P. Entropy generation on the dynamics of volume fraction of nano-particles and Coriolis force impacts on mixed convective nanofluid flow with significant magnetic effect. Numer. Heat Transf. Part A Appl. 2024, 85, 18. [Google Scholar] [CrossRef]
- Analog Devices, Inc. LTspice 24, Free SPICE Simulator Software; Analog Devices, Inc.: Wilmington, MA, USA, 2019. [Google Scholar]
- Hayat, T.; Rashid, M.; Alsaedi, A.; Asghar, S. Nonlinear convective flow of Maxwell nanofluid past a stretching cylinder with thermal radiation and chemical reaction. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 86. [Google Scholar] [CrossRef]
- Chai, L.; Shaukat, R.; Wang, L.; Wang, H.S. A review on heat transfer and hydrodynamic characteristics of nano/microencapsulated phase change slurry (N/MPCS) in mini/microchannel heat sinks. Appl. Therm. Eng. 2018, 135, 334–349. [Google Scholar] [CrossRef]
- Du, X.; Fang, Y.; Cheng, X.; Du, Z.; Zhou, M.; Wang, H. Fabrication and characterization of flame-retardant nano encapsulated n-octadecane with melamine–formaldehyde shell for thermal energy storage. ACS Sustain. Chem. Eng. 2018, 6, 15541–15549. [Google Scholar] [CrossRef]
- Chen, B.; Wang, X.; Zeng, R.; Zhang, Y.; Wang, X.; Niu, J.; Li, Y.; Di, H. An experimental study of convective heat transfer with microencapsulated phase change material suspension: Laminar flow in a circular tube under constant heat flux. Exp. Therm. Fluid Sci. 2008, 32, 1638–1646. [Google Scholar] [CrossRef]
- Zueco, J.; Beg, O.A. Network numerical simulation of hydromagnetic Marangoni mixed convection boundary layers. Chem. Eng. Commun. 2011, 198, 552–571. [Google Scholar] [CrossRef]
- Caravaca Garratón, M.; García-Onsurbe, M.C.; Soto-Meca, A. A new Network Simulation Method for the characterization of delay differential equations. Ain Shams Eng. J. 2023, 14, 102066. [Google Scholar] [CrossRef]
- Liu, C.; Khan, M.U.; Ramzan, M.; Chu, Y.M.; Kadry, S.; Malik, M.Y.; Chinram, R. Nonlinear radiative Maxwell nanofluid flow in a Darcy–Forchheimer permeable media over a stretching cylinder with chemical reaction and bioconvection. Sci. Rep. 2021, 11, 9391. [Google Scholar] [CrossRef] [PubMed]
- Khan, J.A.; Mustafa, M.A. Numerical analysis for non-linear radiation in MHD flow around a cylindrical surface with chemically reactive species. Res. Phys. 2018, 8, 963–970. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Mehryan, S.A.M.; Ayoubloo, K.A.; Hajjar, A.; Islam, M.S.; Younis, O.; Aly, A.M. Thermal behavior and energy storage of a suspension of nano-encapsulated phase change materials in an enclosure. Adv. Powder Tech. 2021, 32, 2004–2019. [Google Scholar] [CrossRef]

| Substance | ||||
|---|---|---|---|---|
| Water | 995.6 | 4180 | 0.615 | 796 |
| Nonadecane (core) | 721 | 2037 | 0.190 | --- |
| Polyurethane (shell) | 786 | 1317 | 0.025 | --- |
| M | Present, NSM −f″(0) | Present, Runge–Kutta −f″(0) | [32] −f″(0) | [33] −f″(0) |
|---|---|---|---|---|
| 0 | 0.9984 | 0.9988 | 1.00000 | 1.00000 |
| 0.2 | 1.0146 | 1.0139 | 1.01981 | 1.01980 |
| 0.5 | 1.0901 | 1.0868 | 1.11803 | 1.11803 |
| 0.8 | 1.2709 | 1.2847 | 1.28062 | 1.28062 |
| 1.0 | 1.4101 | 1.4036 | 1.41421 | 1.41421 |
| Δη = 0.001 | Δη = 0.0001 | |||||||
|---|---|---|---|---|---|---|---|---|
| η | f″(η) | θ(η) | ϕ(η) | χ(η) | f″(η) | θ(η) | ϕ(η) | χ(η) |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0.1726 | 0.4870 | 0.9209 | 0.5116 | 0.1727 | 0.4871 | 0.9210 | 0.5117 |
| 2 | −0.0378 | 0.4870 | 0.9209 | 0.2230 | −0.0378 | 0.2251 | 0.7313 | 0.2230 |
| 3 | −0.0724 | 0.2251 | 0.7312 | 0.0745 | −0.0724 | 0.1117 | 0.4618 | 0.0746 |
| 4 | −0.0492 | 0.1116 | 0.4617 | 0.01881 | −0.04992 | 0.0462 | 0.2140 | 0.0181 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, B.; Ahmed, S.; Zueco, J. Bioconvective Flow Characteristics of NEPCM–Water Nanofluid over an Inclined Cylinder in Porous Medium: An Extended Darcy Model Approach. Mathematics 2024, 12, 4012. https://doi.org/10.3390/math12244012
Das B, Ahmed S, Zueco J. Bioconvective Flow Characteristics of NEPCM–Water Nanofluid over an Inclined Cylinder in Porous Medium: An Extended Darcy Model Approach. Mathematics. 2024; 12(24):4012. https://doi.org/10.3390/math12244012
Chicago/Turabian StyleDas, Bikash, Sahin Ahmed, and Joaquín Zueco. 2024. "Bioconvective Flow Characteristics of NEPCM–Water Nanofluid over an Inclined Cylinder in Porous Medium: An Extended Darcy Model Approach" Mathematics 12, no. 24: 4012. https://doi.org/10.3390/math12244012
APA StyleDas, B., Ahmed, S., & Zueco, J. (2024). Bioconvective Flow Characteristics of NEPCM–Water Nanofluid over an Inclined Cylinder in Porous Medium: An Extended Darcy Model Approach. Mathematics, 12(24), 4012. https://doi.org/10.3390/math12244012






