Clade Size Statistics Under Ford’s α-Model
Abstract
1. Introduction
2. Preliminaries
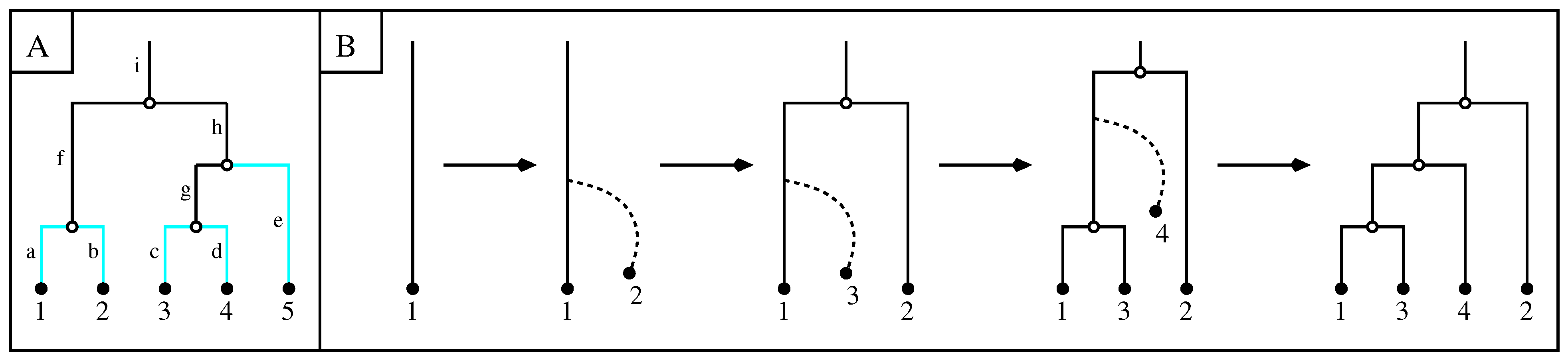
3. Clade Size of a Set of Initially Monophyletic Leaves Subject to -Insertions
- (i)
- The right-hand side of Equation (4) is extended by continuity to the cases of or . In particular, when and , the second factor in the formula reads as , while for and it is provided by . If we instead have and , then the third factor in the formula becomes , while for and it reads as .
- (ii)
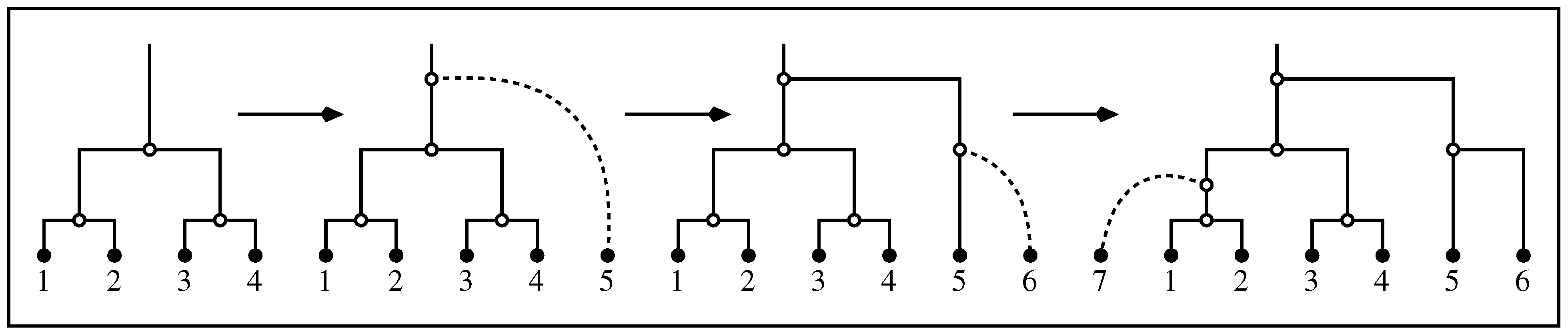
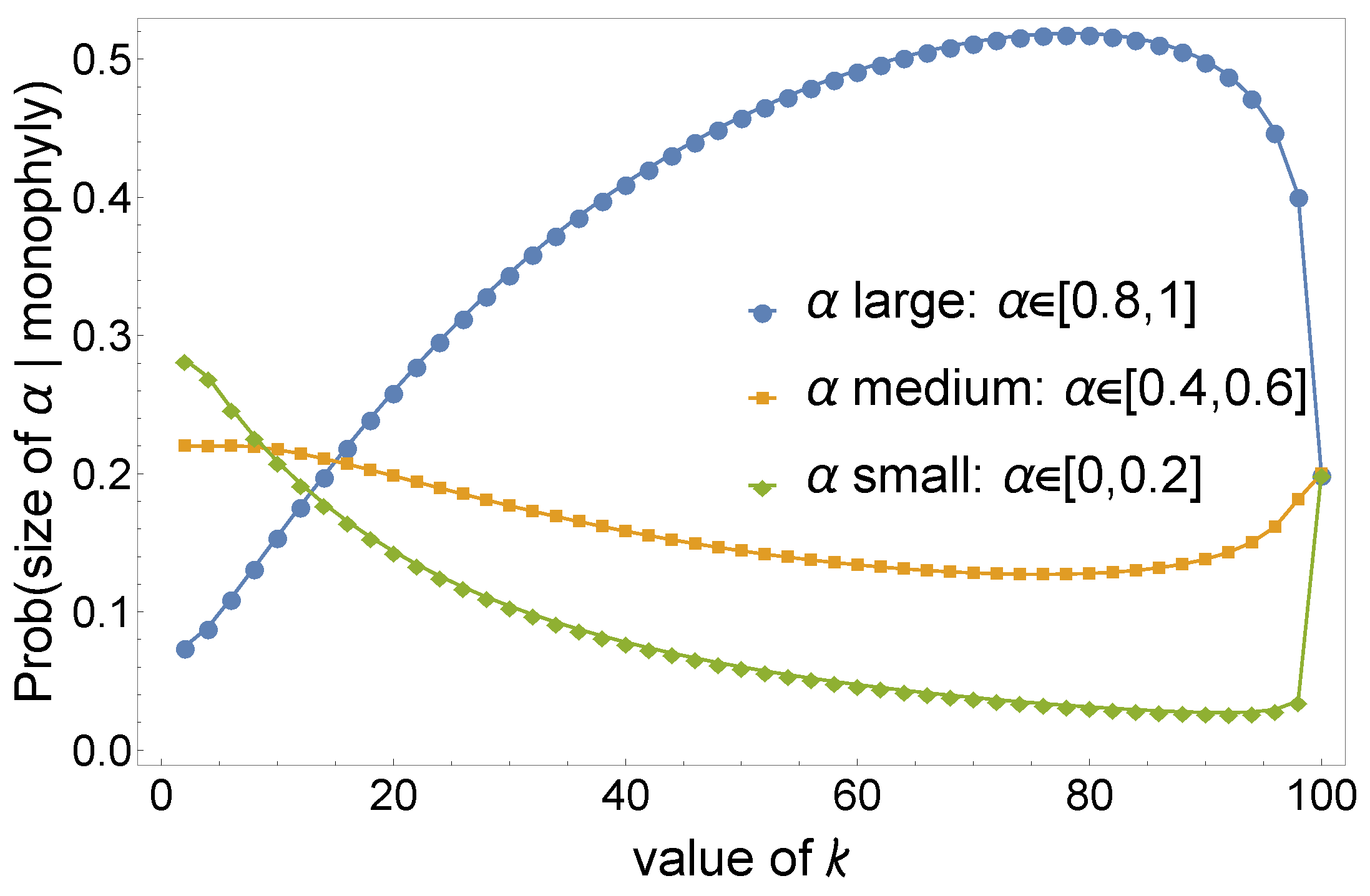
- Lower values of the α parameter determine a larger expected clade size and smaller variance. This is shown in Figure 3, where we perform a sequence of α-insertions (2) starting from a labeled topology of size , then calculate the mean and variance of the clade size of the set of leaves of in the resulting random labeled topology of size n (Figure 2).
- (iii)
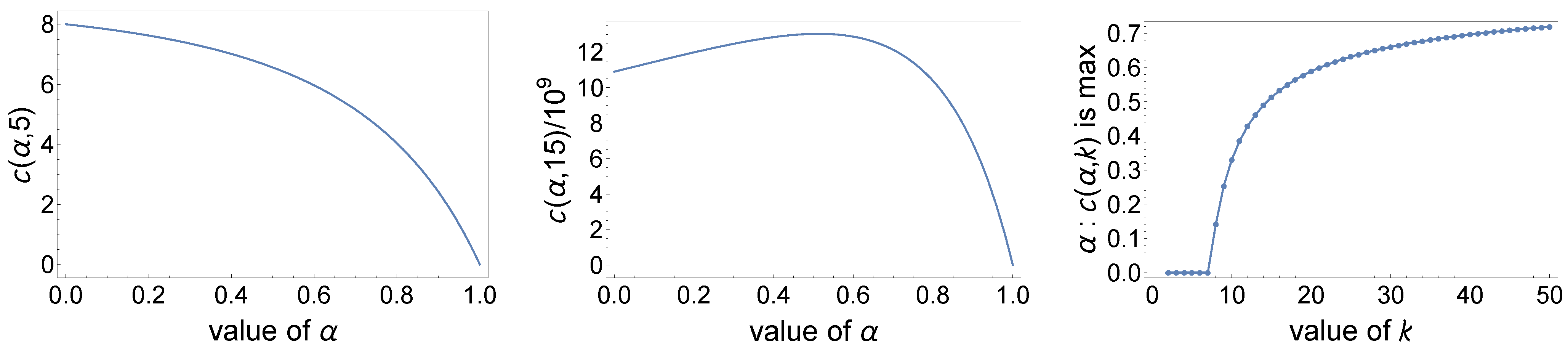
- For fixed values of k and d, the asymptotic formula for , which holds for every complex number , yields the following asymptotic expansion as for the probabilityIn particular, for increasing values of n, the probability of the set of initially monophyletic leaves remaining monophyletic decreases to 0 as quickly as . From Theorem 1, the probability of the clade size of the starting set of leaves being equal to n is instead seen to be . By substituting in (4), we find that for , the probability of the ratio being a fixed satisfies
- (iv)
- It is possible to calculate the probability mass function of the clade size variable without making use of the generalized binomial coefficient. Indeed, by simple algebraic manipulations, from the formula provided in the latter theorem we can also writewhere we admit empty products.
4. Probability of Monophyly for a Set of Random Taxa
- (i)
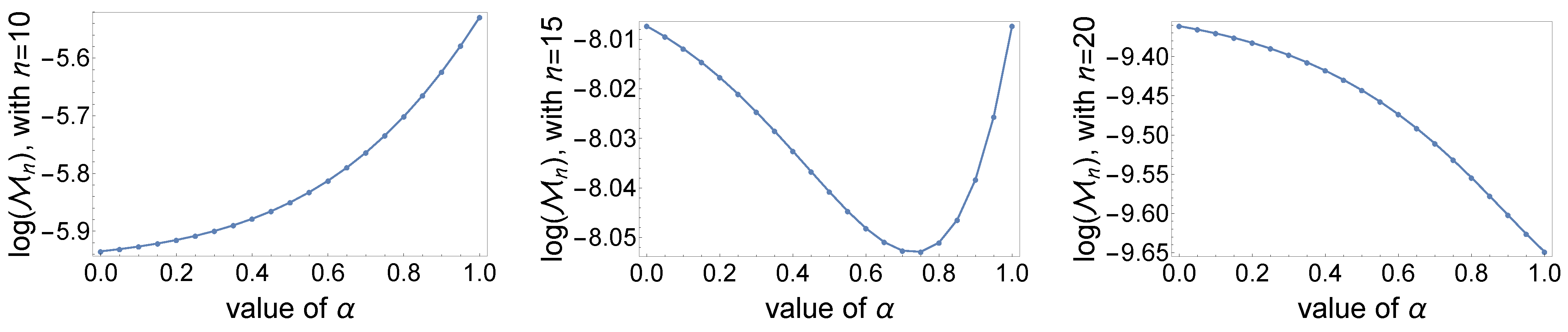
- For different values of n, we can observe a different behavior by plotting the (natural logarithm of the) probability as a function of α (Figure 4). The mentioned probability can be an increasing function of α (left panel), a decreasing function of α (right panel), or a unimodal function of α (middle panel).
- (ii)
- The formula for that appears in (8) calculates the probability of monophyly for a set of k taxa chosen at random from among the leaves of a labeled topology of size n selected under the Ford’s distribution and when or (the latter when we consider the limit ). Indeed, for , by substituting in the third of the following equalities and applying the Chu–Vandermonde identity in the fourth equality, the formula for reduces toFurthermore, when , we can use Legendre’s duplication formula to findFor , we havewhile providesHence,showing that the formula in (8) extended by continuity to yields the right expression for the probability .
- (iii)
- The formula for provided in the latter theorem can be further simplified for fixed values of k. For instance, when or , Equation (8) respectively reduces to the following:andMore generally, explicit expressions for can be determined for fixed values of k by writing the sum in (8) as a telescoping sum:wherefor a polynomial whose coefficients satisfyand the linear systemNote that if satisfies (12) and (13), then as in the first equality of (11) we indeed findbecause and are identical as polynomials of degree in the variable h with leading coefficient and roots .
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aldous, D.J. Stochastic models and descriptive statistics for phylogenetic trees, from Yule to today. Stat. Sci. 2001, 16, 23–34. [Google Scholar] [CrossRef]
- Ford, D.J. Probabilities on cladograms: Introduction to the alpha model. arXiv 2005, arXiv:0511246. [Google Scholar]
- Zhu, S.; Degnan, J.H.; Steel, M. Clades, clans, and reciprocal monophyly under neutral evolutionary models. Theor. Popul. Biol. 2011, 79, 220–227. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Than, C.; Wu, T. Clades and clans: A comparison study of two evolutionary models. J. Math. Biol. 2015, 71, 99–124. [Google Scholar] [CrossRef] [PubMed]
- Di Nunzio, A.; Disanto, F. Clade size distribution under neutral evolutionary models. Theor. Popul. Biol. 2024, 156, 93–102. [Google Scholar] [CrossRef]
- Rosenberg, N.A. The mean and variance of the numbers of r-pronged nodes and r-caterpillars in Yule-generated genealogical trees. Ann. Comb. 2006, 10, 129–146. [Google Scholar] [CrossRef]
- Semple, C.; Steel, M. Phylogenetics; Oxford Univ. Press: Oxford, UK, 2003. [Google Scholar]
- Coronado, T.M.; Mir, A.; Rosselló, F. The probabilities of trees and cladograms under Ford’s α-model. Sci. World J. 2018, 2018, 1916094. [Google Scholar] [CrossRef] [PubMed]
- Czabarka, E.; Székely, L.A.; Wagner, S. Inducibility in Binary Trees and Crossings in Random Tanglegrams. SIAM J. Discret. Math. 2017, 31, 1732–1750. [Google Scholar] [CrossRef]
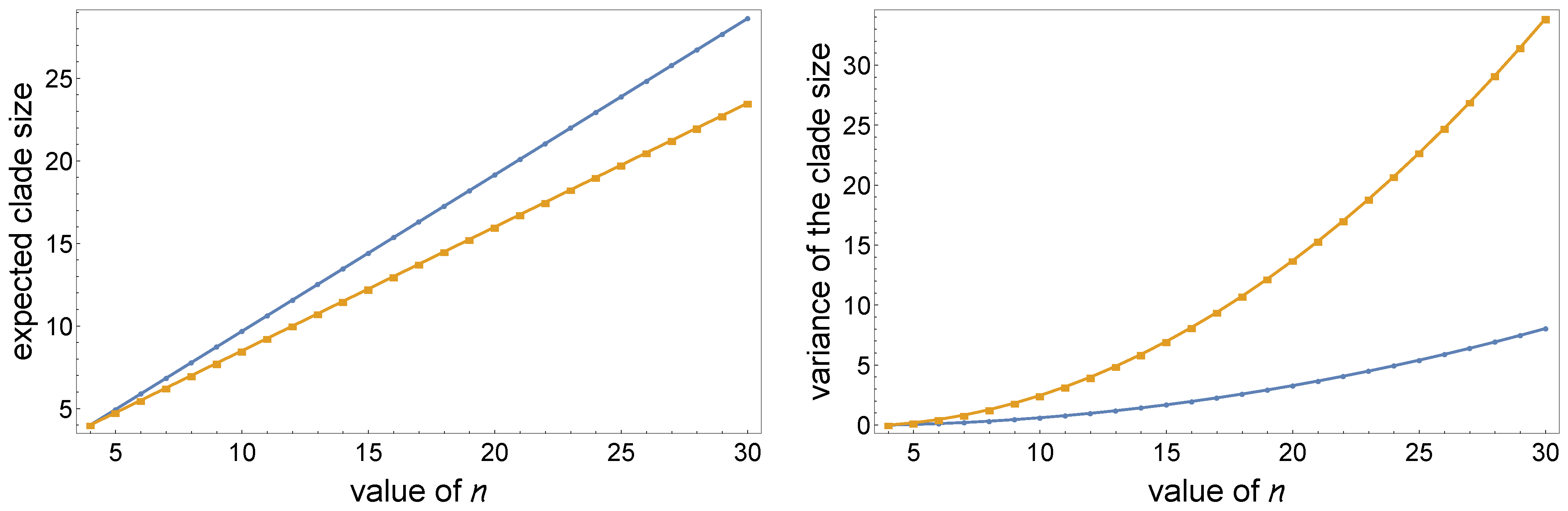
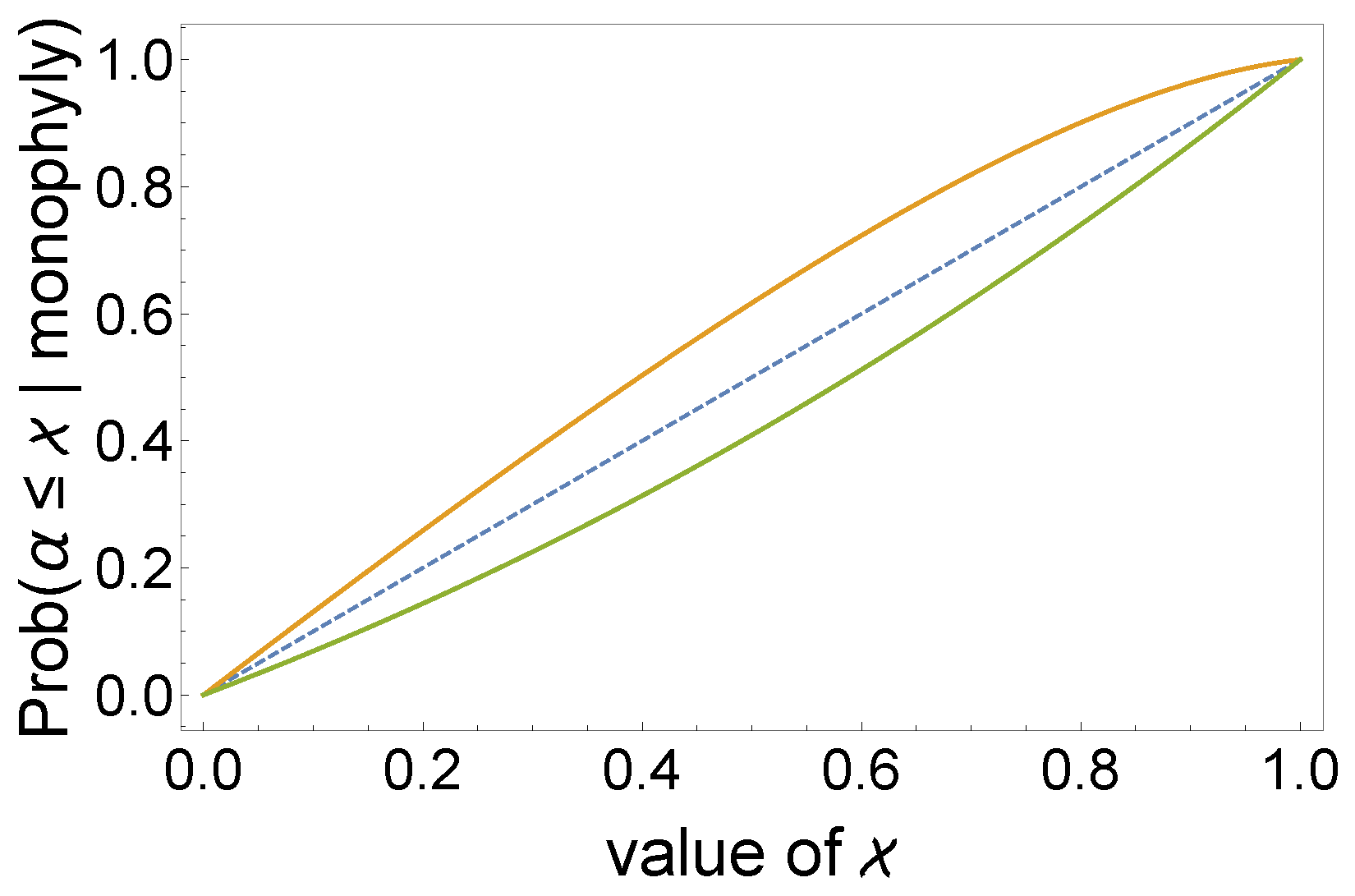
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Nunzio, A.; Disanto, F. Clade Size Statistics Under Ford’s α-Model. Mathematics 2024, 12, 3974. https://doi.org/10.3390/math12243974
Di Nunzio A, Disanto F. Clade Size Statistics Under Ford’s α-Model. Mathematics. 2024; 12(24):3974. https://doi.org/10.3390/math12243974
Chicago/Turabian StyleDi Nunzio, Antonio, and Filippo Disanto. 2024. "Clade Size Statistics Under Ford’s α-Model" Mathematics 12, no. 24: 3974. https://doi.org/10.3390/math12243974
APA StyleDi Nunzio, A., & Disanto, F. (2024). Clade Size Statistics Under Ford’s α-Model. Mathematics, 12(24), 3974. https://doi.org/10.3390/math12243974





