A Novel DV-Hop Localization Method Based on Hybrid Improved Weighted Hyperbolic Strategy and Proportional Integral Derivative Search Algorithm
Abstract
1. Introduction
2. Related Work
2.1. Classical DV-Hop Algorithm
2.2. DV-Hop Error Analysis
- Error in the hop value. Assume there are four neighboring nodes within the communication radius of a node. The hop value to each of the four neighboring nodes is assigned as 1, which is inconsistent with the actual situation. Therefore, there is a hop value error during the hop number acquisition stage [13].
- Average hop distance error. The average hop distance to the nearest beacon node is used to calculate the distance between the unknown node and the beacon node. Since the path between the two beacon nodes is not a straight line, the average hop distance is often smaller than the actual value.
- Coordinate estimation error. A certain amount of error inevitably arises during the node coordinate estimation stage in the distance calculation. As errors accumulate during the solution of the coordinate system equations, the final results deviate more significantly from the actual values [14].
2.3. PID Search Algorithm
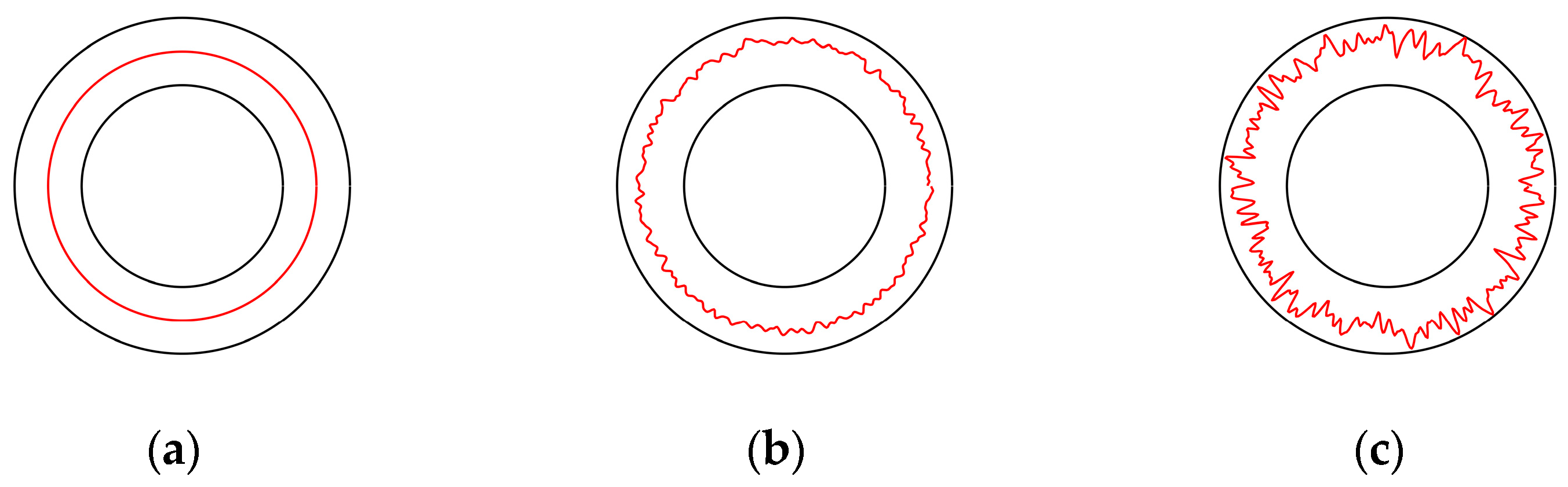
2.4. Irregular Radio Communication and Anisotropic Network
3. Methodology and Model
3.1. IPSA-DV-Hop Algorithm
3.1.1. First Hop Distance Refinement and Weighting
3.1.2. Weighted Hyperbolic Strategy Based on Collinearity
3.1.3. Improved PSA Mechanism
- Calculating system deviations
- 2.
- PID regulation
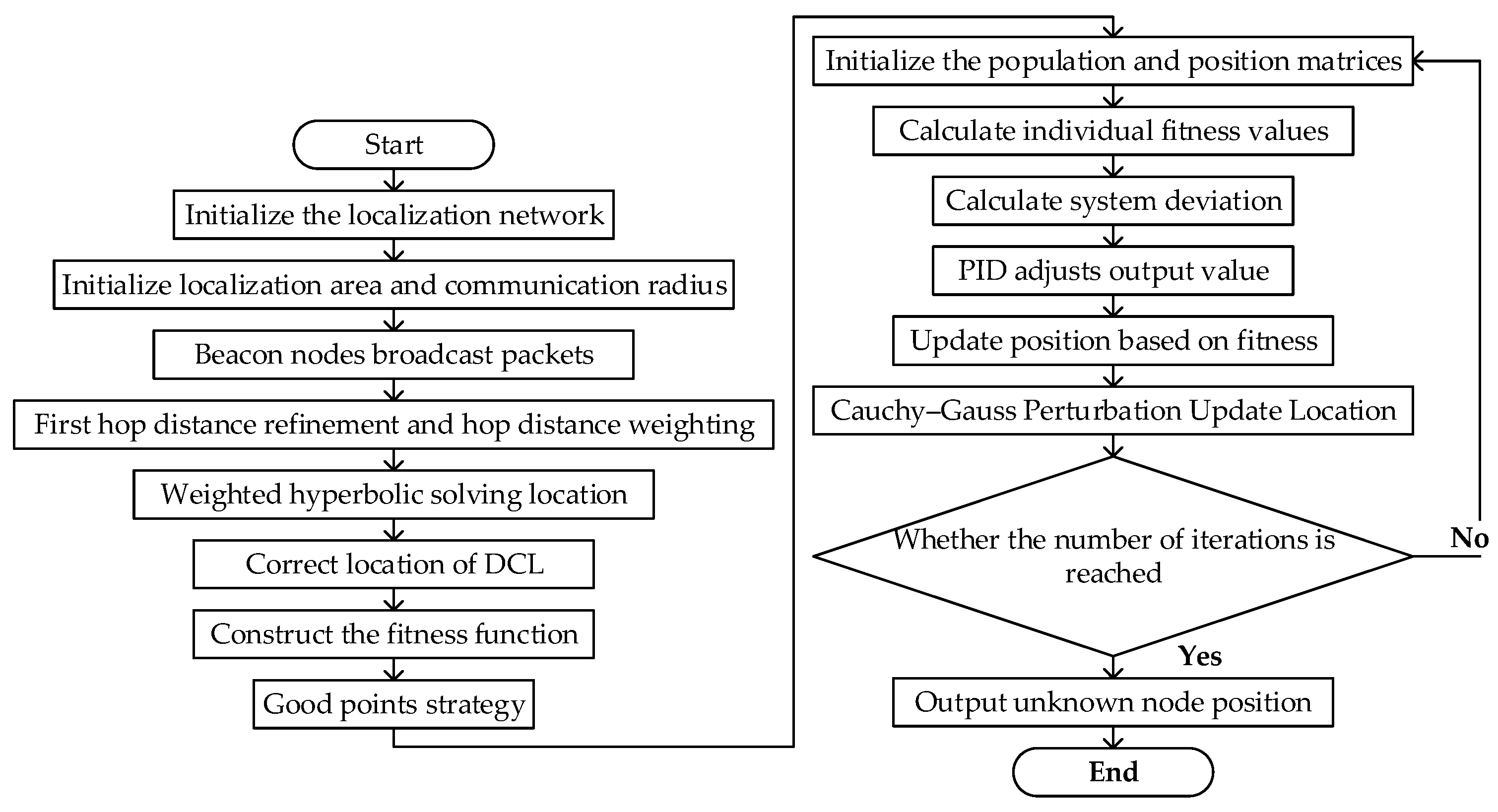
3.2. Two-DimensionalAlgorithm Process
- The initial localization scenario is a square area of meters with nodes and beacon nodes.
- The beacon node broadcasts its location information; the unknown node receives the broadcast packet to obtain the RSSI value and hop distance information between nodes. The unknown node then forwards the hop distance after incrementing it by one, then compares and saves the minimum hop count information to the beacon node.
- The first hop distance is refined using the received RSSI value and the hop count between nodes is calculated based on the refined first hop distance.
- The unknown node calculates its estimated coordinates using the average hop distance and obtains the average hop distance weighted by the distance error.
- The node coordinates are determined using a weighted hyperbolic algorithm, which is combined with the DCL of the node group to further refine the position coordinates.
- The PSA decision variables, constraints, and objective function are initialized. The initial group position coordinates are constructed using the Good Point Set strategy and the fitness function for estimating the unknown node position.
- The system deviation is calculated and iteratively updated using the PID regulation process. The Cauchy–Gaussian perturbation strategy is incorporated in the later stages of the algorithm to output the optimal node position coordinates.
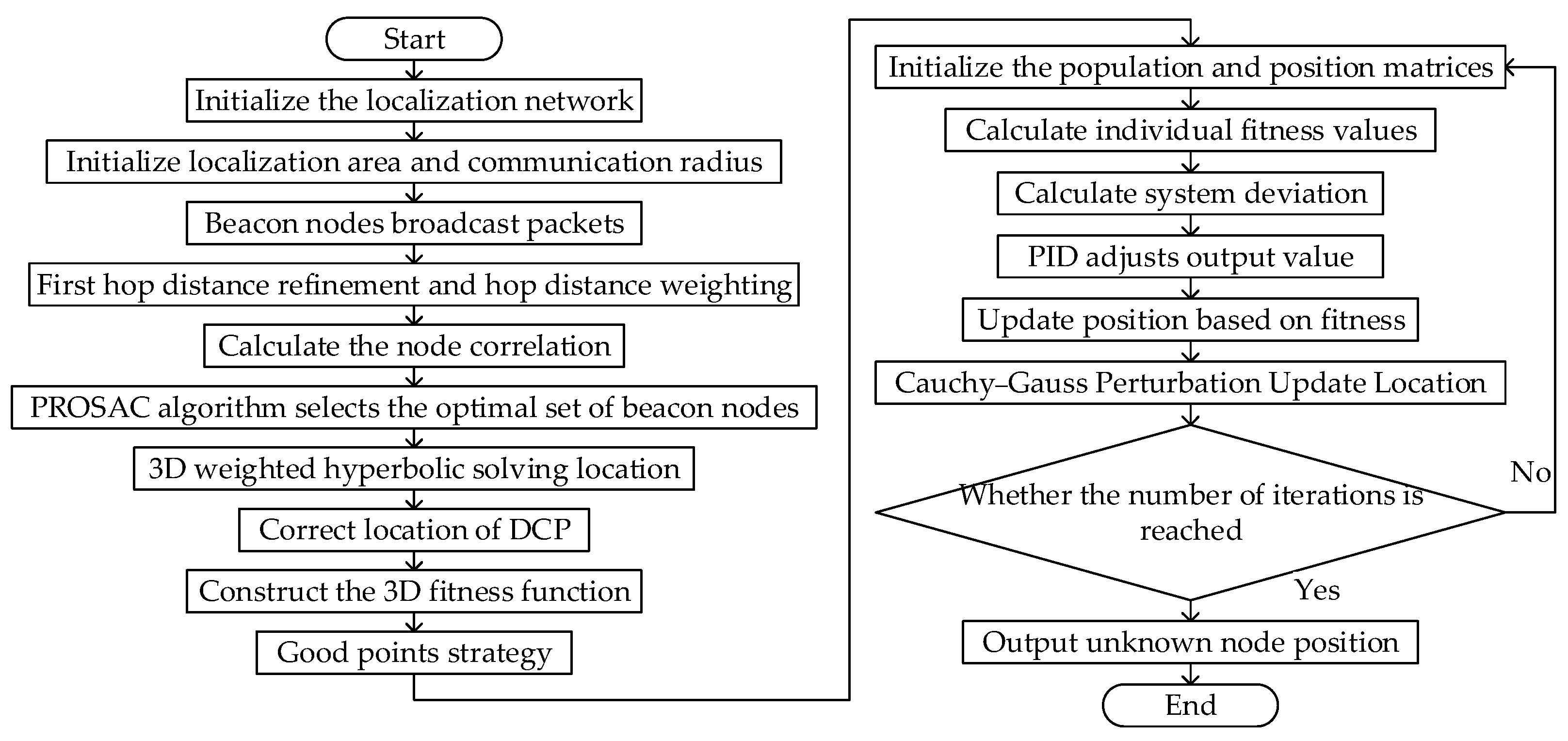
3.3. Three-Dimensional PSA-DV-Hop Algorithm Based on Optimal Subset of Nodes
3.3.1. Node Correlation Degree
3.3.2. The Subset of Optimal Nodes
- Beacon node sorting: All beacon nodes are sorted based on their relevance, which is determined by their correlation to the target node.
- Progressive sampling: Sampling begins from the highest-ranked nodes based on the sorting results, and the sampling set is gradually expanded as the number of iterations increases.
- Model evaluation and selection: The Euclidean distance between the selected beacon nodes is calculated and divided by the hop count to obtain the average distance per hop. The quality of the selected beacon node combination is then evaluated by assessing the stability and consistency of the computed average distance per hop.
- Termination condition: The current optimal combination of beacon nodes is selected if it meets the predetermined accuracy requirement.
3.3.3. The 3D Weighted Hyperbolic Algorithm
3.4. Analysis of Algorithm Complexity
4. Simulation Results and Analysis
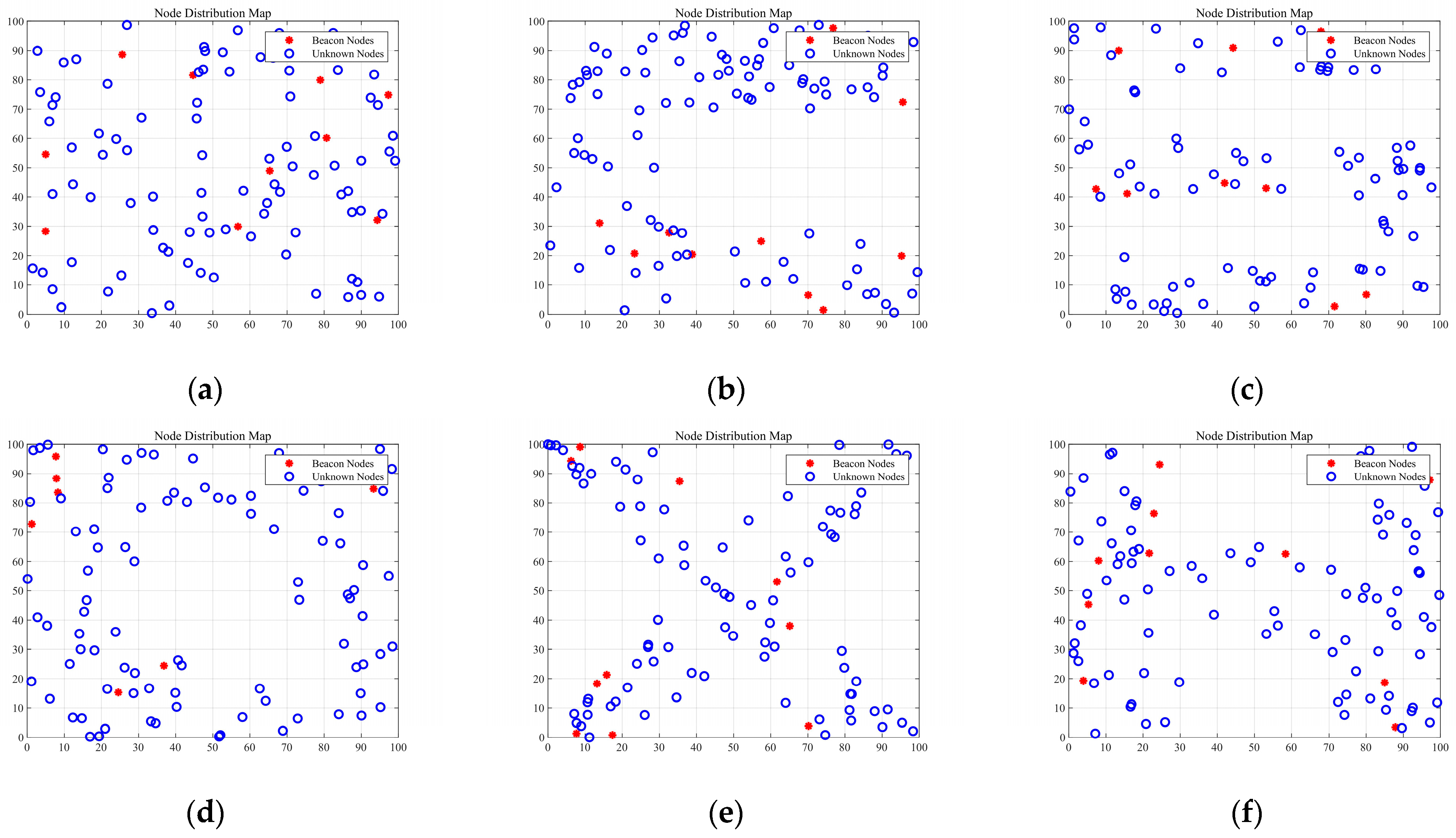
4.1. Two-DimensionalSimulation Parameters and Results
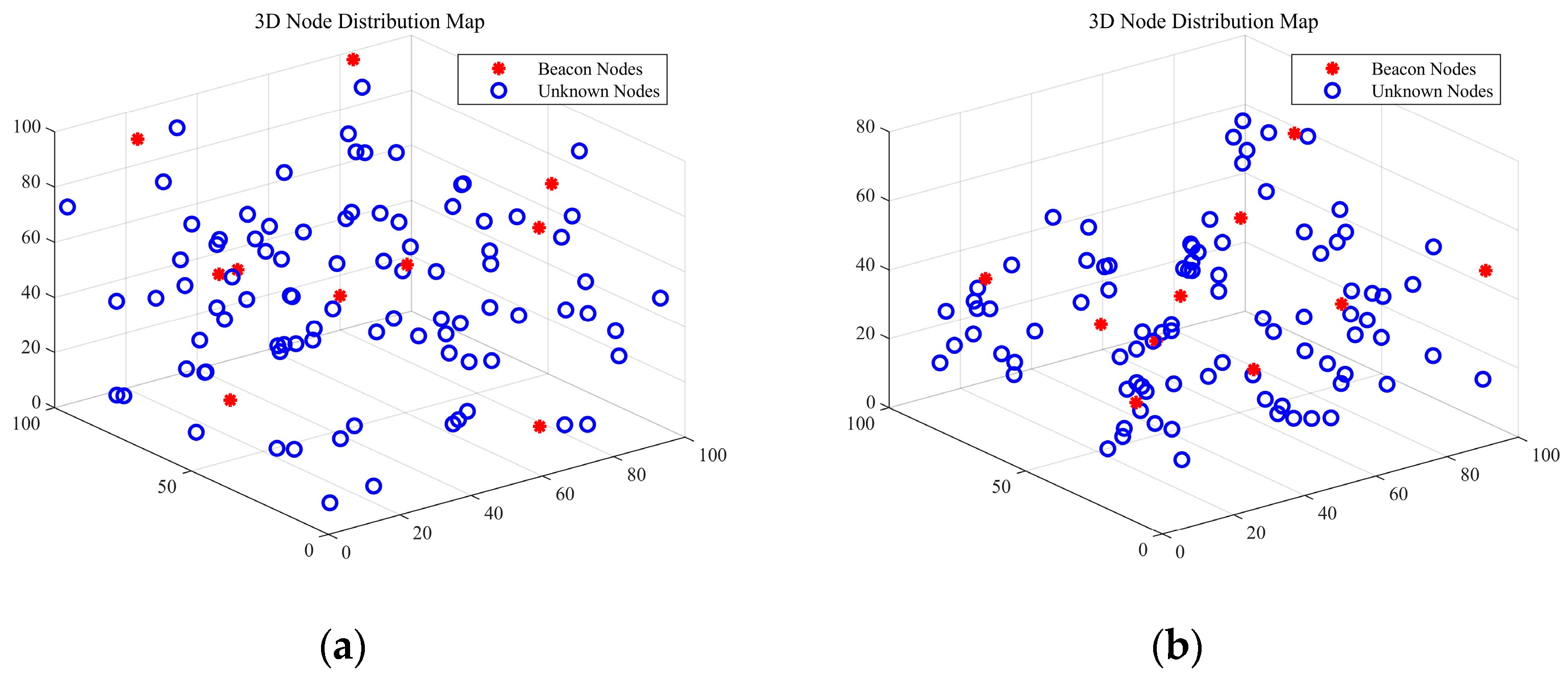
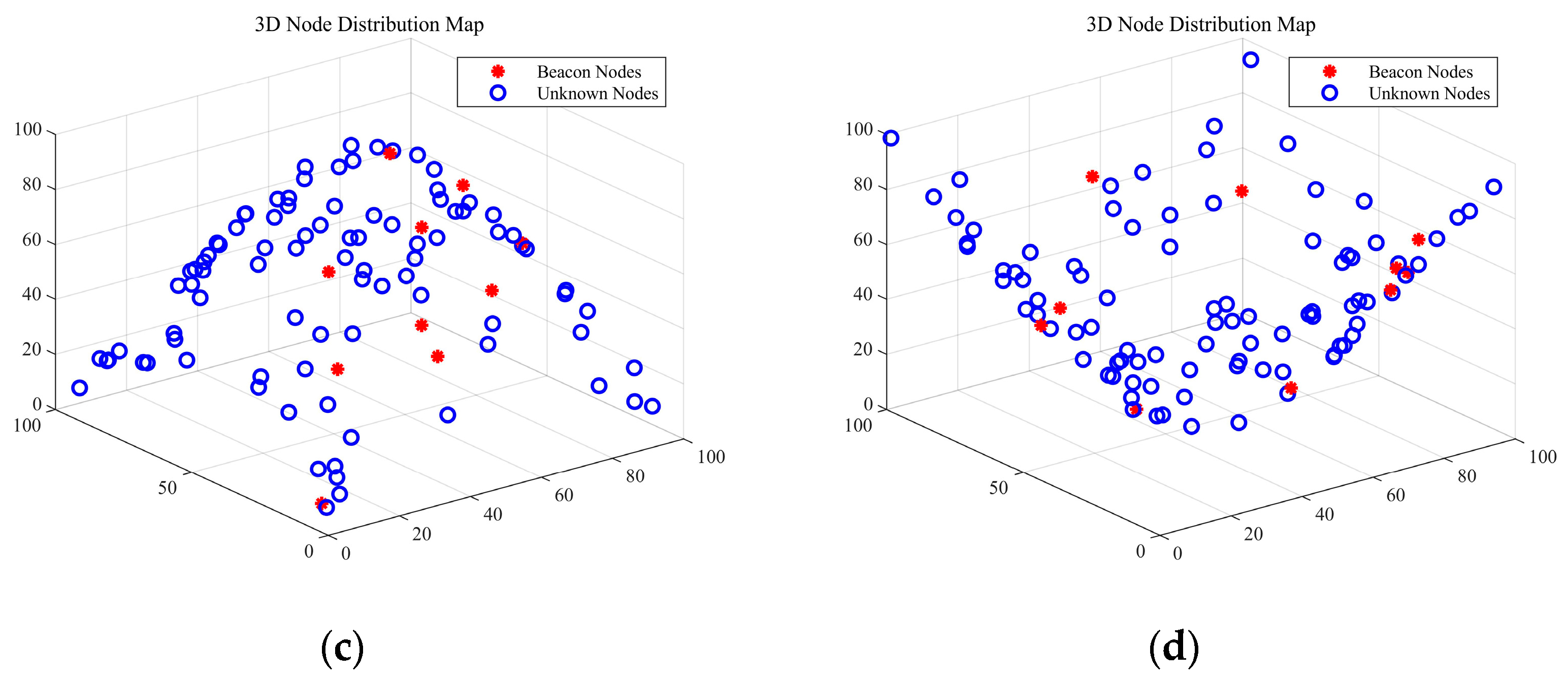
4.2. Three-Dimensional Simulation Parameters and Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Patel, N.R.; Kumar, S. Wireless Sensor Networks’ Challenges and Future Prospects. In Proceedings of the 2018 International Conference on System Modeling & Advancement in Research Trends (SMART), Moradabad, India, 23–24 November 2018; pp. 60–65. [Google Scholar]
- Sivasakthiselvan, S.; Nagarajan, V. Localization Techniques of Wireless Sensor Networks: A Review. In Proceedings of the 2020 International Conference on Communication and Signal Processing (ICCSP), Chennai, India, 28–30 July 2020; pp. 1643–1648. [Google Scholar]
- Park, K.-D.; Yoon, W.-J.; Lee, J.-S. Reduction of Multipath Effect in GNSS Positioning by Applying Pseudorange Acceleration as Weight. Sensors 2024, 24, 6880. [Google Scholar] [CrossRef] [PubMed]
- Saad, E.; Elhosseini, M.; Haikal, A.Y. Recent Achievements in Sensor Localization Algorithms. Alex. Eng. J. 2018, 57, 4219–4228. [Google Scholar] [CrossRef]
- Chadha, J.; Jain, A. Anatomization on Range-Free Localization Algorithms in Wireless Sensor Networks. In Proceedings of the 2019 2nd International Conference on Power Energy, Environment and Intelligent Control (PEEIC), Greater Noida, India, 18–19 October 2019; pp. 489–492. [Google Scholar]
- Cao, Y.; Qian, Y.; Wang, Z. DV-Hop Based Localization Algorithm Using Node Negotiation and Multiple Communication Radii for Wireless Sensor Network. Wirel. Netw. 2023, 29, 3493–3513. [Google Scholar] [CrossRef]
- Achroufene, A. RSSI-Based Geometric Localization in Wireless Sensor Networks. J. Supercomput. 2023, 79, 5615–5642. [Google Scholar] [CrossRef]
- Singh, P.; Mittal, N.; Singh, P. A Novel Hybrid Range-Free Approach to Locate Sensor Nodes in 3D WSN Using GWO-FA Algorithm. Telecommun. Syst. 2022, 80, 303–323. [Google Scholar] [CrossRef]
- Mohanta, T.K.; Das, D.K. A Three-Dimensional Wireless Sensor Network with an Improved Localization Algorithm Based on Orthogonal Learning Class Topper Optimization. Ann. Telecommun. 2023, 78, 475–489. [Google Scholar] [CrossRef]
- Niculescu, D. DV Based Positioning in Ad Hoc Networks. Telecommun. Syst. 2003, 22, 267–280. [Google Scholar] [CrossRef]
- Cai, X.; Hu, K.; Zhang, F.; Li, W.; Li, Y.; Zhang, Z. Research on Node Location Technology Based on Improved Particle Swarm Optimization. In Proceedings of the 2019 IEEE Symposium Series on Computational Intelligence (SSCI), Xiamen, China, 6–9 December 2019; pp. 2833–2837. [Google Scholar]
- Xue, D. Research of Localization Algorithm for Wireless Sensor Network Based on DV-Hop. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 218. [Google Scholar] [CrossRef]
- Sharma, N.; Gupta, V. Meta-Heuristic Based Optimization of WSNs Localisation Problem—A Survey. Procedia Comput. Sci. 2020, 173, 36–45. [Google Scholar] [CrossRef]
- Srivastava, A.; Mishra, P.K. A Survey on WSN Issues with Its Heuristics and Meta-Heuristics Solutions. Wirel. Pers. Commun. 2021, 121, 745–814. [Google Scholar] [CrossRef]
- Gao, Y. PID-Based Search Algorithm: A Novel Metaheuristic Algorithm Based on PID Algorithm. Expert Syst. Appl. 2023, 232, 120886. [Google Scholar] [CrossRef]
- Niu, S.S.; Xiao, D. Basic PID Control. In Process Control; Advances in Industrial Control; Springer International Publishing: Cham, Switzerland, 2022; pp. 67–114. [Google Scholar]
- Bhat, S.J.; Santhosh, K.V. Localization of Isotropic and Anisotropic Wireless Sensor Networks in 2D and 3D Fields. Telecommun. Syst. 2022, 79, 309–321. [Google Scholar] [CrossRef]
- He, T.; Huang, C.; Blum, B.M.; Stankovic, J.A.; Abdelzaher, T. Range-Free Localization Schemes for Large Scale Sensor Networks. In Proceedings of the 9th Annual International Conference on Mobile Computing and Networking, San Diego, CA, USA, 14–19 September 2003; pp. 81–95. [Google Scholar]
- Poggi, C.; Mazzini, G. Collinearity for Sensor Network Localization. In Proceedings of the 2003 IEEE 58th Vehicular Technology Conference. VTC 2003-Fall (IEEE Cat. No.03CH37484), Orlando, FL, USA, 6–9 October 2003; pp. 3040–3044. [Google Scholar]
- Elsawah, A.M.; Fang, K.-T.; Deng, Y.H. Some Interesting Behaviors of Good Lattice Point Sets. Commun. Stat. Simul. Comput. 2021, 50, 3650–3668. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, S.S.; Singh, K.; Bisis, B. Link Prediction Techniques, Applications, and Performance: A Survey. Phys. Stat. Mech. Its Appl. 2020, 553, 124289. [Google Scholar] [CrossRef]
- Lü, L.; Zhou, T. Link Prediction in Complex Networks: A Survey. Phys. Stat. Mech. Its Appl. 2011, 390, 1150–1170. [Google Scholar] [CrossRef]
- Chum, O.; Matas, J. Matching with PROSAC—Progressive Sample Consensus. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 1, pp. 220–226. [Google Scholar]
- Reddy, M.R.; Chandra, M.L.R. An Improved 3D-DV-Hop Localization Algorithm to Improve Accuracy for 3D Wireless Sensor Networks. SN Comput. Sci. 2024, 5, 245. [Google Scholar] [CrossRef]
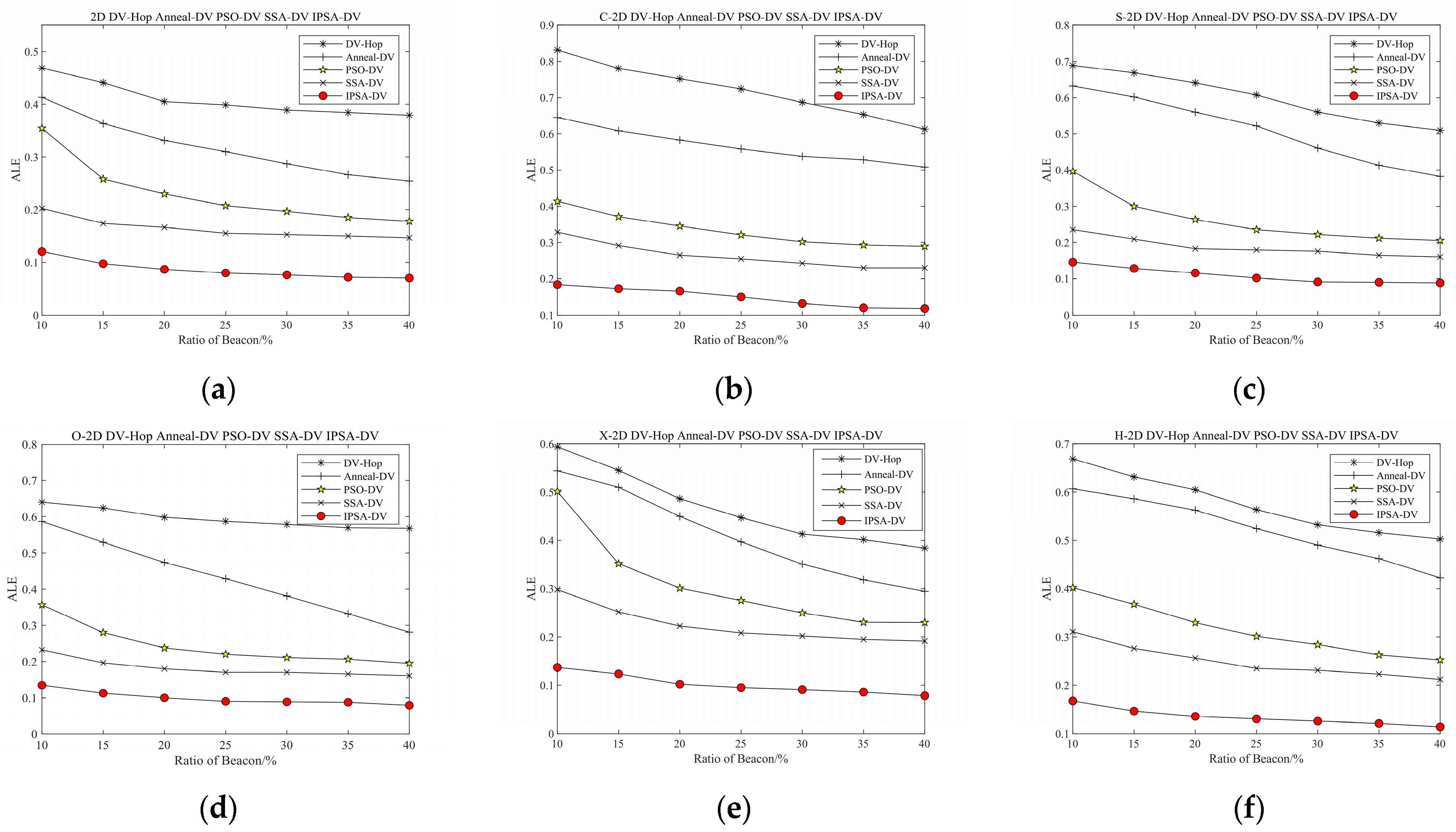

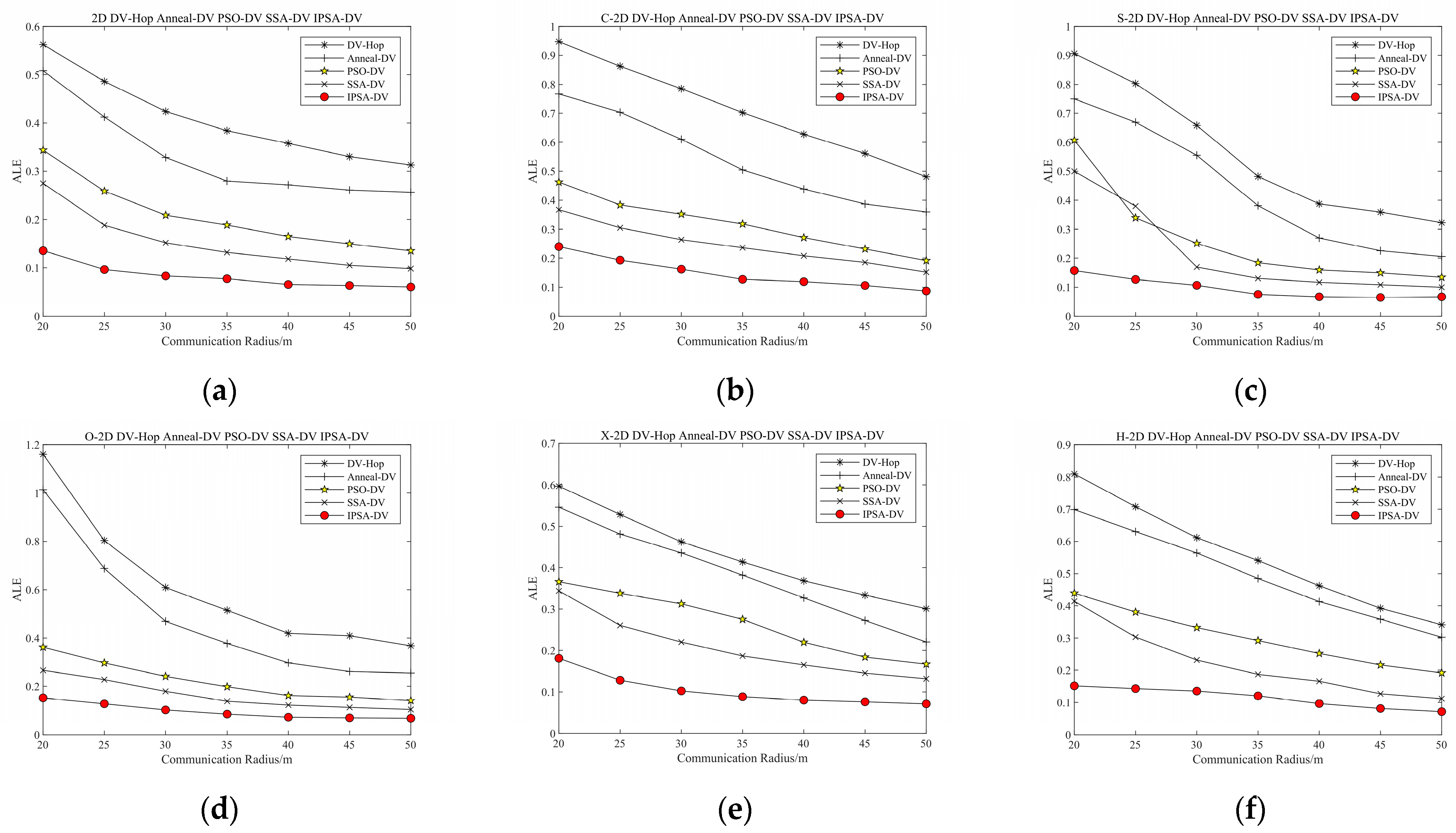

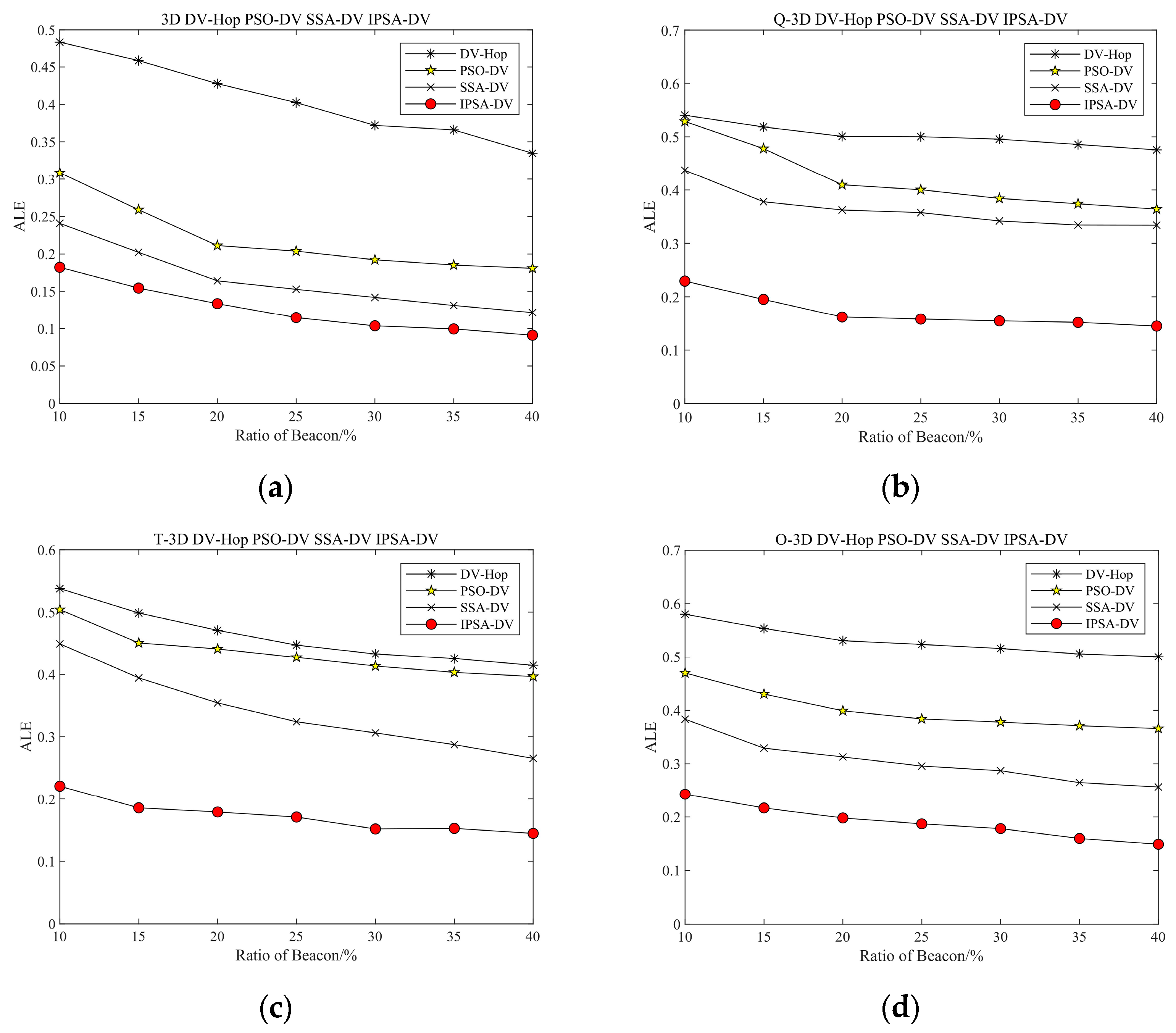
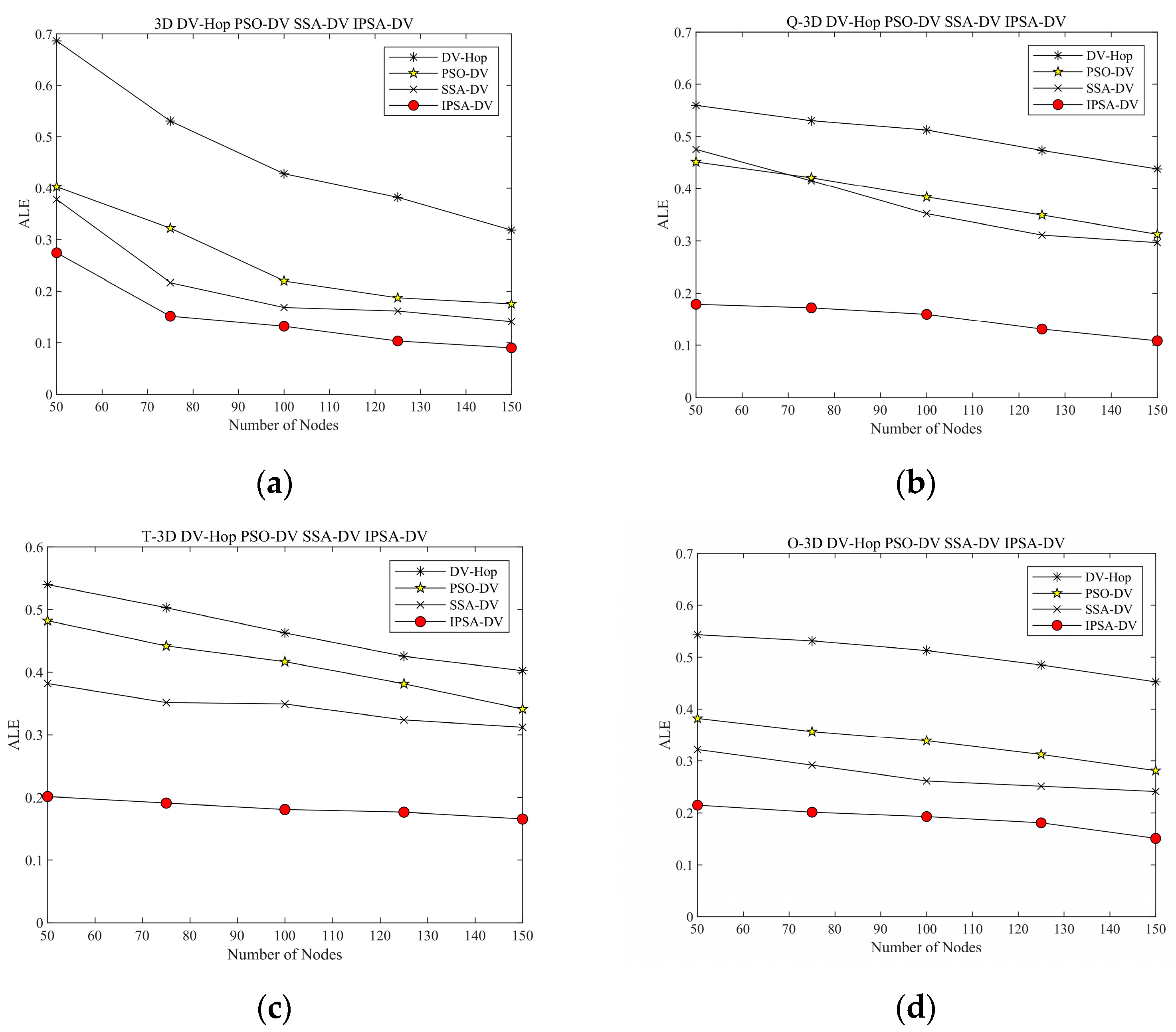
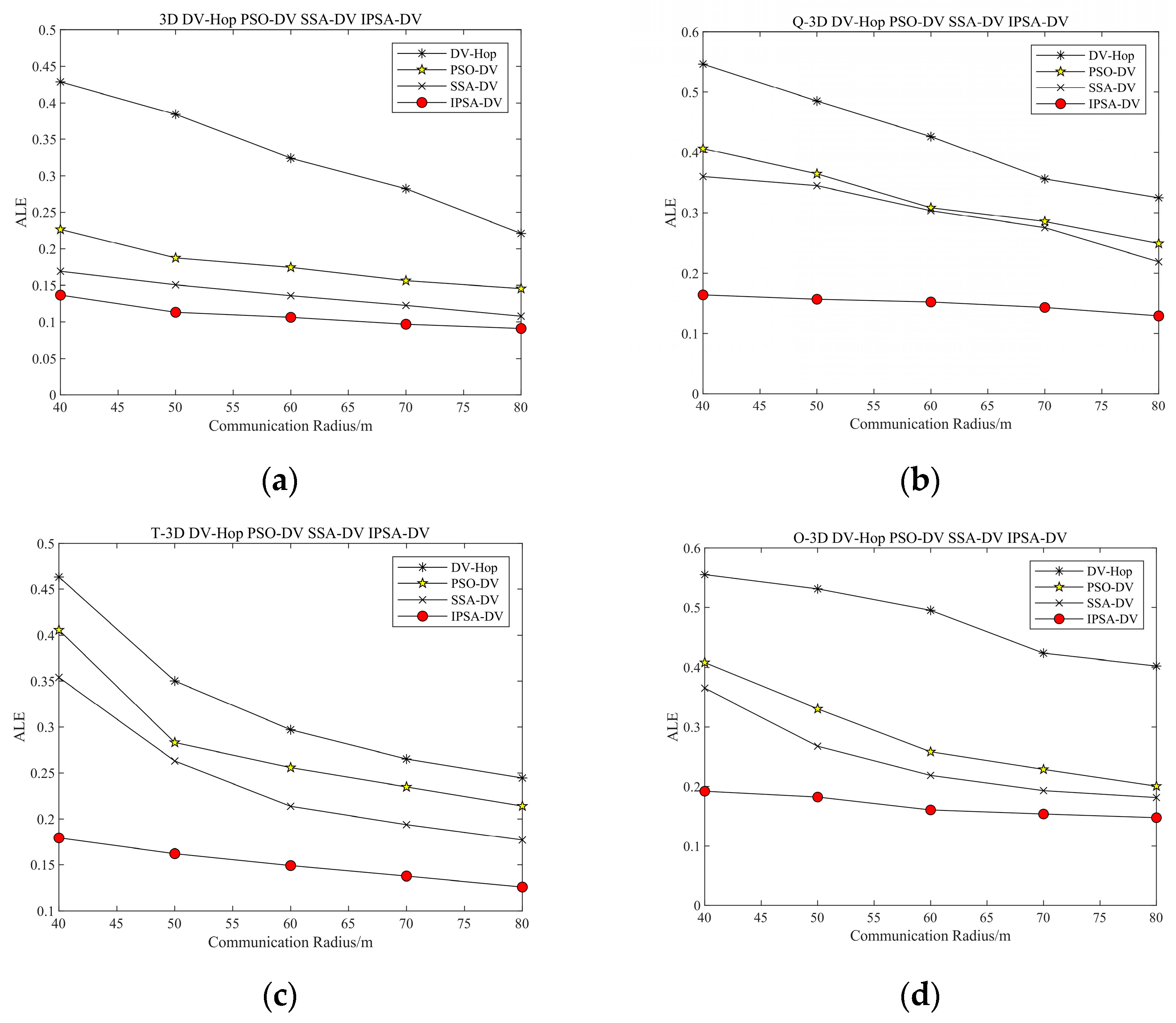
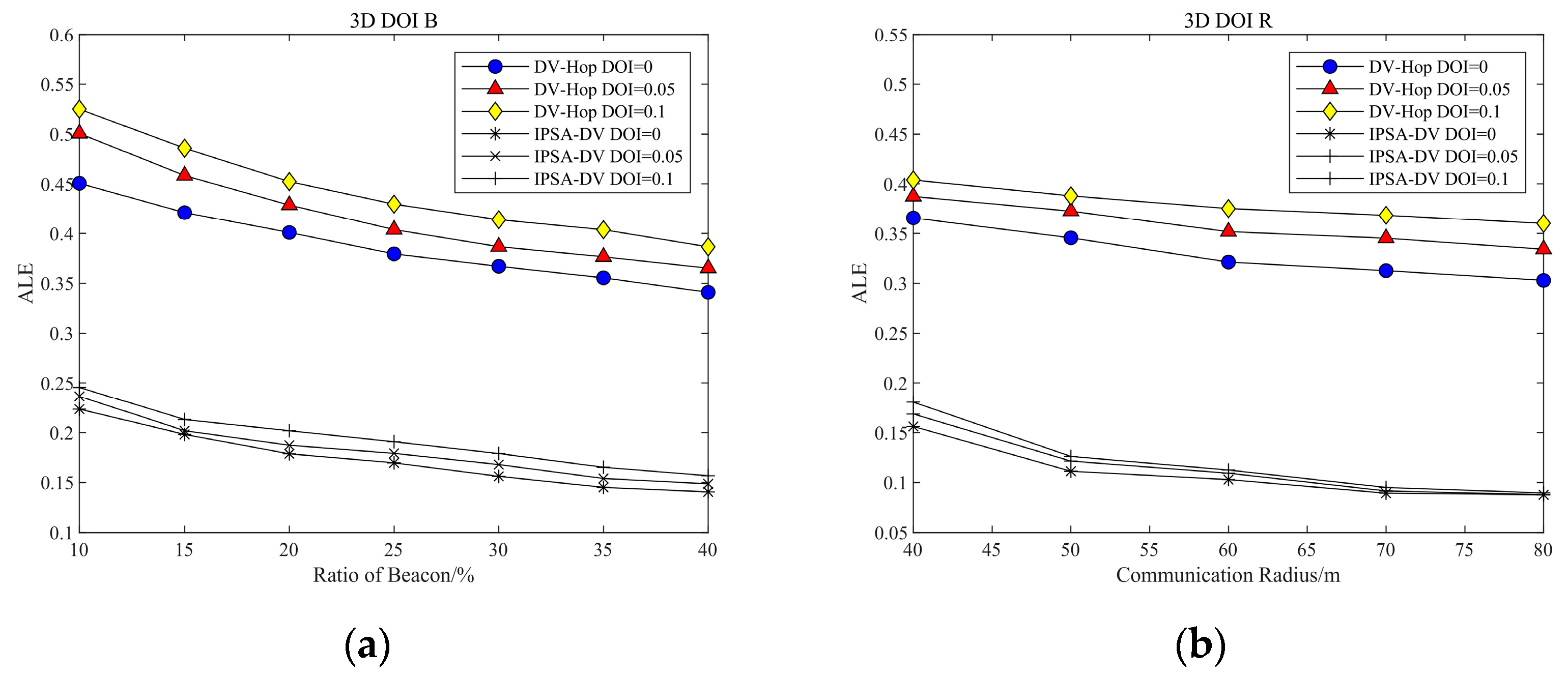
| Simulation Parameters | Value |
|---|---|
| Scenario size | 100 m × 100 m |
| Communication radius | 20–50 m |
| Ratio of beacon | 10–40% |
| Number of nodes | 50–150 |
| DOI | 0–0.1 |
| Algorithms | Rectangular Area | C-Shaped Area | S-Shaped Area | O-Shaped Area | X-Shaped Area | H-Shaped Area |
|---|---|---|---|---|---|---|
| DV-Hop | 1.1 | 1.6 | 1.7 | 1.7 | 1.4 | 1.4 |
| Anneal-DV | 15.2 | 16.2 | 18.2 | 18.5 | 15.6 | 16.3 |
| PSO-DV | 11.1 | 12.9 | 13.5 | 14.6 | 13.2 | 13.4 |
| SSA-DV | 15.1 | 16.5 | 16.7 | 21.8 | 18.1 | 17.6 |
| IPSA-DV | 19.7 | 21.4 | 22.2 | 25.6 | 21.2 | 23.5 |
| Simulation Parameters | Value |
|---|---|
| Scenario size | 100 m × 100 m × 100 m |
| Communication radius | 40–80 m |
| Ratio of beacon | 10–40% |
| Number of nodes | 50–150 |
| DOI | 0–0.1 |
| Algorithms | Cubic Terrain | Rugged Terrain | Hilly Terrain | Valley Terrain |
|---|---|---|---|---|
| 3D DV-Hop | 3.6 | 5.2 | 6.3 | 6.9 |
| 3D PSO-DV | 18.5 | 19.9 | 21.2 | 21.4 |
| 3D SSA-DV | 28.9 | 28.5 | 29.6 | 30.2 |
| 3D PSA-DV | 32.8 | 31.5 | 33.2 | 38.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Li, P.; Hou, B. A Novel DV-Hop Localization Method Based on Hybrid Improved Weighted Hyperbolic Strategy and Proportional Integral Derivative Search Algorithm. Mathematics 2024, 12, 3908. https://doi.org/10.3390/math12243908
Zhang D, Li P, Hou B. A Novel DV-Hop Localization Method Based on Hybrid Improved Weighted Hyperbolic Strategy and Proportional Integral Derivative Search Algorithm. Mathematics. 2024; 12(24):3908. https://doi.org/10.3390/math12243908
Chicago/Turabian StyleZhang, Dejing, Pengfei Li, and Benyin Hou. 2024. "A Novel DV-Hop Localization Method Based on Hybrid Improved Weighted Hyperbolic Strategy and Proportional Integral Derivative Search Algorithm" Mathematics 12, no. 24: 3908. https://doi.org/10.3390/math12243908
APA StyleZhang, D., Li, P., & Hou, B. (2024). A Novel DV-Hop Localization Method Based on Hybrid Improved Weighted Hyperbolic Strategy and Proportional Integral Derivative Search Algorithm. Mathematics, 12(24), 3908. https://doi.org/10.3390/math12243908






