1. Introduction
The challenges associated with packing and covering surfaces with circles or spheres of similar radii have numerous practical applications, ranging from coding theory to Wireless Sensor Networks (WSN). These problems are complementary in nature: the packing problem aims to determine the maximum number of spheres that can fill a given area, while the covering problem seeks to identify the minimum number of spheres required to cover a specified area. While considerable attention has been devoted to the packing problem, the coverage problem remains relatively under explored.
For instance, notable progress has been made in addressing the packing problem, with several significant results including equations, as well as lower and upper bounds for packing density, and patterns that achieve maximum packing [
1]. However, the covering problem has received comparatively less attention, and consistent results regarding the minimal number of spheres, minimal density, or the patterns necessary to achieve optimal coverage are lacking.
1.1. Problem to Investigate
The problem to research is to investigate in what the smallest number of spheres needed to fully cover a cuboid is. In , the sphere and cuboid shapes are defined as follows.
Definition 1. A n-sphere of center and radius is given bywhere is the Euclidean distance in . The volume of the sphere
in
is
, where
is the Euler gamma function defined by
. The first five equations for the sphere volumes are presented in
Table 1.
Definition 2. A n-dimensional cuboid or rectangle given by with is ; denotes the cuboid with . Note that the order relationship is defined on components .
The volume of the n-cuboid is given by .
The coverage problem requires to have the space of the cuboid fully covered by spheres of the same radius.
Definition 3. The cuboid is k-covered with spheres of radius 1 if, , there exist k different spheres , so that .
This definition does not exclude the situation where the spheres have the same center. It is clear that the k-coverage exists when a huge number of spheres are used to cover the points k times. However, it makes sense to find the coverage that uses the smallest number of spheres.
Definition 4. If , then denotes the smallest number of spheres to have a k-coverage for the cuboid .
The problem to investigate can be mathematically formulated as follows: given the cuboid
, find the minimum number of spheres
of radius 1 to
k-cover it, e.g.,
1.2. Related Works
Since 1939, research on one-coverage or circle packing has focused on developing mathematical expressions for optimal covering configurations. Notably, Kershner [
2] studied how to cover any two-dimensional point set with congruent circles, demonstrating that the minimum number of circles,
, required to cover a closed set of points
M satisfies
Furthermore, Verblunsky [
3] demonstrated that the minimum number
of circles with radius 1 required to cover a square of side length
l must satisfy
. These early studies [
2,
3] did not focus on specific circle patterns for minimal coverage, while recent research has explored efficient methods for covering rectangles with congruent circles [
4,
5,
6]. These studies have confirmed the difficulty of achieving optimal packing and the lack of a definitive pattern for achieving optimal coverage.
Recently, many studies have focused on
k-coverage problems in sensor networks, exploring the conditions for achieving coverage and detection algorithms. Some research discusses the minimum density of sensors needed for
k-coverage in a specified area. Adlakha et al. [
7] proposed an exposure-based model to determine the necessary sensor density for complete coverage, concluding that the number of sensors required for one-coverage is approximately
, where
A is the area being covered; however, they did not provide a constant factor for this estimate.
Research by Ammari et al. [
8] focused on k-coverage, a condition where each point in the target area is covered by at least
k sensors. They divided the target area into “Reuleaux” triangles, and found that the target area is k-covered if and only if each “Reuleaux” triangle contains at least k active sensors. Additionally, they determined the minimal sensor density required to guarantee
k-coverage is
, where
r is the radius of the sensing disks, which is directly proportional to
k and inversely proportional to the square of the sensing disk radius.
Tabirca et al. [
9] studied the minimal number of sensors required for 2D coverage, providing mathematical equations as lower and upper bounds for these numbers, as well as some values for small dimensions. Then, similar results were proposed by Tabirca [
10] for the 3D space considering how can cover cuboids.
The exploration of 3D coverage arises from the demand for robust coverage in Wireless Sensor Networks (WSNs) deployed within buildings or integrated into cellular networks. Research efforts have primarily focused on identifying efficient deployments utilizing 3D geometrical shapes such as spheres, octahedrons, or dodecahedrons. Another avenue of investigation involves theoretical analyses of coverage properties like density and uncovered areas. However, transitioning from 2D to 3D coverage presents significantly greater challenges.
Zhang et al. [
11] studied full-coverage deployment using lattice concepts. They connected optimal patterns with natural constructs, and used lattices to model coverage due to their periodicity and homogeneity. The authors proposed new deployment coverage patterns for optimal connectivity under lattice constraints and demonstrated their practical application using sphere sensing and communication models.
Huang et al. [
12] proposed an efficient coverage solution by reducing the 3D problem to 2D and then 1D. They used spheres and sphere caps to develop a polynomial algorithm. They introduced sphere coverage and field sensing and examined coverage of each spherical cap. By projecting circles onto a 1D line, they evaluated coverage levels.
Yun et al. [
13] suggested optimal patterns for sensor deployment achieving full coverage and
k-connectivity in WSNs. They proposed a hexagon-based universally elemental pattern and substantiated its optimality. They also proposed a new deployment polygon-based methodology, and investigated the k-connectivity problem, establishing its optimality for
based on a theoretical result linking coverage with connectivity graph topology.
Priyadarshi et al. [
14] developed a deterministic sensor deployment method using nonlinear optimization. They proposed geometric relationships between sphere radius and area sizes, and integrated these expressions into a multivariable function maximized using Lagrange multipliers. They introduced a three-dimensional coverage pattern and deployment structure based on cuboids, partitioning the monitor region into a three-dimensional grid. Their method significantly reduced the number of sensors compared to traditional methods like cube and regular tetrahedron schemes.
This article’s contribution can be described as twofold. Firstly, some theoretical results will be given to describe the monotonic properties of the numbers . Then, upper and lower bounds are proposed for , and for the minimal density of sensors. Secondly, the article will propose a complex algorithm to approximate the numbers . Based on this computation, some of the values will be presented for 2D and 3D.
2. Smallest Number of Spheres
Lemma 1. The numbers satisfy the following equations: Proof. Since , then a minimal k-cover of gives a k-cover for , so that . Now, the minimal -cover, together with the minimal -cover of , gives a -cover for the cuboid, so that . □
Proof. This is based on
, which means that the specified sphere of radius 1 covers the
n-rectangle, because
Furthermore, the n-sphere circumscribes the rectangle. □
Proof. We use the decomposition of the
n-rectangle
in small rectangles, which can be inscribed in spheres or radius 1. This decomposition takes benefit of the fact that
has all components natural numbers, and is given by
If
, then
, so that
which is covered by an
n-sphere of radius 1. Therefore, Equation (
5) shows that the rectangle
can be decomposed in small rectangles that can be inscribed in spheres of radius 1, so that there is a one-covering with
spheres. □
The proof of this lemma is based on the previous lemmas. Consider
, which gives
. Since
, it results from Lemmas 1 and 2 that
Theorem 1. The numbers satisfy the following equation: One inequality of Equation (
7) is a direct consequence of Lemmas 1 and 4, because
For the second inequality, we observe that
n-spheres of radius 1 fully cover the
n-rectangle
’s volume
k times; this gives the following implications:
which now fully proves the double inequality.
When each component of tends to infinity, e.g., , we can consider that . The following consequence is found when we isolate , then take the limit and use .
Proposition 1. The numbers satisfy the following equation: We can denote
, and call it the minimal density of spheres to achieve
k-coverage in the
n-dimensional space. Therefore, these minimal densities are between the lower and upper bounds listed below for the values of
:
3. Algorithm and Computational Results
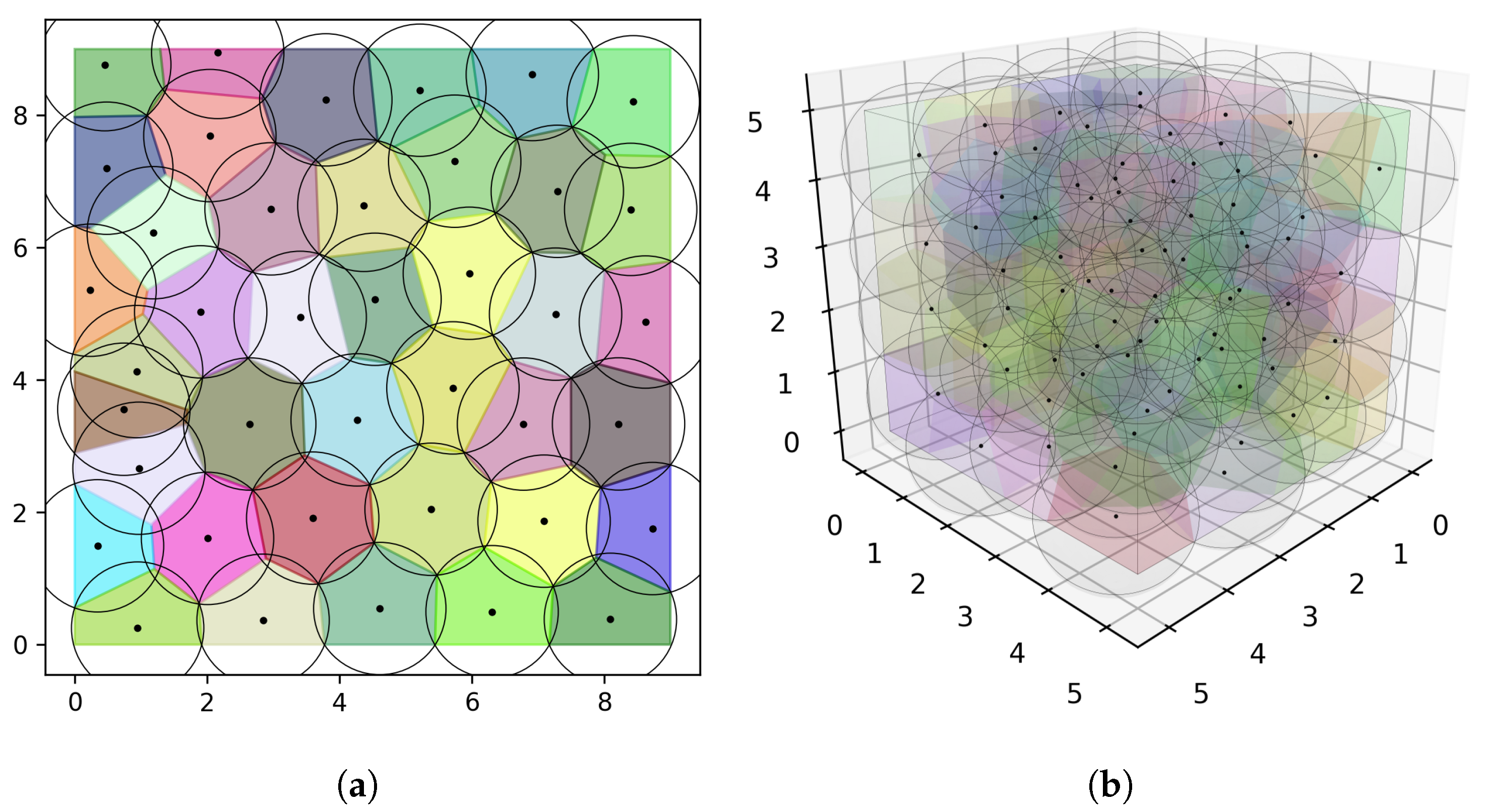
A computational strategy similar to that of Nurmela and Ostergard [
5] is employed to calculate the approximate minimum covering number
, simply denoted as
N in the following, for cuboids
in 2D and 3D, with integer edge lengths not exceeding 9 for two dimensions, and not exceeding 5 for three dimensions (
Figure 1). Algorithm 1 presents the pseudocode for our approach.
For a given set edge lengths a, a binary search method is utilized to find the smallest positive integer N between the theoretical lower and upper bounds established in Theorem 1, such that N unit circles or spheres could cover the cuboid . Specifically, we determined the direction of the binary search by verifying whether N circles or spheres could cover the given cuboid, with the final minimum N value representing the sought-after approximated N.
To verify whether
N circles or spheres could cover a given cuboid
, we initially generated
M sets of random initial positions for
N circle or sphere centers. Subsequently, adopting a strategy akin to [
5], we applied the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm to optimize these center positions, yielding
M local optimal solutions. We constructed a minimization function
, where
represents the position vector of
N circle or sphere centers. If, after BFGS optimization, any solution set corresponded to
N circle positions that completely covered the cuboid
, it was concluded that
N circles or spheres could cover the given cuboid.
| Algorithm 1 Minimum covering number calculation |
- Require:
Cuboid dimensions a, Number of random trials M - Ensure:
Approximated minimum covering number N
- 1:
function FindMinimalCoveringNumber(a, M) - 2:
lower_bound - 3:
upper_bound - 4:
while lower_bound < upper_bound do - 5:
- 6:
if CanCoverCuboid(N, a, M) then - 7:
upper_bound - 8:
else - 9:
lower_bound - 10:
return upper_bound
- 11:
function CanCoverCuboid(N, a, M) - 12:
for trial to M do - 13:
GenerateRandomPositions(N, a) - 14:
BFGS_minimize(f, ) where Loss(, a) - 15:
if Loss(, a) then - 16:
return true - 17:
return false
- 18:
function Loss(, a) - 19:
ConstructVoronoiDiagram() - 20:
uncovered ←CalculateUncoveredVolume(V, , a) - 21:
max_dist_squared ←CalculateMaxDistanceSquared(V, ) - 22:
boundary_violation ←CalculateBoundaryViolation(, a) - 23:
return uncovered + max_dist_squared + boundary_violation
- 24:
function CalculateUncoveredVolume(V, , a) - 25:
covered - 26:
for all point x in do - 27:
The cell in V containing x - 28:
DecomposeIntoSimplices(C) - 29:
The unit circle or sphere centered at point x - 30:
for all simplex s in S do - 31:
covered ← covered + CalculateIntersectionVolume(s, c) - 32:
return covered
- 33:
function CalculateMaxDistanceSquared(V, ) - 34:
max_dist_squared - 35:
for all point x in do - 36:
The cell in V containing x - 37:
for all vertex v in C do - 38:
dist_squared - 39:
max_dist_squared - 40:
return max_dist_squared
- 41:
function CalculateBoundaryViolation(, a) - 42:
sum - 43:
for all point x in do - 44:
sum ← sum - 45:
return sum
|
Diverging from [
5], we found that using only the uncovered area or volume as a loss function could lead to the optimization process becoming trapped in local minima when approaching nearly full coverage, where the area or volume approaches zero. Instead of introducing additional steps to address this issue, as in [
5], we proposed an improved loss function,
where
represents the uncovered area or volume,
is the square of the maximum distance from any point
p in the cuboid to the nearest circle or sphere center
x,
is the set of halfspaces defining the cuboid
, and
is the distance from point
x to halfspace
H.
if and only if point
x is within the cuboid
.
This loss function not only considers the uncovered area or volume, but also introduces a guidance term to take effect when the uncovered area or volume approaches zero, while ensuring circle or sphere centers remain within the cuboid through a penalty term. The cuboid is fully covered by the unit circles or spheres if the loss function , where the uncovered area or volume is 0, and the maximum distance from any point in the cuboid to the nearest circle or sphere center is less than or equal to 1.
To calculate the uncovered area or volume, we first constructed a Voronoi diagram of the circle or sphere centers, then computed the area or volume of the intersection between each Voronoi cell and its corresponding unit circle or sphere, and finally subtracted these areas or volumes from the area or volume of the cuboid
to obtain the total uncovered area or volume. Specifically, we decomposed each Voronoi cell into a triangle or tetrahedron by connecting the simplices on its convex hull with its centroid as a vertex, then calculated the intersection area or volume of these triangles or tetrahedrons with the circle or sphere. The intersection volume was calculated using the method in [
15].
Based on the research of Stoyan and Patsuk [
16,
17], the maximum distance from any point in the cuboid to the nearest circle or sphere center must occur at a vertex of the Voronoi diagram. Therefore, we only needed to calculate the distance from each Voronoi cell vertex to its corresponding circle or sphere center, and take the maximum value to obtain the required maximum distance.
If the edges of the cuboid are aligned with the coordinate axes, with the origin as one of its vertices, the total distance for any point x can be simply calculated as the sum of distances by which each coordinate of x exceeds the cuboid’s boundaries. Formally, this can be calculated as .
With a fixed
, the experimental results for the minimum covering number
of cuboids
are presented in the tables below; note that these numbers are approximation for
. For example,
Table 2 shows the approximated numbers
in 2D, extending the results from [
9]. On the other hand,
Table 3,
Table 4,
Table 5,
Table 6 and
Table 7 show the approximated values of
for a 3D cuboid listed in a sequence of sub-tables generated for
. Note that the Python programs to generate these tables are available at [
18].
4. Conclusions
The article presented some theoretical results related to the minimal number of spheres
to cover a cuboid in an
n-dimensional space. Firstly, It was proven that these numbers
are sub-additive and increasing. Base on these results, some lower and upper bounds were proposed for
in Equation (
7), which then generated Equation (
8) for the minimal density for
k-coverage. Finally, an algorithm was proposed to generate approximations for
for 2D and 3D cuboids. This computation was based on Voronoi diagrams generated for the area to cover. In addition, a loss function is introduced to lead the optimization process. The computation was then used to generate the numbers
for some cuboids in 2D and 3D. More work is now needed to investigate better intervals for these bounds, as well as to find geometrical configurations to achieve the minimal coverage. Furthermore, this work can also be extended to other type of shapes to cover a given area. For example, simplices, like triangles as two-simplex, tetrahedrons as three-simplex, etc., can be considered.