A Trigonometric Variant of Kaneko–Tsumura ψ-Values
Abstract
1. Introduction
2. Main Results
3. Associated Multiple Integrals and 2-Labeled Posets
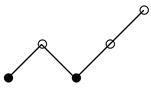
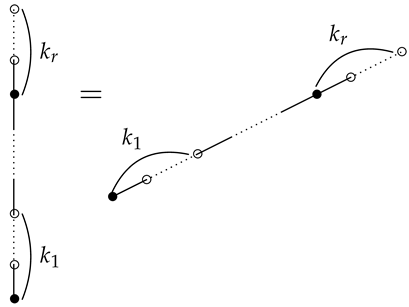
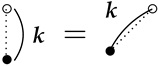 for the diagrams
for the diagrams
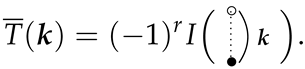

4. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hoffman, M.E. Multiple harmonic series. Pac. J. Math. 1992, 152, 275–290. [Google Scholar] [CrossRef]
- Zagier, D. Values of zeta functions and their applications. In First European Congress of Mathematics; Joseph, A., Mignot, F., Murat, F., Prum, B., Rentschler, R., Eds.; Birkhauser: Basel, Switzerland; Boston, MA, USA; Berlin, Germany, 1994; Volume II, pp. 497–512. [Google Scholar]
- Broadhurst, D.J. Conjectured enumeration of irreducible multiple zeta values, from knots and Feynman diagrams. arXiv 1996, arXiv:hep-th/9612012. [Google Scholar]
- Broadhurst, D.J. Massive 3-loop Feynman diagrams reducible to SC* primitives of algebras of the sixth root of unity. Eur. Phys. J. C (Fields) 1999, 8, 311–333. [Google Scholar] [CrossRef]
- Brown, F. Mixed Tate motives over . Ann. Math. 2012, 175, 949–976. [Google Scholar] [CrossRef]
- Zudilin, W. Multiple q-zeta brackets. Mathematics 2015, 3, 119–130. [Google Scholar] [CrossRef]
- Hoffman, M.E. An odd variant of multiple zeta values. Comm. Number Theory Phys. 2019, 13, 529–567. [Google Scholar] [CrossRef]
- Kaneko, M.; Tsumura, H. On multiple zeta values of level two. Tsukuba J. Math. 2020, 44, 213–234. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, J. Variants of multiple zeta values with even and odd summation indices. Math. Zeit. 2022, 300, 3109–3142. [Google Scholar] [CrossRef]
- Arakawa, T.; Kaneko, M. Multiple zeta values, poly-Bernoulli numbers, and related zeta functions. Nagoya Math. J. 1999, 153, 189–209. [Google Scholar] [CrossRef]
- Kaneko, M.; Tsumura, H. Multi-poly-Bernoulli numbers and related zeta functions. Nagoya Math. J. 2018, 232, 19–54. [Google Scholar] [CrossRef]
- Hoshi, T. On values of zeta functions of Arakawa–Kaneko type. Comment. Math. Univ. Sancti Pauli 2021, 69, 1–22. [Google Scholar]
- Nishibiro, K. On generalization of duality formulas for the Arakawa-Kaneko type zeta functions. arXiv 2023, arXiv:2310.07318. [Google Scholar]
- Nishibiro, K. On explicit relations for values of Kaneko–Tsumura’s λ function. Tokyo J. Math. 2024. [Google Scholar] [CrossRef]
- Umezawa, R. Multiple T-values and iterated log-tangent integrals. arXiv 2023, arXiv:2301.06067. [Google Scholar]
- Euler, L. Meditationes circa singulare serierum genus. Novi Comment. Acad. Sci. Petropolitanae 1776, 20, 140–186. [Google Scholar]
- Kaneko, M.; Pallewatta, M.; Tsumura, H. On poly-cosecant numbers. J. Integer Seq. 2020, 23, 20.6.4. [Google Scholar]
- Bényi, B.; Josuat-Vergès, M. Combinatorial proof of an identity on Genocchi numbers. J. Integer Seq. 2021, 24, 21.7.6. [Google Scholar]
- Bényi, B.; Matsusaka, T. Remarkable relations between the central binomial series, Eulerian polynomials, and poly-Bernoulli numbers. Kyushu J. Math. 2023, 77, 149–158. [Google Scholar] [CrossRef]
- Nishibiro, K. On some properties of polycosecant numbers and polycotangent numbers. arXiv 2022, arXiv:2205.05247. [Google Scholar]
- Khera, J.; Lundberg, E. The distribution of the length of the longest path in random acyclic orientations of a complete bipartite graph. arXiv 2024, arXiv:2408.12716. [Google Scholar]
- Cameron, P.J.; Glass, C.A.; Rekvényi, K.; Schumacher, R.U. Acyclic orientations and poly-Bernoulli numbers. arXiv 2014, arXiv:1412.3685. [Google Scholar]
- Kaneko, M.; Ohno, Y. On a kind of duality of multiple zeta-star values. Int. J. Number Theory 2010, 8, 1927–1932. [Google Scholar] [CrossRef]
- Si, X.; Luo, F. Another proof of Kaneko–Ohno’s duality formula for multiple zeta star values. In Colloquium Mathematicum; Instytut Matematyczny Polskiej Akademii Nauk: Warsaw, Poland, 2023; Volume 174, pp. 1–11. [Google Scholar]
- Kawasaki, N.; Ohno, Y. Combinatorial proofs of identities for special values of Arakawa–Kaneko multiple zeta functions. Kyushu J. Math. 2018, 72, 215–222. [Google Scholar] [CrossRef]
- Yamamoto, S. Multiple zeta functions of Kaneko–Tsumura type and their values at positive integers. Kyushu J. Math. 2022, 76, 497–509. [Google Scholar] [CrossRef]
- Xu, C. Duality formulas for Arakawa–Kaneko zeta values and related variants. Bull. Malays. Math. Sci. Soc. 2021, 44, 3001–3018. [Google Scholar] [CrossRef]
- Luo, F.; Si, X. A note on Arakawa–Kaneko zeta values and Kaneko–Tsumura η-values. Bull. Malays. Math. Sci. Soc. 2023, 46, 21. [Google Scholar] [CrossRef]
- Kaneko, M.; Tsumura, H. Zeta functions connecting multiple zeta values and poly-Bernoulli numbers. Adv. Stud. Pure Math. 2020, 84, 181–204. [Google Scholar]
- Kaneko, M.; Wang, W.; Xu, C.; Zhao, J. Parametric Apéry-type series and Hurwitz-type multiple zeta values. arXiv 2022, arXiv:2209.06770. [Google Scholar]
- Pallewattaa, M.; Xu, C. Some results on Arakawa–Kaneko, Kaneko–Tsumura functions and related functions. Period. Math. Hung. 2024, 89, 175–200. [Google Scholar] [CrossRef]
- Xu, C.; Zhao, J. Alternating Multiple T-values: Weighted sums, duality, and dimension Conjecture. Ramanujan J. 2024, 63, 13–54. [Google Scholar] [CrossRef]
- Zheng, W.; Yang, Y. Parametric Arakawa–Kaneko zeta function and Kaneko–Tsumura η-function. Bull. Belg. Math. Soc. Simon Stevin 2023, 30, 328–340. [Google Scholar] [CrossRef]
- Chen, K.-T. Iterated path integrals. Bull. Am. Math. Soc. 1977, 83, 831–879. [Google Scholar] [CrossRef]
- Chen, K.-T. Algebras of iterated path integrals and fundamental groups. Trans. Am. Math. Soc. 1971, 156, 359–379. [Google Scholar] [CrossRef]
- Kaneko, M.; Tsumura, H. Multiple L-values of level four, poly-Euler numbers, and related zeta functions. Tohoku Math. J. 2024, 76, 361–389. [Google Scholar] [CrossRef]
- Yamamoto, S. Multiple zeta-star values and multiple integrals. RIMS Kôkyûroku Bessatsu 2017, B68, 3–14. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, E.; Lin, X.; Xu, C.; Zhao, J. A Trigonometric Variant of Kaneko–Tsumura ψ-Values. Mathematics 2024, 12, 3771. https://doi.org/10.3390/math12233771
Pan E, Lin X, Xu C, Zhao J. A Trigonometric Variant of Kaneko–Tsumura ψ-Values. Mathematics. 2024; 12(23):3771. https://doi.org/10.3390/math12233771
Chicago/Turabian StylePan, Ende, Xin Lin, Ce Xu, and Jianqiang Zhao. 2024. "A Trigonometric Variant of Kaneko–Tsumura ψ-Values" Mathematics 12, no. 23: 3771. https://doi.org/10.3390/math12233771
APA StylePan, E., Lin, X., Xu, C., & Zhao, J. (2024). A Trigonometric Variant of Kaneko–Tsumura ψ-Values. Mathematics, 12(23), 3771. https://doi.org/10.3390/math12233771





