Bifurcation Branch in a Spatial Heterogeneous Predator–Prey Model with a Nonlinear Growth Rate for the Predator

Abstract

A strongly coupled predator–prey model in a spatially heterogeneous environment with a Holling type-II functional response and a nonlinear growth rate for the predator is considered. Using bifurcation theory and the Lyapunov–Schmidt reduction, we derived a bounded smooth curve formed by the positive solutions and obtained the structure of the bifurcation branches. We also proved that the bounded curve is monotone $\mathbf{S}$-shaped or fish-hook-shaped (⊂-shaped), as the values of the parameters of the model vary; in the latter case, the model has multiple positive steady-state solutions caused by the spatial heterogeneity of the environment.

1. Introduction

The predator–prey model has become important in assessing the interaction between biological species as it can explain the complexity of ecology [1,2,3]. One of the most meaningful questions in ecosystems is whether different species can coexist. In fact, this question is influenced by various factors such as the natural environment, behavioral patterns, and the functional responses between species [4,5,6,7]. For different prey–predator systems, authors have proposed many functional responses, such as Holling I–IV [8,9,10], ratio-dependent [11], and Leslie–Gower [12] responses. Besides functional responses, spatial heterogeneity also has a significant impact on the dynamics of prey–predator systems. For example, Huffaker [13] found through an experiment that the predator–prey system of two species of mites can rapidly collapse and become extinct in small homogeneous environments, while it can last longer in suitable heterogeneous environments.

Based on the effects of functional responses and heterogeneous environments on dynamic behavior, we will investigate the following diffusion predator–prey model with a Holling II functional response in a spatially heterogeneous environment:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\displaystyle \frac{\partial u}{\partial t}}=d_1▵u+u(a_1-k_{1}u-{\displaystyle \frac{b_1(x)v}{1+m_{1}u}}),\hfill & x\in \Omega ,t>0,\hfill \\ {\displaystyle \frac{\partial v}{\partial t}}=d_2▵v+v({\displaystyle \frac{{\alpha }_1}{1+{\beta }_{1}v}}-{\theta }_1+{\displaystyle \frac{c_1(x)u}{1+m_{1}u}}),\hfill & x\in \Omega ,t>0,\hfill \\ {\displaystyle \frac{\partial u}{\partial \nu }}={\displaystyle \frac{\partial v}{\partial \nu }}=0,\hfill & x\in \partial \Omega ,t>0,\hfill \\ u(x,0)=u_0(x)\ge 0,v(x,0)=v_0(x)\ge 0,\hfill & x\in \Omega ,\hfill \end{array}\right.\end{array}$$

(1)

where $\Omega$ is a bounded domain in ${\mathbb{R}}^N$ with a smooth boundary $\partial \Omega$ and an outward normal unit vector $\nu$; $u(x,t)$ and $v(x,t)$ are the densities of the prey and predator at time t and in the spatial position $x\in \Omega$, respectively; $d_1$ and $d_2$ are the diffusion coefficients of the prey and predator; $a_1$ is the intrinsic growth rate of the prey; $a_1/k_1$ is the carrying capacity of the prey; ${\theta }_1$ is the mortality rate of the predator; $b_1(x)\ge 0$ and $c_1(x)\ge 0$ are continuous functions in $\overline{\Omega }$ which measure the maximal predator consumption rate and conversion rate per capita; $m_1$ measures the prey’s ability to evade attack [14,15,16]; ${\displaystyle \frac{{\alpha }_1}{1+{\beta }_{1}v}}$ is the nonlinear growth rate for the predator, which means that the per capita reproduction rate (maximum ${\alpha }_1$) decreases with density; and ${\beta }_1$ is the strength of the density dependence, which is similar to a Beverton–Holt growth function [17,18,19]. The parameters in (1) are all positive constants.

When $b_1(x)=b_1$ and $c_1(x)=c_1$ are non-negative constants and ${\alpha }_1=0$, Model (1) becomes a classic reaction–diffusive predator–prey system with a Holling type-II functional response, and this has been widely studied in [20,21,22]. By using fixed-point index theory and bifurcation theory, Zhou and Mu [23] provided the necessary and sufficient conditions for the existence of coexistence states. Yi et al. investigated Hopf and steady-state bifurcations (with the bifurcation parameter $c_1$) and showed the existence of loops of periodic orbits and steady-state solutions in [24]. When $c_1$ is sufficiently large, Peng and Shi [22] proved the nonexistence of nonconstant positive steady states and implied that the loops of steady-state solutions are bounded, which improves the results in [24].

In a spatially homogeneous environment, i.e., when $b_1(x)=b_1$ and $c_1(x)=c_1$ are non-negative constants in Model (1), Yang et al. [25] used fixed-point index theory, a super-sub solution method, bifurcation theory, and a perturbation technique to prove the existence, stability, and exact number of positive solutions when $m_1$ is large. Then, Chen and Yu [26] obtained the global attractiveness of a constant equilibrium and the nonexistence of a nonconstant positive steady state under strong or weak interactions. Chen and Yu [26] also proposed an interesting problem, which is whether or not System (1) has multiple positive solutions under homogeneous Neumann boundary conditions.

Many interesting papers have discussed the impact of spatially heterogeneous environments on the dynamics of predator–prey systems [27,28,29,30,31]. Through bifurcation theory and the comparison principle, Du and Shi [32] proved that when the predator population is not far from a constant level, the prey population can become extinguished, persist, or blow up based on its initial population conditions, the parameters involved in the system, and the heterogeneous environment. In particular, their results show that the spatial heterogeneity of the environment can play a dominant role in the presence of the Allee effect when the prey’s growth is large.

The purpose of this article is to investigate the influence of spatially heterogeneous environments on the positive solution set of System (1) and to obtain multiple coexisting positive solutions for System (1). That is, we study the non-negative solution of the following strongly semilinear elliptic system:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{d}_1▵u+u(a_1-k_{1}u-{\displaystyle \frac{b_1(x)v}{1+m_{1}u}})=0,\hfill & x\in \Omega ,t>0,\hfill \\ d_2▵v+v({\displaystyle \frac{{\alpha }_1}{1+{\beta }_{1}v}}-{\theta }_1+{\displaystyle \frac{c_1(x)u}{1+m_{1}u}})=0,\hfill & x\in \Omega ,t>0,\hfill \\ {\displaystyle \frac{\partial u}{\partial \nu }}={\displaystyle \frac{\partial v}{\partial \nu }}=0,\hfill & x\in \partial \Omega ,t>0,\hfill \\ u(x,0)=u_0(x)\ge 0,v(x,0)=v_0(x)\ge 0,\hfill & x\in \Omega .\hfill \end{array}\right.\end{array}$$

(2)

For mathematical simplicity, we have carried out some rescaling of System (2). Let $\tilde{u}=k_{1}u/d_1$. After rewriting $\tilde{u}$ as u, System (2) becomes

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}-▵u=u(a-u-{\displaystyle \frac{b(x)v}{1+mu}}):=f(u,v,\delta ),\hfill & x\in \Omega ,\hfill \\ -▵v=v({\displaystyle \frac{\delta -\theta \beta v}{1+\beta v}}+{\displaystyle \frac{c(x)u}{1+mu}}):=g(u,v,\delta ),\hfill & x\in \Omega ,\hfill \\ {\displaystyle \frac{\partial u}{\partial \nu }}={\displaystyle \frac{\partial v}{\partial \nu }}=0,\hfill & x\in \partial \Omega ,\hfill \end{array}\right.\end{array}$$

(3)

where $(a,m,\beta ,\theta ,\alpha )=({\displaystyle \frac{a_1}{d_1}},{\displaystyle \frac{d_1{m}_1}{k_1}},{\beta }_1,{\displaystyle \frac{{\theta }_1}{d_2}},{\displaystyle \frac{{\alpha }_1}{d_2}})$, $(b(x),c(x))=({\displaystyle \frac{b_1(x)}{d_1}},{\displaystyle \frac{d_1{c}_1(x)}{d_2{k}_1}})$, and $\delta =\alpha -\theta$ is a real constant.

From an ecological viewpoint, a positive solution corresponds to the steady-state coexistence of prey and predators. Thus, we are mainly interested in the positive solutions to System (3). To obtain the set of positive solutions, we take $\delta$ as the bifurcation parameter and introduce the following semitrivial solution sets:

$${\Gamma }_u:=\{(u,v,\delta )=(a,0,\delta ):\delta \in \mathbb{R}\},{\Gamma }_v:=\{(u,v,\delta )=(0,{\displaystyle \frac{\delta }{\theta \beta }},\delta ):\delta \in {\mathbb{R}}_{+}\}.$$

We will derive the set of positive solutions which connects ${\Gamma }_u$ with ${\Gamma }_v$ in this paper. More precisely, we will find a negative number ${\delta }_{\ast }={\delta }_{\ast }(a,c(x))<0$ and a positive number ${\delta }^{\ast }={\delta }^{\ast }(a,b(x))>0$ such that the positive solution set forms a bounded continuum $\Gamma$ which bifurcates from $(0,{\displaystyle \frac{{\delta }^{\ast }}{\theta \beta }},{\delta }^{\ast })\in {\Gamma }_v$ and joins $(a,0,{\delta }_{\ast })\in {\Gamma }_u$. Hence, when the bifurcation parameter $\delta$ satisfies ${\delta }_{\ast }<\delta <{\delta }^{\ast }$, System (3) has at least one positive solution.

The main result in this paper is the following theorem.

Theorem 1.

If $a>0$ is sufficiently small, β and m are sufficiently large, then the positive solutions of System (3) (with bifurcation parameter δ) form a bounded smooth curve

$$\Gamma =\{(u(x;ϵ),v(x;ϵ),\delta (ϵ))\subset X\times \mathbb{R}:ϵ\in (0,a)\},$$

where $(u(x;ϵ),v(x;ϵ),\delta (ϵ))$ satisfies $(u(x;0),v(x;0),\delta (0))=(0,{\displaystyle \frac{{\delta }^{\ast }}{\theta \beta }},{\delta }^{\ast })$ and $(u(x;a),v(x;a),\delta (a))=(a,0,{\delta }_{\ast })$. Furthermore, for a sufficiently small constant ${\theta }_0>0$, we have that

(1) When $\theta >{\theta }_0$, there exists a small positive constant $a^{\ast }$ such that the following properties hold:

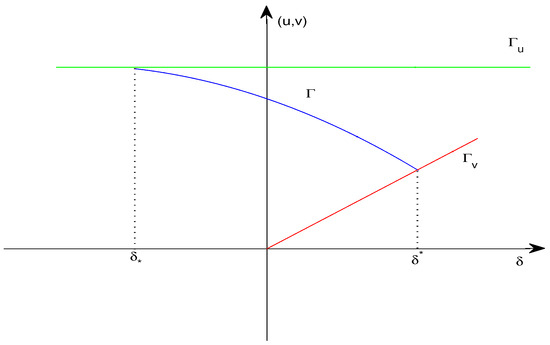
(i) If $0<a\le {\displaystyle \frac{a^{\ast }}{3}}$, then ${\delta }^{\prime }(0)<0$ and Γ subcritically bifurcates from $(0,{\displaystyle \frac{{\delta }^{\ast }}{\theta \beta }},{\delta }^{\ast })$. In this case, System (3) has at least one positive solution as $\delta \in ({\delta }_{\ast },{\delta }^{\ast })$, i.e., the positive solution set of System (3) forms a bounded $\mathbf{S}$-shaped smooth curve bifurcating from $(0,{\displaystyle \frac{{\delta }^{\ast }}{\theta \beta }},{\delta }^{\ast })$, which is shown in Figure 1.

Figure 1. Monotone $\mathbf{S}$-shaped branch of positive solutions in Theorem 1 (1-i) and (2).

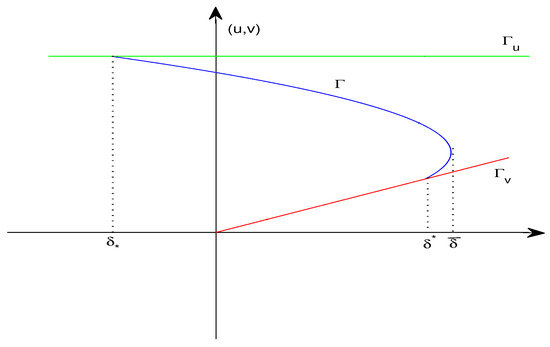
(ii) If ${\displaystyle \frac{2a^{\ast }}{3}}<a\le a^{\ast }$, then ${\delta }^{\prime }(0)>0$ and Γ supercritically bifurcates from $(0,{\displaystyle \frac{{\delta }^{\ast }}{\theta \beta }},{\delta }^{\ast })$. In this case, for $\overline{\delta }:=\underset{0\le ϵ\le a}{max}\delta (ϵ)$, System (3) has no positive solution as $\delta \in (-\infty ,{\delta }_{\ast }]\bigcup (\overline{\delta },+\infty )$, at least one positive solution as $\delta \in \left\{\overline{\delta }\right\}\bigcup ({\delta }_{\ast },{\delta }^{\ast })$, and at least two positive solutions as $\delta \in ({\delta }^{\ast },\overline{\delta })$ i.e., the positive solution set of System (19) forms a bounded fish-hook-shaped smooth curve bifurcating from $(0,{\displaystyle \frac{{\delta }^{\ast }}{\theta \beta }},{\delta }^{\ast })$, which is shown in Figure 2.

Figure 2. Fish-hook-shaped branch of positive solutions in Theorem 1 (1-ii).

(2) When $0<\theta \le {\theta }_0$, then ${\delta }^{\prime }(0)<0$ and Γ subcritically bifurcates from $(0,{\displaystyle \frac{{\delta }^{\ast }}{\theta \beta }},{\delta }^{\ast })$. In this case, System (3) has at least one positive solution as $\delta \in ({\delta }_{\ast },{\delta }^{\ast })$, i.e., the positive solution set of System (3) forms a bounded $\mathbf{S}$-shaped smooth curve bifurcating from $(0,{\displaystyle \frac{{\delta }^{\ast }}{\theta \beta }},{\delta }^{\ast })$, which is shown in Figure 1.

The rest of the paper is organized as follows. In Section 2, we give the nonexistence region of the positive solutions of System (3). In Section 3, by applying the bifurcation theory, we obtain the bounded continuum $\Gamma$ which connects ${\Gamma }_v$ with ${\Gamma }_u$. In Section 4, when $a,\theta ,\delta \to 0$ and $m,\beta \to \infty$, we investigate the limiting system by the Lyapunov–Schmidt reduction and give the proof of Theorem 1. This paper ends with a brief conclusion in Section 5.

2. Nonexistence Region of Positive Solutions

For convenience, we denote the average of $\varphi (x)$ over $\Omega$ by ${\oint }_{\Omega }\varphi (x)dx:={\displaystyle \frac{{\int }_{\Omega }\varphi (x)dx}{|\Omega |}}$, where $|\Omega |$ denotes the measure of $\Omega$. And let

$$X=W^{2,p}(\Omega )\times W^{2,p}(\Omega )andY=L^p(\Omega )\times L^p(\Omega )(p>N),$$

where $W^{2,p}(\Omega )=\{\varphi \in W^{2,p}(\Omega ):{\displaystyle \frac{\partial \varphi }{\partial \nu }}=0,x\in \partial \Omega \}$. The Sobolev embedding theorem implies that $X\subset C^1(\overline{\Omega })\times C^1(\overline{\Omega })$ for $p>N$. Moreover, denote ${\lambda }_1(q)$ as the least eigenvalue of the problem

$$\begin{array}{c}\hfill -\Delta \varphi +q(x)\varphi =\lambda \varphi ,x\in \Omega and{\displaystyle \frac{\partial \varphi }{\partial \nu }}=0,x\in \partial \Omega ,\end{array}$$

(4)

where $q(x)$ is a continuous function in $\overline{\Omega }$. By [33], we know that the mapping $q\to {\lambda }_1(q)$ is continuous, monotone increasing and ${\lambda }_1(0)=0$.

In what follows, we first give a priori estimates of the positive solutions of System (3), and then obtain a sufficient condition for the nonexistence of the positive solutions.

Theorem 2.

Let $(u,v)$ be a positive solution of System (3); then, there exists a positive constant $C_0$ such that ${0<\parallel u\parallel }_{\infty }, {\parallel v\parallel }_{\infty }<C_0$.

Proof. 

From the first equation of (3), we have $▵u+u(a-u)\ge 0$; it follows from the maximum principle [22,34] that $0<u\le {\parallel u\parallel }_{\infty }\le a$. By integrating the first equation of (3) over $\Omega$, we obtain

$${\int }_{\Omega }u(a-u-{\displaystyle \frac{b(x)v}{1+mu}})dx=0.$$

(5)

Then, from the Schwarz inequality, we have

$${\int }_{\Omega }{u}^{2}dx={\int }_{\Omega }u(a-{\displaystyle \frac{b(x)v}{1+mu}})dx\le {\int }_{\Omega }audx\le {a|\Omega |}^{{\displaystyle \frac{1}{2}}}{\parallel u\parallel }_2.$$

Thus, ${\parallel u\parallel }_2\le a{|\Omega |}^{{\displaystyle \frac{1}{2}}}$. From the second equation of (3), we have

$$-▵v=v({\displaystyle \frac{\delta -\theta \beta v}{1+\beta v}}+{\displaystyle \frac{c(x)u}{1+mu}}).$$

And

$$\parallel {\displaystyle \frac{\delta -\theta \beta v}{1+\beta v}}+{\displaystyle \frac{c(x)u}{1+mu}}{\parallel }_2\le (|\delta |+{\theta )|\Omega |}^{{\displaystyle \frac{1}{2}}}+{\parallel c(x)\parallel }_{\infty }{\parallel u\parallel }_2\le {|\Omega |}^{{\displaystyle \frac{1}{2}}}(|\delta |+\theta +{a\parallel c(x)\parallel }_{\infty }).$$

The Harnack inequality [35,36] yields that there exists a positive constant $C_1$ such that

$${\parallel v\parallel }_{\infty }\le C_1\underset{x\in \overline{\Omega }}{min}v(x).$$

(6)

We claim that there exists a positive constant $C_2$ such that ${\parallel v\parallel }_{\infty }\le C_2$. Otherwise, with the aid of (6), there exists a sequence ${\left\{(u_i,v_i)\right\}}_1^{\infty }$ such that

$$\underset{i\to \infty }{lim}{v}_i(x)=\infty ,uniformlyon\overline{\Omega }.$$

Thence, by integrating the first equation of (3) over $\Omega$ and $b(x)\ge 0$, we have

$${\int }_{\Omega }{u}_i(a-u_i-{\displaystyle \frac{b(x)v_i}{1+m{u}_i}})dx<0,forsufficientlylargei,$$

which contradicts (5). This proves the claim. Take $C_0=max\{a,C_2\}$; the proof is complete. □

Generally, when the least eigenvalue defined in (4) is zero, the system is unstable and some bifurcations occur. Hence, we introduce the following sets on the $(a,\delta )$ plane

$$W_u:=\{(a,\delta )\in {\mathbb{R}}^2:{\lambda }_1(-\delta -{\displaystyle \frac{ac(x)}{1+am}})=0\},W_v:=\{(a,\delta )\in {\mathbb{R}}^2:{\lambda }_1(-a+{\displaystyle \frac{\delta b(x)}{\beta \theta }})=0\}.$$

In fact, from [37,38], we know that the existence of positive solutions is possible only if

$${\lambda }_1(-\delta -{\displaystyle \frac{ac(x)}{1+am}})<0and{\lambda }_1(-a+{\displaystyle \frac{\delta }{\beta \theta }}b(x))>0.$$

And the positive solutions bifurcate from $(u,v)=(a,0)$ or $(u,v)=(0,{\displaystyle \frac{\delta }{\beta \theta }})$ if and only if $(a,\delta )\in W_u$ or $(a,\delta )\in W_v$, respectively.

For the sets $W_u$ and $W_v$, we have the following lemma.

Lemma 1.

There exists a monotone decreasing smooth function $\delta ={\delta }_{\ast }(a)$ with ${\delta }_{\ast }(0)=0$ such that $W_u=\{(a,\delta )\in {\mathbb{R}}_{+}\times {\mathbb{R}}_{-}:\delta ={\delta }_{\ast }(a)\}$. And there is a monotone increasing smooth function $\delta ={\delta }^{\ast }(a)$ with ${\delta }^{\ast }(0)=0$ and $\underset{a\to \infty }{lim}{\delta }^{\ast }(a)=\infty$ such that $W_v=\{(a,\delta )\in {\mathbb{R}}_{+}\times {\mathbb{R}}_{+}:$$\delta ={\delta }^{\ast }(a)\}$.

Proof. 

Set $S(a,\delta )={\lambda }_1(-\delta -{\displaystyle \frac{ac(x)}{1+am}})$. From the continuity and monotone increasing property of ${\lambda }_1(q)$ with respect to $q\in C(\overline{\Omega })$ and the fact $c(x)\ge 0$, we know that $S(a,\delta )$ is a continuous and strictly decreasing function about $\delta$ and satisfying

$$S(a,0)={\lambda }_1(-{\displaystyle \frac{ac(x)}{1+am}})<0andS(a,\delta )>0as\delta <-{\displaystyle \frac{{a\parallel c\parallel }_{\infty }}{1+am}}<0.$$

Therefore, the intermediate value theorem implies that there exists a unique ${\delta }_{\ast }(a)\in (-{\displaystyle \frac{{a\parallel c\parallel }_{\infty }}{1+am}},0)$ such that $S(a,{\delta }_{\ast }(a))=0$. Note that $S(a,\delta )$ is a continuous and strictly decreasing function about $a\ge 0$. Hence, $\delta ={\delta }_{\ast }(a)$ is continuous and strictly decreasing with respect to $a\ge 0$, and satisfies ${\delta }_{\ast }(0)=-{\lambda }_1(-{\delta }_{\ast }(0))=-S(0,{\delta }_{\ast }(0))=0$. Thus, the result about $W_u$ is proved.

By the same method, we can prove the result about $W_v$. □

Theorem 3.

If $\delta \le {\delta }_{\ast }(a)$ or $\delta >\beta \theta C_0$, then System (3) has no positive solution, where $C_0$ is defined in Theorem 2.

Proof. 

Let $(u,v)$ be a positive solution of System (3). Then, v satisfies

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}-▵v+v({\displaystyle \frac{\theta \beta v-\delta }{1+\beta v}}-{\displaystyle \frac{c(x)u}{1+mu}})=0,\hfill & x\in \Omega ,\hfill \\ {\displaystyle \frac{\partial v}{\partial \nu }}=0,\hfill & x\in \partial \Omega .\hfill \end{array}\right.\end{array}$$

(7)

Thus,

$$0={\lambda }_1({\displaystyle \frac{\theta \beta v-\delta }{1+\beta v}}-{\displaystyle \frac{c(x)u}{1+mu}})>{\lambda }_1(-\delta -{\displaystyle \frac{c(x)u}{1+mu}}).$$

From Theorem 2, we know that $u\le {\parallel u\parallel }_{\infty }\le a$. Note that the function $-\delta -{\displaystyle \frac{c(x)u}{1+mu}}$ is strictly decreasing with respect to u. From (2), we have

$${\lambda }_1(-\delta -{\displaystyle \frac{c(x)a}{1+ma}})<0.$$

(8)

However, from Lemma 1, we know that ${\lambda }_1(-\delta -{\displaystyle \frac{c(x)a}{1+ma}})\ge 0$ for any $\delta \le {\delta }_{\ast }(a)$, which contradicts (8). Thus, System (3) has no positive solution when $\delta \le {\delta }_{\ast }(a)$.

From Theorem 2, we have $v<C_0$ for all $x\in \Omega$. By integrating the first equation of (7) over $\Omega$, we get

$$0={\int }_{\Omega }v({\displaystyle \frac{\theta \beta v-\delta }{1+\beta v}}-{\displaystyle \frac{c(x)u}{1+mu}})dx<{\int }_{\Omega }{\displaystyle \frac{v(\theta \beta v-\delta )}{1+\beta v}}dx<{\int }_{\Omega }{\displaystyle \frac{v(\theta \beta C_0-\delta )}{1+\beta v}}dx.$$

(9)

Hence, if $\delta >\beta \theta C_0$, then ${\int }_{\Omega }{\displaystyle \frac{v(\theta \beta C_0-\delta )}{1+\beta v}}dx<0$, which contradicts (9). Thus, System (3) has no positive solution if $\delta >\beta \theta C_0$. Then, the proof is complete. □

3. Bounded Continuum of Positive Solutions

Biologically, a nonconstant positive solution corresponds to the coexistence steady state of prey and predator. Thus, we are mainly interested in nonconstant positive solutions of System (3). In this section, we will use the local and global bifurcation theory [39,40] to obtain the bounded continuum of positive solutions of System (3). Let ${\delta }_{\ast }={\delta }_{\ast }(a)$ and ${\delta }^{\ast }={\delta }^{\ast }(a)$ be defined in Lemma 1. Let ${\phi }_{\ast }$ and ${\psi }^{\ast }$ be the positive eigenfunctions of the following system

$$-▵{\phi }_{\ast }-({\delta }_{\ast }+{\displaystyle \frac{c(x)a}{1+ma}}){\phi }_{\ast }=0in\Omega ,{\displaystyle \frac{\partial {\phi }_{\ast }}{\partial \nu }}{|}_{\partial \Omega }=0,{\parallel {\phi }_{\ast }\parallel }_2=1$$

(10)

and

$$-▵{\psi }^{\ast }-(a-{\displaystyle \frac{{\delta }^{\ast }}{\beta \theta }}b(x)){\psi }^{\ast }=0in\Omega ,{\displaystyle \frac{\partial {\psi }^{\ast }}{\partial \nu }}{|}_{\partial \Omega }=0,{\parallel {\psi }^{\ast }\parallel }_2=1.$$

(11)

In what follows, we take $\delta$ as the bifurcation parameter. At first, we present the local bifurcation branch of the positive solution, which bifurcates from the semitrivial solution sets ${\Gamma }_u$ and ${\Gamma }_v$.

Lemma 2.

(i) A branch of positive solutions of System (3) bifurcate from ${\Gamma }_u$ if and only if $\delta ={\delta }_{\ast }<0$. That is, there exist a positive constant $s_{\ast }$ and a function ${\psi }_{\ast }\in X$ such that all positive solutions of System (3) near $(a,0,{\delta }_{\ast })\in X\times {\mathbb{R}}_{-}$ can be parameterized as

$$\{(u,v,\delta )=(a+s({\psi }_{\ast }+s\overline{u}(s)),s({\phi }_{\ast }+s\overline{v}(s)),\overline{\delta }(s))\in X\times {\mathbb{R}}_{-}:0<s<s_{\ast }\},$$

(12)

where $(\overline{u}(s),\overline{v}(s),\overline{\delta }(s))$ is a bounded smooth function with respect to s and satisfies $(\overline{u}(0),\overline{v}(0),$$\overline{\delta }(0))=(0,0,{\delta }_{\ast })$ and ${\int }_{\Omega }\overline{v}{\phi }_{\ast }dx=0$. Moreover, when $c(x)=c>0$ is constant, then ${\overline{\delta }}^{\prime }(0)>0$. That is, bifurcation (12) is supercritical.

(ii) A branch of positive solutions of System (3) bifurcate from ${\Gamma }_v$ if and only if $\delta ={\delta }^{\ast }>0$. That is, there exist a positive constant $s^{\ast }$ and a function ${\phi }^{\ast }\in X$ such that all positive solutions of System (3) near $(0,{\displaystyle \frac{{\delta }^{\ast }}{\beta \theta }},{\delta }^{\ast })\in X\times {\mathbb{R}}_{+}$ can be parameterized as

$$\{(u,v,\delta )=(s({\psi }^{\ast }+s\tilde{u}(s)),{\displaystyle \frac{{\delta }^{\ast }}{\beta \theta }}+s({\phi }^{\ast }+s\tilde{v}(s)),\tilde{\delta }(s))\in X\times {\mathbb{R}}_{+}:0<s<s^{\ast }\},$$

(13)

where $(\tilde{u}(s),\tilde{v}(s),\tilde{\delta }(s))$ is a bounded smooth function with respect to s and satisfies $(\tilde{u}(0),\tilde{v}(0),$$\tilde{\delta }(0))=(0,0,{\delta }^{\ast })$ and ${\int }_{\Omega }\tilde{u}{\psi }^{\ast }dx=0$. Moreover, when $b(x)=b>0$ is constant and $0<{\delta }^{\ast }\le {\displaystyle \frac{\beta \theta }{mb}}$, then ${\tilde{\delta }}^{\prime }(0)<0$. That is, bifurcation (13) is subcritical.

Proof. 

(i) We move the semitrivial solution $(a,0)$ to the origin by the change of variable $U=u-a$ in System (3). Then, we define an operator $\mathcal{F}:X\times {\mathbb{R}}_{-}\to Y$ as

$$\mathcal{F}(U,v,\delta )=\left(\begin{array}{c}▵U+f(U+a,v,\delta )\\ ▵v+g(U+a,v,\delta )\end{array}\right),$$

where f and g are defined as in System (3). We need to find the degenerate point of the linearized operator ${\mathcal{F}}_{(U,v)}(0,0,\delta )$. For any $(\psi ,\phi )\in X$, we have

$${\mathcal{F}}_{(U,v)}(0,0,\delta )[\psi ,\phi ]=\left(\begin{array}{c}▵\psi -a\psi -{\displaystyle \frac{ab(x)}{1+ma}}\phi \\ ▵\phi +(\delta +{\displaystyle \frac{ac(x)}{1+ma}})\phi \end{array}\right).$$

(14)

From (10), we have $▵{\phi }_{\ast }+({\delta }_{\ast }+{\displaystyle \frac{c(x)a}{1+ma}}){\phi }_{\ast }=0$. Set ${\psi }_{\ast }:={(▵-a)}^{-1}{\displaystyle \frac{ab(x)}{1+ma}}{\phi }_{\ast }$. Then, ${\mathcal{F}}_{(U,v)}(0,0,{\delta }_{\ast })[{\psi }_{\ast },{\phi }_{\ast }]=0$, and hence $ker{\mathcal{F}}_{(U,v)}(0,0,{\delta }_{\ast })$ is nontrivial. In fact, we can verify that $ker{\mathcal{F}}_{(U,v)}(0,0,{\delta }_{\ast })=span\left\{({\psi }_{\ast },{\phi }_{\ast })\right\}$.

We need to find the range of ${\mathcal{F}}_{(U,v)}(0,0,{\delta }_{\ast })$, denoted by $R({\mathcal{F}}_{(U,v)}(0,0,{\delta }_{\ast }))$. For $(\overline{\psi },\overline{\phi })\in R({\mathcal{F}}_{(U,v)}(0,0,{\delta }_{\ast }))$, we consider the following system

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}▵\psi -a\psi -{\displaystyle \frac{ab(x)}{1+ma}}\phi =\overline{\psi },\hfill & x\in \Omega ,\hfill \\ ▵\phi +({\delta }_{\ast }+{\displaystyle \frac{ac(x)}{1+ma}})\phi =\overline{\phi },\hfill & x\in \Omega ,\hfill \\ {\displaystyle \frac{\partial \psi }{\partial \nu }}={\displaystyle \frac{\partial \phi }{\partial \nu }}=0,\hfill & x\in \partial \Omega .\hfill \end{array}\right.\end{array}$$

(15)

According to the Fredholm alternative theorem, we know that the second equation of (15) is solvable if and only if ${\int }_{\Omega }\overline{\phi }{\phi }_{\ast }dx=0$. If ${\int }_{\Omega }\overline{\phi }{\phi }_{\ast }dx=0$, then the second equation of (15) has a solution ${\phi }_0$, and hence the first equation of (15) has a unique solution ${\psi }_0={(▵-a)}^{-1}(\overline{\psi }+{\displaystyle \frac{ab(x)}{1+ma}}{\phi }_0)$. Thus,

$$R({\mathcal{F}}_{(U,v)}(0,0,{\delta }_{\ast }))=\{(\overline{\psi },\overline{\phi })\in Y|{\int }_{\Omega }\overline{\phi }{\phi }_{\ast }dx=0\}$$

and $codimR({\mathcal{F}}_{(U,v)}(0,0,{\delta }_{\ast }))=1$. In order to use the local bifurcation theory [39,40] at $(0,0,{\delta }_{\ast })$, we need to verify ${\mathcal{F}}_{(U,v),\delta }(0,0,{\delta }_{\ast })[{\psi }_{\ast },{\phi }_{\ast }]\notin R({\mathcal{F}}_{(U,v)}(0,0,{\delta }_{\ast }))$. From (14), we obtain

$$\begin{array}{c}\hfill {\mathcal{F}}_{(U,v),\delta }(0,0,{\delta }_{\ast })[{\psi }_{\ast },{\phi }_{\ast }]=\left(\begin{array}{c}0\hfill \\ {\phi }_{\ast }\hfill \end{array}\right)\notin R({\mathcal{F}}_{(U,v)}(0,0,{\delta }_{\ast })),\end{array}$$

(16)

since ${\int }_{\Omega }{\phi }_{\ast }^{2}dx>0$.

By the Krein–Rutman theorem [41] [Theorem 4], there is no other bifurcation point except $\delta ={\delta }_{\ast }$. Note that $U=u-a$, we can apply the local bifurcation theorem [39,40] to obtain the assertion of (i). In the sequel, we consider the direction of the bifurcation at $\delta ={\delta }_{\ast }$. By the direction formula of the bifurcation (4.5) of [42] [Theorem 2], we have

$$\begin{array}{c}\hfill {\overline{\delta }}^{\prime }(0)=-{\displaystyle \frac{⟨l_1,{\mathcal{F}}_{(U,v)(U,v)}(0,0,{\delta }_{\ast })[{\psi }_{\ast },{\phi }_{\ast }][{\psi }_{\ast },{\phi }_{\ast }]⟩}{2⟨l_1,{\mathcal{F}}_{(U,v),\delta }(0,0,{\delta }_{\ast })[{\psi }_{\ast },{\phi }_{\ast }]⟩}},\end{array}$$

(17)

where the linear functional $l_1:X\to \mathbb{R}$ defined as $⟨l_1,[{\varphi }_1,{\varphi }_2]⟩={\int }_{\Omega }{\varphi }_2{\phi }_{\ast }dx$. Through direct calculations, we have

$$\begin{array}{c}\hfill {\mathcal{F}}_{(U,v)(U,v)}(0,0,{\delta }_{\ast })[{\psi }_{\ast },{\phi }_{\ast }][{\psi }_{\ast },{\phi }_{\ast }]=2\left(\begin{array}{c}-{\psi }_{\ast }^2-{\displaystyle \frac{b(x)}{{(1+ma)}^2}}{\psi }_{\ast }{\phi }_{\ast }\hfill \\ -({\delta }_{\ast }+\theta )\beta {\phi }_{\ast }^2+{\displaystyle \frac{c(x)}{{(1+ma)}^2}}{\psi }_{\ast }{\phi }_{\ast }\hfill \end{array}\right).\end{array}$$

By (16), (17) and the formula of ${\psi }_{\ast }$, we obtain

$$\begin{array}{ccc}\hfill {\overline{\delta }}^{\prime }(0)& =& {\displaystyle \frac{{\int }_{\Omega }[({\delta }_{\ast }+\theta )\beta {\phi }_{\ast }-\frac{c(x)}{{(1+ma)}^2}{\psi }_{\ast }]{\phi }_{\ast }^{2}dx}{{\int }_{\Omega }{\phi }_{\ast }^{2}dx}}\hfill \\ & =& {\displaystyle \frac{{\int }_{\Omega }[(({\delta }_{\ast }+\theta )\beta {\phi }_{\ast }+\frac{b(x)c(x)}{{(1+ma)}^3}){\phi }_{\ast }-\frac{c(x)}{a{(1+ma)}^2}▵{\psi }_{\ast }]{\phi }_{\ast }^{2}dx}{{\int }_{\Omega }{\phi }_{\ast }^{2}dx}}.\hfill \end{array}$$

When $c(x)=c>0$ is a constant, we get from (10) that ${\phi }_{\ast }={\displaystyle \frac{1}{{|\Omega |}^{\frac{1}{2}}}}$. Then,

$${\overline{\delta }}^{\prime }(0)={\displaystyle \frac{1}{{|\Omega |}^{\frac{3}{2}}}}{\int }_{\Omega }[({\delta }_{\ast }+\theta )\beta +{\displaystyle \frac{b(x)c}{{(1+ma)}^3}}]dx>0.$$

Thus, the assertion (i) is proved.

By the same method, we can prove the result about (ii). □

We have obtained the bifurcations of System (3) at the end points ${\delta }_{\ast }<0$ and ${\delta }^{\ast }>0$. Next, we give the following bounded continuum of positive solutions of System (3) with bifurcation parameter $\delta$.

Theorem 4.

For any fixed $(a,m,\beta ,\theta ,b(x),c(x))$, the positive solution set of System (3) forms a bounded continuum $\Gamma \subset X\times \mathbb{R}$, which bifurcates from $(u,v,\delta )=(0,{\displaystyle \frac{{\delta }^{\ast }}{\beta \theta }},{\delta }^{\ast })\in {\Gamma }_v$ and joins $(u,v,\delta )=(a,0,{\delta }_{\ast })\in {\Gamma }_u$ when δ goes from ${\delta }^{\ast }$ to ${\delta }_{\ast }$. This means that System (3) has at least one positive solution as ${\delta }^{\ast }>\delta >{\delta }_{\ast }$.

Proof. 

In (13), we obtained the local bifurcation branch at $\delta ={\delta }^{\ast }$. Let $\widehat{\Gamma }$ be a maximal connected extension of the local bifurcation branch in $X\times R$ of solutions of System (3). According to the global bifurcation theorem [39,40], $\widehat{\Gamma }$ must satisfy one of the following:

(A) $\widehat{\Gamma }$ meets a certain bifurcation point except for $(u,v,\delta )=(0,{\displaystyle \frac{{\delta }^{\ast }}{\beta \theta }},{\delta }^{\ast })$;

(B) $\widehat{\Gamma }$ is unbounded in $X\times R$.

From Theorem 2, we know that any positive solutions $(u,v)$ of System (3) are bounded in $L^{\infty }(\Omega )\times L^{\infty }(\Omega )$. Thus, by the standard elliptic regularity theory [43], we can find a positive constant $M=M(a,m,\beta ,\theta ,\delta ,b(x),c(x))$ such that ${\parallel (u,v)\parallel }_X\le M$. That means that ${\parallel (u,v)\parallel }_X$ cannot blow up along $\widehat{\Gamma }$, and hence $(A)$ holds true.

Set $P=\{(u,v)\in X|u>0,v>0\}$. From Theorem 2, we know that $\widehat{\Gamma }$ is bounded in $P\times R$. And by a standard argument with the global bifurcation theorem, we can find a certain $(\widehat{u},\widehat{v},\delta )\in \widehat{\Gamma }$ such that $(\widehat{u},\widehat{v})\in \partial P$. Hence, the strong maximum principle yields $\widehat{u}=0$ or $\widehat{v}=0$. $(\widehat{u},\widehat{v})=(0,0)$ is impossible since the trivial solution $(\widehat{u},\widehat{v})=(0,0)$ of System (3) is non-degenerate. Then, $(\widehat{u},\widehat{v})=(a,0)$ or $(\widehat{u},\widehat{v})=(0,{\displaystyle \frac{\delta }{\beta \theta }})$. By Lemma 2, we have that $(\widehat{u},\widehat{v},\delta )=(a,0,{\delta }_{\ast })$ or $(\widehat{u},\widehat{v},\delta )=(0,{\displaystyle \frac{{\delta }^{\ast }}{\beta \theta }},{\delta }^{\ast })$. Note that (A) holds true; we exclude that $(u,v,\delta )=(0,{\displaystyle \frac{{\delta }^{\ast }}{\beta \theta }},{\delta }^{\ast })$, and hence we have $(\widehat{u},\widehat{v},\delta )=(a,0,{\delta }_{\ast })$. This completes the proof. □

4. Limiting System

In Section 3, we obtained the positive solution branch $\Gamma$. Next, we will explore how spatial heterogeneous $b(x)$ and $c(x)$ affect $\Gamma$. So we employ the following scaling

$$\begin{array}{c}\hfill u=\epsilon w,v=\epsilon z,a=\epsilon \mu ,\delta =\epsilon \eta ,\theta =\epsilon \gamma ,,m={\displaystyle \frac{1}{\epsilon }},\beta ={\displaystyle \frac{1}{\epsilon }},\end{array}$$

(18)

where $\epsilon >0$ is a small perturbation parameter, $\mu ,\gamma$ are positive numbers and $\eta$ is a real number. With (18), System (3) becomes:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}▵w+\epsilon F(w,z)=0,\hfill & x\in \Omega ,\hfill \\ ▵z+\epsilon G(w,z,\eta )=0,\hfill & x\in \Omega ,\hfill \\ {\displaystyle \frac{\partial w}{\partial \nu }}={\displaystyle \frac{\partial z}{\partial \nu }}=0,\hfill & x\in \partial \Omega ,\hfill \end{array}\right.\end{array}$$

(19)

where $F(w,z)=w(\mu -w-{\displaystyle \frac{b(x)z}{1+w}})$ and $G(w,z,\eta )=z({\displaystyle \frac{\eta -\gamma z}{1+z}}+{\displaystyle \frac{c(x)w}{1+w}})$.

Note that (18) maps the semitrivial solutions $(a,0)$ and $(0,{\displaystyle \frac{\delta }{\beta \theta }})$ of System (3) to the semitrivial ones $(\mu ,0)$ and $(0,{\displaystyle \frac{\eta }{\gamma }})$ of System (19), respectively. By Lemma 2, we know that the positive solution $\Gamma$ of System (19) bifurcates from the semitrivial solution curve $\{(\mu ,0,\eta ):\eta \in \mathbb{R}\}$ and $\{(0,{\displaystyle \frac{\eta }{\gamma }},\eta ):\eta \in {\mathbb{R}}_{+}\}$ if and only if

$$\begin{array}{c}\hfill \eta ={\eta }_{\ast }(\epsilon ):={\displaystyle \frac{{\delta }_{\ast }(\epsilon \mu )}{\epsilon }}and\eta ={\eta }^{\ast }(\epsilon ):={\displaystyle \frac{{\delta }^{\ast }(\epsilon \mu )}{\epsilon }}.\end{array}$$

(20)

When $\epsilon >0$ is sufficiently small, we derive the detailed structure of the positive solution set of System (19) using the method of Du and Lou [44]. We define a linear operator $H:X\to Y$ and a nonlinear operator $B:X\times \mathbb{R}\to Y$ as follows:

$$H(w,z):={(▵w,▵z)}^{T}andB(w,z,\eta ):={(F(w,z),G(w,z,\eta ))}^T.$$

Thus, System (19) can be written as

$$\begin{array}{c}\hfill H(w,z)+\epsilon B(w,z,\eta )=0.\end{array}$$

(21)

We want to use the Lyapunov–Schmidt reduction to consider the solution of (21). With the Neumann boundary condition ${\partial }_{n}w={\partial }_{n}z=0$, we see that $kerH={\mathbb{R}}^2$. Hence, we decompose $X={\mathbb{R}}^2\times X_1$ and $Y={\mathbb{R}}^2\times Y_1$, where $X_1$ and $Y_1$ represent the ${\mathbb{L}}^2$-orthogonal space of ${\mathbb{R}}^2$ in X and Y, respectively. We introduce a projection to peel off the part of $kerH$ in (21). Let $P:X\to X$ and $Q:Y\to Y$ be projections such that $R(P)=X_1$ and $R(Q)=Y_1$. Thence, any $(w,z)\in X$ of (21) can be decomposed as $(w,z)=(r,s)+\mathbf{u}$, where $(r,s)\in {\mathbb{R}}^2$ and $\mathbf{u}=P(w,z)$. With the actions of the projections Q and $(I-Q)$, (21) is equivalent to the system

$$\begin{array}{c}\hfill \left\{\begin{array}{c}QH(\mathbf{u})+\epsilon QB((r,s)+\mathbf{u},\eta )=0,\hfill \\ (I-Q)B((r,s)+\mathbf{u},\eta )=0.\hfill \end{array}\right.\end{array}$$

(22)

Our goal is to solve the first equation of (22) in $X_1$ for $\mathbf{u}=\mathbf{u}(r,s,\eta ,ϵ)$. Then, by substituting it into the second equation of (22), we obtain $(I-Q)B((r,s)+\mathbf{u}(r,s,\eta ,ϵ),\eta )=0$. If there are some $(r_0,s_0,{\eta }_0,{ϵ}_0)\in {\mathbb{R}}^4$ satisfying $(I-Q)B((r_0,s_0)+\mathbf{u}(r_0,s_0,{\eta }_0,{ϵ}_0),{\eta }_0)=0$, then $(w,z)=(r_0,s_0)+\mathbf{u}(r_0,s_0,{\eta }_0,{ϵ}_0)$ is a solution of (21). By the first equation of (22), we define a mapping $K:{\mathbb{R}}^4\times X_1\to Y_1$ by

$$K(r,s,\eta ,\epsilon ,\mathbf{u})=QH(\mathbf{u})+\epsilon QB((r,s)+\mathbf{u},\eta ).$$

Clearly, the zero points of $K(r,s,\eta ,\epsilon ,\mathbf{u})$ for $\mathbf{u}=\mathbf{u}(r,s,\eta ,\epsilon )$ are the solution of the first equation of (22). Through direct calculations, we have

$$K(r,s,\eta ,0,0)=0and{K}_{\mathbf{u}}(r,s,\eta ,0,0)=QHforany(r,s,\eta )\in {\mathbb{R}}^3.$$

Thus, $K_{\mathbf{u}}(r,s,\eta ,0,0)$ is an isomorphism from $X_1$ onto $Y_1$. Following the same arguments of [45], by the implicit function theorem and a compactness argument, we can obtain a solution of the first equation of (22) for $\mathbf{u}(r,s,\eta ,\epsilon )\in X_1$ with $\mathbf{u}(r,s,\eta ,0)=0$. Hence, we can rewrite $\mathbf{u}(r,s,\eta ,\epsilon )=\epsilon U(r,s,\eta ,\epsilon )$ for a small $\epsilon$. In fact, we can obtain the following result.

Lemma 3.

For any $T>0$, there exists a small ${\epsilon }_0>0$ such that $\mathbf{u}=\mathbf{u}(r,s,\eta ,ϵ)$ is a solution of the first equation of (22) satisfying $\mathbf{u}(r,s,\eta ,0)=0$ and $\mathbf{u}(r,s,\eta ,ϵ)$, which can be parameterized by

$$\mathcal{N}=\{\epsilon U(r,s,\eta ,\epsilon ):|r|,|s|,|\eta |\le T+{\epsilon }_0,\epsilon \le {\epsilon }_0\},$$

where $U(r,s,\eta ,\epsilon )$ is an $X_1$-valued smooth function defined in $\left|r\right|,\left|s\right|,\left|\eta \right|\le T+{\epsilon }_0,\epsilon \le {\epsilon }_0$. Thence, an element $(w,z,\eta ,\epsilon )=((r,s)+\epsilon U(r,s,\eta ,\epsilon ),\eta ,\epsilon )$ is a solution of equation (21) if and only if

$$\begin{array}{c}\hfill {\Phi }^{\epsilon }(r,s,\eta ):=(I-Q)B((r,s)+\epsilon U(r,s,\eta ,\epsilon ),\eta )=0.\end{array}$$

For the detailed proof, one can refer to [45] [Lemma 2].

From Lemma 3, we know that finding the solution of System (19) is equivalent to finding $ker{\Phi }^{\epsilon }(r,s,\eta )$ when $\epsilon \in [0,{\epsilon }_0]$. Firstly, we investigate the structure of $ker{\Phi }^0(r,s,\eta )$. Note that $(I-Q)(w,z)=({\oint }_{\Omega }wdx,{\oint }_{\Omega }zdx)$. We have that

$$\begin{array}{c}\hfill {\Phi }^0(r,s,\eta ):=\left(\begin{array}{c}{\oint }_{\Omega }F(r,s)dx\hfill \\ {\oint }_{\Omega }G(r,s,\eta )dx)\hfill \end{array}\right)=\left(\begin{array}{c}r{\oint }_{\Omega }(\mu -r-{\displaystyle \frac{b(x)s}{1+r}})dx\hfill \\ s{\oint }_{\Omega }({\displaystyle \frac{\eta -\gamma s}{1+s}}+{\displaystyle \frac{c(x)r}{1+r}})dx\hfill \end{array}\right).\end{array}$$

(23)

Therefore, $ker{\Phi }^0(r,s,\eta )$ is a union of the following four sets:

$${\mathcal{L}}_0=\{(0,0,\eta ):\eta \in \mathbb{R}\},{\mathcal{L}}_w=\{(\mu ,0,\eta ):\eta \in \mathbb{R}\},$$

$${\mathcal{L}}_z=\{(0,{\displaystyle \frac{\eta }{\gamma }},\eta ):\eta \in {\mathbb{R}}_{+}\},{\mathcal{L}}_p=\{(r,h(r),l(r)):r\in {\mathbb{R}}_{+}\},$$

where

$$\begin{array}{c}\hfill h(r)={\displaystyle \frac{(\mu -r)(1+r)}{{\oint }_{\Omega }b(x)dx}}andl(r)=\gamma h(r)-{\displaystyle \frac{r(1+h(r))}{1+r}}{\oint }_{\Omega }c(x)dx.\end{array}$$

(24)

In fact, ${\mathcal{L}}_w,{\mathcal{L}}_z$ and ${\mathcal{L}}_p$ can be regarded as the limiting sets of semitrivial solution curves $\{(\mu ,0,\eta ):\eta \in \mathbb{R}\},\{(0,{\displaystyle \frac{\eta }{\gamma }},\eta ):\eta \in {\mathbb{R}}_{+}\}$ and the positive solution set of System (19) when $\epsilon \to 0$, respectively. For the positive solution $\{(r,h(r),l(r)):r\in {\mathbb{R}}_{+}\}$, we need more properties of $h(r)$ and $l(r)$.

From the formulas of $h(r)$ and $l(r)$, we know that

$$h^{\prime }(r)={\displaystyle \frac{\mu -2r-1}{{\oint }_{\Omega }b(x)dx}}and{l}^{\prime }(r)=\gamma h^{\prime }(r)-{\displaystyle \frac{1+h(r)+r(1+r)h^{\prime }(r)}{{(1+r)}^2}}{\oint }_{\Omega }c(x)dx.$$

Thus, we can obtain the following result.

Lemma 4.

The following properties of $h(r)$ and $l(r)$ hold true:

(i) $h(0)={\displaystyle \frac{l(0)}{\gamma }}>0,h(\mu )=0$ and $l(\mu )<0$.

(ii) If $\gamma >{\oint }_{\Omega }c(x)dx$, then $l^{\prime }(\mu )<0$ and $l^{\prime }(0)\left\{\begin{array}{c}>0,if\mu >{\displaystyle \frac{\gamma +{\oint }_{\Omega }b(x)dx{\oint }_{\Omega }c(x)dx}{\gamma -{\oint }_{\Omega }c(x)dx}},\hfill \\ <0,if\mu <{\displaystyle \frac{\gamma +{\oint }_{\Omega }b(x)dx{\oint }_{\Omega }c(x)dx}{\gamma -{\oint }_{\Omega }c(x)dx}}.\hfill \end{array}\right.$

(iii) If $\gamma \le {\oint }_{\Omega }c(x)dx$, then $l^{\prime }(0)<0$.

In Lemma 4, we considered $ker{\Phi }^0(r,s,\eta )$. Now, we concentrate on $ker{\Phi }^{\epsilon }(r,s,\eta )$. Lemma 4 asserts that

$$(0,h(0),l(0))=(0,{\displaystyle \frac{l(0)}{\gamma }},l(0))\in {\mathcal{L}}_{z}and(\mu ,h(\mu ),l(\mu ))=(\mu ,0,l(\mu ))\in {\mathcal{L}}_w.$$

Thus, the bounded curve $\{(r,h(r),l(r)):0<r<\mu \}\subset {\mathcal{L}}_p$ coincides with the limiting set of positive solutions of System (19) as $\epsilon \to 0$. To be more precise, we have the following theorem.

Theorem 5.

For any fixed $(\mu ,\gamma ,b(x),c(x))$, there exists a small constant ${\epsilon }_0$ and a family of bounded smooth curves

$$\{S(ϵ,\epsilon )=(r(ϵ,\epsilon ),s(ϵ,\epsilon ),\eta (ϵ,\epsilon ))\in {\mathbb{R}}^3:(ϵ,\epsilon )\in [0,C_{\epsilon }]\times [0,{\epsilon }_0]\},$$

such that for each $\epsilon \in (0,{\epsilon }_0]$, all positive solutions of system (19) are parameterized as

$$\begin{array}{c}\hfill {\Gamma }_{\epsilon }=\{(w(ϵ,\epsilon ),z(ϵ,\epsilon ),\eta (ϵ,\epsilon ))=((r,s)+\epsilon U(r,s,\eta ,\epsilon ),\eta ):\\ \hfill (r,s,\eta )=(r(ϵ,\epsilon ),s(ϵ,\epsilon ),\eta (ϵ,\epsilon )),ϵ\in (0,C_{\epsilon }]\},\end{array}$$

(25)

where $U(r,s,\eta ,\epsilon )$ is an $X_1$-valued smooth function defined in Lemma 3 and $C_{\epsilon }$ is a smooth function in $\epsilon \in [0,{\epsilon }_0]$ such that $C_0=\mu$. Additionally, $S(ϵ,\epsilon )$ is a smooth function satisfying

$$\begin{array}{c}\hfill S(ϵ,0)=(ϵ,h(ϵ),l(ϵ)),S(0,\epsilon )=(0,{\displaystyle \frac{{\eta }^{\ast }(\epsilon )}{\gamma }},{\eta }^{\ast }(\epsilon )),S(C_{\epsilon },\epsilon )=(\mu ,0,{\eta }_{\ast }(\epsilon )),\end{array}$$

(26)

where functions $h,l$ are defined in (24) and ${\eta }_{\ast }(\epsilon ),{\eta }^{\ast }(\epsilon )$ are defined in (20).

We take several steps to prove Theorem 5. As a first step, we construct the local branches of positive solutions of System (19) near the bifurcation points.

Lemma  5.

There exist a neighbourhood ${\mathcal{U}}_{\ast }$ of $(\mu ,0,-{\displaystyle \frac{\mu }{1+\mu }}{\oint }_{\Omega }c(x)dx)$ and a positive constant ${\zeta }_{\ast }$ such that for any $\epsilon \in [0,{\zeta }_{\ast }]$,

$$\begin{array}{c}\hfill ker{\Phi }^{\epsilon }\bigcap {\mathcal{U}}_{\ast }\bigcap ({\overline{\mathbb{R}}}_{+}^2\times \mathbb{R})=\{(\overline{r}(ϵ,\epsilon ),\overline{s}(ϵ,\epsilon ),\overline{\eta }(ϵ,\epsilon )):ϵ\in [0,{\zeta }_{\ast }]\}\bigcup \{(\mu ,0,\eta )\in {\mathcal{U}}_{\ast }\},\end{array}$$

for a smooth function $(\overline{r}(ϵ,\epsilon ),\overline{s}(ϵ,\epsilon ),\overline{\eta }(ϵ,\epsilon ))$ satisfies $(\overline{r}(ϵ,0),\overline{s}(ϵ,0),\overline{\eta }(ϵ,0))=(\mu -ϵ,h(\mu -ϵ),$$l(\mu -ϵ))$ and $(\overline{r}(0,\epsilon ),\overline{s}(0,\epsilon ),\overline{\eta }(0,\epsilon ))=(\mu ,0,{\eta }_{\ast }(\epsilon ))$.

Proof. 

By Lemma 2(i) and (18), for any $\epsilon >0$, we know that there exist a neighbourhood ${\mathcal{V}}_{\epsilon }$ of $(w,z,\eta )=(\mu ,0,{\eta }_{\ast }(\epsilon ))$ and a positive constant ${\zeta }_{\ast }={\zeta }_{\ast }(\epsilon )$ such that all solutions of System (19) contained in ${\mathcal{V}}_{\epsilon }$ are given by

$$(w(ϵ,\epsilon ),z(ϵ,\epsilon ),\eta (ϵ,\epsilon ))=(\mu +ϵ({\psi }_{\ast }+\overline{w}(ϵ,\epsilon )),ϵ({\phi }_{\ast }+\overline{z}(ϵ,\epsilon )),\overline{\eta }(ϵ,\epsilon ))forϵ\in (0,{\zeta }_{\ast }],$$

where $({\psi }_{\ast },{\phi }_{\ast })$ is defined in (12) and $(\overline{w}(ϵ,\epsilon ),\overline{z}(ϵ,\epsilon ),\overline{\eta }(ϵ,\epsilon ))$ is a smooth function with $\overline{\eta }(0,\epsilon )={\eta }_{\ast }(\epsilon )$ and ${\int }_{\Omega }\overline{z}(ϵ,\epsilon ){\phi }_{\ast }dx=0$. Let $\overline{r}(ϵ,\epsilon )={\oint }_{\Omega }w(ϵ,\epsilon )dx$ and $\overline{s}(ϵ,\epsilon )={\oint }_{\Omega }z(ϵ,\epsilon )dx$. We define the subset ${\mathcal{U}}_{\epsilon }\subset {\mathbb{R}}^3$ by

$${\mathcal{U}}_{\epsilon }=\{(\overline{r},\overline{s},\overline{\eta })\in {\mathbb{R}}^3:(w,z,\overline{\eta })\in {\mathcal{V}}_{\epsilon }\}.$$

Since (19) is equivalent to the equation ${\Phi }^{\epsilon }(r,s,\eta )=0$, we obtain

$$ker{\Phi }^{\epsilon }\bigcap {\mathcal{U}}_{\epsilon }\bigcap ({\overline{\mathbb{R}}}_{+}^2\times \mathbb{R})=\{(\overline{r}(ϵ,\epsilon ),\overline{s}(ϵ,\epsilon ),\overline{\eta }(ϵ,\epsilon )):ϵ\in [0,{\zeta }_{\ast }]\}\bigcup \{(\mu ,0,\eta )\in {\mathcal{U}}_{\epsilon }\}.$$

On the one hand, we can observe (10) from System (19). On the other hand, by integrating (10), we have

$$\begin{array}{c}\hfill {\displaystyle \frac{{\delta }_{\ast }(a)}{a}}{\int }_{\Omega }{\phi }_{\ast }(x,a)dx=-{\displaystyle \frac{1}{1+\mu }}{\int }_{\Omega }{\phi }_{\ast }(x,a)c(x)dx.\end{array}$$

(27)

From Lemma 1, we have ${\delta }_{\ast }(0)=0$. By letting $a\to 0$ in (10), we get $\underset{a\to 0}{lim}{\phi }_{\ast }(x,a)={|\Omega |}^{-1/2}$. Using (27), we can get $\underset{\epsilon \to 0}{lim}{\eta }_{\ast }(\epsilon )=-{\displaystyle \frac{\mu }{1+\mu }}{\oint }_{\Omega }c(x)dx$ since ${\eta }_{\ast }(\epsilon )={\displaystyle \frac{{\delta }_{\ast }(\epsilon \mu )}{\epsilon }}$. Thus, if $\epsilon >0$ is sufficiently small, then ${\mathcal{U}}_{\epsilon }$ contains a neighbourhood ${\mathcal{U}}_{\ast }$ of $(\mu ,0,-{\displaystyle \frac{\mu }{1+\mu }}{\oint }_{\Omega }c(x)dx)$. Therefore, the proof is complete. □

From System (19), we can obtain (11). Hence, we have $\underset{\epsilon \to 0}{lim}{\eta }^{\ast }(\epsilon )={\displaystyle \frac{\gamma \mu }{{\oint }_{\Omega }b(x)dx}}$. Thence, by the similar method of Lemma 5, we have the following lemma.

Lemma 6.

There exist a neighbourhood ${\mathcal{U}}^{\ast }$ of $(0,{\displaystyle \frac{\mu }{{\oint }_{\Omega }b(x)dx}},{\displaystyle \frac{\gamma \mu }{{\oint }_{\Omega }b(x)dx}})$ and a positive constant ${\zeta }^{\ast }$ such that for any $\epsilon \in [0,{\zeta }^{\ast }]$,

$$\begin{array}{c}\hfill ker{\Phi }^{\epsilon }\bigcap {\mathcal{U}}^{\ast }\bigcap {\overline{\mathbb{R}}}_{+}^3=\{(\widehat{r}(ϵ,\epsilon ),\widehat{s}(ϵ,\epsilon ),\widehat{\eta }(ϵ,\epsilon )):ϵ\in [0,{\zeta }^{\ast }]\}\bigcup \{(0,{\displaystyle \frac{\eta }{\gamma }},\eta )\in {\mathcal{U}}^{\ast }\},\end{array}$$

for a smooth function $(\widehat{r}(ϵ,\epsilon ),\widehat{s}(ϵ,\epsilon ),\widehat{\eta }(ϵ,\epsilon ))$ satisfies $(\widehat{r}(ϵ,0),\widehat{s}(ϵ,0),\widehat{\eta }(ϵ,0))=(ϵ,h(ϵ),l(ϵ))$ and $(\widehat{r}(0,\epsilon ),\widehat{s}(0,\epsilon ),\widehat{\eta }(0,\epsilon ))=(0,{\displaystyle \frac{{\eta }^{\ast }(\epsilon )}{\gamma }},{\eta }^{\ast }(\epsilon ))$.

Based on Lemmas 5 and 6, we have the following result.

Lemma 7.

There exists a neighbourhood $\mathcal{U}$ of $\{(r,h(r),l(r)):0\le r\le \mu \}$ such that if $\epsilon >0$ is sufficiently small, all positive solutions of System (19) contained in $\mathcal{U}$ can be parameterized by (25).

Proof. 

Set ${\mathcal{L}}_p[{\displaystyle \frac{{\zeta }^{\ast }}{2}},\mu -{\displaystyle \frac{{\zeta }_{\ast }}{2}}]:=\{(r,h(r),l(r)):r\in [{\displaystyle \frac{{\zeta }^{\ast }}{2}},\mu -{\displaystyle \frac{{\zeta }_{\ast }}{2}}]\}$, where ${\zeta }_{\ast }$ and ${\zeta }^{\ast }$ are defined in Lemmas 5 and 6. From (23), we can obtain

$$\begin{array}{c}\hfill {\Phi }_{(r,s)}^0(r,h(r),l(r))=\left(\begin{array}{cc}{\oint }_{\Omega }(\mu -2r-{\displaystyle \frac{b(x)h(r)}{{(1+r)}^2}})dx\hfill & -{\oint }_{\Omega }{\displaystyle \frac{b(x)r}{1+r}}dx\hfill \\ {\oint }_{\Omega }{\displaystyle \frac{c(x)h(r)}{{(1+r)}^2}}dx\hfill & {\oint }_{\Omega }({\displaystyle \frac{l(r)-2\gamma h(r)-\gamma h^2(r)}{{(1+h(r))}^2}}+{\displaystyle \frac{c(x)r}{1+r}})dx\hfill \end{array}\right).\end{array}$$

Then, we obtain $det{\Phi }_{(r,s)}^0(r,h(r),l(r))=-{\displaystyle \frac{r(\mu -r)l^{\prime }(r)}{1+h(r)}}$. Thus, when $r\in [{\displaystyle \frac{{\zeta }^{\ast }}{2}},\mu -{\displaystyle \frac{{\zeta }_{\ast }}{2}}]$, we have ${\Phi }_{(r,s)}^0(r,h(r),l(r))$ is invertible if and only if $l^{\prime }(r)\ne 0$.

(Case I) If $l^{\prime }(r)\ne 0$ for any fixed $r\in [{\displaystyle \frac{{\zeta }^{\ast }}{2}},\mu -{\displaystyle \frac{{\zeta }_{\ast }}{2}}]$, then ${\Phi }_{(r,s)}^0(r,h(r),l(r))$ is invertible. By implicit function theorem and Lemma 2, we know that there exist a positive constant $\zeta =\zeta (r)$ and a neighbourhood ${\mathcal{W}}_r$ of $(r,h(r))$ such that

$$\begin{array}{c}\hfill ker{\Phi }^{\epsilon }\bigcap {\mathcal{U}}_r=\{(r(\eta ,\epsilon ),s(\eta ,\epsilon ),\eta ):\eta \in (l(r)-\zeta ,l(r)+\zeta )\}\mathrm{for}\mathrm{each}\epsilon \in [0,\zeta ],\end{array}$$

where ${\mathcal{U}}_r={\mathcal{W}}_r\times (l(r)-\zeta ,l(r)+\zeta )$ and $(r(\eta ,\epsilon ),s(\eta ,\epsilon ))$ is a smooth function with $(r(l(r),0),$$s(l(r),0))=(r,h(r))$.

(Case II) If $l^{\prime }(r)=0$ for some $r\in [{\displaystyle \frac{{\zeta }^{\ast }}{2}},\mu -{\displaystyle \frac{{\zeta }_{\ast }}{2}}]$, then $det{\Phi }_{(r,s)}^0(r,h(r),l(r))=0$. This means that $rank{\Phi }_{(r,s)}^0=1$. Thence,

$$\begin{array}{c}\hfill dimker{\Phi }_{(r,s)}^0(r,h(r),l(r))=codimR({\Phi }_{(r,s)}^0(r,h(r),l(r)))=1.\end{array}$$

(28)

Note that

$$\begin{array}{c}\hfill {\Phi }_{\eta }^0(r,h(r),l(r))=\left(\begin{array}{c}0\hfill \\ {\displaystyle \frac{h(r)}{1+h(r)}}\hfill \end{array}\right)\notin R({\Phi }_{(r,s)}^0(r,h(r),l(r))).\end{array}$$

(29)

Thus, from (28), (29) and the spontaneous bifurcation theory of Crandall and Rabinowitz [46], we know that there exist a positive constant $\zeta =\zeta (r)$ and a neighbourhood ${\mathcal{U}}_r$ of $(r,h(r),l(r))$ such that

$$\begin{array}{c}\hfill ker{\Phi }^{\epsilon }\bigcap {\mathcal{U}}_r=\{(r(ϵ,\epsilon ),s(ϵ,\epsilon ),\eta (ϵ,\epsilon )):ϵ\in (-\zeta ,\zeta )\}\mathrm{for} \mathrm{each}\epsilon \in [0,\zeta ],\end{array}$$

where $(r(ϵ,\epsilon ),s(ϵ,\epsilon ),\eta (ϵ,\epsilon ))$ is a smooth function in $(ϵ,\epsilon )\in [-\zeta ,\zeta ]\times [0,\zeta ]$ which satisfies $(r(0,0),$$s(0,0),\eta (0,0))=(r,h(r),l(r))$.

From (Case I) and (Case II), we always have ${\mathcal{L}}_p[{\displaystyle \frac{{\zeta }^{\ast }}{2}},\mu -{\displaystyle \frac{{\zeta }_{\ast }}{2}}]\subset \bigcup \{{\mathcal{U}}_r:r\in [{\displaystyle \frac{{\zeta }^{\ast }}{2}},\mu -{\displaystyle \frac{{\zeta }_{\ast }}{2}}]\}.$ Moreover, from the compactness of ${\mathcal{L}}_p[{\displaystyle \frac{{\zeta }^{\ast }}{2}},\mu -{\displaystyle \frac{{\zeta }_{\ast }}{2}}]$, we can find finitely many points ${\left\{r_j\right\}}_1^n$ such that $(r_j,h(r_j),l(r_j))\in {\mathcal{L}}_p[{\displaystyle \frac{{\zeta }^{\ast }}{2}},\mu -{\displaystyle \frac{{\zeta }_{\ast }}{2}}]$ for $1\le j\le n$ and ${\mathcal{L}}_p[{\displaystyle \frac{{\zeta }^{\ast }}{2}},\mu -{\displaystyle \frac{{\zeta }_{\ast }}{2}}]\subset {\displaystyle \bigcup _{j=1}^n}{\mathcal{U}}_{r_j}$. On the other hand, we put ${\mathcal{U}}_{r_0}={\mathcal{U}}^{\ast }$ and ${\mathcal{U}}_{r_{n+1}}={\mathcal{U}}_{\ast }$, where ${\mathcal{U}}_{\ast },{\mathcal{U}}^{\ast }$ are defined in Lemmas 5 and 6. Without loss of generality, we can assume ${\mathcal{U}}_{r_j}\bigcap {\mathcal{U}}_{r_{j+1}}\ne ⌀$ for $j=0,1,\dots ,n$. Put ${\zeta }_{r_j}=\zeta (r_j)$ for $j=0,1,\dots ,n+1$, where ${\zeta }_{r_0}={\zeta }^{\ast }$ and ${\zeta }_{r_{n+1}}={\zeta }_{\ast }$. With regard to Lemmas 5 and 6, for any $\epsilon \in [0,{\zeta }_{r_j}]$ and $j\in \{0,1,\dots ,n+1\}$, we let

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{J}_j^{\epsilon }:=ker{\Phi }^{\epsilon }\bigcap {\mathcal{U}}_{r_j}=\{(r_j(ϵ,\epsilon ),s_j(ϵ,\epsilon ),{\eta }_j(ϵ,\epsilon )):ϵ\in (-{\zeta }_j,{\zeta }_j)\}for1\le j\le n\hfill \\ J_0^{\epsilon }:=\{(\widehat{r}(ϵ,\epsilon ),\widehat{s}(ϵ,\epsilon ),\widehat{\eta }(ϵ,\epsilon )):ϵ\in [0,{\zeta }^{\ast }]\},\hfill \\ J_{n+1}^{\epsilon }:=\{(\overline{r}(ϵ,\epsilon ),\overline{s}(ϵ,\epsilon ),\overline{\eta }(ϵ,\epsilon )):ϵ\in [0,{\zeta }_{\ast }]\},\hfill \end{array}\right.\end{array}$$

(30)

where $(r_j(ϵ,\epsilon ),s_j(ϵ,\epsilon ),{\eta }_j(ϵ,\epsilon ))$ is a smooth function with $(r_j(0,0),s_j(0,0),{\eta }_j(0,0))=(r_j,$$h(r_j),l(r_j))$ for $1\le j\le n$.

Let $\mathcal{U}:={\displaystyle \bigcup _{j=0}^{n+1}}{\mathcal{U}}_{r_j}$. It follows from (30) that

$$\begin{array}{c}\hfill ker{\Phi }^{\epsilon }\bigcap \mathcal{U}\bigcap ({\overline{\mathbb{R}}}_{+}^2\times \mathbb{R})=\bigcup _{j=0}^{n+1}{J}_j^{\epsilon },forany\epsilon \in [0,\underset{0\le j\le n+1}{min}{\zeta }_{r_j}],\end{array}$$

(31)

which implies that $ker{\Phi }^{\epsilon }\bigcap \mathcal{U}\bigcap ({\overline{\mathbb{R}}}_{+}^2\times \mathbb{R})$ forms a one-dimensional submanifold. Therefore, by the perturbation theory of Du and Lou ([44], Proposition A3), we can construct a bounded smooth curve $S(ϵ,\epsilon )=(r(ϵ,\epsilon ),s(ϵ,\epsilon ),\eta (ϵ,\epsilon ))$ for small $\epsilon >0$ and $ϵ\in [0,C_{\epsilon }]$, which satisfies (26) and $S((0,C_{\epsilon }),\epsilon )={\displaystyle \bigcup _{j=0}^{n+1}}{J}_j^{\epsilon }$, where $C_{\epsilon }$ is defined in Theorem 5. □

In what follows, we will show that System (19) does not has any positive solutions outside $\mathcal{U}$.

Lemma 8.

For any fixed neighbourhood $\mathcal{V}$ of $\{(r,h(r),l(r)):0\le r\le \mu \}$, there exists a small constant ${\zeta }_0>0$ such that any positive solution $(w,z)$ of System (19) can be expressed as $(w,z)=(r,s)+\epsilon U(r,s,\eta ,\epsilon )$ for $\epsilon \in [0,{\zeta }_0]$ and $(r,s,\eta )\in \mathcal{V}$, where $U(r,s,\eta ,\epsilon )$ is an $X_1$-valued smooth function defined in Lemma 3.

Proof. 

We will prove this lemma by a contradictory argument. Let $(w_k,z_k)$ be any positive solution of System (19) with $\eta ={\eta }_k$ and $\epsilon ={\epsilon }_k$, where the positive sequence ${\left\{{\epsilon }_k\right\}}_{k\in \mathbb{N}}$ satisfies $\underset{k\to \infty }{lim}{\epsilon }_k=0$. We suppose that $(w_k,z_k,{\eta }_k)\notin \mathcal{V}$ for all $k\in \mathbb{N}$. To obtain a contradiction, we will find a sequence $\left\{(r_j,s_j)\right\}$ and a subsequence $\left\{(w_{k_j},z_{k_j},{\eta }_{k_j})\right\}$ such that, for all $k_j\in \mathbb{N}$ and some $r\in (0,\mu )$, we have

$$\begin{array}{c}\hfill (w_{k_j},z_{k_j})=(r_j,s_j)+{\epsilon }_{k_j}U(r_j,s_j,{\eta }_{k_j},{\epsilon }_{k_j})and\underset{j\to \infty }{lim}(r_j,s_j,{\eta }_{k_j})=(r,h(r),l(r)).\end{array}$$

(32)

Let ${\overline{w}}_k={\displaystyle \frac{w_k}{\parallel w_k{\parallel }_{\infty }}}$ and ${\overline{z}}_k={\displaystyle \frac{z_k}{\parallel z_k{\parallel }_{\infty }}}$. From System (19), we have

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}▵{\overline{w}}_k={\epsilon }_k{\overline{w}}_k(\mu -w_k-{\displaystyle \frac{b(x)z_k}{1+w_k}}),\hfill & x\in \Omega ,\hfill \\ ▵{\overline{z}}_k=\epsilon {\overline{z}}_k({\displaystyle \frac{\eta -\gamma z_k}{1+z_k}}+{\displaystyle \frac{c(x)w_k}{1+w_k}}),\hfill & x\in \Omega ,\hfill \\ {\displaystyle \frac{\partial {\overline{w}}_k}{\partial \nu }}={\displaystyle \frac{\partial {\overline{z}}_k}{\partial \nu }}=0,\hfill & x\in \partial \Omega ,\hfill \end{array}\right.\end{array}$$

(33)

From Theorems 2, 3 and (18), we know that $\left\{(w_k,z_k,{\eta }_k)\right\}$ is uniformly bounded in $C(\overline{\Omega })\times C(\overline{\Omega })\times \mathbb{R}$. This implies that $\left\{{\overline{w}}_k(\mu -w_k-{\displaystyle \frac{b(x)z_k}{1+w_k}})\right\}$ and $\left\{{\overline{z}}_k({\displaystyle \frac{\eta -\gamma z_k}{1+z_k}}+{\displaystyle \frac{c(x)w_k}{1+w_k}})\right\}$ are also uniformly bounded with respect to k. Thus, by the elliptic regularity theory [43] and compactness argument, we know that there exist a subsequence $\left\{(w_{k_j},z_{k_j},{\eta }_{k_j})\right\}$ and some $\left\{(\overline{w},\overline{z},{\eta }_{\infty })\right\}$ such that

$$\begin{array}{c}\hfill \underset{j\to \infty }{lim}({\overline{w}}_{k_j},{\overline{z}}_{k_j},{\overline{\eta }}_{k_j})=(\overline{w},\overline{z},{\eta }_{\infty })in{C}^1(\overline{\Omega })\times C^1(\overline{\Omega })\times \mathbb{R}.\end{array}$$

(34)

Letting $k\to \infty$ in (33), we have $▵\overline{w}=▵\overline{z}=0$ in $\Omega$ and ${\partial }_n\overline{w}={\partial }_n\overline{z}=0$ on $\partial \Omega$ since $\underset{k\to \infty }{lim}{\epsilon }_k=0$. Note that $\parallel \overline{w}{\parallel }_{\infty }={\parallel \overline{z}\parallel }_{\infty }=1$; then, $\overline{w}=\overline{z}=1$ in $\overline{\Omega }$. Thus, we can find a non-negative constant $(r,s)$ such that

$$\begin{array}{c}\hfill \underset{j\to \infty }{lim}(w_{k_j},z_{k_j})=(r,s)in{C}^1(\overline{\Omega })\times C^1(\overline{\Omega }).\end{array}$$

(35)

From Lemma 3, we have $(w_{k_j},z_{k_j})=(r_j,s_j)+{\epsilon }_{k_j}U(r_j,s_j,{\eta }_{k_j},{\epsilon }_{k_j})$ for sufficiently large $j\in \mathbb{N}$. Combining with (35), we know that $\underset{j\to \infty }{lim}(r_j,s_j)=(r,s)$. By integrating the first and second equation in (33), we have

$$\begin{array}{c}\hfill {\oint }_{\Omega }{\overline{w}}_{k_j}(\mu -w_{k_j}-{\displaystyle \frac{b(x)z_{k_j}}{1+w_{k_j}}})dx=0and{\oint }_{\Omega }{\overline{z}}_{k_j}({\displaystyle \frac{\eta -\gamma z_{k_j}}{1+z_{k_j}}}+{\displaystyle \frac{c(x)w_{k_j}}{1+w_{k_j}}})dx=0.\end{array}$$

(36)

From (34) and (35), by letting $j\to \infty$ in (36), we obtain that

$$\begin{array}{c}\hfill {\oint }_{\Omega }(\mu -r-{\displaystyle \frac{b(x)s}{1+r}})dx=0and{\oint }_{\Omega }({\displaystyle \frac{{\eta }_{\infty }-\gamma s}{1+s}}+{\displaystyle \frac{c(x)r}{1+r}})dx=0.\end{array}$$

Hence, $s=h(r)$ and ${\eta }_{\infty }=l(r)$. So (32) is proved. Hence, Lemma 8 is proved by a contradictory argument. □

From Lemmas 7 and 8, we obtain Theorem 5.

Note that $l^{\prime }(0)$ is important for the direction of ${\Gamma }_{\epsilon }$ at the bifurcation point $(0,{\displaystyle \frac{{\eta }^{\ast }(\epsilon )}{\gamma }},{\eta }^{\ast }(\epsilon ))$ when $\epsilon$ is sufficiently small. From Lemma 4 and Theorem 5, we obtain the following bounded fish-hook-shaped bifurcation branch.

Theorem 6.

(1) Suppose that $\gamma >{\oint }_{\Omega }c(x)dx$ and let ${\mu }^{\ast }={\displaystyle \frac{\gamma +{\oint }_{\Omega }b(x)dx{\oint }_{\Omega }c(x)dx}{\gamma -{\oint }_{\Omega }c(x)dx}}$. For any small positive constant ξ, there exists a small ${\epsilon }_0$ such that if $(\mu ,\epsilon )\in (0,{\mu }^{\ast }-\xi ]\times [0,{\epsilon }_0]$, then ${\displaystyle \frac{\partial \eta }{\partial ϵ}}(0,\epsilon )<0$. That means the bifurcation of ${\Gamma }_{\epsilon }$ at $(0,{\displaystyle \frac{{\eta }^{\ast }(\epsilon )}{\gamma }},{\eta }^{\ast }(\epsilon ))$ is subcritical and the positive solution set of System (19) forms an bounded $\mathbf{S}$-shaped smooth curve which bifurcates from $(0,{\displaystyle \frac{{\eta }^{\ast }(\epsilon )}{\gamma }},{\eta }^{\ast }(\epsilon ))$. On the other hand, if $(\mu ,\epsilon )\in [\mu +\xi ,{\xi }^{-1}]\times [0,{\epsilon }_0]$, then ${\displaystyle \frac{\partial \eta }{\partial ϵ}}(0,\epsilon )>0$. That means that the bifurcation of ${\Gamma }_{\epsilon }$ at $(0,{\displaystyle \frac{{\eta }^{\ast }(\epsilon )}{\gamma }},{\eta }^{\ast }(\epsilon ))$ is supercritical and the positive solution set of System (19) forms a bounded fish-hook-shaped (⊂-shaped) smooth curve which bifurcates from $(0,{\displaystyle \frac{{\eta }^{\ast }(\epsilon )}{\gamma }},{\eta }^{\ast }(\epsilon ))$. Furthermore, when $(\mu ,\epsilon )\in [\mu +\xi ,{\xi }^{-1}]\times [0,{\epsilon }_0]$, then $\eta (ϵ,\epsilon )$ satisfies $\overline{\eta }(\epsilon ):=\underset{0\le ϵ\le C_{\epsilon }}{max}\eta (ϵ,\epsilon )>{\eta }^{\ast }(\epsilon )$, where $C_{\epsilon }$ is defined as in Theorem 5 and we have the following properties:

(i) If $\eta >\overline{\eta }(\epsilon )$ or $\eta \le {\eta }_{\ast }(\epsilon )$, then System (19) has no positive solutions;

(ii) If $\eta =\overline{\eta }(\epsilon )$ or ${\eta }_{\ast }(\epsilon )<\eta \le {\eta }^{\ast }(\epsilon )$, then System (19) has at least one positive solution;

(iii) If ${\eta }^{\ast }(\epsilon )<\eta <\overline{\eta }(\epsilon )$, then System (19) has at least two positive solutions;

(2) Suppose that $\gamma \le {\oint }_{\Omega }c(x)dx$, then ${\displaystyle \frac{\partial \eta }{\partial ϵ}}(0,\epsilon )<0$. That means that the bifurcation of ${\Gamma }_{\epsilon }$ at $(0,{\displaystyle \frac{{\eta }^{\ast }(\epsilon )}{\gamma }},{\eta }^{\ast }(\epsilon ))$ is subcritical. If ${\eta }_{\ast }(\epsilon )<\eta <{\eta }^{\ast }(\epsilon )$, then System (19) has at least one positive solution.

Proof. 

For the curve $S(ϵ,\epsilon )$ defined by Theorem 5, we have $S(ϵ,0)=(ϵ,h(ϵ),l(ϵ))$ and

$$\begin{array}{c}\hfill \underset{\epsilon \to 0}{lim}(s(ϵ,\epsilon ),\eta (ϵ,\epsilon ))=(h(ϵ),l(\epsilon ))in{C}^1([0,\mu ])\times C^1([0,\mu ]).\end{array}$$

(37)

Thence, when $\gamma >{\oint }_{\Omega }c(x)dx$, it follows from Lemma 4 and (37) that, for any small positive constant $\xi$, we can find a small ${\epsilon }_0>0$ such that ${\displaystyle \frac{\partial \eta }{\partial ϵ}}(0,\epsilon )<0$ as $(\mu ,\epsilon )\in (0,{\mu }^{\ast }-\xi ]\times [0,{\epsilon }_0]$ and ${\displaystyle \frac{\partial \eta }{\partial ϵ}}(0,\epsilon )>0$ as $(\mu ,\epsilon )\in [\mu +\xi ,{\xi }^{-1}]\times [0,{\epsilon }_0]$. Note that ${\displaystyle \frac{\partial \eta }{\partial ϵ}}(0,\epsilon )<0$ means that the bifurcation of ${\Gamma }_{\epsilon }$ at $(0,{\displaystyle \frac{{\eta }^{\ast }(\epsilon )}{\gamma }},{\eta }^{\ast }(\epsilon ))$ is subcritical and ${\displaystyle \frac{\partial \eta }{\partial ϵ}}(0,\epsilon )>0$ means the bifurcation of ${\Gamma }_{\epsilon }$ at $(0,{\displaystyle \frac{{\eta }^{\ast }(\epsilon )}{\gamma }},{\eta }^{\ast }(\epsilon ))$ is supercritical.

For any $\epsilon \in [0,{\epsilon }_0]$, if ${\displaystyle \frac{\partial \eta }{\partial ϵ}}(0,\epsilon )>0$, then $\eta$ is any increasing function for small $ϵ>0$. Note that $\eta (0,\epsilon )={\eta }^{\ast }(\epsilon )>0$ and $\eta (C_{\epsilon },\epsilon )={\eta }_{\ast }(\epsilon )<0$. Hence, we can obtain the maximum value of $\eta (ϵ,\epsilon )$ at $ϵ=\overline{ϵ}(\epsilon )$. Denote the maximum value by $\overline{\eta }(\epsilon )$. For each $\eta >0$, set $K_{\epsilon }(\eta )\subset [0,C_{\epsilon }]$ such that $\eta (ϵ,\epsilon )=\eta$ for $ϵ\in K_{\epsilon }(\eta )$. For $\epsilon \in (0,{\epsilon }_0]$, the elements of $K_{\epsilon }(\eta )$ depend on the choices of $\eta$. That is,

(i) If $\eta >\overline{\eta }(\epsilon )$ or $\eta \le {\eta }_{\ast }(\epsilon )$, then $K_{\epsilon }(\eta )=\varnothing$;

(ii) If $\eta =\overline{\eta }(\epsilon )$ or ${\eta }_{\ast }(\epsilon )<\eta \le {\eta }^{\ast }(\epsilon )$, then $K_{\epsilon }(\eta )$ has at least one element;

(iii) If ${\eta }^{\ast }(\epsilon )<\eta <\overline{\eta }(\epsilon )$, then $K_{\epsilon }(\eta )$ has at least two elements.

With the aid of (25), we know that for any fixed $\eta$, the number of elements of $K_{\epsilon }(\eta )$ is equal to the number positive solutions of System (19). The proof of (1) is complete.

By a similar method, we can obtain (2). The proof of Theorem 6 is complete. □

We are ready to prove Theorem 1. For any fixed sufficiently small $\epsilon >0$, let $a=\epsilon \mu ,$$m={\displaystyle \frac{1}{\epsilon }}$ and $\beta ={\displaystyle \frac{1}{\epsilon }}$. Then, System (3) becomes

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}▵u+u(\epsilon \mu -u-{\displaystyle \frac{b(x)z}{1+{\epsilon }^{-1}u}}),\hfill & x\in \Omega ,\hfill \\ ▵v+v({\displaystyle \frac{\delta -\theta {\epsilon }^{-1}v}{1+{\epsilon }^{-1}v}}+{\displaystyle \frac{c(x)u}{1+{\epsilon }^{-1}u}}),\hfill & x\in \Omega ,\hfill \\ {\displaystyle \frac{\partial u}{\partial \nu }}={\displaystyle \frac{\partial v}{\partial \nu }}=0,\hfill & x\in \partial \Omega .\hfill \end{array}\right.\end{array}$$

(38)

By the relationships among (3), (19) and (38), we obtain that $(w,z)$ is a positive solution of System (19) if and only if

$$\begin{array}{c}\hfill (u,v,\delta ,\theta )=\epsilon (w,z,\eta ,\gamma )\end{array}$$

(39)

is a positive solution of System (38).

By Theorems 5 and 6, we know that, for any fixed $(\mu ,b(x),c(x))$, all positive solutions of System (38) can be expressed by

$$\Gamma =\{(u(ϵ,\epsilon ),v(ϵ,\epsilon ),\delta (ϵ,\epsilon )):ϵ\in [0,C_{\epsilon }]\},$$

where $(u(ϵ,\epsilon ),v(ϵ,\epsilon ),\delta (ϵ,\epsilon ))=\epsilon (w(ϵ,\epsilon ),z(ϵ,\epsilon ),\eta (ϵ,\epsilon ))$, $(w(ϵ,\epsilon ),z(ϵ,\epsilon ),\eta (ϵ,\epsilon ))$ and $C_{\epsilon }$ are defined in Theorem 5. Set ${\theta }_0=\epsilon {\oint }_{\Omega }c(x)dx$. Note that $\theta >{\theta }_0$ is equivalent to $\gamma >{\oint }_{\Omega }c(x)dx$ and $\theta \le {\theta }_0$ is equivalent to $\gamma \le {\oint }_{\Omega }c(x)dx$. In both cases of $\theta >{\theta }_0$ and $\theta \le 0$, by the one-to-one correspondence of (39), Theorems 5 and 6 imply Theorem 1.

Remark 1.

In the spatially homogeneous case when $b(x)$ and $c(x)$ are positive constants, it is easily verified that Γ forms a bounded monotone S-type curve of positive constant solutions (see Figure 1). And from the monotonicity, we can know that Model (3) has only one positive solution; in other words, in this case, Model (3) cannot have multiple coexistence steady states.

In the case of spatial heterogeneity, $b(x)$ and $c(x)$ can induce Γ to form a bounded fish-hook-shaped bifurcation branch (see Figure 2) with respect to the bifurcation parameter δ when the natural growth rate of prey a is sufficiently small and the strength of density-dependence β and the prey’s ability to evade attack m are sufficiently large. That is to say, in this case, Model (3) exhibits multiple coexistence steady states.

5. Conclusions

In this paper, we have studied the dynamics of a diffusive predator–prey system with Holling type-II functional response and a nonlinear growth rate for the predator in a spatially heterogeneous environment. When the predator and prey live in a spatially homogeneous environment, i.e., $b_1(x)=b_1\ge 0$ and $c_1(x)=c_1\ge 0$ in System (1), Chen and Yu in [26] have shown that the system at most has one constant positive solution and they proved that it is global attractivity. On the other hand, in the weak interaction case between the predator and prey, i.e., when $c_1/m_1>0$ is small, they leave a gap as some ranges for the model parameters are given where they cannot have an exact description for the existence of a positive solution. In fact, when $b_1(x)=b_1>0,c_1(x)=c_1>0$, the results of this paper also hold. Thence, our results are more general than those of paper [26] especially in the weak interaction case. The steady state bifurcation and pattern formation in the diffusive predator–prey model or other reaction–diffusion systems in spatially heterogeneous environments can be seen as a simple application of our conclusions. It is hoped that our work is of guiding significance to the study of the effects of predation on dynamic bifurcation analysis and pattern formation.

Combining the results in [26] and our results in this paper, we see that System (3) under the homogeneous Neumann boundary condition has rich dynamics. The boundary equilibria can produce subcritical and supercritical bifurcation, and as the bifurcation parameter decreases from ${\delta }^{\ast }$ or $\overline{\delta }$ to ${\delta }_{\ast }$, the positive solution set of System (3) forms a bounded $\mathbf{S}$-shaped or fish-hook-shaped (⊂-shaped) smooth curve. The bifurcation curve can not only yield multiple positive stationary solutions but also show us much more complicated spatiotemporal patterns for System (3). Furthermore, we have shown that System (3) has at least two positive solutions for some suitable ranges of the parameters. Thus, there are some parameter values such that the prey and the predator co-exist in the form of a positive equilibrium for different initial values. In addition, the fractional-order differential equations, which encapsulate the memory impact of dynamical behavior, can successfully formulate many issues in biology and other applied domains [47]. Therefore, we will discuss this system with fractional order in the future.