An Improved Hybrid Genetic-Hierarchical Algorithm for the Quadratic Assignment Problem
Abstract
1. Introduction
- The enhanced two-level (two-layer) hybrid primary (master)-secondary (slave) genetic algorithm is proposed, in particular, in the context of the quadratic assignment problem;
- The augmented universalized multi-strategy perturbation (mutation process)—which is integrated within a multi-level (k-level) hierarchical iterated tabu search algorithm (HITS)—is implemented.
2. An Improved Hybrid Genetic-Hierarchical Algorithm for the QAP
2.1. Preliminaries
2.2. (General) Structure of the Algorithm
| Algorithm 1 Top-level pseudocode of the hybrid genetic-hierarchical algorithm |
| Hybrid_Genetic_Hierarchical_Algorithm; // input: n—problem size, A, B—data matrices // output: p✸—the best found solution // parameters: PS—population size, G—total number of generations, DT—distance threshold, Lidle_gen—idle generations limit, // CrossVar—crossover operator variant, PerturbVar—perturbation/mutation variant begin create the initial population P of size PS; p✸ ← GetBestMember(P); // initialization of the best so far solution for i ← 1 to G do begin // main loop sort the members of the population P in the ascending order of the values of the objective function; select parents p′, p″ ∈ P for crossover procedure; perform the crossover operator on the solution-parents p′, p″ and produce the offspring p′′′; apply improvement procedure Hierarchical_Iterated_Tabu_Search to the offspring p′′′, get the (improved) offspring p✩; if z(p✩) < z(p✸) then p✸ ← p✩; // the best found solution is memorized if idle generations detected then restart from a new population else obtain new population P from the union of the existing parents’ population and the offspring P ∪ {p✩} (such that |P| = PS) endfor; return p✸ end. |
2.3. Initial Population Creation
2.4. Parent Selection
2.5. Crossover Operator
2.6. Population Replacement
2.7. Improvement of Solutions—Hierarchical Iterated Tabu Search
| Algorithm 2 Pseudocode of the multi-level (k-level) hierarchical iterated tabu search algorithm |
| Hierarchical_Iterated_Tabu_Search; // input: p—current solution // output: p✩—the best found solution // parameter: k—current level (k > 0), Q〈k〉, Q〈k− 1〉, …, Q〈0〉—numbers of iterations begin p✩ ← p; for q〈k〉 ← 1 to Q〈k〉 do begin apply k − 1-level hierarchical iterated tabu search algorithm to p and get p∇; if z(p∇) < z(p✩) then p✩ ← p∇; // the best found solution is memorized if q〈k〉 < Q〈k〉 then begin p ← Candidate_Acceptance(p∇, p✩); apply perturbation process to p endif endfor end. |
| Algorithm 3 Pseudocode of the tabu search algorithm |
| Tabu_Search; // input: n—problem size, // p—current solution, Ξ—difference matrix // output: p•—the best found solution (along with the corresponding difference matrix) // parameters: τ—total number of tabu search iterations, h—tabu tenure, α—randomization coefficient, // Lidle_iter—idle iterations limit, HashSize—maximum size of the hash table begin clear tabu list TabuList and hash table HashTable; p• ← p; q ← 1; q′ ← 1; secondary_memory_index ← 0; improved ← FALSE; while (q ≤ τ) or (improved = TRUE) do begin // main cycle Δ′min ← ∞; Δ″min ← ∞; v′ ← 1; w′ ← 1; for i ← 1 to n − 1 do for j ← i + 1 to n do begin // n(n − 1)/2 neighbours of p are scanned Δ ← Ξ(i, j); forbidden ← iif(((TabuList(i, j) ≥ q) or (HashTable((z(p) + Δ) mod HashSize) = TRUE) and (random() ≥ α)), TRUE, FALSE); aspired ← iif(z(p) + Δ < z(p•), TRUE, FALSE); if ((Δ < Δ′min) and (forbidden = FALSE)) or (aspired = TRUE) then begin if Δ < Δ′min then begin Δ″min := Δ′min; v″ := v′; w″ := w′; Δ′min := Δ; v′ := i; w′ := j endif else if Δ < Δ″min then begin Δ″min := Δ; v″ := i; w″ := j endif endif endfor; if Δ″min < ∞ then begin // archiving second solution, Ξ, v″, w″ secondary_memory_index ← secondary_memory_index + 1; (secondary_memory_index) ← p, Ξ, v″, w″ endif; if Δ′min < ∞ then begin // replacement of the current solution and recalculation of the values of ←; recalculate the values of the matrix Ξ; if z(p) < z(p•) then begin p• ← p; q′ ← q endif; // the best so far solution is memorized TabuList(v′, w′) ← q + h; // the elements p(v′), p(w′) become tabu HashTable((z(p) + Δ′min) mod HashSize) ← TRUE endif; improved ← iif(Δ′min < 0, TRUE, FALSE); if (improved = FALSE) and (q − q′ > Lidle_iter) and (q <τ − Lidle_iter) then begin // retrieving solution from the secondary memory random_access_index ← random(β × secondary_memory_index, secondary_memory_index); p, Ξ, v″, w″ ←(random_access_index); ←; recalculate the values of the matrix Ξ; clear tabu list TabuList; TabuList(v″, w″) ← q + h; // the elements p(v″), p(w″) become tabu q′ ← q endif; q ← q + 1 endwhile end. |
2.7.1. Tabu Search Algorithm
2.7.2. Perturbation (Mutation) Process
| Algorithm 4 High-level (abstract) pseudocode of the universalized multi-type (multi-strategy) perturbation procedure |
| Universalized_Multi-Type_Perturbation; // input: p—current solution //—(best) obtained perturbed/reconstructed solution // parameters: ω—perturbation strength (mutation rate) factor, Nperturb—number of perturbation iterations // PerturbVar—perturbation variant begin p⋲← EMPTY_SOLUTION; [apply uniform random perturbation|Lévy perturbation; get permuted solution p; p ← p;] for i ← 1 to Nperturb do begin [apply uniform random perturbation|Lévy perturbation; get permuted solution p; p ← p;] [apply quasi-greedy perturbation 1|2|3; get permuted solution p; memorize best permuted solution as p⋲;] [apply uniform random perturbation|Lévy perturbation; get permuted solution p; p ← p] endfor; [apply uniform random perturbation|Lévy perturbation get permuted solution p;] if p⋲ is not EMPTY_SOLUTION then p← p⋲ end. |
3. Computational Experiments
3.1. Experiment Setup
| Parameters | Values | Remarks |
|---|---|---|
| Population size, | ||
| Initial population size factor, | ||
| Number of generations, | ||
| Distance threshold, | ||
| Idle generations limit, | ||
| Total number of iterations of hierarchical iterated tabu search, Q | ||
| Number of iterations of tabu search, τ | ||
| Tabu tenure, h | h > 0 | |
| Randomization coefficient for tabu search, | ||
| Idle iterations limit, | ||
| Perturbation (mutation) rate factor, ω | ||
| Switch probability, | ||
| Perturbation variant (variation), PerturbVar | ||
| Number of runs of the algorithm, |
3.2. Main Results: Comparison of Algorithms and Discussion
- Based on Table 2, we were able to achieve % success rate for almost all examined instances (in particular, for instances out of ). These instances are solved to (pseudo-)optimality within very reasonable computation times, which are, to our knowledge, record-breaking in many cases. The exception is only a handful of instances (namely, bl100, bl121, bl144, ci144, tai80a, tai100a, tho150, tai343e∗, and tai729e∗). Among these instances, the instances bl100, bl121, bl144, tai100a, tai343e∗, and tai729e∗ are overwhelmingly difficult for the heuristic algorithms and still need new revolutionizing algorithmic solutions.
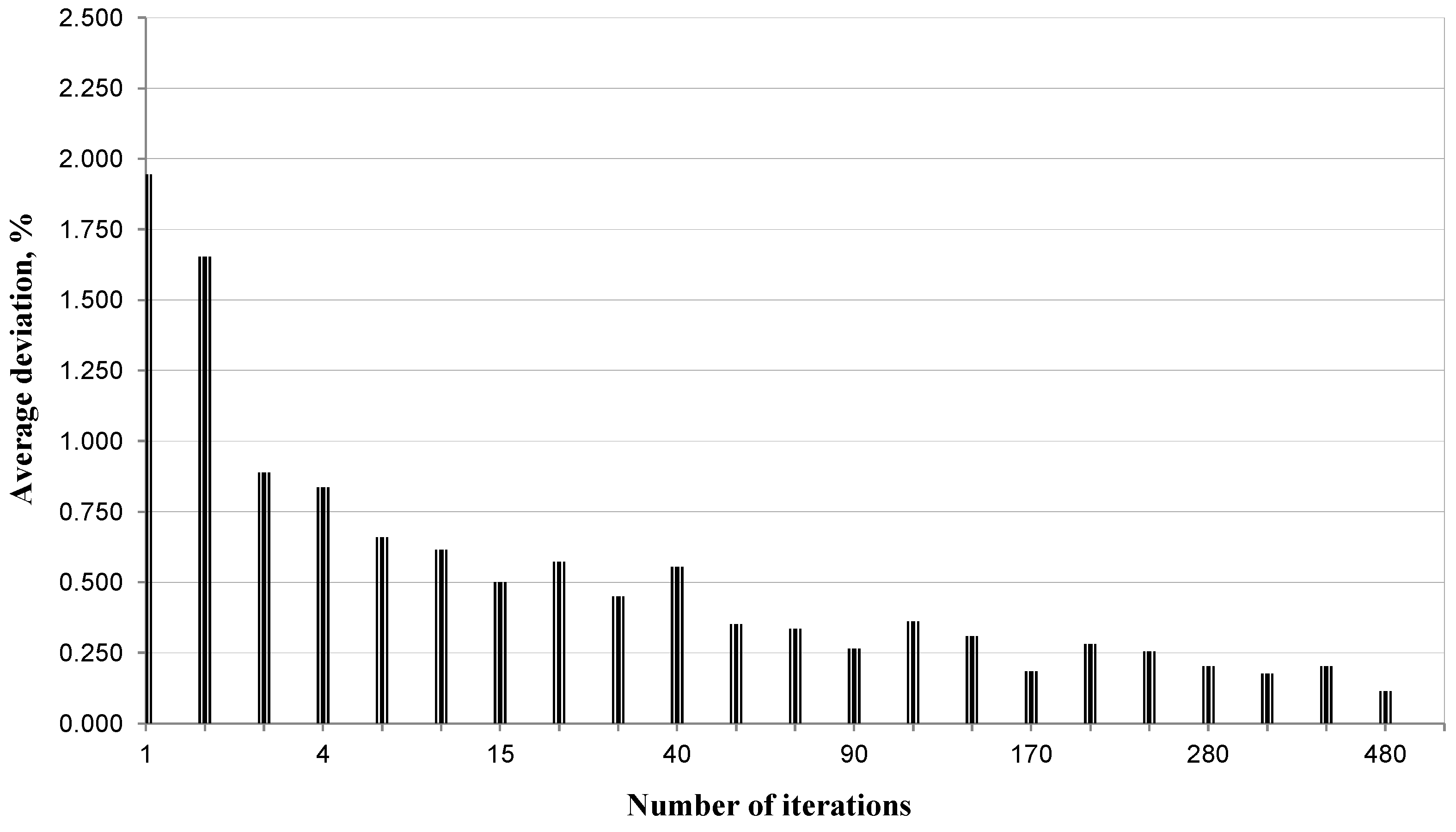
- The best-known solution was, in total, found in runs out of runs ( of the runs). We also found the best-known solution at least once out of runs for instances out of ( of the instances). And we achieved an average deviation of less than for instances out of ( of the instances). The cumulative average deviation over instances is equal to .
4. Concluding Remarks
- Two-level scheme of the hybrid primary (master)-secondary (slave) genetic algorithm is proposed;
- The multi-strategy perturbation process—which is integrated within the hierarchical iterated tabu search algorithm—is introduced.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Perturbation Variations | |||
|---|---|---|---|
| 1—URP | 24—LP, QGP 1, URP | 47—URP, MQGP 3, URP | 70—M(URP, QGP 2), LP |
| 2—LP | 25—LP, QGP 1, LP | 48—URP, MQGP 1, LP | 71—M(URP, QGP 3), LP |
| 3—QGP 1 | 26—LP, QGP 2, URP | 49—URP, MQGP 2, LP | 72—M(LP, QGP 1), LP |
| 4—QGP 2 | 27—LP, QGP 2, LP | 50—URP, MQGP 3, LP | 73—M(LP, QGP 2), LP |
| 5—QGP 3 | 28—LP, QGP 3, URP | 51—LP, MQGP 1, URP | 74—M(LP, QGP 3), LP |
| 6—URP, QGP 1 | 29—LP, QGP 3, LP | 52—LP, MQGP 2, URP | 75—M(QGP 1, URP) |
| 7—URP, QGP 2 | 30—MQGP 1 | 53—LP, MQGP 3, URP | 76—M(QGP 2, URP) |
| 8—URP, QGP 3 | 31—MQGP 2 | 54—LP, MQGP 1, LP | 77—M(QGP 3, URP) |
| 9—LP, QGP 1 | 32—MQGP 3 | 55—LP, MQGP 2, LP | 78—M(QGP 1, LP) |
| 10—LP, QGP 2 | 33—URP, MQGP 1 | 56—LP, MQGP 3, LP | 79—M(QGP 2, LP) |
| 11—LP, QGP 3 | 34—URP, MQGP 2 | 57—M(URP, QGP 1) | 80—M(QGP 3, LP) |
| 12—QGP 1, URP | 35—URP, MQGP 3 | 58—M(URP, QGP 2) | 81—URP, M(QGP 1, URP) |
| 13—QGP 1, LP | 36—LP, MQGP 1 | 59—M(URP, QGP 3) | 82—URP, M(QGP 2, URP) |
| 14—QGP 2, URP | 37—LP, MQGP 2 | 60—M(LP, QGP 1) | 83—URP, M(QGP 3, URP) |
| 15—QGP 2, LP | 38—LP, MQGP 3 | 61—M(LP, QGP 2) | 84—URP, M(QGP 1, LP) |
| 16—QGP 3, URP | 39—MQGP 1, URP | 62—M(LP, QGP 3) | 85—URP, M(QGP 2, LP) |
| 17—QGP 3, LP | 40—MQGP 2, URP | 63—M(URP, QGP 1), URP | 86—URP, M(QGP 3, LP) |
| 18—URP, QGP 1, URP | 41—MQGP 3, URP | 64—M(URP, QGP 2), URP | 87—LP, M(QGP 1, URP) |
| 19—URP, QGP 1, LP | 42—MQGP 1, LP | 65—M(URP, QGP 3), URP | 88—LP, M(QGP 2, URP) |
| 20—URP, QGP 2, URP | 43—MQGP 2, LP | 66—M(LP, QGP 1), URP | 89—LP, M(QGP 3, URP) |
| 21—URP, QGP 2, LP | 44—MQGP 3, LP | 67—M(LP, QGP 2), URP | 90—LP, M(QGP 1, LP) |
| 22—URP, QGP 3, URP | 45—URP, MQGP 1, URP | 68—M(LP, QGP 3), URP | 91—LP, M(QGP 2, LP) |
| 23—URP, QGP 3, LP | 46—URP, MQGP 2, URP | 69—M(URP, QGP 1), LP | 92—LP, M(QGP 3, LP) |

References
- Çela, E. The Quadratic Assignment Problem: Theory and Algorithms; Kluwer: Dordrecht, The Netherland, 1998. [Google Scholar]
- Koopmans, T.; Beckmann, M. Assignment problems and the location of economic activities. Econometrica 1957, 25, 53–76. [Google Scholar] [CrossRef]
- Drezner, Z. The quadratic assignment problem. In Location Science; Laporte, G., Nickel, S., Saldanha da Gama, F., Eds.; Springer: Cham, Switzerland, 2015; pp. 345–363. [Google Scholar] [CrossRef]
- Sahni, S.; Gonzalez, T. P-complete approximation problems. J. ACM 1976, 23, 555–565. [Google Scholar] [CrossRef]
- Anstreicher, K.M.; Brixius, N.W.; Gaux, J.P.; Linderoth, J. Solving large quadratic assignment problems on computational grids. Math. Program. 2002, 91, 563–588. [Google Scholar] [CrossRef]
- Hahn, P.M.; Zhu, Y.-R.; Guignard, M.; Hightower, W.L.; Saltzman, M.J. A level-3 reformulation-linearization technique-based bound for the quadratic assignment problem. INFORMS J. Comput. 2012, 24, 202–209. [Google Scholar] [CrossRef]
- Date, K.; Nagi, R. Level 2 reformulation linearization technique-based parallel algorithms for solving large quadratic assignment problems on graphics processing unit clusters. INFORMS J. Comput. 2019, 31, 771–789. [Google Scholar] [CrossRef]
- Ferreira, J.F.S.B.; Khoo, Y.; Singer, A. Semidefinite programming approach for the quadratic assignment problem with a sparse graph. Comput. Optim. Appl. 2018, 69, 677–712. [Google Scholar] [CrossRef]
- Armour, G.C.; Buffa, E.S. A heuristic algorithm and simulation approach to relative location of facilities. Manag. Sci. 1963, 9, 294–304. [Google Scholar] [CrossRef]
- Buffa, E.S.; Armour, G.C.; Vollmann, T.E. Allocating facilities with CRAFT. Harvard Bus. Rev. 1964, 42, 136–158. [Google Scholar]
- Murthy, K.A.; Li, Y.; Pardalos, P.M. A local search algorithm for the quadratic assignment problem. Informatica 1992, 3, 524–538. [Google Scholar]
- Pardalos, P.M.; Murthy, K.A.; Harrison, T.P. A computational comparison of local search heuristics for solving quadratic assignment problems. Informatica 1993, 4, 172–187. [Google Scholar]
- Angel, E.; Zissimopoulos, V. On the quality of local search for the quadratic assignment problem. Discret. Appl. Math. 1998, 82, 15–25. [Google Scholar] [CrossRef]
- Benlic, U.; Hao, J.-K. Breakout local search for the quadratic assignment problem. Appl. Math. Comput. 2013, 219, 4800–4815. [Google Scholar] [CrossRef]
- Aksan, Y.; Dokeroglu, T.; Cosar, A. A stagnation-aware cooperative parallel breakout local search algorithm for the quadratic assignment problem. Comput. Ind. Eng. 2017, 103, 105–115. [Google Scholar] [CrossRef]
- Misevičius, A. A modified simulated annealing algorithm for the quadratic assignment problem. Informatica 2003, 14, 497–514. [Google Scholar] [CrossRef]
- Taillard, E.D. Robust taboo search for the QAP. Parallel Comput. 1991, 17, 443–455. [Google Scholar] [CrossRef]
- Misevicius, A. A tabu search algorithm for the quadratic assignment problem. Comput. Optim. Appl. 2005, 30, 95–111. [Google Scholar] [CrossRef]
- Fescioglu-Unver, N.; Kokar, M.M. Self controlling tabu search algorithm for the quadratic assignment problem. Comput. Ind. Eng. 2011, 60, 310–319. [Google Scholar] [CrossRef]
- Misevicius, A. An implementation of the iterated tabu search algorithm for the quadratic assignment problem. OR Spectrum 2012, 34, 665–690. [Google Scholar] [CrossRef]
- Shylo, P.V. Solving the quadratic assignment problem by the repeated iterated tabu search method. Cybern. Syst. Anal. 2017, 53, 308–311. [Google Scholar] [CrossRef]
- Drezner, Z. A new genetic algorithm for the quadratic assignment problem. INFORMS J. Comput. 2003, 15, 320–330. [Google Scholar] [CrossRef]
- Misevicius, A. An improved hybrid genetic algorithm: New results for the quadratic assignment problem. Knowl.-Based Syst. 2004, 17, 65–73. [Google Scholar] [CrossRef]
- Benlic, U.; Hao, J.-K. Memetic search for the quadratic assignment problem. Expert Syst. Appl. 2015, 42, 584–595. [Google Scholar] [CrossRef]
- Ahmed, Z.H. A hybrid algorithm combining lexisearch and genetic algorithms for the quadratic assignment problem. Cogent Eng. 2018, 5, 1423743. [Google Scholar] [CrossRef]
- Drezner, Z.; Drezner, T.D. The alpha male genetic algorithm. IMA J. Manag. Math. 2019, 30, 37–50. [Google Scholar] [CrossRef]
- Drezner, Z.; Drezner, T.D. Biologically inspired parent selection in genetic algorithms. Ann. Oper. Res. 2020, 287, 161–183. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, F.; Zhou, Y.; Zhang, Z. A hybrid method integrating an elite genetic algorithm with tabu search for the quadratic assignment problem. Inf. Sci. 2020, 539, 347–374. [Google Scholar] [CrossRef]
- Misevičius, A.; Verenė, D. A hybrid genetic-hierarchical algorithm for the quadratic assignment problem. Entropy 2021, 23, 108. [Google Scholar] [CrossRef]
- Ryu, M.; Ahn, K.-I.; Lee, K. Finding effective item assignment plans with weighted item associations using a hybrid genetic algorithm. Appl. Sci. 2021, 11, 2209. [Google Scholar] [CrossRef]
- Silva, A.; Coelho, L.C.; Darvish, M. Quadratic assignment problem variants: A survey and an effective parallel memetic iterated tabu search. Eur. J. Oper. Res. 2021, 292, 1066–1084. [Google Scholar] [CrossRef]
- Wang, H.; Alidaee, B. A new hybrid-heuristic for large-scale combinatorial optimization: A case of quadratic assignment problem. Comput. Ind. Eng. 2023, 179, 109220. [Google Scholar] [CrossRef]
- Ismail, M.; Rashwan, O. A Hierarchical Data-Driven Parallel Memetic Algorithm for the Quadratic Assignment Problem. Available online: https://ssrn.com/abstract=4517038 (accessed on 22 January 2024).
- Arza, E.; Pérez, A.; Irurozki, E.; Ceberio, J. Kernels of Mallows models under the Hamming distance for solving the quadratic assignment problem. Swarm Evol. Comput. 2020, 59, 100740. [Google Scholar] [CrossRef]
- Pradeepmon, T.G.; Panicker, V.V.; Sridharan, R. A variable neighbourhood search enhanced estimation of distribution algorithm for quadratic assignment problems. OPSEARCH 2021, 58, 203–233. [Google Scholar] [CrossRef]
- Hameed, A.S.; Aboobaider, B.M.; Mutar, M.L.; Choon, N.H. A new hybrid approach based on discrete differential evolution algorithm to enhancement solutions of quadratic assignment problem. Int. J. Ind. Eng. Comput. 2020, 11, 51–72. [Google Scholar] [CrossRef]
- Gambardella, L.M.; Taillard, E.D.; Dorigo, M. Ant colonies for the quadratic assignment problem. J. Oper. Res. Soc. 1999, 50, 167–176. [Google Scholar] [CrossRef]
- Hafiz, F.; Abdennour, A. Particle swarm algorithm variants for the quadratic assignment problems—A probabilistic learning approach. Expert Syst. Appl. 2016, 44, 413–431. [Google Scholar] [CrossRef]
- Dokeroglu, T.; Sevinc, E.; Cosar, A. Artificial bee colony optimization for the quadratic assignment problem. Appl. Soft Comput. 2019, 76, 595–606. [Google Scholar] [CrossRef]
- Samanta, S.; Philip, D.; Chakraborty, S. A quick convergent artificial bee colony algorithm for solving quadratic assignment problems. Comput. Ind. Eng. 2019, 137, 106070. [Google Scholar] [CrossRef]
- Peng, Z.-Y.; Huang, Y.-J.; Zhong, Y.-B. A discrete artificial bee colony algorithm for quadratic assignment problem. J. High Speed Netw. 2022, 28, 131–141. [Google Scholar] [CrossRef]
- Adubi, S.A.; Oladipupo, O.O.; Olugbara, O.O. Evolutionary algorithm-based iterated local search hyper-heuristic for combinatorial optimization problems. Algorithms 2022, 15, 405. [Google Scholar] [CrossRef]
- Wu, P.; Hung, Y.-Y.; Yang, K.-J. A Revised Electromagnetism-Like Metaheuristic For.pdf. Available online: https://www.researchgate.net/profile/Peitsang-Wu/publication/268412372_A_REVISED_ELECTROMAGNETISM-LIKE_METAHEURISTIC_FOR_THE_QUADRATIC_ASSIGNMENT_PROBLEM/links/54d9e45f0cf25013d04353b9/A-REVISED-ELECTROMAGNETISM-LIKE-METAHEURISTIC-FOR-THE-QUADRATIC-ASSIGNMENT-PROBLEM.pdf (accessed on 22 January 2024).
- Riffi, M.E.; Bouzidi, A. Discrete cat swarm optimization for solving the quadratic assignment problem. Int. J. Soft Comput. Softw. Eng. 2014, 4, 85–92. [Google Scholar] [CrossRef]
- Lim, W.L.; Wibowo, A.; Desa, M.I.; Haron, H. A biogeography-based optimization algorithm hybridized with tabu search for the quadratic assignment problem. Comput. Intell. Neurosci. 2016, 2016, 5803893. [Google Scholar] [CrossRef] [PubMed]
- Houssein, E.H.; Mahdy, M.A.; Blondin, M.J.; Shebl, D.; Mohamed, W.M. Hybrid slime mould algorithm with adaptive guided differential evolution algorithm for combinatorial and global optimization problems. Expert Syst. Appl. 2021, 174, 114689. [Google Scholar] [CrossRef]
- Guo, M.-W.; Wang, J.-S.; Yang, X. An chaotic firefly algorithm to solve quadratic assignment problem. Eng. Lett. 2020, 28, 337–342. [Google Scholar]
- Rizk-Allah, R.M.; Slowik, A.; Darwish, A.; Hassanien, A.E. Orthogonal Latin squares-based firefly optimization algorithm for industrial quadratic assignment tasks. Neural Comput. Appl. 2021, 33, 16675–16696. [Google Scholar] [CrossRef]
- Abdel-Baset, M.; Wu, H.; Zhou, Y.; Abdel-Fatah, L. Elite opposition-flower pollination algorithm for quadratic assignment problem. J. Intell. Fuzzy Syst. 2017, 33, 901–911. [Google Scholar] [CrossRef]
- Dokeroglu, T. Hybrid teaching–learning-based optimization algorithms for the quadratic assignment problem. Comp. Ind. Eng. 2015, 85, 86–101. [Google Scholar] [CrossRef]
- Riffi, M.E.; Sayoti, F. Hybrid algorithm for solving the quadratic assignment problem. Int. J. Interact. Multimed. Artif. Intell. 2017, 5, 68–74. [Google Scholar] [CrossRef]
- Semlali, S.C.B.; Riffi, M.E.; Chebihi, F. Parallel hybrid chicken swarm optimization for solving the quadratic assignment problem. Int. J. Electr. Comput. Eng. 2019, 9, 2064–2074. [Google Scholar] [CrossRef]
- Badrloo, S.; Kashan, A.H. Combinatorial optimization of permutation-based quadratic assignment problem using optics inspired optimization. J. Appl. Res. Ind. Eng. 2019, 6, 314–332. [Google Scholar] [CrossRef]
- Kiliç, H.; Yüzgeç, U. Tournament selection based antlion optimization algorithm for solving quadratic assignment problem. Eng. Sci. Technol. Int. J. 2019, 22, 673–691. [Google Scholar] [CrossRef]
- Kiliç, H.; Yüzgeç, U. Improved antlion optimization algorithm for quadratic assignment problem. Malayas. J. Comput. Sci. 2021, 34, 34–60. [Google Scholar] [CrossRef]
- Ng, K.M.; Tran, T.H. A parallel water flow algorithm with local search for solving the quadratic assignment problem. J. Ind. Manag. Optim. 2019, 15, 235–259. [Google Scholar] [CrossRef]
- Kumar, M.; Sahu, A.; Mitra, P. A comparison of different metaheuristics for the quadratic assignment problem in accelerated systems. Appl. Soft Comput. 2021, 100, 106927. [Google Scholar] [CrossRef]
- Yadav, A.A.; Kumar, N.; Kim, J.H. Development of discrete artificial electric field algorithm for quadratic assignment problems. In Proceedings of the 6th International Conference on Harmony Search, Soft Computing and Applications. ICHSA 2020. Advances in Intelligent Systems and Computing, Istanbul, Turkey, 16–17 July 2020; Nigdeli, S.M., Kim, J.H., Bekdaş, G., Yadav, A., Eds.; Springer: Singapore, 2021; Volume 1275, pp. 411–421. [Google Scholar] [CrossRef]
- Dokeroglu, T.; Ozdemir, Y.S. A new robust Harris Hawk optimization algorithm for large quadratic assignment problems. Neural Comput. Appl. 2023, 35, 12531–12544. [Google Scholar] [CrossRef]
- Acan, A.; Ünveren, A. A great deluge and tabu search hybrid with two-stage memory support for quadratic assignment problem. Appl. Soft Comput. 2015, 36, 185–203. [Google Scholar] [CrossRef]
- Chmiel, W.; Kwiecień, J. Quantum-inspired evolutionary approach for the quadratic assignment problem. Entropy 2018, 20, 781. [Google Scholar] [CrossRef]
- Drezner, Z. Taking advantage of symmetry in some quadratic assignment problems. INFOR Inf. Syst. Oper. Res. 2019, 57, 623–641. [Google Scholar] [CrossRef]
- Dantas, A.; Pozo, A. On the use of fitness landscape features in meta-learning based algorithm selection for the quadratic assignment problem. Theor. Comput. Sci. 2020, 805, 62–75. [Google Scholar] [CrossRef]
- Öztürk, M.; Alabaş-Uslu, Ç. Cantor set based neighbor generation method for permutation solution representation. J. Intell. Fuzzy Syst. 2020, 39, 6157–6168. [Google Scholar] [CrossRef]
- Alza, J.; Bartlett, M.; Ceberio, J.; McCall, J. Towards the landscape rotation as a perturbation strategy on the quadratic assignment problem. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, GECCO ’21, Lille, France, 10–14 July 2021; Chicano, F., Ed.; ACM: New York, NY, USA, 2021; pp. 1405–1413. [Google Scholar] [CrossRef]
- Amirghasemi, M. An effective parallel evolutionary metaheuristic with its application to three optimization problems. Appl. Intell. 2023, 53, 5887–5909. [Google Scholar] [CrossRef]
- Zhou, Y.; Hao, J.-K.; Duval, B. Frequent pattern-based search: A case study on the quadratic assignment problem. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1503–1515. [Google Scholar] [CrossRef]
- Baldé, M.A.M.T.; Gueye, S.; Ndiaye, B.M. A greedy evolutionary hybridization algorithm for the optimal network and quadratic assignment problem. Oper. Res. 2021, 21, 1663–1690. [Google Scholar] [CrossRef]
- Ni, Y.; Liu, W.; Du, X.; Xiao, R.; Chen, G.; Wu, Y. Evolutionary optimization approach based on heuristic information with pseudo-utility for the quadratic assignment problem. Swarm Evol. Comput. 2024, 87, 101557. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Saber, S.; Hezam, I.M.; Sallam, K.M.; Hameed, I.A. Binary metaheuristic algorithms for 0–1 knapsack problems: Performance analysis, hybrid variants, and real-world application. J. King Saud Univ.-Comput. Inf. Sci. 2024, 36, 102093. [Google Scholar] [CrossRef]
- Alvarez-Flores, O.A.; Rivera-Blas, R.; Flores-Herrera, L.A.; Rivera-Blas, E.Z.; Funes-Lora, M.A.; Nino-Suárez, P.A. A novel modified discrete differential evolution algorithm to solve the operations sequencing problem in CAPP systems. Mathematics 2024, 12, 1846. [Google Scholar] [CrossRef]
- El-Shorbagy, M.A.; Bouaouda, A.; Nabwey, H.A.; Abualigah, L.; Hashim, F.A. Advances in Henry gas solubility optimization: A physics-inspired metaheuristic algorithm with its variants and applications. IEEE Access 2024, 12, 26062–26095. [Google Scholar] [CrossRef]
- Zhang, J.; Ye, J.-X.; Lin, J.; Song, H.-B. A discrete Jaya algorithm for vehicle routing problems with uncertain demands. Syst. Sci. Control Eng. 2024, 12, 2350165. [Google Scholar] [CrossRef]
- Zhang, Y.; Xing, L. A new hybrid improved arithmetic optimization algorithm for solving global and engineering optimization problems. Mathematics 2024, 12, 3221. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, T.; Cai, L.; Yang, R. Triangulation topology aggregation optimizer: A novel mathematics-based meta-heuristic algorithm for engineering applications. Expert Syst. Appl. 2024, 238 Pt B, 121744. [Google Scholar] [CrossRef]
- Loiola, E.M.; De Abreu, N.M.M.; Boaventura-Netto, P.O.; Hahn, P.; Querido, T. A survey for the quadratic assignment problem. Eur. J. Oper. Res. 2007, 176, 657–690. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Manogaran, G.; Rashad, H.; Zaied, A.N.H. A comprehensive review of quadratic assignment problem: Variants, hybrids and applications. J. Amb. Intel. Hum. Comput. 2018, 9, 1–24. [Google Scholar] [CrossRef]
- Achary, T.; Pillay, S.; Pillai, S.M.; Mqadi, M.; Genders, E.; Ezugwu, A.E. A performance study of meta-heuristic approaches for quadratic assignment problem. Concurr. Comput. Pract. Exp. 2021, 33, 1–29. [Google Scholar] [CrossRef]
- Hussin, M.S.; Stützle, T. Hierarchical iterated local search for the quadratic assignment problem. In Hybrid Metaheuristics, HM 2009, Lecture Notes in Computer Science; Blesa, M.J., Blum, C., Di Gaspero, L., Roli, A., Sampels, M., Schaerf, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5818, pp. 115–129. [Google Scholar] [CrossRef]
- Battarra, M.; Benedettini, S.; Roli, A. Leveraging saving-based algorithms by master–slave genetic algorithms. Eng. Appl. Artif. Intell. 2011, 24, 555–566. [Google Scholar] [CrossRef]
- Liu, S.; Xue, J.; Hu, C.; Li, Z. Test case generation based on hierarchical genetic algorithm. In Proceedings of the 2014 International Conference on Mechatronics, Control and Electronic Engineering, MEIC 2014, Shenyang, China, 15–17 November 2014; Atlantis Press: Dordrecht, The Netherland, 2014; pp. 278–281. [Google Scholar] [CrossRef]
- Ahmed, A.K.M.F.; Sun, J.U. A novel approach to combine the hierarchical and iterative techniques for solving capacitated location-routing problem. Cogent Eng. 2018, 5, 1463596. [Google Scholar] [CrossRef]
- Misevičius, A.; Palubeckis, G.; Drezner, Z. Hierarchicity-based (self-similar) hybrid genetic algorithm for the grey pattern quadratic assignment problem. Memet. Comput. 2021, 13, 69–90. [Google Scholar] [CrossRef]
- Frieze, A.M.; Yadegar, J.; El-Horbaty, S.; Parkinson, D. Algorithms for assignment problems on an array processor. Parallel Comput. 1989, 11, 151–162. [Google Scholar] [CrossRef]
- Merz, P.; Freisleben, B. Fitness landscape analysis and memetic algorithms for the quadratic assignment problem. IEEE Trans. Evol. Comput. 2000, 4, 337–352. [Google Scholar] [CrossRef]
- Li, Y.; Pardalos, P.M.; Resende, M.G.C. A greedy randomized adaptive search procedure for the quadratic assignment problem. In Quadratic Assignment and Related Problems. DIMACS Series in Discrete Mathematics and Theoretical Computer Science; Pardalos, P.M., Wolkowicz, H., Eds.; AMS: Providence, RI, USA, 1994; Volume 16, pp. 237–261. [Google Scholar]
- Drezner, Z. Compounded genetic algorithms for the quadratic assignment problem. Oper. Res. Lett. 2005, 33, 475–480. [Google Scholar] [CrossRef]
- Berman, O.; Drezner, Z.; Krass, D. Discrete cooperative covering problems. J. Oper. Res. Soc. 2011, 62, 2002–2012. [Google Scholar] [CrossRef]
- Tate, D.M.; Smith, A.E. A genetic approach to the quadratic assignment problem. Comput. Oper. Res. 1995, 22, 73–83. [Google Scholar] [CrossRef]
- Misevičius, A.; Kuznecovaitė, D.; Platužienė, J. Some further experiments with crossover operators for genetic algorithms. Informatica 2018, 29, 499–516. [Google Scholar] [CrossRef]
- Sivanandam, S.N.; Deepa, S.N. Introduction to Genetic Algorithms; Springer: Heidelberg, Germany; New York, NY, USA, 2008. [Google Scholar]
- Smyth, K.; Hoos, H.H.; Stützle, T. Iterated robust tabu search for MAX-SAT. In Advances in Artificial Intelligence: Proceedings of the 16th Conference of the Canadian Society for Computational Studies of Intelligence, Halifax, NS, Canada, 11–13 June 2003.; Lecture Notes in Artificial Intelligence; Xiang, Y., Chaib-Draa, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2671, pp. 129–144. [Google Scholar] [CrossRef]
- Mehrdoost, Z.; Bahrainian, S.S. A multilevel tabu search algorithm for balanced partitioning of unstructured grids. Int. J. Numer. Meth. Engng. 2016, 105, 678–692. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Trubian, M. Solution of large weighted equicut problems. Eur. J. Oper. Res. 1998, 106, 500–521. [Google Scholar] [CrossRef]
- Durmaz, E.D.; Şahin, R. An efficient iterated local search algorithm for the corridor allocation problem. Expert Syst. Appl. 2023, 212, 118804. [Google Scholar] [CrossRef]
- Polat, O.; Kalayci, C.B.; Kulak, O.; Günther, H.-O. A perturbation based variable neighborhood search heuristic for solving the vehicle routing problem with simultaneous pickup and delivery with time limit. Eur. J. Oper. Res. 2015, 242, 369–382. [Google Scholar] [CrossRef]
- Lu, Z.; Hao, J.-K.; Zhou, Y. Stagnation-aware breakout tabu search for the minimum conductance graph partitioning problem. Comput. Oper. Res. 2019, 111, 43–57. [Google Scholar] [CrossRef]
- Sadati, M.E.H.; Çatay, B.; Aksen, D. An efficient variable neighborhood search with tabu shaking for a class of multi-depot vehicle routing problems. Comput. Oper. Res. 2021, 133, 105269. [Google Scholar] [CrossRef]
- Qin, T.; Peng, B.; Benlic, U.; Cheng, T.C.E.; Wang, Y.; Lü, Z. Iterated local search based on multi-type perturbation for single-machine earliness/tardiness scheduling. Comput. Oper. Res. 2015, 61, 81–88. [Google Scholar] [CrossRef]
- Canuto, S.A.; Resende, M.G.C.; Ribeiro, C.C. Local search with perturbations for the prize-collecting Steiner tree problem in graphs. Networks 2001, 38, 50–58. [Google Scholar] [CrossRef]
- Shang, Z.; Zhao, S.; Hao, J.-K.; Yang, X.; Ma, F. Multiple phase tabu search for bipartite boolean quadratic programming with partitioned variables. Comput. Oper. Res. 2019, 102, 141–149. [Google Scholar] [CrossRef]
- Lai, X.; Hao, J.-K. Iterated maxima search for the maximally diverse grouping problem. Eur. J. Oper. Res. 2016, 254, 780–800. [Google Scholar] [CrossRef]
- Ren, J.; Hao, J.-K.; Rodriguez-Tello, E.; Li, L.; He, K. A new iterated local search algorithm for the cyclic bandwidth problem. Knowl.-Based Syst. 2020, 203, 106136. [Google Scholar] [CrossRef]
- Avci, M. An effective iterated local search algorithm for the distributed no-wait flowshop scheduling problem. Eng. Appl. Artif. Intell. 2023, 120, 105921. [Google Scholar] [CrossRef]
- Lai, X.; Hao, J.-K. Iterated variable neighborhood search for the capacitated clustering problem. Eng. Appl. Artif. Intell. 2016, 56, 102–120. [Google Scholar] [CrossRef]
- Li, R.; Hu, S.; Wang, Y.; Yin, M. A local search algorithm with tabu strategy and perturbation mechanism for generalized vertex cover problem. Neural Comput. Appl. 2017, 28, 1775–1785. [Google Scholar] [CrossRef]
- Lévy, P. Théorie de l’Addition des Variables Aléatoires; Gauthier-Villars: Paris, France, 1937. [Google Scholar]
- Pavlyukevich, I. Lévy flights, non-local search and simulated annealing. J. Comput. Phys. 2007, 226, 1830–1844. [Google Scholar] [CrossRef]
- Chambers, J.M.; Mallows, C.L.; Stuck, B.W. A method for simulating stable random variables. J. Am. Stat. Assoc. 1976, 71, 340–344. [Google Scholar] [CrossRef]
- Mantegna, R.N. Fast, accurate algorithm for numerical simulation of Lévy stable stochastic processes. Phys. Rev. E 1994, 49, 4677–4683. [Google Scholar] [CrossRef]
- Nemes, G. New asymptotic expansion for the Gamma function. Arch. Math. 2010, 95, 161–169. [Google Scholar] [CrossRef]
- Li, W.; Li, H.; Wang, Y.; Han, Y. Optimizing flexible job shop scheduling with automated guided vehicles using a multi-strategy-driven genetic algorithm. Egypt. Inform. J. 2024, 25, 100437. [Google Scholar] [CrossRef]
- López-Ibáñez, M.; Mascia, F.; Marmion, M.-E.; Stützle, T. A template for designing single-solution hybrid metaheuristics. In Proceedings of the Companion Publication of the 2014 Annual Conference on Genetic and Evolutionary Computation, GECCO Comp ’14, Vancouver, BC, Canada, 12–16 July 2014; Igel, C., Ed.; ACM: New York, NY, USA, 2014; pp. 1423–1426. [Google Scholar] [CrossRef]
- Meng, W.; Qu, R. Automated design of search algorithms: Learning on algorithmic components. Expert Syst. Appl. 2021, 185, 115493. [Google Scholar] [CrossRef]
- Burkard, R.E.; Karisch, S.; Rendl, F. QAPLIB—A quadratic assignment problem library. J. Glob. Optim. 1997, 10, 391–403. [Google Scholar] [CrossRef]
- QAPLIB—A Quadratic Assignment Problem Library—COR@L. Available online: https://coral.ise.lehigh.edu/data-sets/qaplib/ (accessed on 10 November 2023).
- De Carvalho, S.A., Jr.; Rahmann, S. Microarray layout as a quadratic assignment problem. In German Conference on Bioinformatics, GCB 2006, Lecture Notes in Informatics—Proceedings; Huson, D., Kohlbacher, O., Lupas, A., Nieselt, K., Zell, A., Eds.; Gesellschaft für Informatik: Bonn, Germany, 2006; Volume P-83, pp. 11–20. [Google Scholar]
- Drezner, Z.; Hahn, P.M.; Taillard, E.D. Recent advances for the quadratic assignment problem with special emphasis on instances that are difficult for metaheuristic methods. Ann. Oper. Res. 2005, 139, 65–94. [Google Scholar] [CrossRef]
- Taillard—QAP. Available online: http://mistic.heig-vd.ch/taillard/problemes.dir/qap.dir/qap.html (accessed on 30 November 2023).
- Misevičius, A. Letter: New best known solution for the most difficult QAP instance “tai100a”. Memet. Comput. 2019, 11, 331–332. [Google Scholar] [CrossRef]
- Drezner, Z. Tabu search and hybrid genetic algorithms for quadratic assignment problems. In Tabu Search; Jaziri, W., Ed.; In-Tech: London, UK, 2008; pp. 89–108. [Google Scholar] [CrossRef]
- Drezner, Z.; Marcoulides, G.A. On the range of tabu tenure in solving quadratic assignment problems. In Recent Advances in Computing and Management Information Systems; Athens Institute for Education and Research: Athens, Greece, 2009; pp. 157–168. [Google Scholar]
- Drezner, Z.; Misevičius, A. Enhancing the performance of hybrid genetic algorithms by differential improvement. Comput. Oper. Res. 2013, 40, 1038–1046. [Google Scholar] [CrossRef]
- Rodriguez, J.M.; MacPhee, F.C.; Bonham, D.J.; Horton, J.D.; Bhavsar, V.C. Best permutations for the dynamic plant layout problem. In Efficient and Experimental Algorithms: Proceedings of the 12th International Conference on Advances in Computing and Communications (ADCOM 2004), Ahmedabad, India, 15–18 December 2004; Dasgupta, A.R., Iyengar, S.S., Bhatt, H.S., Eds.; Allied Publishers Pvt. Ltd.: New Delhi, India; Ahmedabad, India, 2004; pp. 173–178. [Google Scholar]
| Instance | BKV | Time (s) | Instance | BKV | Time (s) | ||
|---|---|---|---|---|---|---|---|
| bl36 | 3296 | 0.000 | 7.608 | sko100b | 153,890 | 0.000 | 217.000 |
| bl49 | 4548 | 0.000 | 649.900 | sko100c | 147,862 | 0.000 | 347.800 |
| bl64 | 5988 | 0.000 | 1650.000 | sko100d | 149,576 | 0.000 | 346.500 |
| bl81 | 7532 | 0.000 | 50,470.000 | sko100e | 149,150 | 0.000 | 315.700 |
| bl100 | 9256 | 0.099 | 60,740.000 | sko100f | 149,036 | 0.000 | 591.900 |
| bl121 | 11,396 | 0.126 | 125,300.000 | ste36a | 9526 | 0.000 | 0.245 |
| bl144 | 13,432 | 0.229 | 178,300.000 | ste36b | 15,852 | 0.000 | 0.048 |
| chr25a | 3796 | 0.000 | 1.744 | ste36c | 8,239,110 | 0.000 | 0.078 |
| ci36 | 168,611,971 | 0.000 | 1.175 | tai10a | 135,028 | 0.000 | 0.003 |
| ci49 | 236,355,034 | 0.000 | 4.586 | tai10b | 1183,760 | 0.000 | 0.002 |
| ci64 | 325,671,035 | 0.000 | 46.110 | tai12a | 224,416 | 0.000 | 0.003 |
| ci81 | 427,447,820 | 0.000 | 236.500 | tai12b | 39,464,925 | 0.000 | 0.003 |
| ci100 | 523,146,366 | 0.000 | 4562.000 | tai15a | 388,214 | 0.000 | 0.006 |
| ci121 | 653,409,588 | 0.000 | 117,300.000 | tai15b | 51,765,268 | 0.000 | 0.005 |
| ci144 | 794,811,636 | 0.003 | 199,400.000 | tai17a | 491,812 | 0.000 | 0.008 |
| dre15 | 306 | 0.000 | 0.003 | tai20a | 703,482 | 0.000 | 0.103 |
| dre18 | 332 | 0.000 | 0.028 | tai20b | 122,455,319 | 0.000 | 0.008 |
| dre21 | 356 | 0.000 | 0.033 | tai25a | 1167,256 | 0.000 | 0.226 |
| dre24 | 396 | 0.000 | 0.125 | tai25b | 344,355,646 | 0.000 | 0.031 |
| dre28 | 476 | 0.000 | 0.393 | tai27e1 | 2558 | 0.000 | 0.114 |
| dre30 | 508 | 0.000 | 0.629 | tai27e2 | 2850 | 0.000 | 0.207 |
| dre42 | 764 | 0.000 | 6.351 | tai27e3 | 3258 | 0.000 | 0.075 |
| dre56 | 1086 | 0.000 | 53.610 | tai27e4 | 2822 | 0.000 | 0.089 |
| dre72 | 1452 | 0.000 | 160.000 | tai27e5 | 3074 | 0.000 | 0.072 |
| dre90 | 1838 | 0.000 | 1341.000 | tai30a | 1818,146 | 0.000 | 0.261 |
| dre110 | 2264 | 0.000 | 7458.000 | tai30b | 637,117,113 | 0.000 | 0.117 |
| dre132 | 2744 | 0.000 | 51,840.000 | tai35a | 2422,002 | 0.000 | 1.392 |
| els19 | 17,212,548 | 0.000 | 0.009 | tai35b | 283,315,445 | 0.000 | 0.492 |
| esc32a | 130 | 0.000 | 0.119 | tai40a | 3139,370 | 0.000 | 963.200 |
| esc32b | 168 | 0.000 | 0.009 | tai40b | 637,250,948 | 0.000 | 0.395 |
| esc32c | 642 | 0.000 | 0.003 | tai45e1 | 6412 | 0.000 | 0.604 |
| esc32d | 200 | 0.000 | 0.006 | tai45e2 | 5734 | 0.000 | 0.797 |
| esc32e | 2 | 0.000 | 0.002 | tai45e3 | 7438 | 0.000 | 0.839 |
| esc32f | 2 | 0.000 | 0.003 | tai45e4 | 6698 | 0.000 | 0.863 |
| esc32g | 6 | 0.000 | 0.002 | tai45e5 | 7274 | 0.000 | 0.504 |
| esc32h | 438 | 0.000 | 0.006 | tai50a | 4938,796 | 0.000 | 2704.000 |
| esc64a | 116 | 0.000 | 0.019 | tai50b | 458,821,517 | 0.000 | 3.875 |
| esc128 | 64 | 0.000 | 0.178 | tai60a | 7,205,962 | 0.000 | 8965.000 |
| had20 | 6922 | 0.000 | 0.008 | tai80a | 13,499,184 | 0.153 | 68,420.000 |
| kra30a | 88,900 | 0.000 | 0.175 | tai100a | 21,043,560 | 0.201 | 97,600.000 |
| kra30b | 91,420 | 0.000 | 0.278 | tai60b | 608,215,054 | 0.000 | 4.632 |
| kra32 | 88,700 | 0.000 | 0.077 | tai64c | 1,855,928 | 0.000 | 0.019 |
| lipa20a | 3683 | 0.000 | 0.008 | tai75e1 | 14,488 | 0.000 | 18.710 |
| lipa20b | 27,076 | 0.000 | 0.002 | tai75e2 | 14,444 | 0.000 | 19.480 |
| lipa30a | 13,178 | 0.000 | 0.030 | tai75e3 | 14,154 | 0.000 | 23.590 |
| lipa30b | 151,426 | 0.000 | 0.008 | tai75e4 | 13,694 | 0.000 | 34.270 |
| lipa40a | 31,538 | 0.000 | 0.184 | tai75e5 | 12,884 | 0.000 | 17.400 |
| lipa40b | 476,581 | 0.000 | 0.017 | tai80b | 818,415,043 | 0.000 | 23.860 |
| lipa50a | 62,093 | 0.000 | 0.373 | tai100b | 1,185,996,137 | 0.000 | 66.760 |
| lipa50b | 1,210,244 | 0.000 | 0.050 | tai125e1 | 35,426 | 0.000 | 1610.000 |
| lipa60a | 107,218 | 0.000 | 3.647 | tai125e2 | 36,178 | 0.000 | 2156.000 |
| lipa60b | 2,520,135 | 0.000 | 0.137 | tai125e3 | 30,498 | 0.000 | 1414.000 |
| lipa70a | 169,755 | 0.000 | 4.485 | tai125e4 | 33,084 | 0.000 | 2283.000 |
| lipa70b | 4,603,200 | 0.000 | 0.212 | tai125e5 | 37,210 | 0.000 | 2299.000 |
| lipa80a | 253,195 | 0.000 | 18.550 | tai150b | 498,896,643 | 0.000 | 2384.000 |
| lipa80b | 7,763,962 | 0.000 | 0.499 | tai343e1 | 141,048 | 0.098 | 13,110.000 |
| lipa90a | 360,630 | 0.000 | 72.840 | tai343e2 | 148,584 | 0.112 | 12,980.000 |
| lipa90b | 12,490,441 | 0.000 | 0.746 | tai343e3 | 142,092 | 0.232 | 13,070.000 |
| nug28 | 5166 | 0.000 | 0.039 | tai343e4 | 152,966 | 0.134 | 13,440.000 |
| nug30 | 6124 | 0.000 | 0.075 | tai343e5 | 139,114 | 0.143 | 13,280.000 |
| rou20 | 725,522 | 0.000 | 0.064 | tai729e1 | 416,260 | 0.901 | 112,300.000 |
| scr20 | 110,030 | 0.000 | 0.017 | tai729e2 | 422,570 | 0.899 | 111,900.000 |
| sko42 | 15,812 | 0.000 | 0.415 | tai729e3 | 405,004 | 0.945 | 112,400.000 |
| sko49 | 23,386 | 0.000 | 5.763 | tai729e4 | 412,910 | 0.929 | 113,500.000 |
| sko56 | 34,458 | 0.000 | 5.620 | tai729e5 | 418,018 | 0.980 | 112,000.000 |
| sko64 | 48,498 | 0.000 | 6.424 | tho30 | 149,936 | 0.000 | 0.056 |
| sko72 | 66,256 | 0.000 | 25.500 | tho40 | 240,516 | 0.000 | 2.948 |
| sko81 | 90,998 | 0.000 | 65.390 | tho150 | 8,133,398 | 0.000 | 73,000.000 |
| sko90 | 115,534 | 0.000 | 170.200 | wil50 | 48,816 | 0.000 | 2.839 |
| sko100a | 152,002 | 0.000 | 254.200 | wil100 | 273,038 | 0.000 | 548.600 |
| (I) | |||||
| Instance | BKV | IHGHA | FPBS | ||
| Time (s) | Time (s) | ||||
| sko72 | 66,256 | 0.000(10) | 25.500 | 0.000(10) | 288.000 |
| sko81 | 90,998 | 0.000(10) | 65.390 | 0.000(10) | 198.000 |
| sko90 | 115,534 | 0.000(10) | 170.200 | 0.010(n/a) | 144.000 |
| sko100a | 152,002 | 0.000(10) | 254.200 | 0.000(10) | 510.000 |
| sko100b | 153,890 | 0.000(10) | 217.000 | 0.000(10) | 348.000 |
| sko100c | 147,862 | 0.000(10) | 347.800 | 0.000(10) | 522.000 |
| sko100d | 149,576 | 0.000(10) | 346.500 | 0.000(10) | 972.000 |
| sko100e | 149,150 | 0.000(10) | 315.700 | 0.000(10) | 732.000 |
| sko100f | 149,036 | 0.000(10) | 591.900 | 0.003(n/a) | 240.000 |
| wil100 | 273,038 | 0.000(10) | 548.600 | 0.000(10) | 984.000 |
| tho150 | 8,133,398 | 0.000(7) | 73,000.000 | 0.006(n/a) | 3444.000 |
| (II) | |||||
| Instance | BKV | IHGHA | FPBS | ||
| Time (s) | Time (s) | ||||
| tai40a | 3,139,370 | 0.000(10) | 963.200 | 0.037(n/a) | 3150.000 |
| tai50a | 4,938,796 | 0.000(10) | 2704.000 | 0.106(n/a) | 4068.000 |
| tai60a | 7,205,962 | 0.000(10) | 8965.000 | 0.189(n/a) | 3600.000 |
| tai80a | 13,499,184 | 0.153(3) | 68,420.000 | 0.467(0) | 3112.000 |
| tai100a | 21,043,560 | 0.201(0) | 97,600.000 | 0.390(0) | 2166.000 |
| tai50b | 458,821,517 | 0.000(10) | 3.875 | 0.000(10) | 12.000 |
| tai60b | 608,215,054 | 0.000(10) | 4.632 | 0.000(10) | 24.000 |
| tai80b | 818,415,043 | 0.000(10) | 23.860 | 0.000(10) | 84.000 |
| tai100b | 11,185,996,137 | 0.000(10) | 66.760 | 0.000(10) | 174.000 |
| tai150b | 498,896,643 | 0.000(10) | 2384.000 | 0.092(n/a) | 2784.000 |
| (I) | |||||
| Instance | BKV | IHGHA | HGA | ||
| Time (s) | Time (s) | ||||
| dre30 | 508 | 0.000(10) | 0.629 | 0.000(10) | 143.400 |
| dre42 | 764 | 0.000(10) | 6.351 | 1.340(n/a) | 547.800 |
| dre56 | 1086 | 0.000(10) | 53.610 | 17.460(n/a) | 1810.800 |
| dre72 | 1452 | 0.000(10) | 160.000 | 27.280(n/a) | 5591.400 |
| dre90 | 1838 | 0.000(10) | 1341.000 | 33.880(n/a) | 11,557.800 |
| dre110 | 2264 | 0.000(10) | 7458.000 | n/a | n/a |
| dre132 | 2744 | 0.000(10) | 51,840.000 | n/a | n/a |
| (II) | |||||
| Instance | BKV | IHGHA | HGA | ||
| Time (s) | Time (s) | ||||
| tai27e1 | 2558 | 0.000(10) | 0.114 | 0.000(10) | ~60.000 |
| tai27e2 | 2850 | 0.000(10) | 0.207 | 0.000(10) | ~60.000 |
| tai27e3 | 3258 | 0.000(10) | 0.075 | 0.000(10) | ~60.000 |
| tai45e1 | 6412 | 0.000(10) | 0.604 | 0.000(10) | ~300.000 |
| tai45e2 | 5734 | 0.000(10) | 0.797 | 0.000(10) | ~300.000 |
| tai45e3 | 7438 | 0.000(10) | 0.839 | 0.000(10) | ~300.000 |
| tai75e1 | 14,488 | 0.000(10) | 18.710 | 0.000(10) | ~2220.000 |
| tai75e2 | 14,444 | 0.000(10) | 19.480 | 0.339(n/a) | ~2220.000 |
| tai75e3 | 14,154 | 0.000(10) | 23.590 | 0.000(10) | ~2220.000 |
| tai125e1 | 35,426 | 0.000(10) | 1610.000 | n/a | n/a |
| tai125e2 | 36,178 | 0.000(10) | 2156.000 | n/a | n/a |
| tai125e3 | 30,498 | 0.000(10) | 1414.000 | n/a | n/a |
| Instance | BKV | IHGHA | HGA-BIPS | ||
|---|---|---|---|---|---|
| Time (s) | Time (s) | ||||
| bl36 | 3296 | 0.000(10) | 7.608 | 0.000(10) | 135.600 |
| bl49 | 4548 | 0.000(10) | 649.900 | 0.193(n/a) | 959.400 |
| bl64 | 5988 | 0.000(10) | 1650.000 | 0.084(n/a) | 2758.200 |
| bl81 | 7532 | 0.000(10) | 50,470.000 | 0.154(n/a) | 7316.400 |
| bl100 | 9256 | 0.099(3) | 60,740.000 | 0.164(0) | 24,119.000 |
| bl121 | 11,396 | 0.126(1) | 125,300.000 | 0.281(0) | 69,892.000 |
| bl144 | 13,432 | 0.229(1) | 178,300.000 | 0.459(0) | 189,168.000 |
| Instance | BKV | IHGHA | HGA-BIPS | ||
|---|---|---|---|---|---|
| Time (s) | Time (s) | ||||
| ci36 | 168,611,971 | 0.000(10) | 1.175 | 0.000(10) | 142.800 |
| ci49 | 236,355,034 | 0.000(10) | 4.586 | 0.000(10) | 614.400 |
| ci64 | 325,671,035 | 0.000(10) | 46.110 | 0.000(10) | 2285.000 |
| ci81 | 427,447,820 | 0.000(10) | 236.500 | 0.000(10) | 7456.000 |
| ci100 | 523,146,366 | 0.000(10) | 4562.000 | 0.000(10) | 22,753.000 |
| ci121 | 653,409,588 | 0.000(10) | 117,300.000 | 0.005(n/a) | 65,011.000 |
| ci144 | 794,811,636 | 0.003(8) | 199,400.000 | 0.020(n/a) | 177,469.000 |
| Objective Function Value | Algorithm | Authors | Year | References |
|---|---|---|---|---|
| 9432 | GA-TS | J.M. Rodriguez et al. | 2004 | [124] |
| 9272 | HGA | Z. Drezner, G. Marcoulides | 2008/9 | [121,122] |
| 9264 | HGA-DI | Z. Drezner, A. Misevičius | 2013 | [123] |
| 9256 | HGA-AM | Z. Drezner, T.D. Drezner | 2019 | [26] |
| 9248 | IHGHA | A. Misevičius et al. | 2024 | this paper |
| Objective Function Value | Algorithm | Authors | Year | References |
|---|---|---|---|---|
| 11,640 | GA-TS | J.M. Rodriguez et al. | 2004 | [124] |
| 11,412 | HGA | Z. Drezner, G. Marcoulides | 2008/9 | [121,122] |
| 11,400 | HGA-DI | Z. Drezner, A. Misevičius | 2013 | [123] |
| 11,396 | HGA-AM | Z. Drezner, T.D. Drezner | 2019 | [26] |
| 11,392 | IHGHA | A. Misevičius et al. | 2024 | this paper |
| Objective Function Value | Algorithm | Authors | Year | References |
|---|---|---|---|---|
| 13,832 | GA-TS | J.M. Rodriguez et al. | 2004 | [124] |
| 13,472 | HGA | Z. Drezner, G. Marcoulides | 2008/9 | [121,122] |
| 13,460 | HGA-DI | Z. Drezner, A. Misevičius | 2013 | [123] |
| 13,432 | HGA-BIPS | Z. Drezner, T.D. Drezner | 2020 | [27] |
| 13,428 | IHGHA | A. Misevičius et al. | 2024 | this paper |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Misevičius, A.; Andrejevas, A.; Ostreika, A.; Verenė, D.; Žekienė, G. An Improved Hybrid Genetic-Hierarchical Algorithm for the Quadratic Assignment Problem. Mathematics 2024, 12, 3726. https://doi.org/10.3390/math12233726
Misevičius A, Andrejevas A, Ostreika A, Verenė D, Žekienė G. An Improved Hybrid Genetic-Hierarchical Algorithm for the Quadratic Assignment Problem. Mathematics. 2024; 12(23):3726. https://doi.org/10.3390/math12233726
Chicago/Turabian StyleMisevičius, Alfonsas, Aleksandras Andrejevas, Armantas Ostreika, Dovilė Verenė, and Gintarė Žekienė. 2024. "An Improved Hybrid Genetic-Hierarchical Algorithm for the Quadratic Assignment Problem" Mathematics 12, no. 23: 3726. https://doi.org/10.3390/math12233726
APA StyleMisevičius, A., Andrejevas, A., Ostreika, A., Verenė, D., & Žekienė, G. (2024). An Improved Hybrid Genetic-Hierarchical Algorithm for the Quadratic Assignment Problem. Mathematics, 12(23), 3726. https://doi.org/10.3390/math12233726






