Directed Knowledge Graph Embedding Using a Hybrid Architecture of Spatial and Spectral GNNs
Abstract
1. Introduction
- Novel mixed architecture: This is a new hybrid architecture model for directed graphs that can approximate an arbitrary-order filter without over-squashing and over-smoothing issues.
- New directed PE: Concepts from continuous signal processing (SP) are generalized to a discrete directed graph. A new method is adopted to evenly search for a complete set of graph Fourier bases across as wide a frequency band as possible and to further obtain a directed node PE from them.
- Benchmarking: Extensive experiments demonstrate the SOTA and competitive performance of our DSGT compared to baselines and the effectiveness of its module. We experientially analyzed the experimental results.
2. Related Work
2.1. Undirected Graph Neural Network
2.2. Directed Graph Neural Network
2.3. Graph Transformer
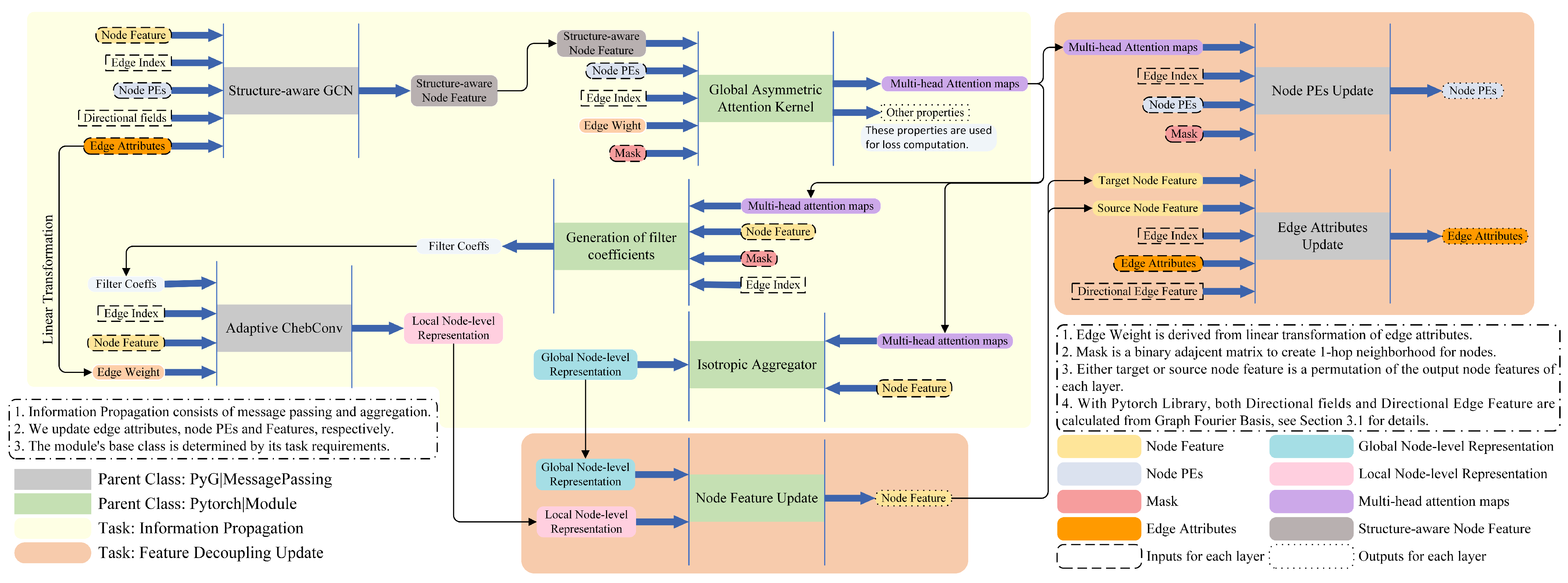
3. Proposed Model
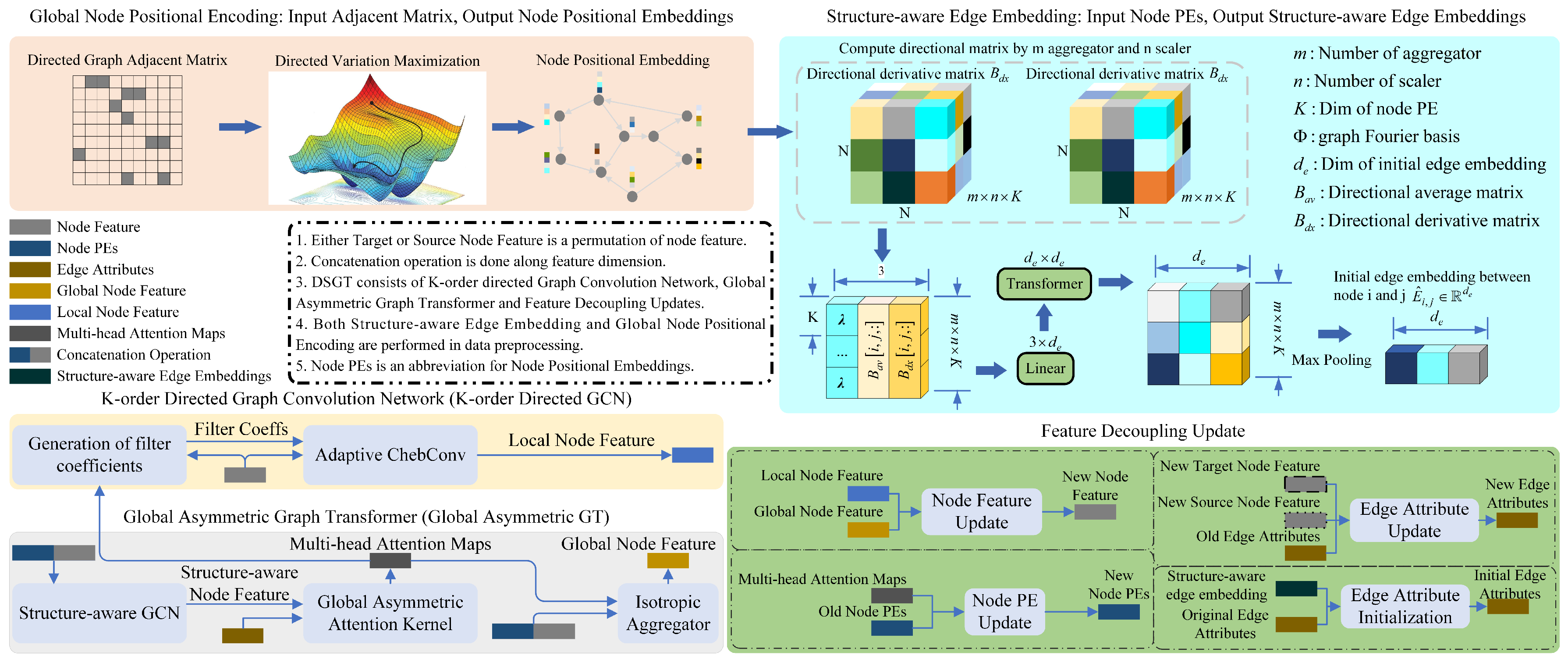
3.1. Graph Preprocessing
3.1.1. Global Node Positional Encoding
| Algorithm 1 Directed variation maximization. |
|
| Algorithm 2 Spectral dispersion minimization. |
|
| Algorithm 3 Non-monotone curvilinear search algorithm. |
|
3.1.2. Structure-Aware Edge Embedding
3.2. Directed Spectral Graph Transformer
3.2.1. Global Asymmetric Graph Transformer
3.2.2. K-Order Directed Graph Convolution Network
3.2.3. Feature Decoupling Update
3.3. End-to-End Optimization for DSGT
| Algorithm 4 Supervised node-level embedding algorithm. |
|
4. Results and Discussion
4.1. Experimental Setup
4.1.1. Dataset Settings
4.1.2. Baselines
4.1.3. Experimental Protocol
4.1.4. Experimental Environment
4.2. Comparative Experiments
4.2.1. Supervised Node Classification
4.2.2. Effectiveness of Node Positional Embeddings
4.3. Ablation Experiment
4.4. Hyperparameter Tuning
4.4.1. The Order of Polynomial Filters
4.4.2. Dimension of Node Positional and Initial Edge Embedding
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. First-Order Extremum Condition for Dual Problems
Appendix A.2. Stationary Condition
Appendix A.3. Advantages over Traditional Attention Kernel
Appendix B
| Abbreviation | Description |
|---|---|
| DSGT | Directed Spectral Graph Transformer |
| Node PE | Node Positional Embedding |
| SP | Signal Processing |
| KSVD | Kernel Singular Value Decomposition |
| TV | (Undirected) Total Variation |
| DV | Directed Total Variation |
| LSSVM | Least-Square Support Vector Machine |
| GLM | Graph Laplacian Matrix |
| GSO | Graph Shifted Operator (e.g., Graph Laplacian Matrix, Graph Adjacent Matrix) |
| GT | Graph Transformer |
| GCN | Graph Convolution Network |
| GNN | Graph Neural Network |
| GFT | Graph Fourier Transformer |
| IGFT | Inverse Graph Fourier Transformer |
| RKBS | Reproducing Kernel Banach Spaces |
| MLP | Multi-Layer Perception |
| GP | Global Maximum Pooling |
| FFN | Forward Feedback Network |
| Symbols | Description |
|---|---|
| N | The total number of nodes in a graph |
| Binary graph adjacent matrix, where | |
| Graph in-degree diagonal matrix, where | |
| The dimension of the node feature | |
| The dimension of the node positional embedding | |
| The dimension of the initial edge embedding | |
| The dimension of the edge attribute | |
| Undirected graph Laplacian matrix | |
| Directed graph Laplacian matrix | |
| Stack operation in the feature dimension | |
| Transformer encoder | |
| Global maximum pooling for the dimension | |
| Nonlinear activation function | |
| s | The dimension of the rank space, in other words, the number of principal components |
| p | The dimension of the basis vector in the rank space |
| · | Matrix multiplication |
| × | Scalar multiplication |
Appendix C
Appendix C.1. Spectral Graph Convolution Theory
Appendix C.2. Nonlinear Kernel SVD
Appendix D







References
- Zhang, G.; Li, D.; Gu, H.; Lu, T.; Shang, L.; Gu, N. Simulating News Recommendation Ecosystems for Insights and Implications. IEEE Trans. Comput. Soc. Syst. 2024, 11, 5699–5713. [Google Scholar] [CrossRef]
- Jain, S.; Hegade, P. E-commerce Product Recommendation Based on Product Specification and Similarity. In Proceedings of the 2021 International Conference on Innovation and Intelligence for Informatics, Computing, and Technologies (3ICT), Zallaq, Bahrain, 29–30 September 2021; pp. 620–625. [Google Scholar] [CrossRef]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral Networks and Locally Connected Networks on Graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar] [CrossRef]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. In Proceedings of the NIPS’16, 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 3844–3852. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2016, arXiv:1609.02907. [Google Scholar] [CrossRef]
- Tong, Z.; Liang, Y.; Sun, C.; Rosenblum, D.S.; Lim, A. Directed Graph Convolutional Network. arXiv 2020, arXiv:2004.13970. [Google Scholar] [CrossRef]
- Zhang, X.; He, Y.; Brugnone, N.; Perlmutter, M.; Hirn, M. MagNet: A Neural Network for Directed Graphs. Adv. Neural Inf. Process. Syst. 2021, 34, 27003–27015. [Google Scholar]
- Ma, Y.; Hao, J.; Yang, Y.; Li, H.; Jin, J.; Chen, G. Spectral-based Graph Convolutional Network for Directed Graphs. arXiv 2019, arXiv:1907.08990. [Google Scholar] [CrossRef]
- Tong, Z.; Liang, Y.; Sun, C.; Li, X.; Rosenblum, D.; Lim, A. Digraph Inception Convolutional Networks. Adv. Neural Inf. Process. Syst. 2020, 33, 17907–17918. [Google Scholar]
- Koke, C.; Cremer, D. HoloNets: Spectral Convolutions do extend to Directed Graphs. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna Austria, 7–11 May 2024; Available online: https://openreview.net/forum?id=EhmEwfavOW (accessed on 10 October 2024).
- Nguyen, K.; Nong, H.; Nguyen, V.; Ho, N.; Osher, S.; Nguyen, T. Revisiting over-smoothing and over-squashing using ollivier-ricci curvature. In Proceedings of the ICML’23, 40th International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023. [Google Scholar]
- Akansha, S. Over-Squashing in Graph Neural Networks: A Comprehensive survey. arXiv 2023, arXiv:2308.15568. [Google Scholar]
- Topping, J.; Di Giovanni, F.; Chamberlain, B.P.; Dong, X.; Bronstein, M.M. Understanding over-squashing and bottlenecks on graphs via curvature. arXiv 2021, arXiv:2111.14522. [Google Scholar] [CrossRef]
- Dwivedi, V.P.; Bresson, X. A Generalization of Transformer Networks to Graphs. arXiv 2020, arXiv:2012.09699. [Google Scholar]
- Bastos, A.; Nadgeri, A.; Singh, K.; Kanezashi, H.; Suzumura, T.; Mulang’, I.O. Investigating Expressiveness of Transformer in Spectral Domain for Graphs. arXiv 2022, arXiv:2201.09332. [Google Scholar] [CrossRef]
- Kreuzer, D.; Beaini, D.; Hamilton, W.; Létourneau, V.; Tossou, P. Rethinking Graph Transformers with Spectral Attention. Adv. Neural Inf. Process. Syst. 2021, 34, 21618–21629. [Google Scholar]
- Dwivedi, V.P.; Luu, A.T.; Laurent, T.; Bengio, Y.; Bresson, X. Graph Neural Networks with Learnable Structural and Positional Representations. arXiv 2021, arXiv:2110.07875. [Google Scholar] [CrossRef]
- Chen, D.; O’Bray, L.; Borgwardt, K. Structure-Aware Transformer for Graph Representation Learning. In Proceedings of the 39th International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; Volume 162, pp. 3469–3489. [Google Scholar]
- Rampášek, L.; Galkin, M.; Dwivedi, V.P.; Luu, A.T.; Wolf, G.; Beaini, D. Recipe for a general, powerful, scalable graph transformer. In Proceedings of the NIPS ’22, 36th International Conference on Neural Information Processing Systems, New Orleans, LA, USA, 28 November–9 December 2022. [Google Scholar]
- Bo, D.; Shi, C.; Wang, L.; Liao, R. Specformer: Spectral Graph Neural Networks Meet Transformers. arXiv 2023, arXiv:2303.01028. [Google Scholar] [CrossRef]
- Singh, R.; Chakraborty, A.; Manoj, B.S. Graph Fourier transform based on directed Laplacian. In Proceedings of the 2016 International Conference on Signal Processing and Communications (SPCOM), Bangalore, India, 12–15 June 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Shafipour, R.; Khodabakhsh, A.; Mateos, G.; Nikolova, E. A Directed Graph Fourier Transform With Spread Frequency Components. IEEE Trans. Signal Process. 2019, 67, 946–960. [Google Scholar] [CrossRef]
- Leus, G.; Segarra, S.; Ribeiro, A.; Marques, A.G. The Dual Graph Shift Operator: Identifying the Support of the Frequency Domain. J. Fourier Anal. Appl. 2021, 27, 49. [Google Scholar] [CrossRef]
- Yun, S.; Jeong, M.; Kim, R.; Kang, J.; Kim, H.J. Graph transformer networks. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Maron, H.; Ben-Hamu, H.; Shamir, N.; Lipman, Y. Invariant and Equivariant Graph Networks. arXiv 2018, arXiv:1812.09902. [Google Scholar]
- Lim, D.; Robinson, J.; Zhao, L.; Smidt, T.E.; Sra, S.; Maron, H.; Jegelka, S. Sign and Basis Invariant Networks for Spectral Graph Representation Learning. arXiv 2022, arXiv:2202.13013. [Google Scholar]
- Ma, G.; Wang, Y.; Wang, Y. Laplacian Canonization: A Minimalist Approach to Sign and Basis Invariant Spectral Embedding. Adv. Neural Inf. Process. Syst. 2023, 36, 11296–11337. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the NIPS’17, 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Nguyen, T.M.; Nguyen, T.; Ho, N.; Bertozzi, A.L.; Baraniuk, R.G.; Osher, S.J. A Primal-Dual Framework for Transformers and Neural Networks. In Proceedings of the Eleventh International Conference on Learning Representations (ICLR), Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Chen, Y.; Tao, Q.; Tonin, F.; Suykens, J.A. Primal-Attention: Self-attention through Asymmetric Kernel SVD in Primal Representation. In Proceedings of the 37th Conference on Neural Information Processing Systems (NeurIPS 2023), New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Suykens, J.A. SVD revisited: A new variational principle, compatible feature maps and nonlinear extensions. Appl. Comput. Harmon. Anal. 2016, 40, 600–609. [Google Scholar] [CrossRef]
- Geisler, S.; Li, Y.; Mankowitz, D.; Cemgil, A.T.; Günnemann, S.; Paduraru, C. Transformers meet directed graphs. In Proceedings of the ICML’23, 40th International Conference on Machine Learning, Honolulu, HI, USA, 23–29 July 2023. [Google Scholar]
- Beaini, D.; Passaro, S.; Letourneau, V.; Hamilton, W.L.; Corso, G.; Liò, P. Directional graph networks. In Proceedings of the International Conference on Learning Representations, Vienna, Austria, 3–7 May 2021. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An imperative style, high-performance deep learning library. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Abadi, M. TensorFlow: Learning functions at scale. In Proceedings of the 21st ACM SIGPLAN International Conference on Functional Programming, Nara, Japan, 18–24 September 2016. [Google Scholar]
- Leon, S.J.; De Pillis, L.; De Pillis, L.G. Linear Algebra with Applications; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- Moret, I.; Novati, P. The computation of functions of matrices by truncated Faber series. Numer. Funct. Anal. Optim. 2001, 22, 1–18. [Google Scholar] [CrossRef]
- Cai, T.; Luo, S.; Xu, K.; He, D.; Liu, T.y.; Wang, L. Graphnorm: A principled approach to accelerating graph neural network training. In Proceedings of the International Conference on Machine Learning. PMLR, Virtual, 18–24 July 2021; pp. 1204–1215. [Google Scholar]
- Maekawa, S.; Sasaki, Y.; Onizuka, M. A Simple and Scalable Graph Neural Network for Large Directed Graphs. arXiv 2023, arXiv:2306.08274. [Google Scholar]
- Hu, W.; Fey, M.; Zitnik, M.; Dong, Y.; Ren, H.; Liu, B.; Catasta, M.; Leskovec, J. Open Graph Benchmark: Datasets for Machine Learning on Graphs. Adv. Neural Inf. Process. Syst. 2020, 33, 22118–22133. [Google Scholar]
- Lim, D.; Hohne, F.; Li, X.; Huang, S.L.; Gupta, V.; Bhalerao, O.; Lim, S.N. Large Scale Learning on Non-Homophilous Graphs: New Benchmarks and Strong Simple Methods. Adv. Neural Inf. Process. Syst. 2021, 34, 20887–20902. [Google Scholar]
- Platonov, O.; Kuznedelev, D.; Diskin, M.; Babenko, A.; Prokhorenkova, L. A critical look at the evaluation of GNNs under heterophily: Are we really making progress? In Proceedings of the Eleventh International Conference on Learning Representations, Virtual Event, 25–29 April 2022.
- Fey, M.; Lenssen, J.E. Fast Graph Representation Learning with PyTorch Geometric. arXiv 2019, arXiv:1903.02428. [Google Scholar]
- Hussain, M.S.; Zaki, M.J.; Subramanian, D. Global Self-Attention as a Replacement for Graph Convolution. In Proceedings of the KDD ’22, 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; pp. 655–665. [Google Scholar] [CrossRef]
| Methods | Directed Graph | Global Asymmetry Attention | Approximate High-Order Filter |
|---|---|---|---|
| Directed GNNs | ✓ | ✗ | ✓ |
| Directed GTs | ✓ | ✓ | ✗ |
| Hybrid Architectures of GNN and GT | ✗ | ✓ | ✓ |
| DSGT (our) | ✓ | ✓ | ✓ |
| Dataset | Cora | Squirrel | Genius | Tolokers | Ogbn-Arxiv | Arxiv-Year |
|---|---|---|---|---|---|---|
| Nodes | 19,793 | 5200 | 421,961 | 11,758 | 169,343 | 169,343 |
| Edges | 126,842 | 217,065 | 984,979 | 1,038,000 | 1,166,243 | 1,166,243 |
| Features | 8710 | 2089 | 12 | 10 | 128 | 128 |
| Classes | 70 | 10 | 2 | 2 | 40 | 35 |
| Directed Edge Ratio | 0.942 | 0.828 | 0.874 | 0.000 | 0.986 | 0.986 |
| Degree Assortativity Coefficient | 0.011 | 0.374 | 0.477 | −0.080 | 0.014 | 0.014 |
| Node Homophily | 0.363 | 0.089 | −0.107 | 0.634 | 0.428 | 0.145 |
| Dataset (Unit: %) | Cora | squirrel | genius | Tolokers | ogbn-arxiv | arxiv-year |
|---|---|---|---|---|---|---|
| DGCN [6] | 62.87 ± 1.36 | 41.64 ± 0.96 | 67.04 ± 2.26 | 70.79 ± 0.49 | 63.01 ± 1.08 | 44.51 ± 0.16 |
| DiGCN [9] | 61.19 ± 0.97 | 47.74 ± 1.54 | 69.56 ± 3.14 | 71.63 ± 0.36 | 63.36 ± 2.06 | 49.09 ± 0.10 |
| Holonet [10] | 76.46 ± 1.07 | 53.71 ± 1.92 | 72.10 ± 3.15 | 74.69 ± 0.36 | 73.09 ± 0.64 | 46.28 ± 0.29 |
| MagNet [7] | 71.77 ± 6.18 | 41.01 ± 1.93 | 80.30 ± 2.07 | 74.33 ± 0.38 | 76.63 ± 0.06 | 51.78 ± 0.26 |
| MagLapNet-I [32] | 77.00 ± 4.96 | 46.06 ± 2.64 | 83.42 ± 1.37 | 75.09 ± 0.45 | 79.92 ± 0.56 | 56.06 ± 1.34 |
| MagLapNet-II [18] | 73.14 ± 3.31 | 49.14 ± 3.66 | 77.94 ± 0.49 | 78.47 ± 0.27 | 76.35 ± 0.19 | 52.17 ± 0.26 |
| GT-WL [14] | 64.38 ± 2.22 | 50.31 ± 1.19 | 68.81 ± 3.27 | 70.77 ± 1.35 | 66.81 ± 1.47 | 47.15 ± 2.39 |
| DSGT(our) | 79.96 ± 3.67 | 50.36 ± 0.25 | 90.05 ± 0.31 | 84.53 ± 0.55 | 80.33 ± 1.19 | 54.62 ± 1.01 |
| Dataset (Unit: %) | Cora | Squirrel | Genius | Tolokers | Ogbn-Arxiv | Arxiv-Year |
|---|---|---|---|---|---|---|
| Magnetic LapPE-ABS [32] | 74.67 ± 0.73 | 46.53 ± 3.63 | 82.08 ± 1.26 | 77.70 ± 5.09 | 74.58 ± 4.01 | 55.13 ± 1.37 |
| Magnetic LapPE-REAL [32] | 73.62 ± 3.01 | 44.07 ± 2.26 | 79.22 ± 1.11 | 77.70 ± 5.09 | 70.44 ± 2.01 | 49.04 ± 0.99 |
| WL PE [14] | 66.59 ± 1.72 | 42.11 ± 1.47 | 77.05 ± 2.06 | 71.55 ± 1.47 | 66.03 ± 3.09 | 44.16 ± 3.25 |
| SVD PE [44] | 78.02 ± 2.35 | 46.96 ± 3.93 | 80.90 ± 5.49 | 81.73 ± 1.59 | 83.34 ± 2.76 | 54.21 ± 2.11 |
| Undirected LapPE [14] | 73.91 ± 1.43 | 43.06 ± 4.14 | 79.85 ± 3.29 | 80.53 ± 0.87 | 75.93 ± 1.26 | 47.14 ± 4.27 |
| Directed PE (ours) [22] | 79.96 ± 3.67 | 50.36 ± 0.25 | 90.05 ± 0.31 | 84.53 ± 0.55 | 80.33 ± 1.19 | 54.62 ± 1.01 |
| Dataset (Unit: %) | Cora | Squirrel | Genius | Tolokers | Ogbn-Arxiv | Arxiv-Year |
|---|---|---|---|---|---|---|
| DSGT-I | 76.93 ± 2.16 | 49.91 ± 0.63 | 86.15 ± 1.93 | 83.55 ± 0.53 | 78.81 ± 2.08 | 53.33 ± 2.10 |
| DSGT-II | 77.87 ± 2.15 | 48.07 ± 3.21 | 83.38 ± 0.76 | 79.96 ± 6.33 | 77.38 ± 0.94 | 55.40 ± 0.96 |
| DSGT-III | 73.00 ± 3.01 | 40.61 ± 1.99 | 77.01 ± 1.24 | 78.18 ± 3.92 | 66.71 ± 1.08 | 46.06 ± 3.87 |
| DSGT-V | 78.67 ± 1.19 | 49.12 ± 1.21 | 85.74 ± 0.75 | 81.96 ± 0.67 | 75.11 ± 1.64 | 53.00 ± 3.33 |
| DSGT-IV | 75.14 ± 1.68 | 47.65 ± 1.01 | 87.41 ± 2.36 | 80.52 ± 0.31 | 78.89 ± 2.21 | 51.31 ± 4.07 |
| DSGT | 79.96 ± 3.67 | 50.36 ± 0.25 | 90.05 ± 0.31 | 84.53 ± 0.55 | 80.33 ± 1.19 | 54.62 ± 1.01 |
| Number of Filter Order K | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Magnetic LapPE-ABS | 66.15 ± 4.86 | 71.78 ± 2.33 | 75.51 ± 2.31 | 74.67 ± 1.73 | 74.07 ± 2.69 | 72.91 ± 1.03 |
| Magnetic LapPE-REAL | 66.05 ± 1.19 | 63.37 ± 5.52 | 70.39 ± 4.17 | 70.96 ± 3.38 | 73.62 ± 3.01 | 72.91 ± 3.43 |
| SVD PE | 68.55 ± 3.50 | 72.18 ± 4.04 | 76.01 ± 2.54 | 78.02 ± 2.35 | 77.96 ± 2.01 | 77.48 ± 2.58 |
| Undirected LapPE | 54.18 ± 3.73 | 60.26 ± 2.96 | 67.87 ± 2.24 | 70.71 ± 2.09 | 70.35 ± 2.05 | 70.91 ± 2.06 |
| Directed PE (our) | 69.09 ± 2.93 | 74.91 ± 2.77 | 76.60 ± 2.58 | 79.96 ± 3.67 | 78.81 ± 1.34 | 77.70 ± 1.35 |
| Dimension of Node PE | 10 | 14 | 18 | 22 | 26 | 30 |
|---|---|---|---|---|---|---|
| Total Parameter Number (Unit: M) | 4.9 | 5.2 | 5.4 | 5.8 | 6.3 | 6.7 |
| Magnetic LapPE-ABS | 73.43 ± 1.11 | 73.73 ± 2.09 | 74.67 ± 1.73 | 74.16 ± 1.27 | 75.44 ± 1.94 | 75.18 ± 1.68 |
| Magnetic LapPE-REAL | 68.99 ± 1.91 | 69.69 ± 2.73 | 70.96 ± 3.38 | 71.02 ± 2.06 | 70.03 ± 1.03 | 71.22 ± 2.57 |
| SVD PE | 74.44 ± 2.11 | 75.68 ± 1.52 | 78.02 ± 2.35 | 78.00 ± 1.78 | 78.64 ± 1.91 | 78.03 ± 2.08 |
| Undirected LapPE | 62.11 ± 1.77 | 66.63 ± 1.73 | 70.71 ± 2.09 | 71.96 ± 2.23 | 72.02 ± 1.99 | 73.36 ± 1.64 |
| Directed PE (our) | 77.21 ± 1.62 | 77.59 ± 2.37 | 79.96 ± 3.67 | 79.93 ± 2.45 | 80.00 ± 1.86 | 80.32 ± 3.69 |
| Dimension of Edge Attributes | 54 | 72 | 90 | 108 | 126 | 144 |
|---|---|---|---|---|---|---|
| Number of Graph Fourier Bases N | 3 | 4 | 5 | 6 | 7 | 8 |
| Total Parameter Number (Unit: M) | 4.7 | 5.0 | 5.2 | 5.4 | 5.6 | 5.8 |
| Cora | 79.24 ± 2.44 | 79.31 ± 3.99 | 79.22 ± 2.63 | 79.96 ± 3.67 | 80.00 ± 2.76 | 79.01 ± 3.03 |
| squirrel | 49.77 ± 1.62 | 49.86 ± 1.23 | 50.11 ± 0.97 | 50.36 ± 0.25 | 50.54 ± 0.61 | 50.44 ± 1.08 |
| genius | 87.53 ± 1.19 | 88.74 ± 0.71 | 89.86 ± 1.10 | 90.05 ± 0.31 | 90.23 ± 0.11 | 90.34 ± 0.23 |
| Tolokers | 83.21 ± 1.00 | 83.00 ± 0.82 | 84.86 ± 1.30 | 84.53 ± 0.55 | 84.07 ± 1.24 | 84.41 ± 0.83 |
| ogbn-arxiv | 77.11 ± 1.20 | 79.23 ± 0.99 | 79.51 ± 1.15 | 80.33 ± 1.19 | 80.34 ± 1.34 | 80.96 ± 0.74 |
| arxiv-year | 53.87 ± 1.37 | 54.16 ± 1.18 | 54.01 ± 1.71 | 54.62 ± 1.01 | 54.44 ± 2.09 | 53.37 ± 1.63 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, G.; Yu, Q.; Chen, F.; Chen, G. Directed Knowledge Graph Embedding Using a Hybrid Architecture of Spatial and Spectral GNNs. Mathematics 2024, 12, 3689. https://doi.org/10.3390/math12233689
Hou G, Yu Q, Chen F, Chen G. Directed Knowledge Graph Embedding Using a Hybrid Architecture of Spatial and Spectral GNNs. Mathematics. 2024; 12(23):3689. https://doi.org/10.3390/math12233689
Chicago/Turabian StyleHou, Guoqiang, Qiwen Yu, Fan Chen, and Guang Chen. 2024. "Directed Knowledge Graph Embedding Using a Hybrid Architecture of Spatial and Spectral GNNs" Mathematics 12, no. 23: 3689. https://doi.org/10.3390/math12233689
APA StyleHou, G., Yu, Q., Chen, F., & Chen, G. (2024). Directed Knowledge Graph Embedding Using a Hybrid Architecture of Spatial and Spectral GNNs. Mathematics, 12(23), 3689. https://doi.org/10.3390/math12233689







