Optimal Tax Trajectory of a Commercial Organisation: Economic and Mathematical Approach

Abstract

The aim of this study is to form a new concept of tax burden calculation—optimal tax trajectory, which meets the needs of economic entities in view of the optimisation of tax payments and state authorities in terms of budget replenishment and subsequent efficient spending of state resources. The presented concept is developed on the basis of mathematical modelling of related economic processes. The model is based on the differential equation. An attempt is made to analyse the impact of building an optimal tax trajectory on the efficiency of the organisation’s activity. It shows that it is possible to increase the tax burden on economic entities in order to replenish the revenue part of the budget, which does not affect their financial situation. The proposed approach expands the instrumental apparatus for calculating tax payments from the position of taxpayers and fiscal authorities. The construction of the optimal tax trajectory facilitates the adoption of point decisions concerning the increase or decrease of the tax burden of an economic entity in mutual account with the factors of the macroeconomic conjuncture. This approach allows for managing the revenue part of the budget and redistributing it later to solve social problems or overcome business downturns.

1. Introduction

The result of the functioning of any commercial structure is determined by its profitability. Profitability as a measure of business efficiency can be achieved by reducing the costs of a business entity. However, there are a number of challenges here too. In addition to increasing fixed and variable costs due to endlessly changing market conditions, entrepreneurs are also experiencing an increasing tax burden. In this context, the development and application of various methods and schemes for optimising the tax payments of a business entity are of paramount importance for building a successful business.

Achieving the necessary optimum in terms of business profitability is carried out by enterprises in several directions. The riskiest of these is the use of illegal methods to minimise a company’s tax payments. Violation of tax legislation leads to serious consequences, manifested, on the one hand, in the form of personal liability of governing structures, and on the other hand, in significant financial losses of the enterprise up to its liquidation. Thus, it is more appropriate for a business structure to operate within the legal framework and use legitimate methods of building an efficient tax payment model. In addition to maintaining a financially sustainable business, this will help maintain or acquire a reputation as a bona fide taxpayer in terms of building financial communications with potential partners and government agencies.

In a number of tax jurisdictions, it is possible to choose the terms and methods of tax accounting. This toolkit is designed to reduce tax pressure on business entities. However, its application does not always lead to the desired result. Often, commercial entities choose to apply a particular tax regime based on general parameters and do not take into account the specificities of their own financial potential and the variability of legal and market conditions. In turn, this limits their financial and investment activity.

The optimal level of taxation can be achieved through the reproductive capacity of organisations, including their large industrial and financial structures and the public economy as a whole. In practice, the economy itself dictates the need to redistribute financial resources from the enterprises. This is caused by structural production factors, financial investments in human capital, socio–economic needs, political reasons, and territorial and regional factors. Large-scale redistributive processes are caused by the accelerated formation of production infrastructure, which requires rapid and massive concentration of capital.

In this context, the factors influencing the selection of the tax payment system should be reflected in the tax policy of the enterprise. However, the tax policy takes into account the strategic directions of realisation of the enterprise taxation system with minimum conditions for operational regulation. Due to the constantly changing market conditions and variability of legal regulation, it is necessary to systematically monitor the quality of taxation of a business entity. This will make it possible to promptly optimise the tax payments of the enterprise within the framework of the current legislation, the relevant financial period, and territorial affiliation.

Considering the problems of applying the system of taxation of organisations, the authors may note that the amount of tax burden is determined based on the impact of several circumstances:

-

Frequent changes in tax legislation and unclear wording of certain provisions resulting in tax accounting errors.

-

Misinterpretation and inconsistency of tax benefits and exemptions from taxpayer obligations.

-

Low level of organisation of tax management at the enterprise (untimely submission of documents, errors in accounting and taxation, incompetence of accounting staff, complexity of relations between taxpayers and tax authorities, negative attitude to the obligation to pay taxes, etc.).

In this regard, it seems appropriate to establish the purpose of the ongoing research as the formation of a new concept for calculating the tax burden, which will meet the needs of both economic entities in view of optimising tax payments and the state authorities in terms of budget replenishment and effective spending of public resources.

In order to achieve the objective of this study, the following tasks are proposed to be solved sequentially:

• Study of existing approaches to calculating the tax burden of companies in order to identify their limitations.
• Definition of the concept “tax trajectory” and development of a mathematical model of the optimal tax trajectory.
• Approbation of the developed mathematical model of the optimal tax trajectory on the example of a specific commercial organisation.

The results obtained in the framework of this study can be used by fiscal authorities in order to manage tax revenues for the budget, and secondly, by taxpayers for the organisation of corporate tax management related to tax optimisation. The scientific novelty of the research consists of the expansion of methodological tools for the optimisation of the tax payments and tax burden of business entities. In particular, existing approaches to optimising the tax burden are mainly based on qualitative changes in the organisation of tax planning (relationship replacement method, relationship splitting method, tax deferral method, and others). In addition, common methods of tax burden calculation are calculations of tax payments (absolute tax burden) or the ratio of tax payments to profit or another financial indicator (relative tax burden) without taking into account the special activity of the business entity. This present study proposes a qualitatively different approach related to the optimisation of the tax trajectory of a commercial organisation over time, taking into account the internal indicators of its activity.

2. Literature and Research Review

The tax burden for an organisation is an indicator of the effectiveness of the tax planning system functioning. Companies formulate accounting policies and forecasts of future expenditures, taking into account the size of the tax burden. The tax burden of organisations is calculated, firstly, to determine the economic behaviour of a business entity. The decrease in the tax burden indicates the effectiveness of the company’s tax policy. The growth of the tax burden is an indicator of the inefficiency of tax policy and tax planning. Second, the tax burden is calculated to determine the likelihood of an onsite tax audit. Thirdly, the tax burden is calculated to forecast for the future the proportion of the organisation’s financial resources that will be payable to the tax authorities in the next tax (or financial) period.

In this regard, it seems reasonable to interpret the concepts of “tax optimization” or “optimisation of tax payments” as a set of actions of a taxpayer, carried out within the legal framework, aimed at reducing the tax burden of an economic entity, taking into account tax risks.

This conclusion has been reached by research that examines different approaches to comparing the terms “tax burden” and “ax pressure” with other concepts. The term “tax burden” itself emerged with the advent of taxes. Already, A. Smith in his scientific work “An Inquiry into the Nature and Cause of the Wealth of Nations” drew attention to the special relationship between the level of tax burden and budget revenues [1].

In the scientific literature, the concepts of “tax burden” and “tax pressure” are usually equated. In this context, the terms are interpreted in the works of A. Laffer and A. I. Povarova [2,3].

Tax pressure has been the subject of academic research since the 18th century. Nevertheless, scientists still cannot agree on its essence. Researchers view tax pressure as the amount of tax paid by an individual or business [4,5]. However, the absolute value of tax payments does not show the full extent of taxation. The absolute value of tax payments cannot be used as the basis for analyses when comparing the tax burden of economic entities.

Gorsky I. V. separates the concepts of “tax pressure” and “tax burden” [6]. By tax pressure, he means “the ratio of the amount of taxes paid by an economic actor to income”. In turn, the tax burden is “the action that is directed by the tax system on economic activity and its subjects”. Indeed, despite the similarity of the concepts, tax burden should be distinguished from tax pressure. Tax pressure and tax burden, regardless of the object of study, imply one or another form of damage or material and financial losses incurred by the subject of economic activity as a result of taxation.

There is an alternative view, according to which the tax pressure arises when a tax liability is incurred. However, the fact that large companies pay several taxes at the same time results in a whole range of tax liabilities. In this vein, the authors define under pressure the tax liability [7] and under tax burden the fact of their calculation and payment [8].

As an independent economic category, tax burden is defined by Evgeny V. Balatsky and Natalia A. Ekimova. In the study, the authors rely on the view that tax pressure is defined as the obligation to pay direct and indirect taxes, while tax burden is the amount of money transferred by a taxpayer to fulfil its own tax obligations [9].

Thus, it seems reasonable to consider tax burden as a value characterising the total amount of tax deductions of a certain company to its revenue. The volume of tax payments of the enterprise is a volatile indicator, as its value is subject to a constant impact of internal and external factors, reflecting the variability of the external environment and the internal potential for the development of the organisation’s activities. In this regard, it seems necessary to establish an acceptable tax burden and assess the factors affecting it.

Currently, there are many different methodologies for estimating a company’s tax burden, but their application is hampered by existing state regulatory standards. This can be explained by the fact that the state authorities have different objectives in setting up a system of tax regulation, one being to increase tax revenue and the other to find the optimum level of tax payments in order to reduce them on the part of the business taxpayer. Often, regulatory documents only mention the quantitative interpretation of the tax burden within the framework of the typical taxation model of an organisation. In turn, this complicates the process of finding and maintaining an acceptable tax burden for the enterprise.

Moreover, the problem of setting up an optimal taxation system for a particular company is also linked to the need to use information systems for managing and controlling tax payments. All this is aimed at the development of the economy as a whole to ensure adequate planned tax revenues in the budget and to reduce the share of the shadow economy. However, the implemented models have certain limitations due to the application of different enterprise taxation regimes, economies of scale, and specifics of the business entity’s activities.

All of the above makes it necessary to build a model of optimal tax trajectory. Achieving the optimum in terms of the tax burden of the enterprise will allow for scale redistributive processes to form a production infrastructure that needs uninterrupted financing. In turn, this will have a favourable impact on socio–economic and territorial–regional disparities. The latter represents the significance of building a model of optimal tax trajectory for large businesses and the largest taxpayers. They largely determine the current and future state of the revenue part of the budget and subsequently its expenditure to realise the functions of the state.

The modern model of the functioning of a large enterprise is often inextricably linked with entering the international market [10]. The company’s international operations in the current environment are subject to significant risks associated with significant fluctuations in the volume of products sold [11], volatility of the national currency exchange rate [12], and instability of prices for exported goods [13]. The oil and gas industry is a good example of a business that is inherently exposed to these risks [14]. The current global economic conjuncture demonstrates that sensitivity to these risks may be so significant that it leads to the bankruptcy of the company.

In the academic literature, various methods are used to stabilise the financial position of a company and the economy as a whole. As a model of the production function, the authors use the Cobb–Douglas model, on the basis of which the necessary level of production is determined and the cost and time of production are optimised. The Cobb–Douglas function as an economic tool expressing in mathematical language the relationship between capital, labour, and output. With almost a hundred years of history, by now, it has many modifications [15]. For example, K. Muro extends the Cobb–Douglas production function to include rent as factor income [16]. M. L. Cheng and Y. Han modified the function and incorporated political factors into it [17]. This demonstrates the wide application of this model and its versatility.

One of the ways to mitigate the impact of risks on the company’s functioning is support from the government. The support can be expressed as additional financial subsidies [10], provision of favourable credit offers [18], tax incentives [19], and others.

Tax support often uses a direct tax rate reduction method. For example, Ellen P. Tanzer shows, using primary and secondary property markets as an example, that a lower property tax rate leads to higher property quality [20]. K. Kopeć proves that a reduction in the value-added tax rate on a particular good or service can lead to an expansion of demand and an increase in sales volumes [21]. At the macro level, the results of the study by A. Zellner and J. K. Ngoie, using data from the US economy, show that a five percentage point reduction in income and corporate tax rates would lead to a three percentage point increase in real gross domestic product [22]. Nevertheless, the general conclusion that the authors draw is that any change in the tax policy of the state should be accompanied in advance by accurate calculations and estimates of the impact of such a policy on the state of the budget.

Despite this, the advantage of the direct tax rate reduction method is the simplicity of its realisability. However, if the company does not make effective use of the support provided, the state may lose the financial resources invested in this support. Moreover, the support may be overwhelming. In turn, this will lead to a decrease in budgetary resources and an increase in the fixed assets of the company. The application of this method or refusal of it is also an element of the taxation system of a business entity. However, due to its specificity, it is not possible to attribute this tool to tax burden or tax optimisation in general.

Thus, it seems appropriate to apply the concept of “tax trajectory”. The construction of a tax trajectory implies the use of a methodology to assess tax payments through a point-by-point selection of tax conditions within the permitted regime and specific parameters of a given company, with a view to their subsequent optimisation. In this way, the company’s tax management gains the ability to respond quickly to changes in legislation and market conditions, and thus the ability to shape the company’s capital structure. In this respect, the company’s tax trajectory is reduced to the construction of a line in the organisation’s tax system, as a line in space along which the movement of its tax burden is carried out and that represents a set of points (specific internal and external factors of influence) within which the company has acted, is acting, or will act in relation to the chosen tax system.

3. Materials and Methods

In this paper, a large oil and gas production company was considered as the object of research. This study models the optimisation of the tax trajectory of this organisation. The trajectory characterises the share of tax deductions depending on the economic performance of the firm.

The subject of this study is the methodological approach to assessing the tax burden and tax trajectory of a company. The research method is the systemic logical analysis using mathematical modelling of economic processes affecting taxation. The analysed data are scientific research and the authors’ results within the framework of research on taxation optimisation processes and their impact on socio–economic systems, the principles of taxation of an organisation, and the basics of development of its economic indicators (residual value of fixed assets, average number of employees, discount rate, average depreciation rate, etc.). The data of the accounting statements of the analysed business entity were taken from the official website of the Corporate Information Disclosure Centre.

The basis of the model is the differential equation. It characterises the dynamics of fixed assets. The key parameter for calculating the dynamics of fixed assets is the function determining the optimal tax trajectory. The function describes the share of tax deductions depending on the economic performance of the company (residual value of fixed assets, average number of employees, discount rate, average depreciation rate, etc.). Functional time dependences of the residual value of fixed assets, average number of employees, ratio of operating cash flow to net income, and ratio of tax payments to operating cash flow were obtained by approximation of the data.

To obtain the function (tax trajectory), we used the Pontryagin maximum principle based on maximisation of the functional that characterises the operating cash flow. The use of Pontryagin’s maximum principle is due to the following reasons. First, this principle allows us to find the best possible control of a dynamical system during its transition from one state to another, especially in the presence of constraints for the input parameters. Second, maximising the Hamiltonian is a relatively simple problem. Instead of maximisation in the function space, the problem is reduced to a stepwise optimisation, which can be implemented by numerical solution. Third, compared to Bellman’s optimality principle, Pontryagin’s maximum principle is more computationally efficient because the conditions it defines need only be fulfilled on a certain trajectory.

The Cobb–Douglas model is chosen to describe the production function. The consistency of the calculation results with the official data determines the choice of model coefficients. Quantitative analysis of the comparison between the calculated tax trajectory and the trajectory obtained from the official data was performed. It is shown that the proposed optimisation of taxation contributes to an increase in the efficiency of the company’s economic activity in the perspective for several years. In the time range 2011–2021, the growth of the residual value of fixed assets due to the optimisation of the tax trajectory is established. It seems expedient to form an assumption of growth in the efficiency of placement of financial and production resources of the organisation within the framework of building a model of optimisation of the tax trajectory.

4. Results

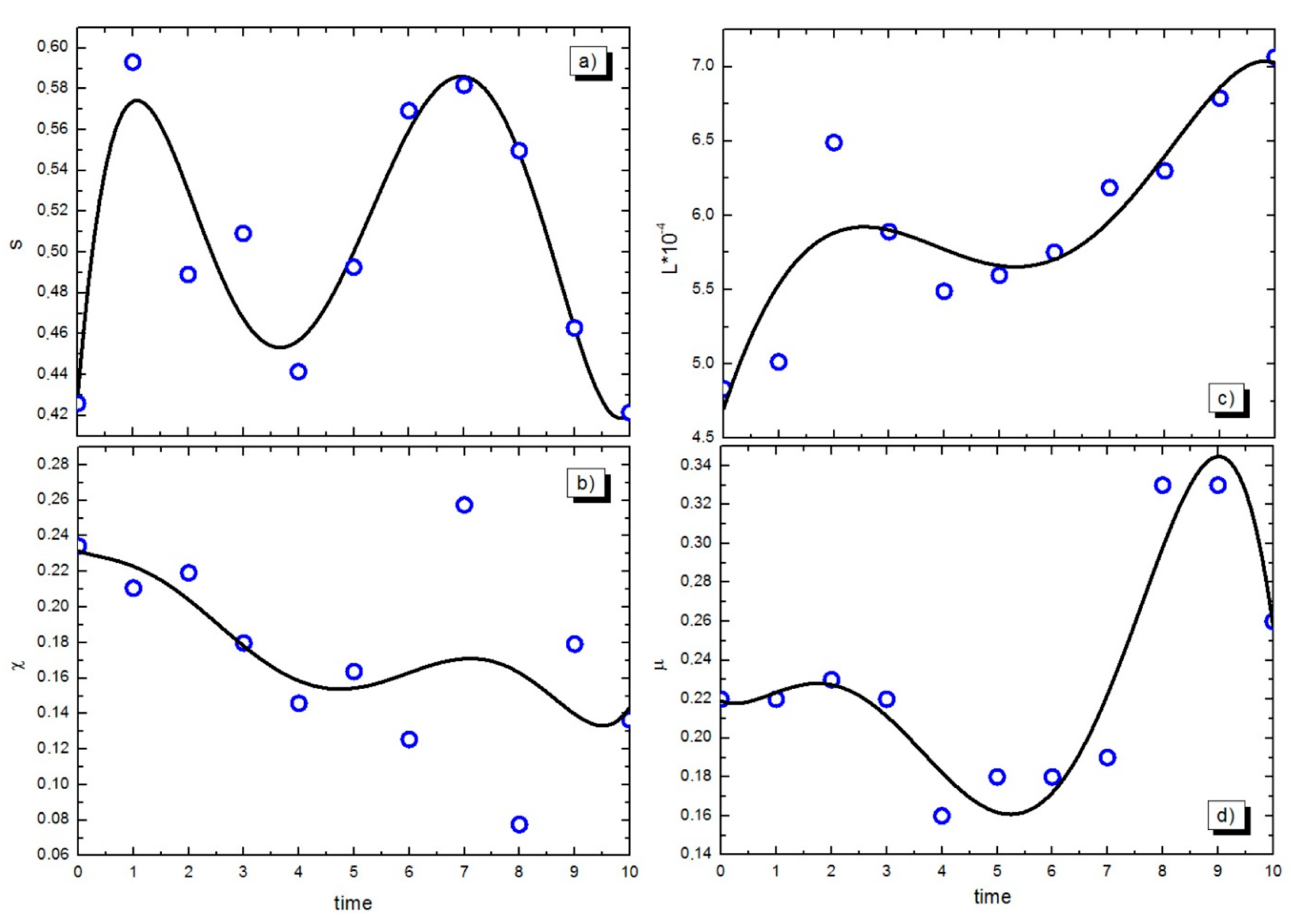
The official data on the following economic indicators of the analysed economic entity were used as input parameters of modelling: K—residual value of fixed assets; C—operating cash flow; I—investment and financial cash flows; N—tax payments; μ—average depreciation rate; L—average number of employees; χ—ratio of tax payments to operating cash flow; s—ratio of operating cash flow to net income. The choice of model parameters was based on theoretical economic considerations, taking into account the economic and financial specificities of a commercial organisation. In particular, these indicators make it possible to provide an aggregated characterisation of the scale of production activity of an economic entity.

The information source for data collection was the accounting statements of the organisation under study (

Table 1. Dynamics of a number of economic indicators of the organisation under study in 2011–2021.

Indicator	Year
	2011	2012	2013	2014	2015	2016
Operating cash flow C (108 $·$ monetary unit)	1.76369	2.31073	2.76736	2.83965	2.85175	3.21297
Investment and financial cash flows I (108 $·$ monetary unit)	1.82982	1.82647	2.68735	3.75365	3.96704	3.92284
Tax payments N (108 ∙ monetary unit)	0.04438	0.25361	0.33514	0.30122	0.09522	0.22158
Average depreciation rate, μ (s−1)	0.22	0.16	0.18	0.18	0.19	0.33
Residual value of fixed assets K (108 ∙ monetary unit)	2.66597	3.70570	4.33071	4.70925	5.10744	3.96332
Average number of employees, L	58,905	54,895	55,975	57,515	61,862	62,998
Ratio of tax payments to operating cash flow, χ	0.17977	0.14577	0.16369	0.12548	0.25748	0.07754
Ratio of operating cash flow to net income, s	0.50920	0.44147	0.49267	0.56931	0.58178	0.54974
Indicator	Year
	2017	2018	2019		2020	2021
Operating cash flow C (108 $·$ monetary unit)	4.21700	5.37523	6.15452		3.58904	2.66151
Investment and financial cash flows I (108 $·$ monetary unit)	3.63410	3.91581	3.63589		3.74165	5.58592
Tax payments N (108 ∙ monetary unit)	0.3653	0.61157	0.59585		0.52502	0.22835
Average depreciation rate, μ (s−1)	0.33	0.26	0.26		0.54	0.37
Residual value of fixed assets K (108 ∙ monetary unit)	4.22587	6.63129	6.63129		3.35241	6.03778
Average number of employees, L	67,882	70,648	78,847		80,420	89,912
Ratio of tax payments to operating cash flow, χ	0.17917	0.13658	0.03450		0.01142	0.03702
Ratio of operating cash flow to net income, s	0.46288	0.42146	0.37137		0.51040	0.67729

Source: compiled by the authors on the basis of [Corporate Information Disclosure Centre, https://www.e-disclosure.ru/portal/files.aspx?id=347&type=3 (accessed on 18 September 2024)].

).

The values of a number of investigated values according to the official data are shown in Figure 1 (open symbols).

Figure 1 shows the data at one-year intervals. However, for numerical modelling, it is necessary for the interval to be significantly smaller to ensure the desired accuracy when solving the corresponding differential equations. In order to reduce the interval, an artificial procedure was undertaken, which is to use a polynomial approximation of the function given tabularly (according to the official data). The approximation was performed in the Origin 9 software package. As a result of approximation, functional dependencies were obtained for the necessary parameters of the model: ratio of tax payments to operating cash flow, ratio of operating cash flow to net income, residual value of fixed assets, average number of employees, and average depreciation rate. The relevant dependencies are as follows (1–5) (the principle of minimisation of approximation variation was used to determine the degree of the polynomial):

$$\mathrm{s}\left(\mathrm{t}\right)=0.42946+0.32528 · \mathrm{t}-0.23573 · {\mathrm{t}}^2+0.06118 · {\mathrm{t}}^3-0.0065 · {\mathrm{t}}^4+2.41828 · {10}^{-4} · {\mathrm{t}}^5,$$

(1)

$$\mathrm{\chi }\left(\mathrm{t}\right)=0.2313-0.00949 · \mathrm{t}+0.00748 · {\mathrm{t}}^2-0.00925 · {\mathrm{t}}^3+0.0027 · {\mathrm{t}}^4-2.99 · {10}^{-4} · {\mathrm{t}}^5+1.14 · {10}^{-5} · {\mathrm{t}}^6,$$

(2)

$$\mathrm{K}\left(\mathrm{t}\right)=1.49754+1.32363 · \mathrm{t}-1.05112 · {\mathrm{t}}^2+0.3848 · {\mathrm{t}}^3-0.05291 · {\mathrm{t}}^4+0.00241 · {\mathrm{t}}^5,$$

(3)

$$\mathrm{L}\left(\mathrm{t}\right)=4.70091+1.11969 · \mathrm{t}-0.30133 · {\mathrm{t}}^2+0.01286 · {\mathrm{t}}^3+0.00328 · {\mathrm{t}}^4-2.44263 · {10}^{-4} · {\mathrm{t}}^5,$$

(4)

$$\mathsf{\mu }\left(\mathrm{t}\right)=0.21909-0.01128 · \mathrm{t}+0.02741 · {\mathrm{t}}^2-0.01384 · {\mathrm{t}}^3+0.00221 · {\mathrm{t}}^4-1.08974 · {10}^{-4} · {\mathrm{t}}^5,$$

(5)

where t = $\tilde{\mathrm{t}}$ − 2011, and $\tilde{\mathrm{t}}$—respective year.

To build a mathematical model, we use a two-parameter production function, where K—residual value of fixed assets, and L—average number of employees. Let us choose the Cobb–Douglas production function Y as a model of the production function (6):

$$\mathrm{Y}=\mathrm{A}{\mathrm{L}}^{\mathsf{\alpha }}{\mathrm{K}}^{\mathsf{\beta }},$$

(6)

where A = 0.9—technological coefficient (as part of this study, A = 1), $\mathsf{\alpha }$—labour elasticity coefficient ($\mathsf{\alpha }\in$ (0; 1)), $\mathsf{\beta }$—capital elasticity coefficient ($\mathsf{\beta }\in$ (0; 1)).

Output is in time dependence Y(t), and the main determinants of formation of which are operating cash flow C(t), investment and financial cash flows I(t), and tax payments N(t) [23] (7):

Y(t) = C(t) + I(t) + N(t)

(7)

Next, let us rewrite expression (8) using the parameter s, which defines the ratio of operating cash flow to net income. The parameter χ determines the ratio of tax payments to operating cash flow:

Y(t) = [1 − χ(t)]{[1 − s(t)]Y(t) + s(t)Y(t)} + χ(t)Y(t)

(8)

Depreciation is a key indicator of the utilisation of active fixed assets K(t). This parameter allows us to characterise the rate μ of the volume of fixed assets withdrawn from production. Having determined the condition of the influence of tax burden on the dynamics of fixed assets over time, let us construct a differential Equation (9):

$${\displaystyle \frac{\mathrm{d}\mathrm{K}}{\mathrm{d}\mathrm{t}}}=\mathrm{s}(\mathrm{t})[1-\mathrm{\chi }(\mathrm{t})]\mathrm{F}[\mathrm{K}(\mathrm{t}), \mathrm{L}]-\mathsf{\mu }\mathrm{K}(\mathrm{t})$$

(9)

In order to quantify the effect of the tax burden on the economic system, let us write down the functional that needs to be maximised (10):

$${\int }_0^{\mathrm{T}}\mathrm{C}\left(\mathrm{t}\right){\mathrm{L}}^{-1}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathsf{\delta }\mathrm{t}\right)\mathrm{d}\mathrm{t}\to \mathrm{m}\mathrm{a}\mathrm{x},$$

(10)

where T—planning horizon, δ—discount rate.

Let us rewrite the expression after replacing the determinant of operating cash flow by output, after which the expression will have the following form (11):

$${\int }_0^{\mathrm{T}}\left[1-\mathrm{\chi }\left(\mathrm{t}\right)\right]\left[1-\mathrm{s}\left(\mathrm{t}\right)\right]{\mathrm{Y}\left(\mathrm{t}\right)\mathrm{L}}^{-1}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathsf{\delta }\mathrm{t}\right)\mathrm{d}\mathrm{t}\to \mathrm{m}\mathrm{a}\mathrm{x}$$

(11)

Thus, let us formulate the optimisation problem in a general formulation. It is necessary to maximise the functional (12):

$${\int }_0^{\mathrm{T}}\left[1-\mathrm{\chi }\left(\mathrm{t}\right)\right]\left[1-\mathrm{s}\left(\mathrm{t}\right)\right]{\mathrm{F}\left[\mathrm{K}\left(\mathrm{t}\right),\mathrm{L}\right]\mathrm{L}}^{-1}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathsf{\delta }\mathrm{t}\right)\mathrm{d}\mathrm{t}\to \mathrm{m}\mathrm{a}\mathrm{x}$$

(12)

under condition (13)

$${\displaystyle \frac{\mathrm{d}\mathrm{K}}{\mathrm{d}\mathrm{t}}}=\mathrm{s}(\mathrm{t})[1-\mathrm{\chi }(\mathrm{t})]\mathrm{F}[\mathrm{K}(\mathrm{t}), \mathrm{L}]-\mathsf{\mu }\mathrm{K}(\mathrm{t})$$

(13)

and constraint s(t) ϵ [0, 1].

We will solve the above maximisation problem using the Pontryagin maximum principle. The main tool for realising the principle is the Hamilton function. To write the Hamiltonian, we will use the connection with the Lagrangian $\tilde{\mathrm{L}}$ (14):

$$\mathrm{H}(\mathrm{K}, \mathrm{\psi }, \mathrm{t})=\mathrm{\psi }{\displaystyle \frac{\mathrm{d}\mathrm{K}}{\mathrm{d}\mathrm{t}}}-\tilde{\mathrm{L}}\left(\mathrm{K},\mathrm{\psi },\mathrm{t}\right)$$

(14)

Drawing an analogy with the apparatus of Hamiltonian mechanics in physics, we can treat the quantity K as a generalised coordinate and ψ, as a dual variable, as a generalised momentum. These conditional definitions are not contrary to common sense. Indeed, the value of K characterises the coordination of the economic system; i.e., its fixed assets. Then, ψ defines the motion of the economic system in the space of generalised coordinates. According to the principle of least action, the integrant in relation (12) defines the Lagrangian with a negative sign [24]. Then, the Hamiltonian is rewritten in the form (15):

$$\mathrm{H}(\mathrm{K}, \mathrm{\psi }, \mathrm{t})=\mathrm{\psi }{\displaystyle \frac{\mathrm{d}\mathrm{K}}{\mathrm{d}\mathrm{t}}}+\left[1-\mathrm{\chi }\left(\mathrm{t}\right)\right]\left[1-\mathrm{s}\left(\mathrm{t}\right)\right]{\displaystyle \frac{\mathrm{Y}\left(\mathrm{t}\right)}{\mathrm{L}}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{\delta }\mathrm{t}\right)$$

(15)

Substituting expression (13) into (15), we obtain the final expression for the Hamiltonian in the form (16):

$$\mathrm{H}(\mathrm{K}, \mathrm{\psi }, \mathrm{t})=\mathrm{\psi }\left\{\mathrm{s}\left(\mathrm{t}\right)\left[1-\mathrm{\chi }\left(\mathrm{t}\right)\right]\mathrm{F}\left[\mathrm{K}\left(\mathrm{t}\right),\mathrm{L}\right]-\mathrm{\mu }\mathrm{K}\left(\mathrm{t}\right)\right\}+\left[1-\mathrm{\chi }\left(\mathrm{t}\right)\right]\left[1-\mathrm{s}\left(\mathrm{t}\right)\right]{\displaystyle \frac{\mathrm{F}\left[\mathrm{K}\left(\mathrm{t}\right),\mathrm{L}\right]}{\mathrm{L}}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{\delta }\mathrm{t}\right)$$

(16)

Let us find the condition under which the Hamilton function takes the maximum value. For this purpose, it is necessary to differentiate it along the optimal trajectory s(t) (17):

$${\displaystyle \frac{\partial \mathrm{H}}{\partial \mathrm{s}}}=\mathrm{\psi }\left[1-\mathrm{\chi }\left(\mathrm{t}\right)\right]\mathrm{F}\left[\mathrm{K}\left(\mathrm{t}\right),\mathrm{L}\right]-\left[1-\mathrm{\chi }\left(\mathrm{t}\right)\right]{\displaystyle \frac{\mathrm{F}\left[\mathrm{K}\left(\mathrm{t}\right),\mathrm{L}\right]}{\mathrm{L}}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{\delta }\mathrm{t}\right)$$

(17)

Let us equate to zero the obtained expression. Then (18):

$$\mathrm{\psi }\left[1-\mathrm{\chi }\left(\mathrm{t}\right)\right]\mathrm{F}\left[\mathrm{K}\left(\mathrm{t}\right),\mathrm{L}\right]-\left[1-\mathrm{\chi }\left(\mathrm{t}\right)\right]{\displaystyle \frac{\mathrm{F}\left[\mathrm{K}\left(\mathrm{t}\right),\mathrm{L}\right]}{\mathrm{L}}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{\delta }\mathrm{t}\right)=0$$

(18)

After some transformations, we obtain (19):

ψ(t) = L⁻¹exp(−δt)

(19)

From expression (19), we can see that the dual variable has a decreasing exponential dependence on time. The discount rate determines the rate of reduction of the dual variable. At the initial point in time, ψ(0) = L−1 is not determined by fixed assets. On the other hand, the dual variable is defined by the canonical Hamilton Equation (20):

$${\displaystyle \frac{\partial \mathrm{\psi }}{\partial \mathrm{t}}}=-{\displaystyle \frac{\partial \mathrm{H}}{\partial \mathrm{K}}}$$

(20)

Then, differentiating the Hamiltonian by the generalised coordinate K, we obtain (21):

$${\displaystyle \frac{\partial \mathrm{\psi }}{\partial \mathrm{t}}}=-\mathrm{\psi }\left(\mathrm{t}\right)\left\{\mathrm{s}\left(\mathrm{t}\right)\left[1-\mathrm{\chi }\left(\mathrm{t}\right)\right]{\displaystyle \frac{\partial }{\partial \mathrm{K}}}\mathrm{F}\left[\mathrm{K}\left(\mathrm{t}\right),\mathrm{L}\right]-\mathrm{\mu }\right\}-{\displaystyle \frac{\left[1-\mathrm{\chi }\left(\mathrm{t}\right)\right]\left[1-\mathrm{s}\left(\mathrm{t}\right)\right]}{\mathrm{L}}}{\displaystyle \frac{\partial }{\partial \mathrm{K}}}\mathrm{F}\left[\mathrm{K}\left(\mathrm{t}\right),\mathrm{L}\right]\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{\delta }\mathrm{t}\right)$$

(21)

According to (14), the left part of expression (16) takes the form $-\mathrm{\delta }{\mathrm{L}}^{-1}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{\delta }\mathrm{t}\right)$. Then (22):

$$-{\displaystyle \frac{\mathrm{\delta }}{\mathrm{L}}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{\delta }\mathrm{t}\right)=-{\displaystyle \frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{\delta }\mathrm{t}\right)}{\mathrm{L}}}\left\{\mathrm{s}\left(\mathrm{t}\right)\left[1-\mathrm{\chi }\left(\mathrm{t}\right)\right]{\displaystyle \frac{\partial \mathrm{F}\left[\mathrm{K}\left(\mathrm{t}\right),\mathrm{L}\right]}{\partial \mathrm{K}}}-\mathrm{\mu }\right\}-{\displaystyle \frac{\left[1-\mathrm{\chi }\left(\mathrm{t}\right)\right]\left[1-\mathrm{s}\left(\mathrm{t}\right)\right]}{\mathrm{L}}}{\displaystyle \frac{\partial \mathrm{F}\left[\mathrm{K}\left(\mathrm{t}\right),\mathrm{L}\right]}{\partial \mathrm{K}}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\mathrm{\delta }\mathrm{t}\right)$$

(22)

After some transformations, we obtain (23):

$$\mathrm{\chi }\left(\mathrm{t}\right)=1-\left(\mathrm{\mu }+\mathrm{\delta }\right){\left\{{\displaystyle \frac{\partial \mathrm{F}\left[\mathrm{K}\left(\mathrm{t}\right),\mathrm{L}\right]}{\partial \mathrm{K}}}\right\}}^{-1}$$

(23)

Expression (23) characterises the optimal management of tax control authorities in order to regulate economic processes. The peculiarity of the obtained expression is its universality in relation to the chosen model of the production function. Let us define the optimal tax control for the Cobb–Douglas production function. Then (24):

$${\displaystyle \frac{\partial \mathrm{F}\left[\mathrm{K}\left(\mathrm{t}\right),\mathrm{L}\right]}{\partial \mathrm{K}}}={\displaystyle \frac{\partial \left[\mathrm{A}{\mathrm{L}}^{\mathsf{\alpha }}{\mathrm{K}}^{\mathsf{\beta }}\right]}{\partial \mathrm{K}}}=\mathrm{A}{\mathrm{L}}^{\mathsf{\alpha }}\mathsf{\beta }{\mathrm{K}}^{\mathsf{\beta }-1}$$

(24)

Let us substitute (24) into the formula for optimal tax (23). After substitution, we have (25):

$${\mathrm{\chi }}_{\mathrm{o}\mathrm{p}\mathrm{t}}\left(\mathrm{t}\right)=1-{\displaystyle \frac{\mathrm{\mu }\left(\mathrm{t}\right)+\mathrm{\delta }\left(\mathrm{t}\right)}{\mathrm{A}\mathsf{\beta }{\mathrm{L}}^{\mathsf{\alpha }}\left(\mathrm{t}\right){\mathrm{K}}^{\mathsf{\beta }-1}\left(\mathrm{t}\right)}}$$

(25)

Ratio (25) describes the optimal tax trajectory of a company, taking into account depreciation rates, discount rate, average number of employees, and residual value of fixed assets. For the purposes of this paper, the discount rate is δ = 0.13.

The next step is to analyse the impact of the tax optimisation process on the dynamics of the residual value of fixed assets. To do this, we need to solve the differential Equation (13) (see expression (13) and Figure 2b). To solve the equation more accurately, it is necessary to reduce the sampling step. To do this, we will use approximations of the key parameters (1)–(5). The numerical solution of Equation (13) is carried out using the Runge–Kutta method of the fourth order of accuracy. The numerical scheme of the solution has the form (26)–(32) [25]:

$${\mathrm{K}}_{\mathrm{n}+1}={\mathrm{K}}_{\mathrm{n}}+{\mathsf{\phi }}_{\mathrm{n}}\Delta \mathrm{t},$$

(26)

$${\mathsf{\phi }}_{\mathrm{n}}={\displaystyle \frac{{\mathsf{\phi }}_{\mathrm{n}}^{\left(1\right)}+2{\mathsf{\phi }}_{\mathrm{n}}^{\left(2\right)}+2{\mathsf{\phi }}_{\mathrm{n}}^{\left(3\right)}+{\mathsf{\phi }}_{\mathrm{n}}^{\left(4\right)}}{6}},$$

(27)

$$\mathrm{f}\left({\mathrm{K}}_{\mathrm{n}},{\mathrm{t}}_{\mathrm{n}}\right)=\mathrm{A}{\mathrm{s}}_{\mathrm{n}}\left(1-{\mathrm{\chi }}_{\mathrm{n}}\right){\mathrm{K}}_{\mathrm{n}}^{\mathsf{\alpha }}{\mathrm{L}}_{\mathrm{n}}^{\mathsf{\beta }}-{\mathrm{\mu }}_{\mathrm{n}}{\mathrm{K}}_{\mathrm{n}},$$

(28)

$${\mathsf{\phi }}_{\mathrm{n}}^{\left(1\right)}=\mathrm{f}\left({\mathrm{K}}_{\mathrm{n}},{\mathrm{t}}_{\mathrm{n}}\right),$$

(29)

$${\mathsf{\phi }}_{\mathrm{n}}^{\left(2\right)}=\mathrm{f}\left({\mathrm{K}}_{\mathrm{n}}+{\displaystyle \frac{{\mathsf{\phi }}_{\mathrm{n}}^{\left(1\right)}\Delta \mathrm{t}}{2}},{\mathrm{t}}_{\mathrm{n}}+{\displaystyle \frac{\Delta \mathrm{t}}{2}}\right),$$

(30)

$${\mathsf{\phi }}_{\mathrm{n}}^{\left(3\right)}=\mathrm{f}\left({\mathrm{K}}_{\mathrm{n}}+{\displaystyle \frac{{\mathsf{\phi }}_{\mathrm{n}}^{\left(2\right)}\Delta \mathrm{t}}{2}},{\mathrm{t}}_{\mathrm{n}}+{\displaystyle \frac{\Delta \mathrm{t}}{2}}\right),$$

(31)

$${\mathsf{\phi }}_{\mathrm{n}}^{\left(4\right)}=\mathrm{f}\left({\mathrm{K}}_{\mathrm{n}}+{\mathsf{\phi }}_{\mathrm{n}}^{\left(3\right)}\Delta \mathrm{t},{\mathrm{t}}_{\mathrm{n}}+\Delta \mathrm{t}\right),$$

(32)

where $\Delta$t = 0.1—sampling step.

For the numerical solution, a computer programme was written in C language using the compiler mingw. The sampling step is chosen for the following reasons. For the first iteration of obtaining the solution, a step equal to 1 was chosen. Then, the step was reduced by 0.1, and the numerical solution was carried out again. As a result, the calculated values of the desired function have changed compared to the values calculated in step 1. The difference was more than 10 percent. Next, the step was again reduced by 0.1, and the above comparison was again made. It should be noted that the subsequent reduction of the step resulted in a smaller difference between the compared function values. The procedure was repeated many times until a minimal difference in function values was found when the step was reduced. Thus, a step of 0.1 conditional time units is chosen to represent the data.

In the framework of this study, the objective was to determine the degree of influence of optimisation of the tax trajectory on the dynamics of the residual value of fixed assets. For the numerical realisation of the set task, the optimal tax trajectory was constructed. When creating a model of optimal tax trajectory, the authors were guided by the following main principles of taxation: joint responsibility, joint financial responsibility, unity of approaches to the formation of tax liabilities, and socio–budgetary efficiency.

Due to the fact that the analysed entity is a member of a consolidated group of taxpayers (during the analysed period), its directors bear subsidiary liability. This means that the tax authorities have the right to make a claim against any member of the consolidated group and recover fines and penalties in the event of insolvency of the responsible participant. This principle significantly increases the possibility of compensation for damage to the state budget.

The same applies to the principle of joint financial liability in respect to the debt obligations of members of a consolidated group of taxpayers. All members of the group are liable for debt reimbursement.

The principle of unity of approaches to the formation of tax liabilities is conditioned by the fact that all members of the consolidated group of taxpayers are equal before the tax legislation with respect to the payment of taxes, as well as with respect to the application of various tax incentives.

Socio–budgetary efficiency determines the effectiveness of the budgetary resources used. This effect is achieved either by determining the optimum resource allocation between all levels of the budgetary system or by implementing programme-targeted methods of budgetary resource allocation. However, when implementing the programme-targeted approach, it is necessary to grant budgetary independence to the authorities that carry out this function. Thus, if all the above conditions are met, it is possible to achieve maximum social impact at minimum state and municipal costs.

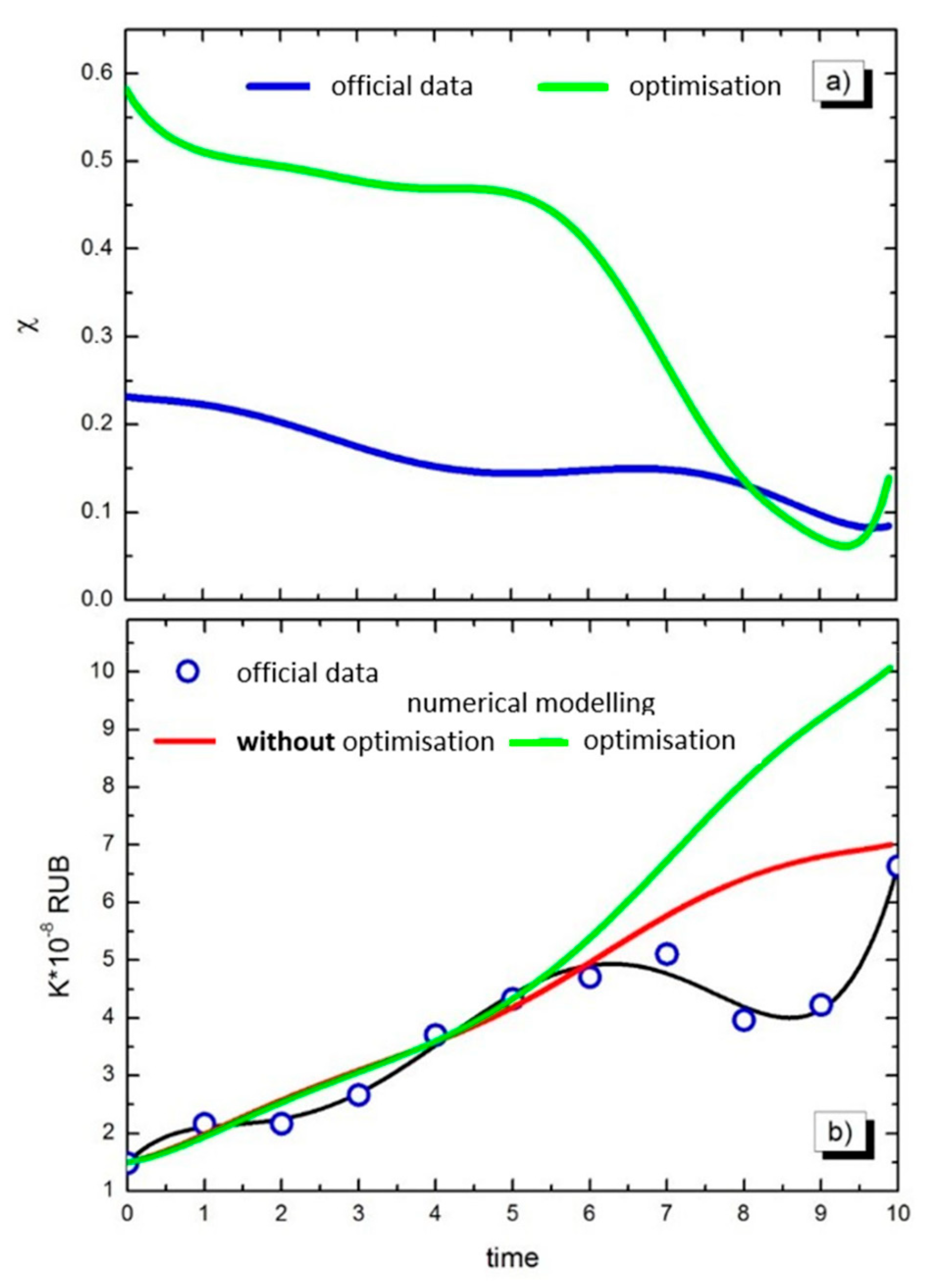
Figure 2 shows the optimal tax trajectory of the analysed commercial organisation and the dynamics of the residual value of its fixed assets. The upper panel shows the actual tax burden curve (blue curve) and the optimal tax trajectory (green curve) constructed based on expression (25). As can be seen, the curves have a strong divergence. In turn, the lower panel shows the curves of the actual (black curve) and approximated (red curve) residual value of fixed assets. The green curve in the lower panel characterises the change in the residual value of fixed assets as a result of the optimisation of the tax trajectory.

According to the blue curve, starting from 2011 to 2018, the tax burden of the analysed economic entity decreases despite the fact that from 2011 to 2014 the world price of the main products of the analysed economic entity (oil, gas) was kept at a fairly high level. Apparently, a general increase in the tax burden (green curve from 2011 to 2014) would allow for a significant increase in the country’s budget, providing substantial financial headroom in other sectors of the economy to withstand crisis situations. Starting in 2014, the model proposes to dramatically reduce the company’s tax burden (green curve from 2014 to 2018). As you know, this period was characterised by a sharp decline in the prices of petroleum products and natural gas, as well as the global financial crisis of 2014.

The influence of these factors has sharply negatively affected the financial condition of the business entity under study and in 2020. Profit growth in the subsequent two-year recovery period did not significantly improve on the pre-crisis figures. In turn, this is due to the lack of a flexible regulatory system that can mitigate the negative impact of the external environment on the activities of economic entities. The construction of this model is also in the interests of the state authorities, as profit is both the tax base and the source of tax payments.

Based on the numerical simulation results, the introduction of optimisation would contribute to the increase of fixed assets even in the crisis period from 2014 to 2021, as Figure 2b shows. A significant increase in the tax burden before 2014 would have done little to reduce the growth of fixed assets.

Let us further note the advantages and limitations of the developed mathematical model of the optimal tax trajectory. The main advantage of the developed mathematical model is a dynamic approach to calculating the tax burden and building an optimal tax trajectory of a commercial organisation, taking into account the internal factors of its economic activity. The existing methods of tax burden optimisation are based only, on the one hand, on a simple arithmetic calculation of tax burden as a ratio of tax payments to a certain financial indicator (e.g., profit, operating cash flow, or other). On the other hand, the available approaches are associated with qualitative changes in tax planning. The developed approach allows us not only to determine the tax burden of an economic entity but also to formulate appropriate management recommendations to change the tax burden of a commercial organisation in order to increase tax revenues to the budget, which does not affect the financial condition of the organisation.

Secondly, the presented mathematical model can be easily formalised as a software product by means of programming languages. Users of the software product are fiscal authorities and taxpayers who, after entering the model parameters into the programme, receive the optimal tax trajectory of the business entity. In turn, this does not require users of the software product to have knowledge of programming languages and numerical mathematical modelling.

Thirdly, the input parameters of the model are standardised. They are independent of a country’s accounting standards and can be extracted from financial and management reporting data. Fourthly, the presented model is universal and applicable to different sectors of the economy.

In turn, the limitations of the developed mathematical model of the optimal tax trajectory are as follows. Basically, the presented mathematical model is oriented to large business entities that contribute significant amounts of tax payments to the budget. The application of the developed model to small or medium-sized businesses is certainly possible but is not well justified by the criterion of labour costs. Moreover, SMEs are often the recipients of various benefits from the state, including tax benefits (for example, in the form of preferential tax regimes). In this case, optimising the tax trajectory of a company, taking into account the application of tax incentives, leads to a certain double effect. With this approach, it is difficult to separate the effectiveness of tax incentives from the optimisation of the tax trajectory. Second, as noted by the authors above, without an appropriate software product and without knowledge of numerical mathematical modelling and programming, the application of the model by taxpayers and fiscal authorities is complicated. However, the software product that the authors plan to develop in the future may offset this limitation.

Thus, the following scheme of application of the mathematical model of the optimal tax trajectory of a commercial organisation can be presented:

• Extracting model input parameters from financial and management reports of the business entity.
• Construction of an optimal tax trajectory.
• Analysis of opportunities and needs to increase or reduce the tax burden of economic entities, formulation of organisational, and managerial recommendations for building a sectoral tax policy (for the tax authority). Assessment of opportunities to reduce the tax burden under the current indicators of economic activity of the organisation (for the taxpayer).

The development of the presented mathematical model can lie in the plane of its unification to the limits of specific types of economic activity and implementation of specific industry indicators into the model as input parameters of the model, as well as the transition from ordinary differential equations to stochastic differential equations.

5. Discussion

Modern conditions of economic activity are characterised by volatility not only in the macroeconomic conjuncture of single countries but also in the mega-economic conjuncture as a whole [26,27]. This is especially true for commodity-based developing economies and economies in transition to developed countries [28]. In turn, the state of the mega-economic conjuncture is largely determined by the global oil and gas market conditions [27]. In a situation of uncertainty and volatility of economic activity, the dichotomy of economic interests of the state and business becomes particularly acute [29]. The state seeks to reduce the budget deficit and increase budget revenues. Businesses, on the other hand, are trying to optimise costs, including by optimising tax payments [30,31]. Obviously, the compromise solution here is a behavioural model of taxation that takes into account the interests of both parties.

The classic indicator reflecting tax pressure on business entities is the indicator of relative tax burden [32]. The disadvantage of this indicator is, firstly, fixing the tax burden only for a certain stage of the financial period. Secondly, the indicator of the relative tax burden does not take into account heterogeneous internal factors of the business entity’s activity. To level these limitations, the authors proposed a qualitatively different approach to optimising tax payments—the optimal tax trajectory.

The optimal tax trajectory constructed for one of the world’s largest oil and gas producers lies above the curve of the economic entity’s actual tax burden (Figure 2a). Thus, it can be argued that it is possible to increase the tax burden in a way that will not affect the resource position of the economic agent. This can be seen in Figure 2b, where the green line shows the increase in the value of the fixed assets of the business entity as a result of optimisation. The following factors explain the existence of this provision for the increase in the tax burden. Firstly, there was an increase in cash flows from operating activities in 2012–2019 (Table 1), which includes the proceeds from the sale of realisable goods. In general, this correlates with the overall global oil market conjuncture [33]. In particular, the world oil price was relatively high in the second quarter of 2011 to the second quarter of 2014 in the post-crisis period and had an overall positive trend during the recovery period in January 2016 to September 2018.

Secondly, the increase in the financial result of the analysed economic entity was facilitated by the commissioning of fields and the lengthening of vertical integration of the production process. A number of expert sources note that the effect of digitalisation and digital transformation of an organisation’s business model (involving cognitive computing, predictive analytics, and big data technologies) is possible [34], although the latter is a hypothesis. The analysis of the impact of digital transformation of an economic entity’s activity on the level of its tax burden can be the object of a separate study.

Thus, the construction of the optimal tax trajectory of an economic entity allows for taking into account the internal factors of economic activity, which depend, in turn, among other things, on general macroeconomic trends. Such an approach, on the one hand, helps to prevent the development of crisis processes at the level of an economic entity and can contribute to its economic growth by optimising expenditures and channelling the freed financial resources to investment projects. This increases the mobility of the tax system to respond to economic trends and provide financial support to certain sectors of the economy.

6. Conclusions

This study proposed a new concept for calculating the tax payments of an economic entity, taking into account the indicators of its activity. The concept is based on building an optimal tax trajectory. The tax trajectory is a method of assessing the tax payments of a company by determining its tax burden point by point, taking into account the company’s performance indicators. Optimisation of the tax trajectory is formally carried out through a numerical solution of the differential equation that characterises the dynamics of fixed assets. The production function of the economic entity put into the model is given by the Cobb–Douglas function.

Constructing a tax trajectory for an organisation can significantly increase the efficiency of financial and production resources by reallocating it using the time factor. In addition, the model demonstrates the possibility of reducing tax payments and thereby redistributing financial resources for the operating activities of an economic entity in certain periods of time, and it reveals potential opportunities for increasing the revenue part of the budget due to the emergence of additional financial opportunities and sources for enterprises. The results of numerical modelling show that this effect can be achieved.

Approbation of the mathematical model of the optimal tax trajectory was made on the basis of the data of accounting and tax reporting of the economic entity of the oil and gas production industry. The results of mathematical modelling demonstrate that an increase in the tax burden in the period from 2011 to 2014 would, on the one hand, make it possible to replenish the consolidated budget of the country. On the other hand, the reallocation of budgetary revenues would support economic sectors vulnerable to crisis situations, in order to consolidate or increase the overall level of business activity, starting from 2014. It is noted that the increase in the tax burden does not affect the financial condition of the economic agent and, moreover, does not reduce the investment of the economic agent in fixed capital. In turn, from 2014 to 2018, the model proposes a reduction in the tax burden due to the unstable mega-economic conjuncture in the oil and gas production industry. Such a reduction in the tax burden would have a favourable impact on the levelling of the financial position of the organisation from 2020 onwards.

Thus, the proposed approach based on the construction of the optimal tax trajectory expands the instrumental apparatus for calculating tax payments of an economic entity. Mathematical modelling of the optimal tax trajectory is in the focus of both public authorities from the position of managing tax revenues to the budget, and economic entities within the framework of their tax management.

The results of mathematical modelling can be scaled (due to the universality of the indicators included in the mathematical model) for a wider range of companies operating in other industries and in different countries.