Model-Following Preview Control for a Class of Linear Descriptor Systems with Actuator Failures

Abstract

This paper considers the model-following preview control problem for a class of continuous-time descriptor systems with actuator failures. Firstly, the model-following problem is transformed into an optimal preview control problem by utilizing restricted equivalent transformations and the construction of augmented systems. After discussing the relationship between the stabilizability and detectability of the augmented system and the corresponding characteristics of the controlled system, the model-following preview controller of the original descriptor system is obtained by integrating on the controller of the augmented system. Finally, an application to electrical circuit system is used for assessment purposes. The simulation results demonstrate the effectiveness of the proposed controller.

1. Introduction

A descriptor system is also known as a differential algebraic system or a singular system, etc. Compared with a normal system, its form is more extensive. It was formed and developed in the 1970s. Rosenbrock first proposed the descriptor system and studied the decoupling zero point and the restricted equivalent transformation of the descriptor system [1]. After that, the existence and uniqueness of the solutions of the descriptor system were discussed in [2]. Since then, many control scholars have begun to explore this new study field; however, there are relatively few research results on model-following control based on descriptor systems.

The model-following control method in the normal system was extended to the descriptor system, and the model-following controller designing method for a class of linear descriptor systems with disturbance was proposed in [3]. Wu et al. presented a model-following control method for a discrete-time nonlinear descriptor system and showed the constraint conditions to ensure that the output tracking error was asymptotically convergent to a zero vector [4]. Zhao and Okubo discussed a model-following controller designing method for a continuous-time nonlinear descriptor system [5]. The H∞ model-following controller was proposed for a class of linear parameter-varying descriptor systems [6]. The robust model reference controller was designed by Tian and Duan for uncertain second-order descriptor systems, and sufficient conditions were given to guarantee the complete parameterization of the robust controller [7]. The robust model-following control problem for high-order descriptor systems with norm-bounded parameter uncertainties was investigated in [8].

Preview control is a control technique that utilizes future information to improve system transient response and enhance tracking performance. At present, the basic theory of preview control has been basically constructed [9,10,11,12,13], which has made progress in the research of the multirate system [14], the descriptor system [15,16,17], the stochastic system [18,19], and the multi-agent system [20,21] and is widely applied to practical projects such as aircraft, wind turbines, vehicle stability control and so on [22,23,24,25].

Model-following control is an important theoretical method in fault-tolerant control. The major idea is to establish a reference model and to realize the tracking of the reference model by designing the controller of the controlled system. Motivated by [26], this article researches the model-following problem for a class of continuous-time descriptor systems with actuator failures by introducing a normal control system with a known input vector as the reference model. The main contributions are summarized as follows:

(1)

Unlike traditional preview control, the output of the reference model is desired to be a signal, and the input of the reference model is a previewable signal.

(2)

The fault-tolerant preview control theory previously proposed for normal systems is extended to a descriptor system, and this theory is successfully applied to a real electrical circuit system.

The structure of this article is as follows: The system model and related assumptions are presented in Section 2. The restricted equivalent transformation of the descriptor system is enunciated in Section 3. Section 4 presents the main results, which contain the establishment of an augmented system and a global optimal preview controller. Conditions for the existence of the controller are drawn in Section 5. In Section 6, the effectiveness of the theoretical results was verified through a simulation. Conclusions are provided in Section 7.

2. Model and Related Assumptions

Consider the following linear continuous-time descriptor system with actuator failures

$$\left\{\begin{array}{cc}\hfill E\dot{x}(t)=& Ax(t)+Bu(t)+Gf(t)\hfill \\ \hfill y(t)=& Cx(t)\hfill \end{array}\right.$$

(1)

where $x(t)\in R^n$, $u(t)\in R^r$, $y(t)\in R^m$, and $f(t)\in R^r$ are state vectors, input vectors, output vectors, and known fault vectors, respectively. $E\in R^{n\times n}$, $A\in R^{n\times n}$, $B\in R^{n\times r}$, $C\in R^{m\times n}$, and $G\in R^{n\times r}$ are known constant matrices, and $\mathrm{rank}(E)=q<n$.

The fault-free reference model is described by

$$\left\{\begin{array}{l}{\dot{x}}_m(t)=A_m{x}_m(t)+B_m{u}_m(t),\\ y_m(t)=C_m{x}_m(t),\end{array}\right.$$

(2)

where $x_m(t)\in R^{n_m}$, $y_m(t)\in R^m$, and $u_m(t)\in R^{r_m}$ are reference state vectors, reference output vectors, and known reference input vectors, respectively. $A_m\in R^{n_m\times n_m}$, $B_m\in R^{n_m\times r_m}$, and $C_m\in R^{m\times n_m}$ are known constant matrices [26].

System (2) describes the ideal dynamic performance of the closed-loop system, and $y_m(t)$ is equivalent to the desired signal in the traditional preview control technology, but the reference signal is generated by the reference input vector $u_m(t)$ (this is a previewable signal) in the given reference model instead of given directly. The failure of the controlled system will lead to an increase in the error between $y(t)$ and $y_m(t)$. Therefore, how to design the controller to make the controlled system still asymptotically track the output vector of the reference model under the condition of failure is a key issue in this paper.

We define the tracking error vector as

$$e(t)=y(t)-y_m(t).$$

(3)

The goal of this article is to design a model-following controller $u(t)$ with preview compensation for descriptor fault system (1) to eliminate the effect of the fault signal on the system output $y(t)$ and to make the output $y(t)$ of closed-loop system (1) track the output $y_m(t)$ of reference model (2) without static error, that is, the output error $e(t)$ is asymptotically stable to the zero vector:

$$\underset{t\to \infty }{\lim }e(t)=\underset{t\to \infty }{\lim }[y(t)-y_m(t)]=0.$$

According to the research objectives of this article, the quadratic performance index function is given as follows:

$$J={\displaystyle {\int }_0^{\infty }\left[e^T(t)Q_{e}e(t)+{\dot{u}}^T(t)R\dot{u}(t)\right]dt},$$

(4)

where $Q_e$ and $R$ are positive definite matrices. Introducing $\dot{u}(t)$ into the performance index function can enable the closed-loop system to include an integrator to help eliminate static errors [11].

The following assumptions are made regarding systems (1) and (2).

Assumption 1.

Suppose system (1) is impulse-free, namely [27]

$$\mathrm{rank}\left[\begin{array}{cc}E& 0\\ A& E\end{array}\right]=n+\mathrm{rank}(E)$$

A necessary condition is that system (1) is regular, but from [27], it is known that the impulse-free descriptor system must be regular, so the system that satisfies Assumption 1 is regular.

Assumption 2.

$(E,A,B)$ is stabilizable, $(E,C,A)$ is detectable, and

$$\mathrm{rank}\left[\begin{array}{cc}A& B\\ C& 0\end{array}\right]=n+m$$

Lemma 1.

The equivalent condition for $(E,A,B)$ to be stabilizable is $\mathrm{rank}\left[\begin{array}{cc}sE-A& B\end{array}\right]=n$, and the equivalent condition for $(E,C,A)$ to be detectable is $\mathrm{rank}\left[\begin{array}{c}sE-A\\ C\end{array}\right]=n$, where $s$ is any complex number that satisfies $\mathrm{Re}(s)\ge 0$ [27].

Assumption 3.

$A_m$ is stable, namely, the eigenvalues of the $A_m$ have a negative real part.

Assumption 4.

The reference input signal $u_m(t)$ is piecewise continuous differentiable and satisfies

$$\underset{t\to \infty }{\lim }{u}_m(t)={\overline{u}}_m,\underset{t\to \infty }{\lim }{\dot{u}}_m(t)=0$$

where ${\overline{u}}_m$ is a constant vector. Moreover, $u_m(s)$ ($t\le s\le t+l_r$) is previewable at each instant of time $t$; $l_r$ is the preview length of $u_m(t)$.

Assumption 5.

The fault signal $f(t)$ is piecewise continuous differentiable and satisfies

$$\underset{t\to \infty }{\lim }f(t)=\overline{f},\underset{t\to \infty }{\lim }\dot{f}(t)=0$$

where $\overline{f}$ is a constant vector. Moreover, $f(t)$ ($t\le s\le t+l_f$) is previewable at each instant of time $t$; $l_f$ is the preview length of $f(t)$.

Remark 1.

Assumptions 4 and 5 are the basic assumptions for previewable signals in preview control theory [28].

3. Restricted Equivalent Transformation

In order to simplify the descriptor system and make use of the conclusion of preview control, we transform system (1) into second restricted equivalent forms by a nonsingular linear transformation. According to $\mathrm{rank}(E)=q$, there always exist nonsingular matrices $Q_1$ and $P_1$, such that $Q_{1}E{P}_1=\left[\begin{array}{cc}{I}_q& 0\\ 0& 0\end{array}\right]$.

Making a nonsingular linear transformation

$$x(t)=P_1\overline{x}(t),$$

substituting into the first equation of system (1), we obtain

$$\left\{\begin{array}{ll}\hfill E{P}_1\dot{\overline{x}}(t)=& A{P}_1\overline{x}(t)+Bu(t)+Gf(t),\hfill \\ \hfill y(t)=& C{P}_1\overline{x}(t)\hfill \end{array}\right.$$

(5)

Taking left transformation matrix $Q_1$ over both sides of (5), we obtain

$$(Q_{1}E{P}_1)\dot{\overline{x}}(t)=(Q_{1}A{P}_1)\overline{x}(t)+(Q_{1}B)u(t)+(Q_{1}G)f(t).$$

Partitioning the matrices $Q_{1}A{P}_1$, $Q_{1}B$, $Q_{1}G$, and $C{P}_1$, denote

$$Q_{1}A{P}_1=\left[\begin{array}{cc}{\overline{A}}_{11}& {\overline{A}}_{12}\\ {\overline{A}}_{21}& {\overline{A}}_{22}\end{array}\right],Q_{1}B=\left[\begin{array}{c}{\overline{B}}_1\\ {\overline{B}}_2\end{array}\right],Q_{1}G=\left[\begin{array}{c}{\overline{G}}_1\\ {\overline{G}}_2\end{array}\right],C{P}_1=\left[\begin{array}{cc}{\overline{C}}_1& {\overline{C}}_2\end{array}\right].$$

Let $\overline{x}(t)=\left[\begin{array}{c}{\overline{x}}_1(t)\\ {\overline{x}}_2(t)\end{array}\right]$, where ${\overline{x}}_1(t)\in R^q$ and ${\overline{x}}_2(t)\in R^{n-q}$. System (1) can be transformed into

$$\left\{\begin{array}{ll}\hfill {\dot{\overline{x}}}_1(t)=& {\overline{A}}_{11}{\overline{x}}_1(t)+{\overline{A}}_{12}{\overline{x}}_2(t)+{\overline{B}}_{1}u(t)+{\overline{G}}_{1}f(t),\hfill \\ \hfill 0=& {\overline{A}}_{21}{\overline{x}}_1(t)+{\overline{A}}_{22}{\overline{x}}_2(t)+{\overline{B}}_{2}u(t)+{\overline{G}}_{2}f(t),\hfill \\ \hfill y(t)=& {\overline{C}}_1{\overline{x}}_1(t)+{\overline{C}}_2{\overline{x}}_2(t).\hfill \end{array}\right.$$

(6)

The above transformation is usually called a restricted equivalent transformation, and system (6) is the second restricted equivalent transformation form of system (1).

It is noted that the restricted equivalent transformation does not change the regularity, stabilizability, detectability, and impulsiveness of the system [27]. Without losing generality, we can study system (1) through system (6).

Remark 2.

By [27], we can see that the following two propositions are equivalent:

(1) 

The descriptor system is impulse-free.

(2) 

Matrix ${\overline{A}}_{22}$ in the second restricted equivalent transformation form of the descriptor system is reversible.

4. Augmented System and Controller Design

By assuming Assumption 1, descriptor system (1) is impulse-free, so the ${\overline{A}}_{22}$ in the second restricted equivalent transformation is reversible. System (6) is composed of a normal system and an algebraic equation. By using the characteristic of matrix ${\overline{A}}_{22}$ as reversible, the algebraic equation is deformed, and we can turn system (6) into a normal control system with state vector ${\overline{x}}_1(t)$.

According to the second form of system (6), we obtain

$${\overline{x}}_2(t)=-{{\overline{A}}_{22}}^{-1}{\overline{A}}_{21}{\overline{x}}_1(t)-{{\overline{A}}_{22}}^{-1}{\overline{B}}_{2}u(t)-{{\overline{A}}_{22}}^{-1}{\overline{G}}_{2}f(t).$$

(7)

Substituting (7) in the first and third forms of (6), system (6) becomes a normal system

$$\left\{\begin{array}{l}{\dot{\overline{x}}}_1(t)=\tilde{A}{\overline{x}}_1(t)+\tilde{B}u(t)+\tilde{G}f(t),\\ y(t)=\tilde{C}{\overline{x}}_1(t)+{\tilde{D}}_{1}u(t)+{\tilde{D}}_{2}f(t),\end{array}\right.$$

(8)

and an Equation (7), where

$\tilde{A}={\overline{A}}_{11}-{\overline{A}}_{12}{{\overline{A}}_{22}}^{-1}{\overline{A}}_{21}$, $\tilde{B}={\overline{B}}_1-{\overline{A}}_{12}{{\overline{A}}_{22}}^{-1}{\overline{B}}_2$, $\tilde{G}={\overline{G}}_1-{\overline{A}}_{12}{{\overline{A}}_{22}}^{-1}{\overline{G}}_2$, $\tilde{C}={\overline{C}}_1-{\overline{C}}_2{{\overline{A}}_{22}}^{-1}{\overline{A}}_{21}$, and ${\tilde{D}}_1=-{\overline{C}}_2{{\overline{A}}_{22}}^{-1}{\overline{B}}_2$, ${\tilde{D}}_2=-{\overline{C}}_2{{\overline{A}}_{22}}^{-1}{\overline{G}}_2$.

Under the premise of maintaining dynamic characteristics, we transform descriptor system (1) with actuator failures into normal system (8) and algebraic equation (7). Therefore, we only need to consider the output tracking problem of system (8) to reference model (2). We construct an augmented system by using the method of the preview control theory.

By taking the derivative on both sides of (3), the state equation in (8) and (2), we can obtain

$$\dot{e}(t)=\dot{y}(t)-{\dot{y}}_m(t)=\tilde{C}{\dot{\overline{x}}}_1(t)+{\tilde{D}}_{1}u(t)+{\tilde{D}}_{2}f(t)-C_m{\dot{x}}_m(t),$$

(9)

$${\ddot{\overline{x}}}_1(t)=\tilde{A}{\dot{\overline{x}}}_1(t)+\tilde{B}\dot{u}(t)+\tilde{G}\dot{f}(t),$$

(10)

$${\ddot{x}}_m(t)=A_m{\dot{x}}_m(t)+B_m{\dot{u}}_m(t).$$

(11)

Combining (9), (10), and (11) and taking $e(t)$ as the output vector, we can yield an augmented system

$$\left\{\begin{array}{l}\dot{X}(t)=\widehat{A}X(t)+\widehat{B}\dot{u}(t)+{\widehat{B}}_m{\dot{u}}_m(t)+\widehat{G}\dot{f}(t),\\ e(t)=\widehat{C}X(t),\end{array}\right.$$

(12)

where

$X(t)=\left[\begin{array}{c}e(t)\\ {\dot{\overline{x}}}_1(t)\\ {\dot{x}}_m(t)\end{array}\right]$, $\widehat{A}=\left[\begin{array}{ccc}0& \tilde{C}& -C_m\\ 0& \tilde{A}& 0\\ 0& 0& A_m\end{array}\right]$, $\widehat{B}=\left[\begin{array}{c}{\tilde{D}}_1\\ \tilde{B}\\ 0\end{array}\right]$, ${\widehat{B}}_m=\left[\begin{array}{c}0\\ 0\\ B_m\end{array}\right]$, $\widehat{G}=\left[\begin{array}{c}{\tilde{D}}_2\\ \tilde{G}\\ 0\end{array}\right]$, $\widehat{C}=\left[\begin{array}{ccc}I& 0& 0\end{array}\right]$.

Remark 3.

$e(t)=y(t)-y_m(t)$ as the output of the augmented system (12) is reasonable due to the output of systems (1) and (2), which are $y(t)$ and $y_m(t)$, respectively.

When using the relevant variables in (12) to represent performance index function (4), it can be rewritten as

$$J={\displaystyle {\int }_0^{\infty }\left[X^T(t)QX(t)+{\dot{u}}^T(t)R\dot{u}(t)\right]}dt,$$

(13)

where $Q=\left[\begin{array}{ccc}{Q}_e& & \\ & 0& \\ & & 0\end{array}\right]$.

So far, the model-tracking problem in this article has been transformed into an optimal preview problem for system (12) and performance index function (13). Similar to [11], we can obtain the following theorem.

Theorem 1.

Suppose $(\widehat{A},\widehat{B})$ is stabilizable and $(Q^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\widehat{A})$ is detectable. The optimal preview input of system (12) under performance index function (13) can be represented as

$$\dot{u}(t)=-R^{-1}{\widehat{B}}^{T}PX(t)-R^{-1}{\widehat{B}}^{T}g(t),$$

(14)

where matrix $P$ is a positive semi-definite matrix satisfying the algebraic Riccati equation

$${\widehat{A}}^{T}P+P\widehat{A}-P\widehat{B}{R}^{-1}{\widehat{B}}^{T}P+Q=0$$

(15)

and

$$g(t)={\displaystyle {\int }_0^{l_f}\left[\exp (\sigma {{\widehat{A}}_c}^T)P\widehat{G}\dot{f}(t+\sigma )\right]d\sigma }+{\displaystyle {\int }_0^{l_r}\left[\exp (\sigma {{\widehat{A}}_c}^T)P{\widehat{B}}_m{\dot{u}}_m(t+\sigma )\right]d\sigma }$$

(16)

the matrix

$${\widehat{A}}_c=\widehat{A}-\widehat{B}{R}^{-1}{\widehat{B}}^{T}P$$

(17)

is stable.

System (12) has the same form as system (3.4) in [11], therefore, the derivation process is similar to that of [11]. It is omitted here.

5. Conditions for the Existence of the Controller

Theorem 1 requires $(\widehat{A},\widehat{B})$ to be stabilizable and $(Q^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\widehat{A})$ to be detectable; we discuss the situations that controlled system (1) needs to satisfy in order to establish these two conditions. Please note that (2) is a given system that must satisfy Assumption 3.

Lemma 2.

Under Assumption 3, the necessary and sufficient condition for $(\widehat{A},\widehat{B})$ to be stabilizable is that $(\tilde{A},\tilde{B})$ must be stabilizable and $\left[\begin{array}{cc}\tilde{A}& \tilde{B}\\ \tilde{C}& \tilde{D}\end{array}\right]$ must be of full row rank.

Proof. 

Based on the PBH criterion [29], the necessary and sufficient condition for $(\widehat{A},\widehat{B})$ to be stabilizable is that the matrix

$$U_c=\left[\begin{array}{cccc}sI& -\tilde{C}& {\tilde{C}}_m& \tilde{D}\\ 0& sI-\tilde{A}& 0& \tilde{B}\\ 0& 0& sI-A_m& 0\end{array}\right]$$

is of full row rank, where $s$ is any complex number that satisfies $\mathrm{Re}(s)\ge 0$. According to Assumption 3, $A_m-sI$ is invertible. Therefore,

$$\begin{array}{ll}\mathrm{rank}(U_c)& =\mathrm{rank}(sI-A_m)+rank\left[\begin{array}{ccc}sI& -\tilde{C}& \tilde{D}\\ 0& sI-\tilde{A}& \tilde{B}\end{array}\right]\\ & =n_m+rank\left[\begin{array}{ccc}sI& -\tilde{C}& \tilde{D}\\ 0& sI-\tilde{A}& \tilde{B}\end{array}\right].\end{array}$$

That is to say, the equivalent condition for matrix $U_c$ to be row full rank is that $\left[\begin{array}{ccc}sI& -\tilde{C}& \tilde{D}\\ 0& sI-\tilde{A}& \tilde{B}\end{array}\right]$ is row full rank. There are two situations to discuss below.

(i)

When $s=0$, it is obvious that the equivalent condition for $\left[\begin{array}{ccc}sI& -\tilde{C}& \tilde{D}\\ 0& sI-\tilde{A}& \tilde{B}\end{array}\right]$ to be row full rank is that $\left[\begin{array}{cc}\tilde{A}& \tilde{B}\\ \tilde{C}& \tilde{D}\end{array}\right]$ is row full rank;

(ii)

When $\mathrm{Re}(s)\ge 0$ and $s\ne 0$, the equivalent condition for $\left[\begin{array}{ccc}sI& -\tilde{C}& \tilde{D}\\ 0& sI-\tilde{A}& \tilde{B}\end{array}\right]$ to be row full rank is that $\left[\begin{array}{cc}sI-\tilde{A}& \tilde{B}\end{array}\right]$ is row full rank.

It can be known that $\left[\begin{array}{cc}sI-\tilde{A}& \tilde{B}\end{array}\right]{|}_{s=0}$ is also full row rank from the discussion of $s=0$. Therefore, we draw the conclusion to be proven by combining these discussions. Lemma 2 is proven. □

Lemma 3.

The necessary and sufficient condition for $(\tilde{A},\tilde{B})$ to be stabilizable is that $(E,A,B)$ is stabilizable [15].

Lemma 4.

The necessary and sufficient condition for $\left[\begin{array}{cc}\tilde{A}& \tilde{B}\\ \tilde{C}& \tilde{D}\end{array}\right]$ to be row full rank is that $\left[\begin{array}{cc}A& B\\ C& 0\end{array}\right]$ is row full rank [15].

From Lemmas 2–4, we obtain the relationship between the stabilizability of the augmented system and the original descriptor system.

Theorem 2.

Under Assumption 3, the necessary and sufficient condition for $(\widehat{A},\widehat{B})$ to be stabilizable is that  $(E,A,B)$ is stabilizable and  $\left[\begin{array}{cc}A& B\\ C& 0\end{array}\right]$ is of full row rank.

Lemma 5.

Under Assumption 3, the necessary and sufficient condition for $(Q^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\widehat{A})$ to be detectable is that $(\tilde{C},\tilde{A})$ is detectable.

Proof. 

In light of the PBH criterion, the equivalent condition for $(Q^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\widehat{A})$ to be detectable is that matrix $U_o=\left[\begin{array}{c}sI-\widehat{A}\\ Q^{1/2}\end{array}\right]$ is column full rank, where $s$ is any complex number that satisfies $\mathrm{Re}(s)\ge 0$. Note that

$$U_o=\left[\begin{array}{ccc}sI& -\tilde{C}& C_m\\ 0& sI-\tilde{A}& 0\\ 0& 0& sI-A_m\\ Q_e^{1/2}& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right].$$

According to the structure of $U_o$ and the invertibility of $A_m-sI$ and $Q_e^{1/2}$, we yield

$$\begin{array}{ll}\mathrm{rank}(U_o)& =\mathrm{rank}\left[\begin{array}{ccc}sI& -\tilde{C}& C_m\\ 0& sI-\tilde{A}& 0\\ 0& 0& sI-A_m\\ Q_e^{1/2}& 0& 0\end{array}\right]\\ & =\mathrm{rank}(Q_e^{1/2})+\mathrm{rank}\left[\begin{array}{cc}-\tilde{C}& C_m\\ sI-\tilde{A}& 0\\ 0& sI-A_m\end{array}\right]\\ & =\mathrm{rank}(Q_e^{1/2})+\mathrm{rank}(A_m-sI)+\mathrm{rank}\left[\begin{array}{c}sI-\tilde{A}\\ \tilde{C}\end{array}\right]\\ & =p+n_m+\mathrm{rank}\left[\begin{array}{c}sI-\tilde{A}\\ \tilde{C}\end{array}\right].\end{array}$$

Lemma 5 is proven. □

Lemma 6.

The necessary and sufficient condition for $(\tilde{C},\tilde{A})$ to be detectable is that $(E,C,A)$ is detectable [15].

From Lemmas 5 and 6, we obtain the connection between the detectability of the augmented system and the original descriptor system.

Theorem 3.

Under Assumption 3, the necessary and sufficient condition for $(Q^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.},\widehat{A})$ to be detectable is that $(E,C,A)$ is detectable.

The most important result of this article can be obtained on the basis of Theorems 1–3.

Theorem 4.

If Assumptions 1–5 hold, and  $Q_e$,  $R$ are positive definite matrices, the Riccati Equation (15) has a unique symmetric positive semi-definite solution, and the optimal preview input of system (1) under the performance index function (4) can be represented as

$$u(t)=u(0)-K_e{\displaystyle {\int }_0^{t}e(\sigma )}d\sigma -K_x[x(t)-x(0)]-K_{x_m}[x_m(t)-x_m(0)]-f_1(t)-f_2(t),$$

(18)

in which  $f_1(t)$,  $f_2(t)$,  $K_e$,  $K_x$ and  $K_{x_m}$ are

$$\begin{gathered} f_1(t)=R^{-1}{\widehat{B}}^T{\displaystyle {\int }_0^{l_r}\exp (\sigma {{\widehat{A}}_c}^T)P{\widehat{B}}_m\left[u_m(t+\sigma )-u_m(\sigma )\right]}d\sigma , \\ {f}_2(t)=R^{-1}{\widehat{B}}^T{\displaystyle {\int }_0^{l_f}\exp (\sigma {{\widehat{A}}_c}^T)P\widehat{G}\left[f(t+\sigma )-f(\sigma )\right]}d\sigma , \end{gathered}$$

$$K=R^{-1}{\widehat{B}}^{T}P=\left[\begin{array}{ccc}{K}_e& K_{{\overline{x}}_1}& K_{x_m}\end{array}\right],$$

(19)

$$K_x=\left[\begin{array}{cc}{K}_{{\overline{x}}_1}& 0\end{array}\right]{P_1}^{-1}.$$

The expression for stable matrix ${\widehat{A}}_c$ is (17). The initial values $u(0)$, $x(0)$ and $x_m(0)$ can be arbitrarily selected.

Proof. 

By integrating the two sides of (14)

$$\dot{u}(t)=-K_{e}e(t)-K_{{\overline{x}}_1}{\dot{\overline{x}}}_1(t)-K_{x_m}{\dot{x}}_m(t)-R^{-1}{\tilde{B}}^{T}g(t),$$

on $[0,t]$, we can obtain

$$u(t)=u(0)-K_e{\displaystyle {\int }_0^{t}e(\sigma )}d\sigma -K_{{\overline{x}}_1}[{\overline{x}}_1(t)-{\overline{x}}_1(0)]-K_{x_m}[x_m(t)-x_m(0)]-R^{-1}{\tilde{B}}^T{\displaystyle {\int }_0^{t}g(s)}ds.$$

(20)

Since $\overline{x}(t)=\left[\begin{array}{c}{\overline{x}}_1(t)\\ {\overline{x}}_2(t)\end{array}\right]$ and nonsingular transformation $x(t)=P_1\overline{x}(t)$, we have $\left[\begin{array}{c}{\overline{x}}_1(t)\\ {\overline{x}}_2(t)\end{array}\right]=P_1^{-1}x(t)$. Order $K_x=\left[\begin{array}{cc}{K}_{{\overline{x}}_1}& 0\end{array}\right]{P_1}^{-1}$, then

$$K_{x}x(t)=\left[\begin{array}{cc}{K}_{{\overline{x}}_1}& 0\end{array}\right]{P_1}^{-1}x(t)=\left[\begin{array}{cc}{K}_{{\overline{x}}_1}& 0\end{array}\right]\left[\begin{array}{c}{\overline{x}}_1(t)\\ {\overline{x}}_2(t)\end{array}\right]=K_{{\overline{x}}_1}{\overline{x}}_1(t),$$

and we can obtain $K_{{\overline{x}}_1}{\overline{x}}_1(0)=K_{x}x(0)$ by making $k=0$ in this formula, and substituting this into (20), we have

$$u(t)=u(0)-K_e{\displaystyle {\int }_0^{t}e(\sigma )}d\sigma -K_x[x(t)-x(0)]-K_{x_m}[x_m(t)-x_m(0)]-R^{-1}{\tilde{B}}^T{\displaystyle {\int }_0^{t}g(s)}ds,$$

(21)

And

$$\begin{array}{ll}{\displaystyle {\int }_0^{t}g(s)}ds& ={\displaystyle {\int }_0^t{\displaystyle {\int }_0^{l_f}\left[\exp (\sigma {{\widehat{A}}_c}^T)P\widehat{G}\dot{f}(s+\sigma )\right]d\sigma }}ds\\ & +{\displaystyle {\int }_0^t{\displaystyle {\int }_0^{l_r}\left[\exp (\sigma {{\widehat{A}}_c}^T)P{\widehat{B}}_m{\dot{u}}_m(s+\sigma )\right]d\sigma }ds}\\ & ={\displaystyle {\int }_0^{l_f}\left\{\exp (\sigma {{\widehat{A}}_c}^T)P\widehat{G}\left[{\displaystyle {\int }_0^t\dot{f}(s+\sigma )ds}\right]\right\}}d\sigma \\ & +{\displaystyle {\int }_0^{l_r}\left\{\exp (\sigma {{\widehat{A}}_c}^T)P{\widehat{B}}_m\left[{\displaystyle {\int }_0^t{\dot{u}}_m(s+\sigma )ds}\right]\right\}}d\sigma \\ & ={\displaystyle {\int }_0^{l_f}\left[\exp (\sigma {{\widehat{A}}_c}^T)P\tilde{W}\left[f(t+\sigma )-f(\sigma )\right]\right]}d\sigma \\ & +{\displaystyle {\int }_0^{l_r}\left[\exp (\sigma {{\widehat{A}}_c}^T)P{\widehat{B}}_m\left[u_m(t+\sigma )-u_m(\sigma )\right]\right]}d\sigma .\end{array}$$

The conclusion is proved by substituting the above formula into (21).

Note that the control effect can be improved by selecting the initial values of $x(0)$, $x_m(0)$ and $u(0)$. □

Remark 4.

In (18), $-K_e{\displaystyle {\int }_0^{t}e(\sigma )}d\sigma$ shows the integrator; $-K_{x}x(t)$ indicates the state feedback of (1); $-K_{x_m}{x}_m(t)$ represents the state feedback of (2); and $f_1(t)$ and $f_2(t)$ express the preview compensation of the reference input signal $u_m(t)$ and fault signal $f(t)$, respectively.

Define the controller given by Equation (18) as a model-following preview controller. It also can be called a fault-tolerant preview controller in the fault-tolerant control problem.

6. Numerical Simulation

When the controller given in (18) is introduced into the original descriptor system (1), we obtain the closed-loop system

$$\left\{\begin{array}{cc}\hfill E\dot{x}(t)& =(A-B{K}_x)x(t)+B\phi (t)+Gf(t),\hfill \\ \hfill y(t)& =Cx(t),\hfill \\ \hfill \phi (t)& =-K_e{\displaystyle {\int }_0^{t}e(\sigma )}d\sigma -f_1(t)-f_2(t)-K_{x_m}{x}_m(t)+u(0)+K_{x}x(0)+K_{x_m}{x}_m(0),\hfill \end{array}\right.$$

(22)

Using the method given by [30], system (22) is discretized to obtain the iteration format

$$\left\{\begin{array}{l}x((k+1)T)=\overline{E}\left\{\overline{A}x(kT)+\frac{T}{2}B\left[\phi (kT)+\phi ((k+1)T)\right]+\frac{T}{2}G\left[f(kT)+f((k+1)T)\right]\right\},\\ x_m((k+1)T)=(T{A}_m+I)x_m(kT)+T{B}_m{u}_m(kT),\\ y(kT)=Cx(kT),\\ y_m(kT)=C_m{x}_m(kT),\\ e(kT)=y(kT)-y_m(kT),\\ \phi (kT)=-K_{e}T{\displaystyle \sum _{i=0}^{k-1}e\left(iT\right)-f_1(kT)-f_2(kT)-K_{x_m}{x}_m\left(kT\right)+u(0)+K_{x}x(0)+K_{x_m}{x}_m(0),}\\ f_1(kT)=R^{-1}{\widehat{B}}^{T}T{\displaystyle \sum _{j=0}^{[l_r/T]-1}\left\{\exp (\sigma {{\widehat{A}}_c}^T)P{\widehat{B}}_m\left[u_m(kT+jT)-u_m(jT)\right]\right\},}\\ f_2(kT)=R^{-1}{\widehat{B}}^{T}T{\displaystyle \sum _{j=0}^{[l_f/T]-1}\left\{\exp (\sigma {{\widehat{A}}_c}^T)P\widehat{G}\left[f(kT+jT)-f(jT)\right]\right\}},\end{array}\right.$$

where

$\overline{E}={\left[E-\frac{T}{2}(A-B{K}_x)\right]}^{-1}$, $\overline{A}=E+\frac{T}{2}(A-B{K}_x)$, T is the sampling period.

Consider the electrical circuit system with actuator failures [31], where the inductance is $1\mathrm{H}$, the capacitance is $1\mathrm{F}$, and the resistance is $1\Omega$.

$$\left\{\begin{array}{cc}\hfill E\dot{x}(t)& =Ax(t)+Bu(t)+Gf(t),\hfill \\ \hfill y(t)& =Cx(t),\hfill \end{array}\right.$$

(23)

where $E=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]$, $A=\left[\begin{array}{cccc}0& 1& 0& 0\\ 1& 0& 0& 0\\ -1& 0& 0& 1\\ 0& 1& 1& 1\end{array}\right]$, $B=\left[\begin{array}{c}0\\ 0\\ 0\\ -1\end{array}\right]$, $G=\left[\begin{array}{c}0\\ 0\\ 0\\ 0.5\end{array}\right]$, $C=\left[\begin{array}{cccc}0& 0& 1& 0\end{array}\right]$.

In this model, the components of the state vector $x(t)={\left[\begin{array}{cccc}{x}_1(t)& x_2(t)& x_3(t)& x_4(t)\end{array}\right]}^T$ represent the current in the circuit, the voltage of the resistance, the voltage of the inductance and the voltage of the capacitance, respectively. Input vector $u(t)$ represents the voltage source. $y(t)$ is the voltage of the capacitance, which can be measured in a physical sense, so it is defined as the output vector of the system. $f(t)$ is a known fault vector

$$f(t)=\left\{\begin{array}{cc}0,& 0\le t\le 15\\ 8,& t>15\end{array}\right.$$

Select reference model (2) as

$$A_m=\left[\begin{array}{cc}-1& 0.2\\ 0& -0.7\end{array}\right],B_m=\left[\begin{array}{c}1\\ 0\end{array}\right],C_m=[\begin{array}{cc}1& 1\end{array}],$$

where the reference input is a step signal

$$u_m(t)=\left\{\begin{array}{cc}0,& 0\le t\le 2\\ 10,& t>2\end{array}\right.$$

Note that output vector $y_m(t)$ of (2) is the ideal value of the voltage of the capacitor.

According to the structure of matrix $E$ in system (22), it should be taken as

$$Q_1=I,P_1=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right].$$

After the restricted equivalent transformation is carried out, system (6) is obtained, where

$$\begin{array}{l}{\overline{A}}_{11}=\left[\begin{array}{cc}0& 0\\ 1& 0\end{array}\right],{\overline{A}}_{12}=\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right],{\overline{A}}_{21}=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right],{\overline{A}}_{21}=\left[\begin{array}{cc}0& 1\\ 1& 1\end{array}\right],\\ {\overline{B}}_2=\left[\begin{array}{c}0\\ -1\end{array}\right],{\overline{G}}_2=\left[\begin{array}{c}0\\ 0.5\end{array}\right],C_1=\left[\begin{array}{cc}0& 1\end{array}\right],\\ {\overline{x}}_1(t)=\left[\begin{array}{c}{x}_1(t)\\ x_3(t)\end{array}\right],{\overline{x}}_2(t)=\left[\begin{array}{c}{x}_2(t)\\ x_4(t)\end{array}\right].\end{array}$$

The corresponding matrices of the augmented system (12) are

$$\begin{array}{l}\widehat{A}=\left[\begin{array}{ccc}0& {\overline{C}}_1& -C_m\\ 0& {\overline{A}}_{11}-{\overline{A}}_{12}{{\overline{A}}_{22}}^{-1}{\overline{A}}_{21}& 0\\ 0& 0& A_m\end{array}\right]=\left[\begin{array}{ccccc}0& 0& 1& -1& -1\\ 0& -1& -1& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 0& -1& 0.2\\ 0& 0& 0& 0& -0.7\end{array}\right],\\ \widehat{B}=\left[\begin{array}{c}0\\ -{\overline{A}}_{12}{{\overline{A}}_{22}}^{-1}{\overline{B}}_2\\ 0\end{array}\right]=\left[\begin{array}{c}0\\ 1\\ 0\\ 0\\ 0\end{array}\right],{\widehat{B}}_m=\left[\begin{array}{c}0\\ 0\\ B_m\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ 1\\ 0\end{array}\right]\widehat{G}=\left[\begin{array}{c}0\\ -{\overline{A}}_{12}{{\overline{A}}_{22}}^{-1}{\overline{G}}_2\\ 0\end{array}\right]=\left[\begin{array}{c}0\\ -0.5\\ 0\\ 0\\ 0\end{array}\right],\\ \widehat{C}=\left[\begin{array}{ccccc}1& 0& 0& 0& 0\end{array}\right].\end{array}$$

Obviously, this example satisfies all the conditions of Assumptions 1–5. The weight matrices of performance index function (4) are taken as $Q_e=3$, $R=1$. The solution of (15) and the gain matrices in (18) are

$$\begin{array}{l}P=\left[\begin{array}{ccccc}5.0958& 1.7321& 3.8278& -2.7548& -3.4797\\ 1.7321& 1.2100& 1.9421& -1.3515& -1.8539\\ 3.8278& 1.9421& 3.7699& -2.6064& -3.3924\\ -2.7548& -1.3515& -2.6064& 1.8415& 2.4102\\ -3.4797& -1.8539& -3.3924& 2.4102& 3.2048\end{array}\right],\\ K_e=1.7321,\\ K_{{\overline{x}}_1}=\left[\begin{array}{cc}1.2100& 1.9421\end{array}\right],\\ K_x=\left[\begin{array}{cccc}1.2100& 0& 1.9421& 0\end{array}\right],\\ K_{x_m}=\left[\begin{array}{cc}-1.3515& -1.8539\end{array}\right],\end{array}$$

where $P$ is symmetric positive definite.

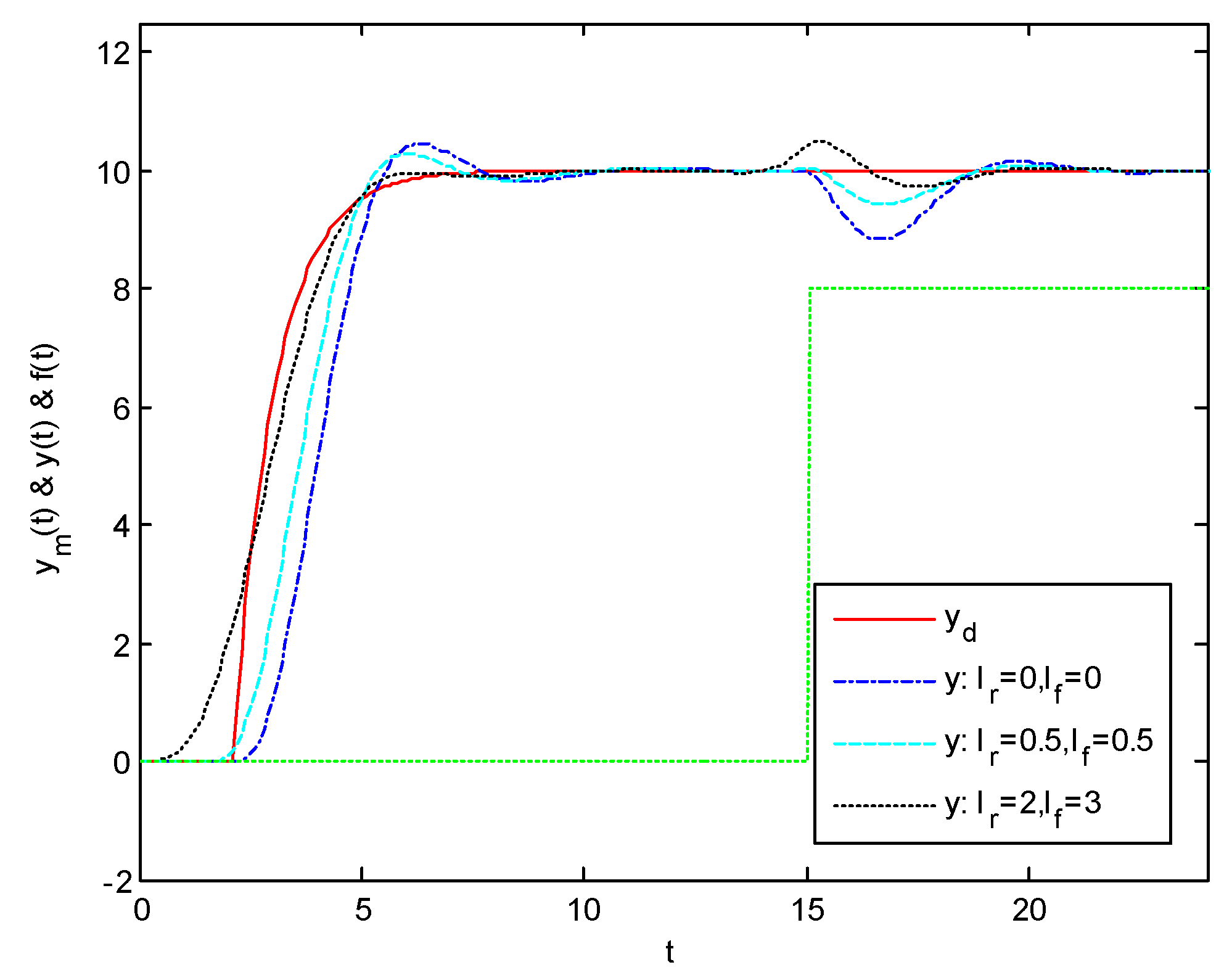
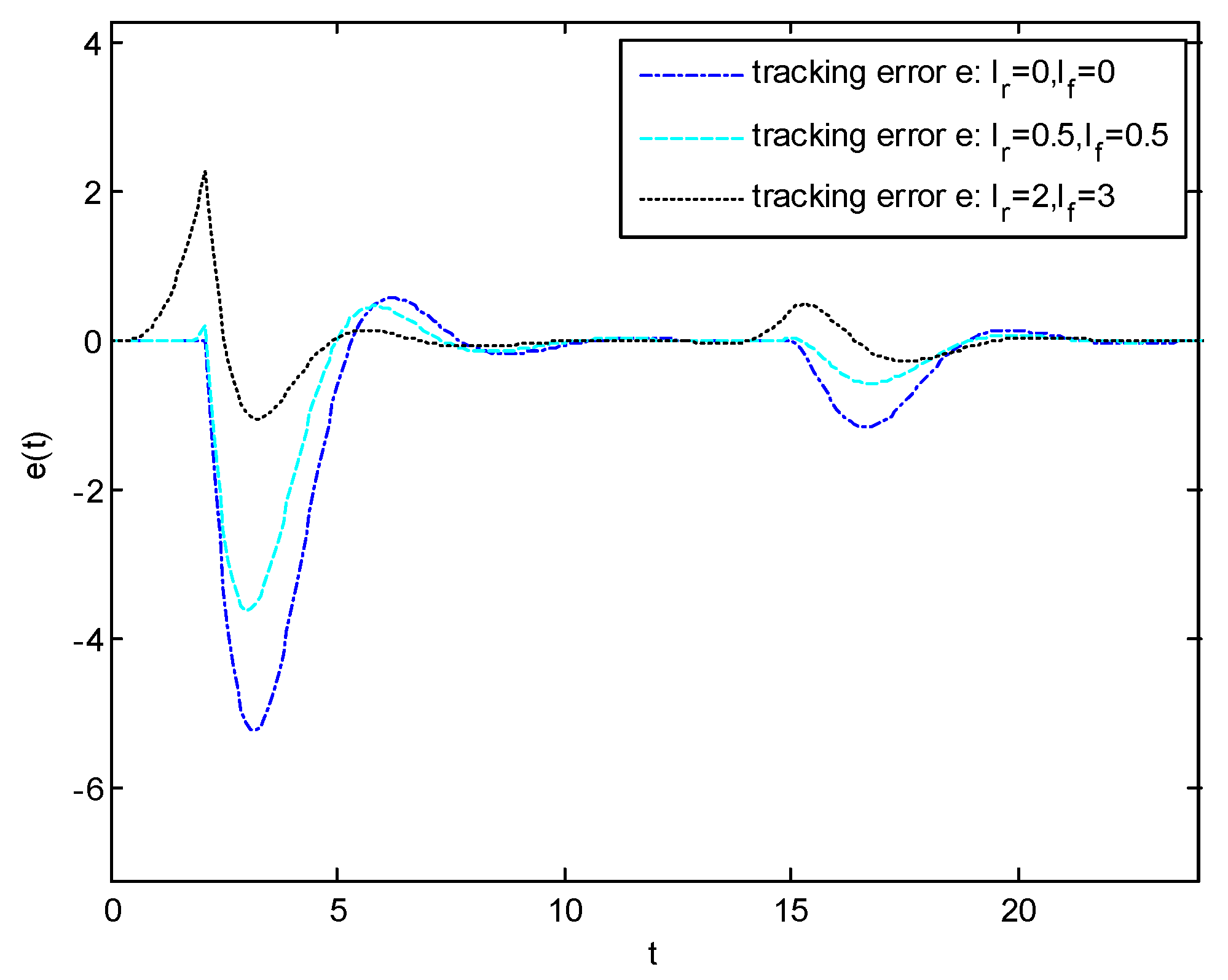
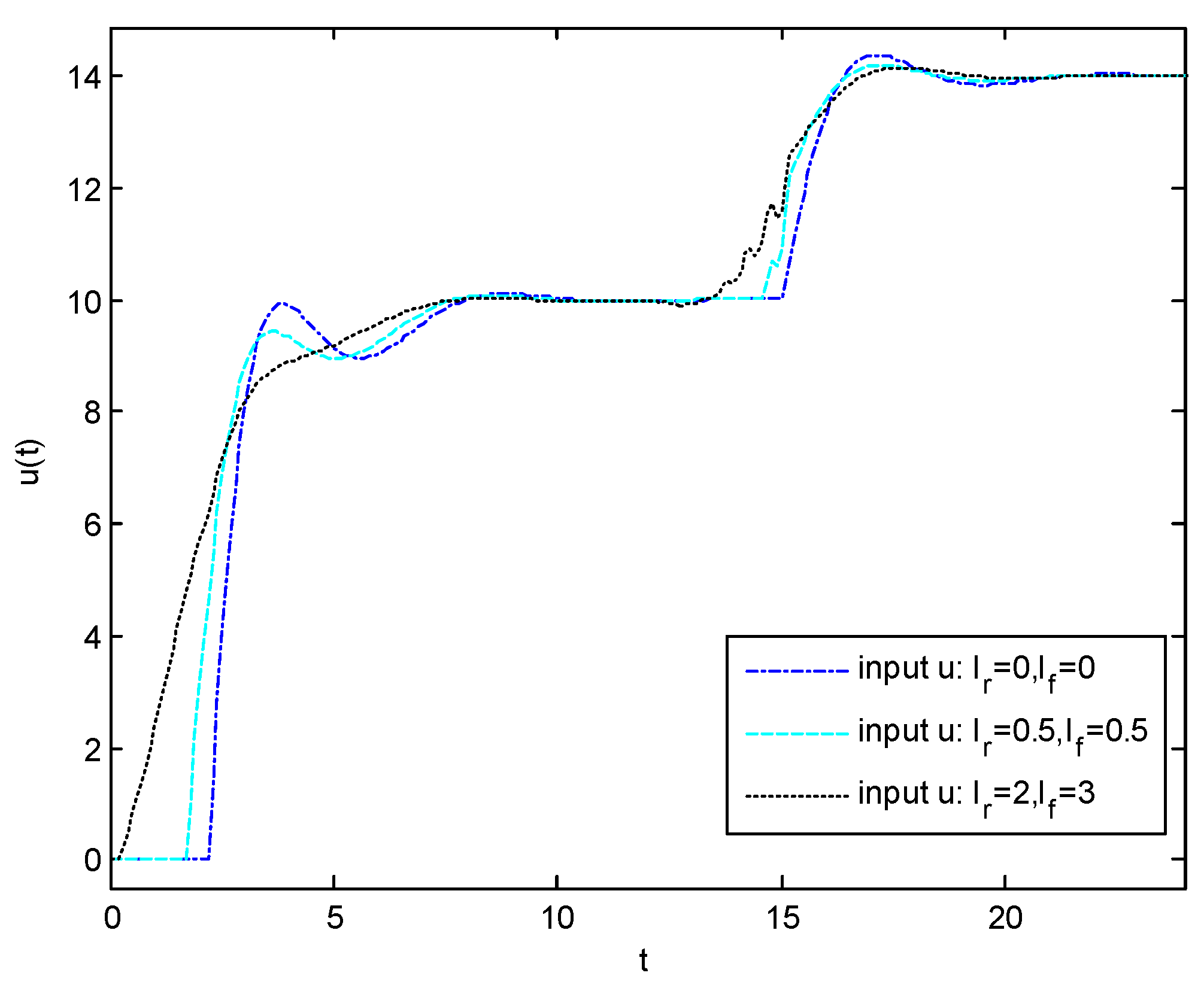
The initial conditions are chosen to be $u(0)=0$, $x(0)={\left[\begin{array}{cccc}0& 0& 0& 0\end{array}\right]}^T$, and $x_m(0)={\left[\begin{array}{cc}0& 0\end{array}\right]}^T$, and the sampling period is $T=0.1$. Figure 1, Figure 2 and Figure 3, respectively, stand for the output response, output tracking error, and the voltage source of the electrical circuit system when the reference input signal and the fault signal are previewable. It can be seen that the preview compensations can effectively suppress the adverse effects caused by fault signals and accelerate the response speed of the system output.

According to calculations, the overshoot of the closed-loop system with different previewable lengths is as follows: ① when $l_r=0$ $\mathrm{s}$, $l_f=0$ $\mathrm{s}$, the overshoot is $12.27\%$; ② when $l_r=0.5$ $\mathrm{s}$, $l_f=0.5$ $\mathrm{s}$, the overshoot is $6.00\%$; and ③ when $l_r=2$ $\mathrm{s}$, $l_f=3$ $\mathrm{s}$, the overshoot is $3.17\%$. Therefore, the longer the previewable length, the smaller the overshoot.

Figure 4, Figure 5 and Figure 6 demonstrate the output response, the tracking error, and the voltage source of the electrical circuit system without fault, respectively. The simulation results reveal that the tracking effect of the capacitance voltage to the ideal value is still remarkable under the reference input preview compensation. When the controlled system does not malfunction, the controller proposed in this article is still valid.

7. Conclusions

Based on the theory of preview control and the model-following control theory of fault-tolerant control, a model-following preview controller for a class of linear continuous-time descriptor systems with actuator failures is designed in this paper. Firstly, the controlled system is transformed into a normal control system through a restricted equivalent transformation. By constructing an augmented system, the model-following problem is converted into the optimal preview control problem for the augmented system. We obtain the required controller for the original descriptor system through the preview control method. Finally, the result is applied to an electrical circuit system with actuator failures, and numerical simulation is carried out to illustrate the effectiveness of the result.

In the future, we consider extending the current results to descriptor systems with stochastic [19,32], multiple input delays, and nonlinearity, which is more challenging.