Fixed-Time Event-Triggered Control of Nonholonomic Mobile Robots with Uncertain Dynamics and Preassigned Transient Performance
Abstract
1. Introduction
2. Problem Formulation and Preliminaries
2.1. Preliminaries
2.2. Universal Barrier Function
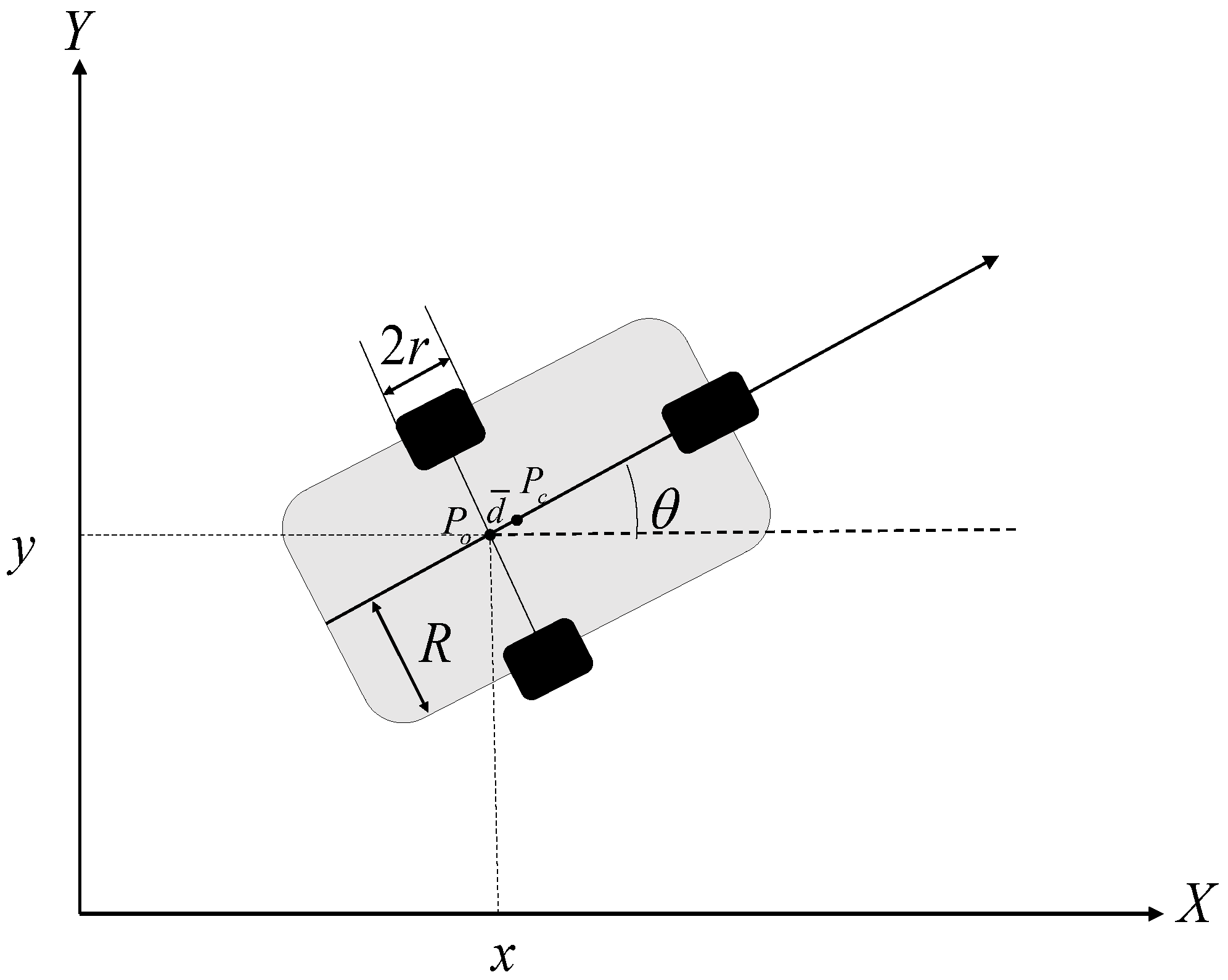
2.3. Robot Dynamics
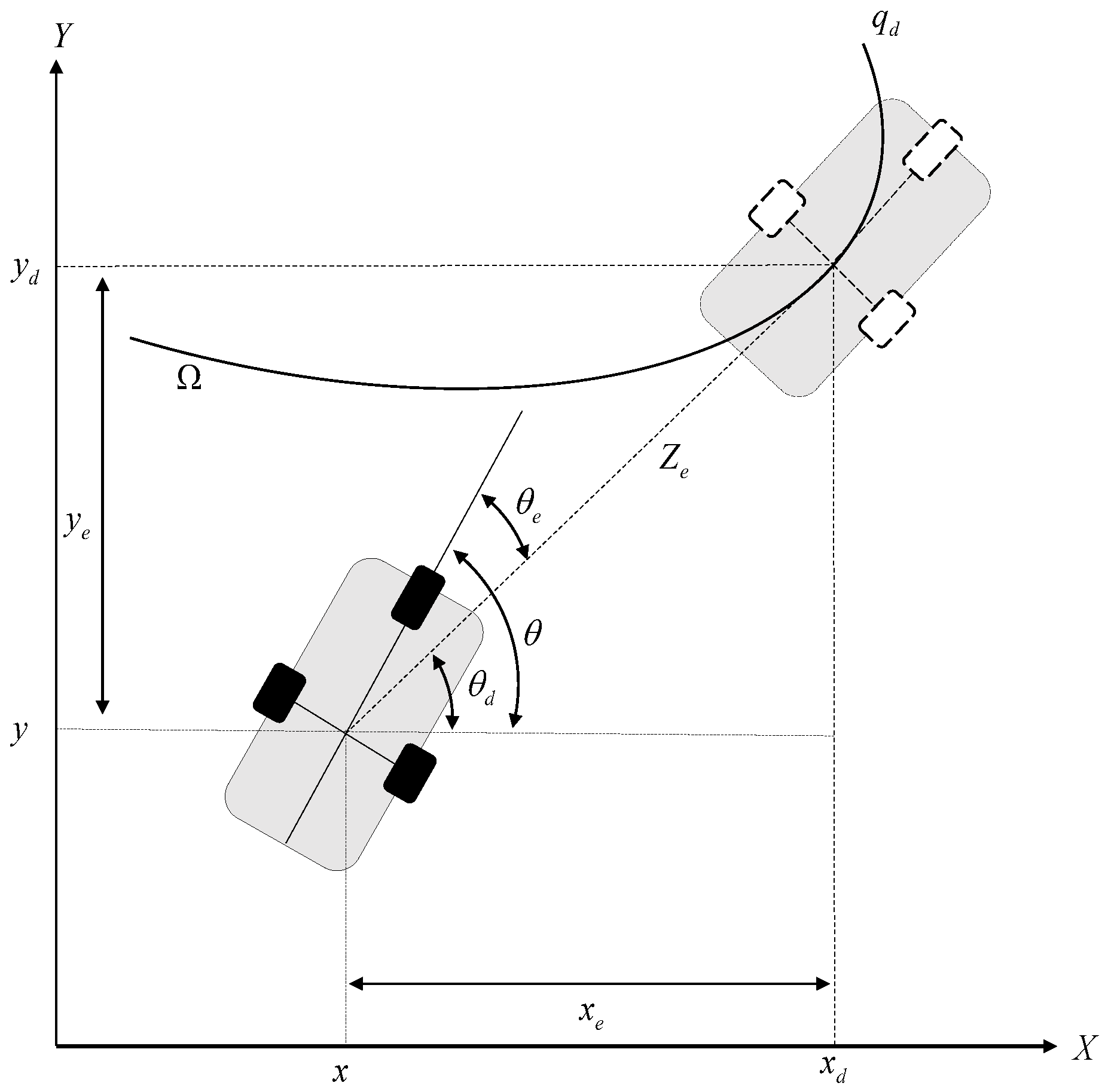
2.4. Control Objective
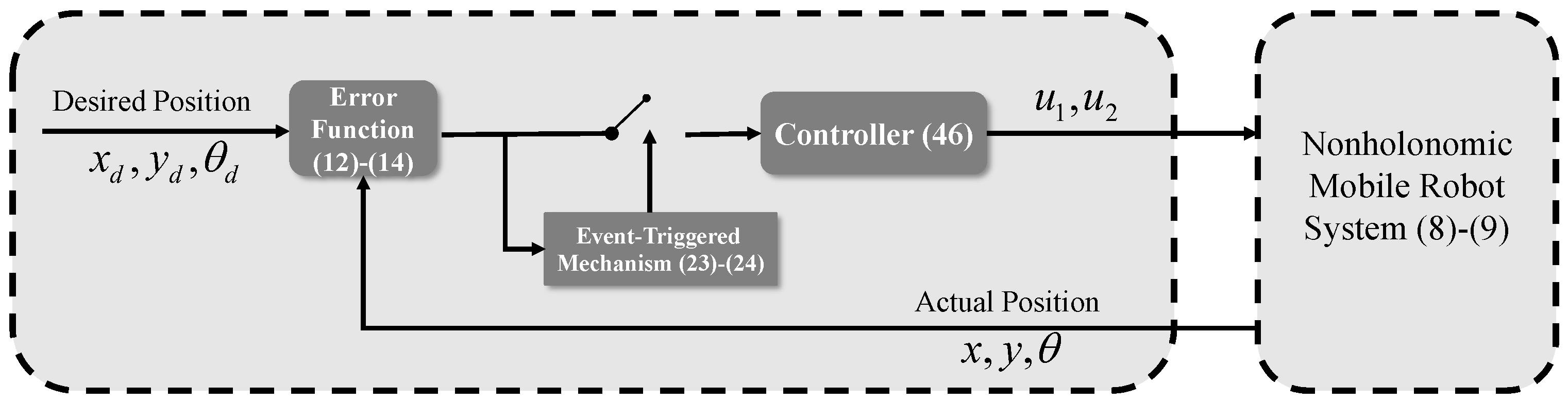
2.5. Time-Varying Relative Threshold Event-Triggered
3. Control Design and Stability Analysis
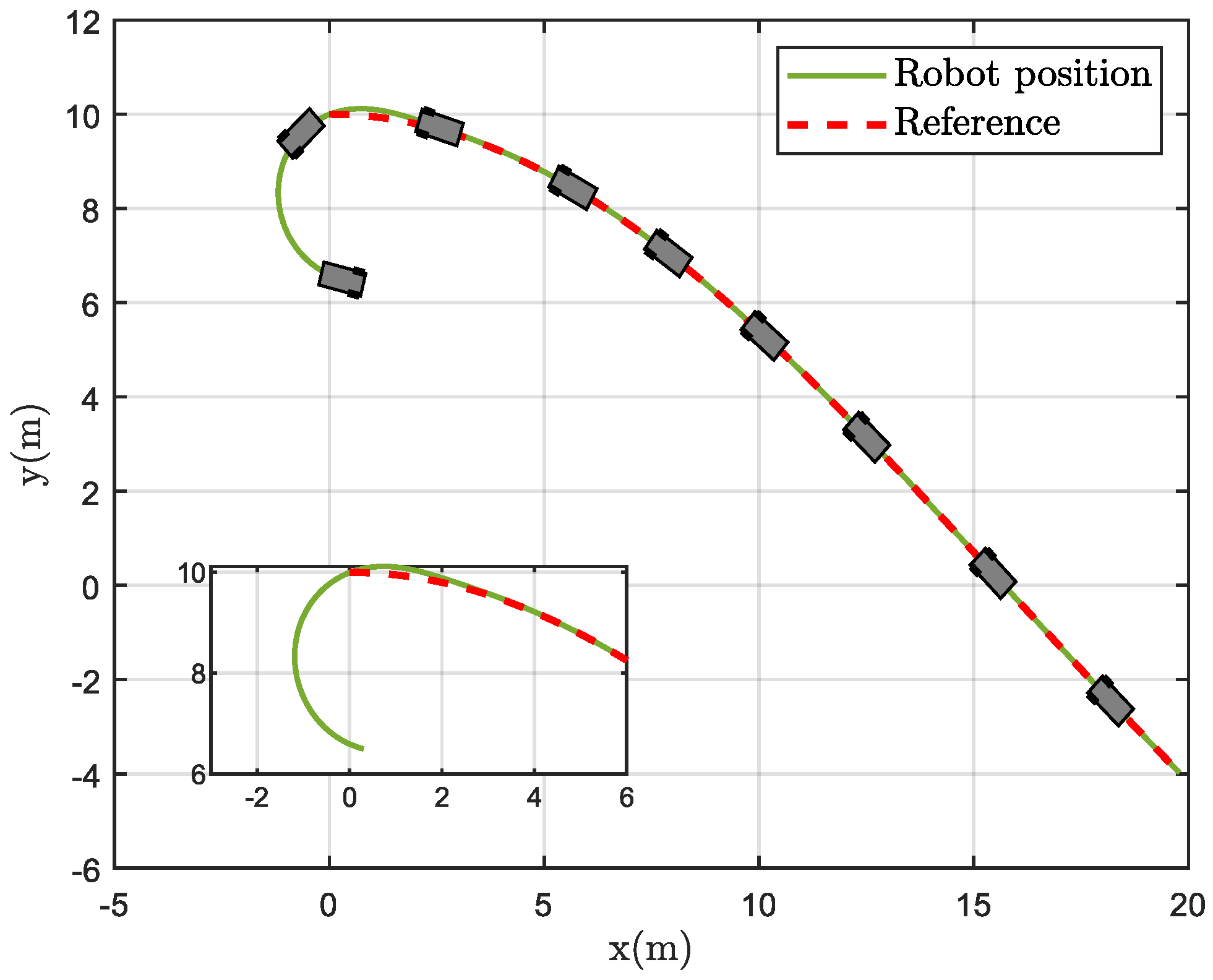
4. Simulations
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rubio, F.; Valero, F.; Llopis-Albert, C. A review of mobile robots: Concepts, methods, theoretical framework, and applications. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419839596. [Google Scholar] [CrossRef]
- Li, Y.; Cai, Y.; Wang, Y.; Li, W.; Wang, G. Simultaneous tracking and stabilization of nonholonomic wheeled mobile robots under constrained velocity and torque. Mathematics 2024, 12, 1985. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, S.; Wu, Y. New stabilization controller of state-constrained nonholonomic systems with disturbances: Theory and experiment. IEEE Trans. Ind. Electron. 2022, 70, 669–677. [Google Scholar] [CrossRef]
- Hou, D.; Gao, F.; Huang, J.; Wu, Y. A switching-based state-scaling design for prescribed-time stabilization of nonholonomic systems with actuator dead-zones. Aerosp. Sci. Technol. 2021, 118, 106986. [Google Scholar] [CrossRef]
- Tian, Y.P.; Li, S. Exponential stabilization of nonholonomic dynamic systems by smooth time-varying control. Automatica 2002, 38, 1139–1146. [Google Scholar] [CrossRef]
- Hespanha, J.P.; Morse, A.S. Stabilization of nonholonomic integrators via logic-based switching. Automatica 1999, 35, 385–393. [Google Scholar] [CrossRef]
- De Wit, C.C.; Siciliano, B.; Bastin, G. Theory of Robot Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Jiang, Z.P.; Nijmeijer, H. Tracking control of mobile robots: A case study in backstepping. Automatica 1997, 33, 1393–1399. [Google Scholar]
- Cardona, M.; Serrano, F.E. Dynamic output feedback and neural network control of a non-Holonomic mobile robot. Sensors 2023, 23, 6875. [Google Scholar] [CrossRef]
- Ou, M.; Sun, H.; Zhang, Z.; Gu, S. Fixed-time trajectory tracking control for nonholonomic mobile robot based on visual servoing. Nonlinear Dyn. 2022, 108, 251–263. [Google Scholar] [CrossRef]
- Lin, L.; Xu, Z.; Zheng, J. Predefined time active disturbance rejection for nonholonomic mobile robots. Mathematics 2023, 11, 2704. [Google Scholar] [CrossRef]
- Meng, H.; Zhang, J.; Li, S. Dual-mode robust model predictive control for the tracking control of nonholonomic mobile robot. Int. J. Robust Nonlinear Control. 2023, 33, 3627–3639. [Google Scholar] [CrossRef]
- Wang, G.; Wang, C.; Du, Q.; Li, L.; Dong, W. Distributed cooperative control of multiple nonholonomic mobile robots. J. Intell. Robot. Syst. 2016, 83, 525–541. [Google Scholar] [CrossRef]
- Wang, G. Consensus algorithm for multiagent systems with nonuniform communication delays and its application to nonholonomic robot rendezvous. IEEE Trans. Control. Netw. Syst. 2022, 10, 1496–1507. [Google Scholar] [CrossRef]
- Wang, W.; Han, Z.; Liu, K.; Lü, J. Distributed adaptive resilient formation control of uncertain nonholonomic mobile robots under deception attacks. IEEE Trans. Circuits Syst. Regul. Pap. 2021, 68, 3822–3835. [Google Scholar] [CrossRef]
- Shi, S.; Yu, X.; Khoo, S. Robust finite-time tracking control of nonholonomic mobile robots without velocity measurements. Int. J. Control. 2016, 89, 411–423. [Google Scholar] [CrossRef]
- Jin, X.; Dai, S.L.; Liang, J.; Guo, D. Adaptive path-following control of an autonomous vehicle with path-dependent constraint requirements. In Proceedings of the 2021 60th IEEE Conference on Decision and Control (CDC), Austin, TX, USA, 13–17 December 2021; pp. 5753–5758. [Google Scholar]
- Huang, X.; Song, Y.; Lai, J. Neuro-adaptive control with given performance specifications for strict feedback systems under full-state constraints. IEEE Trans. Neural Networks Learn. Syst. 2018, 30, 25–34. [Google Scholar] [CrossRef]
- Fachri, R.K.; Romdlony, M.Z.; Rosa, M.R. Multiple waypoint navigation for mobile robot using control Lyapunov-barrier function (clbf). In Proceedings of the 2022 IEEE International Conference on Cybernetics and Computational Intelligence (CyberneticsCom), Malang, Indonesia, 16–18 June 2022; pp. 230–235. [Google Scholar]
- Kong, L.; Yu, X.; Zhang, S. Neuro-learning-based adaptive control for state-constrained strict-feedback systems with unknown control direction. ISA Trans. 2021, 112, 12–22. [Google Scholar] [CrossRef]
- Wang, C.; Wang, J.; Zhang, C.; Du, Y.; Liu, Z.; Chen, C.P. Fixed-time event-triggered consensus tracking control for uncertain nonlinear multiagent systems with dead-zone constraint. Int. J. Robust Nonlinear Control. 2023, 33, 6151–6170. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.; Lu, R.; Zuo, Z.; Li, X. An overview of finite/fixed-time control and its application in engineering systems. IEEE/CAA J. Autom. Sin. 2022, 9, 2106–2120. [Google Scholar] [CrossRef]
- Wang, Y.; Song, Y. Leader-following control of high-order multi-agent systems under directed graphs: Pre-specified finite time approach. Automatica 2018, 87, 113–120. [Google Scholar] [CrossRef]
- Tran, D.; Yucelen, T. Finite-time control of perturbed dynamical systems based on a generalized time transformation approach. Syst. Control. Lett. 2020, 136, 104605. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control. Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Li, H.; Li, C.; Huang, T.; Ouyang, D. Fixed-time stability and stabilization of impulsive dynamical systems. J. Frankl. Inst. 2017, 354, 8626–8644. [Google Scholar] [CrossRef]
- Sharifi, A.; Pourgholi, M. Fixed-time bipartite consensus of nonlinear multi-agent systems using event-triggered control design. J. Frankl. Inst. 2021, 358, 9178–9198. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Yu, Y.; Sun, C. Fixed-time leader–follower consensus of networked nonlinear systems via event/self-triggered control. IEEE Trans. Neural Networks Learn. Syst. 2020, 31, 5029–5037. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, G.; Li, Y.; Li, F.; Wang, C. Distributed event-triggered output feedback control for consensus in higher-order nonlinear multi-agent systems. In Proceedings of the 2023 42nd Chinese Control Conference (CCC), Tianjin, China, 24–26 July 2023; pp. 6057–6062. [Google Scholar]
- Dimarogonas, D.V.; Frazzoli, E.; Johansson, K.H. Distributed event-triggered control for multi-agent systems. IEEE Trans. Autom. Control. 2011, 57, 1291–1297. [Google Scholar] [CrossRef]
- Ding, L.; Han, Q.L.; Ge, X.; Zhang, X.M. An overview of recent advances in event-triggered consensus of multiagent systems. IEEE Trans. Cybern. 2017, 48, 1110–1123. [Google Scholar] [CrossRef]
- Al Issa, S.; Kar, I. Design and implementation of event-triggered adaptive controller for commercial mobile robots subject to input delays and limited communications. Control. Eng. Pract. 2021, 114, 104865. [Google Scholar] [CrossRef]
- Cheng, G.; Kong, L.; Niu, W.; Wu, Y.; Mughal, M.A. Fixed-time event-triggered control for a building-like structure with prescribed performance. IEEE Trans. Syst. Man, Cybern. Syst. 2024, 54, 2711–2722. [Google Scholar] [CrossRef]
- Zhu, Z.; Xia, Y.; Fu, M. Attitude stabilization of rigid spacecraft with finite-time convergence. Int. J. Robust Nonlinear Control. 2011, 21, 686–702. [Google Scholar] [CrossRef]
- Jin, X. Adaptive fixed-time control for MIMO nonlinear systems with asymmetric output constraints using universal barrier functions. IEEE Trans. Autom. Control. 2018, 64, 3046–3053. [Google Scholar] [CrossRef]
- Fukao, T.; Nakagawa, H.; Adachi, N. Adaptive tracking control of a nonholonomic mobile robot. IEEE Trans. Robot. Autom. 2000, 16, 609–615. [Google Scholar] [CrossRef]
- Wang, W.; Huang, J.; Wen, C. Prescribed performance bound-based adaptive path-following control of uncertain nonholonomic mobile robots. Int. J. Adapt. Control. Signal Process. 2017, 31, 805–822. [Google Scholar] [CrossRef]
- Do, K.D.; Jiang, Z.P.; Pan, J. Robust adaptive path following of underactuated ships. Automatica 2004, 40, 929–944. [Google Scholar] [CrossRef]
- Trakas, P.S.; Bechlioulis, C.P. Robust adaptive prescribed performance control for unknown nonlinear systems with input amplitude and rate constraints. IEEE Control. Syst. Lett. 2023, 7, 1801–1806. [Google Scholar] [CrossRef]
- Wang, Z.; Lam, H.K.; Guo, Y.; Xiao, B.; Li, Y.; Su, X.; Yeatman, E.M.; Burdet, E. Adaptive event-triggered control for nonlinear systems with asymmetric state constraints: A prescribed-time approach. IEEE Trans. Autom. Control. 2022, 68, 3625–3632. [Google Scholar] [CrossRef]
- Cheng, L.; Hou, Z.G.; Tan, M. Adaptive neural network tracking control for manipulators with uncertain kinematics, dynamics and actuator model. Automatica 2009, 45, 2312–2318. [Google Scholar] [CrossRef]
- Bayat, F.; Najafinia, S.; Aliyari, M. Mobile robots path planning: Electrostatic potential field approach. Expert Syst. Appl. 2018, 100, 68–78. [Google Scholar] [CrossRef]
- Chen, K.; Gu, Y.; Huang, W.; Zhang, Z.; Wang, Z.; Wang, X. Fixed-time adaptive event-triggered guaranteed performance tracking control of nonholonomic mobile robots under asymmetric state constraints. Mathematics 2024, 12, 1471. [Google Scholar] [CrossRef]
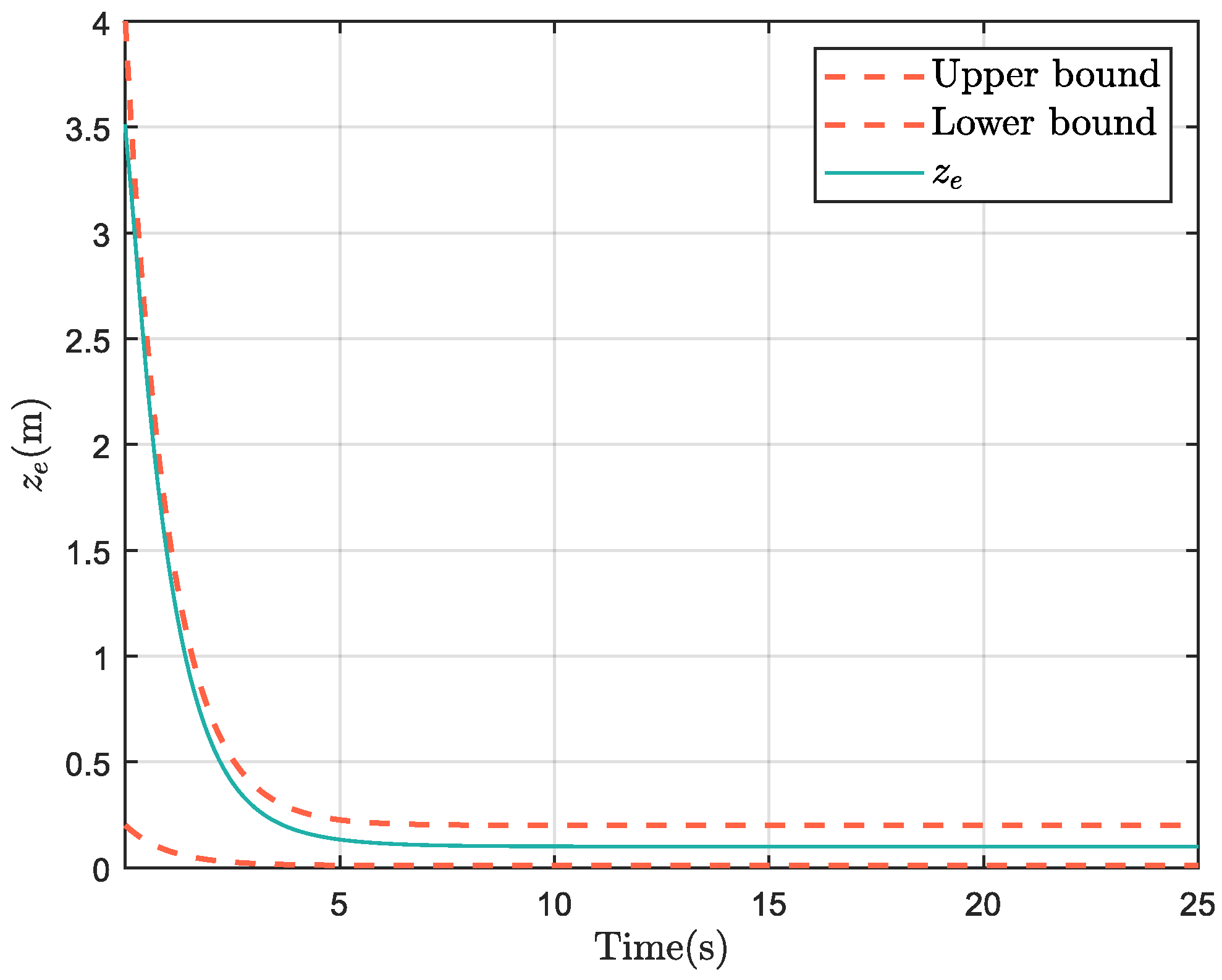
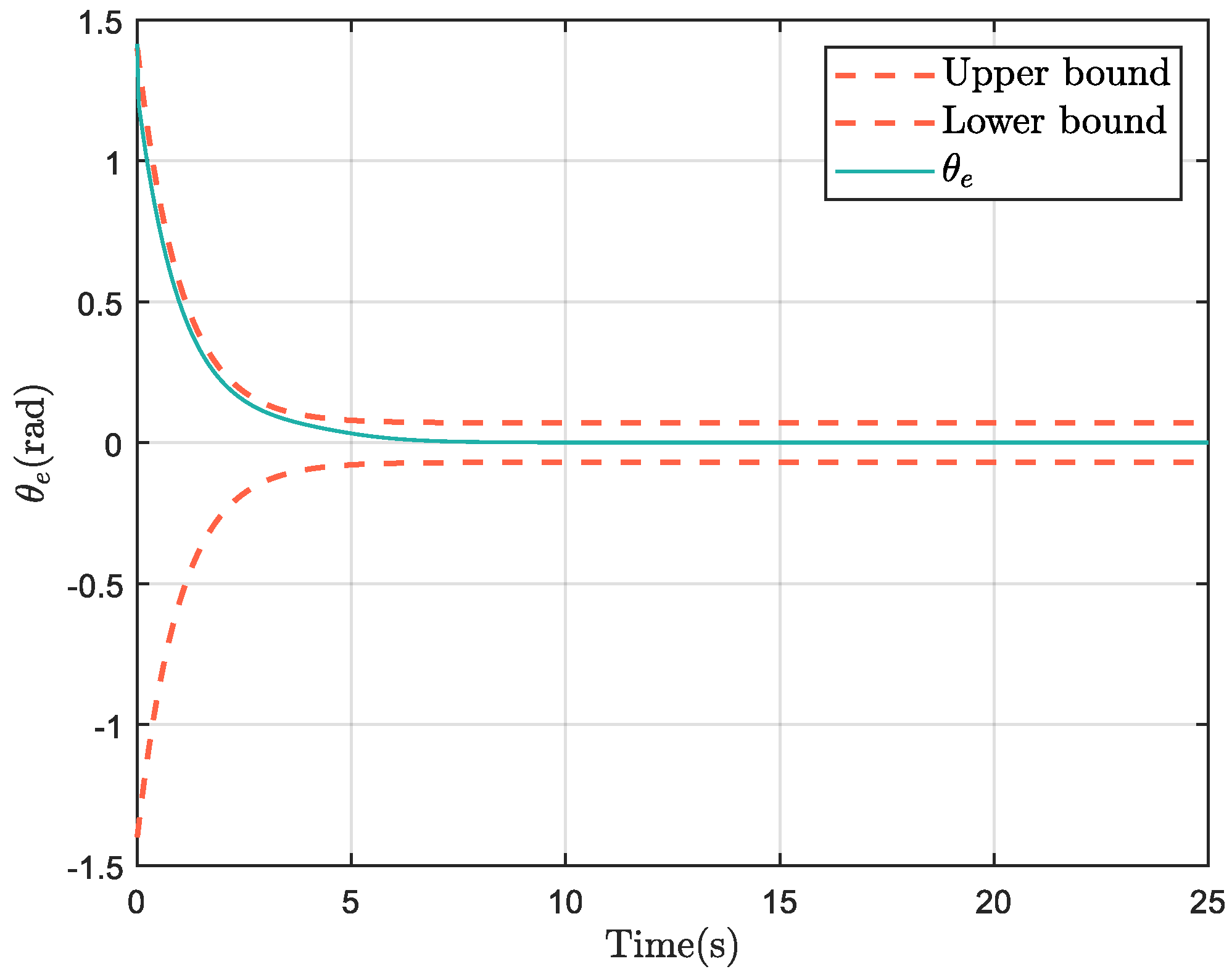
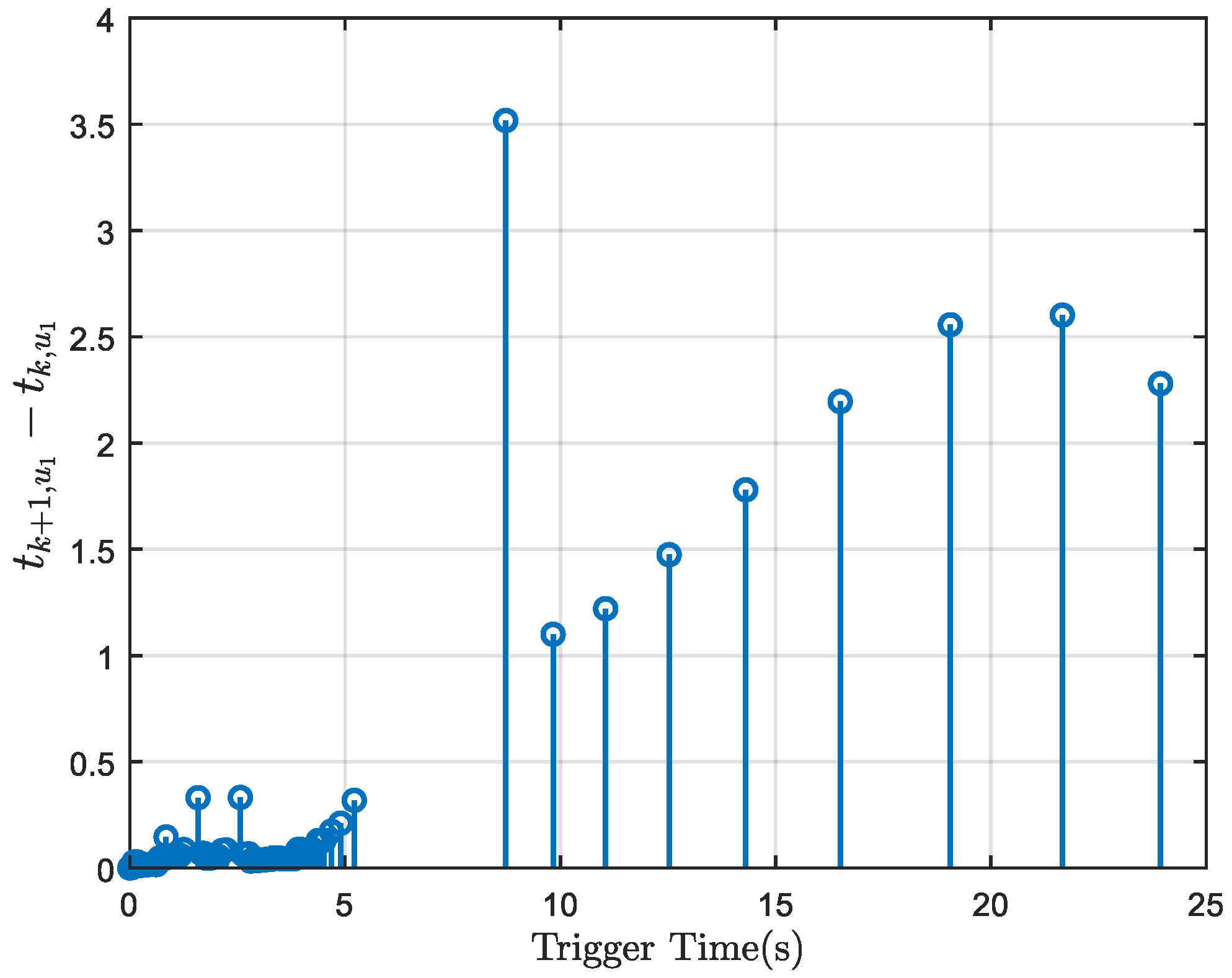
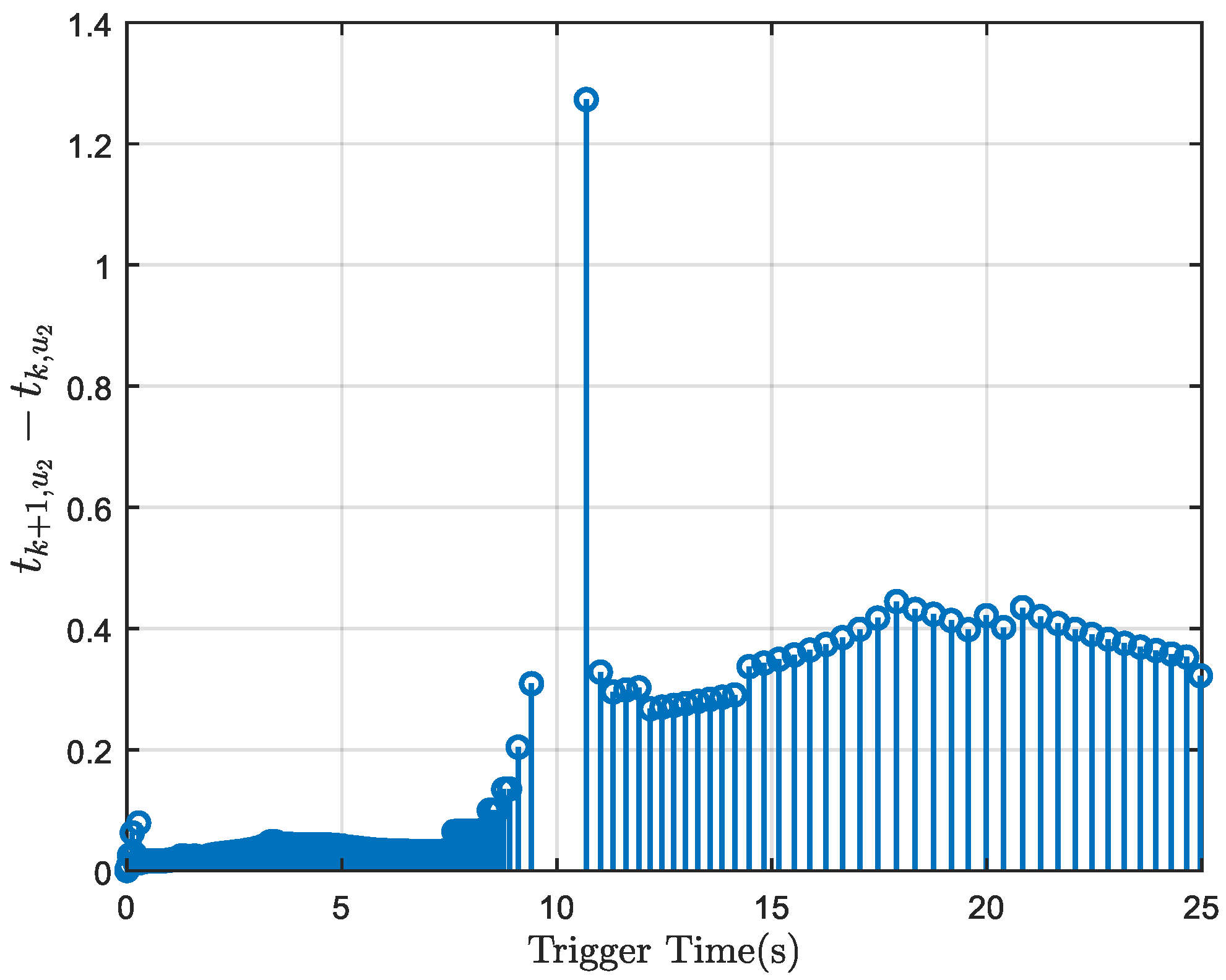
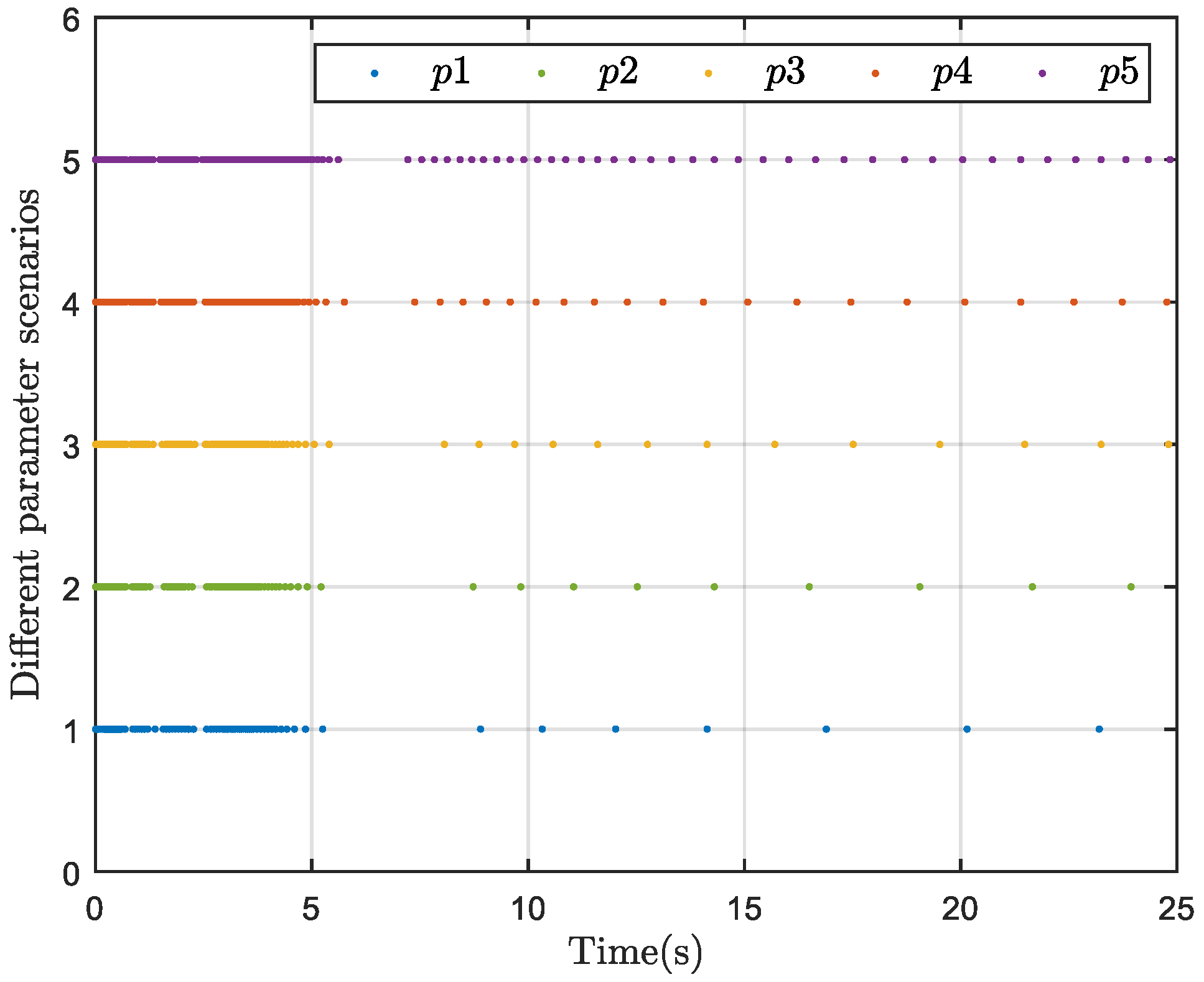
| Parameter | R | r | |||
| Value | 0.75 | 0.3 | 0.15 | 30 | 1 |
| Parameter | |||||
| Value | 15.625 | 0.005 | 0.0025 | 5 | 5 |
| Parameters | |||||
|---|---|---|---|---|---|
| 0.005 | 0.003 | 0.001 | 0.001 | 0.001 | |
| 0.001 | 0.001 | 0.005 | 0.05 | 0.1 |
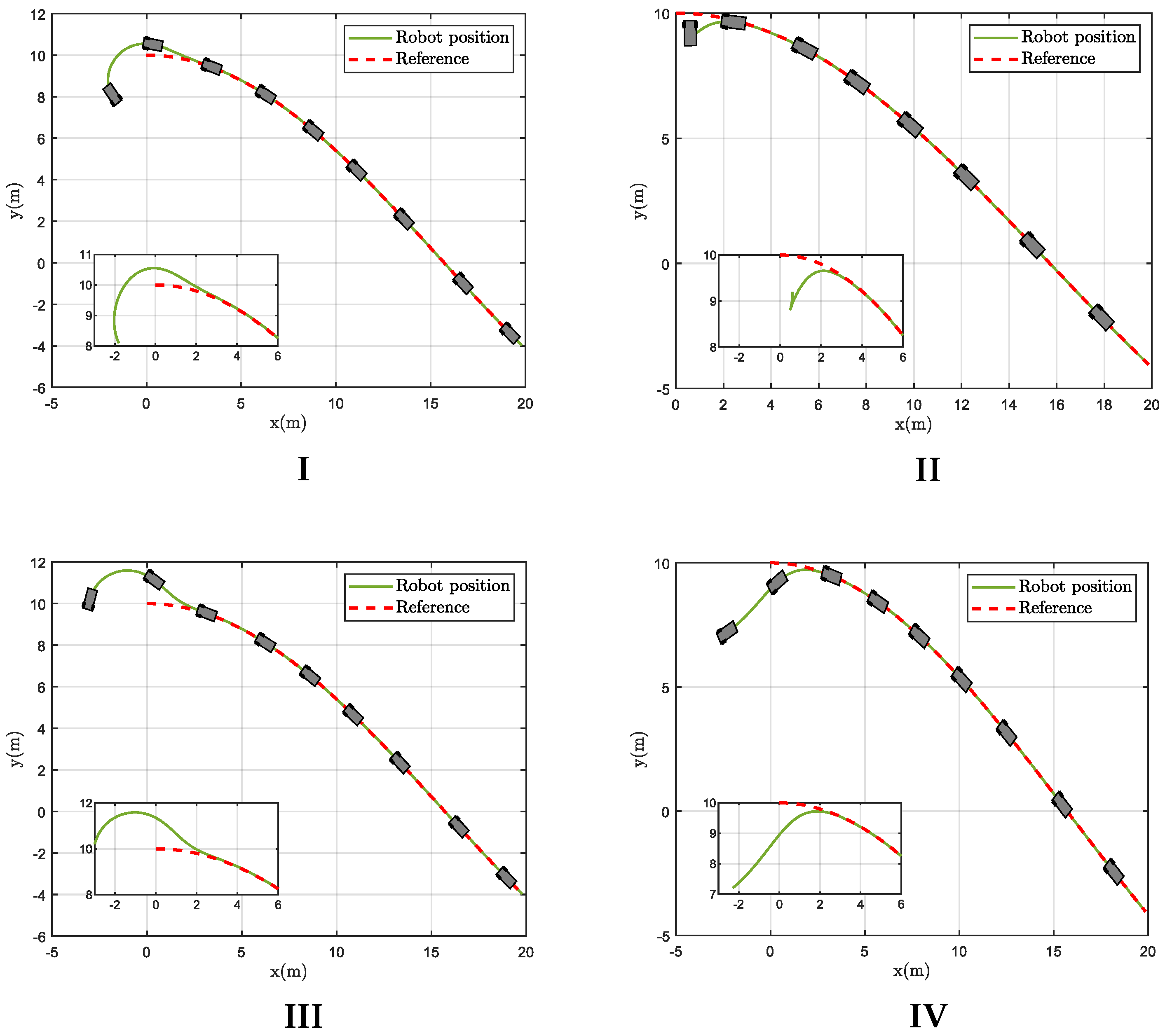
| Case | I | II | III | IV |
|---|---|---|---|---|
| −1.8 | 0.6 | −3.0 | −2.3 | |
| 8.1 | 9.2 | 10.2 | 7.2 | |
| −2.2 | 1.6 | 1.3 | 0.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Ji, Y.; Li, W.; Fang, X. Fixed-Time Event-Triggered Control of Nonholonomic Mobile Robots with Uncertain Dynamics and Preassigned Transient Performance. Mathematics 2024, 12, 3544. https://doi.org/10.3390/math12223544
Wang Y, Ji Y, Li W, Fang X. Fixed-Time Event-Triggered Control of Nonholonomic Mobile Robots with Uncertain Dynamics and Preassigned Transient Performance. Mathematics. 2024; 12(22):3544. https://doi.org/10.3390/math12223544
Chicago/Turabian StyleWang, Yong, Yunfeng Ji, Wei Li, and Xi Fang. 2024. "Fixed-Time Event-Triggered Control of Nonholonomic Mobile Robots with Uncertain Dynamics and Preassigned Transient Performance" Mathematics 12, no. 22: 3544. https://doi.org/10.3390/math12223544
APA StyleWang, Y., Ji, Y., Li, W., & Fang, X. (2024). Fixed-Time Event-Triggered Control of Nonholonomic Mobile Robots with Uncertain Dynamics and Preassigned Transient Performance. Mathematics, 12(22), 3544. https://doi.org/10.3390/math12223544






