Asymptotic and Oscillatory Analysis of Second-Order Differential Equations with Distributed Deviating Arguments

Abstract

This paper focuses on studying the oscillatory properties of a distinctive class of second-order advanced differential equations with distributed deviating arguments in a noncanonical case. Utilizing the Riccati method and the comparison method with first-order equations, in addition to other analytical methods, we have established criteria to test whether the solutions of the studied equation exhibit oscillatory behavior. To verify the validity of the results we obtained and determine their applicability, we present some examples to confirm the strength and accuracy of our proposed criteria.

1. Introduction

The purpose of this research is to investigate the oscillatory behavior of the solutions of the following second-order advanced differential equations:

$${\left(r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }\right)}^{\prime }+{\int }_{k_1}^{k_2}\mu \left(\top ,\varsigma \right)P^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma =0,\top \ge {\top }_0,$$

(1)

where $\alpha$ represents a fraction of two positive odd numbers, and

A1 

$r\in C^1\left([{\top }_0,\infty ),\left(0,\infty \right)\right),$

$${\int }_{{\top }_0}^{\top }{r}^{{\displaystyle \frac{-1}{\alpha }}}\left(\varsigma \right)\mathrm{d}\varsigma <\infty ,$$

(2)

$\mu \in C\left([{\top }_0,\infty )\times \left(k_1,k_2\right),\left(0,\infty \right)\right),$ $\mu \left(\top ,\varsigma \right)\ge 0$ and does not vanish identically;

A2 

$l\in C^1\left([{\top }_0,\infty )\times \left(k_1,k_2\right),\left(0,\infty \right)\right),$ $l\left(\top ,\varsigma \right)\ge \top ,$ and has nonnegative partial derivatives.

By a solution $P\left(\top \right)$ of (1), we mean a real-valued function $P\in C\left([{\top }_x,\infty ),\mathbb{R}\right)$ that satisfies (1) on $[{\top }_x,\infty )$, ${\top }_x\ge {\top }_0$, and $r{\left(P^{\prime }\right)}^{\alpha }\in C^1\left([{\top }_x,\infty ),\left(0,\mathbb{R}\right)\right)$. We consider only those solutions P of (1) that satisfy

$$sup\left\{\left|P\left(\top \right)\right|:{\top }_{*}\le \top <\infty \right\}>0,\mathrm{for}\mathrm{any}{\top }_{*}\ge {\top }_x.$$

The study of oscillations in second-order differential equations holds a pivotal position in mathematical analysis and its applications. Second-order differential equations, which include classical equations of motion, vibration, and wave phenomena, serve as fundamental models in physics, engineering, and other applied sciences. The behavior of the solutions of these equations, particularly their oscillatory nature, reveals critical insights into the periodicity, stability, and resonant properties of the models they represent.

Oscillations in differential equations refer to repetitive variations in the solutions as they traverse through their equilibrium points. These oscillatory behaviors are not only mathematically intriguing but also practically significant. For instance, in mechanical systems, understanding the oscillatory response is essential for predicting the natural frequencies and preventing resonant failures. In electrical circuits, oscillations determine signal propagation and filter design, whereas in biological systems, rhythmic patterns such as heartbeats and neural oscillations are modeled by second-order differential equations [1,2,3,4,5,6]. The foundational theory of oscillations in second-order differential equations was established through the works of pioneers such as Jacob Bernoulli, Leonhard Euler, and Carl Gustav Jacobi. Their contributions laid the foundation for modern techniques in analyzing oscillatory behavior, including qualitative methods, phase plane analysis, and the theory of dynamical systems. Despite these advances, the quest to comprehend the full spectrum of oscillatory phenomena continues to drive contemporary research.

Ordinary differential equations (ODEs) serve as a fundamental tool in understanding and modeling various natural and engineering systems. Despite their widespread use, the complexity and diversity of real-world phenomena often need the introduction of advanced arguments into ODEs to achieve more accurate and comprehensive solutions. The importance of incorporating advanced arguments into ODEs has emerged through, among other things, the behavior exhibited by many nonlinear systems, which cannot be adequately captured by traditional linear differential equations. Advanced nonlinear dynamics allows for a more realistic representation of these systems, leading to better predictions and insights. Furthermore, perturbation methods allow for the analysis of systems subject to small perturbations, providing a means to understand the behavior of complex systems under different conditions. Furthermore, stability analysis is crucial for determining the long-term behavior of ODE solutions, which is essential in fields such as control theory and epidemiology. In recent years, the introduction of advanced arguments into ordinary differential equations has significantly improved our ability to tackle problems by using, for instance, nonlinear dynamics, perturbation methods, stability analysis, and numerical techniques. By integrating these advanced methods, researchers can address challenges such as nonlinearity, sensitivity to initial conditions, and the presence of multiple time scales, which are prevalent in many practical problems [7,8,9,10].

There are two main methods used to determine oscillation criteria for differential equations: the comparison principle method and the Riccati method. The comparison principle method provides a framework for comparing the solutions of differential equations with the solutions of simpler associated differential equations. By identifying the boundaries and relationships between these solutions, sufficient conditions for oscillation can be derived, allowing researchers to infer the behavior of complex systems from more solvable systems. This method relies heavily on the properties of the functions involved and their interactions over time. On the other hand, the Riccati method transforms the original differential equations into a Riccati-type differential equation. This approach takes advantage of the properties of Riccati equations, which have been extensively studied and have established techniques for analyzing their solutions. By converting differential equations into this form, results from Riccati equation theory can be applied to derive oscillation criteria [11,12,13,14].

Both methods contribute valuable insights into the oscillatory phenomena of advanced differential equations, providing researchers with powerful tools for analyzing the stability and dynamics of systems. The comparative strengths and applications of these methods highlight the richness of the techniques available for studying differential equations, ultimately enhancing our understanding of their complex behaviors.

Baculíková et al. [15] and Kusano and Naito [16] analyzed the oscillation of the differential equation

$$P^{″}\left(\top \right)+\mu \left(\top \right)P\left(l\left(\top \right)\right)=0$$

(3)

by various techniques in two cases, for

$$l\left(\top \right)=\left(\top \right),$$

(4)

and

$$l\left(\top \right)\le \top .$$

(5)

Chatzarakis [17] established some properties and relationships that led to achieving the conditions for oscillatory behavior in the half-linear differential equation

$${\left(r\left(\top \right){\left|P^{\prime }\left(\top \right)\right|}^{\alpha -1}{P}^{\prime }\left(\top \right)\right)}^{\prime }+\mu \left(\top \right){\left|P\right|}^{\alpha -1}\left(l\left(\top \right)\right)P\left(l\left(\top \right)\right)=0,$$

where

$$l\left(\top \right)\ge \top$$

(6)

and

$${\int }_{{\top }_0}^{\top }{r}^{{\displaystyle \frac{-1}{\alpha }}}\left(\varsigma \right)\mathrm{d}\varsigma =\infty .$$

(7)

By using standard techniques, the author in [18] was able to reduce the order of the advanced differential equation

$${\left(r\left(\top \right)\left(P^{\prime }\left(\top \right)\right)\right)}^{\prime }+\mu \left(\top \right)P\left(l\left(\top \right)\right)\mathrm{d}\varsigma =0,$$

(8)

and derive some criteria that ensure the oscillation of its solutions.

In [19], the author studied the oscillatory behavior of the equation

$${\left(r{\left(P^{\prime }\right)}^{\alpha }\right)}^{\prime }\left(\top \right)+\mu \left(\top \right)P^{\alpha }\left(l\left(\top \right)\right)=0$$

(9)

assuming (2) and using the condition

$${\int }_{{\top }_0}^{\infty }{\left(r^{-1}\left(\top \right){\int }_{{\top }_0}^{\top }{\left({\int }_{\top }^{\infty }{r}^{-1/\alpha }\left(u\right)\mathrm{d}u\right)}^{\alpha }\mu \left(\varsigma \right)\mathrm{d}\varsigma \right)}^{1/\alpha }\mathrm{d}\top =\infty$$

(10)

to ensure the exclusion of nonoscillatory decreasing solutions.

From the above, most studies have provided results concerning Equation (1) in the presence of either condition (4) or (5) (see [20,21,22,23,24,25,26]). We also noticed that few results subject to (6) are given when (7) holds.

The primary objective of this paper is to study the oscillatory behavior of the solutions of (1) by eliminating the possibility of the existence of nonoscillatory (positive) increasing or decreasing solutions. Unlike most previous studies, we have managed to provide criteria to ensure the oscillation of all solutions of (1) under a single condition. In contrast, previous results either ensured the oscillation of all solutions under two conditions or provided results that guarantee that the solutions of (1) are either oscillatory or tend to zero.

The development of new and distinguished relationships to link the solutions of (1) with their higher-order derivatives has provided us with suitable tools to derive new conditions that differ in nature from those appearing in the previous literature. Consequently, our results expand and enhance previous results given in [7,8,9,16,27,28,29].

2. Main Results

For the sake of brevity, we define the following notations that will be used throughout the paper:

$$\Pi \left(\top \right):={\int }_{\top }^{\infty }{r}^{-1/\alpha }\left(\varsigma \right)\mathrm{d}\varsigma ,$$

and

$$\Phi \left(\top ,u\right)={\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u.$$

Lemma 1.

Let us assume that (1) has a solution $P>0$, (2) is satisfied, and

$${\int }_{{\top }_0}^{\infty }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma =\infty .$$

(11)

Then, the following holds:

• $P^{\prime }<0$, and ${\left(r{\left(P^{\prime }\right)}^{\alpha }\right)}^{\prime }\le 0;$
• ${\left(P/\Pi \right)}^{\prime }\ge 0;$

on $[{\top }_1,\infty ),$ with ${\top }_1\in [{\top }_0,\infty ).$

Proof. 

Assume that $P>0$ satisfies Equation (1) on $[{\top }_1,\infty )$. From (1), we have

$${\left(r{\left(P^{\prime }\right)}^{\alpha }\right)}^{\prime }\left(\top \right)\le -{\int }_{k_1}^{k_2}\mu \left(\top ,\varsigma \right)P^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma .$$

That is, $P^{\prime }<0$ or $P^{\prime }>0$. Suppose that (11) holds, and there is ${\top }_2\ge {\top }_1$ such that $P^{\prime }\left(\top \right)>0$ on $[{\top }_2,\infty )$.

From (1), we have

$${\displaystyle \frac{{\left(r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }\right)}^{\prime }}{P^{\alpha }\left(l\left(\top ,k_1\right)\right)}}\le -{\int }_{k_1}^{k_2}\mu \left(\top ,\varsigma \right)\mathrm{d}\varsigma .$$

(12)

Define

$$w\left(\top \right):={\displaystyle \frac{1}{P^{\alpha }\left(l\left(\top ,k_1\right)\right)}}r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }>0.$$

(13)

In view of (12) and (13), we have

$$\begin{array}{ccc}\hfill w^{\prime }\left(\top \right)& =& {\displaystyle \frac{{\left(r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }\right)}^{\prime }}{P^{\alpha }\left(l\left(\top ,k_1\right)\right)}}-{\displaystyle \frac{r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }}{P^{\alpha }\left(l\left(\top ,k_1\right)\right)}}{\displaystyle \frac{\alpha P^{\alpha -1}\left(l\left(\top ,\varsigma \right)\right)P^{\prime }\left(l\left(\top ,\varsigma \right)\right)l^{\prime }\left(\top ,\varsigma \right)}{P^{\alpha }\left(l\left(\top ,k_1\right)\right)}}\hfill \\ & \le & -{\int }_{k_1}^{k_2}\mu \left(\top ,\varsigma \right)\mathrm{d}\varsigma -w\left(\top \right)l^{\prime }\left(\top ,\varsigma \right){\displaystyle \frac{\alpha P^{\prime }\left(l\left(\top ,\varsigma \right)\right)}{P\left(l\left(\top ,\varsigma \right)\right)}}\hfill \\ & \le & -{\int }_{k_1}^{k_2}\mu \left(\top ,\varsigma \right)\mathrm{d}\varsigma .\hfill \end{array}$$

By integrating both sides of this inequality from ${\top }_2$ to ⊤, we obtain

$$w\left(\top \right)\le w\left({\top }_2\right)-{\int }_{{\top }_2}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma .$$

(14)

From (11), (14) leads to a contradiction with $w\left(\top \right)>0$. Thus, $P^{\prime }\left(\top \right)>0$ cannot hold. Hence, P satisfies the first part of $\left(i\right)$. Since $r{\left(P^{\prime }\right)}^{\alpha }$ is nonincreasing, we have

$$\begin{array}{ccc}\hfill P\left(\top \right)& \ge & -{\int }_{\top }^{\infty }{r}^{-1/\alpha }\left(\varsigma \right)r^{1/\alpha }\left(\varsigma \right)P^{\prime }\left(\varsigma \right)\mathrm{d}\varsigma \hfill \\ & \ge & -r^{1/\alpha }\left(\top \right)P^{\prime }\left(\top \right){\int }_{\top }^{\infty }{r}^{-1/\alpha }\left(\varsigma \right)\mathrm{d}\varsigma ,\hfill \\ & =& -r^{1/\alpha }\left(\top \right)P^{\prime }\left(\top \right)\Pi \left(\top \right),\hfill \end{array}$$

(15)

from which we arrive at

$${\left({\displaystyle \frac{P}{\Pi }}\right)}^{\prime }\left(\top \right)={\displaystyle \frac{1}{r^{1/\alpha }\left(\top \right){\Pi }^2\left(\top \right)}}\left(r^{1/\alpha }\left(\top \right)P^{\prime }\left(\top \right)+P\left(\top \right)\right)\ge 0.$$

(16)

The proof is complete. □

Theorem 1.

Let us assume that (1) has a solution $P>0$ on $[{\top }_1,\infty )$, with ${\top }_1\in [{\top }_0,\infty ),$ (2) holds, and

$${\int }_{{\top }_0}^{\infty }{\left(r^{-1}\left(\top \right){\int }_{{\top }_0}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \right)}^{1/\alpha }\mathrm{d}\top =\infty .$$

(17)

Then, $\left(i\right)$ is satisfied for $\top \ge {\top }_1$ and

$$\underset{\top \to \infty }{lim}P\left(V\right)=0.$$

(18)

Moreover, there exists a ${\top }^{*}\ge {\top }_1$ and $D_1,D_2>0$ such that

$$\begin{array}{ccc}\hfill P\left(\top \right)-D_1\Pi \left(\top \right)& \ge & 0\hfill \\ \hfill P\left(\top \right)-D_2{e}^{\left(-{\int }_{{\top }_0}^{\top }\Pi \left(l\left(\top ,\varsigma \right)\right){\Pi }^{-1}\left(\varsigma \right)r^{-1/\alpha }\left(\varsigma \right){\left({\int }_{{\top }_0}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \right)}^{1/\alpha }\mathrm{d}\varsigma \right)}& \le & 0\mathit{for}\top \ge {\top }^{*}.\hfill \end{array}$$

(19)

Proof. 

Assume that $P>0$ satisfies Equation (1) on $[{\top }_1,\infty ).$ From (17) and (2), we know that $\Phi \left(\top ,u\right)$ is unbounded, and thus, (11) holds. In view of Lemma 1, we see that $\left(i\right)$ holds for $\top \ge {\top }_1$. Since $P^{\prime }<0$, there exists $I\ge 0$ such that ${lim}_{\top \to \infty }P\left(\top \right)=I.$

Assume that $I>0$. Then, we have

$$\begin{array}{ccc}\hfill -{\left(r{\left(P^{\prime }\right)}^{\alpha }\right)}^{\prime }\left(\top \right)& =& {\int }_{k_1}^{k_2}\mu \left(\top ,\varsigma \right)P^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma \hfill \\ & \ge & I^{\alpha }{\int }_{k_1}^{k_2}\mu \left(\top ,\varsigma \right)\mathrm{d}\varsigma \mathrm{for}\top \ge {\top }_2,{\top }_2\in [{\top }_1,\infty ).\hfill \end{array}$$

(20)

By integrating both sides of the inequality in (20) from ${\top }_2$ to ⊤, we find that

$$-r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }+r\left({\top }_2\right){\left(P^{\prime }\left({\top }_2\right)\right)}^{\alpha }\ge -I^{\alpha }{\int }_{{\top }_2}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma ,$$

which implies that

$$P^{\prime }\left(\top \right)+I{\left({\displaystyle \frac{1}{r\left(\top \right)}}{\int }_{{\top }_2}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \right)}^{1/\alpha }\le 0.$$

(21)

Integrating (21) from ${\top }_2$ to ⊤, we obtain

$$P\left(\top \right)+P\left({\top }_2\right)\le -I{\int }_{{\top }_2}^{\top }{\left({\displaystyle \frac{1}{r\left(u\right)}}{\int }_{{\top }_2}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \right)}^{1/\alpha }\mathrm{d}u.$$

Therefore, from (17), we see that $P\left(\top \right)\to -\infty$ as $\top \to \infty$, which leads to a contradiction. Hence, $I=0$.

Now, from $\left(ii\right)$, there is a constant $I_1>0$ such that

$$P\left(\top \right)-I_1\Pi \left(\top \right)\ge 0\mathrm{for}\top \ge {\top }_3\ge {\top }_2.$$

Integrating (1) from ${\top }_3$ to ⊤, we have

$$\begin{array}{ccc}\hfill -r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }+r\left({\top }_3\right){\left(P^{\prime }\left({\top }_3\right)\right)}^{\alpha }& \ge & {\int }_{{\top }_3}^{\top }{\int }_{k_1}^{k_2}\mu \left(\top ,\varsigma \right)P^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma \mathrm{d}u\hfill \\ & \ge & P^{\alpha }\left(l\left(\top ,k_2\right)\right){\int }_{{\top }_3}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \hfill \\ & \ge & P^{\alpha }\left(l\left(\top ,k_2\right)\right){\int }_{{\top }_3}^{{\top }_0}\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \hfill \\ & & -P^{\alpha }\left(l\left(\top ,k_2\right)\right){\int }_{{\top }_0}^{{\top }_3}\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma .\hfill \end{array}$$

Since ${lim}_{\top \to \infty }P\left(\top \right)=0$, there is a ${\top }_4\ge {\top }_3$ such that

$$-r\left({\top }_3\right){\left(P^{\prime }\left({\top }_3\right)\right)}^{\alpha }>P^{\alpha }\left(l\left(\top ,k_2\right)\right){\int }_{{\top }_0}^{{\top }_3}\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \mathrm{for}\top \ge {\top }_4,$$

and thus, we have

$$-r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }-P^{\alpha }\left(l\left(\top ,k_2\right)\right){\int }_{{\top }_0}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \ge 0.$$

Using $\left(ii\right)$, we obtain

$$\begin{array}{ccc}\hfill -r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }& \ge & P^{\alpha }\left(l\left(\top ,k_2\right)\right)\left({\int }_{{\top }_0}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \right){\displaystyle \frac{P^{\alpha }\left(l\left(\top ,\varsigma \right)\right)}{{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)}}\hfill \\ & \ge & P^{\alpha }\left(\top ,k_2\right)\left({\int }_{{\top }_0}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \right){\displaystyle \frac{P^{\alpha }\left(l\left(\top ,\varsigma \right)\right)}{{\Pi }^{\alpha }\left(\top \right)}},\hfill \end{array}$$

that is,

$${\displaystyle \frac{P^{\prime }\left(\top \right)}{P\left(\top \right)}}\le -{\displaystyle \frac{\Pi \left(l\left(\top ,\varsigma \right)\right)}{\Pi \left(\top \right)}}{\displaystyle \frac{{\left({\int }_{{\top }_0}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \right)}^{1/\alpha }}{r^{1/\alpha }\left(\top \right)}}.$$

(22)

By integrating (22) from ${\top }_4$ to ⊤, we obtain

$$\begin{array}{ccc}\hfill P\left(\top \right)& \le & P\left({\top }_4\right)e^{\left(-{\int }_{{\top }_4}^{\top }{\displaystyle \frac{\Pi \left(l\left(u,\varsigma \right)\right)}{\Pi \left(u\right)r^{1/\alpha }\left(u\right)}}{\left({\int }_{{\top }_0}^u\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \right)}^{1/\alpha }\mathrm{d}u\right)}\hfill \\ & =& P\left({\top }_4\right)e^{\left(-{\int }_{{\top }_0}^{{\top }_4}{\displaystyle \frac{\Pi \left(l\left(u,\varsigma \right)\right)}{\Pi \left(u\right)r^{1/\alpha }\left(u\right)}}{\left({\left.\Phi \right|}_{{\top }_0}^u\left(u,\varsigma \right)\right)}^{1/\alpha }\mathrm{d}u\right)}{e}^{\left(-{\int }_{{\top }_0}^{\top }{\displaystyle \frac{\Pi \left(l\left(u,\varsigma \right)\right)}{\Pi \left(u\right)r^{1/\alpha }\left(u\right)}}{\left({\int }_{{\top }_0}^u\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \right)}^{1/\alpha }\mathrm{d}u\right)},\hfill \end{array}$$

which leads to

$$P\left(\top \right)\le D_2{e}^{\left(-{\int }_{{\top }_0}^{\top }{\displaystyle \frac{\Pi \left(l\left(u\right)\right)}{\Pi \left(u\right)r^{1/\alpha }\left(u\right)}}{\left({\int }_{{\top }_0}^u\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \right)}^{1/\alpha }\mathrm{d}u\right)}.$$

The proof is complete. □

Theorem 2.

Assume that condition (2) holds. If

$${\int }_{{\top }_0}^{\infty }{\left(r^{-1}\left(\top \right){\int }_{{\top }_0}^{\top }{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)\mathrm{d}\varsigma \right)}^{1/\alpha }\mathrm{d}\top =\infty ,$$

(23)

then (1) is oscillatory.

Proof. 

Assume that $P>0$ satisfies Equation (1) on $[{\top }_0,\infty ).$ Then, $P\left(l\left(\top ,\varsigma \right)\right)>0$ for $\top \in [{\top }_1,\infty )$. Note that (11) is required for Equation (23) to be true. In view of the fact that

$${\Pi }^{\prime }<0$$

(24)

and (2), the integral

$${\int }_{{\top }_0}^{\top }{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)\mathrm{d}\varsigma$$

is unbounded, and so (11) must be satisfied. Then, by Lemma 1, $\left(i\right)$ holds for $\top \ge {\top }_1$. According to $\left(ii\right)$, it is observed that there is $I>0$ such that

$${\displaystyle \frac{1}{\Pi \left(\top \right)}}P\left(\top \right)\ge I\mathrm{for}\top \ge {\top }_2\ge {\top }_1.$$

(25)

Substituting (25) into (1), we obtain

$$-{\left(r{\left(P^{\prime }\right)}^{\alpha }\right)}^{\prime }\left(\top \right)-I^{\alpha }\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\ge 0.$$

(26)

By integrating the above inequality from ${\top }_2$ to ⊤, we have

$$-r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }-I^{\alpha }{\int }_{{\top }_2}^{\top }\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma \ge 0$$

or

$$-P^{\prime }\left(\top \right)\ge I{\displaystyle \frac{1}{r^{1/\alpha }\left(\top \right)}}{\left({\int }_{{\top }_2}^{\top }\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma \right)}^{1/\alpha }.$$

(27)

By integrating (27) from ${\top }_2$ to ⊤ and using (23), we obtain

$$P\left({\top }_2\right)\le P\left(\top \right)-{\int }_{{\top }_2}^{\top }I{r}^{-1/\alpha }\left(u\right){\left({\int }_{{\top }_2}^{\top }\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma \right)}^{1/\alpha }\mathrm{d}u\to -\infty .$$

This contradiction completes the proof. □

Theorem 3.

Let (2) be satisfied. If

$$\underset{\top \to \infty }{lim\; sup}{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right){\int }_{{\top }_1}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma >1,\forall {\top }_1\ge {\top }_0,$$

(28)

then (1) is oscillatory.

Proof. 

We proceed by contradiction. Let us assume that (28) is false, that is,

$$\underset{\top \to \infty }{lim\; sup}{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right){\int }_{{\top }_1}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \le 1,\forall {\top }_1\ge {\top }_0.$$

Suppose that $P>0$ is a solution of (1) on $[{\top }_0,\infty ).$ Then, $P\left(l\left(\top ,\varsigma \right)\right)>0$ for $\top \in [{\top }_1,\infty )$. Note that (11) is required for (28) and (2) to be true. By Lemma 1, $\left(i\right)$ holds for $\top \ge {\top }_1$. Integrating (1) from ${\top }_1$ to ⊤ and having in mind that $P^{\prime }<0$, we obtain

$$-r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }+r\left({\top }_1\right){\left(P^{\prime }\left({\top }_1\right)\right)}^{\alpha }={\int }_{{\top }_1}^{\top }\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)P^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma ,$$

and then

$$-r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }-P^{\alpha }\left(l\left(\top ,\varsigma \right)\right){\int }_{{\top }_1}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \ge 0.$$

(29)

By Lemma 1, we arrive at (15), which, together with (29), produces

$$\begin{array}{ccc}\hfill -r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }& \ge & -r\left(l\left(\top \right)\right){\left(P^{\prime }\left(l\left(\top ,\varsigma \right)\right)\right)}^{\alpha }{\Pi }^{\alpha }\left(l\left(\top \right)\right){\int }_{{\top }_1}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \hfill \\ & \ge & -r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right){\int }_{{\top }_1}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma ,\hfill \end{array}$$

which contradicts

$$\underset{\top \to \infty }{lim\; sup}{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right){\int }_{{\top }_1}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \le 1.$$

This completes the proof of the theorem. □

Theorem 4.

Let (2) and (17) be satisfied. If

$$\underset{\top \to \infty }{lim\; sup}{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right){\int }_{{\top }_0}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma >1,$$

(30)

then (1) is oscillatory.

Proof. 

We employ a proof by contradiction. Let us assume that (30) is false, and thus,

$$\underset{\top \to \infty }{lim\; sup}{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right){\int }_{{\top }_0}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \le 1.$$

From the proof of Theorem 3, we conclude (29). Using the fact (18), we obtain

$$-r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }>P^{\alpha }\left(l\left(\top ,\varsigma \right)\right){\int }_{{\top }_0}^{{\top }_1}\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma ,\top \ge {\top }_2>{\top }_1$$

and

$$\begin{array}{ccc}\hfill -r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }& \ge & -r\left({\top }_1\right){\left(P^{\prime }\left({\top }_1\right)\right)}^{\alpha }+P^{\alpha }\left(l\left(\top ,\varsigma \right)\right){\int }_{{\top }_0}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma -P^{\alpha }\left(l\left(\top \right)\right){\int }_{{\top }_0}^{{\top }_1}\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \hfill \\ & \ge & P^{\alpha }\left(l\left(\top ,\varsigma \right)\right){\int }_{{\top }_0}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma ,\mathrm{for}\top \ge {\top }_2.\hfill \end{array}$$

(31)

By Lemma 1, we arrive at (15), which, together with (29), gives

$$\begin{array}{ccc}\hfill -r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }& \ge & -r\left(l\left(\top ,\varsigma \right)\right){\left(P^{\prime }\left(l\left(\top \right)\right)\right)}^{\alpha }{\Pi }^{\alpha }\left(l\left(\top \right)\right){\int }_{{\top }_0}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \hfill \\ & \ge & -r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right){\int }_{{\top }_0}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma ,\hfill \end{array}$$

which contradicts

$$\underset{\top \to \infty }{lim\; sup}{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right){\int }_{{\top }_0}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \le 1.$$

This completes the proof. □

Theorem 5.

Let (2) be satisfied. If

$$\underset{\top \to \infty }{lim\; inf}{\int }_{\top }^{l\left(\top ,\varsigma \right)}\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma >{\displaystyle \frac{1}{e}},$$

(32)

then (1) is oscillatory.

Proof. 

Assume that $P>0$ satisfies Equation (1) on $[{\top }_0,\infty ).$ Then, $P\left(l\left(\top ,\varsigma \right)\right)>0$ for $\top \in [{\top }_1,\infty )$. We note that (32) and (2) give (11). Also, (32) implies

$${\int }_{{\top }_0}^{\infty }\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma =\infty .$$

(33)

From (24) and (33), we find that (11) is satisfied. By Lemma 1, $\left(i\right)$ holds. From (1) and (15), we note that the advanced differential inequality

$$x^{\prime }\left(\top \right)-\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\Pi }^{\alpha }\left(l\left(\top \right)\right)x\left(l\left(\top ,\varsigma \right)\right)\ge 0$$

(34)

has a solution $x>0,$ where $x:=-r{\left(P^{\prime }\right)}^{\alpha }.$ Furthermore, the condition

$$\underset{\top \to \infty }{lim\; inf}{\int }_{\top }^{l\left(\top ,\varsigma \right)}\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma >{\displaystyle \frac{1}{e}}$$

implies the oscillation of (34) according to ([30] Theorem 2.4.1). That is, (1) does not admit a positive solution $x>0$. This concludes the proof. □

Theorem 6.

Let (2) be satisfied. If

$$\underset{\top \to \infty }{lim\; inf}{\int }_{\top }^{l\left(\top ,\varsigma \right)}\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\tilde{\Pi }}^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma >{\displaystyle \frac{1}{e}},$$

(35)

where

$$\tilde{\Pi }\left(\top \right)=\Pi \left(\top \right)+{\displaystyle \frac{1}{\alpha }}{\int }_{\top }^{\infty }{\displaystyle \frac{\Pi \left(\varsigma \right)}{{\Pi }^{-\alpha }\left(l\left(\top ,\varsigma \right)\right)}}\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)\mathrm{d}\varsigma ,$$

then (1) is oscillatory.

Proof. 

Assume that $P>0$ satisfies Equation (1) on $[{\top }_0,\infty ).$ Then, $P\left(l\left(\top ,\varsigma \right)\right)>0$ for $\top \in [{\top }_1,\infty )$. Similar to Theorem 6, this indicates that (35) and (2) lead to (11). By Lemma 1, we see that $\left(i\right)$ holds for $\top \ge {\top }_1$. It is clear that

$${\left(P+r^{1/\alpha }{P}^{\prime }\Pi \right)}^{\prime }\left(\top \right)=\Pi \left(\top \right){\left(r^{1/\alpha }{P}^{\prime }\right)}^{\prime }\left(\top \right).$$

Applying the chain rule, we obtain

$${\left(r{\left(P^{\prime }\right)}^{\alpha }\right)}^{\prime }\left(\top \right)-\alpha {\left(r^{1/\alpha }\left(\top \right)P^{\prime }\left(\top \right)\right)}^{\alpha -1}{\left(r^{1/\alpha }{P}^{\prime }\right)}^{\prime }\left(\top \right)=0$$

and

$${\left(P+r^{1/\alpha }{P}^{\prime }\Pi \right)}^{\prime }\left(\top \right)-{\displaystyle \frac{1}{\alpha }}\Pi \left(\top \right){\left(r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }\right)}^{\prime }{\left(r^{1/\alpha }\left(\top \right)P^{\prime }\left(\top \right)\right)}^{1-\alpha }=0,$$

which, by (1), leads to

$${\left(P\left(\top \right)+r^{1/\alpha }\left(\top \right)P^{\prime }\left(\top \right)\Pi \left(\top \right)\right)}^{\prime }=-{\displaystyle \frac{1}{\alpha }}\Pi \left(\top \right){\left(r^{1/\alpha }\left(\top \right)P^{\prime }\left(\top \right)\right)}^{1-\alpha }\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)P^{\alpha }\left(l\left(\top ,\varsigma \right)\right)<0.$$

(36)

Let us define the decreasing function

$$\varphi \left(\top \right):=P\left(\top \right)+r^{1/\alpha }\left(\top \right)\Pi \left(\top \right)P^{\prime }\left(\top \right)>0.$$

Integrating (36) from ⊤ to ∞ and using (15), we have

$$\begin{array}{ccc}\hfill \varphi \left(\top \right)& =& {\displaystyle \frac{1}{\alpha }}{\int }_{\top }^{\infty }{\displaystyle \frac{\Pi \left(\varsigma \right)}{{\left(r^{1/\alpha }\left(\varsigma \right)P^{\prime }\left(\varsigma \right)\right)}^{\alpha -1}}}\left({\int }_{k_1}^{k_2}\mu \left(v,u\right)\mathrm{d}u\right)P^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma +\varphi \left(\infty \right)\hfill \\ & \ge & {\displaystyle \frac{1}{\alpha }}{\int }_{\top }^{\infty }{\displaystyle \frac{\Pi \left(\varsigma \right)}{{\left(r^{1/\alpha }\left(\varsigma \right)P^{\prime }\left(\varsigma \right)\right)}^{\alpha -1}}}\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)P^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma \hfill \\ & \ge & {\displaystyle \frac{1}{\alpha }}{\int }_{\top }^{\infty }{\displaystyle \frac{\Pi \left(\varsigma \right)}{{\left(r^{1/\alpha }\left(\varsigma \right)P^{\prime }\left(\varsigma \right)\right)}^{\alpha -1}}}{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\left(-r^{1/\alpha }l\left(\varsigma \right)P^{\prime }\left(l\left(\top ,\varsigma \right)\right)\right)}^{\alpha }\mathrm{d}\varsigma \hfill \\ & \ge & {\displaystyle \frac{1}{\alpha }}{\int }_{\top }^{\infty }{\displaystyle \frac{\Pi \left(\varsigma \right)}{{\left(r^{1/\alpha }\left(\varsigma \right)P^{\prime }\left(\varsigma \right)\right)}^{\alpha -1}}}{\Pi }^{\alpha }\left(l\left(\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\left(-r^{1/\alpha }\left(\varsigma \right)P^{\prime }\left(\varsigma \right)\right)}^{\alpha }\mathrm{d}\varsigma \hfill \\ & =& {\displaystyle \frac{1}{\alpha }}{\int }_{\top }^{\infty }\Pi \left(\varsigma \right){\Pi }^{\alpha }\left(l\left(\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)\left(-r^{1/\alpha }\left(\varsigma \right)P^{\prime }\left(\varsigma \right)\right)\mathrm{d}\varsigma .\hfill \end{array}$$

This implies

$$\varphi \left(\top \right)\ge -{\alpha }^{-1}{r}^{1/\alpha }\left(\top \right)P^{\prime }\left(\top \right){\int }_{\top }^{\infty }\Pi \left(\varsigma \right){\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)\mathrm{d}\varsigma .$$

Thus,

$$\begin{array}{ccc}\hfill P\left(\top \right)& \ge & -{\displaystyle \frac{P^{\prime }\left(\top \right)}{r^{1/\alpha }\left(\top \right)}}\left(\Pi \left(\top \right)+{\alpha }^{-1}{\int }_{\top }^{\infty }\Pi \left(\varsigma \right){\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)\mathrm{d}\varsigma \right)\hfill \\ & =& -{\displaystyle \frac{P^{\prime }\left(\top \right)\tilde{\Pi }\left(\top \right)}{r^{-1/\alpha }\left(\top \right)}}.\hfill \end{array}$$

(37)

Taking into account (1), we find that the advanced differential inequality

$$x^{\prime }\left(\top \right)-\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\tilde{\Pi }}^{\alpha }\left(l\left(\top ,\varsigma \right)\right)x\left(l\left(\top ,\varsigma \right)\right)\ge 0$$

(38)

has a solution $x:=-r{\left(P^{\prime }\right)}^{\alpha }>0$. From ([30] Theorem 2.4.1), we find that the condition

$$\underset{\top \to \infty }{lim\; inf}{\int }_{\top }^{l\left(\top \right)}\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\tilde{\Pi }}^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma >{\displaystyle \frac{1}{e}}$$

implies the oscillation of (38). That is, (1) does not admit a positive solution $x>0$, which is a contradiction. The proof is complete. □

Lemma 2

([31] Lemma 2.3). Let

$$g\left(h\right)=B_{1}h-B_2{\left(h-B_3\right)}^{\left(\alpha +1\right)/\alpha },$$

with $B_1>0$, and with $B_2$ and $B_3$ being real constants. Then, g attains its maximum value at

$$h^{*}=B_3+{\displaystyle \frac{{\alpha }^{\alpha }}{{\left(\alpha +1\right)}^{\alpha }}}{\left({\displaystyle \frac{B_1}{B_2}}\right)}^{\alpha },$$

and

$$g\left(h^{*}\right)=B_1{B}_3+{\displaystyle \frac{{\alpha }^{\alpha }}{{\left(\alpha +1\right)}^{\alpha +1}}}{\displaystyle \frac{B_1^{\alpha +1}}{B_2^{\alpha }}}.$$

(39)

Theorem 7.

Let (2) and (11) be satisfied. If there is a function ψ belonging to the class $C^1\left([{\top }_0,\infty )\right.$, $\left.\left(0,\infty \right)\right)$ such that

$$\underset{\top \to \infty }{lim\; sup}\left\{{\Pi }^{\alpha }\left(\top \right){\psi }^{-1}\left(\top \right){\int }_{{\top }_2}^{\top }\left(\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)*\psi \left(\varsigma \right){\left({\displaystyle \frac{\Pi \left(l\left(\top ,\varsigma \right)\right)}{\Pi \left(\varsigma \right)}}\right)}^{\alpha }-{\displaystyle \frac{r\left(\varsigma \right)}{{\psi }^{\alpha }\left(\varsigma \right)}}{\left({\displaystyle \frac{{\psi }^{\prime }\left(\varsigma \right)}{\alpha +1}}\right)}^{\alpha +1}\right)\mathrm{d}\varsigma \right\}>1,$$

(40)

for $\top ,{\top }_2\in [{\top }_0,\infty )$, then (1) is oscillatory.

Proof. 

Assume that $P>0$ satisfies Equation (1) on $[{\top }_0,\infty ).$ Then, $P\left(l\left(\top ,\varsigma \right)\right)>0$ for $\top \in [{\top }_1,\infty )$. From Lemma 1, we find that $\left(i\right)$ holds. Moreover, from (15), we can define a nonnegative function

$$w:=\psi \left({\displaystyle \frac{r{\left(P^{\prime }\right)}^{\alpha }}{P^{\alpha }}}+{\Pi }^{-\alpha }\right)\mathrm{on}[{\top }_1,\infty ),$$

(41)

which verifies

$$\begin{array}{ccc}\hfill w^{\prime }& =& {\displaystyle \frac{1}{\psi }}{\psi }^{\prime }w+\psi {\displaystyle \frac{1}{P^{\alpha }}}{\left(r{\left(P^{\prime }\right)}^{\alpha }\right)}^{\prime }-\alpha \psi r{\left({\displaystyle \frac{P^{\prime }}{P}}\right)}^{\alpha +1}+\alpha {\displaystyle \frac{1}{r^{1/\alpha }}}\psi {\Pi }^{-\left(\alpha +1\right)}\hfill \\ & \le & {\displaystyle \frac{1}{\psi }}{\psi }^{\prime }w+\psi {\displaystyle \frac{1}{P^{\alpha }}}{\left(r{\left(P^{\prime }\right)}^{\alpha }\right)}^{\prime }-{\left(w-{\displaystyle \frac{\psi }{{\Pi }^{\alpha }}}\right)}^{\left(\alpha +1\right)/\alpha }\alpha {\left(\psi r\right)}^{-1/\alpha }\hfill \\ & & +{\Pi }^{-\left(\alpha +1\right)}\alpha \psi {\displaystyle \frac{1}{r^{1/\alpha }}}.\hfill \end{array}$$

(42)

In view of (1) and $\left(ii\right)$, we obtain

$${\left(r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }\right)}^{\prime }+{\displaystyle \frac{{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)}{{\Pi }^{\alpha }\left(\top \right)}}\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)P^{\alpha }\left(\top \right)\le 0\mathrm{for}\top \ge {\top }_2\ge {\top }_1,$$

(43)

which, with (42), gives

$$\begin{array}{ccc}\hfill w^{\prime }\left(\top \right)& \le & -\psi \left(\top \right){\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right){\Pi }^{-\alpha }\left(\top \right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)+{\displaystyle \frac{1}{\psi \left(\top \right)}}w\left(\top \right){\psi }^{\prime }\left(\top \right)\hfill \\ & & -\alpha {\left(\psi r\left(\top \right)\right)}^{-1/\alpha }{\left(w\left(\top \right)-{\displaystyle \frac{\psi \left(\top \right)}{{\Pi }^{\alpha }\left(\top \right)}}\right)}^{\left(\alpha +1\right)/\alpha }+\alpha {\displaystyle \frac{1}{r^{1/\alpha }\left(\top \right)}}\psi \left(\top \right){\Pi }^{-\left(\alpha +1\right)}\left(\top \right).\hfill \end{array}$$

Taking

$$B_1:={\displaystyle \frac{1}{\psi \left(\top \right)}}{\psi }^{\prime }\left(\top \right),B_2:=\alpha {\displaystyle \frac{1}{{\left(r\left(\top \right)\psi \left(\top \right)\right)}^{1/\alpha }}},B_3:={\displaystyle \frac{1}{{\Pi }^{\alpha }\left(\top \right)}}\psi \left(\top \right),$$

in (39), we arrive at

$$\begin{array}{ccc}\hfill w^{\prime }\left(\top \right)& \le & -\psi \left(\top \right){\displaystyle \frac{1}{{\Pi }^{\alpha }\left(\top \right)}}{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)+{\psi }^{\prime }\left(\top \right){\displaystyle \frac{1}{{\Pi }^{\alpha }\left(\top \right)}}\hfill \\ & & +{\left(\alpha +1\right)}^{-\left(\alpha +1\right)}{\displaystyle \frac{1}{{\psi }^{\alpha }\left(\top \right)}}r\left(\top \right){\left({\psi }^{\prime }\right)}^{\alpha +1}\left(\top \right)+\alpha {\displaystyle \frac{1}{r^{1/\alpha }\left(\top \right)}}\psi \left(\top \right){\Pi }^{-\left(\alpha +1\right)}\left(\top \right)\hfill \\ & =& -\psi \left(\top \right){\displaystyle \frac{1}{{\Pi }^{\alpha }\left(\top \right)}}{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)+{\left({\displaystyle \frac{\psi }{{\Pi }^{\alpha }}}\right)}^{\prime }\left(\top \right)\hfill \\ & & +{\left(\alpha +1\right)}^{-\left(\alpha +1\right)}{\displaystyle \frac{1}{{\psi }^{\alpha }\left(\top \right)}}r\left(\top \right){\left({\psi }^{\prime }\left(\top \right)\right)}^{\alpha +1}.\hfill \end{array}$$

(44)

Integrating (44) from ${\top }_2$ to ⊤, we obtain

$$\begin{array}{ccc}& & {\int }_{{\top }_2}^{\top }\left(\psi \left(\varsigma \right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\left({\displaystyle \frac{\Pi \left(l\left(\top ,\varsigma \right)\right)}{\Pi \left(\varsigma \right)}}\right)}^{\alpha }-{\left(\alpha +1\right)}^{-\left(\alpha +1\right)}r\left(\varsigma \right){\left({\psi }^{\prime }\left(\varsigma \right)\right)}^{\alpha +1}{\psi }^{-\alpha }\left(\varsigma \right)\right)\mathrm{d}\varsigma \hfill \\ & & -{\displaystyle \frac{\psi \left(\top \right)}{{\Pi }^{\alpha }\left(\top \right)}}+{\displaystyle \frac{\psi \left({\top }_2\right)}{{\Pi }^{\alpha }\left({\top }_2\right)}}\hfill \\ & \le & w\left({\top }_2\right)-w\left(\top \right).\hfill \end{array}$$

From (41), we obtain

$$\begin{array}{ccc}& & {\int }_{{\top }_2}^{\top }\left(\psi \left(\varsigma \right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\left({\displaystyle \frac{\Pi \left(l\left(\top ,\varsigma \right)\right)}{\Pi \left(\varsigma \right)}}\right)}^{\alpha }-r\left(\varsigma \right){\left({\psi }^{\prime }\left(\varsigma \right)\right)}^{\alpha +1}{\left(\alpha +1\right)}^{-\left(\alpha +1\right)}{\psi }^{-\alpha }\left(\varsigma \right)\right)\mathrm{d}\varsigma \hfill \\ & \le & \psi \left({\top }_2\right)r\left({\top }_2\right){\left(P^{\prime }\left({\top }_2\right)\right)}^{\alpha }{P}^{-\alpha }\left({\top }_2\right)-\psi \left(\top \right)r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }{P}^{-\alpha }\left(\top \right).\hfill \end{array}$$

(45)

It follows from (15) that

$$-\psi \left(\top \right){\displaystyle \frac{1}{{\Pi }^{\alpha }\left(\top \right)}}\le \psi \left(\top \right)r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }{\displaystyle \frac{1}{P^{\alpha }\left(\top \right)}}\le 0,$$

which, together with (45), gives

$$\begin{array}{ccc}& & {\int }_{{\top }_2}^{\top }\left(\psi \left(\varsigma \right){\displaystyle \frac{{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)}{{\Pi }^{\alpha }\left(\varsigma \right)}}\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)-{\displaystyle \frac{{\left(\alpha +1\right)}^{-\left(\alpha +1\right)}}{{\psi }^{\alpha }\left(\varsigma \right)}}r\left(\varsigma \right){\left({\psi }^{\prime }\left(\varsigma \right)\right)}^{\alpha +1}\right)\mathrm{d}\varsigma \hfill \\ & \le & {\displaystyle \frac{1}{{\Pi }^{\alpha }\left(\top \right)}}\psi \left(\top \right).\hfill \end{array}$$

(46)

Thus,

$$\underset{\top \to \infty }{lim\; sup}\left\{{\Pi }^{\alpha }\left(\top \right){\psi }^{-1}\left(\top \right){\int }_{{\top }_2}^{\top }\left(\psi \left(\varsigma \right){\displaystyle \frac{{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)}{{\Pi }^{\alpha }\left(\varsigma \right)}}\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)-r\left(\varsigma \right){\psi }^{-\alpha }\left(\varsigma \right){\displaystyle \frac{{\left({\psi }^{\prime }\left(\varsigma \right)\right)}^{\alpha +1}}{{\left(\alpha +1\right)}^{\alpha +1}}}\right)\mathrm{d}\varsigma \right\}\le 1.$$

This contradiction completes the proof of the theorem. □

Corollary 1.

Let (2) and (11) be satisfied. If

$$\underset{\top \to \infty }{lim\; sup}{\Pi }^{\alpha -1}\left(\top \right){\int }_{{\top }_2}^{\top }\left({\displaystyle \frac{{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)}{{\Pi }^{\alpha -1}\left(\top \right)}}\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)-{\displaystyle \frac{r^{-1/\alpha }\left(\varsigma \right)}{{\Pi }^{\alpha }\left(\varsigma \right){\left(\alpha +1\right)}^{\left(\alpha +1\right)}}}\right)\mathrm{d}\varsigma >1,$$

(47)

or

$$\underset{\top \to \infty }{lim\; sup}{\Pi }^{\alpha }\left(\top \right){\int }_{{\top }_2}^{\top }{\displaystyle \frac{{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)}{{\Pi }^{\alpha }\left(\varsigma \right)}}\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)\mathrm{d}\varsigma >1,\forall \top \in [{\top }_0,\infty ),$$

(48)

or

$$\underset{\top \to \infty }{lim\; sup}{\int }_{{\top }_2}^{\top }{\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)-{\displaystyle \frac{1}{r^{1/\alpha }\left(\varsigma \right)}}{\displaystyle \frac{{\alpha }^{\alpha +1}}{{\left(\alpha +1\right)}^{\alpha +1}}}{\Pi }^{-1}\left(\varsigma \right)\mathrm{d}\varsigma >1,$$

(49)

then (1) is oscillatory.

Proof. 

In Theorem 7, choose $\psi \left(\top \right)=1$, $\psi \left(\top \right)=\Pi \left(\top \right)$, and $\psi \left(\top \right)={\Pi }^{\alpha }\left(\top \right),$ consecutively; we obtain conditions (47), (48), and (49), respectively. □

Lemma 3.

Let (2) and (11) be satisfied. Moreover, suppose that for

$$j<1-v,$$

(50)

with j, $v\ge 0$,

$${\displaystyle \frac{j}{\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\Pi \left(\top \right)r^{1/\alpha }\left(\top \right)}}\le 1$$

(51)

holds, and

$${\displaystyle \frac{v}{\Pi \left(l\left(\top ,\varsigma \right)\right){\left({\int }_{{\top }_1}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \right)}^{\alpha }}}\le 1.$$

(52)

Then, there is a ${\top }_{*}\in [{\top }_1,\infty )$ such that

$$P/{\Pi }^{1-j}\mathit{is}\mathit{nondecreasing}$$

(53)

and

$$P/{\Pi }^v\mathit{is}\mathit{nonincreasing}$$

(54)

on $[{\top }_{*},\infty ).$

Proof. 

From Lemma 1, we find that $\left(i\right)$ holds. Using (1), (15), and (51), we have

$$\begin{array}{ccc}\hfill {\left(-r{\left(P^{\prime }\right)}^{\alpha }{\Pi }^j\right)}^{\prime }\left(\top \right)& =& -{\left(r{\left(P^{\prime }\right)}^{\alpha }\right)}^{\prime }\left(\top \right){\Pi }^j\left(\top \right)+jr\left(\top \right)r^{-1/\alpha }\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }{\Pi }^{j-1}\left(\top \right)\hfill \\ & =& {\Pi }^j\left(\top \right)P^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)+jr\left(\top \right)r^{-1/\alpha }\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }{\Pi }^{j-1}\left(\top \right)\hfill \\ & \ge & -r\left(\top \right){\Pi }^j\left(\top \right){\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\left(P^{\prime }\left(\top \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)\hfill \\ & & +jr\left(\top \right)r^{-1/\alpha }\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }{\Pi }^{j-1}\left(\top \right).\hfill \end{array}$$

Hence, it is

$${\left(-r{\left(P^{\prime }\right)}^{\alpha }{\Pi }^j\right)}^{\prime }\left(\top \right)=-r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }{\Pi }^j\left(\top \right)\left(\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\Pi }^{\alpha }\left(l\left(\top ,\varsigma \right)\right)-j{\Pi }^{-1}\left(\top \right)r^{-1/\alpha }\left(\top \right)\right),$$

which produces

$${\left(-r{\left(P^{\prime }\right)}^{\alpha }{\Pi }^j\right)}^{\prime }\left(\top \right)\ge 0\mathrm{for}\top \ge {\top }_2,{\top }_2\in [{\top }_1,\infty ).$$

(55)

Using property (55), we obtain

$$\begin{array}{ccc}\hfill P\left(\top \right)& \ge & -{\int }_{\top }^{\infty }{P}^{\prime }\left(\varsigma \right){\displaystyle \frac{1}{r^{1/\alpha }\left(\varsigma \right){\Pi }^j\left(\varsigma \right)}}{r}^{1/\alpha }\left(\varsigma \right){\Pi }^j\left(\varsigma \right)\mathrm{d}\varsigma \hfill \\ & \ge & -{\int }_{\top }^{\infty }{P}^{\prime }\left(\varsigma \right)r^{1/\alpha }\left(\varsigma \right){\Pi }^j\left(\varsigma \right)r^{-1/\alpha }\left(\varsigma \right){\Pi }^{-j}\left(\varsigma \right)\mathrm{d}\varsigma \hfill \\ & \ge & -P^{\prime }\left(\top \right)r^{1/\alpha }\left(\varsigma \right){\Pi }^j\left(\top \right){\int }_{\top }^{\infty }{r}^{-1/\alpha }\left(\varsigma \right){\Pi }^{-j}\left(\varsigma \right)\mathrm{d}\varsigma .\hfill \end{array}$$

(56)

It is clear that

$${\int }_{\top }^{\infty }{r}^{-1/\alpha }\left(\varsigma \right){\Pi }^{-j}\left(\varsigma \right)\mathrm{d}\varsigma ={\displaystyle \frac{1}{\left(1-j\right){\Pi }^{j-1}\left(\top \right)}},$$

(57)

and thus, we have

$$P\left(\top \right)\ge -{\displaystyle \frac{1}{1-j}}{r}^{1/\alpha }\left(\top \right)P^{\prime }\left(\top \right)\Pi \left(\top \right),$$

(58)

which leads to

$${\left({\displaystyle \frac{P}{{\Pi }^{1-j}}}\right)}^{\prime }\left(\top \right)={\displaystyle \frac{r^{-1/\alpha }\left(\top \right){\Pi }^{2-j}\left(\varsigma \right)}{\left(1-j\right)}}\left(r^{1/\alpha }\left(\top \right)P^{\prime }\left(\top \right)\Pi \left(\top \right)+P\right),$$

and thus,

$${\left({\displaystyle \frac{P}{{\Pi }^{1-j}}}\right)}^{\prime }\left(\top \right)\ge 0.$$

As in the proof of Theorem 1, we arrive at (22), that is,

$$P\left(\top \right)+r^{1/\alpha }\left(\top \right)P^{\prime }\left(\top \right){\displaystyle \frac{1}{\Pi \left(l\left(\top ,\varsigma \right)\right)}}\Pi \left(\top \right){\left({\int }_{{\top }_1}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \right)}^{-1/\alpha }\le 0.$$

(59)

Using inequality (59) in the equality

$${\left({\displaystyle \frac{P}{{\Pi }^v}}\right)}^{\prime }\left(\top \right)={\displaystyle \frac{P^{\prime }\left(\top \right)}{{\Pi }^v\left(\top \right)}}+{\displaystyle \frac{vP\left(\top \right)}{{\Pi }^{v+1}\left(\top \right)r^{1/\alpha }\left(\top \right)}},$$

and using (52), we obtain

$$\begin{array}{ccc}\hfill {\left({\displaystyle \frac{P}{{\Pi }^v}}\right)}^{\prime }\left(\top \right)& \le & P^{\prime }\left(\top \right){\displaystyle \frac{1}{{\Pi }^v\left(\top \right)}}-v{P}^{\prime }\left(\top \right){\displaystyle \frac{1}{{\Pi }^v\left(\top \right)\Pi \left(l\left(\top ,\varsigma \right)\right)}}{\left({\int }_{{\top }_1}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \right)}^{-1/\alpha }\hfill \\ & =& P^{\prime }\left(\top \right){\displaystyle \frac{1}{{\Pi }^v\left(\top \right)}}\left(1-v{\Pi }^{-1}\left(l\left(\top ,\varsigma \right)\right){\left({\int }_{{\top }_1}^{\top }\Phi \left(\top ,\varsigma \right)\mathrm{d}\varsigma \right)}^{-1/\alpha }\right)\hfill \\ & \le & 0.\hfill \end{array}$$

Therefore, $\left({\displaystyle \frac{P}{{\Pi }^v}}\right)$ is nonincreasing. This ends the proof. □

Theorem 8.

Let (2) be satisfied, and let j and v be constants satisfying (50)–(52). If

$${\displaystyle \frac{1}{{\left(1-P\right)}^{\alpha }}}\underset{\top \to \infty }{lim\; sup}{\displaystyle \frac{{\Pi }^{j\alpha }\left(\top \right)}{{\Pi }^{\alpha \left(j+v-1\right)}\left(l\left(\top ,\varsigma \right)\right)}}{\int }_{{\top }_1}^{\top }{\Pi }^{v\alpha }\left(l\left(\top ,\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)\mathrm{d}\varsigma >1,$$

(60)

for ${\top }_1\ge {\top }_0$, then (1) is oscillatory.

Proof. 

Assume that $P>0$ satisfies Equation (1) on $[{\top }_0,\infty ).$ Then, $P\left(l\left(\top ,\varsigma \right)\right)>0$ for $\top \in [{\top }_1,\infty )$. We find that (23) requires (11) to be held. Note that (2) gives

$${\displaystyle \frac{1}{{\Pi }^{j+v+1}\left(l\left(\top ,\varsigma \right)\right)}}{\Pi }^j\left(\top \right)\le {\displaystyle \frac{1}{{\Pi }^{v-1}\left(\top \right)}}\to 0\mathrm{as}\top \to \infty .$$

That is, the function

$${\int }_{{\top }_0}^{\top }\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\Pi }^{v\alpha }\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma$$

is unbounded. Thus, $\Phi \left(\top ,u\right)$ must be unbounded, and we find that $\left(i\right)$ holds. Integrating (1) from ${\top }_1$ to ⊤ and using Lemma 3, we conclude that

$${\left(P/{\Pi }^v\right)}^{\prime }\le 0\mathrm{and}{\left(P/{\Pi }^{1-j}\right)}^{\prime }\ge 0,$$

and consequently,

$$\begin{array}{ccc}\hfill -r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }& =& -r\left({\top }_1\right){\left(P^{\prime }\left({\top }_1\right)\right)}^{\alpha }+{\int }_{{\top }_1}^{\top }{P}^l\left(l\left(\top ,\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)\mathrm{d}\varsigma \hfill \\ & \ge & P^{\alpha }\left(l\left(\top \right)\right){\Pi }^{-v\alpha }\left(l\left(\top \right)\right){\int }_{{\top }_1}^{\top }{\Pi }^{v\alpha }\left(l\left(\top ,\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)\mathrm{d}\varsigma \hfill \\ & =& {\displaystyle \frac{1}{{\Pi }^v\left(l\left(\top \right)\right){\Pi }^{1-j}\left(l\left(\top \right)\right)}}{\left(P\left(l\left(\top ,\varsigma \right)\right){\Pi }^{1-j}\left(l\left(\top ,\varsigma \right)\right)\right)}^{\alpha }{\int }_{{\top }_1}^{\top }{\Pi }^{v\alpha }\left(l\left(\top ,\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)\mathrm{d}\varsigma ,\hfill \end{array}$$

that is,

$$-r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }\ge {\left(P\left(\top \right){\Pi }^{j-v-1}\left(l\left(\top ,\varsigma \right)\right){\Pi }^{j-1}\left(\top \right)\right)}^{\alpha }{\int }_{{\top }_1}^{\top }{\Pi }^{v\alpha }\left(l\left(\top ,\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)\mathrm{d}\varsigma .$$

(61)

Using (61) in (58), we obtain

$$-r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }\ge -r\left(\top \right){\left(P^{\prime }\left(\top \right)\right)}^{\alpha }{\left({\displaystyle \frac{{\Pi }^j\left(\top \right)}{\left(1-j\right){\Pi }^{j+v-1}\left(l\left(\top ,\varsigma \right)\right)}}\right)}^{\alpha }{\int }_{{\top }_1}^{\top }{\Pi }^{v\alpha }\left(l\left(\top ,\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)\mathrm{d}\varsigma ,$$

which produces

$${\left({\displaystyle \frac{1}{\left(1-j\right){\Pi }^{j+v-1}\left(l\left(\top ,\varsigma \right)\right)}}{\Pi }^j\left(\top \right)\right)}^{\alpha }{\int }_{{\top }_1}^{\top }{\Pi }^{v\alpha }\left(l\left(\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)\mathrm{d}\varsigma \le 1$$

or

$$\underset{\top \to \infty }{lim\; sup}{\Pi }^{j\alpha }\left(\top \right){\displaystyle \frac{1}{{\Pi }^{\alpha \left(j+v-1\right)}\left(l\left(\top ,\varsigma \right)\right)}}{\int }_{{\top }_1}^{\top }{\Pi }^{v\alpha }\left(l\left(\top ,\varsigma \right)\right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)\mathrm{d}\varsigma \le {\left(1-P\right)}^{\alpha }.$$

This completes the proof. □

Theorem 9.

Suppose that (2) holds,

$$0\le j<1,$$

(62)

and (51) is satisfied. If

$$e{\left(1-j\right)}^{-\alpha }\underset{\top \to \infty }{lim\; inf}{\int }_{\top }^{l\left(\top ,\varsigma \right)}\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\Pi }^l\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma >1,$$

then (1) is oscillatory.

Proof. 

The proof can be obtained by following arguments similar to those in the proof of Theorem 5, using (15) instead of (58). □

Theorem 10.

Let us assume that (2), (11), and (62) are satisfied. Also, suppose that (51) is satisfied. If there is a function $\psi \in C^1\left([{\top }_0,\infty ),\left(0,\infty \right)\right)$ such that

$$\underset{\top \to \infty }{lim\; sup}\left\{{\displaystyle \frac{{\Pi }^{\alpha }\left(\top \right)}{\psi \left(\top \right)}}{\int }_{{\top }_2}^{\top }\left({\displaystyle \frac{\psi \left(\varsigma \right)\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right)}{{\left(\Pi \left(l\left(\top ,\varsigma \right)\right){\Pi }^{-1}\left(\varsigma \right)\right)}^{-\alpha \left(P-1\right)}}}-{\displaystyle \frac{r\left(\varsigma \right){\psi }^{-\alpha }\left(\top \right){\left({\psi }^{\prime }\left(\top \right)\right)}^{\alpha +1}}{{\left(\alpha +1\right)}^{\alpha +1}}}\right)\mathrm{d}\varsigma \right\}>1,$$

(63)

$\top \in [{\top }_0,\infty ),$ then (1) is oscillatory.

Proof. 

The proof can be obtained similarly to the proof of Theorem 7, replacing $\left(ii\right)$ with (53) in (43). □

Corollary 2.

Let (2) be satisfied, and assume that (62) and (51) hold. If

$$\underset{\top \to \infty }{lim\; sup}{\int }_{\top }^{\top }\left(\left({\int }_{k_1}^{k_2}\mu \left(\top ,u\right)\mathrm{d}u\right){\Pi }^{\alpha \left(1-P\right)}\left(l\left(\top ,\varsigma \right)\right){\Pi }^{\alpha j}\left(\varsigma \right)-{\displaystyle \frac{{\left(\alpha /\alpha +1\right)}^{\alpha +1}{r}^{-1/\alpha }\left(\varsigma \right)}{\Pi \left(\varsigma \right)}}\right)\mathrm{d}\varsigma >1,$$

(64)

$\forall \top \in [{\top }_0,\infty ),$ then (1) is oscillatory.

3. Examples and Remarks

Example 1.

Consider the following advanced differential equation:

$${\left({\top }^{\alpha +1}{\left(P^{\prime }\left(\top \right)\right)}^{\alpha }\right)}^{\prime }+{\int }_{k_1}^{k_2}{\mu }_0{P}^{\alpha }\left(\lambda \top \right)\mathrm{d}\varsigma =0,{\mu }_0>0,\lambda \in [1,\infty ),\top \in [1,\infty ).$$

(65)

We see that

$$\Pi \left(\top \right)={\int }_{\top }^{\infty }{\displaystyle \frac{1}{{\varsigma }^{\left(\alpha +1\right)/\alpha }}}\mathrm{d}\varsigma =\alpha {\displaystyle \frac{1}{{\top }^{1/\alpha }}}.$$

We can conclude the following:

1: 

According to Theorem 1,

$\left(\mathbf{e}\mathbf{1}\right)$ Condition (17) holds. Therefore, any nonoscillatory solution of (65) satisfies (18).

$\left(\mathbf{e}\mathbf{2}\right)$ A lower bound of the solution $P\left(\top \right)$ is $D_1{\top }^{-1/\alpha }$, and an upper bound of the solution $P\left(\top \right)$ is $D_2{\top }^{-{\left({\mu }_0/\lambda \right)}^{1/\alpha }},$ where $D_1$ and $D_2$ are positive constants.

2: 

According to Theorem 2, (23) does not apply; so, Theorem 2 fails.

3: 

According to Theorem 3, all solutions of (65) oscillate if

$${\mu }_0{\displaystyle \frac{{\alpha }^{\alpha }}{\lambda }}>1.$$

(66)

4: 

According to Theorem 5, all solutions of (65) are oscillatory if

$${\mu }_{0}e{\alpha }^{\alpha }ln\lambda {\displaystyle \frac{1}{\lambda }}>1.$$

(67)

5: 

According to Theorem 6, all solutions of (65) are oscillatory if

$${\mu }_{0}e{\alpha }^{\alpha }{\left(1+{\alpha }^{\alpha -1}{\lambda }^{-1}{\mu }_0\right)}^{\alpha }ln\lambda {\displaystyle \frac{1}{\lambda }}>1.$$

(68)

6: 

According to Corollary 1 (condition (49)), all solutions of (65) are oscillatory if

$${\mu }_0{\left(\alpha +1\right)}^{\left(\alpha +1\right)}{\displaystyle \frac{1}{{\lambda }^{\alpha }}}>1.$$

(69)

Remark 1.

We note that condition (68) improves condition (67).

Example 2.

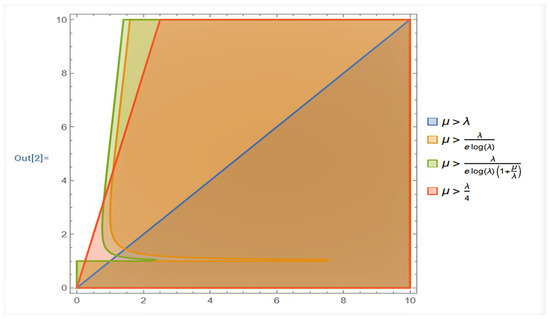
Consider the advanced differential Equation (65) in the linear case as follows:

$${\left({\top }^2\left(P^{\prime }\left(\top \right)\right)\right)}^{\prime }+{\int }_{k_1}^{k_2}{\mu }_{0}P\left(\lambda \top \right)\mathrm{d}\varsigma =0.$$

(70)

By applying the results obtained in Example 1 as a special case ($\alpha =1)$ for (65) and by taking certain values for λ, we obtain the oscillation criteria for (70) (see Figure 1 and Table 1).

Figure 1. Test of the quality of criteria for Equation (70).

Table 1. The most effective theorems according to the change in the values of $\lambda$.

More efficient Theorems when	$\lambda$ has larger values	$\lambda$ has smaller values
	Theorems 5 and 6	Theorems 3 and 7

Remark 2.

We note that both Theorems 5 and 6 fail to apply when $\lambda =1,$ while condition (69) resulting from Theorem 7 leads to

$${\mu }_0>1/4,$$

and this is considered a sharp criterion for the Euler equation.

Example 3.

Consider the advanced differential Equation (65) with

$$j:={\alpha }^{\alpha +1}{\displaystyle \frac{{\mu }_0}{\lambda }}\mathit{and}v:=\alpha {\left({\displaystyle \frac{{\mu }_0}{\lambda }}\right)}^{1/\alpha }.$$

Now, assuming that (50) holds, we conclude the following:

1: 

(66) can be written as

$${\mu }_0{\displaystyle \frac{1}{{\alpha }^{-\alpha }}}{\displaystyle \frac{{\lambda }^{j-1}}{{\left(1-j\right)}^{\alpha }\left(1-v\right)}}>1;$$

2: 

(67) can be written as

$${\mu }_0{\displaystyle \frac{1}{{\alpha }^{-\alpha }}}{\displaystyle \frac{eln\lambda }{\lambda \left(1-j\right)}}>1;$$

3: 

(69) can be written as

$${\mu }_0{\displaystyle \frac{1}{\left(\alpha +1\right)}}{\displaystyle \frac{1}{{}^{-\left(\alpha +1\right)}\lambda ^{\alpha \left(1-j\right)}}}>1.$$

Remark 3.

From the above example, we find that Theorem 8, Theorem 9, and Theorem 10 improve the results stated in Theorem 3, Theorem 5, and Theorem 7, respectively.

Example 4.

Consider the following advanced differential equation:

$${\left({\top }^2{P}^{\prime }\left(\top \right)\right)}^{\prime }+{\displaystyle \frac{{\mu }_0}{2}}P\left(2\varsigma \right)=0.$$

(71)

Clearly,

$$\Pi \left(\top \right)={\int }_{\top }^{\infty }{\varsigma }^{-2}\mathrm{d}\varsigma ={\displaystyle \frac{1}{\top }}.$$

We can conclude the following:

1: 

From Theorem 3, it follows that all solutions of (71) are oscillatory if

$${\mu }_0>4.$$

2: 

From Theorem 5, it follows that all solutions of (71) are oscillatory if

$${\mu }_0>{\displaystyle \frac{4}{eln2}}.$$

3: 

From Theorem 6, it follows that (71) is oscillatory if

$${\mu }_0>{\displaystyle \frac{4}{eln2\left(1+\frac{1}{4}{\mu }_0\right)}}.$$

4: 

From (49), it follows that all solutions of (71) are oscillatory if

$${\mu }_0>1.$$

Remark 4.

Most of the previous literature that studied special cases of (1) shows results that ensure the oscillation of the solutions of the studied equations under two conditions. For example, the author of [19] studied Equation (9) and provided condition (10) to guarantee the exclusion of nonoscillatory decreasing solutions. Subsequently, using various methods, different conditions were provided to exclude nonoscillatory increasing solutions. Thus, the results given in [19] require two conditions, whereas we used a single condition to ensure the exclusion of all nonoscillatory solutions (see Theorems 2, 3, 5, and 6).

Furthermore, the use of the generalized Riccati assumption in Theorem 3, in the presence of the function $\psi \left(\top \right)$, offers us multiple opportunities to test the oscillation of (1) (see Theorem 7 and Corollary 1).

4. Conclusions

Studying the behavior of solutions to equations in a noncanonical case is more challenging than in a canonical case due to the difficulty in establishing relationships between the solution and its various derivatives. These relationships are crucial for obtaining criteria to exclude the possibility of multiple derivative-positive, nonoscillatory solutions. By employing the Riccati method and the comparison principle, along with other analytical methods, we obtained different criteria. We presented distinctive results that do not require additional restrictions, as is usually the case in most previous studies. We provided a single criterion that ensures the exclusion of the possibility of nonoscillatory solutions of the increasing/decreasing positive type.

In addition, concerning future research, we see an opportunity to expand the scope of this study. We specifically suggest exploring the possibility of applying the same methods to establish criteria for the oscillation of neutral differential equations of the form

$${\left(r\left(\top \right){\left({\left(P\left(\top \right)+G\left(\top \right)P\left(\sigma \left(\top \right)\right)\right)}^{\prime }\right)}^{\alpha }\right)}^{\prime }+{\int }_{k_1}^{k_2}\mu \left(\top ,\varsigma \right)P^{\alpha }\left(l\left(\top ,\varsigma \right)\right)\mathrm{d}\varsigma =0.$$

This expansion could contribute to enhancing the applicability of the methods established in this paper to a broader range of differential equations, thereby promoting ongoing advancement in this field.