A Generalised Difference Equation and Its Dynamics and Solutions
Abstract
1. Introduction
2. Preliminaries
3. Dynamics of Equation (1)
- (i)
- If , then the equilibrium point of Equation (5) is locally asymptotically stable;
- (ii)
- If then the equilibrium points and are unstable.
3.1. The Difference Equation
3.2. The Difference Equation
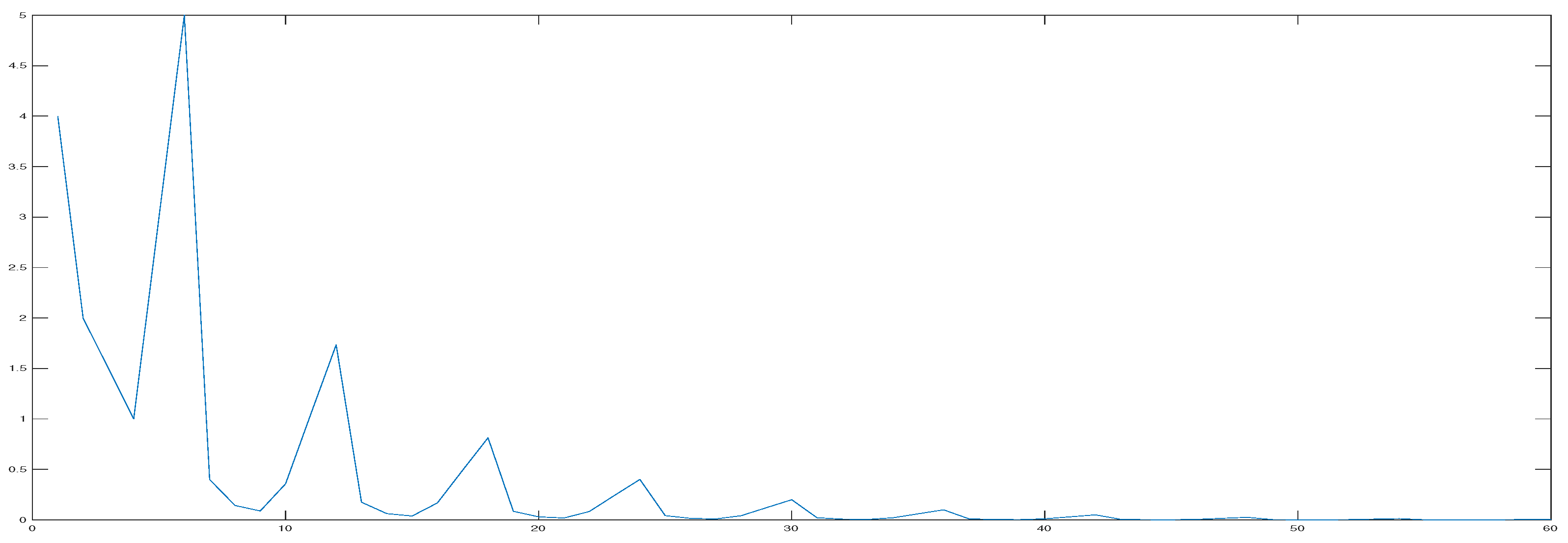
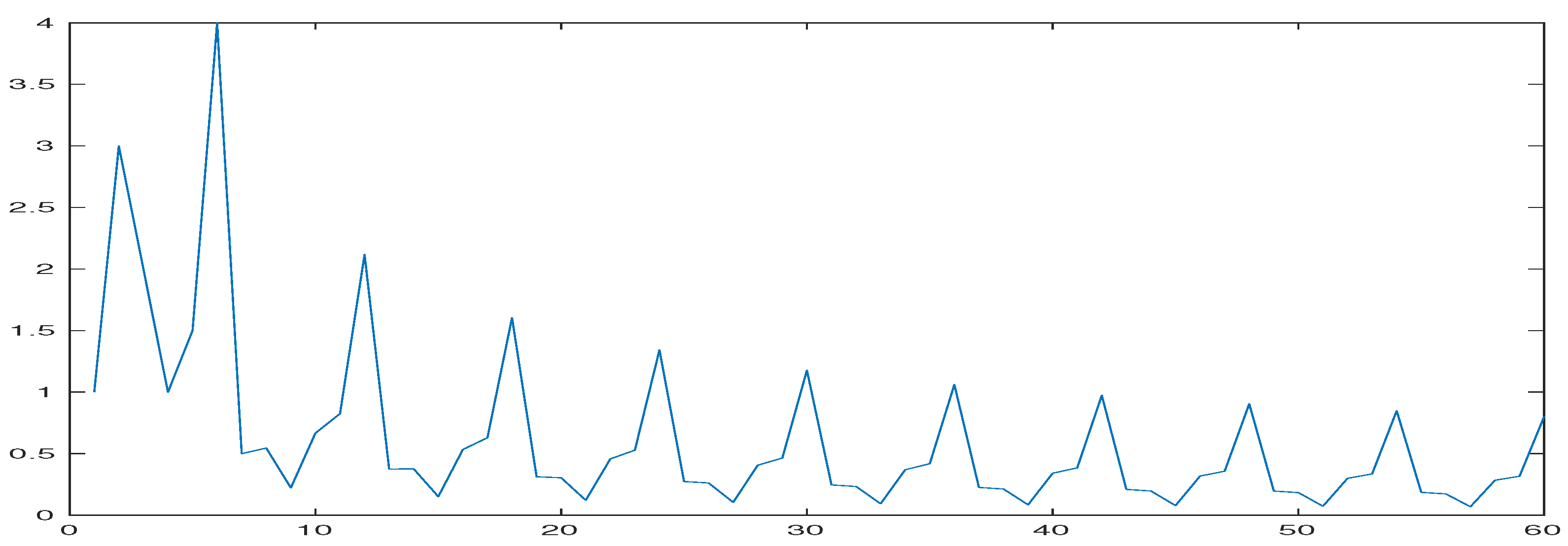
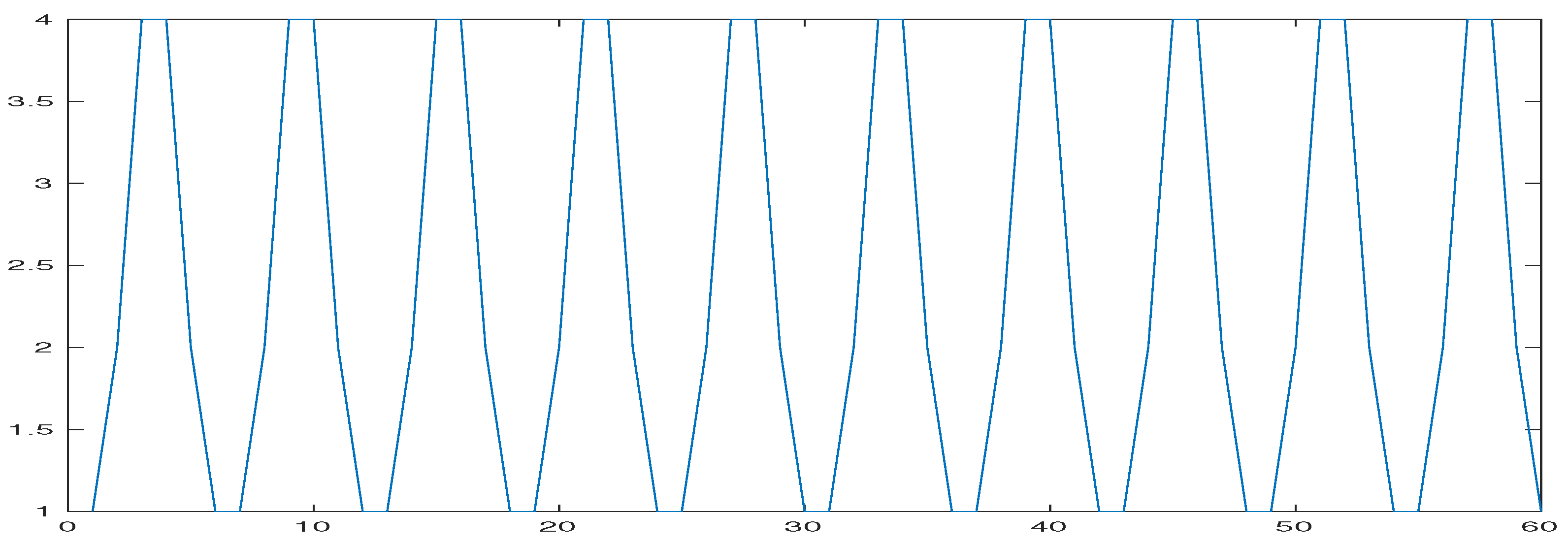
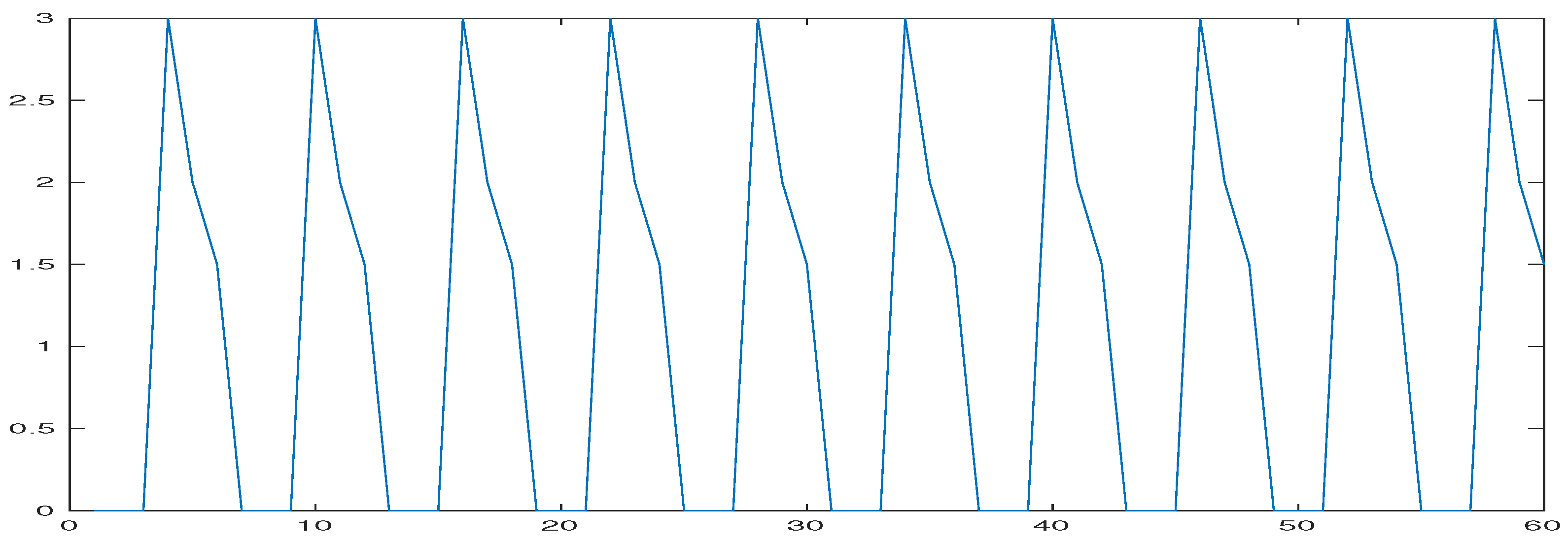
4. Numerical Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Andruch-Sobilo, A.; Migda, M. Further properties of the rational recursive sequence . Opusc. Math. 2006, 26, 387–394. [Google Scholar]
- Elsayed, E.M. On the solutions of a rational recursive sequence of a big order. Folia Math. 2008, 15, 25–39. [Google Scholar]
- Elsayed, E.M. On the difference equation . Thai J. Math. 2009, 7, 1–8. [Google Scholar]
- Elsayed, E.M. Solutions of a recursive sequence of order ten. Gen. Math. 2011, 19, 145–162. [Google Scholar]
- Elsayed, E.M. On the solution of some difference equations. Eur. J. Pure Appl. Math. 2011, 4, 287–303. [Google Scholar]
- Aloqeili, M. Dynamics of a rational difference equation. Appl. Math. Comput. 2006, 176, 768–774. [Google Scholar] [CrossRef]
- Ghazel, M.; Elsayed, E.M.; Matouk, A.E.; Mousallam, A.M. Investigating dynamical behaviors of the difference equation . J. Nonlinear Sci. Appl. 2017, 10, 4662–4679. [Google Scholar] [CrossRef]
- Abo-Zeid, R. Global Behavior of the difference equation . Arch. Math. (Brno) 2015, 51, 77–85. [Google Scholar] [CrossRef]
- Karatas, R. On the solutions of the recursive sequence . Fasc. Math. 2010, 45, 37–45. [Google Scholar]
- Karatas, R. On positive solutions of the difference equation . Int. J. Contemp. Math. Sci. 2006, 1, 495–500. [Google Scholar] [CrossRef]
- Karatas, R. A solution form of a rational difference equation. Konuralp J. Math. 2023, 11, 20–23. [Google Scholar]
- Ibrahim, T.F. Dynamics of a rational recursive sequence of order two. Int. J. Math. Comput. 2009, 5, 98–105. [Google Scholar]
- Kocic, V.L.; Ladas, G. Global Behavior of Nonlinear Difference Equations of High Order with Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Gelisken, A.; Karatas, R. On a solvable difference equation with sequence coefficients. Adv. Appl. Disc. Math 2022, 30, 27–33. [Google Scholar] [CrossRef]
- Ahmed, A.M. On the dynamics of a higher order rational difference equation. Discret. Dyn. Nat. Soc. 2011, 419789, 8. [Google Scholar] [CrossRef]
- Simsek, D.; Abdullayev, F. On the recursive sequence . J. Math. Sci. 2018, 234, 73–81. [Google Scholar] [CrossRef]
- Simsek, D.; Ogul, B.; Çınar, C. Solution of the rational difference equation . Filomat 2019, 33, 1353–1359. [Google Scholar] [CrossRef]
- Tollu, D.T.; Yazlık, Y.; Taşkara, N. Behavior of positive solutions of a difference equation. J. Appl. Math. Inf. 2017, 35, 217–230. [Google Scholar] [CrossRef]
- El-Metwally, H.; Grove, A.; Ladas, E.A.; Levins, G.; Radin, M. On the difference equation xn+1 = α + βxn−1e−xn. Nonlinear Anal. Theory Methods Appl. 2003, 47, 4623–4634. [Google Scholar] [CrossRef]
- Almatrafi, M.B.; Elsayed, E.M.; Alzahrani, F. Investigating some properties of a fourth order difference equation. J. Comput. Anal. Appl. 2020, 28, 243–253. [Google Scholar]
- Gümüş, M.; Soykan, Y. The dynamics of the positive solutions of a higher order fractional difference equation with arbitrary powers. J. Appl. Math. Inform. 2017, 35, 267–276. [Google Scholar] [CrossRef]
- Karatas, R. Global behavior of a higher order difference equation. Comput. Math. Appl. 2010, 60, 830–839. [Google Scholar] [CrossRef]
- Karatas, R. Global behavior of a rational recursive sequence. Ars Combinatoria 2010, 97A, 421–428. [Google Scholar]
- Ergin, S.; Karatas, R. On the solutions of the recursive sequence . Thai J. Math. 2016, 14, 391–397. [Google Scholar]
- Ergin, S.; Karatas, R. On the dynamics of a recursive sequence. Ars Comb. 2013, 109, 353–360. [Google Scholar]
- Saary, T.I. Modern Nonlinear Equations; McGraw Hill: New York, NY, USA, 1967. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karatas, R.; Gelişken, A.; Arı, M. A Generalised Difference Equation and Its Dynamics and Solutions. Mathematics 2024, 12, 3531. https://doi.org/10.3390/math12223531
Karatas R, Gelişken A, Arı M. A Generalised Difference Equation and Its Dynamics and Solutions. Mathematics. 2024; 12(22):3531. https://doi.org/10.3390/math12223531
Chicago/Turabian StyleKaratas, Ramazan, Ali Gelişken, and Murat Arı. 2024. "A Generalised Difference Equation and Its Dynamics and Solutions" Mathematics 12, no. 22: 3531. https://doi.org/10.3390/math12223531
APA StyleKaratas, R., Gelişken, A., & Arı, M. (2024). A Generalised Difference Equation and Its Dynamics and Solutions. Mathematics, 12(22), 3531. https://doi.org/10.3390/math12223531





