The High Relative Accuracy of Computations with Laplacian Matrices

Abstract

This paper provides an efficient method to compute an $LDU$ decomposition of the Laplacian matrix of a connected graph with high relative accuracy. Several applications of this method are presented. In particular, it can be applied to efficiently compute the eigenvalues of the mentioned Laplacian matrix. Moreover, the method can be extended to graphs with weighted edges.

1. Introduction

In graph theory, the Laplacian matrix, also called the Kirchhoff matrix, is a matrix representation of a graph that has played a key role in many applications (see [1,2]). It can be viewed as a discrete analog of the Laplacian operator in multivariable calculus. In fact, it is a matrix form of the negative discrete Laplace operator on a graph approximating the negative continuous Laplacian obtained by the finite difference method. The Laplacian matrix also arises in the analysis of random walks and electrical networks on graphs [3] and, in particular, in the computation of resistance distances. Other application fields of Laplacian matrices include graph isomorphism problems, numerical methods for differential equations, physical chemistry, organic chemistry, biochemistry, computer science, and design of statistical experiments. Further references on these applications can be found in [4,5].

As far as we know, there is no study concerning accurate computations with Laplacian matrices. As for the conditioning of Laplacian matrices, we can mention [6]. In this paper, we present an efficient method to compute an $LDU$ decomposition of the Laplacian matrix of a connected graph with high relative accuracy. The first application of this result is devoted to the computation of the number of spanning trees of a connected graph with high relative accuracy. The second application deals with the computation of the eigenvalues of a Laplacian matrix with high relative accuracy.

It is well known that the number of connected components of a graph coincides with the multiplicity of 0 as an eigenvalue of the Laplacian matrix and that the Laplacian matrix is a symmetric positive semidefinite matrix. In a connected graph, the second smallest eigenvalue of the Laplacian matrix provides the algebraic connectivity of the graph and has many important applications. So, it is convenient to accurately approximate this minimal positive eigenvalue of the Laplacian matrix. Furthermore, the lowest k eigenvalues and their corresponding eigenvectors have a direct application to data science in spectral clustering (see, for example, [7]). However, to date, the accurate computation of the eigenvalues of a matrix has only been obtained for matrices satisfying very restrictive conditions. We show in this paper that, for Laplacian matrices of connected graphs, their eigenvalues can be computed with an efficient method with high relative accuracy. This application of the minimal positive eigenvalue of the Laplacian matrix is an example of the application of the spectrum of the Laplacian matrix to the graph structure, which corresponds to the area of spectral graph theory [8]. Many other applications could be mentioned and, for them, our accurate and efficient method could be used.

High relative accuracy (HRA) is a very desirable property because, if an algorithm is performed to HRA in floating-point arithmetic, then the relative errors in the computations have the order of the unit round-off (or machine precision). In fact, a real value $y\ne 0$ is said to be computed to HRA whenever the computed $\tilde{y}$ satisfies

$${\displaystyle \frac{|y-\tilde{y}|}{|y|}}<ku,$$

where u is the unit round-off (or machine precision), and $k>0$ is a constant that does not depend on the arithmetic precision. It is known that an algorithm computes with HRA when it only uses products, quotients, additions of numbers with the same sign, or subtractions of initial data (cf. [9]); that is, the only forbidden operation is the subtraction of numbers (which are not initial data) with the same sign. Up to now, HRA linear algebra computations have only been guaranteed for a few classes of matrices and using an adequate parametrization of the matrices. Among them, we can mention some subclasses of totally positive matrices (see, for instance, [10,11,12,13]) or matrices related to diagonal dominance (cf. [14,15,16] ). In this last case, rank-revealing decompositions, which will be presented below, have played a crucial role.

Given an $n\times n$ matrix A, let X be $n\times r$, D be $r\times r$ and Y be $r\times n$ matrices. We say that $A=XD{Y}^T$ is a rank-revealing decomposition (RRD) if X and Y are well conditioned, and D is a nonsingular diagonal matrix. The interest in obtaining an RRD of a matrix comes from the fact that it can be used to compute its singular values (and so, its eigenvalues when it is symmetric) efficiently and with HRA using the algorithm introduced in Section 3 of [9]. Here, we present an efficient algorithm to obtain an RDD of a Laplacian matrix of a connected graph.

The paper is organized as follows: Section 2 presents the basic definitions, notations, and results. Section 3 provides the HRA and efficient method to obtain an $LDU$ decomposition of a Laplacian matrix of a connected graph, and we also include the corresponding algorithm in pseudocode. The main result is applied to compute the number of spanning trees of a connected graph with high relative accuracy, which is illustrated with an example from chemistry in Section 3.1. In Section 3.2, the main result is applied to the computation of the eigenvalues of a Laplacian matrix of a connected graph with high relative accuracy using an RRD of the matrix. The concept of the Laplacian matrix extends naturally to a graph with non-negative weights on the edges (cf. [2,17]). Section 4 extends the result of Section 3 to these graphs. Section 5 includes numerical examples to illustrate the accuracy of the proposed methods. Finally, Section 6 summarizes the main conclusions of the paper.

2. Basic Definitions, Notations, and Results

We say that a real matrix $A={\left(a_{ij}\right)}_{1\le i,j\le n}$ is a Z-matrix if all its off-diagonal entries are nonpositive, i.e., $a_{ij}\le 0$ for all $(i,j)$ such that $i\ne j$.

We say that $A={\left(a_{ij}\right)}_{1\le i,j\le n}$ is a (row) diagonally dominant (DD) matrix if

$$|a_{ii}|\ge \sum _{j\ne i}|a_{ij}|\mathrm{for}\mathrm{all}i=1,\dots ,n,$$

(1)

and we say that $A={\left(a_{ij}\right)}_{1\le i,j\le n}$ is a column DD matrix if $A^T$ is a row DD matrix. Let us recall that the singular value decomposition (SVD) of a real $n\times n$ matrix A is the factorization $A=U\Sigma V^T$, where U and V are orthogonal matrices, and $\Sigma$ is non-negative and diagonal. The diagonal entries of $\Sigma$ are the singular values of A. For the particular case that A is positive semidefinite, the singular values are equal to the eigenvalues.

Let us denote by $Q_{k,n}$ the set of strictly increasing sequences of k integers chosen from $\{1,\dots ,n\}$. Let $\alpha =({\alpha }_1,\dots ,{\alpha }_{k_1})$ and $\beta =({\beta }_1,\dots ,{\beta }_{k_2})$ be sequences of $Q_{k_1,n}$ and $Q_{k_2,n}$, respectively. Then, $A[\alpha |\beta ]$ denotes the $k_1\times k_2$ submatrix of A formed using the rows numbered by ${\alpha }_1,\dots ,{\alpha }_{k_1}$ and the columns numbered by ${\beta }_1,\dots ,{\beta }_{k_2}$. If $\alpha =\beta$, we use the abbreviated notation $A\left[\alpha \right]:=A[\alpha |\alpha ]$.

Given a simple graph $\mathcal{G}$ with n vertices $v_1,\dots ,v_n$ and a set of edges connecting different pairs of nodes, we build the adjacency matrix $A={\left(a_{ij}\right)}_{1\le i,j\le n}$ of G as

$${\displaystyle a_{ij}:=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}{v}_i\mathrm{is}\mathrm{connected}\mathrm{to}{v}_j,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.}$$

The degree deg$\left(v_i\right)$ is defined as the number of neighbors of the node $v_i$. The degree matrix$D:=\mathrm{diag}(d_1,\dots ,d_n)$ is a diagonal matrix such that $d_i=\mathrm{deg}\left(v_i\right)$. Then, the Laplacian matrix$\mathcal{L}={\left(l_{ij}\right)}_{1\le i,j\le n}$ is defined as $\mathcal{L}=D-A$. Hence, its entries are given by

$${\displaystyle l_{ij}:=\left\{\begin{array}{cc}deg\left(v_i\right),\hfill & \mathrm{if}i=j,\hfill \\ -1,\hfill & \mathrm{if}i\ne j\mathrm{and}{v}_i\mathrm{is}\mathrm{adjacent}\mathrm{to}{v}_j,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.}$$

(2)

This special structure of the Laplacian matrix translates into many interesting properties. The Laplacian spectra provide a lot of information about the graph and have many applications. For instance,

$$l_{ii}=\sum _{k\ne i}-l_{ik},i=1,\dots ,n.$$

(3)

Hence, $\mathcal{L}e=0$, where $e={(1,\dots ,1)}^T$ and so it has zero as an eigenvalue. Moreover, the multiplicity of ${\lambda }_1=0$ as an eigenvalue shows the number of connected components of the graph. The second smallest eigenvalue, ${\lambda }_2$ (the first nonzero eigenvalue), is known as the Fiedler eigenvalue and gives information about the connectivity of the graph [8]. Moreover, the lowest k eigenvalues and their corresponding eigenvectors have a direct application to data science in spectral clustering (see, for example, [7]).

In this article, we consider the computation of an LDU factorization of the Laplacian matrix to HRA. Then, we will show some applications of this factorization such as the computation of the number of spanning trees of G, $t\left(G\right)$, and the obtention of a rank-revealing decomposition that can be used to obtain the eigenvalues of $\mathcal{L}$ to HRA. In particular, property (3) will be key to achieving accurate computations with this class of matrices. Given a DD Z-matrix with non-negative diagonal entries, a parametrization that can be used to achieve accurate computations is given by its off-diagonal entries and the row sums. Taking these parameters as input, we can then use a modified version of Gaussian elimination to compute an LDU factorization with HRA that serves as an RRD. RRD has been recalled in the Introduction, and we also highlighted that it can be used to compute singular values efficiently and with HRA using the algorithm introduced in Section 3 of [9]. The RRD obtained in this paper uses unit triangular DD matrices. In order to illustrate that these matrices are very well conditioned, let us recall the bound below for the condition number of such matrices introduced in [15]. Previously, recall that, given a nonsingular matrix A, we can consider the following condition: number

$${\kappa }_{\infty }\left(A\right):={\parallel A\parallel }_{\infty }{\parallel A^{-1}\parallel }_{\infty }.$$

Proposition 1

(Proposition 2.1 of [15]). Let $T={\left(t_{ij}\right)}_{1\le i,j\le n}$ be a unit triangular matrix diagonally dominant by columns (resp. rows). Then, the elements of $T^{-1}$ are bounded in absolute value by 1 and ${\kappa }_{\infty }\left(T\right)\le n^2$ (respectively, ${\kappa }_{\infty }\left(T\right)\le 2n$).

In the main result of this manuscript, we will show that it is possible to obtain an LDU decomposition of a Laplacian matrix with HRA using an adapted version of Gaussian elimination without pivoting. This LDU decomposition can be used to compute the number of spanning trees of a graph with HRA and obtain an RRD. In ref. [14], pivoting was used to derive RRD for DD M-matrices. Recall that a nonsingular Z-matrix A is an M-matrix if $A^{-1}$ is non-negative. Applications of M-matrices and related classes can be found in [18,19] and references therein. Our approach does not use pivoting and leads to a factorization $L\widehat{D}{L}^T$ with L lower triangular and column DD (and $L^T$ row DD) in contrast to the factorization obtained in [14] with complete symmetric pivoting, where $L^T$ only satisfies if the diagonal entries have absolute values greater than or equal to the absolute value of the entries of their rows. Moreover, no pivoting reduces the computational cost, and it also has the additional important advantage that, when the Laplacian matrix is banded, no pivoting preserves its banded structure.

There is a sufficient condition to assure the high relative accuracy of an algorithm, the condition of no inaccurate cancellations (NICs) (cf. [20]): the algorithm only uses multiplications, divisions, sums of real numbers of the same sign, and subtractions of initial data. So, an algorithm that avoids subtractions (with the exception of subtractions of initial data) can be carried out with high relative accuracy. An algorithm that avoids all subtractions is called subtraction-free (SF), and it also satisfies the NIC condition. Hence, SF algorithms assure high relative accuracy.

3. Main Result and Some Consequences

We start this section by presenting the main result of the paper. We give an efficient method with HRA to obtain an LDU decomposition of a Laplacian matrix of a connected graph. The corresponding algorithm is included later. After that, we will show two applications of this factorization to achieve accurate computations with the Laplacian matrices.

Theorem 1.

Let $\mathcal{L}={\left(l_{ij}\right)}_{1\le i,j\le n}$ be the Laplacian matrix of a connected graph. Then, we can compute its LDU decomposition $\mathcal{L}=L\widehat{D}{L}^T$ with an SF algorithm (and so, with HRA) of at most $\mathcal{O}\left(n^3\right)$ elementary operations, where L is column DD, and $\widehat{D}$ is non-negative.

Proof. 

Let $\mathcal{L}={\left(l_{ij}\right)}_{1\le i,j\le n}$ be a Laplacian matrix of a connected graph of n nodes. By Lemma 13.1.1 of [2], $\mathrm{rank}\mathcal{L}=n-1$. Let us apply Gaussian elimination to $\mathcal{L}$. Since $\mathcal{L}$ has the special sign structure of a Z-matrix, we can adapt Gaussian elimination to be an SF algorithm. Let us recall that Gaussian elimination is an algorithm that produces zeros below the main diagonal of a matrix. It consists of $n-1$ steps when applied to an $n\times n$ matrix, producing matrices ${\mathcal{L}}^{\left(t\right)}={\left(l_{ij}^{\left(t\right)}\right)}_{1\le i,j\le n}$, $t\le n$:

$$\mathcal{L}={\mathcal{L}}^{\left(1\right)}\to {\mathcal{L}}^{\left(2\right)}\to \dots \to {\mathcal{L}}^{\left(n\right)},$$

where ${\mathcal{L}}^{\left(n\right)}$ is an upper triangular matrix. While the pivots are nonzero, the matrix ${\mathcal{L}}^{(t+1)}$ can be obtained from ${\mathcal{L}}^{\left(t\right)}$ in the following way: We produce zeros at the t-th column by subtracting multiples of the t-th row from the rows below it as follows:

$$l_{ij}^{(t+1)}=\left\{\begin{array}{cc}{l}_{ij}^{\left(t\right)},& if1\le i\le t,\\ l_{ij}^{\left(t\right)}-{\displaystyle \frac{l_{it}^{\left(t\right)}}{l_{tt}^{\left(t\right)}}}{l}_{tj}^{\left(t\right)},& ift<i\le n.\end{array}\right.$$

Observe that the first pivot $l_{11}^{\left(1\right)}=l_{11}$ is nonzero and thus positive by (3) because $\mathcal{L}$ is a Z-matrix. In fact, if $l_{11}^{\left(1\right)}=l_{11}=0$ then, by (3), $0={\sum }_{j>1}-l_{1j}$, which implies that $l_{1j}=0$ for all j since $\mathcal{L}$ is a Z-matrix. This contradicts that $\mathcal{L}$ is the Laplacian of a connected graph.

Let $k>1$ be the first index such that $l_{kk}^{\left(k\right)}=0$. Let us see that all submatrices ${\mathcal{L}}^{\left(r\right)}[r,\dots ,n]$ with $r\le k$ preserve the property (3):

$$l_{ii}^{\left(r\right)}=\sum _{j\ne i}-l_{ij}^{\left(r\right)},r\le k.$$

(4)

Property (3) is equivalent to $\mathcal{L}e=0$, where $e={(1,\dots ,1)}^T$. After t ($t<k$) steps of Gaussian elimination, e is again the solution of the equivalent linear system with coefficient matrix ${\mathcal{L}}^{(t+1)}$: ${\mathcal{L}}^{(t+1)}e=0$. So, ${\mathcal{L}}^{\left(r\right)}e=0$ for $r=1,\dots ,k$ and then the diagonal entries of ${\mathcal{L}}^{\left(r\right)}$ satisfy (4).

Let us now see that we can obtain matrices ${\mathcal{L}}^{\left(2\right)}[2,\dots ,n],\dots ,{\mathcal{L}}^{\left(k\right)}[k,\dots ,n]$ with an SF algorithm.

For the first step of Gaussian elimination, we subtract multiples of the first row of ${\mathcal{L}}^{\left(1\right)}$ from the rows below it to produce zeros in the first column. All the off-diagonal entries of ${\mathcal{L}}^{\left(2\right)}[2,\dots ,n]$ are computed as the sum of two nonpositive numbers so that they can be obtained without subtractions, and they are again nonpositive. Only the diagonal entries would be computed as a true subtraction. However, these entries can be computed without subtractions using (4) for $r=2$ and we also infer that they are non-negative. In particular, we can compute the second diagonal entry after performing the first elimination step as $l_{22}^{\left(2\right)}=-{\sum }_{j=3}^n{l}_{2j}^{\left(2\right)}$, and if it is nonzero, then we use it as a pivot for the next elimination step. Analogously, all off-diagonal entries of matrices ${\mathcal{L}}^{\left(3\right)}[3,\dots ,n],\dots ,{\mathcal{L}}^{(k-1)}[k-1,\dots ,n]$ are nonpositive. Hence, by (4), all the pivots $l_{tt}^{\left(t\right)}$ are given by

$$l_{tt}^{\left(t\right)}=-\sum _{j=t+1}^n{l}_{tj}^{\left(t\right)},\mathrm{for}t=1,\dots ,k-1,$$

(5)

so they are non-negative and can be computed with HRA.

Let us now assume that $k<n$, and we shall arrive at a contradiction. If $k<n$, then $l_{kk}^{\left(k\right)}=0$ for $k<n$. By (4) for $r=k$, and taking into account that the off-diagonal entries of ${\mathcal{L}}^{\left(k\right)}$ are nonpositive, we have that the first row of ${\mathcal{L}}^{\left(k\right)}[k,\dots ,n]$ is null and, since it is well known that all matrices ${\mathcal{L}}^{\left(r\right)}[r,\dots ,n]$ ($r\le k$) inherit the symmetry of $\mathcal{L}$, the first column of ${\mathcal{L}}^{\left(k\right)}[k,\dots ,n]$ is also null. Then, we can continue the Gaussian elimination with the pivot $l_{k+1,k+1}^{(k+1)}:=l_{k+1,k+1}^{\left(k\right)}$, which must be nonzero because, otherwise, ${\mathcal{L}}^{\left(k\right)}[k+1,\dots ,n]$ would also have nulls its first row and column. Then, $\mathrm{rank}\mathcal{L}=\mathrm{rank}{\mathcal{L}}^{\left(k\right)}\le n-2$, a contradiction with $\mathrm{rank}\mathcal{L}=n-1$. Analogously, all remaining pivots $l_{tt}^{\left(t\right)}\ne 0$ for $t=k+1,\dots ,n$ and (4) also holds for all $r=k+1,\dots ,n$. But (4) for $r=n$ implies that $l_{nn}^{\left(n\right)}=0$ and, since we also have $l_{kk}^{\left(k\right)}=0$, we again obtain a contradiction with $\mathrm{rank}\mathcal{L}=n-1$. In conclusion, since $\mathrm{rank}\mathcal{L}=n-1$, $k=n$.

Taking into account that $\mathcal{L}$ is a symmetric matrix, the result of Gaussian elimination is therefore a factorization $\mathcal{L}=L\widehat{D}{L}^T$, where L is a lower triangular with unit diagonal, and $\widehat{D}$ is a diagonal matrix with first $n-1$ positive diagonal entries and a last zero diagonal entry. Since the t-th row of the upper triangular matrix $\widehat{D}{L}^T$ is formed by $t-1$ zeros and the entries $l_{tj}^{\left(t\right)},$$j\ge t$, we deduce from the positivity of $l_{tt}^{\left(t\right)}$ and the nonpositivity of the off-diagonal entries that $L^T$ is a Z-matrix. Formula (5) for $k=n$ also implies that the sum of the entries of the first $n-1$ rows of $L^T$ is zero. So, L is column DD.    □

In Algorithm 1, we present the pseudocode for the SF Gaussian elimination that computes the matrices L and D for the LDU decomposition $\mathcal{L}=L\widehat{D}{L}^T$.

Algorithm 1 Adapted Gaussian elimination

Require: The off-diagonal entries of $\mathcal{L}$ : $\mathcal{L}=\left(l_{ij}\right)(i\ne j)$ Ensure: L and $\widehat{D}$ to HRA     for $k=1:n-1$ do           $l_{kk}=-{\sum }_{j=k+1}^n{l}_{kj}$           for $i=k+1:n$ do                 $l_{ik}=l_{ik}/l_{kk}$                 for $j=k+1:n$ do                       If $i\ne j$ then $l_{ij}=l_{ij}-l_{ik}*l_{kj}$                 end for           end for     end for     $L=tril\left(\mathcal{L}\right)$                 ▷ Taking the lower triangular part of L     for $i=1:n-1$ do           $x_{ii}=1$     end for     $\widehat{D}=diag\left(\mathcal{L}\right)$             ▷ Diagonal matrix with the diagonal entries of L

From the LDU decomposition, we can easily obtain the number of spanning trees of G based on the well-known matrix-tree theorem.

Theorem 2

(Theorem 13.2.1 in [2]). Let G be a graph with a Laplacian matrix $\mathcal{L}$. If u is an arbitrary vertex of G numbered by i, then $det\mathcal{L}[1,\dots ,i-1,i+1,\dots ,n]$ is equal to the number of spanning trees of G, $t\left(G\right)$.

The number $t\left(G\right)$ has been used in [21] to compute the number of spanning trees of a polycyclic graph in the context of Chemistry.

Remark 1.

Let us notice that $t\left(G\right)$ can be obtained using Theorem 2 by computing the determinant of the matrix $\mathcal{L}[1,\dots ,n-1]$ obtained after removing the last column and row of $\mathcal{L}$. Since we know how to compute the decomposition $L\widehat{D}U$ of $\mathcal{L}$ with high relative accuracy by Theorem 1, we can obtain this number with HRA from the matrix D of that decomposition as the product of the nonzero diagonal entries.

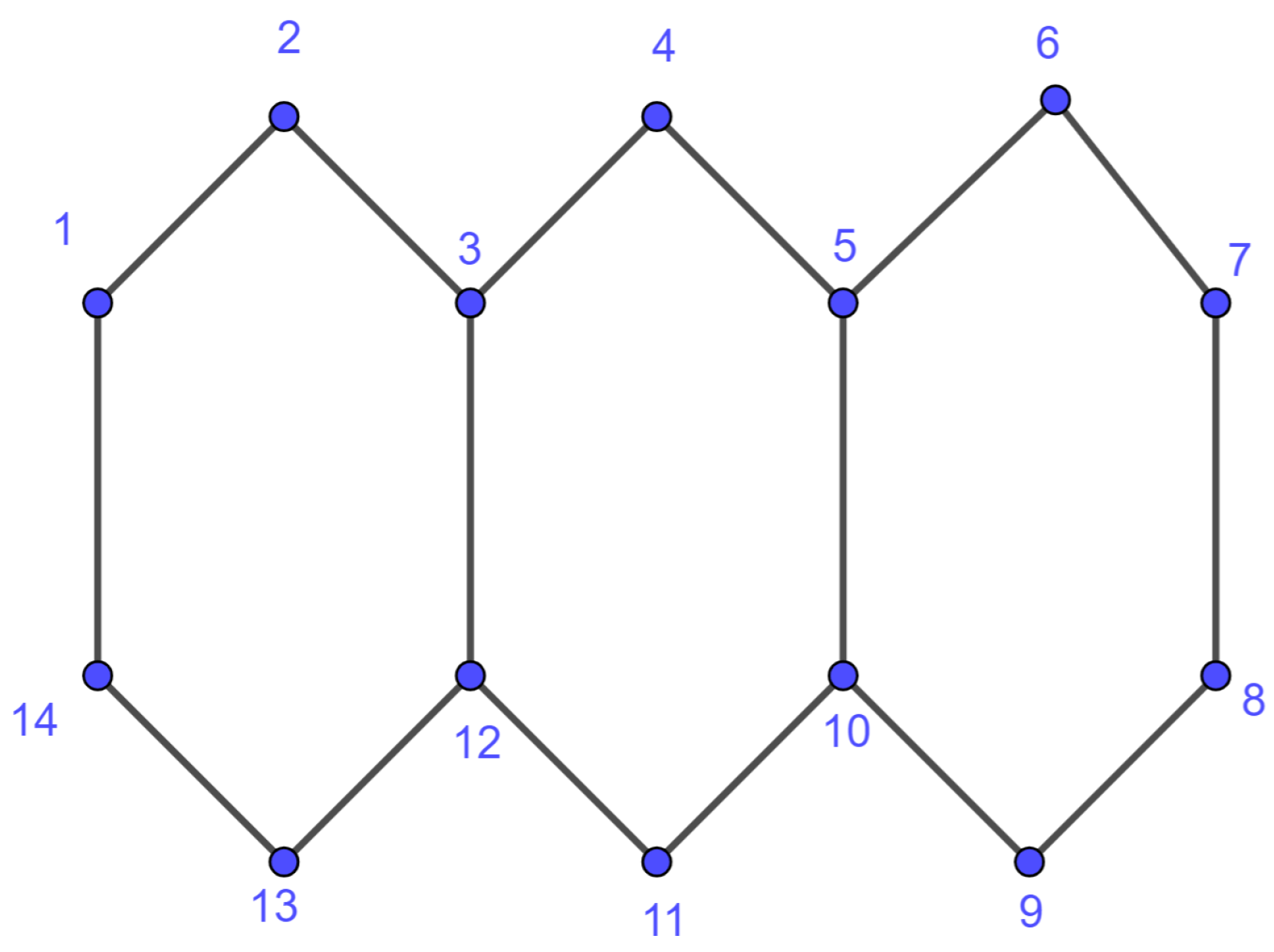
3.1. Example

In this subsection, we will illustrate an example of a Laplacian and its LDU factorization taking a well-known example from chemistry. We considered the polycyclic graph associated with a molecule of anthracene corresponding to Figure 1.

Figure 1. Molecule of anthracene with numbered vertices.

We numbered the nodes from 1 to 14. Then, we built the matrix $\mathcal{L}$ associated with G and applied Algorithm 1 to $\mathcal{L}$. The result is the decomposition $\mathcal{L}=LD{L}^T$, with

$$L=\left(\begin{array}{cccccccccccccc}1.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000\\ -0.500& 1.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000\\ 0.000& -0.667& 1.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000\\ 0.000& 0.000& -0.429& 1.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000\\ 0.000& 0.000& 0.000& -0.636& 1.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000\\ 0.000& 0.000& 0.000& 0.000& -0.423& 1.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000\\ 0.000& 0.000& 0.000& 0.000& 0.000& -0.634& 1.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000\\ 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& -0.732& 1.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000\\ 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& -0.789& 1.000& 0.000& 0.000& 0.000& 0.000& 0.000\\ 0.000& 0.000& 0.000& 0.000& -0.423& -0.268& -0.196& -0.155& -0.953& 1.000& 0.000& 0.000& 0.000& 0.000\\ 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& -0.782& 1.000& 0.000& 0.000& 0.000\\ 0.000& 0.000& -0.429& -0.273& -0.115& -0.073& -0.054& -0.042& -0.035& -0.164& -0.955& 1.000& 0.000& 0.000\\ 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& 0.000& -0.793& 1.000& 0.000\\ -0.500& -0.333& -0.143& -0.091& -0.038& -0.024& -0.018& -0.014& -0.012& -0.055& -0.045& -0.207& -1.000& 1.000\end{array}\right),$$

and $\widehat{D}=\mathrm{diag}(2,1.5,2.3333,1.5714,2.3636,1.5769,1.3659,1.2679,1.2113,1.2791,1.2182,1.2612,1.2071,0)$.

From this factorization, we can compute $t\left(G\right)$ as the product of the nonzero diagonal entries of $\widehat{D}$. Hence, $t\left(G\right)=204$. From L and $\widehat{D}$, we can also obtain a rank-revealing decomposition erasing the last column of L and the last row and column of $\widehat{D}$ as we will remark in the next subsection.

3.2. Rank-Revealing Decomposition

From the accurate LDU decomposition of $\mathcal{L}$ obtained in Theorem 1, we can obtain an RRD for this matrix. This representation of a Laplacian matrix can be used to achieve HRA when we compute its singular values and eigenvalues, as recalled in the Introduction.

Corollary 1.

Let $\mathcal{L}={\left(l_{ij}\right)}_{1\le i,j\le n}$ be the Laplacian matrix of a connected graph. Then, we can compute its rank-revealing decomposition $\mathcal{L}=XD{X}^T$ with an SF algorithm of most $\mathcal{O}\left(n^3\right)$ elementary operations, where X is column DD. Moreover, all the eigenvalues of $\mathcal{L}$ can be computed to HRA with an algorithm of complexity of most $\mathcal{O}\left(n^3\right)$ elementary operations.

Proof. 

By Theorem 1, we obtain the factorization $\mathcal{L}=L\widehat{D}{L}^T$ with HRA. Let us notice that this factorization implies that $\mathcal{L}$ is a positive semidefinite matrix since $\widehat{D}$ is a non-negative diagonal matrix. Hence, its singular values coincide with its eigenvalues. Let us define the matrices $X:=L[1,\dots ,n|1,\dots ,n-1]$ and $D:=\widehat{D}[1,\dots ,n-1]$; thus, we obtain the decomposition $\mathcal{L}=XD{X}^T$, where X is a DD matrix by columns. This fact implies that X is very well conditioned (cf. Proposition 1). Since our adaptation of Gaussian elimination was SF, $A=XD{X}^T$ gives an RRD decomposition that can be taken as input to compute the singular values with HRA applying the algorithm presented in cf. [9]. □

4. An Extension of the Main Result

Let us notice that the proof of Theorem 1 can be extended to more general matrices. In fact, the proposition below shows which hypotheses are sufficient in the proof of Theorem 1 to assure the computation of the eigenvalues with HRA with an algorithm of $\mathcal{O}\left(n^3\right)$ elementary operations.

Proposition 2.

Let $A={\left(a_{ij}\right)}_{1\le i,j\le n}$ be a symmetric Z-matrix that satisfies Property (3) and such that rank$\left(A\right)=n-1$. Then, we can compute its LDU decomposition $A=LD{L}^T$ with an SF algorithm of most $\mathcal{O}\left(n^3\right)$ elementary operations, where L is column DD.

Thanks to Proposition 2, we can extend Theorem 1 to the Laplacian of weighted connected graphs. Let us consider a weighted graph G, where $w_{ij}$ is the non-negative weight associated with the edge between the nodes i and j, with $1\le i,j\le n$. Then, the Laplacian of G is the $n\times n$ matrix $L={\left({\widehat{l}}_{ij}\right)}_{1\le i,j\le n}$, defined as follows:

$${\displaystyle {\widehat{l}}_{ij}:=\left\{\begin{array}{cc}{w}_i,\hfill & \mathrm{if}i=j,\hfill \\ -w_{ij},\hfill & \mathrm{if}i\ne j\mathrm{and}{v}_i\mathrm{is}\mathrm{adjacent}\mathrm{to}{v}_j,\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.}$$

(6)

where $w_i=-\sum l_{ij}$ is the degree of the node i, which is the sum of the weights of edges incident on vertex i. Whenever G is a connected graph, the vector $e=(1,\dots ,1)$ is the only eigenvector associated with the eigenvalue $\lambda =0$ of L, and we have that rank$L=n-1$. Hence, the Laplacian of a weighted connected graph satisfies Proposition 2. Finally, for the Laplacian of a weighted graph, we can obtain an RRD following the same strategy.

Corollary 2.

Let $A={\left(a_{ij}\right)}_{1\le i,j\le n}$ be a symmetric Z-matrix that satisfies Property (3) and such that rank$\left(A\right)=n-1$. Then, we can compute its rank-revealing decomposition $A=XD{X}^T$ with an SF algorithm (and so, with HRA) of most $\mathcal{O}\left(n^3\right)$ elementary operations, where X is column DD. Moreover, all the eigenvalues of A can be computed with HRA with an algorithm of complexity of most $\mathcal{O}\left(n^3\right)$ elementary operations.

5. Numerical Experiments

In this section, we will introduce some examples to showcase some of the results presented in this article. In Theorem 1, we have seen that we can compute an RRD decomposition of a Laplacian matrix with HRA. We extended this result to more classes of matrices in Proposition 2. Now, we will consider some ill-conditioned examples belonging to this class.

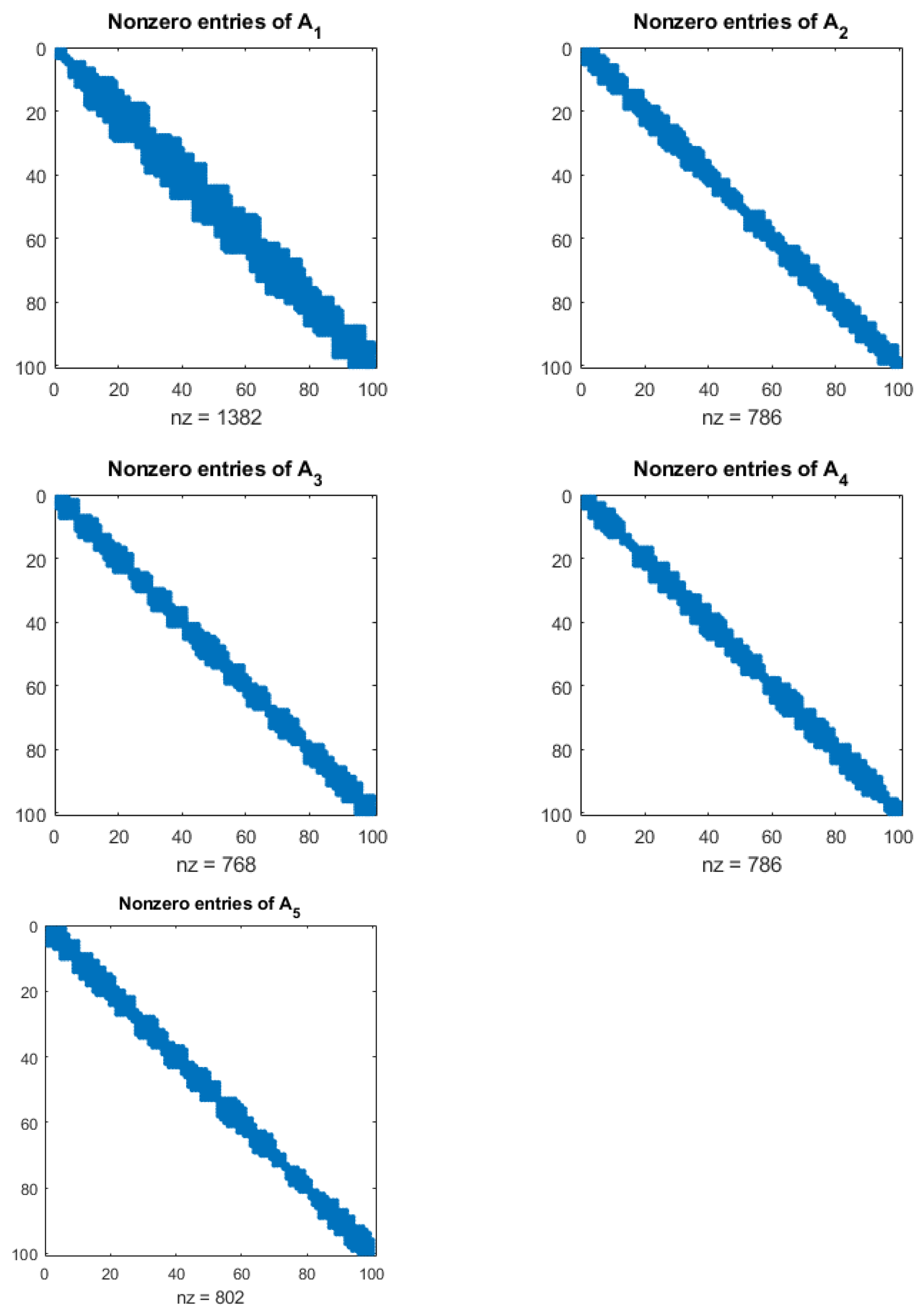
We generated some $100\times 100$ banded matrices that satisfy the hypotheses of Proposition 2, i.e., they are the Laplacian of a weighted undirected graph. We called these matrices $A_k$ for $k=1,2,3,4,5$. These matrices have 100 columns and 100 rows, and most of their entries are zero. The nonzero entries always appear in the diagonal entries, and the off-diagonal entries are closer to the diagonal. In order to decide how many off-diagonal entries below the main diagonal are different from zero, we chose a random integer $b_i$ between 1 and 5 for every column. For example, the first column of the matrix $A_1$ has the first two off-diagonal entries different from zero, i.e., $b_1$ was chosen as 2. Then, we would do the same for the second column, the third column, etc. The only extra condition used is that, whenever the number $b_i$ chosen for the i-th column is equal or smaller than $b_{i-1}-2$, we would set it to $b_i=b_{i-1}-1$ instead. In the case of the matrix $A_1$, the second, third and fourth columns have one off-diagonal entry below the main diagonal different from zero. Then, the fifth row has $b_5=4$, and hence, four entries below the main diagonal were chosen to be different from zero. For all the examples, we used this procedure to decide the nonzero entries below the main diagonal, and then we ensured that the matrices were symmetric. By doing so, we obtained the block structure of nonzero entries, which is illustrated in Figure 2. The quantities $nz$ appearing in these graphics refer to the number of nonzero entries of the matrices. For each of these examples, we generated random integers $c_{ij}$ between 1 and 100 for the off-diagonal nonzero entries of the lower part. Finally, we built the symmetrical matrix $A_k={\left(a_{ij}\right)}_{1\le i,j\le 100}$ such that

$$a_{ij}=\left\{\begin{array}{cc}-{\left(c_{ij}\right)}^7& \mathrm{if}i>j,\\ -{\left(c_{ji}\right)}^7& \mathrm{if}i<j,\\ -\sum _{j\ne i}{a}_{ij}& \mathrm{if}i=j.\end{array}\right.$$

Figure 2. Structure of the nonzero entries of the numerical examples.

In order to test the advantages of using our proposed HRA method, we used Matlab to implement both classical Gaussian elimination without pivoting and an adaptation of Gaussian elimination following the pseudocode presented in Algorithm 1. We used both methods to compute the same $L_i{D}_i{L}_i^T$ decomposition of the matrix $A_i$. Then, we computed this decomposition in Mathematica using a 100-digit precision. In Table 1, we show the largest componentwise relative errors for the approximations of the matrix L computed with both Matlab methods, considering the results from Mathematica as exact.

Table 1. Largest componentwise relative errors for nonzero entries of $L_i$ in the decomposition $A_i=L_i{D}_i{L}_i^T$.

i	${\mathit{\kappa }}_{\mathit{\infty }}\left({\mathit{A}}_{\mathit{i}}[1,\mathit{\dots },\mathit{n}-1]\right)$	${\mathit{\kappa }}_{\mathit{\infty }}\left({\mathit{L}}_{\mathit{i}}\right)$	$max\frac{|{\mathit{x}}_{\mathit{ij}}-{\widehat{\mathit{x}}}_{\mathit{ij}}|}{|{\mathit{x}}_{\mathit{ij}}|}$ for HRA	$max\frac{|{\mathit{x}}_{\mathit{ij}}-{\widehat{\mathit{x}}}_{\mathit{ij}}|}{|{\mathit{x}}_{\mathit{ij}}|}$ for Gauss
1	$1.8471\times {10}^{11}$	474.4763	$4.5563\times {10}^{-16}$	$5.1702\times {10}^{-8}$
2	$1.0001\times {10}^{11}$	436.1355	$4.0695\times {10}^{-16}$	$5.1630\times {10}^{-7}$
3	$5.6660\times {10}^6$	410.2576	$4.0484\times {10}^{-16}$	$3.9087\times {10}^{-12}$
4	$7.2833\times {10}^8$	387.2842	$3.9370\times {10}^{-16}$	$2.2108\times {10}^{-9}$
5	$4.7916\times {10}^{10}$	393.6934	$4.7924\times {10}^{-16}$	$7.0798\times {10}^{-7}$

Let us remark that even though the original matrix is quite ill conditioned, the matrix $L_i$ computed by this method is well conditioned as expected. In Table 1, we also compare the conditioning of the matrix $A_i$ with the condition number of the matrix $L_i$. For the estimation of the condition number of the matrix $A_i$, we considered the submatrix obtained by deleting the last row and column since the matrix is singular, and the multiplicity of the eigenvalue $\lambda =0$ is one. We can see that ${\kappa }_{\infty }\left(L_i\right)$ satisfies the bound given in Proposition 1.

6. Conclusions

A method for efficient computation of the LDU decomposition of the Laplacian matrix of a connected graph was presented. Moreover, it was proved that the method can be performed with high relative accuracy. In particular, it provides a rank-revealing decomposition of the Laplacian matrix of a connected graph, which in turn can be the starting point of the methods in [9] to compute all its eigenvalues with high relative accuracy.

We also highlighted another application of our method, namely computing the number of spanning trees of a connected graph. We also showed the extension of our method to graphs with weighted edges. Numerical examples confirmed the theoretical results.