Abstract
In structural stochastic dynamic analysis, the consideration of the randomness in the physical parameters of the structure necessitates the establishment of numerous stochastic finite element models and the subsequent computation of their corresponding vibration modes. When the complete analysis is applied to calculate the vibration modes for each sample of the stochastic finite element model, a substantial computational expense is incurred. To enhance computational efficiency, this work presents an extended subspace iteration method aimed at rapidly determining the vibration modal parameters of statically indeterminate structures. The essence of this proposed method revolves around efficiently constructing reduced basis vectors during the subspace iteration process, utilizing flexibility disassembly perturbation and the Krylov subspace. This extended subspace iteration method proves particularly advantageous for the modal analysis of finite element models that incorporate a multitude of random variables. The proposed modal random analysis method has been validated using both a truss structure and a beam structure. The results demonstrate that the proposed method achieves substantial savings in computational time. Specifically, for the truss structure, the calculation time of the proposed method is approximately 1.2% and 65% of that required by the comprehensive analysis method and the combined approximation method, respectively. For the beam structure, on average, the computational time of the proposed method is roughly 2.1% of a full analysis and approximately 48.2% of the Ritz vector method’s time requirement. Compared to existing stochastic modal analysis algorithms, the proposed method offers improved computational accuracy and efficiency, particularly in scenarios involving high-discreteness random analyses.
Keywords:
modal random analysis; subspace iteration; stochastic finite element; flexibility disassembly perturbation; Krylov subspace MSC:
65F15
1. Introduction
The material properties and geometric dimensions of a real engineering structure are random [1,2,3]. Therefore, the finite element model (FEM) containing many random variables is more in line with the real situation of a structure. When considering the randomness of the structure, it is usually necessary to take thousands of FEM samples and calculate the corresponding static or dynamic response to analyze the reliability of the structure. Taking dynamic modal analysis as an example, the common methods for solving dynamic eigenvalue problems include the inverse iteration (II) method [4,5], the subspace iteration (SI) method [6,7], model reduction [8], and so on. Among them, the subspace iteration method is the most widely used due to its computational efficiency and ease of programming. Lin and Simoncini [9] applied the subspace iteration method to solve the continuous algebraic Riccati equation. Gu [10] considered randomness within the framework of the subspace iteration method and proposed a new error analysis method. Lasecka and Lewandowski [11] extended the subspace iteration method and applied it to systems of viscoelastic damping elements described by both classical and fractional models. However, for a structure with over ten thousand degrees of freedom (DOFs), conducting a complete dynamic modal analysis generally requires a significant computational cost based on the above methods. If thousands of samples are taken, using the above methods to calculate the modal parameters of each FEM sample will require a huge amount of computation, which may make the stochastic dynamic analysis difficult to carry out. Thus, many dynamic modal reanalysis methods have been proposed in recent years to fast calculate the modal parameters of a random structure based on the modal data of the original structure. Chen et al. [12,13] performed a comparative analysis evaluating the computational efficiency of the matrix perturbation, combined approximation (CA), and extended CA algorithms. Following this, Kirsch et al. [14,15] integrated CA with II and SI techniques for the reanalysis of structural vibrations. Yang et al. [16] applied the CA algorithm in dynamic reanalysis, focusing on various topology revision scenarios. Hong et al. [17] introduced a condensation model that expedited the recalculation of modified modal data through substructure combination. Xu et al. [18] enhanced the CA algorithm for dynamic reanalysis by incorporating the frequency-shift process. Norouzi et al. [19] utilized reanalysis algorithms to assess the fatigue life of structures. Mourelatos et al. [20] conducted dynamic reanalysis of large-scale structures, leveraging model reduction and the CA algorithm. Zheng et al. [21] combined CA with frequency-shift to rapidly compute the modal data of revised structures. Liu et al. [22] solved the modal reanalysis problem post-structural revision using the modal synthesis algorithm. Li et al. [23] facilitated aircraft design through the application of the modal reanalysis algorithm. Zheng et al. [24] explored the modal reanalysis method in response to an increase in structural degrees of freedom. Huang et al. [25] performed displacement and modal reanalysis of structures with nonlinear boundary conditions. He et al. [26,27] devised a dynamic reanalysis method that fused pseudo-random number initialization, independent and coupled II, and Rayleigh–Ritz analysis. Chang et al. [28] developed an SMW formula-based model reduction algorithm for structural modal reanalysis. Recently, Li et al. [29] investigated the modal reanalysis of large structural modifications incorporating local nonlinearity.
Despite notable strides in dynamic reanalysis, the prevailing methodologies continue to grapple with limitations, notably low computational precision and instability in complex stochastic dynamic assessments involving myriad random parameters. In this context, the emergence of flexibility disassembly perturbation (FDP) [30,31] as a game-changer for static structural analyses is significant. FDP has demonstrated remarkable effectiveness in static reanalysis [30] and static sensitivity reanalysis [31] of large-scale, high-complexity scenarios. Driven by the achievements, FDP is employed in this work to strengthen the subspace iteration algorithm, making it capable of performing dynamic random analysis on large-scale, statically indeterminate structures. The essence of this method lies in swiftly generating reduced basis vectors during subspace iteration, leveraging flexibility disassembly perturbation and Krylov subspace techniques for enhanced efficiency. This innovative modal stochastic analysis approach, validated through a truss structure, outperforms conventional methods in terms of computational efficiency and stability. The article is structured as follows: Section 2 initially offers a concise review of the subspace iteration algorithm’s calculation steps and key formulas utilized in modal computation. Subsequently, FDP is implemented to enhance the subspace iteration method, specifically tailored for conducting modal random analysis on individual FEM samples of the structure. Section 3 showcases a numerical illustration to validate the proposed method and benchmark it against existing approaches. Lastly, Section 4 summarizes the key takeaways and contributions of this research endeavor.
2. Theoretical Development
2.1. Subspace Iteration Method for Vibration Modal Computation
For a -DOF structure, the modal parameters of free vibration can be obtained by the eigen-pair equation as:
where and denote the dimensional stiffness and mass matrices of the initial FEM; is the eigenvector matrix; is a diagonal matrix of eigenvalues; and denote the first eigenvalues and eigenvectors; and denotes an identity matrix. The subspace iteration method is the most commonly used algorithm for solving the above dynamic eigen-pair problem, which can compute low-order eigen-pairs at once. The main steps of the subspace iteration method are as follows:
Step 1. Construct an initial eigenvector matrix using linearly independent vectors. The parameter should be greater than the number of desired eigenvalue pairs . Based on existing research [6,7], can be taken as the smaller value between and , i.e., .
Step 2. For the -th iteration, calculate the new eigenvector matrix through:
In Equation (5), represents the inverse matrix of .
Step 3. Calculate the condensed stiffness matrix and mass matrix through:
Step 4. Solve the simplified eigen-pair problem of the reduced system to achieve the corresponding eigenvalues and eigenvectors as follows:
Step 5. For the -th iteration, the solution of the eigenvalues of the original system is . The solution of the eigenvectors of the original system is calculated through:
Step 6. The iteration can be terminated when the results of two adjacent iterations are very close.
2.2. Extended Subspace Iteration Method Using FDP
For stochastic modal analysis, the stiffness and mass matrices of the structure are both random matrices due to the randomness of physical parameters such as elastic modulus and density of the material. For each random sampling, the modified stiffness matrix and mass matrix can be expressed as follows:
where and are variations caused by structural randomness. The modal eigen-pairs of this sample can also be obtained by solving the following generalized eigenvalue problem:
Similarly, the complete analysis by the subspace iteration method for this FEM sample is as follows:
Step 1. Construct an initial eigenvector matrix using linearly independent vectors ().
Step 2. For the -th iteration, calculate the new eigenvector matrix through:
Step 3. Calculate the condensed stiffness matrix and mass matrix through:
Step 4. Solve the simplified eigen-pair problem of the reduced system to obtain the corresponding eigenvalues and eigenvectors as follows:
Step 5. For the -th iteration, the solution of the eigenvalues of the random system is . The solution of the eigenvectors of the random system is calculated through:
Step 6. The iteration can be terminated when the results of two adjacent iterations are very close.
Analyzing the outlined steps, it becomes evident that the primary computational bottleneck stems from the inverting matrix in Equation (16). When dealing with thousands of samples, this task becomes overwhelmingly intensive, potentially rendering random modal analysis unfeasible. To address this, we employ the Flexibility Disassembly Perturbation (FDP) formula, which swiftly approximates , significantly boosting the computational speed of the subspace iteration method. FDP’s cornerstone lies in transforming random physical parameters into a diagonal matrix by cleverly decomposing and combining elementary stiffness matrices. For this purpose, the overall stiffness matrix of the structure is elegantly represented by the cumulative sum of the elementary stiffness matrices as follows:
where denotes the -th elementary stiffness matrix, . The spectral decomposition of can be expressed as follows:
where are the non-zero eigenvalues of , and are the corresponding eigenvectors. For instance, performing the spectral decomposition on a plane beam–element stiffness matrix in a local coordinate system is performed as follows [28]:
In Equation (23), represents the modulus of elasticity; signifies the cross-sectional area; denotes the moment of inertia; and stands for the length of the beam element. Notably, the random parameters are consolidated within the diagonal elements of the matrix . Substituting Equation (22) into (21) yields the following:
In Equation (25), and are and dimensional matrices, respectively. Notably, assumes a square form with dimensionality for statically determinate structures, while it adopts a rectangular shape with dimensions for statically indeterminate structures. Typically, stochastic variables such as the elastic modulus and cross-sectional size solely impact the diagonal matrix , leading to its variation. Consequently, the revised stiffness matrix can be formulated as a function of these altered diagonal elements:
where () are the random coefficients. It is a well-established fact that the structural flexibility matrix serves as the inverse of the stiffness matrix, i.e.,
It is noted that the matrix in Equation (29) is a diagonal square matrix of dimension , and each diagonal element in is not equal to zero because the probability that the random coefficient exactly equals −1 in random sampling is almost zero. Therefore, the matrix is invertible. For a statically determinate structure, the FDP formula can be straightforwardly derived from Equation (28), offering a simplified and direct path to its computation as follows:
For a statically indeterminate structure, a generalized FDP formula is developed from Equation (28) with the help of the matrix generalized inverse:
The superscript “+” represents the matrix generalized inverse, and it is evident that for a statically determinate structure, Equation (35) reduces to Equation (32). The FDP formulas, as shown in Equation (35), are used for fast estimating in the subspace iteration method to improve the computational efficiency of random modal reanalysis. For statically indeterminate structures, since Equation (35) is an approximate estimate of , it is usually necessary to add extra basis vectors to the initial subspace to construct a new subspace to further improve the calculation accuracy. The extended subspace is designed as follows:
where are the eigenvectors of the original system without considering randomness; are the added basis vectors; and is a positive integer less than . These added basis vectors are calculated based on FDP and Krylov’s subspace as follows:
Using FDP and the extended subspace, the operational process of the extended subspace iteration algorithm for random modal analysis of a statically indeterminate structure is as follows:
- (1)
- Construct an initial subspace matrix using Equations (37) and (38).
- (2)
- For the -th iteration, calculate the new eigenvector matrix using Equation (35) as follows:
- (3)
- Calculate the condensed stiffness matrix and mass matrix through:
- (4)
- Solve the simplified eigen-pair problem of the reduced system to obtain the corresponding eigenvalues and eigenvectors as follows:
- (5)
- For the -th iteration, the solution of the eigenvalues of the random system are the first diagonal elements of . The solution of the eigenvectors is the first column vector obtained through:
- (6)
- The iteration can be terminated when the results of two adjacent iterations are very close.
Figure 1 shows the operation flow of the proposed random modal analysis method for statically indeterminate structures more intuitively.
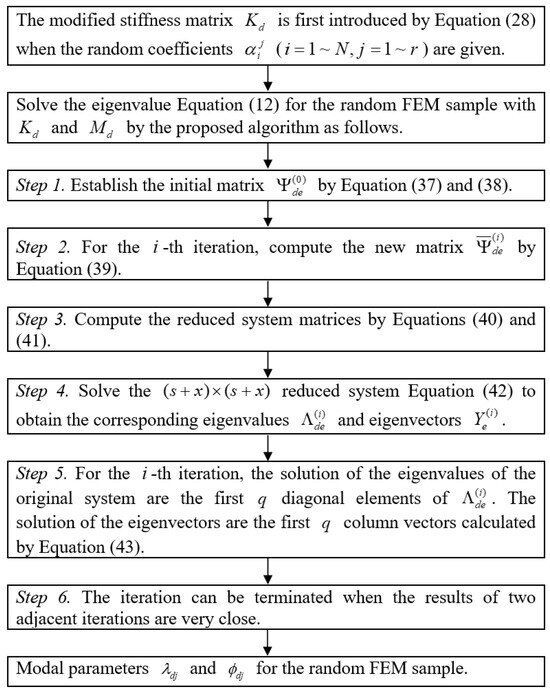
Figure 1.
The operation flow of the proposed algorithm for random modal analysis of statically indeterminate structures.
3. Numerical Examples
3.1. Example 1: A Truss Structure
A 58-bar structure depicted in Figure 2 was utilized as the example to validate the proposed algorithm. This structure has 51 degrees of freedom (DOFs) and 7 redundant constraints, indicating it is statically indeterminate with a proportion of redundant constraints of about 10% of total members. Each horizontal or vertical rod measures 0.5 m in length, and all members share a cross-sectional area of 314 mm2. The density of the material is 7800 kg/m3. It is assumed that the elastic modulus of the material adheres to a normal distribution, with a mean value being assigned as 200 GPa. Within this context, three scenarios for the standard deviation are contemplated: they are determined as 0.1, 0.15, and 0.2 times the mean value, respectively. In a modal stochastic analysis, 5000 random samples were analyzed, and the first three modes post-sampling were computed using the proposed method, the CA reanalysis method [13], and a complete analysis.
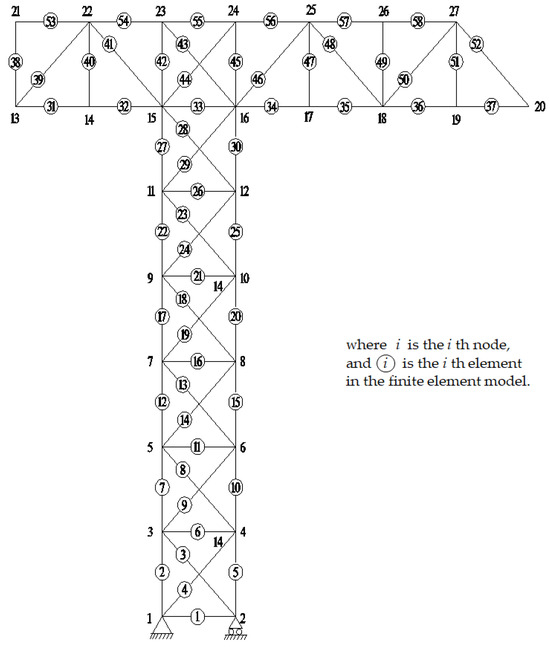
Figure 2.
A truss structure with 58 rods.
For the case where the standard deviation is 0.1 times the mean value, the computation times required for the complete analysis, the CA algorithm, and the new algorithm (with three added basis vectors) are listed in Table 1. According to Table 1, the computation times for both the CA and new algorithms are significantly shorter than those of the full analysis. Specifically, the CA algorithm takes approximately 1.8% of the time required by full analysis, whereas the proposed algorithm requires only 1.2% of the full analysis time and 65% of the CA algorithm’s time. Evidently, the proposed method demonstrates the highest level of computational efficiency among the three. Figure 3 presents the first eigenvalues for the 5000 samples calculated by the three methods. As shown in Figure 3, the first-order eigenvalues of each sample calculated by the three methods are concentrated near the median, with a distribution pattern similar to a normal distribution. This indicates that when random sampling is performed for elastic modulus according to a normal distribution, the eigenvalues of the obtained samples also basically follow a normal distribution. The range, mean, and standard deviation of the first eigenvalues are listed in Table 2. Note that the results obtained from the complete analysis seem to be the exact solutions for comparison purposes. As can be seen from Table 2, the results obtained by the two rapid algorithms are basically the same as the exact solution. In addition, Figure 4 provides the relative errors of the CA and new methods. The comparative errors of the eigenvalues and eigenvectors are computed by:
where represents the two-norm of a vector. As shown in Figure 4, the calculation error of the proposed method is obviously smaller than that of the CA method. Similarly, Figure 5, Figure 6, Figure 7 and Figure 8 and Table 3 and Table 4 present the calculation results for the second and third eigenvalues by the three methods. Figure 5 and Figure 7 show that the second-order and third-order eigenvalues of the samples calculated by the three methods are also concentrated near the median, with a distribution pattern similar to a normal distribution. Figure 6 and Figure 8 show that the calculation errors of the second-order and third-order eigenvalues obtained by the proposed method are also smaller than those of the CA method. It has been shown that the proposed method can achieve higher calculation accuracy than the CA method in less calculation time.

Table 1.
Computation time when the standard deviation is 0.1 times the mean value.
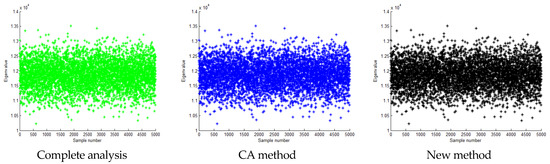
Figure 3.
Calculation result of the first eigenvalue when the standard deviation is 0.1 times the mean value.

Table 2.
Statistical characteristics of the first eigenvalue when the standard deviation is 0.1 times the mean value.
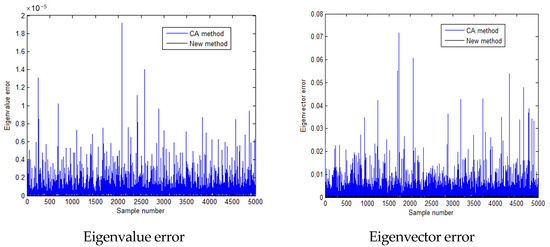
Figure 4.
Calculation errors of the first eigen-pairs when the standard deviation is 0.1 times the mean value.
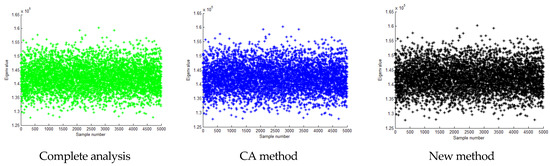
Figure 5.
Calculation result of the second eigenvalue when the standard deviation is 0.1 times the mean value.
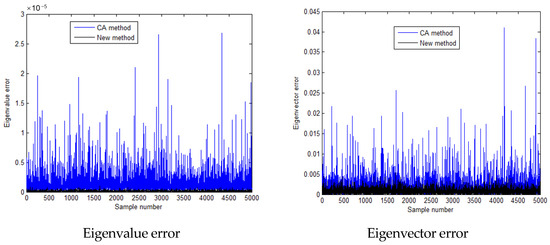
Figure 6.
Calculation errors of the second eigen-pairs when the standard deviation is 0.1 times the mean value.
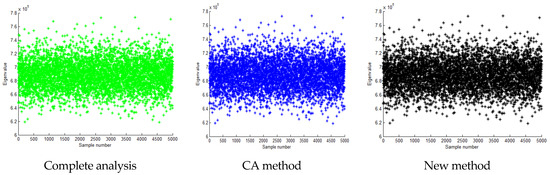
Figure 7.
Calculation result of the third eigenvalue when the standard deviation is 0.1 times the mean value.
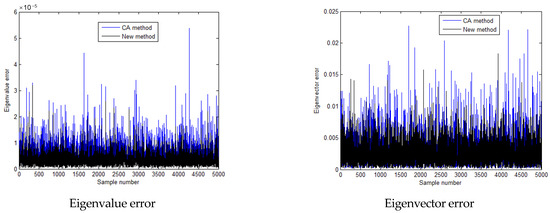
Figure 8.
Calculation errors of the third eigen-pairs when the standard deviation is 0.1 times the mean value.

Table 3.
Statistical characteristics of the second eigenvalue when the standard deviation is 0.1 times the mean value.

Table 4.
Statistical characteristics of the third eigenvalue when the standard deviation is 0.1 times the mean value.
In the scenario where the standard deviation is 0.15 times the mean value, Table 5 outlines the computation times necessary for the comprehensive analysis, the CA algorithm, and the new algorithm. As evident from Table 5, both the CA and the novel algorithm exhibit substantial reductions in computation time compared to the full analysis. Specifically, the CA algorithm consumes roughly 1.9% of the full analysis’s time, while the proposed algorithm further optimizes, requiring just 1.2% of the full analysis’s duration and 60% of the CA algorithm’s time. Clearly, the proposed method emerges as the most computationally efficient among the three. Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 and Table 6, Table 7 and Table 8 display the outcomes of the first, second, and third eigenvalue calculations using these three methods. Figure 9, Figure 11, and Figure 13, respectively, show that the first, second, and third-order eigenvalues of the samples obtained by the three methods are concentrated near the median, resembling a normal distribution. Figure 10, Figure 12, and Figure 14, respectively, show that the calculation errors of the first, second, and third-order eigenvalues obtained by the proposed method are all smaller than those of the CA method. These results demonstrate that the proposed method aligns more closely with the exact solution derived from the full analysis than those of the CA method. This underscores the ability of the proposed method to attain higher calculation accuracy within a shorter computation time compared to the CA method.

Table 5.
Computation time when the standard deviation is 0.15 times the mean value.
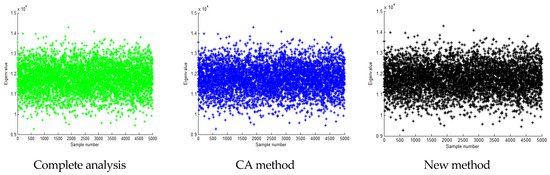
Figure 9.
Calculation result of the first eigenvalue when the standard deviation is 0.15 times the mean value.
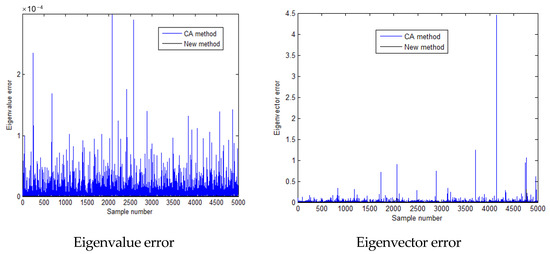
Figure 10.
Calculation errors of the first eigen-pairs when the standard deviation is 0.15 times the mean value.
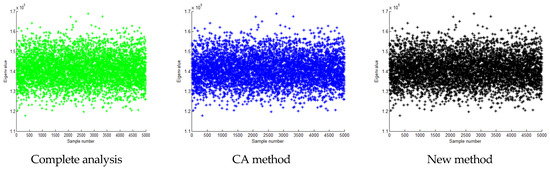
Figure 11.
Calculation result of the second eigenvalue when the standard deviation is 0.15 times the mean value.
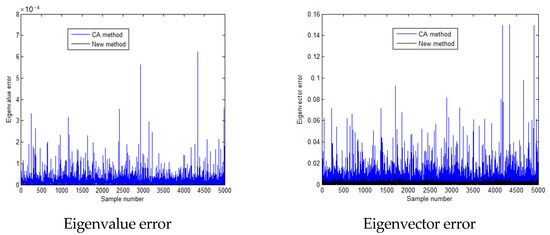
Figure 12.
Calculation errors of the second eigen-pairs when the standard deviation is 0.15 times the mean value.
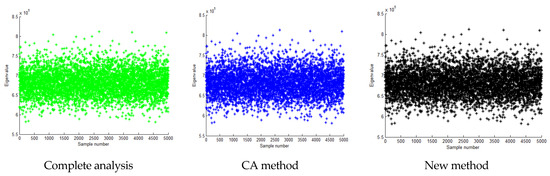
Figure 13.
Calculation result of the third eigenvalue when the standard deviation is 0.15 times the mean value.
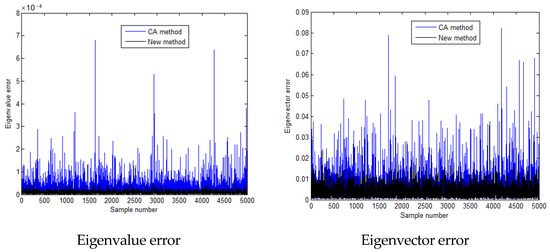
Figure 14.
Calculation errors of the third eigen-pairs when the standard deviation is 0.15 times the mean value.

Table 6.
Statistical characteristics of the first eigenvalue when the standard deviation is 0.15 times the mean value.

Table 7.
Statistical characteristics of the second eigenvalue when the standard deviation is 0.15 times the mean value.

Table 8.
Statistical characteristics of the third eigenvalue when the standard deviation is 0.15 times the mean value.
In the scenario where the standard deviation is equivalent to 0.2 times the mean value, Table 9 details the computational time demands for a comprehensive analysis, the CA algorithm, and the innovative algorithm. As evident from Table 9, both the CA algorithm and the novel algorithm exhibit markedly reduced computation times compared to the exhaustive analysis. Precisely, the CA algorithm consumes approximately 1.8% of the time utilized by the full analysis, whereas the presented algorithm requires an even more streamlined 1.2% of the full analysis duration, being 67% as time-consuming as the CA algorithm. Evidently, the proposed method outperforms both in terms of computational efficiency. Additionally, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20 and Table 10, Table 11 and Table 12 showcase the eigenvalue computation outcomes for the first, second, and third eigenvalues utilizing these three methodologies. Figure 15, Figure 17, and Figure 19, respectively, illustrate that the first, second, and third-order eigenvalues of the samples, calculated using the three methods, are centered around the median, exhibiting a normal distribution-like pattern. Similarly, Figure 16, Figure 18, and Figure 20 reveal that the calculation errors associated with the first, second, and third-order eigenvalues, respectively, obtained through the proposed method are consistently lower than those obtained via the CA method. The analysis reveals that the calculation error of the proposed method is lower than that of the CA method, with its results aligning more closely with the exact solution derived from the exhaustive analysis. Thus, it is demonstrated that the proposed algorithm achieves higher accuracy while maintaining a shorter computation time compared to the CA method.

Table 9.
Computation time when the standard deviation is 0.2 times the mean value.
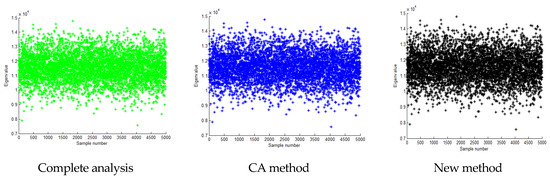
Figure 15.
Calculation result of the first eigenvalue when the standard deviation is 0.2 times the mean value.
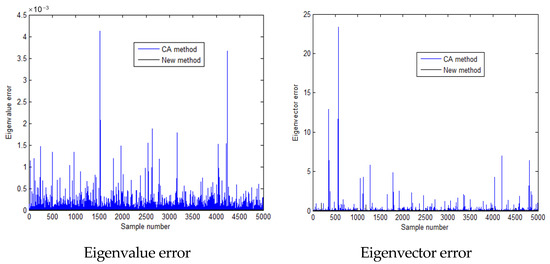
Figure 16.
Calculation errors of the first eigen-pairs when the standard deviation is 0.2 times the mean value.
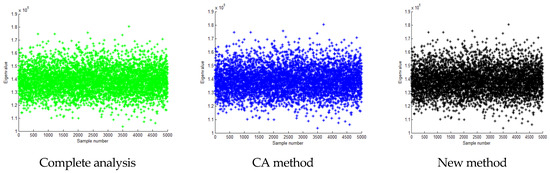
Figure 17.
Calculation result of the second eigenvalue when the standard deviation is 0.2 times the mean value.
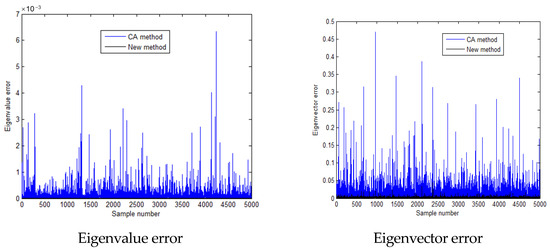
Figure 18.
Calculation errors of the second eigen-pairs when the standard deviation is 0.2 times the mean value.
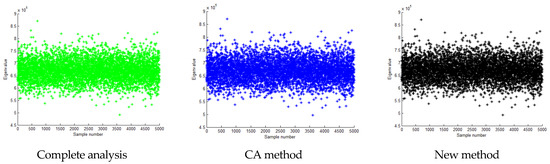
Figure 19.
Calculation result of the third eigenvalue when the standard deviation is 0.2 times the mean value.
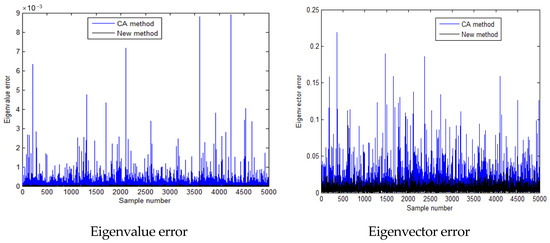
Figure 20.
Calculation errors of the third eigen-pairs when the standard deviation is 0.2 times the mean value.

Table 10.
Statistical characteristics of the first eigenvalue when the standard deviation is 0.2 times the mean value.

Table 11.
Statistical characteristics of the second eigenvalue when the standard deviation is 0.2 times the mean value.

Table 12.
Statistical characteristics of the third eigenvalue when the standard deviation is 0.2 times the mean value.
According to Table 2, Table 3 and Table 4, Table 6, Table 7 and Table 8, and Table 10, Table 11 and Table 12, the ratios of the standard deviations to the means for the first three eigenvalues calculated by the proposed method are listed in Table 13. As can be seen from Table 13, as the standard deviation of the elastic modulus increases, the ratio of the standard deviation to the mean of the eigenvalues calculated by the proposed method also gradually increases. In other words, the degree of dispersion of the eigenvalues increases with the increase in the standard deviation of the elastic modulus.

Table 13.
The ratios of the standard deviations to the means for the first three eigenvalues calculated by the proposed method.
3.2. Example 2: A Beam Structure
The purpose of the second example is to compare the performance of the proposed method with the Ritz vector method [32] in stochastic modal analysis and, additionally, to investigate the computational performance of the proposed method as the number of random variables increases. As shown in Figure 21, this beam structure spans 50 m and is evenly divided into 100 elements. The cross-sectional height of the beam structure is 0.5 m and the width is 0.3 m, with a material density of 2700 kg/m3. Assuming that the elastic moduli follow a normal distribution with a mean of 35 GPa and a standard deviation equal to 0.2 times the mean, the following three sets of samples with different numbers of random variables are examined: the elastic moduli of the first 30 elements are treated as random variables, the elastic moduli of the first 60 elements are treated as random variables, and the elastic moduli of all elements are treated as random variables. During the modal stochastic analysis, 10,000 random samples were examined, and subsequently, the first three modes were calculated using three approaches: the proposed method, the Ritz vector method, and a comprehensive analysis. Table 14 presents a comparison of the computation times for the three methods. From Table 14, the computation times for both the Ritz vector method and the new algorithm are significantly shorter than those of the full analysis. For example, when the elastic modulus of all elements is treated as a random variable, the Ritz vector algorithm takes approximately 4.3% of the time required by the full analysis, whereas the proposed algorithm requires only 2.0% of the full analysis time and 46.8% of the Ritz vector algorithm’s time. On average, the computational time of the proposed method is approximately 2.1% of that required for a full analysis and roughly 48.2% of the Ritz vector method. This demonstrates that the proposed method has the highest computational efficiency. In terms of computational accuracy, Table 15, Table 16, Table 17, Table 18, Table 19, Table 20, Table 21, Table 22 and Table 23 provide the statistical results of the first three eigenvalues obtained by three methods for the three sets of samples with different numbers of random variables, respectively. As can be seen from Table 15, Table 16, Table 17, Table 18, Table 19, Table 20, Table 21, Table 22 and Table 23, the computational accuracy of the proposed method is also superior to that of the Ritz vector method. According to Table 15, Table 16, Table 17, Table 18, Table 19, Table 20, Table 21, Table 22 and Table 23, the ratios of the standard deviations to the means for the first three eigenvalues calculated by the proposed method are listed in Table 24. As can be seen from Table 24, as the number of random variables increases, the ratio of the standard deviation to the mean of the eigenvalues calculated by the proposed method also gradually increases. In other words, the degree of dispersion of the eigenvalues increases with the increase in the number of random variables.

Figure 21.
A beam structure.

Table 14.
Computation time for the three sets of samples with different numbers of random variables.

Table 15.
Statistical characteristics of the first eigenvalue for example 2 when the elastic moduli of the first 30 elements are treated as random variables.

Table 16.
Statistical characteristics of the second eigenvalue for example 2 when the elastic moduli of the first 30 elements are treated as random variables.

Table 17.
Statistical characteristics of the third eigenvalue for example 2 when the elastic moduli of the first 30 elements are treated as random variables.

Table 18.
Statistical characteristics of the first eigenvalue for example 2 when the elastic moduli of the first 60 elements are treated as random variables.

Table 19.
Statistical characteristics of the second eigenvalue for example 2 when the elastic moduli of the first 60 elements are treated as random variables.

Table 20.
Statistical characteristics of the third eigenvalue for example 2 when the elastic moduli of the first 60 elements are treated as random variables.

Table 21.
Statistical characteristics of the first eigenvalue for example 2 when the elastic moduli of all elements are treated as random variables.

Table 22.
Statistical characteristics of the second eigenvalue for example 2 when the elastic moduli of all elements are treated as random variables.

Table 23.
Statistical characteristics of the third eigenvalue for example 2 when the elastic moduli of all elements are treated as random variables.

Table 24.
The ratios of the standard deviations to the means for the first three eigenvalues of example 2 calculated by the proposed method.
4. Conclusions
This research presents a novel fast algorithm designed to drastically reduce the computational burden associated with modal random analysis of structures. The core concept revolves around enhancing the efficiency of the subspace iteration method through the integration of the FDP technique and the utilization of extended basis vectors. Initially, the FDP formula is employed to swiftly approximate the perturbed flexibility matrix of a random FEM sample characterized by a high number of random variables. Subsequently, this perturbed flexibility matrix is incorporated into the subspace iteration algorithm to promptly extract the perturbed modal parameters of the FEM sample. For statically indeterminate structures, a dedicated formula is introduced to generate additional basis vectors, thereby expanding the subspace and further refining the calculation accuracy. To demonstrate the accuracy and efficiency of the proposed algorithm, a truss structure and a beam structure are analyzed. The comparative study yields the following key insights: (1) The novel modal random analysis algorithm achieves substantial savings in computational time. For the 58-bar structure, the calculation time of the proposed method is approximately 1.2% and 65% of that required by the comprehensive analysis method and the CA method, respectively. For the beam structure, on average, the computational time of the proposed method is approximately 2.1% of that required for a full analysis and roughly 48.2% of the time needed for the Ritz vector method. (2) The results obtained using the proposed method closely approximate the exact solution derived from the comprehensive analysis, demonstrating superior accuracy and efficiency compared to the CA method and Ritz vector method. (3) Notably, the performance of the proposed method remains stable even as the discreteness of structural parameters increases, making it an ideal choice for modal random analysis of highly discrete structures, balancing both computational time and accuracy.
Author Contributions
Conceptualization, H.C., B.X. and Q.Y.; methodology, H.C. and F.Q.; software and validation, X.P.; investigation, H.C. and X.P.; writing—original draft preparation, H.C., X.P., F.Q. and Q.Y.; writing—review and editing, Q.Y.; visualization, F.Q.; project administration, H.C. and B.X.; funding acquisition, B.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Ningbo Public Welfare Science and Technology Plan Project (No. 2024S078) and the Zhejiang Provincial Natural Science Foundation of China (No. LGF22E080021 and No. LY24E080010).
Data Availability Statement
The data used to support the findings of this study are included in this study and are also available from the corresponding author upon request.
Conflicts of Interest
Xi Peng and Bin Xu was employed by the company Ningbo Roaby Technology Industrial Group Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The funders had no role in the collection, analysis, or interpretation of data or in the decision to publish the results.
References
- Men, P.; Wang, X.; Liu, D.; Zhang, Z.; Zhang, Q.; Lu, Y. On use of polyvinylpyrrolidone to modify polyethylene fibers for improving tensile properties of high strength ECC. Constr. Build. Mater. 2024, 417, 135354. [Google Scholar] [CrossRef]
- Peng, X.; Shi, F.; Yang, J.; Yang, Q.; Wang, H.; Zhang, J. Modification of construction waste derived recycled aggregate via CO2 curing to enhance corrosive freeze-thaw durability of concrete. J. Clean. Prod. 2023, 405, 137016. [Google Scholar] [CrossRef]
- Zhang, G.Z.; Liu, C.; Cheng, P.F.; Li, Z.; Han, Y.; Wang, X.Y. Enhancing the Interfacial Compatibility and Self-Healing Performance of Microbial Mortars by Nano-SiO2-Modified Basalt Fibers. Cem. Concr. Compos. 2024, 152, 105650. [Google Scholar] [CrossRef]
- Clough, R.W.; Penzien, J.P. Dynamics of Structures; McGraw–Hill: New York, NY, USA, 1993. [Google Scholar]
- Bathe, K.J. Finite Element Procedures; Prentice–Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Dong, B.; Parker, R.G. Sector-model subspace iteration for vibration of multi-stage, cyclically symmetric systems. J. Sound Vib. 2023, 544, 117378. [Google Scholar] [CrossRef]
- Xu, H.; Liu, B. Hierarchical subspace evolution method for super large parallel computing: A linear solver and an eigensolver as examples. Int. J. Numer. Methods Eng. 2023, 124, 5–39. [Google Scholar] [CrossRef]
- Friswell, M.I.; Garvey, S.D.; Penny, J.E.T. Model reduction using dynamic and iterated IRS techniques. J. Sound Vib. 1995, 186, 311–323. [Google Scholar] [CrossRef]
- Lin, Y.; Simoncini, V. A new subspace iteration method for the algebraic Riccati equation. Numer. Linear Algebra Appl. 2015, 22, 26–47. [Google Scholar] [CrossRef]
- Gu, M. Subspace iteration randomization and singular value problems. SIAM J. Sci. Comput. 2015, 37, A1139–A1173. [Google Scholar] [CrossRef]
- Lasecka-Plura, M.; Lewandowski, R. The subspace iteration method for nonlinear eigenvalue problems occurring in the dynamics of structures with viscoelastic elements. Comput. Struct. 2021, 254, 106571. [Google Scholar] [CrossRef]
- Chen, S.H.; Yang, X.W.; Lian, H.D. Comparison of several eigenvalue reanalysis methods for modified structures. Struct. Multidiscip. Optim. 2000, 20, 253–259. [Google Scholar]
- Chen, S.H.; Yang, X.W. Extended Kirsch combined method for eigenvalue reanalysis. AIAA J. 2000, 38, 927–930. [Google Scholar] [CrossRef]
- Kirsch, U. Approximate vibration reanalysis of structures. AIAA J. 2003, 41, 504–511. [Google Scholar] [CrossRef]
- Kirsch, U.; Bogomolni, M. Procedures for approximate eigenproblem reanalysis of structures. Int. J. Numer. Methods Eng. 2004, 60, 1969–1986. [Google Scholar] [CrossRef]
- Yang, Z.J.; Chen, S.H.; Wu, X.M. A method for modal reanalysis of topological modifications of structures. Int. J. Numer. Methods Eng. 2006, 65, 2203–2220. [Google Scholar] [CrossRef]
- Hong, S.-K.; Epureanu, B.I.; Castanier, M.P.; Gorsich, D.J. Parametric reduced-order models for predicting the vibration response of complex structures with component damage and uncertainties. J. Sound Vib. 2011, 330, 1091–1110. [Google Scholar] [CrossRef]
- Xu, T.; Guo, G.; Zhang, H. Vibration reanalysis using frequency-shift combined approximations. Struct. Multidiscip. Optim. 2011, 44, 235–246. [Google Scholar] [CrossRef]
- Norouzi, M.; Nikolaidis, E. Efficient method for reliability assessment under high-cycle fatigue. Int. J. Reliab. Qual. Saf. Eng. 2012, 19, 1250022. [Google Scholar] [CrossRef]
- Mourelatos, Z.P.; Nikolaidis, E. An efficient re-analysis methodology for vibration of large-scale structures. Int. J. Veh. Des. 2013, 61, 86–107. [Google Scholar] [CrossRef]
- Zheng, S.P.; Wu, B.S.; Li, Z.G. Vibration reanalysis based on block combined approximations with shifting. Comput. Struct. 2015, 149, 72–80. [Google Scholar] [CrossRef]
- Liu, H.; Wang, H.; Tan, G.; Liu, Z. Reanalysis of the structural dynamic characteristics based on double coordinate free-interface mode synthesis & matrix perturbation method. Vibroengineering Procedia 2016, 10, 83–88. [Google Scholar]
- Li, D.; Zhou, Q.; Chen, G.; Li, Y. Structural dynamic reanalysis method for transonic aeroelastic analysis with global structural modifications. J. Fluids Struct. 2017, 74, 306–320. [Google Scholar] [CrossRef]
- Zheng, S.P.; Wu, B.S.; Li, Z.G. Free vibration reanalysis of structures with added degrees of freedom. Comput. Struct. 2018, 206, 31–41. [Google Scholar] [CrossRef]
- Huang, G.; Chen, X.; Yang, Z.; Wu, B. Exact analysis and reanalysis methods for structures with nonlinear boundary conditions. Comput. Struct. 2018, 198, 12–22. [Google Scholar] [CrossRef]
- He, J.; Chen, X.; Xu, B. Structural modal reanalysis for large, simultaneous and multiple type modifications. Mech. Syst. Signal Process. 2015, 62, 207–217. [Google Scholar]
- He, J.; Xu, B. Quick and Highly Efficient Modal Analysis Method Based on the Reanalysis Technique for Large Complex Structure and Topology Optimization. Int. J. Comput. Methods 2020, 17, 1850134. [Google Scholar] [CrossRef]
- Chang, S.; Cho, M. Dynamic-condensation-based reanalysis by using the Sherman–Morrison–Woodbury formula. AIAA J. 2021, 59, 905–911. [Google Scholar] [CrossRef]
- Li, W.; Chen, S. An improved model order reduction method for dynamic analysis of large-scale structures with local nonlinearities. Appl. Math. Model. 2023, 120, 786–811. [Google Scholar] [CrossRef]
- Yang, Q.W. Fast and Exact Algorithm for Structural Static Reanalysis Based on Flexibility Disassembly Perturbation. AIAA J. 2019, 57, 3599–3607. [Google Scholar] [CrossRef]
- Yang, Q.W.; Peng, X. A Fast Calculation Method for Sensitivity Analysis Using Matrix Decomposition Technique. Axioms 2023, 12, 179. [Google Scholar] [CrossRef]
- Koh, H.S.; Yoon, G.H. Ritz vector-based substructuring method using interface eigenmode-shape pseudo-forces. Finite Elem. Anal. Des. 2023, 227, 104023. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).