Computability of Generalized Graphs

Abstract

We investigate conditions under which a semicomputable set is computable. In particular, we study topological pairs $(A,B)$ which have a computable type, which means that in any computable topological space, a semicomputable set S is computable if there exists a semicomputable set T such that $(S,T)$ is homeomorphic to $(A,B)$. It is known that $(G,E)$ has a computable type if G is a topological graph and E is the set of all its endpoints. Furthermore, the same holds if G is a so-called chainable graph. We generalize the notion of a chainable graph and prove that the same result holds for a larger class of spaces.

1. Introduction

A compact set $S\subseteq {\mathbb{R}}^n$ is semicomputable if its complement ${\mathbb{R}}^n\setminus S$ can be effectively exhausted by rational open balls. On the other hand, a compact set $S\subseteq {\mathbb{R}}^n$ is computable if it is semicomputable and we can effectively enumerate all rational open balls which intersect S. By the mere definition, it is clear that each computable set is semicomputable, while there exist some examples which show that the reverse implication does not hold. For instance, there exists $\gamma >0$ such that $[0,\gamma ]$ is a semicomputable set and $\gamma$ itself is not a computable number (therefore, $[0,\gamma ]$ is not a computable set) [1]. Here, by the computable number we mean every real number that can be effectively approximated by a rational point for any given precision. Moreover, there exists a nonempty semicomputable subset of $\mathbb{R}$ which does not contain any computable point [2]. The notions of a semicomputable and a computable set can be naturally defined in the setting of computable metric and topological spaces.

Although the implication

$$S \mathrm{semicomputable}\Rightarrow S \mathrm{computable}$$

(1)

is not true, in general, there are certain additional assumptions on S under which (1) holds. For example, each semicomputable compact manifold is computable. Therefore, each semicomputable topological circle is computable, but also a Warsaw circle, which is not a manifold, is computable if it is semicomputable. Moreover, if S is a semicomputable circularly chainable continuum that is not chainable, then S is computable. Also, the same is true if S is a continuum chainable from a to b, where a and b are computable points (i.e., $\{a,b\}$ is a semicomputable set) [3,4,5].

We say that a topological space A has a computable type if for any computable topological space $(X,\mathcal{T},(I_i))$ the following holds: if S is semicomputable in $(X,\mathcal{T},(I_i))$ and homeomorphic to A, then S is computable in $(X,\mathcal{T},(I_i))$. For example, the previously mentioned result for compact manifolds now can be stated in the following way: each compact manifold has a computable type.

The fact that there exists $\gamma >0$ such that $[0,\gamma ]$ is semicomputable, but not computable, means that $[0,1]$ does not have a computable type. Related to this situation, we have the following concept of computable type.

If A is a topological space and B its subspace, then we say that $(A,B)$ is a topological pair. We say that a topological pair $(A,B)$ has a computable type if for any computable topological space $(X,\mathcal{T},(I_i))$ the following holds: if $f:A\to X$ is an (topological) embedding such that $f(A))$ and $f(B)$ are semicomputable sets, then $f(A)$ is a computable set.

Using this terminology, we can say that $(S,\{a,b\})$ has a computable type if S is a continuum chainable from a to b. In particular, $([0,1],\{0,1\})$ has a computable type.

Recently, Amir and Hoyrup examined conditions under which a finite polyhedron has a computable type (see [6]). They also examined the computable type and strong computable type in [7].

Some results regarding computable type and (in)computability of semicomputable sets can be found in [8,9,10].

Inspired by the notion of a topological graph, in [11] the authors have defined the notion of a chainable graph and have proven that the claims stated for topological graphs, hold for chainable graphs, as well. Namely, a topological graph is considered to be any topological space obtained as a union of finitely many arcs such that every two of them which intersect, intersect in exactly one point which is an endpoint of both of them. The definition of chainable graph arcs has been replaced by chainable continua. It is proved in [12] that $(G,E)$ has computable type if G is a graph and E is the set of all its endpoints. In [11] it was proved that the same holds for chainable graphs.

In this paper, we generalize the notion of a chainable graph from [11] and we define the notion of a generalized graph. While in a chainable graph, every two edges can intersect only in their endpoints, in the definition of a generalized graph we only demand that two edges (which are chainable continua) intersect finitely many points. More precisely, we say that a triple $(G,\mathcal{K},V)$ is a generalized graph if G is a topological space, V is a finite set and $\mathcal{K}$ is a finite set of pairs $(K,\{a,b\})$, where $a,b\in V$ are distinct points and $K\subseteq A$ is a Hausdorff continuum chainable from a to b, such that the following holds: A is the union of V and all such K and for all $(K,\{a,b\}),(L,\{c,d\})\in \mathcal{K}$ such that $K\ne L$ we have that $K\cap L$ is a finite set. We show that generalized graphs are indeed a generalization of chainable graphs. We prove that $(G,E)$ has a computable type if $(G,\mathcal{K},V)$ is a generalized graph and E is the set of all its endpoints.

It should be mentioned that Amir and Hoyrup in [7] showed that, for the purpose of studying computable type, computable topological spaces are no more general than computable metric spaces, or in fact the Hilbert cube. However, for the techniques that we use in this paper, a computable topological space is a natural ambient space.

2. Preliminaries

In this section, we recall some basic notions, both from computability and topology, needed to state our main result. For background on computable analysis and some recent results we refer the reader to [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34].

2.1. Computable Functions

Let $k\in \mathbb{N}$, $k\ge 1$. A function $f:{\mathbb{N}}^k\to \mathbb{Q}$ is said to be computable if there are computable (i.e., recursive) functions $a,b,c:{\mathbb{N}}^k\to \mathbb{N}$ such that

$$f(x)={(-1)}^{c(x)}{\displaystyle \frac{a(x)}{b(x)+1}},$$

for each $x\in {\mathbb{N}}^k$. A function $f:{\mathbb{N}}^k\to \mathbb{R}$ is said to be computable if there exists a computable function $F:{\mathbb{N}}^{k+1}\to \mathbb{Q}$ such that

$$|f(x)-F(x,i)|<2^{-i},$$

for each $x\in {\mathbb{N}}^k$, $i\in \mathbb{N}$.

For a set X, let $\mathcal{F}(X)$ denote the family of all finite subsets of X. A function $\Theta :\mathbb{N}\to \mathcal{F}(\mathbb{N})$ is called computable if the set

$$\{(x,y)\in {\mathbb{N}}^2\mid y\in \Theta (x)\}$$

is computable and if there is a computable function $\phi :\mathbb{N}\to \mathbb{N}$ such that

$$\Theta (x)\subseteq \{0,\dots ,\phi (x)\}$$

for each $x\in \mathbb{N}$.

From now on, let $\mathbb{N}\to \mathcal{F}(\mathbb{N})$, $j\to [j]$ be some fixed computable function whose range is the set of all nonempty finite subsets of $\mathbb{N}$.

2.2. Computable Metric Space

Let $(X,d)$ be a metric space and $\alpha =({\alpha }_i)$ be a sequence in X such that $\alpha (\mathbb{N})\subseteq X$ is dense in $(X,d)$. A triple $(X,d,\alpha )$ is said to be a computable metric space if the function ${\mathbb{N}}^2\to \mathbb{R}$, $(i,j)\mapsto d({\alpha }_i,{\alpha }_j)$, is computable.

For example, $({\mathbb{R}}^n,d,\alpha )$ is a computable metric space, where d is the Euclidean metric on ${\mathbb{R}}^n$ for $n\in \mathbb{N}\setminus \{0\}$, and $\alpha :\mathbb{N}\to {\mathbb{Q}}^n$ is some effective enumeration of ${\mathbb{Q}}^n$.

If $(X,d)$ is a metric space, $x\in X$ and $r>0$, then by $B(x,r)$ we denote the open ball of radius r centered at x and by $\overline{B}(x,r)$ we denote the corresponding closed ball. If $A\subseteq X$, we will denote by $\overline{A}$ the closure of A in $(X,d)$.

Let $(X,d,\alpha )$ be a fixed computable metric space. Let $i\in \mathbb{N}$ and $r\in \mathbb{Q}$, $r>0$. We say that $B({\alpha }_i,r)$ is an (open) rational ball in a computable metric space $(X,d,\alpha )$.

Let $q:\mathbb{N}\to \mathbb{Q}$ and ${\tau }_1,{\tau }_2:\mathbb{N}\to \mathbb{N}$ be fixed computable functions such that the image of q is the set of all positive rational numbers and such that $\{({\tau }_1(i),{\tau }_2(i))\mid i\in \mathbb{N}\}={\mathbb{N}}^2$. For $i\in \mathbb{N}$ we denote

$$I_i=B({\alpha }_{{\tau }_1(i)},q_{{\tau }_2(i)}).$$

(2)

Note that $\{I_{\mid }i\in \mathbb{N}\}$ is the set of all rational balls in $(X,d,\alpha )$. For $j\in \mathbb{N}$ let

$$J_j=\bigcup _{i\in [j]}{I}_i.$$

Then, $\{J_j\mid j\in \mathbb{N}\}$ is the set of all finite (nonempty) unions of rational balls.

Now we can state the following definitions:

• a closed set $S\subseteq X$ in $(X,d)$ is a computably enumerable (c.e.) set in $(X,d,\alpha )$ if the set $\{i\in \mathbb{N}\mid S\cap I_i\ne \varnothing \}$ is a c.e. subset of $\mathbb{N}$;
• a compact set $S\subseteq X$ in $(X,d)$ is a semicomputable set in $(X,d,\alpha )$ if the set $\{j\in \mathbb{N}\mid S\subseteq J_j\}$ is a c.e. subset of $\mathbb{N}$;
• a compact set $S\subseteq X$ in $(X,d)$ is a computable set in $(X,d,\alpha )$ if S is both c.e. and semicomputable in $(X,d,\alpha )$.

These definitions do not depend on the choice of the functions q, ${\tau }_1$, ${\tau }_2$ and ${([j])}_{j\in \mathbb{N}}$.

2.3. Computable Topological Space

Let $(X,\mathcal{T})$ be a topological space and let $(I_i)$ be a sequence in $\mathcal{T}$ such that the set $\{I_i\mid i\in \mathbb{N}\}$ is a basis for $\mathcal{T}$. A triple $(X,\mathcal{T},(I_i))$ is called a computable topological space if there exist c.e. subsets $C,D\subseteq {\mathbb{N}}^2$ such that:

• if $i,j\in \mathbb{N}$ are such that $(i,j)\in C$, then $I_i\subseteq I_j$;
• if $i,j\in \mathbb{N}$ are such that $(i,j)\in D$, then $I_i\cap I_j=\varnothing$;
• if $x\in X$ and $i,j\in \mathbb{N}$ are such that $x\in I_i\cap I_j$, then there is $k\in \mathbb{N}$ such that $x\in I_k$ and $(k,i),(k,j)\in C$;
• if $x,y\in X$ are such that $x\ne y$, then there are $i,j\in \mathbb{N}$ such that $x\in I_i$, $y\in I_j$ and $(i,j)\in D$.

If $(X,d,\alpha )$ is a computable metric space, then it can be shown (see [35]) that $(X,\mathcal{T},(I_i))$ is a computable metric space, where ${\mathcal{T}}_d$ is the topology induced by d and $I_i$ is the sequence of rational open balls defined earlier.

Let $(X,\mathcal{T},(I_i))$ be a computable topological space and, for $j\in \mathbb{N}$, let $J_j:={\bigcup }_{i\in [j]}{I}_i$.

We define semicomputable, computably enumerable and computable sets in $(X,\mathcal{T},(I_i))$ in the same way as in the case of computable metric spaces. As before, these definitions do not depend on the choice of the sequence ${([j])}_{j\in \mathbb{N}}$).

If $(X,d,\alpha )$ is a computable metric space and $S\subseteq X$, then S is c.e./semicomputable/computable in $(X,d,\alpha )$ if and only if S is c.e./semicomputable/computable in $(X,{\mathcal{T}}_d,(I_i))$.

It should be mentioned that if $(X,\mathcal{T},(I_i))$ is a computable topological space, then the topological space $(X,\mathcal{T})$ need not be metrizable (see Example 3.2 in [35]).

Note that $(X,\mathcal{T})$ is Hausdorff and second countable if $(X,\mathcal{T},(I_i))$ is a computable topological space. So, if S is a compact set in $(X,\mathcal{T})$, then S, as a subspace of $(X,\mathcal{T})$, is a compact Hausdorff second countable space, which implies that S is a normal second countable space, and therefore, it is metrizable. We will use this fact later.

The proofs of the following facts, which will be used frequently in this paper, can be found in [35].

Theorem 1.

Let $(X,\mathcal{T},(I_i))$ be a computable topological space. There exist c.e. subsets $\mathcal{C},\mathcal{D}\subseteq {\mathbb{N}}^2$ such that:

1.

if $i,j\in \mathbb{N}$ are such that $(i,j)\in \mathcal{C}$, then $J_i\subseteq J_j$;

2.

if $i,j\in \mathbb{N}$ are such that $(i,j)\in \mathcal{D}$, then $J_i\cap J_j=\varnothing$;

3.

if $\mathcal{F}$ is a finite family of nonempty compact sets in $(X,\mathcal{T})$ and $A\subseteq \mathbb{N}$ is a finite subset of $\mathbb{N}$, then for each $K\in \mathcal{F}$ there is $i_K\in \mathbb{N}$ such that

(i)

$K\subseteq J_{i_k}$;

(ii)

if $K,L\in \mathcal{F}$ are such that $K\cap L=\varnothing$, then $(i_K,i_L)\in \mathcal{D}$;

(iii)

if $a\in A$ and $K\in \mathcal{F}$ are such that $K\subseteq J_a$, then $(i_k,a)\in \mathcal{C}$.

Proposition 1.

Let $(X,\mathcal{T},(I_i))$ be a computable topological space, let $S\subseteq X$ be a semicomputable set in this space and let $m\in \mathbb{N}$. Then, the set $S\setminus J_m$ is semicomputable in $(X,\mathcal{T},(I_i))$.

We say that $x\in X$ is a computable point in $(X,\mathcal{T},(I_i))$ if $\{i\in \mathbb{N}\mid x\in I_i\}$ is a c.e. subset of $\mathbb{N}$. The proof of the following proposition can be found in [12].

Proposition 2.

Let $(X,\mathcal{T},(I_i))$ be a computable topological space and let $x_0,\dots ,x_n\in X$. Then, the following holds:

$$x_0,\dots ,x_n\mathit{are}\mathit{computable}\mathit{points}\iff \{x_0,\dots ,x_n\}\mathit{is}a\mathit{semicomputable}\mathit{set}$$

$$\iff \{x_0,\dots ,x_n\}\mathit{is}a\mathit{computable}\mathit{set}.$$

Let us recall the notion of computable type. We say that a topological space A has a computable type if the following holds: if S is a semicomputable set in a computable topological space $(X,\mathcal{T},(I_i))$ such that S is homeomorphic to A, then S is computable $(X,\mathcal{T}$, $(I_i))$. Furthermore, we say that a topological pair $(A,B)$ has a computable type if the following holds: if S and T are semicomputable sets in a computable topological space $(X,\mathcal{T},(I_i))$ such that $(S,T)$ is homeomorphic to $(A,B)$, then S is computable in $(X,\mathcal{T},(I_i))$.

2.4. Chainable and Circularly Chainable Hausdorff Continua

Let X be a set and $\mathcal{C}=(C_0,\dots ,C_m)$ be a finite sequence of subsets of X. We say that $\mathcal{C}$ is a chain in X if the following holds:

$$C_i\cap C_j=\varnothing \iff 1<|i-j|,$$

for all $i,j\in \{0,\dots ,m\}$. Also, we say that $\mathcal{C}$ is a circular chain in X if the following holds:

$$C_i\cap C_j=\varnothing \iff 1<|i-j|<m,$$

for all $i,j\in \{0,\dots ,m\}$.

Let $A\subseteq X$ and $a,b\in A$. We say that $C_0,\dots ,C_m$ covers A if $A\subseteq C_0\cup \cdots \cup C_m$, and we say it covers A from a to b if it is also $a\in C_0$ and $b\in C_m$.

Let $(X,d)$ be a metric space. A (circular) chain $C_0,\dots ,C_m$ is said to be an $ϵ$-(circular) chain for some $ϵ>0$, if $diam{C}_i<ϵ,$ for each $i\in \{0,\dots ,m\}$ and it is said to be an open (circular) chain if every $C_i$ is open in $(X,d)$. In the same way, we define the notion of a compact (circular) chain.

Let $(X,d)$ be a continuum, i.e., a connected and compact metric space. We say that $(X,d)$ is a (circularly) chainable continuum if for every $ϵ>0$ there exists an open $ϵ$-(circular) chain in $(X,d)$ which covers X. For $a,b\in X$, we say that $(X,d)$ is a continuum chainable from a to b if for every $ϵ>0$ there exists an open $ϵ$-chain $C_0,\dots ,C_m$ which covers X from a to b.

The proofs of the following facts can be found in [5].

Proposition 3.

Let $(X,d)$ be a continuum and $a,b\in X$.

1.

$(X,d)$ is a chainable continuum from a to b if and only if for each $ϵ>0$ there is a compact ϵ-chain in $(X,d)$ which covers X from a to b.

2.

$(X,d)$ is a (circularly) chainable continuum if and only if for each $ϵ>0$ there is a compact ϵ-(circular) chain in $(X,d)$ which covers X.

A Hausdorff continuum is a connected and compact Hausdorff topological space.

Let $\mathcal{A}$ and $\mathcal{B}$ be families of sets. We say that $\mathcal{A}$ refines $\mathcal{B}$ if for each $A\in \mathcal{A}$ there exists $B\in \mathcal{B}$ such that $A\subseteq B$.

Let X be a Hausdorff continuum. We say that X is a (circularly) chainable Hausdorff continuum if for each open cover $\mathcal{U}$ of X there is an open (circular) chain $C_0,\dots ,C_m$ in X which covers X such that $\{C_0,\dots ,C_m\}$ refines $\mathcal{U}$. We similarly define that a Hausdorff continuum is chainable from a to b.

It follows easily that a metric space $(X,d)$ is a (circularly) chainable continuum if and only if topological space $(X,{\mathcal{T}}_d)$ is a (circularly) chainable Hausdorff continuum (where ${\mathcal{T}}_d$ is the topology induced by d). Also, $(X,d)$ is a continuum chainable from a to b if and only if $(X,{\mathcal{T}}_d)$ is a Hausdorff continuum chainable from a to b. See Section 3 in [3].

Remark 1.

Let X and Y be topological spaces and let $f:X\to Y$ be a homeomorphism. Then is easy to see that X is a (circularly) chainable Hausdorff continuum if and only if Y is a (circularly) chainable Hausdorff continuum. Furthermore, if $a,b\in X$, then X is a Hausdorff continuum chainable from a to b if and only if Y is a Hausdorff continuum chainable from $f(a)$ to $f(b)$.

2.5. Topological and Chainable Graph

Here, we recall the notions of the topological graph (see [12]) and its generalization, the chainable graph (see [11]).

Let $\mathcal{I}$ be a nonempty finite family of (non-degenerate) line segments in ${\mathbb{R}}^n$, $n\in \mathbb{N}$, such that for all $I,J\in \mathcal{I}$, $I\ne J$ holds: if $I\cap J\ne \varnothing$ then $I\cap J=\{a\}$, where a is an endpoint of both I and J. Any topological space G homeomorphic to ${\bigcup }_{I\in \mathcal{I}}I$ is called a graph.

For the graph G we say that $x\in G$ is an endpoint of G if there exists an open neighborhood N of x in G such that N is homeomorphic to $[0,\infty )$ by a homeomorphism which maps x to 0. If $\mathcal{I}$ is the family from the definition of G, then x is an endpoint of G if and only if there exists a unique $I\in \mathcal{I}$ such that x is an endpoint of I (see [12]). See Figure 1.

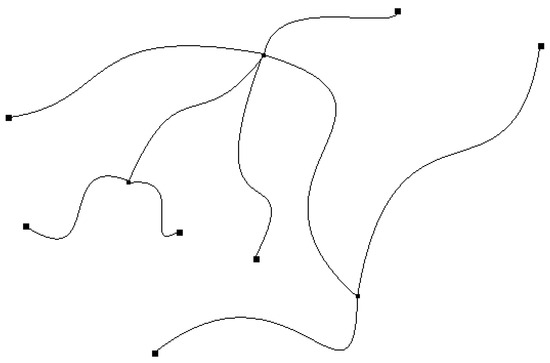
Figure 1. Graph. The highlighted points are its endpoints.

The following result was proved in [12].

Theorem 2.

Let G be a graph and let E be the set of all endpoints of G. Then $(G,E)$ has computable type.

Let A be a topological space. Suppose V is a finite subset of A and let $\mathcal{K}$ be a finite family of pairs $(K,\{a,b\})$, where $a,b\in V$, $a\ne b$, and K is a subspace of A such that K is a Hausdorff continuum chainable from a to b and such that $K\cap V=\{a,b\}$. Suppose

$$A=V\cup \bigcup _{(K,\{a,b\})\in \mathcal{K}}K$$

and the following holds:

(i)

for all $a,b\in V$, $a\ne b$, there exists at most one K such that $(K,\{a,b\})\in \mathcal{K}$;

(ii)

if $(K,\{a,b\})\in \mathcal{K}$ and $(K,\{c,d\})\in \mathcal{K}$, then $\{a,b\}=\{c,d\}$;

(iii)

if $(K,\{a,b\}),(L,\{c,d\})\in \mathcal{K}$ and $K\ne L$, then $K\cap L\subseteq V$.

Then, we say that the triple $(A,\mathcal{K},V)$ is a chainable graph. Also, we say that $a\in V$ is an endpoint of $(A,\mathcal{K},V)$ if there exists a unique $K\subseteq A$ such that $(K,\{a,b\})\in \mathcal{K}$ for some $b\in V$ (note that such a b also has to be unique by (ii)). See Figure 2.

Figure 2. Chainable graph. The highlighted points are its endpoints. Three of these chainable continua are homeomorphic to the continuum K from Example 1.

For example, if K is a Hausdorff continuum chainable from a to b, $a\ne b$, then $(K,\{(K,\{a,b\})\},\{a,b\})$ is a chainable graph and a and b are all of its endpoints.

If G is a topological graph, then it is not hard to see that there exist $\mathcal{K}$ and V such that $(G,\mathcal{K},V)$ is a chainable graph. On the other hand, if $(G,\mathcal{K},V)$ is a chainable graph, then G need not be a graph. See [11].

The proof of the following proposition, a generalization of Theorem 2, can be found in [11].

Theorem 3.

If $(A,\mathcal{K},V)$ is a chainable graph and B is the set of all its endpoints, then $(A,B)$ has a computable type.

3. Generalized Graph

In this section, we consider spaces more general than chainable graphs (and graphs), so-called generalized graphs, and we generalize Theorem 3 by showing that an analog version of this theorem holds for generalized graphs, as well.

Suppose A is a topological space. Let $V\subseteq A$ be a finite subset of A and let $\mathcal{K}$ be a finite family of pairs $(K,\{a,b\})$ where $a,b\in V$, $a\ne b$, and K is a subspace of A such that K is a Hausdorff continuum chainable from a to b. Suppose

$$A=V\cup \bigcup _{(K,\{a,b\})\in \mathcal{K}}K$$

and that the following holds: if $(K,\{a,b\})$, $(L,\{c,d\})\in \mathcal{K}$ and $K\ne L$, then $card(K\cap L)<{\aleph }_0$.

Then the triple $(A,\mathcal{K},V)$ is called a generalized graph.

Let $(A,\mathcal{K},V)$ be a chainable graph and let $a\in V$. We say that a is an endpoint of $(A,\mathcal{K},V)$ if there exists a unique $K\subseteq A$ such that $(K,\{a,b\})\in \mathcal{K}$ for some $b\in V$.

If $(K,\{a,b\})\in \mathcal{K}$, we can think of K as an edge of the generalized graph $(A,\mathcal{K},V)$. Then, $a\in V$ is an endpoint of $(A,\mathcal{K},V)$ if it is an endpoint of only one of its edges. Also, we can say that the main difference between a chainable and a generalized graph is that we let the edges of the generalized graph intersect in more than two, yet finitely many, points.

Note that each chainable graph is a generalized graph.

Example 1.

Let

$$K=\left(\{0\}\times [-1,1]\right)\cup \left\{\left(x,sin{\displaystyle \frac{1}{x}}\right)\mid 0<x\le 1\right\}.$$

Let $a=(0,-1)$ and $b=(1,sin1)$. It is known that K is a continuum chainable from a to b. Therefore, the triple $(K,\{(K,\{a,b\})\},\{a,b\})$ is both a chainable and a generalized graph. Now, let $c=(0,1)$. Since K is also a continuum chainable from b to c, triple $(K,\{(K,\{a,c\}),(K,\{b,c\})\},\{a,b,c\})$ is a generalized graph but is not a chainable graph since it does not satisfy the property (ii) from the definition of a chainable graph.

The previous example shows us one more distinction between chainable and generalized graphs. Namely, if $(A,\mathcal{K},V)$ is a generalized graph and K is its edge, there can exist different pairs of endpoints of K which is not the case in a chainable graph.

We have shown that there exists triple $(A,\mathcal{K},V)$ which is a generalized graph but not a chainable graph. In the next three examples we show even more: there is such space A for which there are $\mathcal{K}$ and V such that $(A,\mathcal{K},V)$ is a generalized graph but there are no such $\mathcal{K}$ and V for which $(A,\mathcal{K},V)$ is a chainable graph.

Example 2.

Let

$$A=\left(\left[-1,0\right]\times \{-1,1\}\right)\cup \left(\{0\}\times \left[-1,1\right]\right)\cup \left\{\left(t,sin\left({\displaystyle \frac{1}{t}}\right)\right)\mid t\in ⟨\left.0,1\right]\right\}$$

and

$$a=(-1,-1),b=(-1,1)\mathrm{and}c=(1,sin1).$$

See Figure 3.

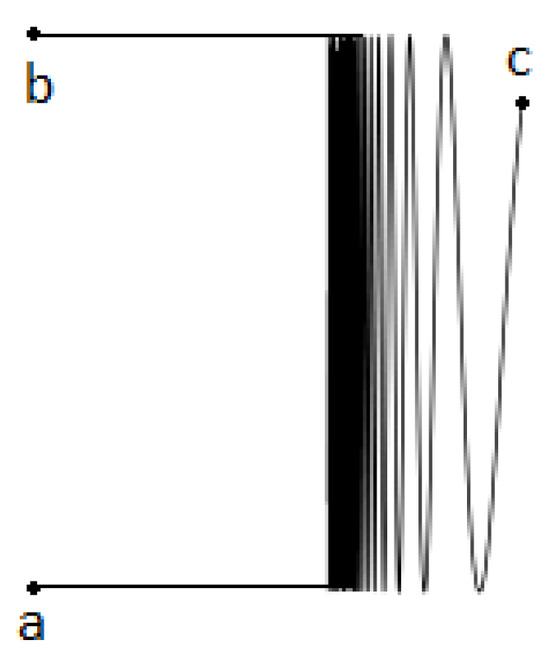
Figure 3. Set A.

It is easy to see that there exist $\mathcal{K}$ and V such that $(A,\mathcal{K},V)$ is a generalized graph.

Example 3.

Let A be as in Example 2. Assume that there are $\mathcal{K}$ and V such that $(A,\mathcal{K},V)$ is a chainable graph. Then, there are no $a,b\in V$ such that $(K,\{a,b\})\in \mathcal{K}$ if

$$K=\left(\left[{\gamma }_1,0\right]\times \{-1\}\right)\cup \left(\left[{\gamma }_2,0\right]\times \{1\}\right)\cup \left(\{0\}\times \left[-1,1\right]\right)\cup \left\{\left(t,sin\left({\displaystyle \frac{1}{t}}\right)\right)\mid t\in ⟨\left.0,\beta \right]\right\},$$

${\gamma }_1,{\gamma }_2\in \left[-1,0⟩,\beta \in ⟨0,1\right].$

To prove so, let us assume the opposite, i.e., let $a,b\in V$ be such that $(K,\{a,b\})\in \mathcal{K}$. We will distinguish three cases.

Firstly, let $a,b\notin \left[{\gamma }_1,0\right]\times \{-1\}$. Let $0<ϵ<min\{\left|{\gamma }_1\right|,2\}$. Since continuum K is chainable from a to b, there is an open ϵ-chain $C_0,\dots ,C_m$ in K which covers K from a to b. If $i\in \{0,\dots ,m\}$ is such that $({\gamma }_1,-1)\in C_i$, then

$$\begin{array}{c}\hfill \left(\left[{\gamma }_2,0\right]\times \{1\}\right)\cup \left(\{0\}\times \left[-1,1\right]\right)\cup \left\{\left(t,sin\left({\displaystyle \frac{1}{t}}\right)\right)\mid t\in ⟨\left.0,\beta \right]\right\}\subseteq \\ \hfill \subseteq \left(C_0\cup \cdots \cup C_{i-1}\right)\cup \left(C_{i+1}\cup \cdots \cup C_m\right)\end{array}$$

(3)

which contradicts the connectednes of the set on the left side of the equation since $C_0\cup \cdots \cup C_{i-1}$ and $C_{i+1}\cup \cdots \cup C_m$ are disjoint by the definition of a chain. Namely, if $(x,y)\in \left[{\gamma }_2,0\right]\times \{1\}$ then $(x,y)\in C_i$ would mean that

$$2\le \sqrt{{\left({\gamma }_1-x\right)}^2+2^2}=d\left(({\gamma }_1,-1),(x,1)\right)\le diam(C_i)<ϵ<2$$

which is a contradiction. Similarly, if $(x,y)\in \{0\}\times \left[-1,1\right]$, assuming that $(x,y)\in C_i$ leads to

$$\left|{\gamma }_1\right|\le d\left(({\gamma }_1,-1),(0,y)\right)<ϵ<\left|{\gamma }_1\right|;$$

a contradiction. Finally, if $(x,y)\in \left\{\left(t,sin\left({\displaystyle \frac{1}{t}}\right)\right)\mid t\in ⟨\left.0,\beta \right]\right\}$, we similarly obtain

$$\left|{\gamma }_1\right|\le |{\gamma }_1-x|\le d\left(({\gamma }_1,-1),(x,y)\right)<ϵ<\left|{\gamma }_1\right|,$$

if $(x,y)\in C_i$.

If $a,b\notin \left[{\gamma }_2,0\right]\times \{1\}$, we obtain a contradiction in the same way.

Hence, we are left with the third case when both $\left[{\gamma }_1,0\right]\times \{-1\}$ and $\left[{\gamma }_2,0\right]\times \{1\}$ contain exactly one of the points a and b which will also leads to a contradiction (and that will prove the claim). Namely, let $0<ϵ<\beta$. Again, since continuum K is chainable from a to b, there is an open ϵ-chain $C_0,\dots ,C_m$ in K which covers K from a to b. Let $i\in \{0,\dots ,m\}$ be such that $\left(\beta ,sin\left({\displaystyle \frac{1}{\beta }}\right)\right)\in C_i$. Similarly as before we can prove that

$$\left(\left[{\gamma }_1,0\right]\times \{-1\}\right)\cup \left(\left[{\gamma }_2,0\right]\times \{1\}\right)\cup \left(\{0\}\times \left[-1,1\right]\right)\subseteq \left(C_0\cup \cdots \cup C_{i-1}\right)\cup \left(C_{i+1}\cup \cdots \cup C_m\right)$$

which then contradicts the connectedness of the set on the left side of the equation.

Example 4.

Let A be as in Example 2. We are going to show that there are no $\mathcal{K}$ and V such that $(A,\mathcal{K},V)$ is a chainable graph. To prove so, let us assume the opposite. Then, by the definition of the chainable graph, there is $(K,\{a,b\})\in \mathcal{K}$ such that $(0,0)\in K$ (otherwise $\{(0,0)\}$ would be an open set in A, which follows easily from the definition of a chainable graph, but it is clear that $\{(0,0)\}$ is not open in A). Since K is connected and $card(K)\ge 2$ for each $ϵ>0$

$$B((0,0),ϵ)\cap \left(K\setminus \{(0,0)\}\right)\ne \varnothing .$$

(4)

This allows us to conclude that for each $ϵ>0$ there is $t\in ⟨0,ϵ⟩$ such that $\left(t,sin\left({\displaystyle \frac{1}{t}}\right)\right)\in K$. Indeed, let us assume that there exists $\delta >0$ such that for each $t\in ⟨0,\delta ⟩$ it holds $\left(t,sin\left({\displaystyle \frac{1}{t}}\right)\right)\notin K$. Using (4) we conclude that for ${\delta }^{\prime }=min\{\delta ,{\displaystyle \frac{1}{2}}\}$ there is

$$(x,y)\in B\left((0,0),{\delta }^{\prime }\right)\cap K\setminus \{(0,0)\},$$

i.e., there is $(x,y)\in K$, $(x,y)\ne (0,0)$ such that

$$\sqrt{x^2+y^2}=d\left((x,y),(0,0)\right)<{\delta }^{\prime }.$$

(5)

If $(x,y)\in \left[-1,0\right]\times \{-1,1\}$, by (5) we have that

$$1\le \sqrt{x^2+1}=\sqrt{x^2+y^2}<{\delta }^{\prime }<{\displaystyle \frac{1}{2}},$$

is a contradiction. Also, if $(x,y)\in \left\{\left(t,sin\left({\displaystyle \frac{1}{t}}\right)\right)\mid t\in ⟨\left.0,1\right]\right\}$, then there is $t^{\prime }\in ⟨\left.0,1\right]$ such that $\left(t^{\prime },sin\left({\displaystyle \frac{1}{t^{\prime }}}\right)\right)\in K$ and, because of (5), it is

$$0<t^{\prime }=\left|t^{\prime }\right|\le \sqrt{{(t^{\prime })}^2+{sin}^2\left({\displaystyle \frac{1}{t^{\prime }}}\right)}<{\delta }^{\prime }<\delta ;$$

i.e., $t^{\prime }\in ⟨0,\delta ⟩$ which contradicts the assumption. This leaves us with the last case possible, $(x,y)\in \{0\}\times \left[-1,1\right]$. Using (5), this means that

$$x=0\mathrm{and}\left|y\right|<{\displaystyle \frac{1}{2}}.$$

Now, using (4) and the same arguments as above (K is infinite since it is connected, Hausdorff and $card(K)\ge 2$), we conclude that there is $z\in ⟨-{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}}⟩$ such that

$$(0,z)\in B\left((0,0),{\delta }^{\prime }\right)\cap K\setminus \{(0,0),(0,y)\}.$$

Obviously, there is $r\in \{0,y,z\}$ such that $(0,r)\ne a,b$, i.e.,

$$(0,r)\in K\setminus \{a,b\}.$$

Because $K\setminus \{a,b\}$ is an open set in A (which is not hard to conclude from the definition of a chainable graph), there is $0<\mu <\delta$ such that

$$B\left((0,r),\mu \right)\subseteq K\setminus \{a,b\}.$$

Since

$$(0,r)\in \overline{\left\{\left(t,sin\left({\displaystyle \frac{1}{t}}\right)\right)\mid t\in ⟨\left.0,1\right]\right\}}$$

we have that

$$B\left((0,r),\mu \right)\cap \left\{\left(t,sin\left({\displaystyle \frac{1}{t}}\right)\right)\mid t\in ⟨\left.0,1\right]\right\}$$

which, again, contradicts the assumption. Hence, for each $ϵ>0$ there is $t\in ⟨0,ϵ⟩$ such that $\left(t,sin\left({\displaystyle \frac{1}{t}}\right)\right)\in K$.

Now, let $p:{\mathbb{R}}^2\to \mathbb{R}$ be a projection on the first coordinate. A compact and connected $p(K)\subseteq \mathbb{R}$ is a segment. Since $(0,0)\in K$, obviously $0\in p(K)$, and since for each $ϵ>0$ there is $t\in ⟨0,ϵ⟩$ such that $t\in p(K)$, there are $\alpha ,\beta \in \mathbb{R}$, $\alpha \le 0<\beta$ such that $p(K)=\left[\alpha ,\beta \right]$. Since

$$\left.⟨0,\beta \right]\subseteq \left[\alpha ,\beta \right]=p(K)$$

and ${p|}_{A\cap \{(u,v)\mid u>0\}}$ is a bijection, we conclude that

$$\left\{\left(t,sin\left({\displaystyle \frac{1}{t}}\right)\right)\mid t\in ⟨\left.0,\beta \right]\right\}\subseteq K$$

and, therefore,

$$\overline{\left\{\left(t,sin\left({\displaystyle \frac{1}{t}}\right)\right)\mid t\in ⟨\left.0,\beta \right]\right\}}\subseteq \overline{K},$$

i.e.,

$$\{0\}\times \left[-1,1\right]\cup \left\{\left(t,sin\left({\displaystyle \frac{1}{t}}\right)\right)\mid t\in ⟨\left.0,\beta \right]\right\}\subseteq K.$$

(6)

Now, we show that in (6), equality does not hold. Indeed, let us assume that

$$\{0\}\times \left[-1,1\right]\cup \left\{\left(t,sin\left({\displaystyle \frac{1}{t}}\right)\right)\mid t\in ⟨\left.0,\beta \right]\right\}=K.$$

If $\beta <1$, then $(0,-1),(0,1),\left(\beta ,sin\left({\displaystyle \frac{1}{\beta }}\right)\right)\in \overline{K^c}\cap K$. Since $\overline{K^c}\subseteq \overline{{\left(K\setminus \{a,b\}\right)}^c}={\left(K\setminus \{a,b\}\right)}^c=K^c\cup \{a,b\}$, we conclude that

$$\left\{(0,-1),(0,1),\left(\beta ,sin\left({\displaystyle \frac{1}{\beta }}\right)\right)\right\}\subseteq \{a,b\},$$

a contradiction. If $\beta =1$, as above, we conclude that $\left\{(0,-1),(0,1)\right\}\subseteq \{a,b\}$, i.e., $\left\{(0,-1),(0,1)\right\}=\{a,b\}$. Therefore, K is chainable from $(0,-1)$ to $(0,1)$, so there is an open ${\displaystyle \frac{1}{2}}$ – chain in K which covers K from $(0,-1)$ to $(0,1)$. If $i\in \{0,\dots ,n\}$ is such that $\left(1,sin1\right)\in C_i$, similarly as in Example 3, we obtain that

$$\{0\}\times \left[0,1\right]\subseteq (C_0\cup \cdots \cup C_{i-1})\cup (C_{i+1}\cup \cdots \cup C_n),$$

which is impossible since $\{0\}\times \left[0,1\right]$ is connected. Therefore,

$$\{0\}\times \left[-1,1\right]\cup \left\{\left(t,sin\left({\displaystyle \frac{1}{t}}\right)\right)\mid t\in ⟨\left.0,\beta \right]\right\}\subset K$$

which means that

$$K\cap \left(\left[-1,0⟩\right.\times \{-1,1\}\right)\ne \varnothing .$$

But, we can conclude even more. It is true that

$$K\cap \left(\left[-1,0⟩\right.\times \{-1\}\right)\ne \varnothing \mathrm{and}K\cap \left(\left[-1,0⟩\right.\times \{1\}\right)\ne \varnothing .$$

Indeed, if assume the opposite, for example, $K\cap \left(\left[-1,0⟩\right.\times \{-1\}\right)=\varnothing$, then $K\cap \left(\left[-1,0⟩\right.\times \{1\}\right)\ne \varnothing$. Since $p(K)=\left[\alpha ,\beta \right]$ and ${p|}_{K\cap \{(u,v)\{u<0\}}$ is a bijection, we obtain that

$$K\cap \left(\left[-1,0⟩\right.\times \{1\}\right)=\left[\alpha ,0⟩\right.\times \{1\}$$

so

$$K=\left(\left[\alpha ,0\right]\times \{1\}\right)\cup \left(\{0\}\times \left[-1,1\right]\right)\cup \left\{\left(t,sin\left({\displaystyle \frac{1}{t}}\right)\right)\mid t\in ⟨\left.0,\beta \right]\right\}.$$

We have $(0,1)\in \overline{K^c}\cap K$ and so $(0,-1)\in \{a,b\}$, which implies that $\{a,b\}\subseteq \{0\}\times [-1,1]\cup \{(t,sin({\displaystyle \frac{1}{t}})\mid t\in ⟨0,\beta ]\}$ or $\{a,b\}\subseteq [\alpha ,0]\times \{1\}\cup \{0\}\times [-1,1]$. In both cases we obtain a contradiction with the fact that K is chainable from a to b, as in Example 3.

So

$$K\cap \left(\left[-1,0\right]\times \{-1\}\right)\ne \varnothing \mathrm{and}K\cap \left(\left[-1,0\right]\times \{1\}\right)\ne \varnothing .$$

(7)

and we prove that both of these sets are connected. To show that, assume that $K\cap \left(\left[-1,0\right]\times \{1\}\right)$ is not connected. Therefore, there exists a separation $(F,G)$ of $K\cap \left(\left[-1,0\right]\times \{1\}\right)$. Without loss of generality, let $(0,1)\in G$, so we can write

$$K=F\cup \left(G\cup \left(K\setminus \left(\left[-1,0⟩\right.\times \{1\}\right)\right)\right).$$

(8)

Both F and G are closed in $K\cap \left(\left[-1,0\right]\times \{1\}\right)$, and therefore, they are closed in A (since $K\cap \left(\left[-1,0\right]\times \{1\}\right)$ is closed in A). Since $F,G\subseteq K$, F and G are closed in K. Similarly, $K\setminus \left(\left[-1,0⟩\right.\times \{1\}\right)$ is closed in A since $\left[-1,0⟩\right.\times \{1\}$ is open in A. Therefore, (8) gives us a separation of K which is connected, a contradiction. So, since $K\cap \left(\left[-1,0\right.⟩\times \{-1\}\right)\ne \varnothing$ and $K\cap \left(\left[-1,0\right]\times \{-1\}\right)$ is connected and compact, there exists ${\gamma }_2\in \mathbb{R},-1\le {\gamma }_2<0$ such that

$$K\cap \left(\left[-1,0\right]\times \{1\}\right)=\left[{\gamma }_2,0\right]\times \{1\}.$$

Similarly, there exists ${\gamma }_1\in \mathbb{R},-1\le {\gamma }_1<0$ such that

$$K\cap \left(\left[-1,0\right]\times \{-1\}\right)=\left[{\gamma }_1,0\right]\times \{-1\},$$

i.e.,

$$K=\left(\left[{\gamma }_1,0\right]\times \{-1\}\right)\cup \left(\left[{\gamma }_2,0\right]\times \{1\}\right)\cup \left(\{0\}\times \left[-1,1\right]\right)\cup \left\{\left(t,sin\left({\displaystyle \frac{1}{t}}\right)\right)\mid t\in ⟨\left.0,\beta \right]\right\},$$

${\gamma }_1,{\gamma }_2\in \left[-1,0⟩,\beta \in ⟨0,1\right]$ which is impossible by Example 3.

In this section we are going to prove the following result:

Theorem 4.

If $(A,\mathcal{K},V)$ is a generalized graph and B is the set of all its endpoints, then $(A,B)$ has computable type.

Remark 2.

Using Remark 1, we conclude the following: if $(A,\mathcal{K},V)$ is a generalized graph, B the set of all its endpoints, $A^{\prime }$ a topological space and $f:A\to A^{\prime }$ a homeomorphism, then

$$(A^{\prime },\{(f(K),\{f(a),f(b)\})\mid (K,\{a,b\})\in \mathcal{K}\},f(V))$$

is generalized graph and $f(B)$ is the set of all its endpoints. Namely, if $(K,\{a,b\}),(L,\{c,d\})\in \mathcal{K}$ are such that $f(K)\ne f(L)$, then $K\ne L$, and therefore, $K\cap L$ is a finite set which, together with the fact that $f(K)\cap f(L)=f(K\cap L)$, implies that $f(K)\cap f(L)$ is a finite set.

Let $(X,\mathcal{T},(I_i))$ be a computable topological space and let S and T be subsets of X such that $S\subseteq T$. We say that S is computably enumerable (c.e) up to T if there exists a c.e. subset $\Omega$ of $\mathbb{N}$ such that for each $i\in \mathbb{N}$ the following holds:

$$\mathrm{if}{I}_i\cap S\ne \varnothing ,\mathrm{then}i\in \Omega ;$$

$$\mathrm{if}i\in \Omega ,\mathrm{then}{I}_i\cap T\ne \varnothing .$$

It is obvious that if S is closed and S is c.e. up to S, then S is a c.e. set in $(X,\mathcal{T},(I_i))$.

Remark 3.

Let $(X,\mathcal{T},(I_i))$ be a computable topological space and let $S_0$,…, $S_k$ and T be subsets of X such that $S_i$ is c.e. up to T for each $i\in \{0,\dots ,k\}$. Then, it readily follows that $S_0,$ …, $S_k$ is c.e. up to T.

Now we are ready to prove Theorem 4. In view of Remark 2 it is enough to prove the following proposition.

Proposition 4.

Let $(X,\mathcal{T},{(I)}_i)$ be a computable topological space and let S and T be semicomputable sets in this space. Suppose there are $\mathcal{K}$ and V such that $(S,\mathcal{K},V)$ is a generalized graph and T is the set of all its endpoints. Then, S is computable.

Despite the obvious similarities between chainable and generalized graphs, there are more than slightly differences in the proofs of the main results. In the case of the chainable graph, if we take a continuum (i.e., an edge) K chainable from a to b we know that the intersection with an other edge M can occur only in one of the points a and b, let us say in a, and a is also an endpoint of M, so we can use that fact to write $M=M_1\cup M_2\cup M_3$, where $M_1,M_2,M_3$ are compacts such that $M_1\cap M_3=\varnothing$ and $a\in M_1$. That is not the case if we have a generalized graph and some technical lemmas are needed in order to solve that problem. So, before giving the proof of Proposition 4, we need certain further facts about chainable continua. Specifically, we have to prove that if it is given a chainable continuum K and its arbitrary point c, we can find a nontrivial subcontinuum L of K which contains c and is small enough. More precisely, we need to show the following:

Lemma 1.

Let $(K,d)$ be a continuum chainable from a to b, $a,b\in K$ and let $c\in K$ be arbitrary. For each $ϵ>0$ there is a nontrivial continuum $L\subseteq K$ such that $c\in L$ and $L\subseteq B\left(c,ϵ\right).$

Firstly, we give straightforward proofs of a few lemmas needed to prove the aforementioned one.

Lemma 2.

Let $(K,d)$ be a continuum chainable from a to b. For each $ϵ>0$ there exists an open ϵ-chain $C_0,\dots ,C_m$ in $(K,d)$ which covers K from a to b such that $\overline{C_0},\dots ,\overline{C_m}$ is also a chain.

Proof.

Since $(K,d)$ is a continuum chainable from a to b, there exists a compact ${\displaystyle \frac{ϵ}{4}}$-chain $K_0,\dots ,K_m$ in $(K,d)$ which covers K from a to b. Let us define

$$\delta =min\left\{min\left\{d(K_i,K_j)\mid \left|i-j\right|\ge 2\right\},ϵ\right\}.$$

(9)

Since $d(K_i,K_j)>0$ for disjoint sets $K_i$ and $K_j$, the number $\delta$ is positive.

For each $i\in \{0,\dots ,m\}$, because $K_i$ is compact, there exist $k_i\in \mathbb{N}$ and $x_0^i,\dots ,x_{k_i}^i\in K_i$ such that

$$K_i\subseteq \bigcup _{l=0}^{k_i}B\left(x_l^i,{\displaystyle \frac{\delta }{4}}\right).$$

(10)

Let us define

$$C_i=\bigcup _{l=0}^{k_i}B\left(x_l^i,{\displaystyle \frac{\delta }{4}}\right).$$

Above the defined $C_i$ are open sets and because of (10) it is $a\in C_0$, $b\in C_m$ and

$$K\subseteq C_0\cup \cdots \cup C_m$$

and $C_i\cap C_j\ne \varnothing$ for all $i,j\in \{0,\dots ,m\}$ such that $\left|i-j\right|\le 1$. In particular, $\overline{C_i}\cap \overline{C_j}\ne \varnothing$.

Furthermore, for arbitrary $x,y\in C_i$, there are $l,p\in \{0,\dots ,k_i\}$ such that $x\in B\left(x_l^i,{\displaystyle \frac{\delta }{4}}\right)$ and $y\in B\left(x_p^i,{\displaystyle \frac{\delta }{4}}\right)$. Therefore,

$$d(x,y)\le d(x,x_l^i)+d(x_l^i,x_p^i)+d(x_p^i,y)<{\displaystyle \frac{\delta }{4}}+diam{K}_i+{\displaystyle \frac{\delta }{4}}<{\displaystyle \frac{\delta }{4}}+{\displaystyle \frac{ϵ}{4}}+{\displaystyle \frac{\delta }{4}}\le {\displaystyle \frac{3ϵ}{4}}<ϵ,$$

i.e., $diam{C}_i<ϵ$ for each $i\in \{0,\dots ,m\}$.

It is clear that for all $i,j\in \{0,\dots ,m\}$ such that $\left|i-j\right|\ge 2$ and $l\in \{0,\dots ,k_i\}$, $s\in \{0,\dots ,k_j\}$ it is

$$\overline{B}\left(x_l^i,{\displaystyle \frac{\delta }{4}}\right)\cap \overline{B}\left(x_s^j,{\displaystyle \frac{\delta }{4}}\right)=\varnothing$$

because otherwise we would have that

$$d(x_l^i,x_s^j)\le {\displaystyle \frac{\delta }{4}}+{\displaystyle \frac{\delta }{4}}<\delta \le d(K_i,K_j),$$

which is impossible.

Since, for each $i\in \{1,\dots ,m\}$,

$$\overline{C_i}=\overline{\bigcup _{l=0}^{k_i}B\left(x_l^i,{\displaystyle \frac{\delta }{4}}\right)}=\bigcup _{l=0}^{k_i}\overline{B\left(x_l^i,{\displaystyle \frac{\delta }{4}}\right)}\subseteq \bigcup _{l=0}^{k_i}\overline{B}\left(x_l^i,{\displaystyle \frac{\delta }{4}}\right),$$

we conclude that $\overline{C_i}\cap \overline{C_j}=\varnothing$ for all $i,j\in \{0,\dots ,m\}$ such that $\left|i-j\right|\ge 2$. In particular, $C_i\cap C_j=\varnothing$. Therefore, $C_0,\dots ,C_m$ is an appropriate chain. □

Lemma 3.

Let $(K,d)$ be a continuum chainable from a to b, $a,b\in K$ and let $c\in K$ be arbitrary. For each $ϵ>0$ there exists an open ϵ-chain $C_0,\dots ,C_m$ in $(K,d)$ which covers K from a to b such that:

1.

$\overline{C_0},\dots ,\overline{C_m}$ is also a chain;

2.

there exists a unique $u\in \{0,\dots ,m\}$ such that $c\in C_u$.

Proof.

Since $(K,d)$ is a continuum chainable from a to b, by previous lemma, there is an open ${\displaystyle \frac{ϵ}{3}}$-chain $D_0,\dots ,D_n$ in $(K,d)$ which covers K from a to b such that $\overline{D_0},\dots ,\overline{D_n}$ is also a chain. Let $k\in \{0,\dots ,n\}$ be such that $c\in D_k$. If $k=0$ then $C_0=D_0\cup D_1$ and $C_i=D_{i+1}$ for each $i\in \{1,\dots ,n-1\}$, defines an appropriate chain. Similarly, if $k=n$ the chain is defined by $C_i=D_i$ for each $i\in \{0,\dots ,n-2\}$, and $C_{n-1}=D_{n-1}\cup D_n$. Finally, if $k\ne 0,n$ then the desired chain is $D_0,\dots ,D_{k-2},D_{k-1}\cup D_k\cup D_{k+1},D_{k+2},\dots ,D_n$. □

Lemma 4.

Let X be a set and let $C_0,\dots ,C_m$ and $D_0,\dots ,D_n$ be two chains in X such that $\{D_0,\dots ,D_n\}$ refines $\{C_0,\dots ,C_m\}$. Furthermore, suppose that $i,j,k\in \{0,\dots ,m\}$ and $p,g\in \{0,\dots ,n\}$ are such that $i<k<j$, $D_p\subseteq C_i$ and $D_q\subseteq C_j$. Then, there exists $r\in \{0,\dots ,n\}$ such that $min\{p,q\}<r<max\{p,q\}$ and $D_r\subseteq C_k$.

Proof.

We have $p\ne q$ since $C_i\cap C_j=\varnothing$. If $p<q$ the conclusion follows from Lemma 3.8 in [5]. Otherwise, if $p>q$, the same lemma, only applied on the chain $D_0^{\prime },\dots ,D_n^{\prime }$ defined by $D_j^{\prime }=D_{n-j}$ for each $j\in \{0,\dots ,n\}$, proves the claim. □

In order to prove Lemma 1, one must consider cases when $c=a$ or $c=b$ and when c is neither a nor b. We have the following definition. If $\mathcal{A}=(A_0,\dots ,A_m)$ and $\mathcal{B}=(B_0,\dots ,B_n)$ are finite sequences of subsets of a set X, we say that $\mathcal{A}$ strongly refines $\mathcal{B}$ if $\{A_0,\dots ,A_m\}$ refines $\{B_0,\dots ,B_n\}$, $A_0\subseteq B_0$ and $A_m\subseteq B_n$.

The proof of the following lemma can be found in [4].

Lemma 5.

Let $(X,d)$ be a compact metric space. Let $({\mathcal{C}}^i)$, where ${\mathcal{C}}^i=(C_0^i,\dots ,C_{m_i}^i)$, $i\in \mathbb{N}$, be a sequence of chains such that $\overline{C_0^{i+1}},\dots ,\overline{C_{m_{i+1}}^{i+1}}$ strongly refines $C_0^i,\dots ,C_{m_i}^i$ and such that $diam(C_j^i)<2^{-i}$ for each $i\in \mathbb{N}$ and for each $j\in \{0,\dots ,m_i\}$. Let

$$S=\bigcap _{i\in \mathbb{N}}(\overline{C_0^i}\cup \cdots \cup \overline{C_{m_i}^i}).$$

Then, S is a continuum chainable from a to b, where $a\in {\bigcap }_{i\in \mathbb{N}}{C}_0^i$, $b\in {\bigcap }_{i\in \mathbb{N}}{C}_{m_i}^i$.

The proof of this one can be found in [11].

Lemma 6.

Let $(K,d)$ be a continuum chainable from a to b, $a,b\in K$, $a\ne b$. Let $ϵ>0$ be arbitrary. Then, there exist $c\in K$ and $L\subseteq K$ such that $c\ne a$, L is a continuum chainable from a to c and $L\subseteq B(a,ϵ)$.

Now, we give the proof of one more lemma, the crucial one for the proof of Lemma 1.

Lemma 7.

Let $(X,d)$ be a compact metric space. Let $({\mathcal{C}}^i)$, where ${\mathcal{C}}^i=(C_0^i,\dots ,C_{m_i}^i)$, $i\in \mathbb{N}$, be a sequence of open chains such that $\overline{C_0^{i+1}},\dots ,\overline{C_{m_{i+1}}^{i+1}}$ refines $C_0^i,\dots ,C_{m_i}^i$, such that $diam(C_j^i)<2^{-i}$ for each $i\in \mathbb{N}$ and for each $j\in \{0,\dots ,m_i\}$ and such that $(\overline{C_0^i}\dots ,\overline{C_{m_i}^i})$ is also a chain for each $i\in \mathbb{N}$.

Let

$$S=\bigcap _{i\in \mathbb{N}}\left(\overline{C_0^i}\cup \cdots \cup \overline{C_{m_i}^i}\right).$$

Then, S is nonempty, connected and compact (i.e., a nonempty continuum).

Proof.

Let us denote

$$F_i=\overline{C_0^i}\cup \cdots \cup \overline{C_{m_i}^i}.$$

Because $\overline{C_0^{i+1}},\dots ,\overline{C_{m_{i+1}}^{i+1}}$ refines $C_0^i,\dots ,C_{m_i}^i$ (and therefore, $\overline{C_0^i},\dots ,\overline{C_{m_i}^i}$), $(F_i)$ is a descending sequence of closed and nonempty subsets of $(X,d)$ and since $(X,d)$ is compact we have ${\bigcap }_{i\in \mathbb{N}}{F}_i\ne \varnothing$, i.e., $S\ne \varnothing$.

Furthermore, since S is an intersection of closed subsets of $(X,d)$, S is also closed in X which, together with the fact that $(X,d)$ is compact, implies that S is also compact.

Now, we only have to prove that S is connected. Let us assume the opposite, i.e., let $(A,B)$ be a separation of S. Let

$$r=d(A,B)=inf\left\{d(a,b)\mid a\in A,b\in B\right\}.$$

Since A and B are compact and disjoint, we have that $r>0$. Let $i_0\in \mathbb{N}$ be such that $diam(C_j^{i_0})<{\displaystyle \frac{r}{2}}$ for each $j\in \{0,\dots ,m_{i_0}\}$.

Now, we will define a sequence ${(k_i)}_{i\ge i_0}$, where $k_i\in \{0,\dots ,m_i\}$ is such that

$$\overline{C_{k_{i+1}}^{i+1}}\subseteq C_{k_i}^i,$$

for each $i\ge i_0$.

Firstly, notice that each element of the chain ${\mathcal{C}}^{i_0}$ intersects at most one of the sets A and B. Indeed, let us assume that there exists $j\in \{0,\dots ,m_{i_0}\}$ such that $C_j^{i_0}\cap A\ne \varnothing$ and $C_j^{i_0}\cap B\ne \varnothing$. Then, for $a\in C_j^{i_0}\cap A$ and $b\in C_j^{i_0}\cap B$ we have that

$$d(a,b)\le diam{C}_j^{i_0}<{\displaystyle \frac{r}{2}}<r=d(A,B),$$

which is obviously a contradiction. Therefore, for each $j\in \{0,\dots ,m_{i_0}\}$, we conclude that

$$(C_j^{i_0}\cap A\ne \varnothing \Rightarrow C_j^{i_0}\cap B=\varnothing )\mathrm{and}(C_j^{i_0}\cap B\ne \varnothing \Rightarrow C_j^{i_0}\cap A=\varnothing ).$$

(11)

Since $(A,B)$ is a separation of S and because $\overline{C_0^{i_0+1}},\dots ,\overline{C_{m_{i_0+1}}^{i_0+1}}$ refines $C_0^{i_0},\dots ,C_{m_{i_0}}^{i_0}$, it is

$$S=A\cup B\subseteq \overline{C_0^{i_0+1}}\cup \cdots \cup \overline{C_{m_{i_0+1}}^{i_0+1}}\subseteq C_0^{i_0}\cup \cdots \cup C_{m_{i_0}}^{i_0},$$

so there exist $u_{i_0},v_{i_0}\in \{0,\dots ,m_{i_0}\}$ such that

$$C_{u_{i_0}}^{i_0}\cap A\ne \varnothing \mathrm{and}{C}_{v_{i_0}}^{i_0}\cap B\ne \varnothing .$$

(12)

Because of (11), we conclude that

$$C_{u_{i_0}}^{i_0}\cap B=\varnothing \mathrm{and}{C}_{v_{i_0}}^{i_0}\cap A=\varnothing .$$

(13)

Also, (12) implies

$$\left|u_{i_0}-v_{i_0}\right|\ge 2.$$

(14)

Namely, if we assume the opposite, i.e., $\left|u_{i_0}-v_{i_0}\right|\le 1$ then $C_{u_{i_0}}^{i_0}\cap C_{v_{i_0}}^{i_0}\ne \varnothing$. So, for $x\in C_{u_{i_0}}^{i_0}\cap C_{v_{i_0}}^{i_0}$ and $a\in C_{u_{i_0}}^{i_0}\cap A$, $b\in C_{v_{i_0}}^{i_0}\cap B$ we have that

$$d(a,b)\le d(a,x)+d(x,b)\le diam{C}_{u_{i_0}}^{i_0}+diam{C}_{v_{i_0}}^{i_0}<{\displaystyle \frac{r}{2}}+{\displaystyle \frac{r}{2}}=r=d(A,B),$$

(15)

i.e., we obtain a contradiction.

We now show that there exists $k_{i_0}\in \{0,\dots ,m_{i_0}\}$, $min\left\{u_{i_0},v_{i_0}\right\}<k_{i_0}<max\left\{u_{i_0},v_{i_0}\right\}$ such that

$$C_{k_{i_0}}^{i_0}\cap A=C_{k_{i_0}}^{i_0}\cap B=\varnothing .$$

(16)

Indeed, let us assume the opposite, i.e., that

$$C_w^{i_0}\cap A\ne \varnothing \mathrm{or}{C}_w^{i_0}\cap B\ne \varnothing$$

for each $w\in \{min\left\{u_{i_0},v_{i_0}\right\}+1,\dots ,max\left\{u_{i_0},v_{i_0}\right\}-1\}$. Firstly, let us assume that $v_{i_0}>u_{i_0}$. If $C_w^{i_0}\cap A=\varnothing$ for each $w\in \left\{u_{i_0}+1,\dots ,v_{i_0}-1\right\}$, then by assumption we conclude that $C_w^{i_0}\cap B\ne \varnothing$ for each $w\in \left\{u_{i_0}+1,\dots ,v_{i_0}-1\right\}$. Therefore, for some $x\in C_{u_{i_0}}^{i_0}\cap C_{u_{i_0}+1}^{i_0}$ and $a\in C_{u_{i_0}}^{i_0}\cap A$, $b\in C_{u_{i_0}+1}^{i_0}\cap B$ we obtain a contradiction similarly as in (15). Now, if there is $w\in \left\{u_{i_0}+1,\dots ,v_{i_0}-1\right\}$ such that $C_w^{i_0}\cap A\ne \varnothing$ then

$$z=max\left\{k\in \left\{u_{i_0}+1,\dots ,v_{i_0}-1\right\}\mid C_k^{i_0}\cap A\ne \varnothing \right\}$$

is well defined and we can conclude that $C_{z+1}^{i_0}\cap B\ne \varnothing$. Again as before, for some $x\in C_z^{i_0}\cap C_{z+1}^{i_0}$ and $a\in C_z^{i_0}\cap A$, $b\in C_{z+1}^{i_0}\cap B$ we obtain a contradiction. The same conclusions arise if $v_{i_0}<u_{i_0}$.

Suppose $i\ge i_0$ and $u_i,k_i,v_i\in \{0,\dots ,m_i\}$ are such that:

• $min\{u_i,v_i\}<k_i<max\{u_i,v_i\}$;
• $C_{u_i}^i\cap A\ne \varnothing$;
• $C_{v_i}^i\cap B\ne \varnothing$;
• $C_{k_i}^i\cap A=C_{k_i}^i\cap B=\varnothing$.

We now show that there exist $u_{i+1},k_{i+1},v_{i+1}\in \{0,\dots ,m_{i+1}\}$ such that:

(a)

$min\{u_{i+1},v_{i+1}\}<k_{i+1}<max\{u_{i+1},v_{i+1}\};$

(b)

$C_{u_{i+1}}^{i+1}\cap A\ne \varnothing ;$

(c)

$C_{v_{i+1}}^{i+1}\cap B\ne \varnothing ;$

(d)

$C_{k_{i+1}}^{i+1}\cap A=C_{k_{i+1}}^{i+1}\cap B=\varnothing ;$

(e)

$\overline{C_{k_{i+1}}^{i+1}}\subseteq C_{k_i}^i.$

Namely, by 3 there is $x\in B$ such that

$$x\in C_{v_i}^i.$$

(17)

Similarly as before,

$$B\subseteq S\subseteq \overline{C_0^{i+2}}\cup \cdots \cup \overline{C_{m_{i+2}}^{i+2}}\subseteq C_0^{i+1}\cup \cdots \cup C_{m_{i+1}}^{i+1},$$

so there is $v_{i+1}\in \{0,\dots ,m_{i+1}\}$ such that

$$x\in C_{v_{i+1}}^{i+1}.$$

(18)

Obviously,

$$C_{v_{i+1}}^{i+1}\cap B\ne \varnothing .$$

(19)

Similarly, using 2., we conclude that there exists $u_{i+1}\in \{0,\dots ,m_{i+1}\}$ such that

$$C_{u_{i+1}}^{i+1}\cap A\ne \varnothing \mathrm{and}{C}_{u_{i+1}}^{i+1}\cap C_{u_i}^i\ne \varnothing .$$

(20)

By (19), (20) and 4., one can easily conclude that

$$\overline{C_{v_{i+1}}^{i+1}}⊈C_{k_i}^i\mathrm{and}\overline{C_{u_{i+1}}^{i+1}}⊈C_{k_i}^i.$$

Let us now assume that $u_i<v_i$, i.e., $u_i<k_i<v_i$. There exists $s\in \{k_i+1,\dots ,m_i\}$ such that

$$\overline{C_{v_{i+1}}^{i+1}}\subseteq C_s^i.$$

(21)

Indeed, if we assume the opposite, then there exists $q\in \{0,\dots ,k_i-1\}$ such that

$$\overline{C_{v_{i+1}}^{i+1}}\subseteq C_q^i,$$

which together with (17) and (18), implies that $C_{v_i}^i\cap C_q^i\ne \varnothing$, which is a contradiction since $q<k_i<v_i$, i.e., $v_i-q\ge 2$. Analogously, there is $p\in \{0,\dots ,k_i-1\}$ such that

$$\overline{C_{u_{i+1}}^{i+1}}\subseteq C_p^i.$$

(22)

Because of (19) and (20) it is clear that $u_{i+1}\ne v_{i+1}$ and $p<k_i<s$, so by applying Lemma 4 to (21) and (22), we see that there is $k_{i+1}\in \{0,\dots ,m_{i+1}\}$, $min\{u_{i+1},v_{i+1}\}<k_{i+1}<max\{u_{i+1},v_{i+1}\}$ such that

$$\overline{C_{k_{i+1}}^{i+1}}\subseteq C_{k_i}^i.$$

Using similar arguments, we obtain the same conclusion if $v_i<u_i$, i.e., $v_i<k_i<u_i$. This concludes the inductive construction of $u_{i+1},v_{i+1}$ and $k_{i+1}$ such that (a)–(e) hold.

Now, to summarize, for each $i\ge i_0$ we have found $k_i\in \{0,\dots ,m_i\}$ such that $\overline{C_{k_{i+1}}^{i+1}}\subseteq C_{k_i}^i.$ In that way, we have constructed a descending sequence ${(\overline{C_{k_i}^i})}_{i\ge i_0}$ of closed subsets of $(X,d)$, so there exists

$$x\in \bigcap _{i\ge i_0}\overline{C_{k_i}^i}.$$

In particular, $x\in \overline{C_{k_{i_0+1}}^{i_0+1}}\subseteq C_{k_{i_0}}^{i_0}$ so by (16) $x\notin S$. On the other hand,

$$x\in \bigcap _{i\ge i_0}\overline{C_{k_i}^i}\subseteq \bigcap _{i\ge i_0}\left(\overline{C_0^i}\cup \cdots \cup \overline{C_{m_i}^i}\right)=\bigcap _{i\in \mathbb{N}}\left(\overline{C_0^i}\cup \cdots \cup \overline{C_{m_i}^i}\right)=S.$$

Therefore, S is connected. □

Finally, we give the proof of Lemma 1.

Proof.

If $c=a$ or $c=b$, the conclusion arises from Lemma 6.

Assume now that $c\ne a,b$. Firstly, we will construct a sequence of open chains $({\mathcal{C}}^i)$, ${\mathcal{C}}^i=(C_0^i,\dots ,C_{m_i}^i)$, $i\in \mathbb{N}$, such that for each $i\in \mathbb{N}$:

• ${\mathcal{C}}^i$ covers K from a to b and $diam(C_j^i)<2^{-i}$ for each $j\in \{0,\dots ,m_i\}$;
• $\overline{C_0^i},\dots ,\overline{C_{m_i}^i}$ is also a chain;
• $\overline{C_0^{i+1}},\dots ,\overline{C_{m_{i+1}}^{i+1}}$ refines $C_0^i,\dots ,C_{m_i}^i$;
• $\exists !$ $u_i\in \{0,\dots ,m_i\}$ such that $c\in C_{u_i}^i$;
• $diam{C}_j^0<{\displaystyle \frac{ϵ}{5}}$ for each $j\in \{0,\dots ,m_0\}$ and $4\le u_0\le m_0-4$.

Firstly, we define

$$\mu =min\{1,{\displaystyle \frac{ϵ}{5}},{\displaystyle \frac{d(a,c)}{4}},{\displaystyle \frac{d(c,b)}{4}}\}.$$

By Lemma 3, there is an open $\mu$-chain $C_0^0,\dots ,C_{m_0}^0$ in $(K,d)$ which covers K from a to b such that $\overline{C_0^0},\dots ,\overline{C_{m_0}^0}$ is also a chain and that there exists a unique $u_0\in \{0,\dots ,m_0\}$ such that $c\in C_{u_0}^0.$ Obviously, $mesh{\mathcal{C}}^0<1,{\displaystyle \frac{ϵ}{5}}.$ In order for ${\mathcal{C}}^0$ to satisfy all the other conditions, it remains to prove that $4\le u_0\le m_0-4$. Since $a\in C_0^0$ and $c\in C_{u_0}^0$, it is

$$d(a,c)\le diam(C_0^0\cup \cdots \cup C_{u_0}^0)\le diam{C}_0^0+\cdots +diam{C}_{u_0}^0<(u_0+1){\displaystyle \frac{d(a,c)}{4}},$$

so it follows that $u_0+1>4$, i.e., $u_0\ge 4$. Similarly, because $b\in C_{m_0}^0$

$$d(c,b)\le diam(C_{u_0}^0\cup \cdots \cup C_{m_0}^0)\le diam{C}_{u_0}^0+\cdots +diam{C}_{m_0}^0<(m_0-u_0+1){\displaystyle \frac{d(c,b)}{4}},$$

so $m_0-u_0+1>4$, i.e., $u_0\le m_0-4.$ Note that condition 5 implies $m_0\ge 8$.

Let us assume that ${\mathcal{C}}^i=(C_0^i,\dots ,C_{m_i}^i)$ is an open chain in $(K,d)$ that satisfies properties 1–4. Since $\mathcal{U}=\{C_0^i,\dots ,C_{m_i}^i\}$ is an open cover of $(K,d)$, there is a Lebesque number $\lambda >0$ of $\mathcal{U}$. Because $(K,d)$ is a chainable continuum, by Lemma 3 there is an open $min\{2^{-(i+1)},\lambda \}$-chain ${\mathcal{C}}^{i+1}=(C_0^{i+1},\dots ,C_{m_{i+1}}^{i+1})$ in $(K,d)$ which covers K from a to b such that $\overline{C_0^{i+1}},\dots ,\overline{C_{m_{i+1}}^{i+1}}$ is also a chain and that there is a unique $u_{i+1}\in \{0,\dots ,m_{i+1}\}$ such that $c\in C_{u_{i+1}}^{i+1}$. Because $diam\overline{C_j^{i+1}}=diam{C}_j^{i+1}<\lambda$ for each $j\in \{0,\dots ,m_{i+1}\}$, $\overline{C_0^{i+1}},\dots ,\overline{C_{m_{i+1}}^{i+1}}$ refines $C_0^i,\dots ,C_{m_i}^i$.

This concludes the recursive construction of the sequence $({\mathcal{C}}^i)$ such that 1–5 hold.

Let

$$v_0=u_0-2\mathrm{and}{w}_0=u_0+2.$$

(23)

Now, for each $i\in \mathbb{N}$, we want to choose $v_i,w_i\in \{0,\dots ,m_i\}$ such that

$$v_i\le u_i\le w_i$$

(24)

and

$$\overline{C_{v_{i+1}}^{i+1}},\dots ,\overline{C_{w_{i+1}}^{i+1}}\mathrm{refines}{C}_{v_i}^i,\dots ,C_{w_i}^i.$$

(25)

Let us assume that $i\in \mathbb{N}$ and for each $k\le i$ numbers $v_k,w_k\in \{0,\dots ,m_k\}$ are such that (24) and (25) hold. Let

$$v_{i+1}=max\left\{j<u_{i+1}\mid \left(\forall r\in \left\{v_i,\dots ,w_i\right\}\right)\overline{C_j^{i+1}}⊈C_r^i\right\}+1$$

(26)

and

$$w_{i+1}=min\left\{j>u_{i+1}\mid \left(\forall r\in \left\{v_i,\dots ,w_i\right\}\right)\overline{C_j^{i+1}}⊈C_r^i\right\}-1.$$

(27)

The number $v_{i+1}$ is well defined because $0<u_{i+1}$ and $\overline{C_0^{i+1}}⊈C_r^i$ for each $r\in \{v_i,\dots ,w_i\}$. Namely, if we assume that $u_{i+1}=0$, then $a\in \overline{C_{u_{i+1}}^{i+1}}$. Because of properties 3 and 4 we have

$$\overline{C_{u_{i+1}}^{i+1}}\subseteq C_{u_i}^i\subseteq \overline{C_{u_i}^i}\subseteq \cdots \subseteq C_{u_0}^0,$$

i.e., $a\in C_{u_0}^0$, which is impossible since $u_0\ge 4$ and $a\in C_0^0$. Furthermore, let us assume that there exists $r\in \left\{v_i,\dots ,w_i\right\}$ such that $\overline{C_0^{i+1}}\subseteq C_r^i$. This, together with multiple use of (25), implies

$$\overline{C_0^{i+1}}\subseteq C_{v_i}^i\cup \cdots \cup C_{w_i}^i\subseteq \overline{C_{v_i}^i}\cup \cdots \cup \overline{C_{w_i}^i}\subseteq C_{v_{i-1}}^{i-1}\cup \cdots \cup C_{w_{i-1}}^{i-1}\subseteq \cdots \subseteq C_{v_0}^0\cup \cdots \cup C_{w_0}^0.$$

So, there exists $v_0\le j\le w_0$ such that $a\in C_j^0$. By (23) and 5, it is $j\ge 2$ and this yields a contradiction since $a\in C_0^0$. Similarly, the number $w_{i+1}$ is also well defined since $m_{i+1}>u_{i+1}$ and $\overline{C_{m_{i+1}}^{i+1}}⊈C_r^i$ for each $r\in \{v_i,\dots ,w_i\}$. Obviously, $v_{i+1}\le u_{i+1}\le w_{i+1}$.

Now, we are left to prove that $\overline{C_{v_{i+1}}^{i+1}},\dots ,\overline{C_{w_{i+1}}^{i+1}}\mathrm{refines}{C}_{v_i}^i,\dots ,C_{w_i}^i$.

Let us assume the opposite, i.e., let $r\in \{v_{i+1},\dots ,w_{i+1}\}$ be such that for each $s\in \{v_i,\dots ,w_i\}$ we have $\overline{C_r^{i+1}}⊈C_s^i$. It is clear that $r\ne u_{i+1}$ since $\overline{C_{u_{i+1}}^{i+1}}\subseteq C_{u_i}^i$. Furthermore, if $v_{i+1}\le r<u_{i+1}$, the number r is greater than the maximum $v_{i+1}-1$ defined by (26) which is obviously a contradiction. Similarly, in case $u_{i+1}<r\le w_{i+1}$, a contradiction is obtained using (27). Therefore, we conclude that $\overline{C_{v_{i+1}}^{i+1}},\dots ,\overline{C_{w_{i+1}}^{i+1}}\mathrm{refines}{C}_{v_i}^i,\dots ,C_{w_i}^i$. But we can prove even more. Namely, for each $i\in \mathbb{N}$

$$\overline{C_{v_{i+1}}^{i+1}}\subseteq C_{v_i}^i\mathrm{or}\overline{C_{v_{i+1}}^{i+1}}\subseteq C_{w_i}^i$$

(28)

and

$$\overline{C_{w_{i+1}}^{i+1}}\subseteq C_{v_i}^i\mathrm{or}\overline{C_{w_{i+1}}^{i+1}}\subseteq C_{w_i}^i.$$

(29)

Let us assume the opposite of (28), i.e.,

$$\overline{C_{v_{i+1}}^{i+1}}⊈C_{v_i}^i\mathrm{and}\overline{C_{v_{i+1}}^{i+1}}⊈C_{w_i}^i,$$

from which, together with (25), we infer that

$$\overline{C_{v_{i+1}}^{i+1}}\subseteq C_p^i,$$

(30)

for some $p\in \{v_i+1,\dots ,w_i-1\}$. Because of (26), it is $\overline{C_{v_{i+1}-1}^{i+1}}⊈C_j^i$ for each $j\in \{v_i,\dots ,w_i\}$. Considering property 3 this implies that

$$\overline{C_{v_{i+1}-1}^{i+1}}\subseteq C_q^i$$

(31)

for some $q\in \left\{0,\dots ,v_i-1\right\}\cup \{w_i+1,\dots ,m_i\}$. Therefore, because $\left|p-q\right|\ge 2$, it is $C_p^i\cap C_q^i=\varnothing$ and since (30) and (31) imply $\overline{C_{v_{i+1}}^{i+1}}\cap \overline{C_{v_{i+1}-1}^{i+1}}=\varnothing$, a contradiction is obtained and (28) is proven. Similarly, one can easily show that (29) holds, too.

So, we define

$$L=\bigcap _{i\in \mathbb{N}}\left(\overline{C_{v_i}^i}\cup \cdots \cup \overline{C_{w_i}^i}\right),$$

and we conclude, using Lemma 7, that L is a nonempty continuum in $(K,d)$.

Now we shall prove that L is nontrivial. Let S be the set of all finite sequences of the form $(a_0,\dots ,a_n)$, $n\in \mathbb{N}$, such that $a_i\in \{v_i,w_i\}$ and $\overline{C_{a_{i+1}}^{i+1}}\subseteq C_{a_i}^i$ for each $i\in \{0,\dots ,n-1\}$ and let for a sequence $(a_0,\dots ,a_n)\in S$,

$$S_{\left(a_0,\dots ,a_n\right)}=\left\{(b_0,\dots ,b_k)\in S\mid k\ge n\mathrm{and}{a}_0=b_0,\dots ,a_n=b_n\right\}.$$

It is obvious that S is infinite and because $S=S_{v_0}\cup S_{w_0}$, either $S_{v_0}$ or $S_{w_0}$ is infinite. Let us define $f(0)=v_0$, if $S_{v_0}$ is infinite and $f(0)=w_0$, otherwise. Obviously, $S_{f(0)}$ is then infinite. Note that because of (23), $C_{f(0)}^0\cap C_{u_0}^0=\varnothing$. Now, assume that we have defined $f(0),\dots ,f(n)$ such that $S_{\left(f(0),\dots ,f(n)\right)}$ is infinite. Since

$$S_{\left(f(0),\dots ,f(n)\right)}=S_{\left(f(0),\dots ,f(n),v_{n+1}\right)}\cup S_{\left(f(0),\dots ,f(n),w_{n+1}\right)},$$

we put $f(n+1)=v_{n+1}$, if $S_{\left(f(0),\dots ,f(n),v_{n+1}\right)}$ is infinite and $f(n+1)=w_{n+1}$, otherwise. It is clear that $S_{\left(f(0),\dots ,f(n+1)\right)}$ is infinite. Therefore, we have constructed a sequence $\left(f(n)\right)$, $\overline{C_{f(n+1)}^{n+1}}\subseteq C_{f(n)}^n$. We can conclude that there is $d\in {\bigcap }_{i\in \mathbb{N}}\overline{C_{f(n)}^n}$ and because

$$\bigcap _{i\in \mathbb{N}}\overline{C_{f(n)}^n}\subseteq \overline{C_{f(1)}^1}\subseteq C_{f(0)}^0\mathrm{and}{C}_{f(0)}^0\cap C_{u_0}^0=\varnothing ,$$

we conclude that $d\ne c$. Clearly, $d\in L$. Also, for each $i\in \mathbb{N}$, it is $c\in C_{u_i}^i$, so it is $c\in \overline{C_{v_i}^i}\cup \cdots \cup \overline{C_{w_i}^i}$ for each $i\in \mathbb{N}$. Therefore, $c\in L$. Hence, L is nontrivial.

Now, we are only left to prove that $L\subseteq B(c,ϵ)$, which is clear since

$$c\in L\subseteq \overline{C_{v_1}^1}\cup \cdots \cup \overline{C_{w_1}^1}\subseteq C_{v_0}^0\cup \cdots \cup C_{w_0}^0$$

and

$$diam\left(C_{v_0}^0\cup \cdots \cup C_{w_0}^0\right)\le diam{C}_{u_0-2}^0+\cdots +diam{C}_{u_0+2}^0<5·{\displaystyle \frac{ϵ}{5}}=ϵ.$$

This concludes the proof. □

Now, we are ready to prove Proposition 4.

Proof.

Suppose $S\ne \varnothing$, because otherwise the claim is clear. Recall that S has to be metrizable. Let d be the metric on S which induces the topology on S (the relative topology on S in $(X,\mathcal{T}))$. For each $(K,\left\{a,b\right\})\in \mathcal{K}$, K is a Hausdorff continuum chainable from a to b, and therefore, the metric space $(K,d{|}_{K\times K})$ is a continuum chainable from a to b. Let

$${\mathcal{K}}^{\prime }=\left\{K\subseteq X\mid \exists a,b\in V\mathrm{such}\mathrm{that}(K,\{a,b\})\in \mathcal{K}\right\}.$$

Then, by the definition of a generalized graph

$$S=\bigcup {\mathcal{K}}^{\prime }\cup \left(V\setminus \bigcup {\mathcal{K}}^{\prime }\right)$$

(32)

Since $\bigcup {\mathcal{K}}^{\prime }$ and $\left(V\setminus \bigcup {\mathcal{K}}^{\prime }\right)$ are compact in $(X,\mathcal{T})$ and disjoint, by Theorem 1 there exists $m\in \mathbb{N}$ such that

$$\bigcup {\mathcal{K}}^{\prime }\subseteq J_m\mathrm{and}\left(V\setminus \bigcup {\mathcal{K}}^{\prime }\right)\cap J_m=\varnothing .$$

Together with (32), we have that

$$V\setminus \bigcup {\mathcal{K}}^{\prime }=S\setminus J_m,$$

which means that $V\setminus \bigcup {\mathcal{K}}^{\prime }$ is semicomputable in $(X,\mathcal{T},(I_i))$. Since it is finite, Proposition 2 implies that $V\setminus \bigcup {\mathcal{K}}^{\prime }$ is computable. In particular, it is c.e. so it is (trivially) c.e. up to S.

In order to prove that S is c.e. in $(X,\mathcal{T},(I_i))$, we want to prove that K is c.e. up to S for each $K\in {\mathcal{K}}^{\prime }$. In that way, S will be a c.e. up to itself as a finite union of such sets, and therefore, a c.e. set. Together with the fact that S is semicomputable (by assumption), S will be computable and the proof will be completed.

So, let $K\in {\mathcal{K}}^{\prime }$ be arbitrary. Then, there are $a,b\in V$ such that $(K,\{a,b\})\in \mathcal{K}$. For the sake of simplicity, we will denote

$${\mathcal{K}}^{\prime \prime }={\mathcal{K}}^{\prime }\setminus \left\{K\right\}.$$

Note that each endpoint is a computable point by Proposition 2, since T is semicomputable and finite.

Let us assume that ${\mathcal{K}}^{\prime \prime }=\varnothing$. Then a and b are endpoints of $(S,\mathcal{K},V)$, so a and b are computable points. If $V\setminus K=\varnothing$, then $K=S$, so K is semicomputable by the assumption. Hence, K is computable as a semicomputable chainable continuum with computable endpoints [3], in particular, K is c.e. up to S. But if $V\setminus K\ne \varnothing$, then equality

$$S=K\cup \left(V\setminus K\right)$$

implies, similarly as before, that there exists $m^{\prime }\in \mathbb{N}$ such that $K=S\setminus J_{m^{\prime }}$, and therefore, K is semicomputable. As in the previous case we conclude that K is c.e. up to S.

Now, assume that ${\mathcal{K}}^{\prime \prime }\ne \varnothing$ and let us denote

$$W_K^{\prime }=\{w\in K\mid \exists L\in {\mathcal{K}}^{\prime \prime }\mathrm{such}\mathrm{that}w\in L\},$$

(33)

i.e., let $W_K^{\prime }$ be the set of all elements of K such that they are also contained in some $L\in {\mathcal{K}}^{\prime }$, $L\ne K$. Obviously, $W_K^{\prime }$ is finite (by the definition of a generalized graph).

Let us first suppose that $W_K^{\prime }=\varnothing$. Then, for each $F\in {\mathcal{K}}^{\prime \prime }$ we have $F\cap K=\varnothing$, i.e.,

$$S\setminus K=\left(V\setminus K\right)\cup \bigcup {\mathcal{K}}^{\prime \prime }.$$

(34)

Since $S\setminus K$ is a finite union of compact sets, it is also compact and obviously disjoint from K so, as before, we have $K=S\setminus J_{m^{\prime \prime }}$ for some $m^{\prime \prime }\in \mathbb{N}$. It follows that K is a semicomputable continuum chainable from a to b, where both a and b are computable points (a and b are endpoints of $(S,\mathcal{K},V)$ since $W_K^{\prime }=\varnothing$). Therefore, K is a computable set and, in particular, c.e. up to S.

Finally, consider the case $W_K^{\prime }\ne \varnothing .$ Let us enumerate the set $W_K^{\prime }$, i.e., let

$$W_K^{\prime }=\{w_0,\dots ,w_n\},$$

$w_i\ne w_j$ for $i,j\in \{0,\dots ,n\}$, $i\ne j$, and let

$$ϵ=min\left\{d(w_i,w_j)\mid i,j\in \{0,\dots ,n\},i\ne j\right\}.$$

(35)

Using the definition of $ϵ$ it follows that for all $i,j\in \{0,\dots ,n\}$ such that $i\ne j$ we have

$$\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)\cap \overline{B}\left(w_j,{\displaystyle \frac{ϵ}{3}}\right)=\varnothing .$$

(36)

Now, we want to prove that the sets A and B defined by

$$A=S\setminus \left(K\cup \bigcup _{0\le i\le n}B\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)\right)$$

(37)

and

$$B=K\cup \bigcup _{0\le i\le n}\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{4}}\right)$$

(38)

are disjoint and both compact in $(X,\mathcal{T})$.

Firstly, B is compact in $(X,\mathcal{T})$ as a finite union of compact sets (a closed ball in a compact S is also compact). To prove that A is compact, it is clearly enough to prove the following identity:

$$A=\left(S\setminus \bigcup _{0\le i\le n}B\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)\right)\cap \left(\left(V\setminus K\right)\cup \bigcup {\mathcal{K}}^{\prime \prime }\right).$$

(39)

Since

$$S\setminus K\subseteq \left(V\setminus K\right)\cup \bigcup {\mathcal{K}}^{\prime \prime },$$

to prove (39), we only have to prove the non trivial inclusion.

So, assume that

$$x\in \left(S\setminus \bigcup _{0\le i\le n}B\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)\right)\cap \left(\left(V\setminus K\right)\cup \bigcup {\mathcal{K}}^{\prime \prime }\right).$$

(40)

It is clear that

$$x\in S\setminus \bigcup _{0\le i\le n}B\left(w_i,{\displaystyle \frac{ϵ}{3}}\right),$$

(41)

so in order to prove that $x\in A$, it suffices to show that

$$x\in S\setminus K.$$

Indeed, let us assume the opposite, i.e., $x\in K$. Then, obviously $x\notin V\setminus K$. Also, there is no $K^{\prime }\in {\mathcal{K}}^{\prime \prime }$ such that $x\in K^{\prime }$ because then there would exist $j\in \{0,\dots ,n\}$ such that $x=w_j$ which would contradict (41). Hence, $x\notin \bigcup {\mathcal{K}}^{\prime \prime }$, i.e., $x\notin \left(V\setminus K\right)\cup \bigcup {\mathcal{K}}^{\prime \prime }$, which contradicts (40). So $x\in S\setminus K$.

Since (39) holds, A is compact in $(X,\mathcal{T})$. It is obvious that $A\cap B=\varnothing$. So, since A and B are disjointed and compacted in $(X,\mathcal{T})$, by Theorem 1 there are $\mu ,{\mu }^{\prime }\in \mathbb{N}$ such that

$$A\subseteq J_{\mu }\mathrm{and}B\subseteq J_{{\mu }^{\prime }}$$

and

$$J_{\mu }\cap J_{{\mu }^{\prime }}=\varnothing .$$

Hence,

$$B\subseteq S\setminus J_{\mu }\subseteq S\setminus A,$$

which, together with (37) and (38), implies that

$$K\cup \bigcup _{0\le i\le n}\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{4}}\right)\subseteq S\setminus J_{\mu }\subseteq K\cup \bigcup _{0\le i\le n}\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right).$$

(42)

Now, we distinguish four cases depending on whether a and/or b are elements of $W_K^{\prime }$.

Firstly, suppose $a,b\in W_K^{\prime }$. Then, without loss of generality we may assume that $a=w_0$ and $b=w_n$. Since $a\in W_K^{\prime }$, there is $L_1\in {\mathcal{K}}^{\prime }$, $L_1\ne K$ such that $a\in L_1$. Similarly, there is $N_1\in {\mathcal{K}}^{\prime }$, $N_1\ne K$ such that $b\in N_1$. By Lemma 1 there are nontrivial continua $L\subseteq L_1$ and $N\subseteq N_1$ such that

$$a\in L\mathrm{and}L\subseteq B\left(a,{\displaystyle \frac{ϵ}{4}}\right)$$

(43)

and

$$b\in N\mathrm{and}N\subseteq B\left(b,{\displaystyle \frac{ϵ}{4}}\right).$$

(44)

Because L and N are connected and $a\in L\cap K$ and $b\in N\cap K$, $L\cup K\cup N$ is also connected. Furthermore, by (42)–(44) we conclude that

$$L\cup K\cup N\subseteq S\setminus J_{\mu }.$$

(45)

Now, choose $c\in L$, $c\ne a$ (which exists since L is nontrivial). Because of (36) and (43) we conclude that

$$c\notin \bigcup _{1\le i\le n}\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right).$$

(46)

Moreover,

$$c\notin K.$$

(47)

Indeed, if we assume that $c\in K$ then we have $c\in W_K^{\prime }$ (because $c\in L_1$ and $L_1\ne K$). By (46), we obtain $c=w_0$, i.e., $c=a$ which is not true. Combining (46) and (47) we obtain that

$$c\notin K\cup \bigcup _{1\le i\le n}\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right),$$

so, by Theorem 1, there exists $\alpha \in \mathbb{N}$ such that

$$K\cup \bigcup _{1\le i\le n}\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)\subseteq J_{\alpha }$$

(48)

and

$$c\notin J_{\alpha }.$$

(49)

Similarly, there exist $d\in N$, $d\ne b$ and $\beta \in \mathbb{N}$ such that

$$K\cup \bigcup _{0\le i\le n-1}\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)\subseteq J_{\beta }$$

(50)

and

$$d\notin J_{\beta }.$$

(51)

Let $\mathcal{C}$ and $\mathcal{D}$ be the subsets of ${\mathbb{N}}^2$ from Theorem 1 and let $f:\mathbb{N}\to \mathbb{N}$ be a recursive function such that $\{i\}=[f(i)]$ for each $i\in \mathbb{N}$.

Now, let $\xi \in \mathbb{N}$ be such that $I_{\xi }\cap K\ne \varnothing$. Then, $I_{\xi }\cap \left(K\setminus W_K^{\prime }\right)\ne \varnothing$. Namely, if we assume the opposite, i.e., $I_{\xi }\cap K\subseteq W_K^{\prime }$, then $I_{\xi }\cap K$ is finite, and therefore, closed in K. Since it is also open in K and K is connected, we have $I_{\xi }\cap K=K$. Now, because K is finite and Hausdorff it is discrete and this is a contradiction with the fact that K is connected and $cardK\ge 2$ ($a,b\in K$).

So, there exist $x\in I_{\xi }\cap (K\setminus W_K^{\prime })$ and $0<r<min\{d(x,w)\mid w\in W_K^{\prime }\}$ such that

$$B(x,r)\subseteq I_{\xi }=J_{f(\xi )}.$$

(52)

Furthermore, since $(K,d{|}_{K\times K})$ is a continuum chainable from a to b, there is a compact r-chain $K_0,\dots ,K_m$ in $(K,d{|}_{K\times K})$ which covers K and such that $a\in K_0$ and $b\in K_m$.

Without loss of generality (as in the proof of Lemma 3) we may assume that

$$a\notin K_j,\mathrm{for}j\ne 0\mathrm{and}b\notin K_j,\mathrm{for}j\ne m.$$

(53)

Let $p\in \{0,\dots ,m\}$ be such that $x\in K_p$. It follows from (52) and $diam{K}_p<r$ that

$$K_p\subseteq J_{f(\xi )}.$$

(54)

For each $i\in \{0,\dots ,n\}$ let $l_i\in \{0,\dots ,m\}$ be such that

$$w_i\in K_{l_i}.$$

By (53) we have

$$l_0=0\mathrm{and}{l}_n=m.$$

Because of the definition of r, we also conclude that $K_p\cap W_K^{\prime }=\varnothing$ so

$$p\ne l_i$$

(55)

for each $i\in \{0,\dots ,n\}.$ This, in particular, implies that

$$p\ne 0,m.$$

(56)

Let us now define

$$F=K_0\cup \cdots \cup K_{p-1}\cup \bigcup _{\stackrel{0\le i\le n}{l_i<p}}\left(\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)\cap \left(\left(V\setminus K\right)\cup \bigcup {\mathcal{K}}^{\prime \prime }\right)\right)$$

and

$$G=K_{p+1}\cup \cdots \cup K_m\cup \bigcup _{\stackrel{0\le i\le n}{l_i>p}}\left(\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)\cap \left(\left(V\setminus K\right)\cup \bigcup {\mathcal{K}}^{\prime \prime }\right)\right).$$

Sets $F,K_p$ and G are all compact since $\left(V\setminus K\right)\cup \bigcup {\mathcal{K}}^{\prime \prime }$ is compact.

Note that for each $i\in \{0,\dots ,n\}$, by (36), we have that

$$\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)\cap W_K^{\prime }=\{w_i\}.$$

(57)

Now, for each $l_i<p$, since

$$w_i\in K_{l_i}$$

it holds, for each $j>p$,

$$w_i\notin K_j$$

(58)

and then

$$\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)\cap \left(\left(V\setminus K\right)\cup \bigcup {\mathcal{K}}^{\prime \prime }\right)\cap \left(K_{p+1}\cup \cdots \cup K_m\right)=$$

$$=\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)\cap \left(\bigcup {\mathcal{K}}^{\prime \prime }\cap \left(K_{p+1}\cup \cdots \cup K_m\right)\right)\stackrel{(58)}{\subseteq }$$

$$\stackrel{(58)}{\subseteq }\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)\cap \left(W_K^{\prime }\setminus \{w_i\}\right)\stackrel{(57)}{=}\varnothing .$$

Similarly we have that

$$\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)\cap \left(\left(V\setminus K\right)\cup \bigcup {\mathcal{K}}^{\prime \prime }\right)\cap \left(K_0\cup \dots \cup K_{p-1}\right)=\varnothing ,$$

for $l_i>p$. This, together with (36) and the fact that $K_0,\dots ,K_m$ is a chain implies that the sets F and G are disjointed.

Using (57), one can easily show that

$$K\cup \bigcup _{0\le i\le n}\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)=F\cup K_p\cup G.$$

(59)

By (48) and (50) we have that $F\subseteq J_{\beta }$ and $G\subseteq J_{\alpha }$. Therefore, there exist $u,v,w\in \mathbb{N}$ such that $F\subseteq J_u$, $K_p\subseteq J_v$, $G\subseteq J_w$, $(u,w)\in \mathcal{D}$, $(v,f(\xi ))\in \mathcal{C}$, $(u,\beta )\in \mathcal{C}$ and $(w,\alpha )\in \mathcal{C}$. Note that, by (42) and (59), it holds $S\setminus J_{\mu }\subseteq J_u\cup J_v\cup J_w$.

So, if $\xi \in \mathbb{N}$ is such that $I_{\xi }\cap K\ne \varnothing$, then there exist $u,v,w\in \mathbb{N}$ such that:

(i)

$S\setminus J_{\mu }\subseteq J_u\cup J_v\cup J_w$;

(ii)

$(u,w)\in \mathcal{D}$;

(iii)

$(v,f(\xi ))\in \mathcal{C}$;

(iv)

$(w,\alpha )\in \mathcal{C}$;

(v)

$(u,\beta )\in \mathcal{C}$.

Let $\Omega$ be the set of all $(\xi ,u,v,w)\in {\mathbb{N}}^4$ for which the statements (i)–(v) hold. Since $S\setminus J_{\mu }$ is a semicomputable set in $(X,\mathcal{T},(I_i))$, the set of all $(\xi ,u,v,w)\in {\mathbb{N}}^4$ such that (i) holds is a c.e set. Now, it follows easily that $\Omega$ is a c.e. set. Let $\Gamma$ be the set of all $\xi \in \mathbb{N}$ for which there exist $u,v,w\in \mathbb{N}$ such that $(\xi ,u,v,w)\in \Omega$. Then, $\Gamma$ is c.e by the Projection theorem.

On the other hand, suppose $\xi \in \Gamma$. Then, there exist $u,v,w\in \mathbb{N}$ such that (i)–(v) hold. We want to prove that $I_{\xi }\cap S\ne \varnothing$.

Suppose the opposite, i.e., $I_{\xi }\cap S=\varnothing$. Since $J_v\subseteq I_{\xi }$ by (iii), we have

$$S\setminus J_{\mu }\subseteq J_u\cup J_w$$

and, by (45), it holds

$$L\cup K\cup N\subseteq J_u\cup J_w.$$

Clearly $J_u$ and $J_w$ are open in $(X,\mathcal{T})$ and disjointed. Since $L\cup K\cup N$ is connected, in order to yield a contradiction, it is enough to show that both $J_u$ and $J_v$ intersect $L\cup K\cup N$. It is clear that $c,d\in L\cup K\cup N$. By (51) $d\notin J_{\beta }$, therefore, because of (v), we have $d\notin J_u$ so $d\in J_w$. Similarly, by (49), $c\in J_u$ and a contradiction is obtained, i.e., $I_{\xi }\cap S\ne \varnothing$. We have proven the following:

$$\mathrm{if}{I}_{\xi }\cap K\ne \varnothing \mathrm{then}\xi \in \Gamma ,$$

$$\mathrm{if}\xi \in \Gamma \mathrm{then}{I}_{\xi }\cap S\ne \varnothing .$$

This means that K is c.e. up to S.

Now suppose $a\in W_K^{\prime }$ and $b\notin W_K^{\prime }$. Similarly as before, we conclude that b is a computable point in $(X,\mathcal{T},(I_i))$ and we can assume that $a=w_0$.

Again, since $a\in W_K^{\prime }$, there is $L_1\in {\mathcal{K}}^{\prime }$, $L_1\ne K$ such that $a\in L_1$. By Lemma 1, there is a nontrivial continuum $L\subseteq L_1$ such that

$$a\in L\mathrm{and}L\subseteq B\left(a,{\displaystyle \frac{ϵ}{4}}\right).$$

Because L is connected and $a\in L\cap K$, $L\cup K$ is also connected. Furthermore, by (42),

$$L\cup K\subseteq S\setminus J_{\mu }.$$

(60)

Now, choose $c\in L$, $c\ne a$. Similarly, as before, we obtain

$$c\notin K\cup \bigcup _{1\le i\le n}\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right),$$

so by Theorem 1 there exists $\gamma \in \mathbb{N}$ such that

$$K\cup \bigcup _{1\le i\le n}\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)\subseteq J_{\gamma }$$

(61)

and

$$c\notin J_{\gamma }.$$

(62)

Suppose $\xi \in \mathbb{N}$ is such that $I_{\xi }\cap K\ne \varnothing$. Similarly, as before, there exist $x\in I_{\xi }\cap (K\setminus (W_K^{\prime }\cup \{b\}))$ and $0<r<min\left\{min\left\{d(x,w)\mid w\in W_K^{\prime }\right\},d(x,b)\right\}$ such that

$$B(x,r)\subseteq I_{\xi }=J_{f(\xi )}.$$

(63)

Furthermore, since $(K,d{|}_{K\times K})$ is a continuum chainable from a to b, there is a compact r-chain $K_0,\dots ,K_t$ in $(K,d{|}_{K\times K})$ which covers K from a to b. Let $p\in \{0,\dots ,t\}$ be such that $x\in K_p$. For each $i\in \{0,\dots ,n\}$ let $l_i\in \{0,\dots ,t\}$ be such that $w_i\in K_{l_i}$. We have $p\ne l_j$ for each $j\in \{0,\dots ,n\}$ and

$$K_p\subseteq J_{f(\xi )}.$$

As above, we define

$$F=K_0\cup \cdots \cup K_{p-1}\cup \bigcup _{\stackrel{0\le i\le n}{l_i<p}}\left(\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)\cap \left(\left(V\setminus K\right)\cup \bigcup {\mathcal{K}}^{\prime \prime }\right)\right)$$

and

$$G=K_{p+1}\cup \cdots \cup K_t\cup \bigcup _{\stackrel{0\le i\le n}{l_i>p}}\left(\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)\cap \left(\left(V\setminus K\right)\cup \bigcup {\mathcal{K}}^{\prime \prime }\right)\right).$$

Now, the same as earlier, we conclude that the sets $F,K_p$ and G are compact in $(X,\mathcal{T})$ and that

$$K\cup \bigcup _{0\le i\le n}\overline{B}\left(w_i,{\displaystyle \frac{ϵ}{3}}\right)=F\cup K_p\cup G.$$

(64)

Note that, by (64) and (42), it holds $S\setminus J_{\mu }\subseteq J_u\cup J_v\cup J_w$.

As before, F and G are disjointed and by (61) we have that $G\subseteq J_{\gamma }$ so there exist $u,v,w\in \mathbb{N}$ such that $F\subseteq J_u$, $K_p\subseteq J_v$, $G\subseteq J_w$, $(u,w)\in \mathcal{D}$, $(v,f(\xi ))\in \mathcal{C}$, $(w,\gamma )\in \mathcal{C}$ and $b\in J_w.$

So, if $\xi \in \mathbb{N}$ is such that $I_{\xi }\cap K\ne \varnothing$, then there exist $u,v,w\in \mathbb{N}$ such that:

(i)

$S\setminus J_{\mu }\subseteq J_u\cup J_v\cup J_w$;

(ii)

$(u,w)\in \mathcal{D}$;

(iii)

$(v,f(\xi ))\in \mathcal{C}$;

(iv)

$(w,\gamma )\in \mathcal{C}$;

(v)

$b\in J_w$.

Let ${\Omega }^{\prime }$ be the set of all $(\xi ,u,v,w)\in {\mathbb{N}}^4$ for which the statements (i)–(v) hold and let $\Gamma$ be the set of all $\xi \in \mathbb{N}$ for which there exist $u,v,w\in \mathbb{N}$ such that $(\xi ,u,v,w)\in {\Omega }^{\prime }$. Since b is a computable point, the set of all $(\xi ,u,v,w)\in {\mathbb{N}}^4$ such that (v) holds is a c.e set. Now, it follows easily that ${\Omega }^{\prime }$ is a c.e. set and then $\Gamma$ is also c.e.

On the other hand, suppose $\xi \in \Gamma$. Then, there exist $u,v,w\in \mathbb{N}$ such that (i)–(v) hold. We claim that $I_{\xi }\cap S\ne \varnothing$. Suppose the opposite, i.e., $I_{\xi }\cap S=\varnothing$. Since $J_v\subseteq I_{\xi }$ by (iii), then

$$S\setminus J_{\mu }\subseteq J_u\cup J_w$$

and, because of (60),

$$L\cup K\subseteq J_u\cup J_w.$$

Clearly $J_u$ and $J_w$ are open and disjointed. Since $L\cup K$ is connected, in order to yield a contradiction, it is enough to show that both $J_u$ and $J_v$ intersect $L\cup K$, which is clear since $b,c\in L\cup K$, $b\in J_w$ by (v) and $c\in J_u$ (otherwise, $c\in J_w$ would by (iv) mean that $c\in J_{\gamma }$, which contradicts (62)). Hence, $I_{\xi }\cap S\ne \varnothing$. To summarize,

$$\mathrm{if}{I}_{\xi }\cap K\ne \varnothing \mathrm{then}\xi \in \Gamma$$

and

$$\mathrm{if}\xi \in \Gamma \mathrm{then}{I}_{\xi }\cap S\ne \varnothing ,$$

i.e., K is c.e. up to S.

Now, we are left with the last case: $a,b\notin W_K^{\prime }$. Obviously $a,b\in T$ so both a and b are computable points.

Suppose $\xi \in \mathbb{N}$ is such that $I_{\xi }\cap K\ne \varnothing$. Similarly, as before, there exist $x\in I_{\xi }\cap (K\setminus (W_K^{\prime }\cup \{a,b\}))$ and $0<r<min\left\{min\left\{d(x,w)\mid w\in W_K^{\prime }\right\},d(x,b),d(x,a)\right\}$ such that

$$B(x,r)\subseteq I_{\xi }=J_{f(\xi )}.$$

(65)

Furthermore, since $(K,d{|}_{K\times K})$ is a continuum chainable from a to b, there exists a compact r-chain $K_0,\dots ,K_s$ in $(K,d{|}_{K\times K})$ which covers K from a to b. Let $p\in \left\{0,\dots ,s\right\}$ be such that $x\in K_p$. It follows

$$K_p\subseteq J_{f(\xi )}.$$

In the same way as before, we define the sets F and G and conclude that there exist $u,v,w\in \mathbb{N}$ such that:

(i)

$S\setminus J_{\mu }\subseteq J_u\cup J_v\cup J_w$;

(ii)

$(u,w)\in \mathcal{D}$;

(iii)

$(v,f(\xi ))\in \mathcal{C}$;

(iv)

$a\in J_u$;

(v)

$b\in J_w$.

Let ${\Omega }^{\prime \prime }$ be the set of all $(\xi ,u,v,w)\in {\mathbb{N}}^4$ for which the statements (i)–(v) hold and let $\Gamma$ be the set of all $\xi \in \mathbb{N}$ for which there exist $u,v,w\in \mathbb{N}$ such that $(\xi ,u,v,w)\in {\Omega }^{\prime \prime }$. As before, it follows that ${\Omega }^{\prime \prime }$ is a c.e. set and that $\Gamma$ is also c.e.

On the other hand, suppose $\xi \in \Gamma$. Then, there exist $u,v,w\in \mathbb{N}$ such that (i)–(v) hold. We want to show that $I_{\xi }\cap S\ne \varnothing$. Suppose $I_{\xi }\cap S=\varnothing$. Since $J_v\subseteq I_{\xi }$ by (iii), we have

$$S\setminus J_{\mu }\subseteq J_u\cup J_w.$$

It follows $K\subseteq J_u\cup J_w$, $a\in K\cap J_u$ and $b\in K\cap J_w$, which is impossible since K is connected. So $I_{\xi }\cap S\ne \varnothing$. We have proved that

$$\mathrm{if}{I}_{\xi }\cap K\ne \varnothing \mathrm{then}\xi \in \Gamma$$

and

$$\mathrm{if}\xi \in \Gamma \mathrm{then}{I}_{\xi }\cap S\ne \varnothing ,$$

i.e., K is c.e. up to S.

We conclude that each $K\in {\mathcal{K}}^{\prime }$ is c.e. up to S. As stated before, that is enough to obtain that S is computable in $(X,\mathcal{T},(I_i))$. □

4. Discussion

In this paper, we have shown that the topological pair of a generalized graph and the set of its endpoints has a computable type. A notion of a generalized graph is inspired by a notion of a graph—a union of finitely many arcs such that distinct arcs intersect in at most one endpoint. However, by the definition of a generalized graph, we let its edges intersect in multiple points as long as there are finitely many of them. A question arises naturally—if we allow infinite intersections of edges, can we state an analogous result for such an object. The answer is negative. Namely, there is continuum $L_1$ in ${\mathbb{R}}^2$ chainable from $(0,1)$ to $(1,1)$ which intersects continuum $L_2$ chainable from $(0,-1)$ to $(1,-1)$ in inifinitely many, yet countable, points. Union $L_1\cup L_2$ is a semicomputable set that is not computable (see Example 6.2 in [36]). In fact, $L_1$ and $L_2$ are arcs.

In [7] the authors examined the strong computable type. We will now describe the notion of the strong computable type using terminology from recursive function theory.

Let $\mathcal{O}$ be any class of functions ${\mathbb{N}}^k\to \mathbb{N}$ ($k\in \mathbb{N}\setminus \{0\}$) such that $\mathcal{O}$ contains initial (basic) functions and is closed to composition, primitive recursion and the $\mu$-operator. Note that any (total) computable function belong to $\mathcal{O}$. We say that $S\subseteq {\mathbb{N}}^n$ is c.e. relative to $\mathcal{O}$ if $S=\varnothing$ or $S=f(\mathbb{N})$, where $f:\mathbb{N}\to {\mathbb{N}}^n$ is a function such that each component function of f belongs to $\mathcal{O}$. If $(X,\mathcal{T},(I_i))$ is a computable topological space and S is a closed set in $(X,\mathcal{T})$, we say that S is c.e. in $(X,\mathcal{T},(I_i))$ relative to $\mathcal{O}$ if the set $\{i\in \mathbb{N}\mid I_i\cap S\ne \varnothing \}$ is c.e. relative to $\mathcal{O}$. A compact set S in $(X,\mathcal{T})$ is said to be semicomputable in $(X,\mathcal{T},(I_i))$ relative to $\mathcal{O}$ if the set $\{j\in \mathbb{N}\mid S\subseteq J_j\}$ is c.e. relative to $\mathcal{O}$. Finally, S is computable in $(X,\mathcal{T},(I_i))$ relative to $\mathcal{O}$ if it is both c.e. and semicomputable relative to $\mathcal{O}$.

We say that a topological space A has strong computable type if in any computable topological space $(X,\mathcal{T},(I_i))$ for any $\mathcal{O}$ the following holds: if S is semicomputable in $(X,\mathcal{T},(I_i))$ relative to $\mathcal{O}$ and S is homeomorphic to A, then S is computable in $(X,\mathcal{T},(I_i))$ relative to $\mathcal{O}$. We say that a topological pair $(A,B)$ has a strong computable type if in any computable topological space $(X,\mathcal{T},(I_i))$ for any $\mathcal{O}$ the following holds: if S and T are semicomputable in $(X,\mathcal{T},(I_i))$ relative to $\mathcal{O}$ and $(S,T)$ is homeomorphic to $(A,B)$, then S is computable in $(X,\mathcal{T},(I_i))$ relative to $\mathcal{O}$.

It is straightforward to check that all proofs in this paper also work if, instead of computable functions, we use functions from any fixed class $\mathcal{O}$ (where $\mathcal{O}$ is a class with the property described above). We conclude the following: if $(A,\mathcal{K},V)$ is a generalized graph and B is the set of all its endpoints, then $(A,B)$ has strong computable type.

Also, we would like to highlight how this result helps us to better understand the relationship between computability and topology. We know that for a semicomputable set, in order to be a computable one, it suffices to be computably enumerable, but this is usually not easy to check. Sometimes, the topological properties of a semicomputable set are strong enough that they, together with some additional conditions, imply the computability of the whole set. We have proven that in the case of a generalized graph, computable enumerability (and, therefore, the computability) of the set as a whole follows from the mere topological structure of the set and from the computability of the finitely many specific points (endpoints). Other known results on the computable type also show that there is a strong relationship between topology and computability theory.

In the end, let us mention that in a computable metric space, a semicomputable arc (which, in general, is not computable) can always be approximated by a computable subarc with arbitrary given precision (in the sense of the Hausdorff metric). Moreover, a similar statement holds for semicomputable decomposable chainable continua, see [5]. In view of this, a natural question is as follows: what can be said about approximations of semicomputable generalized graphs by computable generalized graphs? This can be a further direction of investigation regarding the topic of generalized graphs.