Continuous-Time Dynamic Graph Networks Integrated with Knowledge Propagation for Social Media Rumor Detection

Abstract

The proliferation of the Internet and mobile devices has made it increasingly easy to propagate rumors on social media. Widespread rumors can incite public panic and have detrimental effects on individuals. In recent years, researchers have found that both the spatial structure of rumor diffusion and the temporal features of propagation can be effective in identifying rumors. However, existing methods tend to focus on either spatial structure or temporal information in isolation, and few models can effectively capture both types of information. Additionally, most existing methods treat continuously changing temporal information as static snapshots, neglecting the precise timing of propagation. Moreover, as users repost and comment, background knowledge associated with the posts also evolves dynamically, which is often ignored. To address these limitations, we propose CGNKP (Continuous-time Dynamic Graph Networks integrated with Knowledge Propagation), a model that jointly captures the spatial structure and continuous-time features of post propagation to fully understand the dynamics of background knowledge. Specifically, we introduce a novel method for encoding continuous-time dynamic graphs, modeling the propagation process through two dynamic graphs: a temporal propagation graph (for posts diffusion) and a temporal knowledge graph (for knowledge diffusion). Extensive experiments on real-world datasets demonstrate that CGNKP significantly outperforms multiple strong baselines, achieving accuracies of 0.861 on the Twitter15 dataset and 0.903 on the Twitter16 dataset.

1. Introduction

With the rapid development of the Internet, we have witnessed the emergence of many online social media (OSM) tools in the past decade, such as Twitter, Facebook, Weibo, Instagram, etc. These OSMs have gradually become the primary source of information in people’s daily lives and have fundamentally changed how people share information [1,2,3,4]. However, OSMs can be a double-edged sword. On the one hand, they allow the creation of social connections during periods of social distance and facilitate the dissemination of knowledge in various contexts. On the other hand, they may cause people to share quick and superficial ideas and spread them rapidly, such as rumors. In this paper, rumors are defined as information that is unconfirmed or has been proven to be false [5,6]. The explosive spread of rumors threatens the credibility of the Internet and has serious adverse effects on individuals and society. For instance, it impacts the stability of the country, the fairness of elections, and public health. During the 2016 U.S. presidential election, over 500 rumors about Donald Trump and Hillary Clinton circulated on Twitter. The spread of these rumors on Twitter significantly damaged the reputation of the candidates and interfered with voters’ judgment, thus ultimately affecting the outcome of the US presidential election. In the case of the COVID-19 pandemic, a newly published study revealed that at least 800 people died from rumors of high levels of alcohol consumption [7]. The severity of rumor generation has stimulated the need to detect misinformation effectively in OSMs [8]. However, rumors’ brief and fast-spreading nature makes them difficult to detect automatically. Therefore, automatic rumor detection has attracted the attention of an increasing number of researchers.

Early rumor detection methods primarily depended on manual feature selection. The selected features focused on extracting many lexical and semantic features from the original and forwarded messages [9] and relying on traditional machine learning methods to learn models from the labeled data [9]. Machine learning-based methods require a lot of labor and time to select the appropriate features. Therefore, researchers have introduced deep learning methods in social rumor detection problems. Deep learning methods possess powerful feature learning capabilities, enabling their models to learn features that are more accurate and representative of the original data than those obtained through feature engineering in traditional machine learning algorithms. Thus, better classification results can be achieved.

Recent studies have shown that modeling diffusion as a propagation tree or graph can effectively identify rumors. Huang et al. [10] used a tree-like Recurrent Neural Network (RNN) as an architecture for rumor detection and designed both Bottom-up and Top-down ways to encode the propagation structure. Bian et al. [11] modeled propagation as a graph structure and encoded the propagation using a Bi-directional Graph Convolutional Network (Bi-GCN). However, these spatial structure-based approaches often ignore or oversimplify the temporal structure of rumor propagation.

The temporal structure of rumor propagation is characterized by a time series of comments or reposts, which can further distinguish diffusion patterns [12]. Ma et al. [13] input source posts and reposts into an RNN in a temporal order to capture the context information of relevant posts. Sun et al. [14] view the diffusion process as multiple ordered static snapshots and encode temporal information by feeding these snapshots into a Graph Convolutional Network (GCN) in sequential order.

Meanwhile, another parallel line introduces external knowledge related to rumor identification [15,16,17]. Such approaches usually use the knowledge related to the content of source posts to extend the semantics and thus improve the quality of the posts’ representation. An underlying logic is that posts are usually short in length and contain many abbreviations, proper nouns, nicknames, etc. Traditional classification models often have difficulty understanding their meanings. The knowledge bases include the background knowledge corresponding to these unique words. Adding this knowledge to the text representation can greatly help models determine a post’s trustworthiness.

Although existing deep learning-based rumor detection methods have made significant progress, they still confront several limitations:

(L1) A lack of joint learning of spatial and temporal structure: the vast majority of rumor detection methods tend to focus only on either diffusion’s spatial structure [10] or temporal structure [12,13,18], while few models can effectively learn spatial and temporal structure features jointly.

(L2) Coarse temporal granularity: Existing temporal-based rumor detection methods either input posts into an RNN in temporal order [10,13] or view the dynamic diffusion process as a discrete-time dynamic graph, i.e., an ordered set of static graph snapshots, and input each static graph into a Graph Neural Network (GNN) to simulate temporal features [14]. However, these methods do not represent temporal information with enough specificity or refinement. Because the propagation of posts has exact times and is a constantly changing process, the propagation process of posts can be modeled as a continuous-time dynamic graph. As shown in Figure 1, a continuous-time dynamic graph can represent the propagation process of posts with exact times and thus can represent the temporal information precisely. In contrast, a discrete-time dynamic graph can only extract the interval time’s static propagation structure, so the time series’s granularity is relatively coarse.

(L3) Lack of background knowledge of comments: User comments often contain a large amount of useful information, and semantic expansion of user comments facilitates the detection of rumors. The vast majority of existing approaches for knowledge enhancement use only the background knowledge related to source posts while ignoring the background knowledge related to user comments [15,16,17]. At the same time, knowledge information also propagates with diffusion, and the existing methods ignore the dynamic structure of knowledge.

To address the aforementioned limitations (L1–L3), we propose a new rumor detection model, CGNKP. First, inspired by Yu et al. [19] and Chen et al. [20], we introduce a novel Continuous-Time Dynamic Encoder (CTDE) to capture the temporal propagation patterns of rumors. This approach effectively captures the content semantics, spatial structure, and temporal information of the post-propagation process. We model post propagation using continuous-time dynamic graphs rather than discrete-time graphs, as propagation in social networks is continuous and evolves over time [21,22]. Moreover, we extract conceptualized knowledge related to the source post and individual comments from external knowledge bases, constructing temporal knowledge graphs that evolve over time. Similarly, we apply the continuous-time dynamic encoder to capture the dynamic knowledge propagation process. Finally, we employ a subgraph-level attention mechanism to adaptively fuse dynamic post information with dynamic knowledge information for enhanced rumor detection.

Our main contributions in addressing the limitations of rumor detection are as follows:

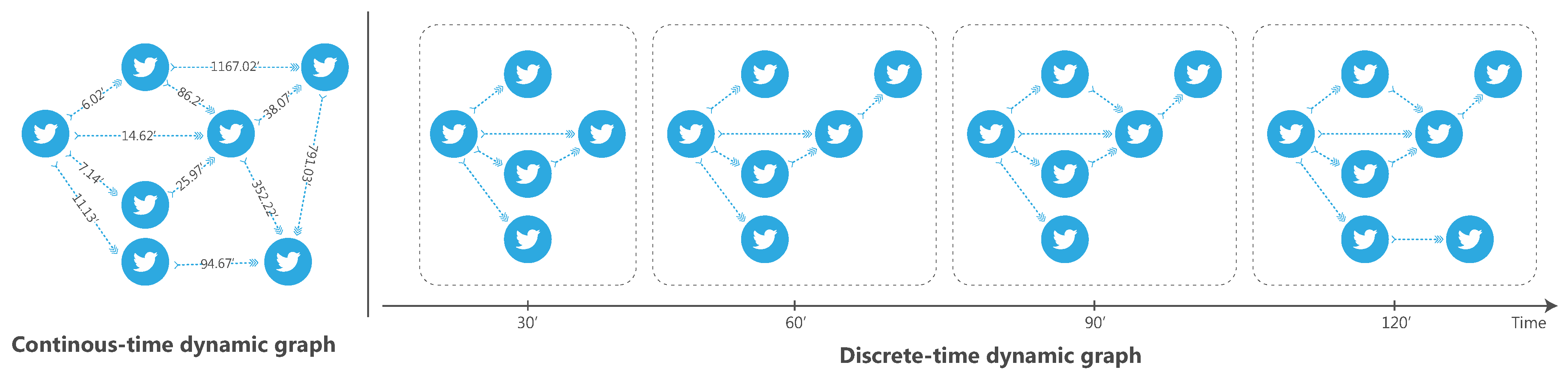
• Joint Spatial and Temporal Structure (L1): We introduce a new continuous-time dynamic encoder to precisely capture the spatio-temporal structural features of rumor propagation.
• Combining Fine-Grained Temporal Features (L2): In contrast to existing methods, CGNKP employs continuous-time dynamic graphs to represent the diffusion process of rumors, utilizing exact temporal information instead of static graph snapshots. This allows for a more refined representation of the temporal diffusion process.
• Dynamic Knowledge Information (L3): CGNKP focuses not only on the diffusion of posts but also on the diffusion of knowledge. Specifically, we construct temporal knowledge graphs that expand over time using external knowledge bases and encode them using the continuous-time dynamic encoder to obtain dynamic knowledge information.

The rest of this paper is organized as follows. Section 2 reviews existing approaches to rumor detection and related work on dynamic graph networks. Section 3 formalizes the problem of our study. Section 4 elaborates on the framework of CGNKP. Section 5 explores the comprehensive performance of CGNKP, the performance of each component, and the ability to detect early rumors. Section 6 is the conclusion.

2. Related Work

2.1. Spatial Structure-Based Rumor Detection

Spatial structure-based rumor detection typically constructs a tree or graph structure of the diffusion between the source post and individual comments to seek to identify rumors by propagation patterns. Earlier approaches relied on machine learning methods that used manually created features to extract spatial structure features. Ma et al. [23] proposed a kernel-based propagation tree approach to identify rumors by evaluating the similarity between propagation trees. Recently, due to the rapid development of deep learning, a large number of works based on using deep learning methods to capture the content semantics and propagation patterns have appeared. Huang et al. [10] encoded propagation trees using GCN. Bian et al. [11] considered propagation trees as two parts, top-down propagation and bottom-down diffusion, and then, Bi-GCN was used to encode the two structures, sequentially. Wei et al. [24] combined Bayesian criterion and GCN to encode the uncertainty relationship between nodes in the propagation tree and optimize the model by enhancing the consistency of the relationship.

2.2. Temporal Structure-Based Rumor Detection

The temporal structure is another effective feature for detecting rumors. Ma et al. [13] used recurrent neural networks, which learn hidden representations that capture contextual information about relevant posts over time.

Recently, some works have explored the joint modeling of spatial and temporal structures. Huang et al. [12] construct propagation trees to model the spatial structure while extracting temporal information using RNNs. However, RNNs are not particularly effective for spatial feature extraction. In contrast, Sun et al. [14] treat the temporal structure as a snapshot of multiple ordered graphs, utilizing a GNN to encode the spatial structure. Nevertheless, this approach fails to capture specific temporal information, as the granularity of the encoded temporal data remains coarse.

The temporal structure-based approach considers the time sequence of propagation but struggles to effectively integrate the spatial diffusion path of information. To address these limitations, CGNKP incorporates both temporal and spatial information, allowing it to capture the speed, path, and spatial diffusion characteristics of rumor propagation. Furthermore, CGNKP models propagation as a continuous-time dynamic graph, leveraging specific time attributes to jointly encode the spatio-temporal structure more effectively.

2.3. Knowledge-Enhanced Rumor Detection

Most knowledge-based rumor detection methods use external knowledge to enrich the representation of posts. Wang et al. [16] jointly modeled the semantic representation of text, external knowledge, and visual information and used it for misinformation detection. Dun et al. [17] combined attention mechanisms to incorporate superficial knowledge into textual representation to identify fake news. Similarly, Gao et al. [15] proposed a multi-modal model that integrates external knowledge graphs with textual and visual data to improve the representation of news articles.

However, these methods primarily depend on static knowledge, which does not adequately capture the temporal dynamics of knowledge. From the social and cognitive perspectives, knowledge is essential for understanding how information spreads. Modeling the dynamic changes in knowledge can simulate the evolution of people’s understanding of a topic, reflecting shifts in social beliefs and public perception. To address these limitations, we propose a rumor detection method based on dynamic knowledge. This approach models not only the propagation of messages but also the evolution of related knowledge. By capturing these dynamics, our model can more effectively identify rumors.

2.4. Dynamic Graph Networks

There are two primary types of dynamic graph models. Discrete-time dynamic graphs are a series of snapshots of a static graph captured at intervals of time, while continuous-time dynamic graphs are more general. They can be represented as a timed list of events, including edge additions or deletions, node additions or deletions, and node or edge feature modifications [21].

Early learning methods for dynamic graphs focused on discrete-time dynamic graphs. This method either aggregates graph snapshots and applies static algorithms to combine them into tensors and decompose them or encodes each snapshot to generate a sequence of embeddings. In the latter scenario, the embeddings are either incorporated into a temporal sequence model or employed as components in an RNN [25,26].

Discrete-time dynamic graphs represent the temporal graph network as a sequence of snapshots with a coarser granularity. In contrast, continuous-time dynamic graphs represent the temporal graph network as a sequence of timed events, which can more finely describe the temporal change characteristics. Rossi et al. [21] proposed the temporal graph network framework, which encodes node embeddings with a graph attention layer and addresses the staleness problem using a memory module. Yu et al. [19] proposed DyGFormer to encode node interactions using a neighbor co-occurrence scheme while leveraging a patching technique to capture long-term temporal dependencies. Chen et al. [20] introduced TempME, a temporal motif-based method aimed at enhancing the explainability of temporal graph neural networks. Inspired by Yu et al. [19] and Chen et al. [20], we introduce a continuous-time dynamic encoder to capture the spatial and continuous-time features of rumor propagation.

3. Problem Definition

The rumor detection dataset consists of a collection of events $\epsilon =\left\{{\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_n\right\}$, where ${\epsilon }_i$ represents the i-th event. Each event contains a source post and associated responsive posts. We define the set of a source post $s_i$ and responsive posts $p_i$ contained in the i-th event as ${\epsilon }_i^p=\left\{s_i,p_{i1},p_{i2},\dots ,p_{im}\right\}$, where m denotes the number of responsive posts in ${\epsilon }_i$, and $s_i$ can be used as $p_{i0}$. We can also obtain the release time sequence ${\epsilon }_i^t=\left\{t_{i0},t_{i1},\dots ,t_{im}\right\}$ associated with the event ${\epsilon }_i$, where $t_{i0}=0$. ${\epsilon }_i^p$ and ${\epsilon }_i^t$ are combined to obtain ${\epsilon }_i=\left\{\left(p_{i0},t_{i0}\right),\left(p_{i1},t_{i1}\right),\dots ,\left(p_{im},t_{im}\right)\right\}$. We need to learn a model $f:\epsilon \to y$ to classify events ${\epsilon }_i$ into predefined categories $y=\{0,1\}$, where the ground-truth label of the event is represented by 0 for non-rumor and 1 for rumor.

4. Model

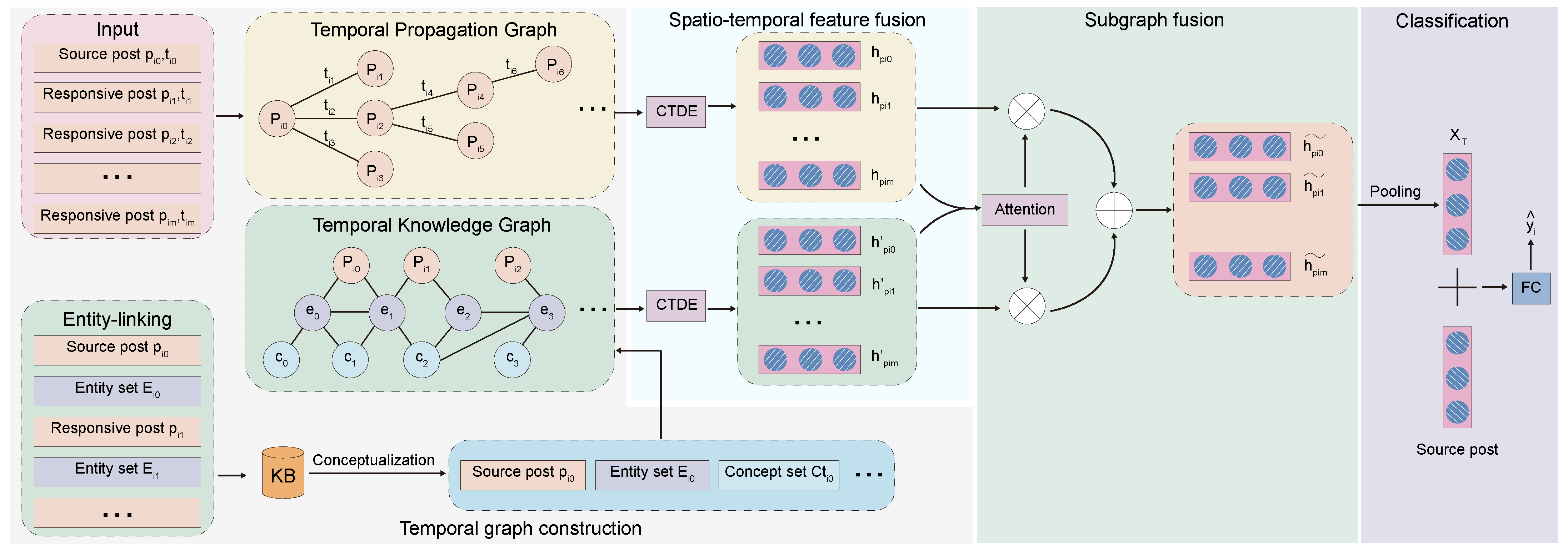
4.1. Model Framework

Figure 2 shows the structure of CGNKP, which is divided into four components: (1) Temporal graph construction module: we construct temporal propagation graphs and temporal knowledge graphs to model the spatio-temporal propagation information of posts and knowledge, respectively. (2) Spatio-temporal feature fusion module: this is used to finely process the spatial and temporal information and output the node embedding of each subgraph. (3) Subgraph fusion module: used to efficiently fuse the two subgraphs’ information and generate each post’s final representation. (4) Classification module: a classification module for aggregating the final text semantics, spatial structure, temporal structure, and predict categories.

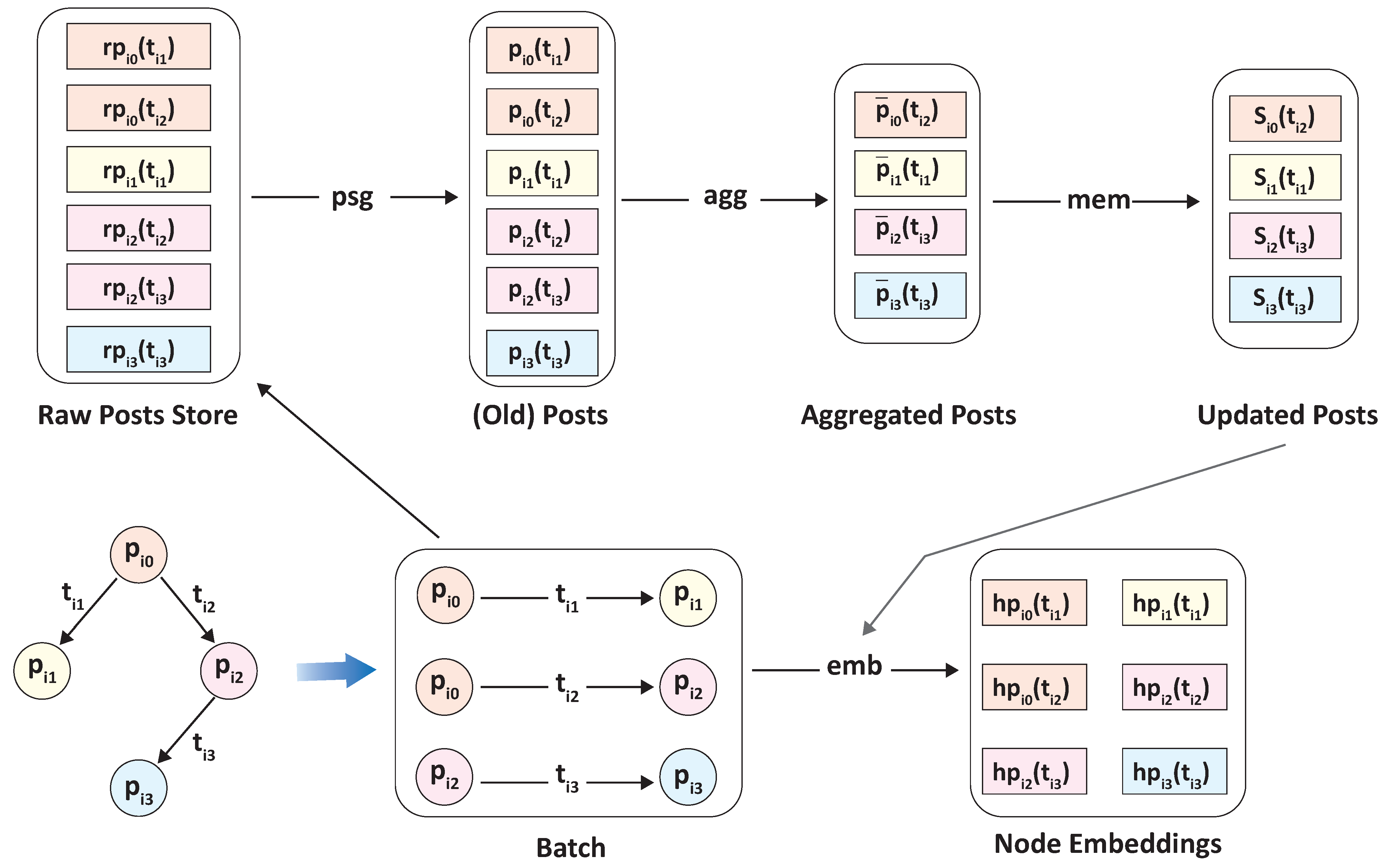
4.2. Temporal Graph Construction Module

In this section, we construct two dynamic graphs, a temporal propagation graph and a temporal knowledge graph. We will describe each separately.

4.2.1. Temporal Propagation Graph Construction

For an event ${\epsilon }_i$, based on its source post and responsive posts, we construct a propagation graph $G_i^p=〈V_i^p,E_i^p〉$. Where the node set $V_i^p$ represents the source post as well as the responsive posts. The edge set $E_i^p$ represents the interaction between the source post and responsive posts and the interaction between responsive posts. For example, if $p_{i2}$ is a comment of $p_{i1}$, then in $G_i^p$, there exists an edge to connect them. For simplicity, we do not consider the direction of edges and denote $G_i^p$ as an undirected graph. Its adjacency matrix is $A_i\in {\{0,1\}}^{(m+1)\times (m+1)}$. For each node, we apply the embedding vector to initialize its representation.

4.2.2. Temporal Knowledge Graph Construction

Most rumors are short texts containing many entities, proper nouns, and abbreviations. Understanding the meaning of these entities requires converting them to their corresponding concepts. Therefore, we introduce external knowledge related to posts, allowing knowledge information to be involved in message propagation. We construct a temporal knowledge graph to capture the temporal knowledge propagation. We extract knowledge information and model the source post, responsive posts, entities, and structured relationships between knowledge to achieve richer semantics.

First, we describe the process of extracting knowledge. Given a post, We use ChatGPT to extract entities in posts.

For each identified entity, we obtain its corresponding concept in the existing knowledge graphs (such as YAGO [27] and Microsoft concept graph [28]) by conceptualization. We extract concepts in terms of is-A relationships. For example, given a post “Colorado McDonald’s offers first marijuana-friendly smoking section in a restaurant”. Using entity links, we can extract a set of entities E = {Colorado, McDonald, marijuana}. After that, we conceptualize these entities, i.e., we obtain the relevant setting of concepts from the external knowledge base ${\mathrm{Concept}}_{\mathrm{colorado}}$ = {state, the U.S. State}, ${\mathrm{Concept}}_{\mathrm{McDonald}}$ = {restaurant, restaurant chain, multinational corporation}, and ${\mathrm{Concept}}_{\mathrm{marijuana}}$ = {drug, plant extracts}. Following this process, we can obtain the set of entities $E_i$ and the set of concepts $C_i$.

For the event ${\epsilon }_i$, we construct a temporal knowledge graph $G_i^k=\langle V_i^k,E_i^k\rangle$, where the set of nodes $V_i^k$ is the concatenated set of $V_i^p$,$E_i$ and $C_i$. For each node in $G_i^k$, we apply an embedding vector to initialize its representation. We construct the temporal knowledge graph mainly to simulate the temporal propagation of knowledge information. Thus, unlike the temporal propagation graph, we do not build edges between posts. For the construction of other node edges, we follow the following rules:

Post-entity edges: If a post in $V_i^p$ contains a word that can be linked to an entity in $E_i$, we add an edge between the post node and the entity node.

Entity-entity edges, entity-concept edges, concept-concept edges: Point Mutual Information (PMI) is used to measure entity-entity, entity-concept, and concept-concept correlations. Specifically, a fixed-size sliding window is used to count the correlation of nodes in the global corpus, and then, we calculate the PMI score between node pairs. We retain the edges with positive PMI values and remove the edges with non-positive PMI values.

4.3. Spatio-Temporal Feature Fusion Module

The constructed temporal propagation graph and temporal knowledge graph are each fed into separate CTDE modules. Figure 3 shows the flow of CTDE to generate node embedding, and then, we introduce the core modules of CTDE in detail.

Memory: The memory component is designed to remember the historical information of a node. The vector s (state) of each node seen by the model at time t forms the memory. The node’s memory will be updated after an event (e.g., interaction with another node or node-wise change). In this way, CTDE can remember the long-term dependencies of each node in the graph. If a new node appears, its memory is initialized to a 0 vector. The node is updated when an event involving it occurs.

Post Function: There are two posts for each interaction event containing nodes i and j:

$$p_i\left(t\right)={\mathrm{psg}}_s\left(s_i\left(t^{-}\right),s_j\left(t^{-}\right),\Delta t,e_{ij}\left(t\right)\right)$$

(1)

$$p_j\left(t\right)={\mathrm{psg}}_d\left(s_j\left(t^{-}\right),s_i\left(t^{-}\right),\Delta t,e_{ij}\left(t\right)\right)$$

(2)

For an event containing only node i, this would correspond to a post:

$$p_i\left(t\right)={\mathrm{psg}}_n\left(s_i\left(t^{-}\right),t,v_i\left(t\right)\right)$$

(3)

where $s_i\left(t^{-}\right)$ denotes the memory of node i before t. Three layers of MLP are used for $ps{g}_s, ps{g}_d,$ and $ps{g}_n$, respectively.

Posts Aggregator: To improve efficiency, we use batch processing to reduce the computation time. However, this results in multiple events involving node i in the same batch. We use an aggregation function to aggregate $p_i\left(t_1\right),\dots ,p_i\left(t_b\right)$ for $t_1,\dots ,t_b\le t$.

$${\overline{p}}_i\left(t\right)=\mathrm{agg}\left(p_i\left(t_1\right),\dots ,p_i\left(t_b\right)\right)$$

(4)

For the sake of simplicity, we choose the average operation as the $agg(·)$ function.

Posts updater: Posts updater updates itself mainly based on the node’s memory and event message.

$$s_i\left(t\right)=\mathrm{GRU}\left({\overline{p}}_i\left(t\right),s_i\left(t^{-}\right)\right)$$

(5)

When an interaction event between node i and node j occurs, the memory of both nodes is updated after the event. For a single node event, only the memory of the involved node is updated, not the other nodes.

Embedding: The Embedding module generates the temporal embedding of node i at time t. The primary goal of the embedding module is to ensure that the node representations remain relevant over time, even if the updates to the memory occur only during events. This approach helps maintain the accuracy of node embeddings, especially when there are extended periods without new events. We use CTDE as the embedding module. A series of L graph attention layers compute the embedding of node i by aggregating information from its L-hop temporal neighborhoods. The inputs to layer l are the upper layer representation $h_i^{(l-1)}\left(t\right)$ of node i, the current time step t, the neighbor representations $\left\{h_1^{(l-1)}\left(t\right),\dots ,h_N^{(l-1)}\left(t\right)\right\}$ of node i, timestamps $t_{1,\dots ,}{t}_N$, and the features $e_{i1}\left(t_1\right),\dots ,e_{iN}\left(t_N\right)$ of node i’s edges at each time step:

$$\begin{array}{cc}\hfill & {\mathbf{h}}_i^{\left(l\right)}\left(t\right)={\mathrm{MLP}}^{\left(l\right)}({\mathbf{h}}_i^{(l-1)}\left(t\right)\parallel {\tilde{\mathbf{h}}}_i^{\left(l\right)}\left(t\right))\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & \begin{array}{cc}\hfill {\tilde{\mathbf{h}}}_i^{\left(l\right)}\left(t\right)=& {\mathrm{MultiHeadAttention}}^{\left(l\right)}({\mathbf{q}}^{\left(l\right)}\left(t\right),\hfill \\ \hfill & {\mathbf{K}}^{\left(l\right)}\left(t\right),{\mathbf{V}}^{\left(l\right)}\left(t\right))\hfill \end{array}\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & {\mathbf{q}}^{\left(l\right)}\left(t\right)={\mathbf{h}}_i^{(l-1)}\left(t\right)\parallel \mathit{\varphi }\left(0\right)\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & {\mathbf{K}}^{\left(l\right)}\left(t\right)={\mathbf{V}}^{\left(l\right)}\left(t\right)={\mathbf{C}}^{\left(l\right)}\left(t\right)\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & \begin{array}{cc}\hfill {\mathbf{C}}^{\left(l\right)}\left(t\right)=& [{\mathbf{h}}_1^{(l-1)}\left(t\right)\parallel {\mathbf{e}}_{i1}\left(t_1\right)\parallel \mathit{\varphi }(t-t_1),\dots ,\hfill \\ \hfill & {\mathbf{h}}_N^{(l-1)}\left(t\right)\parallel {\mathbf{e}}_{iN}\left(t_N\right)\parallel \mathit{\varphi }(t-t_N)]\hfill \end{array}\hfill \end{array}$$

(10)

Here, ‖ denotes the concatenation operation, and  $\varphi (·)$ denotes the temporal encoder [22]. Multi-head-attention is performed at each layer, where the query ${\mathbf{q}}^{\left(l\right)}\left(t\right)$ represents the reference node (e.g., the target node or an L-1-hop neighbor), and keys ${\mathbf{K}}^{\left(l\right)}\left(t\right)$ and ${\mathbf{V}}^{\left(l\right)}\left(t\right)$ represent its neighbors. The last MLP is used to fuse the features ${\mathbf{h}}_i^{(l-1)}\left(t\right)$ of node i in the previous layer and the features ${\tilde{\mathbf{h}}}_i^{\left(l\right)}\left(t\right)$ of node i after aggregating the neighboring nodes.

Raw Posts Store: The complexity of our training strategy is that the memory-related modules (Posts Function, Posts Aggregator, and Posts Updater) do not directly affect the loss, nor do they receive a gradient. To solve this problem, we update the information in memory with posts from previous batches (these posts are stored in the Raw Posts Store) and generate node embeddings. Figure 3 illustrates the training process of the memory-related modules. The Raw Posts Store contains the raw posts $r{p}_i$ of each node i, which are generated since the last interaction before time t. When the model processes the next post of node i, it generates the raw posts $r{p}_i$. The updated memory is then used to compute the embedding of the node. New interactions generated after this interaction are then stored in the Raw Posts Store.

For an event ${\epsilon }_i$, the temporal propagation graph and the temporal knowledge graph we construct based on ${\epsilon }_i$ are processed by two CTDE modules to obtain two sets of nodes embedding $X_{TP}=\left\{h_{p_{i0}},h_{p_{i1}},h_{p_{i2}},\dots ,h_{p_{in}}\right\},X_{TK}=\left\{h_{p_{i0}^{\prime }}^{\prime },h_{p_{i1}}^{\prime },h_{p_{i2}}^{\prime },\dots ,h_{p_{in}}^{\prime }\right\}$ at the final moment $t_m$.

4.4. Subgraph Fusion Module

The node embedding $X_{TP}$ obtained from the temporal propagation graph and the node embedding $X_{TK}$ obtained from the temporal knowledge graph contain different information. The $X_{TP}$ encodes the propagation relationship between each post, while the $X_{TK}$ encodes the propagation relationship between the knowledge associated with each post. We must effectively fuse the different information to accurately identify rumors. Therefore, CGNKP needs to learn the weights of the two embeddings containing different information, i.e., the subgraph-level attention mechanism is used to generate a set of node embeddings that fuse the structural information of the two subgraphs.

To learn the weights of the two subgraphs, we first apply a linear layer to the subgraph representation to convert it into a low-dimensional vector. Then, the similarity between each node and the subgraph attention vector q is calculated as the node importance score in the current subgraph. The average importance score of all nodes in the same subgraph is used as the subgraph importance score. The formula for calculating the importance $w_{TP\left(TK\right)}$ of the temporal propagation graph and the temporal knowledge graph is as follows:

$$\begin{array}{cc}\hfill w_{TP\left(TK\right)}=& {\displaystyle \frac{1}{\mid X_{TP\left(TK\right)}\mid }}\sum _{h_{pi}\in X_{TP\left(TK\right)}}{q}^T\hfill \\ \hfill & ·tanh(W_{sub}{h}_{pi}+b)\hfill \end{array}$$

(11)

where $W_{sub}$ is the weight matrix and b is the bias. The subgraph level attention vector q, the weight $W_{sub}$, and the bias b of the linear layer are shared by the two subgraphs. After obtaining the subgraph importance scores $w_{TP\left(TK\right)}$, we normalize the scores to the weight coefficients:

$${\alpha }_{TP\left(TK\right)}={\displaystyle \frac{exp\left(w_{TP\left(TK\right)}\right)}{exp\left(w_{TP}\right)+exp\left(w_{TK}\right)}}$$

(12)

Eventually, using the weight coefficients of the learned subgraphs, we obtain a node embedding set $X_T$ that incorporates information from both graphs:

$$\begin{array}{cc}\hfill \widetilde{X_T}& =\widetilde{h_{p_{i0}}},\widetilde{h_{p_{i1}}},\dots ,\widetilde{h_{p_{in}}}\hfill \\ \hfill \widetilde{h_{p_{ij}}}& ={\alpha }_{TP}·h_{p_{ij}}+{\alpha }_{TK}·h_{p_{ij}}^{\prime }\hfill \end{array}$$

(13)

4.5. Classification Module

We apply a mean-pooling operation to fuse the structured information representation of the nodes in $\widetilde{X_T}$, formalized as:

$$X_T=\text{mean-pooling}\left(\widetilde{X_T}\right)$$

(14)

Then, we apply BERT [29] to encode the source post information, and then concatenate and fuse it with $X_T$.

$$S_i=\mathrm{linear}\left(\mathrm{BERT}\left(p_{i0}\right)\parallel X_T\right)$$

(15)

Finally, we feed $S_i$ into a classifier to obtain the prediction results:

$$\widehat{y_i}=\mathrm{softmax}\left(\mathrm{linear}\left(S_i\right)\right)$$

(16)

To train the model, we use the cross-entropy loss and a regularization term to guide the training. The formula is given as.

$$L\left(y_i,\widehat{y_i}\right)=-\sum _{i\in [1,n]}{y}_{i}log\widehat{y_i}+\lambda {\parallel \theta \parallel }_2^2$$

(17)

where $y_i$ is the ground truth label of the i-th event, $\lambda$ represents the trade-off coefficient, and $\theta$ represents the set of all parameters. ${\parallel ·\parallel }_2^2$ indicates the L2 regularization term to prevent overfitting. The entire training process of CGNKP is outlined in Algorithm 1.

Algorithm 1: Training of CGNKP

5. Experiments

We now show the relevant findings of our experiments. We compare the performance of CGNKP in rumor detection with state-of-the-art baselines. In addition, we designed ablation experiments that compare several variants of CGNKP to investigate the effects of different components. In particular, we quantify our concerns as follows.

RQ1: How does CGNKP perform compared to the state-of-the-art baselines on rumor detection?

RQ2: What is the impact of each CGNKP component on the overall performance?

RQ3: Is CGNKP able to detect rumors in the early propagation stage?

5.1. Experimental Settings

5.1.1. Datasets

We construct our experiments on two real-world datasets: Twitter15 and Twitter16 [23]. The statistics are presented in

Table 1. Statistics of the datasets.

	Twitter15	Twitter16
# of events	1490	818
# of posts	331,612	204,820
# of true-rumors	374	205
# of false-rumors	370	205
# of unverified rumors	374	203
# of non-rumors	372	205
Avg. time length/event(hours)	1337	848
Avg. # of posts/event	223	251
Max # of posts/event	1768	2765
Min # of posts/event	55	81

. The labels of each event on Twitter15 and Twitter16 are labeled according to the real labels of tweets on rumor sites. The Twitter datasets contain four tags: Non-rumor (NR), False Rumor (FR), True Rumor (TR), and Unverified Rumor (UR). We divided the two datasets into training, validation, and test sets in a ratio of 7:1:2. Table 1 shows the statistics for these datasets.

5.1.2. Baseline Models

We compare CGNKP with feature-based, deep learning-based, and the recently proposed state-of-the-art methods.

DTR [30]: A decision tree-based ranking model that clusters posts and selects the top k clustering results as rumors.

DTC [31]: A decision tree-based model incorporating manually designed post features to distinguish rumors.

RFC [32]: A random forest classifier that combines manual features such as content, structural attributes, and user attributes of the spread for detection.

SVM-TK [23]: An SVM classifier based on Tree Kernel that attempts to capture the structural features of propagation by kernel-learning.

GRU-RNN: An RNN with GRU units that models the response time features of comments.

TD-RvNN and BU-RvNN [33]: A tree-structured recurrent neural network with GRU units, where the RvNN obtains its representation from a bottom-up (BU-RvNN) or a top-down (TD-RvNN) propagation structure.

PLAN [34]: A transformer-based rumor detection model to model long-range post-pair interactions.

Bi-GCN [11]: A GCN-based rumor detection method using bidirectional propagation structures (propagation and diffusion structures) and textual content(source post and comments).

STS-NN [12]: An RNN-based model that models spatial and temporal structure by modifying RNNs.

GCRES [35]: A deep residual graph convolutional network that fuses content and propagation structure to detect rumors, leveraging the interaction characteristics of heterogeneous graphs for enhanced accuracy.

RA [36]: A misinformation detection method based on Large Language Models (LLMs). It identifies whether a post matches any of the nine predefined misinformation characteristics.

LeRuD [37]: An LLM-based method that utilizes specific prompts to guide the model to focus on key clues in news content and comments, dividing the propagation information into a “Chain of Propagation” for step-by-step analysis and reasoning.

5.1.3. Implementation Setting

CGNKP is implemented using the PyTorch framework, and the parameters are optimized by the Adam algorithm. BERT-base was used as the encoder for the source post and pretrained on the datasets. The learning rate of BERT is set to 5 × 10⁻⁵, the learning rate of other parameters is set to 1 × 10⁻³, and the training epoch is set to 5. We select the optimal parameter settings on the validation set and evaluate the performance of CGNKP on the test set. We employ Accuracy (Acc) in all categories and the F1 score in each category to evaluate the performance of the models.

5.2. Overall Performance (RQ1)

The performance comparison between CGNKP and other baselines is presented in

Table 2. Performance comparison on the Twitter15 and Twitter16 datasets. The best result is shown in bold, and the second best is shown as underlined.

Model	Twitter15					Twitter16
	Acc	F1				Acc	F1
		UR	NR	TR	FR		UR	NR	TR	FR
DTR	0.409	0.501	0.311	0.364	0.473	0.414	0.394	0.273	0.630	0.344
DTC	0.454	0.733	0.355	0.317	0.415	0.465	0.643	0.393	0.419	0.403
RFC	0.565	0.810	0.422	0.401	0.543	0.585	0.752	0.415	0.547	0.563
GRU-RNN	0.641	0.684	0.634	0.688	0.571	0.633	0.617	0.715	0.577	0.527
SVM-TK	0.667	0.619	0.669	0.772	0.645	0.662	0.643	0.623	0.783	0.655
BU-RvNN	0.708	0.695	0.728	0.759	0.653	0.718	0.723	0.712	0.779	0.659
TD-RvNN	0.723	0.682	0.758	0.821	0.654	0.737	0.662	0.743	0.835	0.708
PLAN	0.787	0.775	0.775	0.768	0.807	0.799	0.779	0.754	0.836	0.821
STS-NN	0.809	0.797	0.811	0.856	0.773	0.821	0.739	0.814	0.883	0.845
Bi-GCN	0.829	0.752	0.772	0.851	0.827	0.837	0.818	0.772	0.885	0.847
GCRES	0.842	0.811	0.801	0.852	0.839	0.882	0.857	0.765	0.904	0.832
RA	0.713	0.682	0.735	0.762	0.661	0.729	0.715	0.711	0.826	0.692
LeRuD	0.706	0.691	0.686	0.797	0.638	0.715	0.702	0.733	0.809	0.716
CGNKP (ours)	0.861	0.897	0.861	0.865	0.841	0.903	0.862	0.883	0.935	0.889

.

This yields the following observations:

• Feature-based models such as DTR, DTC, and RFC perform poorly since they use hand-developed features based on the overall statistics of posts. However, these features are too coarse and have low generalizability. RFC performs better than the other two models. This is because RFC uses additional structural features and temporal features.
• Deep learning-based models automatically extract effective features due to the use of neural networks, leading to significantly better performance than feature-based approaches. The performance of GRU-RNN is relatively poor because it only utilizes the content of the posts and ignores other useful information, such as the rumors’ propagation structure and temporal information. BU-RvNN and TD-RvNN perform better than GRU-RNN, indicating that simulating spatial and temporal structures is effective for rumor detection. PLAN performs well on the two datasets, showing that capturing the interaction between posts is effective. STS-NN and Bi-GCN model the propagation structure and temporal information between the source post and comments. Bi-GCN outperforms STS-NN because it can distinguish between spatial and temporal structure patterns. Additionally, Bi-GCN does not incorporate linguistic features but focuses on feature mining of rumor propagation and diffusion. As the number of nodes in the propagation tree decreases, the information that can be provided decreases accordingly, leading to a drop in model performance. The strong performance of GCRES among baseline models demonstrates the effectiveness of leveraging deep residual graph networks to learn content and structure interaction information in network propagation models.
• The RA and LeRuD methods, which are based on LLMs, offer a flexible and interpretative approach to rumor detection. Their use of prompt engineering allows them to guide the model’s focus on specific characteristics, making them adaptable across various scenarios. However, because LLMs are not specifically trained for rumor detection, they may not capture certain nuanced features as effectively as deep learning-based approaches that are fine-tuned for this task, while RA and LeRuD excel in leveraging language understanding and can provide insights through interpretability, they sometimes face challenges in processing complex temporal and contextual information, especially when relying on predefined prompts. In contrast, deep learning models, particularly those using graph neural networks, are adept at extracting dynamic features across time and space, benefiting from specialized training on structured data. This allows them to learn intricate patterns within propagation networks.
• CGNKP achieves the best results on the two datasets. This is for several reasons. First, we use dynamic graphs to adequately model the structural features of rumor propagation and the temporal features, which are crucial for distinguishing rumors. Second, we model the temporal propagation structure as continuous-time dynamic graphs instead of discrete-time dynamic graphs, which can represent the temporal propagation structure in a more fine-grained way with specific temporal information. Finally, we model the dynamic background knowledge information for source posts and comments, which helps CGNKP to achieve the best results (we elaborate on this in Section 5.3). Finally, we use a subgraph-level attention mechanism to dynamically fuse the two subgraphs’ representations instead of simply concatenating them. This allows the model to adjust the proportion of the representation vector occupied by the two types of information.

5.3. Ablation Experiments (RQ2)

In this section, we construct ablation experiments on the two datasets to fully analyze the key components of CGNKP. In particular, we build comparisons by removing some components in the following variants of CGNKP.

• -source: remove source post content enhancement, i.e., use only pooled graph representation as input to the Classification Module.
• -structure: ignore structured features of rumor propagation, but keep content, temporal, and knowledge features.
• -time_GAT: remove temporal information, i.e., keep rumor propagation structure, and aggregate graph structure information with GAT.
• -time_GCN: remove temporal information, i.e., keep the rumor propagation structure, and use vanilla GCN to aggregate the graph structure information.
• -CTDE: Remove the CTDE module and replace CTDE with TGAT [22].
• -Knowledge: remove the dynamic knowledge structure, i.e., keep only the temporal propagation graph.
• -sub_Atten: remove the subgraph-level attention, i.e., concatenate the temporal propagation graph with the temporal knowledge graph representation.

The performance of these variants is summarized in Figure 4, leading to the following observations:

• As the results show, CGNKP outperforms all other variants, and the removal of these components degrades the performance of rumor detection. The content of the source post (-source) remains the most important signal for identifying rumors among the various features. However, relying solely on content-based features is insufficient for effectively identifying rumors.
• -structure suffers a significant decrease, indicating that structured information is crucial for detecting rumors. Both -time_GAT and -time_GCN use a static graph neural network approach, while -time_GCN has poorer performance than -time_GAT, reflecting the negative attention in reducing the weights of noisy nodes. The static graphs approach is much less accurate than the dynamic graphs method (-CTDE), which has much lower accuracy on the two datasets. This indicates that temporal information is a significant feature for detecting rumors. This result also explains why the methods proposed by Bian et al. [11] are not as effective as CGNKP, since the former focuses on simulating temporal information while the latter mainly explores the diffusion process. CGNKP utilizes dynamic graph neural networks, which can fully use temporal information and capture structured features.
• CGNKP has better performance than -knowledge. This indicates that the dynamic diffusion structure of knowledge can also be an important feature for identifying rumors.
• The absence of subgraph-level attention (-sub_Atten) prevents CGNKP from achieving peak performance. Because subgraph-level attention can assign weights to both subgraphs and adaptively adjust the weight size to obtain the best representation.

5.4. Performance on Early Detection (RQ3)

Identifying rumors in the early stages of propagation is crucial for effectively curbing their spread. Early detection enables relevant authorities to take prompt action, thereby enhancing public safety and mitigating the negative impact of rumors on society. We will now examine the performance of early rumor detection by comparing the detection accuracy of different models across various elapsed times and post counts [33]. The sooner the model detects the rumor, the less information it has to work with. We assess its performance based on the accuracy achieved at specific checkpoints. Figure 5 shows the comparison of CGNKP and the baseline models in terms of early detection performance.

First, the accuracy of all models climbs as the deadline elapses or post count increases. In particular, CGNKP achieves the highest accuracy at each deadline or post count compared to the other models.

Second, DTR and SVM-TK have poor early detection performance compared to deep learning-based methods because they only use hand-created features. Compared with TD-RvNN and BU-RvNN, which capture only one-way propagation or diffusion structures, Bi-GCN captures bi-directional structures using bi-directional GCNs and thus is more beneficial for early detection of rumors.

We observe that CGNKP performs particularly well when only a limited sample of observations is available. CGNKP takes only a short time to identify misinformation because it captures the dynamic rumor propagation structure and background knowledge information. From Figure 5, we also note that the accuracy of CGNKP on the Twitter15 and Twitter16 datasets fluctuates in the early stages. This could be due to the noise in the early stages of propagation causing a disturbance to the detection process, whereas the structured and temporal information becomes more valuable in later stages. Notably, CGNKP performs significantly better than other models at each evaluation point. This further demonstrates the effectiveness of CGNKP for early rumor detection.

6. Conclusions

This paper introduces a rumor detection model, CGNKP, designed to capture spatial structure, continuous temporal information, external knowledge, and text semantics within a unified framework. Initially, the propagation graph and knowledge graph are constructed based on the diffusion of posts and the dynamic evolution of background knowledge. In particular, for temporal information, we use exact time instead of simply viewing the temporal graph as discrete snapshots of the ordered graph. Subsequently, the temporal graph network framework is employed to capture both the continuous temporal and spatial structures of the propagation. Lastly, a subgraph-level attention mechanism is utilized to adaptively integrate the distinct information from the two subgraphs, creating a representation for each post. The experimental results indicate that CGNKP is highly effective for rumor detection across two real-world datasets and markedly surpasses other state-of-the-art models in tasks related to early rumor detection.