A Bimodal Exponential Regression Model for Analyzing Dengue Fever Case Rates in the Federal District of Brazil
Abstract
1. Introduction
2. Materials and Methods
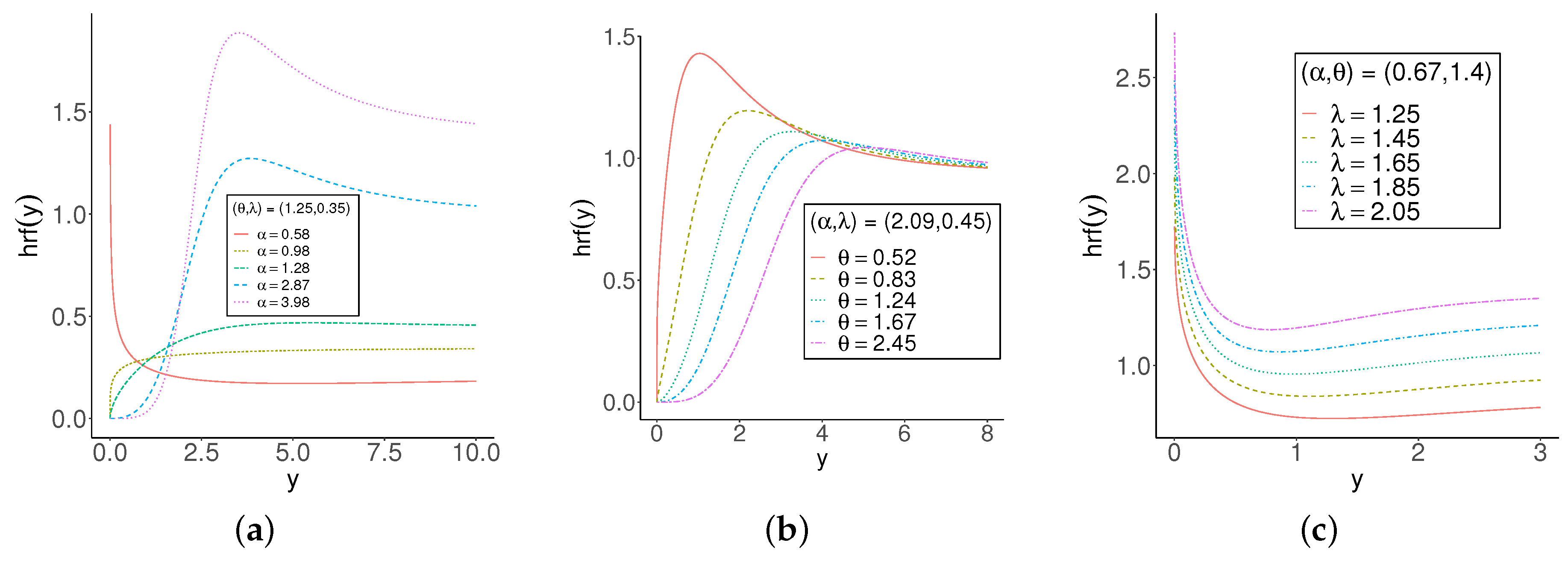
2.1. Main Properties
2.1.1. Representation
2.1.2. Quantile Function
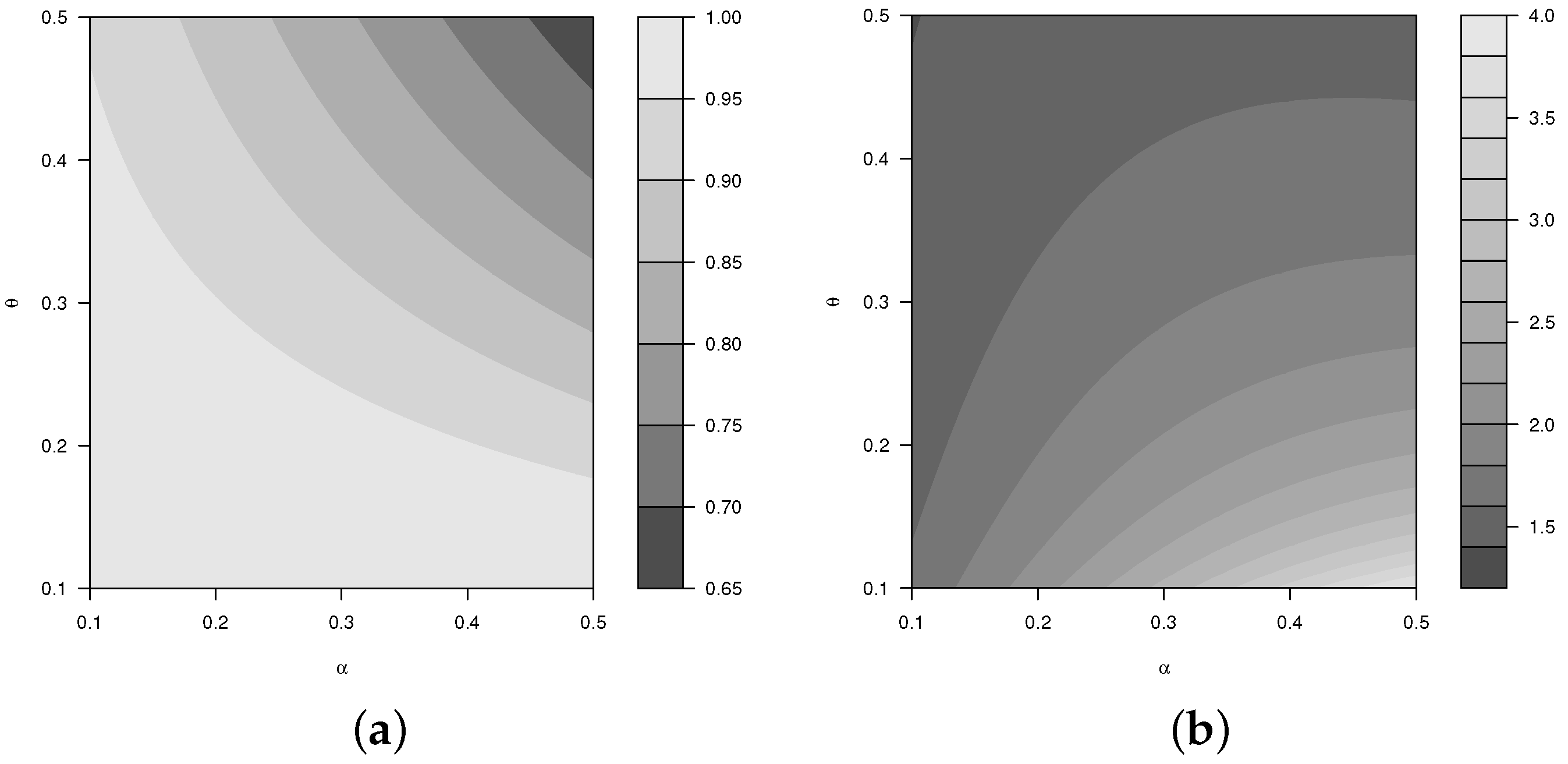
2.1.3. Moments
2.1.4. Generating Function
2.1.5. Estimation
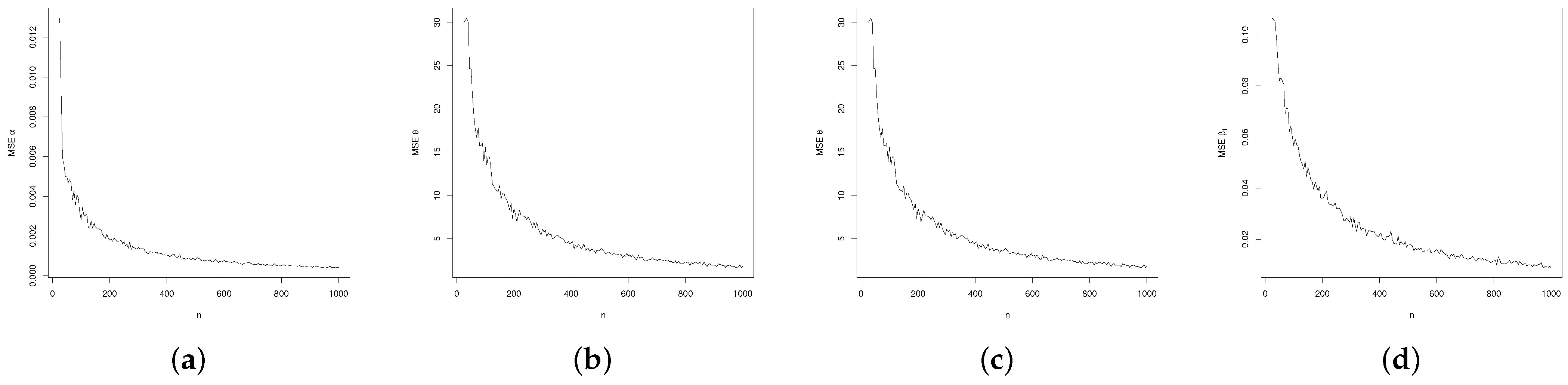
2.1.6. Simulation Study
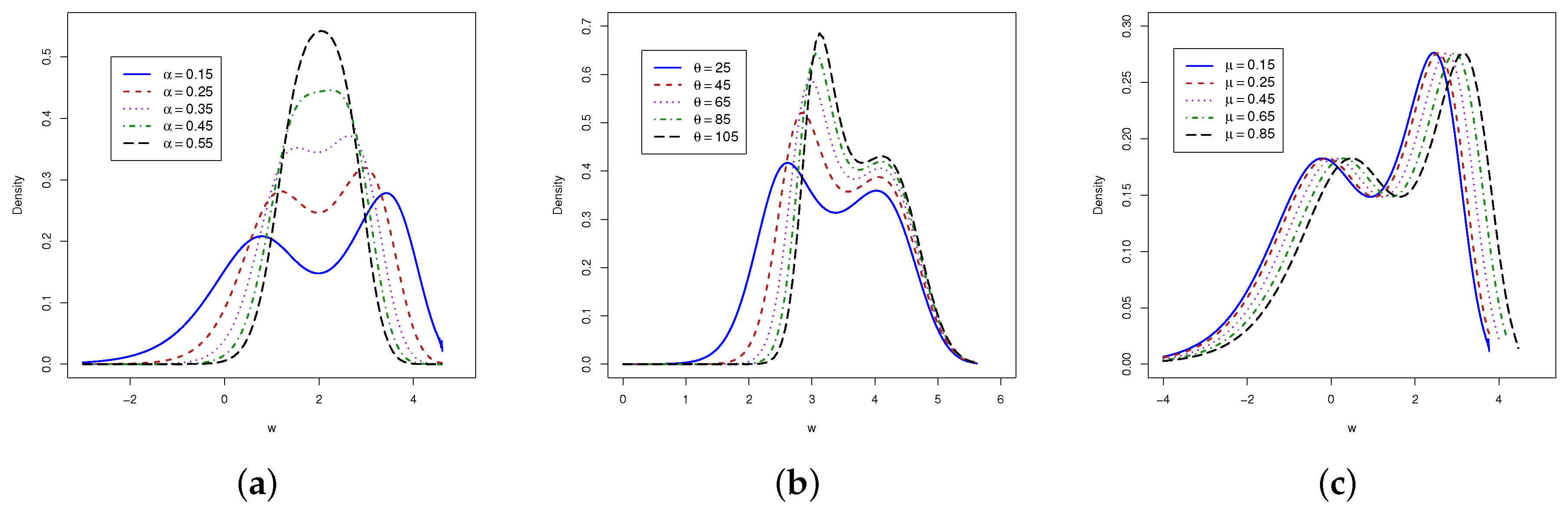
3. The Proposal LGOLLE Distribution
3.1. The New LGOLLE Regression Model
3.2. Estimation
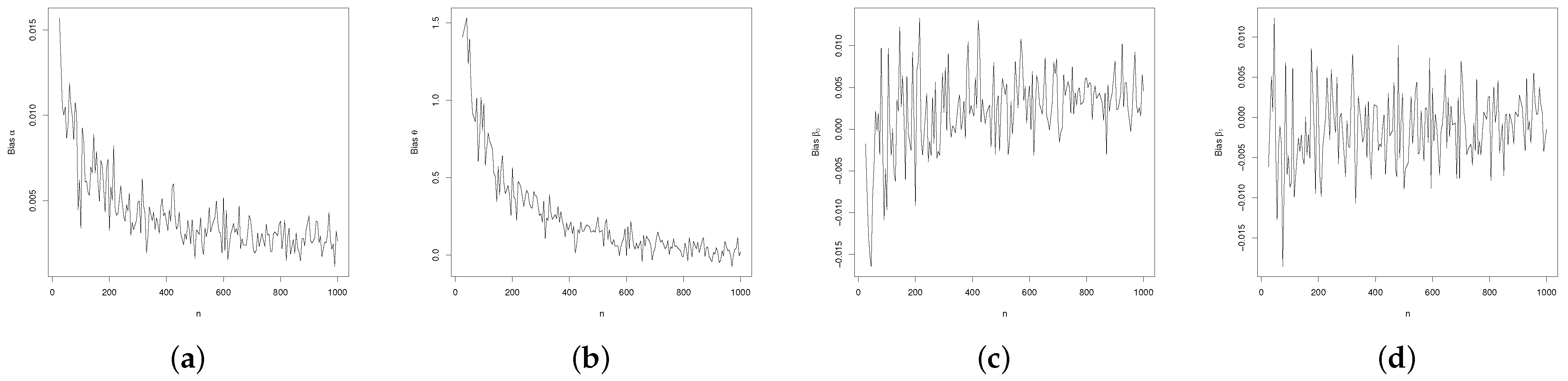
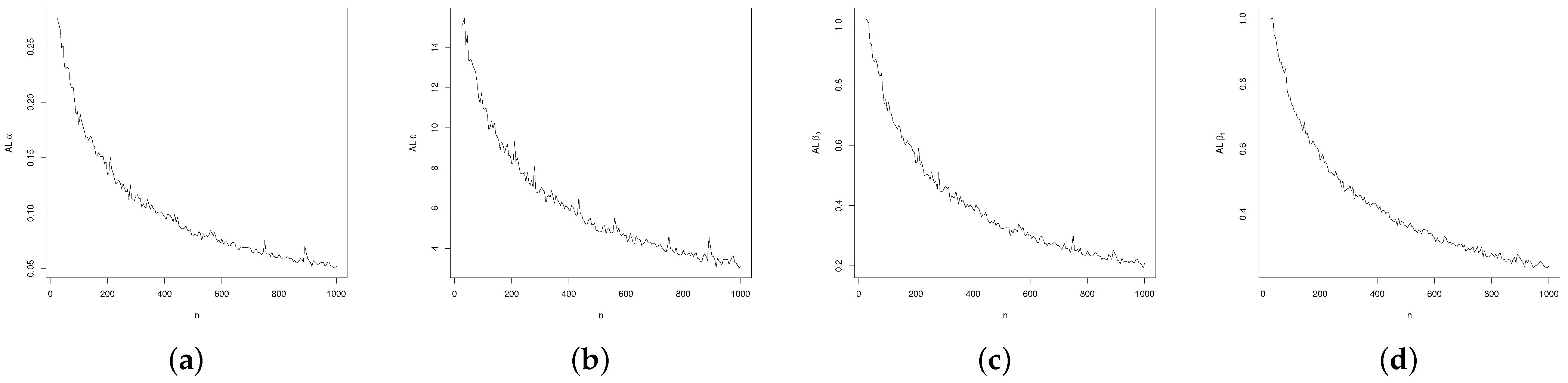
3.3. Regression Simulation Study
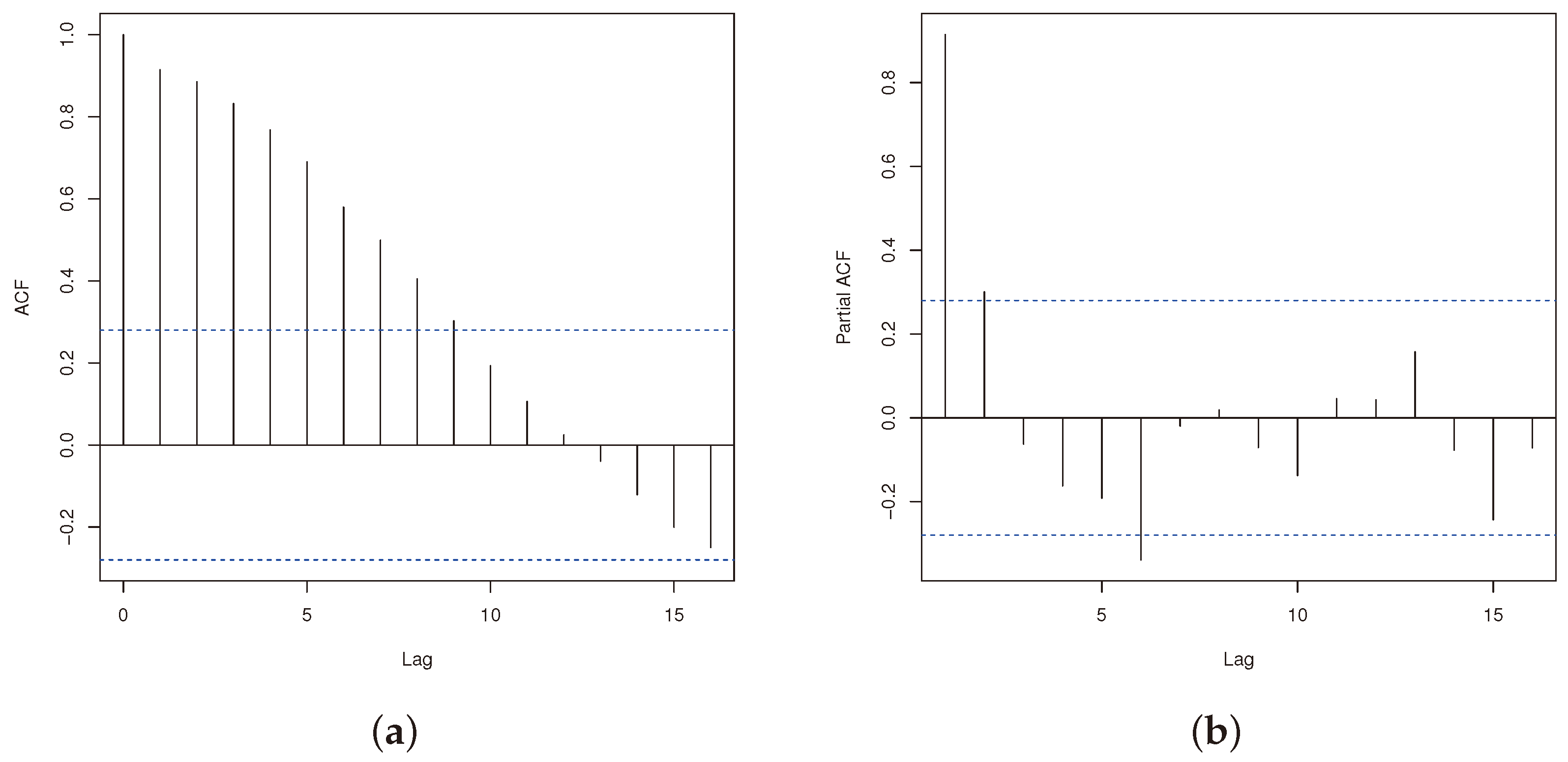
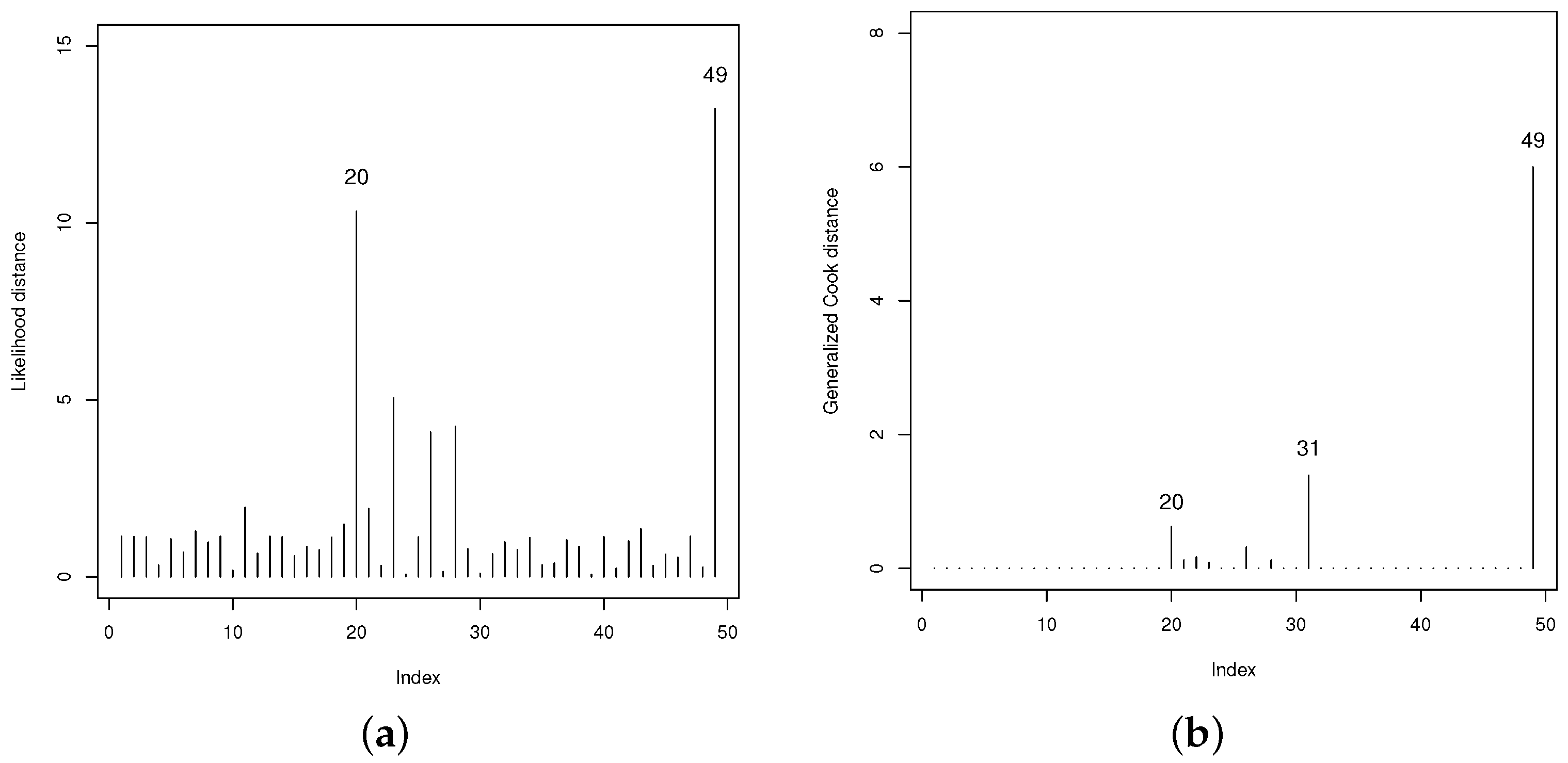
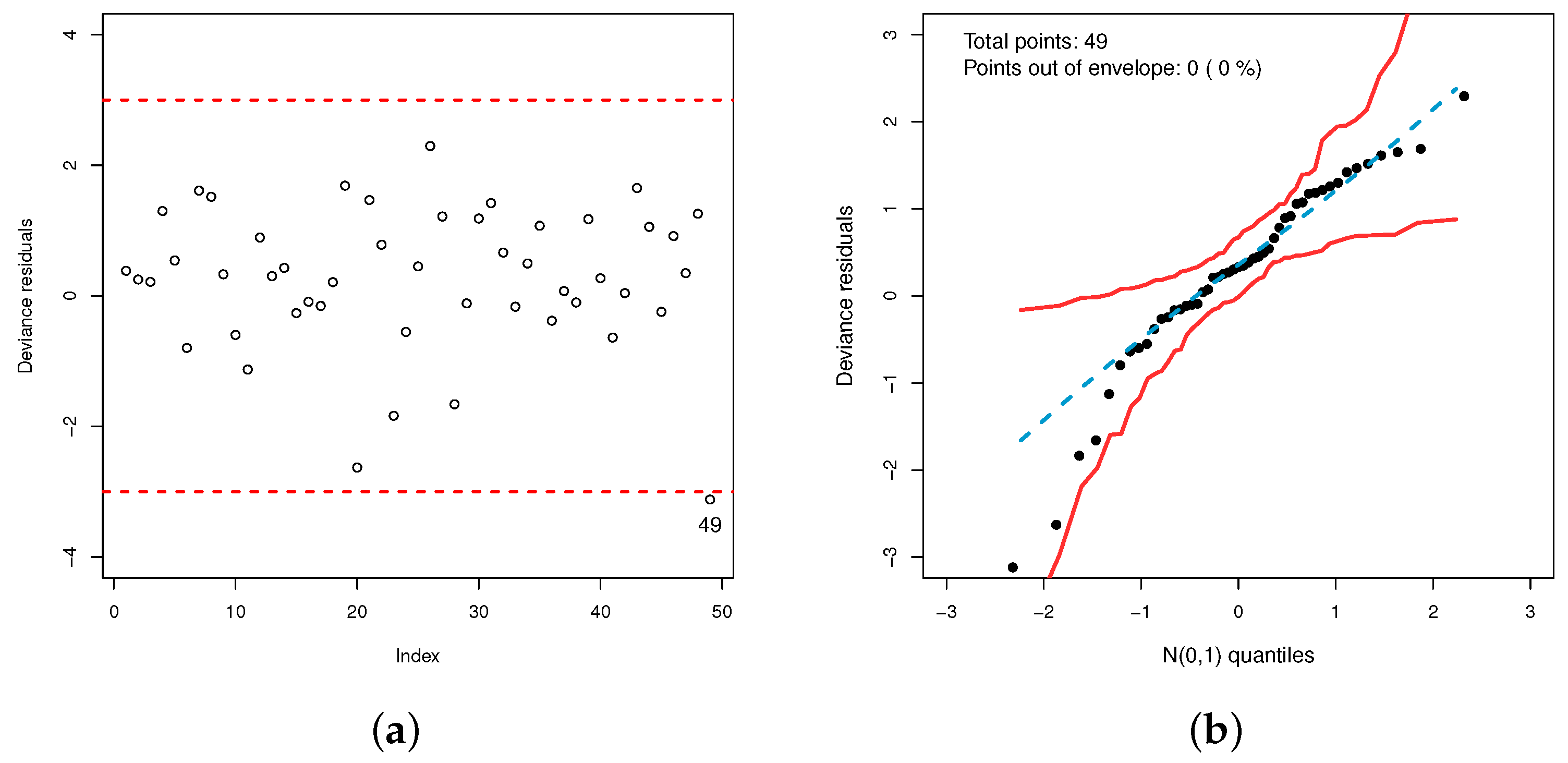
3.4. Model Checking
4. Application: Dengue Fever Cases Data
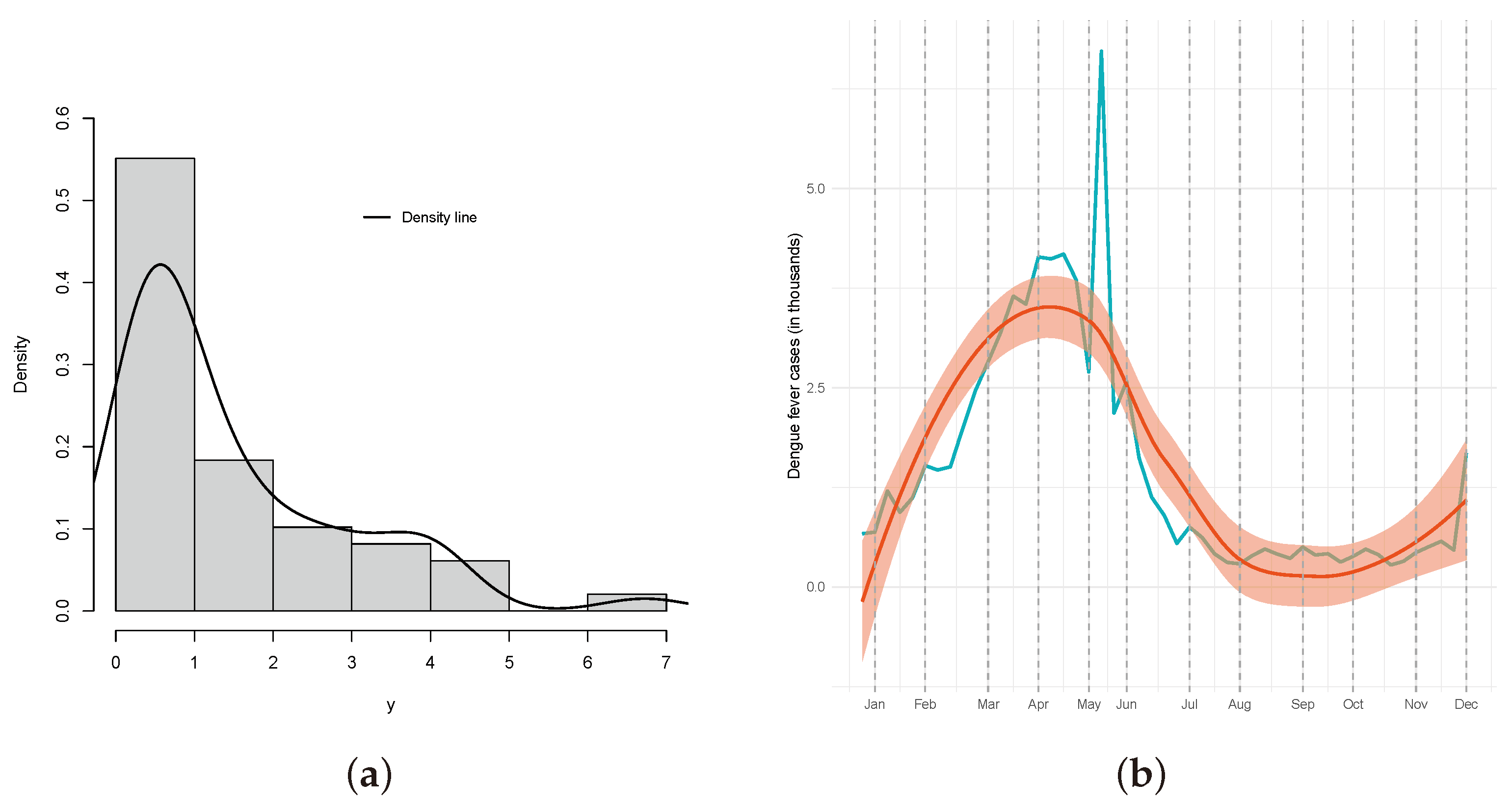
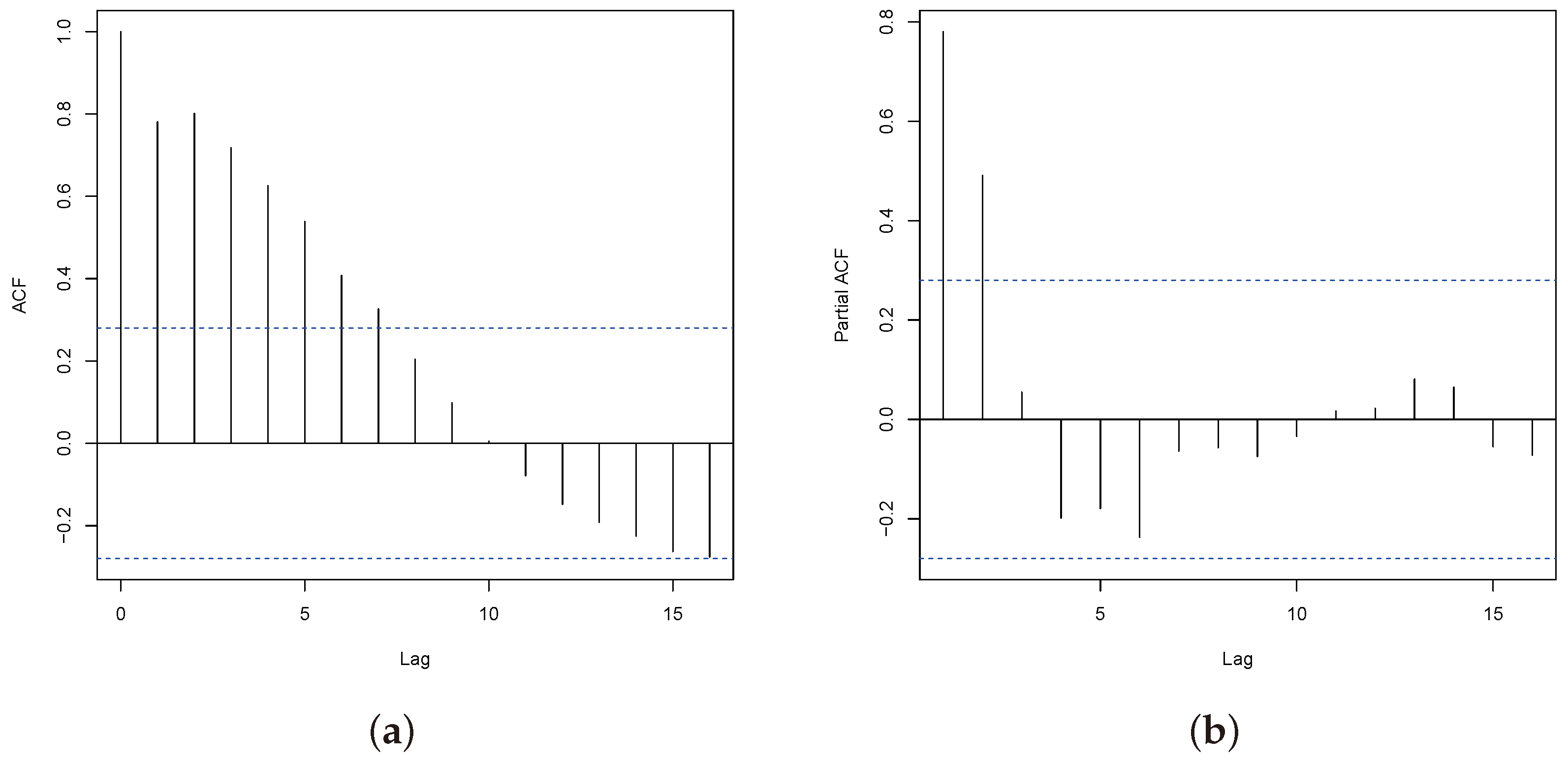
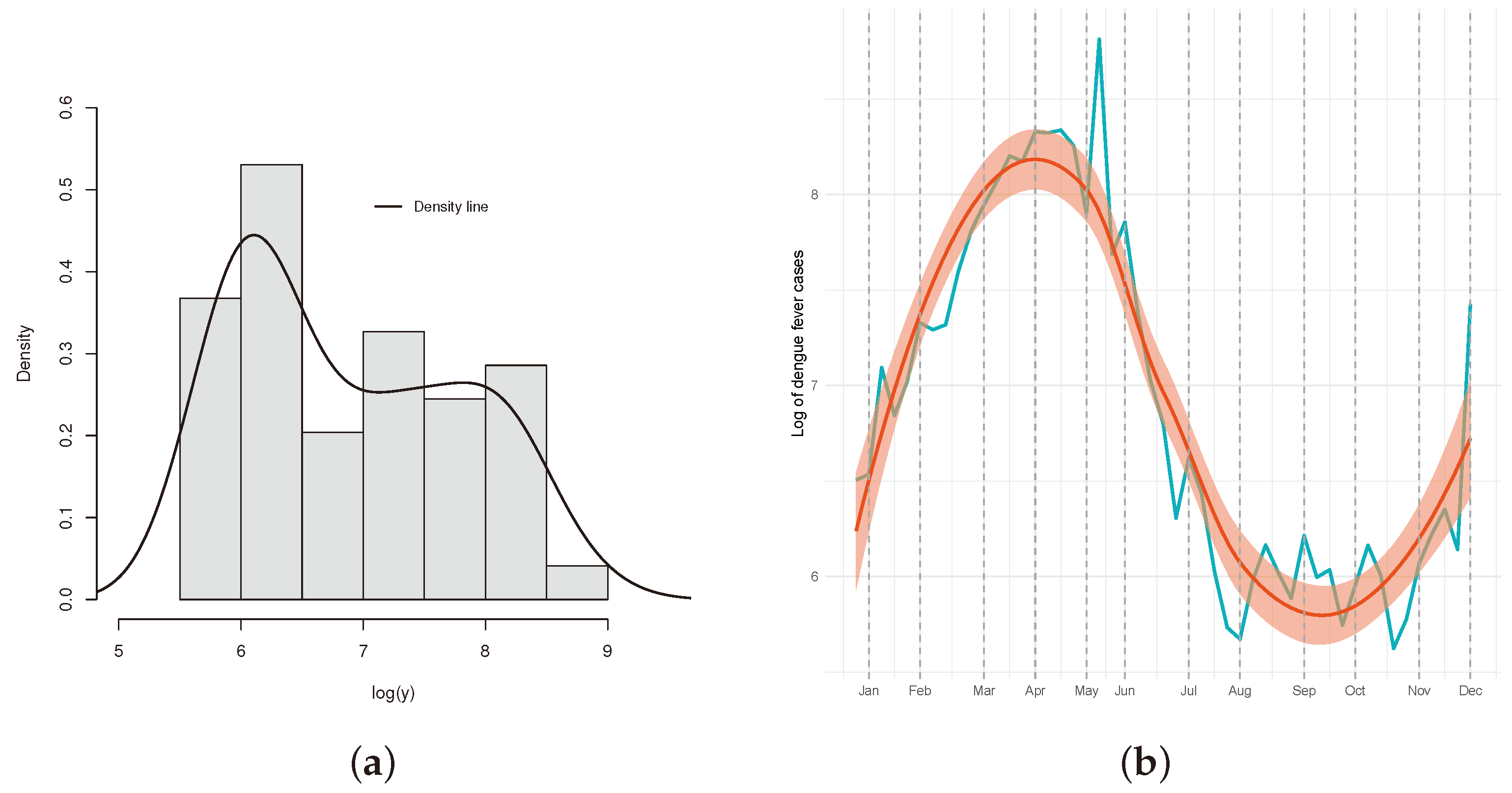
4.1. Descriptive of the Data
- : total dengue fever cases of a epidemiological week (DG) (response variable);
- : month (levels: 0—January to 11—December). Thus, for and , dummy variables.
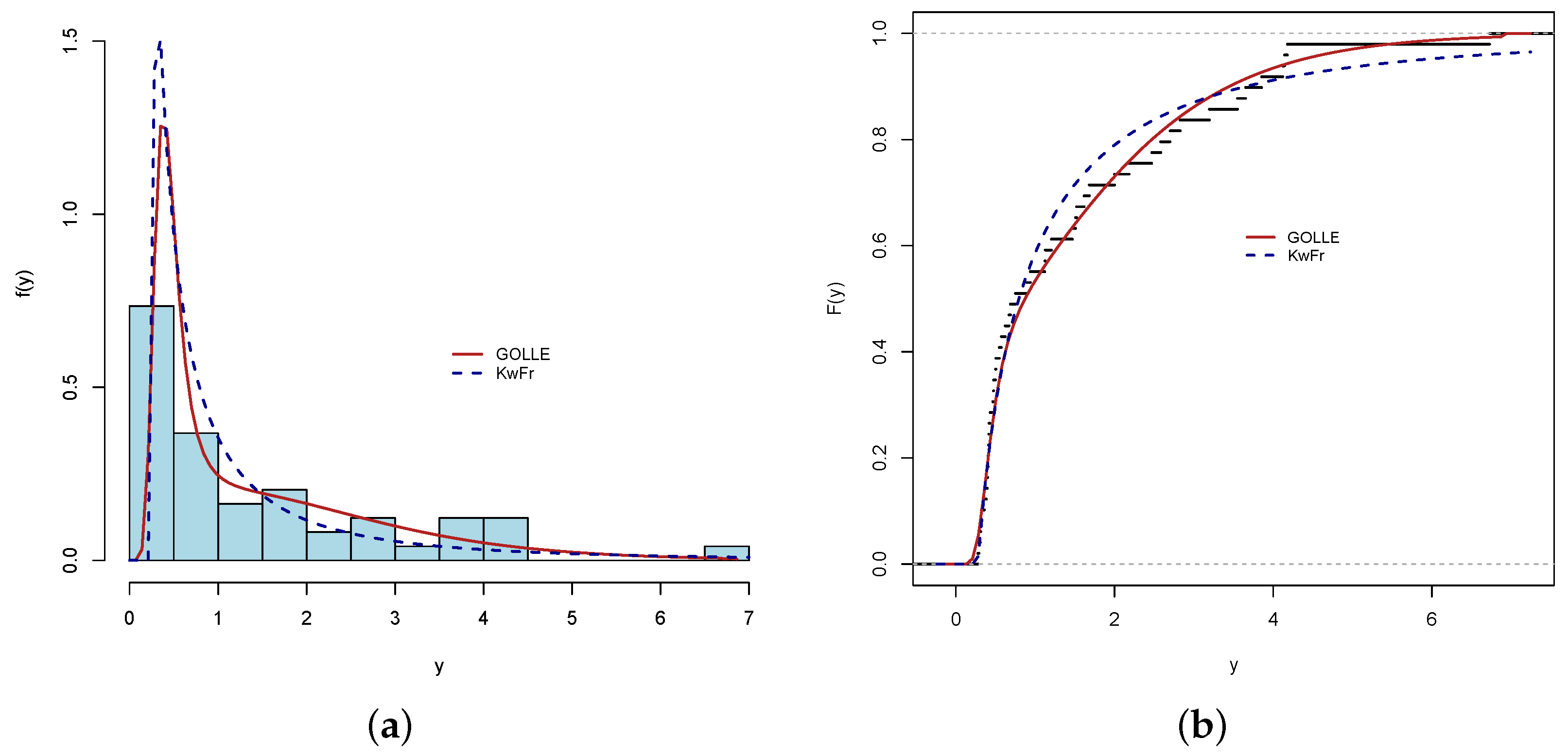
4.2. Findings from GOLLE Distribution
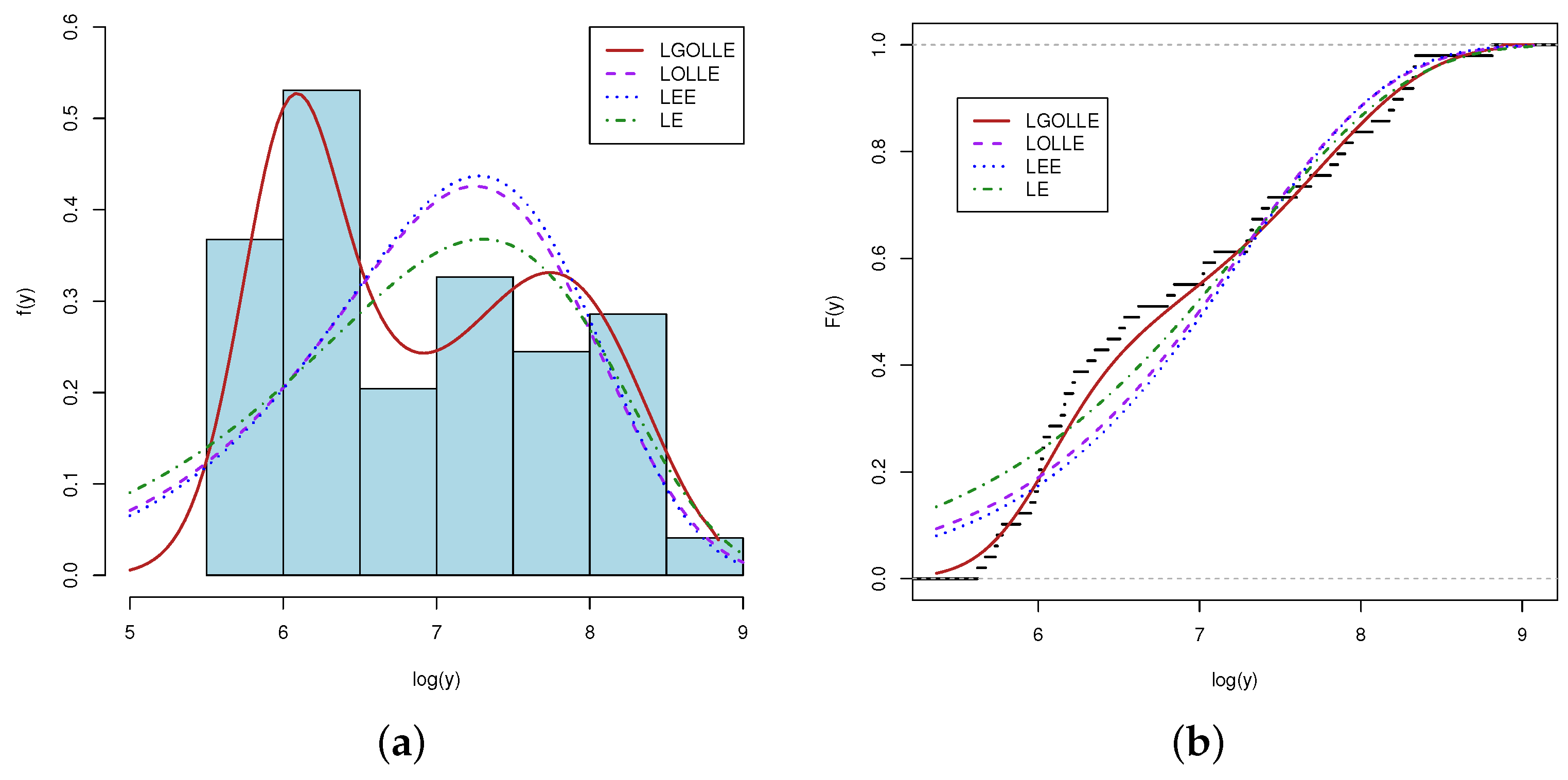
4.3. Findings from LGOLLE Regression Model
4.4. Discussion
- Except for the covariates and , referring to the months of July and December, all other covariates are significant at a level of significance. This indicates that there is a difference in dengue fever cases registered in the Federal District between the other months and January. The months of July and December are probably not significant due to their behavior being similar to the reference month;
- The months of February to June have positive estimates, which is significant, showing an increase in comparison to January. This can be seen in Figure 12b, which shows an extreme event occurring between May and June in the data for that time window;
- The months of August to November have negative values, indicating a decline in dengue fever cases compared to January. During this period, the Federal District experiences a drought, which corroborates the study’s findings (https://portal.inmet.gov.br/uploads/notastecnicas/Estado-do-clima-no-Brasil-em-2022-OFICIAL.pdf, accessed on 2 July 2024).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Anderson Darling | |
| ACF | autocorrelation function |
| AE | average estimate |
| AL | average estimate length |
| ARIMA | autoregressive integrated moving average model |
| BFr | beta-Fréchet |
| cdf | cumulative distribution function |
| CI | confidence interval |
| COVID-19 | corona virus disease 2019 |
| DG | dengue fever cases |
| E | exponential distribution |
| EE | exponentiated exponential distribution |
| EVT | extreme value theory |
| Fr | Fréchet |
| GCD | generalized Cook distance |
| GEV | generalized extreme value |
| GE | gamma-exponential distribution |
| GFr | gamma-Fréchet distribution |
| GOLLE | generalized odd log-logistic exponential distribution |
| GOLL-G | generalized odd log-logistic distribution |
| hrf | hazard rate function |
| KS | Kolmogorov-Sminorv |
| KwE | Kumaraswamy exponential distribution |
| KwFr | Kumaraswamy Fréchet distribution |
| LD | loglikelihood distance |
| LE | log exponential distribution |
| LGOLLE | log generalized odd log-logistic exponential distribution |
| LLE | log exponentiated exponential distribution |
| LOLLE | log odd log-logistic exponential distribution |
| LR | likelihood ratio |
| mgf | moment generation function |
| MLE | maximum likelihood estimate |
| MSE | mean squared error |
| OLLE | odd log-logistic exponential distribution |
| PACF | partial autocorrelation function |
| probability distribution function | |
| qf | quantile function |
| RMSE | root mean squared error |
| SE | standard error |
| SINAN | sistema de informação de agravos de notificação |
| T-X | transformer-transformer generator |
| Cramér-von Misses |
References
- Joseph, J.; Gillariose, J. A novel discrete Slash family of distributions with application to epidemiology informatics data. Int. J. Data Sci. Anal. 2024, 1–17. [Google Scholar] [CrossRef]
- Li, Y.; Dou, Q.; Lu, Y.; Xiang, H.; Yu, X.; Liu, S. Effects of ambient temperature and precipitation on the risk of dengue fever: A systematic review and updated meta-analysis. Environ. Res. 2020, 191, 110043. [Google Scholar] [CrossRef]
- Lim, J.T.; Dickens, B.S.L.; Cook, A.R. Modelling the epidemic extremities of dengue transmissions in Thailand. Epidemics 2020, 33, 100402. [Google Scholar] [CrossRef]
- Diop, A.; Deme, E.H.; Diop, A. zero-inflated generalized extreme value regression model for binary response data and application in health study. J. Stat. Comput. Simul. 2023, 93, 1–24. [Google Scholar] [CrossRef]
- Marani, M.; Katul, G.G.; Pan, W.K.; Parolari, A.J. Intensity and frequency of extreme novel epidemics. Proc. Natl. Acad. Sci. USA 2021, 35, e2105482118. [Google Scholar] [CrossRef]
- Thomas, M.; RootzÉn, H. Real-time prediction of severe influenza epidemics using extreme value statistics. J. R. Stat. Soc. Ser. C Appl. Stat. 2022, 71, 376–394. [Google Scholar] [CrossRef]
- Lin, H.; Zhang, Z. Extreme co-movements between infectious disease events and crude oil futures prices: From extreme value analysis perspective. Energy Econ. 2022, 110, 106054. [Google Scholar] [CrossRef]
- Tian, N.; Zheng, J.-X.; Guo, Z.-Y.; Li, L.-H.; Xia, S.; Lv, S.; Zhou, X.-N. Dengue incidence trends and its burden in major endemic regions from 1990 to 2019. Trop. Med. Infect. Dis. 2022, 7, 180. [Google Scholar] [CrossRef]
- Lun, X.; Wang, Y.; Zhao, C.; Wu, H.; Zhu, C.; Ma, D.; Xu, M.; Wang, J.; Liu, Q.; Xu, L.; et al. Epidemiological characteristics and temporal-spatial analysis of overseas imported dengue fever cases in outbreak provinces of China, 2005–2019. Infect. Dis. Poverty 2022, 11, 12. [Google Scholar] [CrossRef]
- Sandeep, M.; Padhi, B.K.; Yella, S.S.T.; Sruthi, K.G.; Venkatesan, R.G.; Sasanka, K.S.; Krishna, B.S.; Satapathy, P.; Mohanty, A.; Al-Tawfiq, J.A.; et al. Myocarditis manifestations in dengue cases: A systematic review and meta-analysis. J. Infect. Public Health 2023, 16, 1761–1768. [Google Scholar] [CrossRef]
- de Oliveira-Júnior, J.F.; Souza, A.; Abreu, M.C.; Nunes, R.S.C.; Nascimento, L.S.; Silva, S.D.; Correia Filho, W.L.F.; Silva, E.B. Modeling of dengue by cluster analysis and probability distribution functions in the state of Alagoas in Brazilian. Braz. Arch. Biol. Technol. 2023, 66, e23220086. [Google Scholar] [CrossRef]
- Qoshja, A.; Muça, M. A new modified generalized odd log-logistic distribution with three parameters. Math. Theory Model. 2018, 8, 2224–5804. Available online: https://www.researchgate.net/publication/331483356_A_NEW_MODIFIED_GENERALIZED_ODD_LOG-LOGISTIC_DISTRIBUTION_WITH_THREE_PARAMETERS (accessed on 28 June 2024).
- Afify, A.Z.; Suzuki, A.K.; Zhang, C.; Nassar, M. On three-parameter exponential distribution: Properties, Bayesian and non-Bayesian estimation based on complete and censored samples. Commun. Stat.-Simul. Comput. 2021, 50, 3799–3819. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Alizadeh, M.; Ozel, G.; Hosseini, B.; Ortega, E.M.M.; Altun, E. The generalized odd log-logistic family of distributions: Properties, regression models and applications. J. Stat. Comput. Simul. 2017, 87, 908–932. [Google Scholar] [CrossRef]
- da Costa, N.S.S.; Cordeiro, G.M. A new normal regression with medical applications. Appl. Math. Inf. Sci. 2023, 17, 309–322. [Google Scholar] [CrossRef]
- da Costa, N.S.S.; do Carmo, M.d.C.S.; Cordeiro, G.M. Analyzing county-level COVID-19 vaccination rates in Texas: A new Lindley regression model. COVID 2023, 3, 1761–1780. [Google Scholar] [CrossRef]
- Alzaatreh, A.; Lee, C.; Famoye, F. A new method for generating families of continuous distributions. Metron 2013, 71, 63–79. [Google Scholar] [CrossRef]
- Gleaton, J.U.; Lynch, J.D. Properties of generalized log-logistic families of lifetime distributions. J. Probab. Stat. Sci. 2006, 4, 51–64. Available online: https://www.researchgate.net/publication/283595537_Properties_of_generalized_log-logistic_families_of_lifetime_distributions (accessed on 28 June 2024).
- Gupta, R.C.; Gupta, R.D. Proportional reversed hazard rate model and its applications. J. Stat. Plan. Inference 2007, 137, 3525–3536. [Google Scholar] [CrossRef]
- Gupta, R.C.; Gupta, R.D. Exponentiated exponential family: An alternative to gamma and Weibull distributions. Biom. J. J. Math. Methods Biosci. 2001, 43, 117–130. [Google Scholar] [CrossRef]
- R Core Team. R Core Team: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2024. [Google Scholar]
- Cox, D.R.; Snell, E.J. A general definition of residuals. J. R. Stat. Soc. Ser. B (Methodol.) 1968, 30, 248–275. [Google Scholar] [CrossRef]
- Cook, R.D.; Weisberg, S. Residuals and Influence in Regression; Chapman & Hall: London, UK, 1982. [Google Scholar]
- Ortega, E.M.M.; Paula, G.A.; Bolfarine, H. Deviance residuals in generalized log-gamma regression models with censored observations. J. Stat. Comput. Simul. 2008, 78, 747–764. [Google Scholar] [CrossRef]
- Silva, G.O.; Ortega, E.M.M.; Paula, G.A. Residuals for log-Burr XII regression models in survival analysis. J. Appl. Stat. 2011, 38, 1435–1445. [Google Scholar] [CrossRef]
- Atkinson, A.C. Plots, Transformations, and Regression: An Introduction to Graphical Methods of Diagnostic Regression Analysis; Clarendon Press: Oxford, UK, 1987. [Google Scholar] [CrossRef]
- Mead, M.E.A. A note on Kumaraswamy Fréchet distribution. Australia 2014, 8, 294–300. Available online: http://www.ajbasweb.com/old/ajbas/2014/September/294-300.pdf (accessed on 28 June 2024).
- Adepoju, K.A.; Chukwu, O.I. Maximum likelihood estimation of the Kumaraswamy exponential distribution with applications. J. Mod. Appl. Stat. Methods 2015, 14, 208–214. [Google Scholar] [CrossRef]
- Silva, R.; Andrade, T.; Maciel, D.; Campos, R.; Cordeiro, G. A new lifetime model: The gamma extended Frechet distribution. J. Stat. Theory Appl. 2013, 12, 39. [Google Scholar] [CrossRef]
- Kudriavtsev, A.A. On the representation of gamma-exponential and generalized negative binomial distributions. Inform. Its Appl. 2019, 13, 76–80. [Google Scholar] [CrossRef]
- Nadarajah, S.; Kotz, S. The beta exponential distribution. Reliab. Eng. Syst. Saf. 2006, 91, 689–697. [Google Scholar] [CrossRef]
- Fréchet, M. Sur La Loi de Probabilité de L’écart Maximum. Annales de La Societe Polonaise de Mathematique. Available online: https://cir.nii.ac.jp/crid/1572261550191409280 (accessed on 28 June 2024).
- Marinho, P.R.D.; Silva, R.B.; Bourguignon, M.; Cordeiro, G.M.; Nadarajah, S. AdequacyModel: An R package for probability distributions and general purpose optimization. PLoS ONE 2019, 14, e0221487. [Google Scholar] [CrossRef]

| Sub-Model | ||
|---|---|---|
| - | 1 | Generalized log-logistic family [18] |
| 1 | - | Proportional reversed hazard rate family [19] |
| 1 | 1 | Baseline |
| Sub-Model | ||
|---|---|---|
| - | 1 | Odd log-logistic exponential (OLLE) distribution, see [18] |
| 1 | - | Exponentiated-exponential (EE) distribution, see [20] |
| 1 | 1 | Exponential (E) distribution |
| Scenario 1—GOLLE (0.67, 1.40, 1.25) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Par | n = 50 | n = 150 | n = 300 | ||||||
| AE | AB | RMSE | AE | AB | RMSE | AE | AB | RMSE | |
| 0.817 | 0.147 | 0.750 | 0.742 | 0.072 | 0.381 | 0.724 | 0.054 | 0.292 | |
| 2.609 | 1.209 | 3.157 | 1.756 | 0.356 | 1.194 | 1.557 | 0.157 | 0.728 | |
| 1.729 | 0.479 | 1.364 | 1.393 | 0.143 | 0.713 | 1.307 | 0.057 | 0.508 | |
| Par | n = 500 | n = 750 | n = 1000 | ||||||
| 0.707 | 0.037 | 0.212 | 0.676 | 0.006 | 0.155 | 0.681 | 0.011 | 0.135 | |
| 1.477 | 0.077 | 0.537 | 1.496 | 0.096 | 0.433 | 1.452 | 0.052 | 0.351 | |
| 1.269 | 0.019 | 0.392 | 1.301 | 0.051 | 0.317 | 1.273 | 0.023 | 0.267 | |
| Scenario 2—GOLLE (0.22, 1.13, 7.50) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Par | n = 50 | n = 150 | n = 300 | ||||||
| 0.261 | 0.041 | 0.185 | 0.240 | 0.020 | 0.104 | 0.231 | 0.011 | 0.063 | |
| 1.413 | 0.283 | 0.877 | 1.212 | 0.082 | 0.465 | 1.151 | 0.021 | 0.308 | |
| 9.167 | 1.667 | 5.438 | 7.954 | 0.454 | 2.990 | 7.655 | 0.155 | 2.206 | |
| Par | n = 500 | n = 750 | n = 1000 | ||||||
| 0.223 | 0.003 | 0.044 | 0.224 | 0.004 | 0.040 | 0.222 | 0.002 | 0.030 | |
| 1.155 | 0.025 | 0.223 | 1.141 | 0.011 | 0.197 | 1.141 | 0.011 | 0.156 | |
| 7.625 | 0.125 | 1.448 | 7.577 | 0.077 | 1.214 | 7.589 | 0.089 | 1.008 | |
| Distribution | Reference |
|---|---|
| Kumaraswamy-Fréchet (KwFr) | [27] |
| Kumaraswamy-Exponential (KwE) | [28] |
| Gamma-Fréchet (GFr) | [29] |
| Gamma-Exponentital (GE) | [30] |
| Beta-Exponentital (BE) | [31] |
| Fréchet (Fr) | [32] |
| Variable | Min. | Max. | Mean | Median | SD | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| DG | 277 | 6726 | 1483 | 752 | 1445.35 | 1.509 | 4.998 |
| Model | Parameters | KS | |||||
|---|---|---|---|---|---|---|---|
| GOLLE † () | 0.154 | 76.500 | 5.402 | 0.060 | 0.400 | 0.077 | |
| (0.018) | (0.019) | (0.003) | (0.914) | ||||
| OLLE() | 1.180 | 1 | 0.634 | 0.318 | 1.929 | 0.160 | |
| (0.142) | (-) | (0.086) | (0.145) | ||||
| EE() | 1 | 1.391 | 0.830 | 0.313 | 1.898 | 0.175 | |
| (-) | (0.284) | (0.147) | (0.088) | ||||
| E() | 1 | 1 | 0.674 | 0.316 | 1.913 | 0.170 | |
| (-) | (-) | (0.096) | (0.103) | ||||
| KwFr() | 3.851 | 51.070 | 0.172 | 0.271 | 0.087 | 0.559 | 0.097 |
| (1.409) | (71.389) | (0.060) | (0.008) | (0.705) | |||
| KwE() | 4.500 | 0.151 | 5.402 | 0.242 | 1.482 | 0.205 | |
| (0.005) | (0.022) | (0.003) | (0.028) | ||||
| GFr() | 0.465 | 0.777 | 0.225 | 0.128 | 0.830 | 0.120 | |
| (0.082) | (0.142) | (0.039) | (0.443) | ||||
| BE() | 3.027 | 0.150 | 5.402 | 0.253 | 1.548 | 0.197 | |
| (1.054) | (0.023) | (0.003) | (0.038) | ||||
| GE() | 1.323 | 0.892 | 0.317 | 1.917 | 0.173 | ||
| (0.241) | (0.197) | (0.096) | |||||
| Fr() | 1.791 | −0.281 | 0.235 | 1.449 | 0.173 | ||
| (0.285) | (0.076) | (0.094) | |||||
| Models | Statistic w | p-Value |
|---|---|---|
| GOLLE vs. E | 29.657 | <0.0001 |
| GOLLE vs. EE | 27.143 | <0.0001 |
| GOLLE vs. OLLE | 27.937 | <0.0001 |
| Model | Parameters | KS | ||||
|---|---|---|---|---|---|---|
| LGOLLE † () | 0.1517 | 78.7499 | 5.2352 | 0.054 | 0.3664 | 0.0862 |
| (0.0178) | (0.0274) | (0.0034) | (0.8293) | |||
| LOLLE() | 1.1798 | 1 | 7.3631 | 0.3184 | 1.9289 | 0.1601 |
| (0.1423) | (-) | (0.1353) | (0.1453) | |||
| LEE() | 1 | 1.3911 | 7.0935 | 0.3132 | 1.8975 | 0.1750 |
| (-) | (0.2839) | (0.1769) | (0.0879) | |||
| LE() | 1 | 1 | 7.3019 | 0.3161 | 1.9131 | 0.1704 |
| (-) | (-) | (0.1429) | (0.1032) | |||
| Models | Statistic w | p-Value |
|---|---|---|
| LGOLLE vs LE | 29.650 | <0.0001 |
| LGOLLE vs LEE | 27.136 | <0.0001 |
| LGOLLE vs LOLLE | 27.930 | <0.0001 |
| Parameter | Estimate | SE | CI (95%) | p-Value |
|---|---|---|---|---|
| (Fev) | 0.5511 | 0.1836 | (0.1913; 0.9109) | 0.0049 |
| (Mar) | 1.0827 | 0.1909 | (0.7085; 1.4569) | <0.0001 |
| (Apr) | 1.6788 | 0.1764 | (1.3331; 2.0245) | <0.0001 |
| (May) | 1.7125 | 0.1822 | (1.3554; 2.0696) | <0.0001 |
| (Jun) | 1.4393 | 0.2262 | (0.9960; 1.8826) | <0.0001 |
| (Jul) | 0.3091 | 0.1935 | (−0.0702; 0.6884) | <0.1192 |
| (Ago) | −0.5881 | 0.2006 | (−0.9813; −0.1949) | 0.0059 |
| (Sep) | −0.4623 | 0.1723 | (−0.8000; −0.1246) | 0.0110 |
| (Oct) | −0.5778 | 0.1776 | (−0.9259; −0.2297) | 0.0025 |
| (Nov) | −0.5749 | 0.1802 | (−0.9281; −0.2217) | 0.0030 |
| (Dec) | −0.1612 | 0.1928 | (−0.5391; 0.2167) | 0.4088 |
| 47.1443 | 6.4074 | (34.5861; 59.7026) | - | |
| 0.0751 | 0.0054 | (0.0645; 0.0857) | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
da Costa, N.S.S.; Lima, M.d.C.S.d.; Cordeiro, G.M. A Bimodal Exponential Regression Model for Analyzing Dengue Fever Case Rates in the Federal District of Brazil. Mathematics 2024, 12, 3386. https://doi.org/10.3390/math12213386
da Costa NSS, Lima MdCSd, Cordeiro GM. A Bimodal Exponential Regression Model for Analyzing Dengue Fever Case Rates in the Federal District of Brazil. Mathematics. 2024; 12(21):3386. https://doi.org/10.3390/math12213386
Chicago/Turabian Styleda Costa, Nicollas S. S., Maria do Carmo Soares de Lima, and Gauss Moutinho Cordeiro. 2024. "A Bimodal Exponential Regression Model for Analyzing Dengue Fever Case Rates in the Federal District of Brazil" Mathematics 12, no. 21: 3386. https://doi.org/10.3390/math12213386
APA Styleda Costa, N. S. S., Lima, M. d. C. S. d., & Cordeiro, G. M. (2024). A Bimodal Exponential Regression Model for Analyzing Dengue Fever Case Rates in the Federal District of Brazil. Mathematics, 12(21), 3386. https://doi.org/10.3390/math12213386








