Attack-Dependent Adaptive Event-Triggered Security Fuzzy Control for Nonlinear Networked Cascade Control Systems Under Deception Attacks

Abstract

This article investigates the issue of $H_{\infty }$ security output feedback control for a nonlinear networked cascade control system with deception attacks. First, to further reduce the amount of communication data, reasonably schedule network resources, and alleviate the impact of multi-channel deception attacks, an attack-dependent adaptive event-triggered mechanism is introduced into the primary network channel, and its adaptive triggered threshold can be adjusted according to the random attack probability. Secondly, the output dynamic quantization of the secondary network channel is considered. Then, a novel security cascade output feedback controller design framework based on the Takagi–Sugeno (T-S) fuzzy networked cascade control system under deception attacks is established. In addition, by introducing the Lyapunov–Krasovskii stability theory, the design conditions of the controller are given. Finally, the effectiveness and superiority of the proposed design strategies are verified by two simulation examples of power plant boiler–turbine system and power plant boiler power generation control system.

1. Introduction

Since the cascade control strategy was proposed [1], it has become an effective means to optimize the control system performance. Especially in the presence of external disturbances, the performance improvement effect is remarkable. The cascade control systems are composed of two subsystems in series, which are divided into the primary loop and the secondary loop. Since the secondary loop has a faster response speed than the primary loop, the secondary loop can effectively suppress the system disturbance, and the primary loop is responsible for adjusting the steady-state performance of the system [2]. It is precisely because the cascade control system has the advantages of reducing the disturbance of the secondary loop and improving the control quality, that the cascade control strategy is widely used in many industrial production process controls such as heat exchange systems [3] and cyber-physical systems [4].

In recent years, networked control systems (NCSs) have been widely used in intelligent transportation, intelligent manufacturing, and daily life due to their advantages of low cost, space saving, and easy maintenance [5,6,7]. Compared with the cascade control systems that do not transmit signal through the network, the networked cascade control systems (NCCSs) of signals transmission through the network combine the advantages of cascade control systems and NCSs. Based on this, many studies related to NCCSs have been published; for example, in [8], a passivity-based $H_{\infty }$ controller design method for NCCSs was proposed and verified by a boiler–turbine system. The issue of $H_{\infty }$ control for NCCSs with uncertain time-delay was considered in [9]. However, the open network environment may lead to many important data being eavesdropped or maliciously attacked, which will lead to unreliable or unavailable communication data, and even serious security incidents [10]. Therefore, the problem of security controller design for NCCSs in practical engineering applications has attracted the attention of many scholars, and some results have been published. For example, in [11], a novel design method of networked cascade controller based on event-triggered control was proposed under stochastic nonlinear constraints and actuator faults. Considering the denial-of-service (DoS) attacks and the possible saturation problem of the actuator, the event-triggered controller of the NCCS was investigated in [12]. By proposing a switching method, the $H_{\infty }$ stabilization problem of event-triggered NCCSs under DoS attacks was proposed in [13].

However, in the cascade security control strategy studied above, only the threat of DoS attacks to the system was concerned. Unlike the purpose of DoS attacks to block data transmission by occupying network bandwidth, deception attacks mainly achieve the purpose of attack by destroying the integrity and availability of transmitted data. At the same time, it is more covert and sensitive than DoS attacks. After the transmitted data are tampered with by the attacker, it is difficult for the data receiver to detect [14]. Furthermore, deception attacks can also be subdivided into: (1) false data injection attacks [15,16,17]; that is, the attacker knows the system state information, and (2) replay attacks [18]; that is, the attacker is unknown to the system state information. In addition, it is worth noting that stealth attacks can also be regarded as a kind of covert false data injection attacks with better concealment [19].

In this article, we focus on the study of random deception attacks in which the attacker knows the system state information in advance, such as [20], considering the influence of primary loop random deception attacks and actuator saturation, and the $H_{\infty }$ control problem of NCCSs based on hybrid drive mechanism was studied. However, most of the existing literature only focuses on the threat of deception attacks on a single channel, and the research on deception attacks on any multi-channel is not sufficient [21,22], especially the security control problem of NCCSs under the threat of multi-channel deception attacks. Malicious adversaries that launch deception attacks on any multi-channel will seriously damage the integrity of the data transmitted by the main loop and the secondary loop of the NCCSs, thus affecting the adjustment of the entire NCCSs and affecting the performance and stability of the NCCSs. Therefore, the security cascade control strategy under the threat of arbitrary multi-channel deception attacks deserves further study.

In addition, we review the existing cascade control strategies based on event-triggered mechanism (ETM) under the influence of network attacks [8,13,14,20]. The design of event-triggered conditions or triggered thresholds only considers system-related information and ignores the impact of network attack sequences on event-triggered results. How to design the attacks-dependent adaptive ETM (ADAETM), obtain more stringent triggered conditions, and enhance the non-vulnerability of the triggered mechanism is a proposition worth exploring. On the other hand, the secondary network channel of the NCCSs also needs attention due to the transmission delay, packet disorder, and other threats caused by bandwidth constraints. Therefore, it is necessary to dynamically quantify the transmission signal of the secondary network channel. In recent years, many results on the controller and filter design of NCCSs under the joint framework of event-triggered and quantizer strategies have been published [23,24,25,26,27]. This inspires us to further explore the joint design method of ADAETM and dynamic quantization for NCCSs.

As an effective modeling method for nonlinear systems, the T-S fuzzy model is based on the principle of fuzzy logic. By setting appropriate membership functions (MFs), a series of local subsystems were smoothly connected to approximate the nonlinear systems [28]. Due to the advantages of the T-S fuzzy model, the related research results based on T-S fuzzy systems are remarkable, especially the control synthesis and filter design of nonlinear NCCSs in recent years [27,29,30,31,32,33]. For instance, the security fuzzy controller design problem of nonlinear NCCSs based on event-triggered and quantization strategy was studied in the network attacks environment [27]. The reachable set control problem for the T-S fuzzy singular Markov jump system was studied in [31]. Considering the DC microgrid system based on T-S fuzzy model, the security fuzzy control strategy under the influence of time-constrained DoS attacks was given in [32]. Moreover, considering the unmeasurable or unavailable state variables in NCCs, the output feedback control strategy is more reasonable than the state feedback control strategy and closer to the practical application background. The excellent results of NCSs output feedback have been reported in [34,35,36,37]. For example, in [34], the quantized output feedback security tracking controller design problem was studied, and a novel design framework was given. Considering the problem of time delay and packet loss, ref. [36] designed a output feedback controller under finite-time stability for NCCS. However, it is found that the output feedback control problem of nonlinear NCCS based on the T-S fuzzy model has not been solved in the existing literature, which inspires this work.

On the basis of the above existing research works, we will consider the design of fuzzy security cascade output feedback controller (SCOFC) based on ADAETM for the nonlinear NCCSs under the multi-channel deception attacks and secondary-loop signal dynamic quantization. The contributions of the proposed design strategy are as follows:

1.

Different from the results of single-channel deception attacks in [20,27], this article focuses on the multi-channel deception attacks from the primary sensor to the primary controller communication link and from the secondary controller to the actuator communication link.

2.

A novel ADAETM is proposed. Its adaptive law can flexibly adjust the adaptive triggered threshold by random deception attacks probability, which further alleviates the impact of deception attacks on the NCCS.

3.

Compared with [8,9,11,12,13,20,26,27], the signal dynamic quantization of the secondary loop channel is considered for the first time. The data transmission amount of the secondary network channel is reduced, and the network channel burden is further reduced.

4.

A novel SCOFC design strategy is proposed under the framework of ADAETM, dynamic quantization, and deception attacks. Based on this framework, the theoretical results of the developed security fuzzy controller are expressed by linear matrix inequalities (LMIs), and the mean square asymptotically stable with $H_{\infty }$ performance is ensured for the resulting system.

The structure of the follow-up research content of this article is as follows. The problem formulation of SCOFC is given in Section 2. In Section 3, the novel SCOFC design strategy and design results are given by LMIs. In Section 4, two simulation examples of power plant boiler–turbine system (PPBTS) and power plant boiler power generation control system (PPBPGCS) are shown the effectiveness of the proposed design strategy. The main conclusion of the article is concluded in Section 5.

Notations: Let ${\mathbb{R}}^n$ and ${\mathbb{R}}^{m\times n}$ represent the n-dimensional Euclidean space and the $m\times n$ real matrices sets, respectively. The matrices ${\mathcal{N}}^T$ and ${\mathcal{N}}^{-1}$ denote the matrix $\mathcal{N}$ transposition and inverse, respectively. $\mathrm{diag}\{·\}$ stands for the block-diagonal matrix and ${\mathbf{I}}_n$, ${\mathbf{0}}_n$ represent the n columns identity matrices and zero matrices with appropriate dimensions, respectively. Let ${\mathcal{H}}_e\left\{\mathcal{N}\right\}$ denotes $\mathcal{N}+{\mathcal{N}}^T$, and $l_2[0,\infty )$ stands for the square-integrable function space. The symbol $i\in ⟨r⟩$ means that $i=1,2,3,\dots ,r$.

2. Problem Formulation

This article is concerned with security control for nonlinear NCCSs. As shown in Figure 1, the nonlinear NCCS is described by the T-S fuzzy model, which is mainly composed of primary and secondary systems in series. The primary loop consists of primary plant–${\mathrm{Plant}}^1$, primary sensor–${\mathrm{Sensor}}^1$, primary controller–${\mathrm{Controller}}^1$, and actuator. The secondary loop consists of secondary plant–${\mathrm{Plant}}^2$, secondary sensor–${\mathrm{Sensor}}^2$, secondary controller–${\mathrm{Controller}}^2$, and actuator.

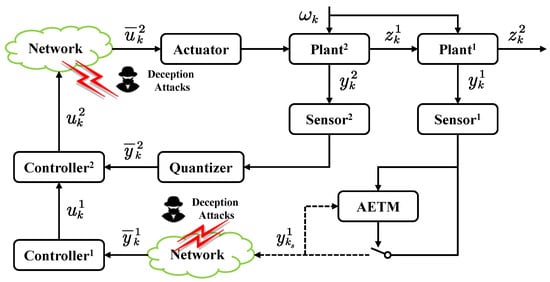
Figure 1. Framework of an NCCS under deception attacks.

Combining the advantages of NCCSs and traditional cascade control systems, the definition of NCCSs is mainly reflected in the sensor–controller, and the data between the controller and actuator are transmitted through the wireless network. Considering the characteristics of the NCCS, a dynamic quantizer is introduced in the secondary loop, and an ADAETM is introduced in the primary loop. At the same time, the risk of deception attacks from primary sensor–${\mathrm{Sensor}}^1$ to primary controller–${\mathrm{Controller}}^1$ and from secondary sensor–${\mathrm{Sensor}}^2$ to actuator is considered.

2.1. System Description

In the nonlinear NCCS, the discrete-time T-S fuzzy primary system–${\mathrm{Plant}}^1$ is described as follows:

${\mathrm{Plant}}^1\mathrm{Rule}i$: $\mathbf{IF}$ $d_1\left(x_k^1\right)$ is ${\mathcal{D}}_1^i,\dots$, and $d_p\left(x_k^1\right)$ is ${\mathcal{D}}_p^i$, $\mathbf{THEN}$

$$\left\{\begin{array}{cc}\hfill x_{k+1}^1& =A_{1i}{x}_k^1+B_{1i}{z}_k^2\hfill \\ \hfill z_k^1& =C_{1i}{x}_k^1+D_{1i}{\omega }_k\hfill \\ \hfill y_k^1& =E_{1i}{x}_k^1\hfill \end{array}\right.$$

(1)

where ${\mathcal{D}}_l^i(i\in ⟨r⟩,l\in ⟨p⟩)$ denotes the fuzzy sets, $d_l\left(x_k^1\right)$ is premise variable and $d\left(x_k^1\right)=[d_1\left(x_k^1\right)\dots d_p\left(x_k^1\right)]$; $x_k^1\in {\mathbb{R}}^{n_{x^1}}$, $z_k^1\in {\mathbb{R}}^{n_{z^1}}$, $y_k^1\in {\mathbb{R}}^{n_{y^1}}$ and $z_k^2\in {\mathbb{R}}^{n_{z^2}}$ denote the state vector, measured output, regulated output of ${\mathrm{Plant}}^1$, and the measurement output of ${\mathrm{Plant}}^2$, respectively; ${\omega }_k\in {\mathbb{R}}^{n_{\omega }}$ belongs to $l_2[0,\infty )$ and represents the exogenous disturbances. $A_{1i}$, $B_{1i}$, $C_{1i}$, $D_{1i}$, and $E_{1i}$ are the known system matrices of the appropriate dimensions.

By using a standard fuzzy inference approach, the fuzzy primary system (1) is inferred as follows:

$$\left\{\begin{array}{cc}\hfill x_{k+1}^1& ={\displaystyle \sum _{i=1}^r}{g}_i^1\left(d\left(x_k^1\right)\right)[A_{1i}{x}_k^1+B_{1i}{z}_k^2]\hfill \\ \hfill z_k^1& ={\displaystyle \sum _{i=1}^r}{g}_i^1\left(d\left(x_k^1\right)\right)[C_{1i}{x}_k^1+D_{1i}{\omega }_k]\hfill \\ \hfill y_k^1& ={\displaystyle \sum _{i=1}^r}{g}_i^1\left(d\left(x_k^1\right)\right)E_{1i}{x}_k^1\hfill \end{array}\right.$$

(2)

where $g_i^1\left(d\left(x_k^1\right)\right)$ are the normalized MFs satisfying that $g_i^1\left(d\left(x_k^1\right)\right)={\displaystyle \frac{w_i\left(x_k^1\right)}{{\sum }_{i=1}^r{w}_i\left(x_k^1\right)}}\ge 0$, ${\sum }_{i=1}^r{g}_i^1\left(d\left(x_k^1\right)\right)=1$ with $w_i\left(x_k^1\right)={\prod }_{l=1}^q{\mathcal{D}}_l^i\left(d_l\left(x_k^1\right)\right)$ which denotes the MFs of the primary system with premise variable $d_l\left(x_k^1\right)$.

In addition, the introduction of event-triggered strategy in the network channel will lead to the problem of asynchronous signal transmission. And the asynchrony and mismatch of premise variables of the fuzzy primary controller–${\mathrm{Controller}}^1$ are considered.

${\mathrm{Controller}}^1\mathrm{Rule}j$: $\mathbf{IF}$ $d_1\left({\overline{x}}_k^1\right)$ is ${\mathcal{E}}_1^j,\dots$, and $d_p\left({\overline{x}}_k^1\right)$ is ${\mathcal{E}}_p^j$, $\mathbf{THEN}$

$$\begin{array}{c}\hfill u_k^1=K_{1j}{\overline{y}}_k^1\end{array}$$

(3)

where $K_{1j}$ are the ${\mathrm{Controller}}^1$ gains, ${\overline{y}}_k^1$ is the final input of the ${\mathrm{Controller}}^1$ after event-triggered and deception attacks, and $u_k^1\in {\mathbb{R}}^{n_{u^1}}$ denote control input of ${\mathrm{Plant}}^1$. ${\mathcal{E}}_l^j(j\in ⟨r⟩,l\in ⟨p⟩)$ denotes the fuzzy sets, $d_l\left({\overline{x}}_k^1\right)$ is premise variable, and $d\left({\overline{x}}_k^1\right)=[d_1\left({\overline{x}}_k^1\right)\dots d_p\left({\overline{x}}_k^1\right)]$.

By using single-point fuzzification, product reasoning, and the central weighted average defuzzification method, the output form of the fuzzy ${\mathrm{Controller}}^1$ is as follows:

$$\begin{array}{c}\hfill u_k^1={\displaystyle \sum _{j=1}^r}{g}_j^1\left(d\left({\overline{x}}_k^1\right)\right)K_{1j}{\overline{y}}_k^1\end{array}$$

(4)

where $g_j^1\left(d\left({\overline{x}}_k^1\right)\right)$ are the normalized MFs satisfying that $g_j^1\left(d\left({\overline{x}}_k^1\right)\right)={\displaystyle \frac{w_j\left({\overline{x}}_k^1\right)}{{\sum }_{j=1}^r{w}_j\left({\overline{x}}_k^1\right)}}\ge 0$, ${\sum }_{j=1}^r{g}_j^1\left(d\left({\overline{x}}_k^1\right)\right)=1$ with $w_j\left({\overline{x}}_k^1\right)={\prod }_{l=1}^p{\mathcal{E}}_l^j\left(d_l\left({\overline{x}}_k^1\right)\right)$ which denotes the MFs of the ${\mathrm{Controller}}^1$ with premise variable $d_l\left({\overline{x}}_k^1\right)$.

Based on the reconstruction strategy in [22], the asynchronous problem of MFs caused by event-triggered strategy was effectively solved. Suppose the minimum values of $g_j^1\left(d\left(x_k^1\right)\right)>0$ and $g_j^1\left(d\left({\overline{x}}_k^1\right)\right)>0$, the relationship between $g_j^1\left(d\left(x_k^1\right)\right)$ and $g_j^1\left(d\left({\overline{x}}_k^1\right)\right)$ is interpreted as

$$\begin{array}{c}\hfill |g_j^1\left(d\left({\overline{x}}_k^1\right)\right)-g_j^1\left(d\left(x_k^1\right)\right)|\le {\Lambda }_j\end{array}$$

where $g_j^1\left(d\left({\overline{x}}_k^1\right)\right)={\varrho }_j{g}_j^1\left(d\left(x_k^1\right)\right)$, ${\Lambda }_j$ are some positive constants, ${\varrho }_j={\varrho }_j(d\left(x_k^1\right),d\left({\overline{x}}_k^1\right))$ is a parameter related with $g_j^1\left(d\left(x_k^1\right)\right)$, and $g_j^1\left(d\left({\overline{x}}_k^1\right)\right)$.

Based on the conditions mentioned above, one obtains

$$\begin{array}{c}\hfill {\underline{\varrho }}_j=1-{\displaystyle \frac{{\Lambda }_j}{g_j^1\left(d\left(x_k^1\right)\right)}}\le {\varrho }_j\le 1+{\displaystyle \frac{{\Lambda }_j}{g_j^1\left(d\left(x_k^1\right)\right)}}={\overline{\varrho }}_j\end{array}$$

(5)

where ${\underline{\varrho }}_j$ and ${\overline{\varrho }}_j$ denote the known lower bound and upper bound of ${\varrho }_j$, which yields that

$$\begin{array}{c}\hfill {\displaystyle \frac{{\underline{\varrho }}_j}{{\overline{\varrho }}_j}}\triangleq {\displaystyle \frac{min\left\{{\varrho }_i\right\}}{max\left\{{\varrho }_j\right\}}}\le {\displaystyle \frac{{\varrho }_i}{{\varrho }_j}}\le {\displaystyle \frac{max\left\{{\varrho }_i\right\}}{min\left\{{\varrho }_j\right\}}}\triangleq {\displaystyle \frac{{\overline{\varrho }}_j}{{\underline{\varrho }}_j}}.\end{array}$$

Setting ${\varrho }_{min}=min\left\{{\underline{\varrho }}_j\right\}$ and ${\varrho }_{max}=max\left\{{\overline{\varrho }}_j\right\}$ for i, $j\in ⟨r⟩$, one has

$$\begin{array}{c}\hfill {\vartheta }_1\triangleq {\displaystyle \frac{{\varrho }_{min}}{{\varrho }_{max}}}\le {\displaystyle \frac{{\varrho }_i}{{\varrho }_j}}\le {\displaystyle \frac{{\varrho }_{max}}{{\varrho }_{min}}}\triangleq {\vartheta }_2.\end{array}$$

(6)

In the nonlinear NCCS, the discrete-time T-S fuzzy secondary system–${\mathrm{Plant}}^2$ is described as follows:

${\mathrm{Plant}}^2\mathrm{Rule}q$: $\mathbf{IF}$ $f_1\left(x_k^2\right)$ is ${\mathcal{F}}_1^q,\dots$, and $f_p\left(x_k^2\right)$ is ${\mathcal{F}}_p^q$, $\mathbf{THEN}$

$$\left\{\begin{array}{cc}\hfill x_{k+1}^2& =A_{2q}{x}_k^2+B_{2q}{\overline{u}}_k^2+B_{3q}{\omega }_k\hfill \\ \hfill z_k^2& =C_{2q}{x}_k^2+D_{2q}{\omega }_k\hfill \\ \hfill y_k^2& =E_{2q}{x}_k^2\hfill \end{array}\right.$$

(7)

where ${\mathcal{F}}_l^q(q\in ⟨r⟩,l\in ⟨p⟩)$ denotes the fuzzy sets, $f_l\left(x_k^2\right)$ are fuzzy premise variables and $f\left(x_k^2\right)=[f_1\left(x_k^2\right)\dots f_p\left(x_k^2\right)]$; $x_k^2\in {\mathbb{R}}^{n_{x^2}}$ and ${\overline{u}}_k^2\in {\mathbb{R}}^{n_{u^2}}$ denote the state vector and the final control input of ${\mathrm{Plant}}^2$, respectively; The remaining parameters are defined with reference to ${\mathrm{Plant}}^1$. $A_{2q}$, $B_{2q}$, $B_{3q}$, $C_{2q}$, $D_{2q}$, and $E_{2q}$ are the known system matrices of the appropriate dimensions.

Then, based on fuzzy inference approach, the secondary system–${\mathrm{Plant}}^2$ (7) is inferred as follows:

$$\left\{\begin{array}{cc}\hfill x_{k+1}^2& ={\displaystyle \sum _{q=1}^r}{g}_q^2\left(f\left(x_k^2\right)\right)[A_{2q}{x}_k^2+B_{2q}{\overline{u}}_k^2+B_{3q}{\omega }_k]\hfill \\ \hfill z_k^2& ={\displaystyle \sum _{q=1}^r}{g}_q^2\left(f\left(x_k^2\right)\right)[C_{2q}{x}_k^2+D_{2q}{\omega }_k]\hfill \\ \hfill y_k^2& ={\displaystyle \sum _{q=1}^r}{g}_q^2\left(f\left(x_k^2\right)\right)E_{2q}{x}_k^2\hfill \end{array}\right.$$

(8)

where $g_q^2\left(f\left(x_k^2\right)\right)$ are the normalized MFs satisfying that $g_q^2\left(f\left(x_k^2\right)\right)={\displaystyle \frac{w_q\left(x_k^2\right)}{{\sum }_{q=1}^r{w}_q\left(x_k^2\right)}}\ge 0$, ${\sum }_{q=1}^r{g}_q^2\left(f\left(x_k^2\right)\right)=1$ with $w_q\left(x_k^2\right)={\prod }_{l=1}^p{\mathcal{F}}_l^q\left(f_l\left(x_k^2\right)\right)$ denotes the MFs of the system with premise variable $f_l\left(x_k^2\right)$.

The model of secondary controller–${\mathrm{Controller}}^2$ considering quantization in network channel is given as follows:

$$\begin{array}{c}\hfill u_k^2=K_2{\overline{y}}_k^2+u_k^1\end{array}$$

(9)

where $K_2$ is the ${\mathrm{Controller}}^2$ gain and ${\overline{y}}_k^2$ is the quantized system measurement output.

2.2. Dynamic Quantizer

In this article, consider the following form of dynamic quantizer:

$$\begin{array}{c}\hfill q_{\mu }\left({\nu }_k\right)={\mu }_{k}q\left({\displaystyle \frac{{\nu }_k}{{\mu }_k}}\right),{\mu }_k>0\end{array}$$

(10)

where ${\mu }_k$ is the dynamic parameter and suppose that the dynamic quantizer (10) satisfies the following constraints:

$$\begin{array}{cc}\hfill & \parallel q\left({\nu }_k\right)-{\nu }_k\parallel \le \Delta ,if\parallel {\nu }_k\parallel \le M\hfill \end{array}$$

(11a)

$$\begin{array}{cc}\hfill & \parallel q\left({\nu }_k\right)\parallel >M-\Delta ,if\parallel {\nu }_k\parallel >M\hfill \end{array}$$

(11b)

where $M>0$ and $\Delta >0$ represent the quantization range and quantization error bound of dynamic quantizer, respectively.

Then, the quantized measurement output signal of ${\mathrm{Plant}}^2$ is in the following form:

$$\begin{array}{c}\hfill {\overline{y}}_k^2=q_{\mu }\left(y_k^2\right)={\mu }_{k}q\left({\displaystyle \frac{y_k^2}{{\mu }_k}}\right)=h_k^{\mu }+y_k^2\end{array}$$

(12)

where $q_{\mu }(\ast )$ is a dynamic quantizer defined by (10), and $h_k^{\mu }={\mu }_k(q\left({\displaystyle \frac{y_k^2}{{\mu }_k}}\right)-{\displaystyle \frac{y_k^2}{{\mu }_k}})$. The measurement output signal quantization process and parameter update of dynamic quantizer are shown in Algorithm 1.

Remark 1. 

Due to the introduction of network in cascade control systems, it is necessary to consider the network phenomenon of each loop. Different from the existing literature [8,9,11,12,13,20,26,27], this article considers the signal quantization problem of the secondary loop for the first time. In addition, in order to balance the number of packets and quantization error in the network signal, based on the method proposed in [34], the quantization error term can be well processed.

Algorithm 1 Calculation of ${\mu }_k$ and ${\overline{y}}_k^2$ in dynamic quantizer

Input:  $\Delta$, M, and ℏ Output:  ${\mu }_k$, $h_k^{\mu }$ and ${\overline{y}}_k^2$ Step 1: At the sampling instant k, the dynamic quantizer receives $y_k^2$. if  $\parallel y_k^2/{\mu }_k\parallel \le M$   then    $\parallel q(y_k^2/{\mu }_k)-(y_k^2/{\mu }_k)\parallel \le \Delta$ else    $\parallel q(y_k^2/{\mu }_k)\parallel >M-\Delta$ end if Step 2: Update dynamic parameter ${\mu }_k$ and quantization data ${\overline{y}}_k^2$. ${\mu }_k=(\hslash /M)\parallel y_k^2\parallel$, $h_k^{\mu }=[(\hslash \Delta )/M]sin\left(y_k^2\right)$, ${\overline{y}}_k^2=h_k^{\mu }+y_k^2$ Step 3: Let $k=k+1$ and go to Step 1. return  ${\mu }_k$, $h_k^{\mu }$ and ${\overline{y}}_k^2$. The dynamic quantizer parameter ${\mu }_k$ and quantization data ${\overline{y}}_k^2$ are obtained.

2.3. Multi-Channel Deception Attacks

The deception attacks in the NCCSs mainly inject the wrong data into the communication channel intermittently, and replace the real data at the same time, which affect the stability and performance of the systems. Therefore, the security problem of NCCSs interfered by multi-channel deception attacks cannot be ignored.

Considering the characteristics of the deception attacks signals ${\mathfrak{f}}_k^1\in {\mathbb{R}}^{n_{y^1}}$ and ${\mathfrak{f}}_k^2\in {\mathbb{R}}^{n_{u^2}}$, which assumes that the following constraints are satisfied:

$$\begin{array}{c}\hfill \parallel {\mathfrak{f}}_k^1{\parallel }_2\le \parallel {\mathcal{F}}_1{\widehat{y}}_k^1{\parallel }_2,\parallel {\mathfrak{f}}_k^2{\parallel }_2\le {\parallel {\mathcal{F}}_2{u}_k^2\parallel }_2\end{array}$$

(13)

where ${\mathcal{F}}_1$ and ${\mathcal{F}}_2$ are constant matrices denoting the upper bound of the error data function with nonlinear characteristics. Bernoulli variables ${\alpha }_{1k}$ and ${\alpha }_{2k}$ are used to describe the probabilistic characteristics of deception attacks, satisfying

$$\begin{array}{c}\hfill \mathbb{E}\left\{{\alpha }_{\iota k}\right\}={\overline{\alpha }}_{\iota },\mathbb{E}\left\{{({\alpha }_{\iota k}-{\overline{\alpha }}_{\iota })}^2\right\}={\rho }_{\iota }^2,\iota \in ⟨2⟩.\end{array}$$

Then, the signals ${\overline{y}}_k^1$ and ${\overline{u}}_k^2$ transmitted to the communication network after being deception attacks are expressed as follows:

$$\begin{array}{cc}\hfill {\overline{y}}_k^1& ={\alpha }_{1k}{\mathfrak{f}}_k^1+(1-{\alpha }_{1k}){\widehat{y}}_k^1\hfill \\ \hfill {\overline{u}}_k^2& ={\alpha }_{2k}{\mathfrak{f}}_k^2+(1-{\alpha }_{2k})u_k^2.\hfill \end{array}$$

(14)

Remark 2. 

Different from [20,27], this article also considers the impact of deception attacks between the primary loop ${\mathit{Sensor}}^1$ to ${\mathit{Controller}}^1$ network channel and ${\mathit{Controller}}^2$ to actuator network channel. Compared with [20,27], the controller design method proposed in this article under multi-channel deception attacks is closer to the actual situation and more meaningful.

Remark 3. 

It is worth noting that the success of network attacks is random, which is determined by the built-in hardware and software protection in the device, the data transmitted based on the network protocol, and the network conditions with random fluctuation characteristics; that is, network congestion, network load, and so on [17,20]. Therefore, this article discusses random multi-channel deception attacks, and assumes that the deception attacks occur in the primary loop ${\mathit{Sensor}}^1$ to ${\mathit{Controller}}^1$ network channel and ${\mathit{Controller}}^2$ to actuator network channel. At the same time, the way deception attacks destroy data integrity is to completely replace real data with false data attack signals [15] (refer to (14)).

Remark 4. 

It should be further pointed out that the attack signal of the network attacks is generated by the attacker’s strategy formulation of the attack object, so the network attacks may be difficult to detect or undetectable, and the attack signal may be associated with the systems state data, output data, control data, and other information [14]. Referring to the description of the attack signal in [20], the two deception attack signals considered in this article are modeled as nonlinear functions related to the output data of ${\mathit{Plant}}^1$ and the control signal of ${\mathit{Controller}}^2$, respectively, and satisfy the constraints in (13).

2.4. Attacks-Dependent Adaptive Event-Triggered Mechanism

In order to alleviate the impact of deception attacks on the triggered effect and system performance, the following form of ADAETM is given:

$$\begin{array}{c}\hfill k_{s+1}=\underset{k}{inf}\left\{k>k_s|e_{sk}^T\Omega e_{sk}>{\delta }_k{y}_{k_s}^{1T}\Omega y_{k_s}^1\right\}\end{array}$$

(15)

where $e_{sk}=y_{k_s}^1-y_k^1$, $y_k^1$ is the current sampled measurement output and $y_{k_s}^1$ is the latest measurement output signal that satisfies the triggered condition, $\Omega >0$ is the event-triggered weighting matrix to be designed, and ${\delta }_k$ is an adaptive parameter and satisfies the following adaptive law:

$$\begin{array}{c}\hfill {\delta }_k={\delta }_1-{\delta }_2{\displaystyle \frac{2{\overline{\alpha }}_1}{\pi }}\mathrm{atan}({ϵ}_1\parallel y_{k_s}^1{\parallel }^{{ϵ}_2})+{\delta }_{3}exp(-{ϵ}_3\parallel {\Omega }^{{\displaystyle \frac{1}{2}}}{e}_{sk}{\parallel }^{{ϵ}_4})\end{array}$$

where $\mathrm{atan}(\ast )$ is the inverse-tangent function. ${ϵ}_1$, ${ϵ}_2$, ${ϵ}_3$, and ${ϵ}_4$ are the event-triggered threshold adjustment positive parameters. ${\delta }_1$, ${\delta }_2$, and ${\delta }_3$ are known constant thresholds. Then, the ADAETM operating mechanism is shown in Algorithm 2.

Remark 5. 

Considering the influence of deception attacks, attack probability ${\overline{\alpha }}_1$ is introduced to design the random adaptive law ${\delta }_k$. It is obvious that the expression ${\delta }_2{\displaystyle \frac{2{\overline{\alpha }}_1}{\pi }}\mathit{atan}({ϵ}_1\parallel y_{k_s}^1{\parallel }^{{ϵ}_2})$ is always greater than 0. When the attack intensity increases, that is, the attack probability ${\overline{\alpha }}_1$ becomes larger, then the term $-{\delta }_2{\displaystyle \frac{2{\overline{\alpha }}_1}{\pi }}\mathit{atan}({ϵ}_1\parallel y_{k_s}^1{\parallel }^{{ϵ}_2})$ makes the adaptive law ${\delta }_k$ smaller, the triggered condition is easier to meet, so that more sampling data are transmitted to compensate for the impact of the deception attacks. On the other hand, when the communication channel data are transmitted normally, the ${\delta }_k$ will degrade into ${\delta }_1+{\delta }_{3}exp(-{ϵ}_3\parallel {\Omega }^{{\displaystyle \frac{1}{2}}}{e}_{sk}{\parallel }^{{ϵ}_4})$; thus, ${\delta }_k$ will relatively increase. Such changes can make the triggered condition more stringent, help to further reduce the triggered data, and improve resource utilization. The detailed operation process can be understood by Algorithm 2.

Consider the network induced delay ${\eta }_{k_s}$ satisfying ${\eta }_{k_s}\in [0,{\eta }_M)$, where ${\eta }_M$ is a positive integer. Based on the analysis process in [29], define the following:

$$\begin{array}{c}\hfill {\widehat{y}}_k^1=y_{k_s},k\in [k_s+{\eta }_{k_s},k_{s+1}+{\eta }_{k_s+1}-1].\end{array}$$

(16)

Then, the introduced time-varying delay variable ${\tau }_k$ and output data error $e_{sk}$ are expressed as

$$\begin{array}{cc}\hfill {\tau }_k& =\left\{\begin{array}{cc}k-k_s,\hfill & k\in {\mathcal{S}}_0\hfill \\ k-k_s-\ell ,\hfill & k\in {\mathcal{S}}_{\ell }\hfill \\ k-k_s-\overline{\ell },\hfill & k\in {\mathcal{S}}_{\overline{\ell }}\hfill \end{array}\right.\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill e_{sk}& =\left\{\begin{array}{cc}0,\hfill & k\in {\mathcal{S}}_0\hfill \\ y_{k_s}^1-y_{k_s+\ell }^1,\hfill & k\in {\mathcal{S}}_{\ell }\hfill \\ y_{k_s}^1-y_{k_s+\overline{\ell }}^1,\hfill & k\in {\mathcal{S}}_{\overline{\ell }}\hfill \end{array}\right.\hfill \end{array}$$

(18)

where ${\mathcal{S}}_0=[k_s+{\eta }_{k_s},k_s+{\eta }_M+1]$, ${\mathcal{S}}_{\ell }=[k_s+{\eta }_M+\ell ,k_s+{\eta }_M+\ell +1]$, ${\mathcal{S}}_{\overline{\ell }}=[k_s+{\eta }_M+\overline{\ell },k_{s+1}+{\eta }_{k_s+1}-1]$, $\ell =1,2,\dots ,\overline{\ell }-1$.

Then, the range of ${\tau }_k$ is as follows:

$$\begin{array}{c}\hfill 0<{\eta }_{k_s}\le {\tau }_k\le 1+{\eta }_M=\overline{\tau }\end{array}$$

(19)

where $\overline{\tau }$ is a constant, which is the upper bound of event-triggered data transmission delay. Then, the signal ${\widehat{y}}_k^1$ transmitted to the ${\mathrm{Controller}}^1$ can be obtained as

$$\begin{array}{c}\hfill {\widehat{y}}_k^1=y_{k-{\tau }_k}+e_{sk}.\end{array}$$

(20)

Algorithm 2  Calculation of ${\delta }_k$ and (k, $y_k^1$) in ADAETM

Input:  $\Omega$, ${\overline{\alpha }}_1$, ${\delta }_1$, ${\delta }_2$, ${\delta }_3$, ${ϵ}_1$, ${ϵ}_2$, ${ϵ}_3$, and ${ϵ}_4$. Initial set $k_0=0$, $y_{k_0}^1=0$, $k=1$, $s=0$. Output:  ${\delta }_k$ and (k, $y_k^1$). Step 1: At the sampling instant k, the network channel receives $y_k^1$. if  attack probability ${\overline{\alpha }}_1=0$  then    the term $-{\delta }_2{\displaystyle \frac{2{\overline{\alpha }}_1}{\pi }}\mathrm{atan}({ϵ}_1\parallel y_{k_s}^1{\parallel }^{{ϵ}_2})=0$, ${\delta }_1+{\delta }_{3}exp(-{ϵ}_3\parallel {\Omega }^{{\displaystyle \frac{1}{2}}}{e}_{sk}{\parallel }^{{ϵ}_4})\Rightarrow {\delta }_k\uparrow$ else if attack probability ${\overline{\alpha }}_1\uparrow$ then    the term ${\delta }_2{\displaystyle \frac{2{\overline{\alpha }}_1}{\pi }}\mathrm{atan}({ϵ}_1\parallel y_{k_s}^1{\parallel }^{{ϵ}_2})\uparrow \Rightarrow {\delta }_k\downarrow$ else    the term ${\delta }_2{\displaystyle \frac{2{\overline{\alpha }}_1}{\pi }}\mathrm{atan}({ϵ}_1\parallel y_{k_s}^1{\parallel }^{{ϵ}_2})\downarrow \Rightarrow {\delta }_k\uparrow$ end if Step 2: Update attacks dependent adaptive law ${\delta }_k$ and data packet if  $e_{sk}^T\Omega e_{sk}>{\delta }_k{y}_{k_s}^{1T}\Omega y_{k_s}^1$   then    the buffer stores the data packet (k, $y_k^1$) with $k_0=k$, $y_{k_0}^1=y_k^1$, releases the data packet to the communication channel else    the data packet is not transmission end if Step 3: Let $k=k+1$ and go to Step 1. return  $k_s$, $y_{k_s}^1$, and ${\delta }_k$. The attacks-dependent adaptive law ${\delta }_k$ and latest output data packet (k, $y_k^1$) are obtained.

2.5. System Formulation

By combining (2), (4), (8), (9), (12), (14), (20), and defining $g_i^1=g_i^1\left(d\left(x_k^1\right)\right)$, $g_j^1=g_j^1\left(d\left({\overline{x}}_k^1\right)\right)$, $g_q^2=g_q^2\left(f\left(x_k^2\right)\right)$, it can yield a new model for NCCSs as follows:

$$\begin{array}{cc}\hfill x_{k+1}^1& ={\displaystyle \sum _{i=1}^r}{\displaystyle \sum _{j=1}^r}{g}_i^1{g}_q^2[A_{1i}{x}_k^1+B_{1i}{C}_{2q}{x}_k^2+B_{1i}{D}_{2q}{\omega }_k]\hfill \\ \hfill x_{k+1}^2& ={\displaystyle \sum _{i=1}^r}{\displaystyle \sum _{j=1}^r}{\displaystyle \sum _{q=1}^r}{g}_i^1{g}_j^1{g}_q^2[(A_{2q}+(1-{\alpha }_{2k})B_{2q}{K}_2{E}_{2q})x_k^2\hfill \\ \hfill & +(1-{\alpha }_{1k})(1-{\alpha }_{2k})B_{2q}{K}_{1j}{E}_{1i}{x}_{k-{\tau }_k}^1\hfill \\ \hfill & +(1-{\alpha }_{1k})(1-{\alpha }_{2k})B_{2q}{K}_{1j}{e}_{sk}\hfill \\ \hfill & +(1-{\alpha }_{2k}){\alpha }_{1k}{B}_{2q}{K}_{1j}{\mathfrak{f}}_k^1+{\alpha }_{2k}{B}_{2q}{\mathfrak{f}}_k^2\hfill \\ \hfill & +(1-{\alpha }_{2k})B_{2q}{K}_2{h}_k^{\mu }+B_{3q}{\omega }_k]\hfill \\ \hfill z_k^1& ={\displaystyle \sum _{i=1}^r}{g}_i^1[C_{1i}{x}_1\left(k\right)+D_{1i}{\omega }_k].\hfill \end{array}$$

(21)

The nonlinear NCCS is considered in this article, and under the influence of multi-channel deception attacks, the ADAETM and dynamic quantizer are introduced, so that the designed SCOFC satisfies the following objectives:

1.

The system (21) is mean square asymptotically stable in the absence of external disturbances, i.e., ${\omega }_k=0$;

2.

Under zero initial conditions, for all ${\omega }_k\ne 0$, there exists a positive scalar $\gamma >0$, such that the following condition holds: ${\sum }_{k=0}^{\infty }{z}_k^{1T}{z}_k^1\le {\gamma }^2{\sum }_{k=0}^{\infty }{\omega }_k^T{\omega }_k$.

3. Main Results

In this section, the design conditions that guarantee the mean square asymptotically stable and $H_{\infty }$ performance of the system (21) are given. Then, the design results of the security fuzzy controller gains under event-triggered and dynamic quantization strategy are given.

Theorem 1. 

For given scalars ${\overline{\alpha }}_1>0$, ${\overline{\alpha }}_2>0$, ${\delta }_1>0$, ${\delta }_2>0$, ${\delta }_3>0$, $\Delta >0$, $M>0$, $\tau >0$, $\overline{\tau }>0$, and ${\vartheta }_j>0(j\in ⟨2⟩)$, the system (21) is mean square asymptotically stable and satisfies the predetermined $H_{\infty }$ performance index γ if there exist positive definite symmetric matrices $P_1$, $P_2$, $Q_1$, $Q_2$, $Q_3$, $R_1$, $R_2$, Ω, and slack matrix $R_3$ with appropriate dimensions, such that the following inequalities hold for $i<j$:

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}{R}_2& \ast \\ R_3& R_2\end{array}\right]& >0\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}{\Pi }_i^{11}& \ast \\ {\Pi }_{iiq}^{21}& {\Pi }_{22}\end{array}\right]& <0\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill \left[\begin{array}{ccc}{\Pi }_i^{11}+{\vartheta }_j{\Pi }_j^{11}& \ast & \ast \\ {\Pi }_{ijq}^{21}& {\Pi }_{22}& \ast \\ \sqrt{{\vartheta }_2}{\Pi }_{jiq}^{21}& 0& {\Pi }_{22}\end{array}\right]& <0,i,j,q\in ⟨r⟩\hfill \end{array}$$

(24)

where

$$\begin{array}{cc}\hfill {\Pi }_i^{11}& =\left[\begin{array}{cc}{\Pi }_i^1& \ast \\ {\Pi }_i^3& {\Pi }_2\end{array}\right],{\Pi }_i^1=\mathit{diag}\{-{\Pi }_1,{\overline{\Pi }}_i^1,-P_2\}\hfill \\ \hfill {\overline{\Pi }}_i^1& =\left[\begin{array}{ccc}{Q}_2-Q_1-R_2& \ast & \ast \\ R_2-R_3& -{\Pi }_{3i}& \ast \\ R_1+R_3& R_2-R_3& -{\Pi }_4\end{array}\right]\hfill \\ \hfill {\Pi }_1& =P_1+R_1-Q_1-Q_3,{\Pi }_4=Q_2+Q_3+R_1+R_2\hfill \\ \hfill {\Pi }_{3i}& =2R_1-{\mathcal{H}}_e\left\{R_3\right\}-\delta E_{1i}^T\Omega E_{1i},\delta ={\delta }_1+{\delta }_2+{\delta }_3\hfill \\ \hfill {\Pi }_i^3& ={\left[{\Pi }_{1i}^{3T}0000\right]}^T,{\Pi }_{1i}^3=[{\mathbf{0}}_2\delta \Omega E_{1i}{\mathbf{0}}_2]\hfill \\ \hfill {\Pi }_2& =\mathit{diag}\left\{(\delta -1)\Omega ,-{\displaystyle \frac{M^2}{{\Delta }^2}}I,-{\overline{\alpha }}_1,-{\overline{\alpha }}_2,-{\gamma }^{2}I\right\}\hfill \\ \hfill {\Pi }_{ijq}^{21T}& =[{\Pi }_{ijq}^{211T},{\Pi }_{ijq}^{212T},{\Pi }_{ijq}^{213T}],{\Pi }_{ijq}^{211}=\left[{\Sigma }_{ijq}^3{\Sigma }_{ijq}^4\right]\hfill \\ \hfill {\Sigma }_{ijq}^3& ={\mathcal{E}}_1{\left[{\Sigma }_i^{31T}{\Sigma }_q^{32T}{\Sigma }_i^{33T}{\Sigma }_{ijq}^{34T}{\Sigma }_{ij}^{35T}\right]}^T\hfill \\ \hfill {\Sigma }_{ijq}^4& ={\mathcal{E}}_1{\left[{\Sigma }_i^{41T}0{\Sigma }^{43T}{\Sigma }_j^{44T}{\Sigma }_j^{45T}\right]}^T\hfill \\ \hfill {\Pi }_{ijq}^{212}& ={\mathcal{E}}_2{\left[{\Sigma }_{iq}^{5T}{\Sigma }_{iq}^{6T}{\Sigma }_{iq}^{6T}\right]}^T,{\Pi }_{ijq}^{213}={\mathcal{E}}_3\left[{\Sigma }_{ijq}^7{\Sigma }_{ijq}^8\right]\hfill \\ \hfill {\Sigma }_i^{31}& =\left[C_{1i}{\mathbf{0}}_4\right],{\Sigma }_q^{32}=\left[{\mathbf{0}}_4{E}_{2q}\right],{\Sigma }_i^{33}=\left[{\mathbf{0}}_2{\mathcal{F}}_1{E}_{1i}{\mathbf{0}}_2\right]\hfill \\ \hfill {\Sigma }_{ijq}^{34}& =\left[{\mathbf{0}}_2{\overrightarrow{\alpha }}_1{\mathcal{F}}_2{K}_{1j}{E}_{1i}0{\mathcal{F}}_2{K}_2{E}_{2q}\right]\hfill \\ \hfill {\Sigma }_{ij}^{35}& =[{\mathbf{0}}_2-K_{1j}{E}_{1i}{\mathbf{0}}_2],{\Sigma }_i^{41}=\left[{\mathbf{0}}_4{D}_{1i}\right],{\Sigma }^{43}=\left[{\mathcal{F}}_1{\mathbf{0}}_4\right]\hfill \\ \hfill {\Sigma }_j^{44}& =\left[{\overrightarrow{\alpha }}_1{\mathcal{F}}_2{K}_{1j}0{\overline{\alpha }}_1{\mathcal{F}}_2{K}_{1j}{\mathbf{0}}_2\right],{\Sigma }_j^{45}=[-K_{1j}0K_{1j}{\mathbf{0}}_2]\hfill \\ \hfill {\Sigma }_{iq}^5& =\left[A_{1i}{\mathbf{0}}_3{B}_{1i}{C}_{2q}{\mathbf{0}}_4{B}_{1i}{D}_{2q}\right]\hfill \\ \hfill {\Sigma }_{iq}^6& =[A_{1i}-I{\mathbf{0}}_3{B}_{1i}{C}_{2q}{\mathbf{0}}_4{B}_{1i}{D}_{2q}]\hfill \\ \hfill {\Sigma }_{ijq}^7& =\left[\begin{array}{ccccc}{\mathbf{0}}_2& {\overrightarrow{\alpha }}_1{\overrightarrow{\alpha }}_2{\mathcal{B}}_{ijq}^1& 0& {\overrightarrow{\alpha }}_2{\mathcal{B}}_q^2& {\overrightarrow{\alpha }}_1{\overrightarrow{\alpha }}_2{\mathcal{B}}_{jq}^3\\ {\mathbf{0}}_2& -{\overrightarrow{\alpha }}_2{\mathcal{B}}_{ijq}^1& 0& 0& -{\overrightarrow{\alpha }}_2{\mathcal{B}}_{jq}^3\\ {\mathbf{0}}_2& -{\overrightarrow{\alpha }}_1{\mathcal{B}}_{ijq}^1& 0& -{\mathcal{B}}_q^2& -{\overrightarrow{\alpha }}_1{\mathcal{B}}_{jq}^3\\ {\mathbf{0}}_2& {\mathcal{B}}_{ijq}^1& 0& -{\mathcal{B}}_q^2& {\mathcal{B}}_{jq}^3\end{array}\right]\hfill \\ \hfill {\Sigma }_{ijq}^8& =\left[\begin{array}{cccc}{\overrightarrow{\alpha }}_2{B}_{2q}{K}_2& {\overrightarrow{\alpha }}_2{\overline{\alpha }}_1{\mathcal{B}}_{jq}^3& {\overline{\alpha }}_2{B}_{2q}& B_{3q}\\ 0& {\overrightarrow{\alpha }}_2{\mathcal{B}}_{jq}^3& 0& 0\\ -B_{2q}{K}_2& -{\overline{\alpha }}_1{\mathcal{B}}_{jq}^3& B_{2q}& 0\\ -B_{2q}{K}_2& -{\mathcal{B}}_{jq}^3& B_{2q}& 0\end{array}\right]\hfill \\ \hfill {\Pi }_{22}& =\mathit{diag}\{{\Pi }_{22}^1,{\Pi }_{22}^2,{\Pi }_{22}^3\},{\overrightarrow{\alpha }}_{\iota }=1-{\overline{\alpha }}_{\iota }\hfill \\ \hfill {\Pi }_{22}^1& =\mathit{diag}\{-I,-I,-I,-I,-I\}\hfill \\ \hfill {\Pi }_{22}^2& =\mathit{diag}\{-P_1^{-1},-R_1^{-1},-R_2^{-1}\}\hfill \\ \hfill {\Pi }_{22}^3& =\mathit{diag}\{-P_2^{-1},-P_2^{-1},-P_2^{-1},-P_2^{-1}\}\hfill \\ \hfill {\mathcal{B}}_{ijq}^1& =B_{2q}{K}_{1j}{E}_{1i},{\mathcal{B}}_q^2=B_{2q}{K}_2{E}_{2q},{\mathcal{B}}_{jq}^3=B_{2q}{K}_{1j}\hfill \\ \hfill {\mathcal{E}}_1& =\mathit{diag}\{I,\hslash ,\sqrt{{\overline{\alpha }}_1},\sqrt{{\overline{\alpha }}_2},\sqrt{{\overline{\alpha }}_2}{\rho }_1\}\hfill \\ \hfill {\mathcal{E}}_2& =\mathit{diag}\{I,\overline{\tau }I,\tau I\},{\mathcal{E}}_3=\mathit{diag}\{I,{\rho }_{1}I,{\rho }_{2}I,{\rho }_1{\rho }_{2}I\}.\hfill \end{array}$$

Proof. 

Consider the discrete-time piecewise Lyapunov–Krasovskii functional in the following form:

$$\begin{array}{c}\hfill V_k=V_{1k}+V_{2k}+V_{3k}\end{array}$$

(25)

where

$$\begin{array}{cc}\hfill V_{1k}& =x_k^{1T}{P}_1{x}_k^1+x_k^{2T}{P}_2{x}_k^2\hfill \\ \hfill V_{2k}& ={\displaystyle \sum _{v=k-\underline{\tau }}^{k-1}}{x}_v^{1T}{Q}_1{x}_v^1+{\displaystyle \sum _{v=k-\overline{\tau }}^{k-\underline{\tau }-1}}{x}_v^{1T}{Q}_2{x}_v^1+{\displaystyle \sum _{v=k-\overline{\tau }}^{k-1}}{x}_v^{1T}{Q}_3{x}_v^1\hfill \\ \hfill V_{3k}& =\overline{\tau }{\displaystyle \sum _{l=-\overline{\tau }}^{-1}}{\displaystyle \sum _{v=k+l}^{k-1}}{\varrho }_v^{1T}{R}_1{\varrho }_v^1+\tau {\displaystyle \sum _{l=-\overline{\tau }}^{-\underline{\tau }-1}}{\displaystyle \sum _{v=k+l}^{k-1}}{\varrho }_v^{1T}{R}_2{\varrho }_v^1\hfill \\ \hfill {\varrho }_k^1& =x_{k+1}^1-x_k^1,\tau =\overline{\tau }-\underline{\tau }.\hfill \end{array}$$

Then, defining $\Delta V_k=V_{k+1}-V_k$, the piecewise Lyapunov–Krasovskii functional difference equation under the mathematical expectation can be obtained as

$$\begin{array}{cc}\hfill \mathbb{E}\{\Delta V_{1k}\}& ={\displaystyle \sum _{i=1}^r}{\displaystyle \sum _{j=1}^r}{\displaystyle \sum _{q=1}^r}{g}_i^1{g}_j^1{g}_q^2\left\{x_{k+1}^{1T}{P}_1{x}_{k+1}^1-x_k^{1T}{P}_1{x}_k^1+\mathbb{E}\left\{x_{k+1}^{2T}{P}_2{x}_{k+1}^2\right\}-x_k^{2T}{P}_2{x}_k^2\right\}\hfill \\ \hfill \mathbb{E}\{\Delta V_{2k}\}& =x_k^{1T}(Q_1+Q_3)x_k^1+x_{k-\underline{\tau }}^{1T}(Q_2-Q_1)x_{k-\underline{\tau }}^1-x_{k-\overline{\tau }}^{1T}(Q_2+Q_3)x_{k-\overline{\tau }}^1\hfill \\ \hfill \mathbb{E}\{\Delta V_{3k}\}& ={\displaystyle \sum _{i=1}^r}{\displaystyle \sum _{j=1}^r}{\displaystyle \sum _{q=1}^r}{g}_i^1{g}_j^1{g}_q^2\{{\varrho }_k^{1T}({\overline{\tau }}^2{R}_1+{\tau }^2{R}_2){\varrho }_k^1-\overline{\tau }{\displaystyle \sum _{v=k-\overline{\tau }}^{k-1}}{\varrho }_v^{1T}{R}_1{\varrho }_v^1\hfill \\ \hfill & -\tau {\displaystyle \sum _{v=k-\overline{\tau }}^{k-\underline{\tau }-1}}{\varrho }_v^{1T}{R}_2{\varrho }_v^1\}.\hfill \end{array}$$

(26)

According to (21) and (26), one has

$$\begin{array}{cc}\hfill & \mathbb{E}\left\{x_{k+1}^{2T}{P}_2{x}_{k+1}^2\right\}={\displaystyle \sum _{i=1}^r}{\displaystyle \sum _{j=1}^r}{\displaystyle \sum _{q=1}^r}{g}_i^1{g}_j^1{g}_q^2\left\{{\mathcal{A}}^T{P}_2\mathcal{A}+{\rho }_1^2{\mathcal{B}}^T{P}_2\mathcal{B}+{\rho }_2^2{\mathcal{C}}^T{P}_2\mathcal{C}+{\rho }_1^2{\rho }_2^2{\mathcal{D}}^T{P}_2\mathcal{D}\right\}\hfill \end{array}$$

(27)

where

$$\begin{array}{cc}\hfill \mathcal{A}& =A_{2q}{x}_k^2+{\overrightarrow{\alpha }}_2{B}_{2q}{K}_2{E}_{2q}{x}_k^2+{\overrightarrow{\alpha }}_1{\overrightarrow{\alpha }}_2{B}_{2q}{K}_{1j}{E}_{1i}{x}_{k-{\tau }_k}^1+{\overrightarrow{\alpha }}_1{\overrightarrow{\alpha }}_2{B}_{2q}{K}_{1j}{e}_{sk}+{\overrightarrow{\alpha }}_2{\overline{\alpha }}_1{B}_{2q}{K}_{1j}{\mathfrak{f}}_k^1\hfill \\ \hfill & +{\overline{\alpha }}_2{B}_{2q}{\mathfrak{f}}_k^2+{\overrightarrow{\alpha }}_2{B}_{2q}{K}_2{h}_k^{\mu }+B_{3q}{\omega }_k\hfill \\ \hfill \mathcal{B}& =-{\overrightarrow{\alpha }}_2{B}_{2q}{K}_{1j}{E}_{1i}{x}_{k-{\tau }_k}^1-{\overrightarrow{\alpha }}_2{B}_{2q}{K}_{1j}{e}_{sk}+{\overrightarrow{\alpha }}_2{B}_{2q}{K}_{1j}{\mathfrak{f}}_k^1\hfill \\ \hfill \mathcal{C}& =-B_{2q}{K}_2{E}_{2q}{x}_k^2-{\overrightarrow{\alpha }}_1(B_{2q}{K}_{1j}{E}_{1i}{x}_{k-{\tau }_k}^1+B_{2q}{K}_{1j}{e}_{sk})-{\overline{\alpha }}_1{B}_{2q}{K}_{1j}{\mathfrak{f}}_k^1-B_{2q}{\mathfrak{f}}_k^2-B_{2q}{K}_2{h}_k^{\mu }\hfill \\ \hfill \mathcal{D}& =-B_{2q}{K}_2{E}_{2q}{x}_k^2+B_{2q}{K}_{1j}{E}_{1i}{x}_{k-{\tau }_k}^1+B_{2q}{K}_{1j}(e_{sk}-{\mathfrak{f}}_k^1)+B_{2q}{\mathfrak{f}}_k^2-B_{2q}{K}_2{h}_k^{\mu }\hfill \\ \hfill {\overrightarrow{\alpha }}_1=1-{\overline{\alpha }}_1,{\overrightarrow{\alpha }}_2=1-{\overline{\alpha }}_2.\end{array}$$

Considering $\underline{\tau }\le {\tau }_k\le \overline{\tau }$, one has

$$\begin{array}{cc}\hfill & -\overline{\tau }{\displaystyle \sum _{v=k-\overline{\tau }}^{k-1}}{\varrho }_v^{1T}{R}_1{\varrho }_v^1-\tau {\displaystyle \sum _{v=k-\overline{\tau }}^{k-\underline{\tau }-1}}{\varrho }_v^{1T}{R}_2{\varrho }_v^1\hfill \\ \hfill & \le -{[x_k^1-x_{k-\overline{\tau }}^1]}^T{R}_1[x_k^1-x_{k-\overline{\tau }}^1]-{\theta }_k^{13T}\left[\begin{array}{cc}{R}_2& \ast \\ R_3& R_2\end{array}\right]{\theta }_k^{13}\hfill \end{array}$$

(28)

where ${\theta }_k^{13}={[x_{k-\underline{\tau }}^{1T}-x_{k-{\tau }_k}^{1T}{x}_{k-{\tau }_k}^{1T}-x_{k-\overline{\tau }}^{1T}]}^T$.

Without loss of generality, the dynamic parameters for the dynamic quantizer considered in this article are defined as ${\mu }_k={\displaystyle \frac{\hslash }{M}}\left|y_k^2\right|$ with $\hslash \ge 1$. Then, as in [35], according to the definition of the dynamic quantizer given in (11) and the homogeneity property of Euclidean norm, it can be obtained that

$$\begin{array}{c}\hfill h_k^{\mu T}{h}_k^{\mu }\le {\displaystyle \frac{{\hslash }^2{\Delta }^2}{M^2}}{y}_k^{2T}{y}_k^2.\end{array}$$

(29)

Considering the constraint of nonlinear deception attack signals ${\mathfrak{f}}_k^1$ and ${\mathfrak{f}}_k^2$, we obtain

$$\begin{array}{cc}\hfill {\overline{\alpha }}_1{(y_{k-{\tau }_k}^1+e_{sk})}^T{\mathcal{F}}_1^T{\mathcal{F}}_1(y_{k-{\tau }_k}^1+e_{sk})-{\overline{\alpha }}_1{\mathfrak{f}}_k^{1T}{\mathfrak{f}}_k^1& \ge 0\hfill \\ \hfill {\overline{\alpha }}_2{(K_2{\overline{y}}_k^2+u_k^1)}^T{\mathcal{F}}_2^T{\mathcal{F}}_2(K_2{\overline{y}}_k^2+u_k^1)-{\overline{\alpha }}_2{\mathfrak{f}}_k^{2T}{\mathfrak{f}}_k^2& \ge 0.\hfill \end{array}$$

(30)

Based on the event-triggered condition (15), one has

$$\begin{array}{c}\hfill e_{sk}^T\Omega e_{sk}\le {\delta }_k{(y_{k-{\tau }_k}^1+e_{sk})}^T\Omega (y_{k-{\tau }_k}^1+e_{sk}).\end{array}$$

(31)

Combining (26)–(31), by defining ${\zeta }_k={\left[x_k^{1T}{x}_{k-\underline{\tau }}^{1T}{x}_{k-{\tau }_k}^{1T}{x}_{k-\overline{\tau }}^{1T}{x}_k^{2T}{e}_{sk}^T{\mathfrak{f}}_k^{1T}{\mathfrak{f}}_k^{2T}{h}_k^{\mu T}{\omega }_k^T\right]}^T$, we can deduce that

$$\begin{array}{cc}\hfill & \mathbb{E}\{\Delta V_k\}+z_k^{1T}{z}_k^1-{\gamma }^2{\omega }_k^T{\omega }_k\hfill \\ \hfill & \le {\displaystyle \sum _{i,j,q=1}^r}{g}_i^1{g}_j^1{g}_q^2{\varrho }_j{\zeta }_k^T({\Pi }_{ijq}^{11}+{\Pi }_{ijq}^{21T}{\Pi }_{22}^{-1}{\Pi }_{ijq}^{21}){\zeta }_k\hfill \\ \hfill & ={\displaystyle \sum _{i,q=1}^r}{\varrho }_i^2{\left(g_i^1\right)}^2{g}_q^2{\zeta }^T\left(k\right)({\Pi }_{iiq}^{11}+{\Pi }_{iiq}^{21T}{\Pi }_{22}^{-1}{\Pi }_{iiq}^{21}){\zeta }_k\hfill \\ \hfill & ={\displaystyle \sum _{i,q=1}^r}{\displaystyle \sum _{i<j}^r}{g}_i^1{g}_j^1{g}_q^2{\varrho }_j{\zeta }_k^T\left({\Pi }_{ijq}^{11}+\frac{{\varrho }_i}{{\varrho }_j}{\Pi }_{ijq}^{11}+{\Pi }_{ijq}^{21T}{\Pi }_{22}^{-1}{\Pi }_{ijq}^{21}+\frac{{\varrho }_i}{{\varrho }_j}{\Pi }_{jiq}^{21T}{\Pi }_{22}^{-1}{\Pi }_{jiq}^{21}\right){\zeta }_k.\hfill \end{array}$$

(32)

Then, it is obtained from conditions (23) and (24) that

$$\begin{array}{cc}\hfill {\Pi }_{iiq}^{11}+{\Pi }_{iiq}^{21T}{\Pi }_{22}^{-1}{\Pi }_{iiq}^{21}& <0\hfill \\ \hfill {\Pi }_{ijq}^{11}+{\vartheta }_j{\Pi }_{jiq}^{11}+{\Pi }_{ijq}^{21T}{\Pi }_{22}^{-1}{\Pi }_{ijq}^{21}+{\vartheta }_j{\Pi }_{jiq}^{21T}{\Pi }_{22}^{-1}{\Pi }_{jiq}^{21}& <0,j\in ⟨2⟩.\hfill \end{array}$$

Due to $({\vartheta }_2-[{\varrho }_i/{\varrho }_j]){\Pi }_{jiq}^{21T}{\Pi }_{22}^{-1}{\Pi }_{jiq}^{21}>0$, we have

$$\begin{array}{c}\hfill {\Pi }_{ijq}^{11}+{\displaystyle \frac{{\varrho }_i}{{\varrho }_j}}{\Pi }_{jiq}^{11}+{\Pi }_{ijq}^{21T}{\Pi }_{22}^{-1}{\Pi }_{ijq}^{21}+{\displaystyle \frac{{\varrho }_i}{{\varrho }_j}}{\Pi }_{jiq}^{21T}{\Pi }_{22}^{-1}{\Pi }_{jiq}^{21}<0.\end{array}$$

Then, the following result can be obtained:

$$\begin{array}{c}\hfill \mathbb{E}\{\Delta V_k\}+z_k^{1T}{z}_k^1-{\gamma }^2{\omega }_k^T{\omega }_k<0.\end{array}$$

(33)

The sum of the two sides of the inequality (33) from $k=0$ to $k=\infty$ can have

$$\begin{array}{c}\hfill \mathbb{E}\{V_{\infty }-V_0\}+{\displaystyle \sum _{k=0}^{\infty }}\{z_k^{1T}{z}_k^1-{\gamma }^2{\omega }_k^T{\omega }_k\}<0.\end{array}$$

(34)

Considering the fact that $V_{\infty }>0$ and $V_0=0$, the following conclusions can be obtained:

$$\begin{array}{c}\hfill {\displaystyle \sum _{k=0}^{\infty }}{z}_k^{1T}{z}_k^1-{\gamma }^2{\displaystyle \sum _{k=0}^{\infty }}{\omega }_k^T{\omega }_k<0\end{array}$$

(35)

which implies the system is mean square asymptotically stable without disturbance and satisfies the $H_{\infty }$ performance index $\gamma$. The proof is completed.    □

Remark 6. 

Through the proof of Theorem 1, the sufficient conditions that the system satisfies $H_{\infty }$ performance and mean square asymptotic stability are obtained. Specifically, this article considers the impact of event-triggered, dynamic quantization, and deception attacks on the system. To reduce the conservatism of the design results, the artificial time delay caused by event-triggered control is introduced, and the performance and stability of the system are analyzed by constructing the Lyapunov–Krasovskii functional. In the mean square sense, the inequality (22) and integral inequality (28) are used to reduce the inevitable time-delay summation term, and the inequality constraints (29)–(31) is introduced in a targeted manner. The preliminary inequality result is obtained in (32). Furthermore, the related design conditions of MFs are considered. Due to the introduction of ETM, the asynchronous phenomenon of MFs are inevitable. Through the method in [12] and Schur complement lemma, the final sufficient design conditions (23) and (24) are obtained.

Remark 7. 

It should be noted that, if the assumptions of cascade controller gain, dynamic quantizer parameters, and event-triggered weight matrix are removed, there will be some nonlinear terms and coupling terms in inequality conditions (23) and (24). This makes the inequality difficult to solve. In Theorem 2, this difficulty can be solved by some variable substitutions, basic inequalities, and matrix decoupling techniques.

Theorem 2. 

For given ${\overline{\alpha }}_1>0$, ${\overline{\alpha }}_2>0$, ${\delta }_1>0$, ${\delta }_2>0$, ${\delta }_3>0$, $\Delta >0$, $M>0$, $\tau >0$, $\overline{\tau }>0$, and ${\vartheta }_j>0(j\in ⟨2⟩)$, the system (21) is mean square asymptotically stable and satisfies the $H_{\infty }$ performance index γ if there exist positive definite symmetric matrices $P_1$, $P_2$, $Q_1$, $Q_2$, $Q_3$, $R_1$, $R_2$, Ω, and slack matrix $R_3$ with appropriate dimensions, such that (22) and the following inequalities hold for $i<j$:

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}{\overrightarrow{\Pi }}_{iiq}^1& \ast \\ {\overrightarrow{\Pi }}_{iiq}^{21}& {\overrightarrow{\Pi }}_i^3\end{array}\right]& <0\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill \left[\begin{array}{ccc}{\overrightarrow{\Pi }}_{ijq}^{{\vartheta }_j}& \ast & \ast \\ {\overrightarrow{\Pi }}_{ijq}^{21}& {\overrightarrow{\Pi }}_i^3& \ast \\ \sqrt{{\vartheta }_2}{\overrightarrow{\Pi }}_{jiq}^{31}& 0& {\overrightarrow{\Pi }}_j^3\end{array}\right]& <0,i,j,q\in ⟨r⟩\hfill \end{array}$$

(37)

where

$$\begin{array}{cc}\hfill {\overrightarrow{\Pi }}_i^1& =\left[\begin{array}{cc}{\Pi }_{iiq}^{11}& \ast \\ {\widehat{\Pi }}_{iiq}^{21}& {\widehat{\Pi }}_{22}\end{array}\right],{\overrightarrow{\Pi }}_{iiq}^{21}=\varsigma {\overrightarrow{\Pi }}_{iq}^2+{\overrightarrow{\Pi }}_{iiq}^3\hfill \\ \hfill {\overrightarrow{\Pi }}_{ijq}^{{\vartheta }_j}& =\left[\begin{array}{ccc}{\Pi }_i^{11}+{\vartheta }_j{\Pi }_j^{11}& \ast & \ast \\ {\widehat{\Pi }}_{ijq}^{21}& {\widehat{\Pi }}_{22}& \ast \\ \sqrt{{\vartheta }_2}{\widehat{\Pi }}_{jiq}^{21}& 0& {\widehat{\Pi }}_{22}\end{array}\right],{\overrightarrow{\Pi }}_{ijq}^{21}=\varsigma {\overrightarrow{\Pi }}_{iq}^4+{\overrightarrow{\Pi }}_{ijq}^5\hfill \\ \hfill {\overrightarrow{\Pi }}_{jiq}^{31}& =\varsigma {\overrightarrow{\Pi }}_{jq}^6+{\overrightarrow{\Pi }}_{jiq}^7,{\widehat{\Pi }}_{22}=\mathit{diag}\{{\Pi }_{22}^1,{\widehat{\Pi }}_{22}^2,{\widehat{\Pi }}_{22}^3\}\hfill \\ \hfill {\widehat{\Pi }}_{22}^2& =\mathit{diag}\{-P_1,-2\epsilon P_1+{\epsilon }^2{R}_1,-2\epsilon P_1+{\epsilon }^2{R}_2\}\hfill \\ \hfill {\widehat{\Pi }}_{22}^3& =\mathit{diag}\{-P_2,-P_2,-P_2,-P_2\}\hfill \end{array}$$

in which ${\widehat{\Pi }}_{iiq}^{21}\left({\widehat{\Pi }}_{ijq}^{21}\right)$ is obtained from ${\Pi }_{iiq}^{21}\left({\Pi }_{ijq}^{21}\right)$ by substituting $P_2{B}_{2q}{K}_{1j}{E}_{1i}$, $P_2{B}_{2q}{K}_{1j}$, $P_2{B}_{2q}{K}_2{E}_{2q}$, $P_2{B}_{2q}{K}_2$, $P_1{\mathcal{F}}_2{K}_{1j}{E}_{1i}$, $P_1{K}_{1j}{E}_{1i}$, and $P_2{\mathcal{F}}_2{K}_2{E}_{2q}$ with $B_{2q}{J}_{1j}{E}_{1i}$, $B_{2q}{J}_{1j}$, $B_{2q}{J}_2{E}_{2q}$, $B_{2q}{J}_2$, ${\mathcal{F}}_2{J}_{1j}{E}_{1i}$, $J_{1j}{E}_{1i}$, and ${\mathcal{F}}_2{J}_2{E}_{2q}$, and 

$$\begin{array}{cc}\hfill {\overrightarrow{\Pi }}_{iq}^2& =\left[{\overrightarrow{\Pi }}_i^{21}{\overrightarrow{\Pi }}_{iq}^{22}\right],{\overrightarrow{\Pi }}_{iiq}^3=\left[{\overrightarrow{\Pi }}_{iiq}^{31}{\overrightarrow{\Pi }}_i^{32}\right],{\overrightarrow{\Pi }}_{iq}^4=\left[{\overrightarrow{\Pi }}_i^{21}{\overrightarrow{\Pi }}_{iq}^{22}0\right]\hfill \\ \hfill {\overrightarrow{\Pi }}_{ijq}^5& =\left[{\overrightarrow{\Pi }}_{ijq}^{31}{\overrightarrow{\Pi }}_j^{32}0\right],{\overrightarrow{\Pi }}_{jq}^6=\left[{\overrightarrow{\Pi }}_j^{21}0{\overrightarrow{\Pi }}_{jq}^{22}\right],{\overrightarrow{\Pi }}_{jiq}^7=\left[{\overrightarrow{\Pi }}_{jiq}^{31}0{\overrightarrow{\Pi }}_j^{32}\right]\hfill \\ \hfill {\overrightarrow{\Pi }}_i^3& ={\mathcal{H}}_e\{-\varsigma {\mathbb{N}}_i\},{\overrightarrow{\Pi }}_j^3={\mathcal{H}}_e\{-\varsigma {\mathbb{N}}_j\}\hfill \\ \hfill {\mathbb{N}}_j& =\mathit{diag}\{N_{1j},N_2,N_{1j},N_2,N_{1j}\}.\hfill \end{array}$$

In addition, the gains of ${\mathit{Controller}}^1$ and ${\mathit{Controller}}^2$ are given as follows:

$$\begin{array}{c}\hfill K_{1j}=N_{1j}^{-1}{J}_{1j},K_2=N_2^{-1}{J}_2.\end{array}$$

(38)

Proof. 

Perform congruence transformation to (23) by $diag\{{\mathbf{I}}_{10},\mathcal{P}\}$ with $\mathcal{P}=\mathit{diag}\{{\mathbf{I}}_5,P_1,P_1,P_1,P_2,P_2,P_2,P_2\}$, the inequality (23)–(25) can be rewritten as

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}{\Pi }_i^{11}& \ast \\ {\tilde{\Pi }}_{iiq}^{21}& {\widehat{\Pi }}_{22}\end{array}\right]& <0\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill \left[\begin{array}{ccc}{\Pi }_i^{11}+{\vartheta }_j{\Pi }_j^{11}& \ast & \ast \\ {\tilde{\Pi }}_{ijq}^{21}& {\widehat{\Pi }}_{22}& \ast \\ \sqrt{{\vartheta }_2}{\tilde{\Pi }}_{jiq}^{21}& 0& {\widehat{\Pi }}_{22}\end{array}\right]& <0\hfill \end{array}$$

(40)

where ${\tilde{\Pi }}_{ijq}^{21T}=\mathcal{P}\left[{\Pi }_{ijq}^{211T}{\Pi }_{ijq}^{212T}{\Pi }_{ijq}^{213T}{\Pi }_{ijq}^{214T}\right]$.

Defining $J_{1j}=N_{1j}{K}_{1j},J_2=N_2{K}_2$. Then, the condition (39), (40) can be reexpressed as

$$\begin{array}{cc}\hfill {\overrightarrow{\Pi }}_{iiq}^1+{\mathcal{H}}_e\left\{{\overrightarrow{\Pi }}_{iq}^{2T}{\mathbb{N}}_i^{-1}{\overrightarrow{\Pi }}_{iiq}^3\right\}<& 0\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill {\overrightarrow{\Pi }}_{ijq}^{{\vartheta }_j}+{\mathcal{H}}_e\{{\overrightarrow{\Pi }}_{iq}^{4T}{\mathbb{N}}_i^{-1}{\overrightarrow{\Pi }}_{ijq}^5+{\sqrt{\vartheta }}_2{\overrightarrow{\Pi }}_{jq}^{6T}{\mathbb{N}}_j^{-1}{\overrightarrow{\Pi }}_{jiq}^7\}<& 0\hfill \end{array}$$

(42)

the definitions of ${\overrightarrow{\Pi }}_{iq}^2$, ${\overrightarrow{\Pi }}_{iiq}^3$, ${\overrightarrow{\Pi }}_{iq}^4$, ${\overrightarrow{\Pi }}_{ijq}^5$, ${\overrightarrow{\Pi }}_{jq}^6$, ${\overrightarrow{\Pi }}_{jiq}^7$, and ${\mathbb{N}}_j$ are shown in Theorem 2, and 

$$\begin{array}{cc}\hfill {\overrightarrow{\Pi }}_j^{21}& ={\left[{\overrightarrow{{\rm Y}}}_j^{1T}{\overrightarrow{{\rm Y}}}^{2T}{\overrightarrow{{\rm Y}}}_j^{1T}0{\overrightarrow{{\rm Y}}}_j^{3T}\right]}^T\hfill \\ \hfill {\overrightarrow{\Pi }}_{jq}^{22}& ={\left[{\overrightarrow{{\rm Y}}}_{jq}^{4T}{\overrightarrow{{\rm Y}}}_q^{5T}{\overrightarrow{{\rm Y}}}_{jq}^{4T}{\overrightarrow{{\rm Y}}}_q^{6T}{\overrightarrow{{\rm Y}}}_{jq}^{7T}\right]}^T\hfill \\ \hfill {\overrightarrow{{\rm Y}}}_j^1& =[{\mathbf{0}}_{13}{\overrightarrow{\alpha }}_1{\widehat{\mathbb{N}}}_{1j}-{\widehat{\mathbb{N}}}_{3j}{\mathbf{0}}_3],{\overrightarrow{{\rm Y}}}_j^2=\left[{\mathbf{0}}_{13}{\widehat{\mathbb{N}}}_{2}0{\mathbf{0}}_3\right]\hfill \\ \hfill {\overrightarrow{{\rm Y}}}_j^3& =\left[{\mathbf{0}}_{13}{\overrightarrow{\alpha }}_1{\widehat{\mathbb{N}}}_{1j}{\widehat{\mathbb{N}}}_{3j}{\mathbf{0}}_3\right]\hfill \\ \hfill {\overrightarrow{{\rm Y}}}_{jq}^4& =[{\overrightarrow{\alpha }}_1{\overrightarrow{\alpha }}_2{\widehat{\mathbb{N}}}_{5jq}-{\overrightarrow{\alpha }}_2{\widehat{\mathbb{N}}}_{6jq}-{\overrightarrow{\alpha }}_1{\widehat{\mathbb{N}}}_{7jq}{\overrightarrow{\alpha }}_1{\widehat{\mathbb{N}}}_{8jq}]\hfill \\ \hfill {\overrightarrow{{\rm Y}}}_q^5& =[{\overrightarrow{\alpha }}_1{\widehat{\mathbb{N}}}_{4q}0-{\widehat{\mathbb{N}}}_{4q}-{\widehat{\mathbb{N}}}_{4q}]\hfill \\ \hfill {\overrightarrow{{\rm Y}}}_q^6& =[{\overrightarrow{\alpha }}_2{\widehat{\mathbb{N}}}_{4q}0-{\widehat{\mathbb{N}}}_{4q}-{\widehat{\mathbb{N}}}_{4q}]\hfill \\ \hfill {\overrightarrow{{\rm Y}}}_{jq}^7& =[{\overrightarrow{\alpha }}_2{\overline{\alpha }}_1{\widehat{\mathbb{N}}}_{5jq}{\overrightarrow{\alpha }}_2{\widehat{\mathbb{N}}}_{6jq}-{\overline{\alpha }}_1{\widehat{\mathbb{N}}}_{7jq}-{\widehat{\mathbb{N}}}_{8jq}]\hfill \\ \hfill {\overrightarrow{\Pi }}_{ijq}^{31}& =\left[\begin{array}{cc}{\overrightarrow{{\rm Y}}}_{ij}^8& {\overrightarrow{{\rm Y}}}_q^9\\ 0& 0\end{array}\right],{\overrightarrow{\Pi }}_j^{32}=\left[\begin{array}{cc}0& 0\\ {\overrightarrow{{\rm Y}}}_j^{10}& 0\end{array}\right],{\overrightarrow{{\rm Y}}}_{ij}^8=\left[\begin{array}{cc}{\mathbf{0}}_2& J_{1j}{E}_{1i}\\ {\mathbf{0}}_2& 0\end{array}\right]\hfill \\ \hfill {\overrightarrow{{\rm Y}}}_q^9& =\mathrm{diag}\{0,J_2{E}_{2q}\},{\overrightarrow{{\rm Y}}}_j^{10}=\mathrm{diag}\{J_{1j},J_2,J_{1j}\}\hfill \\ \hfill {\widehat{\mathbb{N}}}_{1j}& =\sqrt{{\overline{\alpha }}_2}{({\mathcal{F}}_2-{\mathcal{F}}_2{N}_{1j})}^T,{\widehat{\mathbb{N}}}_2=\sqrt{{\overline{\alpha }}_2}{({\mathcal{F}}_2-{\mathcal{F}}_2{N}_2)}^T\hfill \\ \hfill {\widehat{\mathbb{N}}}_{3j}& =\sqrt{{\overline{\alpha }}_2}{\rho }_1{(I-N_{1j})}^T,{\widehat{\mathbb{N}}}_{4q}={(P_2{B}_{2q}-B_{2q}{N}_2)}^T\hfill \\ \hfill {\widehat{\mathbb{N}}}_{5jq}& ={(P_2{B}_{2q}-B_{2q}{N}_{1j})}^T,{\widehat{\mathbb{N}}}_{6jq}={\rho }_1{\widehat{\mathbb{N}}}_{5jq}\hfill \\ \hfill {\widehat{\mathbb{N}}}_{7jq}& ={\rho }_2{\widehat{\mathbb{N}}}_{5jq},{\widehat{\mathbb{N}}}_{8jq}={\rho }_1{\rho }_2{\widehat{\mathbb{N}}}_{5jq}.\hfill \end{array}$$

It is easy to know that (41), (42) can hold if the conditions (36), (37) are satisfied by applying Lemma 2 in [34]. The proof is completed.    □

Remark 8. 

Through the proof of Theorem 2, the sufficient conditions for solving the cascade controller gain, quantizer parameter, and ADAETM weighting matrix are obtained. In the proof process, the nonlinear terms and coupling terms that affect the inequality solution are eliminated by congruence transformation, basic inequality transformation, and matrix decoupling technology, such as $P_2{B}_{2q}{K}_{1j}{E}_{1i}$, $P_2{B}_{2q}{K}_{1j}$, $P_2{B}_{2q}{K}_2{E}_{2q}$, and so on. Then, the solution of LMIs is a convex optimization problem. Many existing optimization methods and numerical tools, such as the YALMIP toolbox in MATLAB, can be used to solve convex optimization problems. Based on Theorem 2 and the existing solving tools, the design results can be more easily obtained by off-line execution. The detailed solution process is given by Algorithm 3.

Remark 9. 

The computational complexity $\mathcal{C}={\mathcal{N}}^3\mathcal{L}$ of the LMIs in Theorem 2 is determined by the number of decision variables $\mathcal{N}$ and the dimension $\mathcal{L}$ of the LMIs. Based on Theorem 2, we have $\mathcal{N}=3n_{x^1}\times (n_{x^1}+1)+{\displaystyle \frac{1}{2}}{n}_{x^2}(n_{x^2}+1)+{\displaystyle \frac{1}{2}}{n}_{y^1}(n_{y^1}+1)+n_{x^1}\times n_{x^1}+n_{u^1}\times (n_{y^1}+n_{u^1})+n_{u^2}\times \left(n_{y^2}{n}_{u^2}\right)+1$ and $\mathcal{L}=2n_{x^1}+{\displaystyle \frac{1}{2}}{r}^2(r+1)(7n_{x^1}+5n_{x^2}+4n_{y^1}+n_{y^2}+n_{\omega }+5n_{u^1}+3n_{u^2})+{\displaystyle \frac{1}{2}}{r}^2(r+1)(10n_{x^1}+4n_{x^2}+4n_{y^1}+n_{y^2}+n_{\omega }+8n_{u^1}+5n_{u^2})$.

Algorithm 3  Solve the control gains, quantizer parameter, and ADAETM weighting matrix

Input:  parameter matrices $A_{1i}$, $B_{1i}$, $C_{1i}$, $D_{1i}$, $E_{1i}$, $A_{2q}$, $B_{2q}$, $B_{3q}$, $C_{2q}$, $D_{2q}$, $E_{2q}$, and parameter scalars ${\delta }_1$, ${\delta }_2$, ${\delta }_3$, ${\overline{\alpha }}_1$, ${\overline{\alpha }}_2$, $\Delta$, M, $\overline{\tau }$, $\tau$, $\gamma$, ${\vartheta }_1$, and ${\vartheta }_2$. Output:  $K_{1j}$, $K_2$, ℏ, and $\Omega$. YALMIP toolbox in MATLAB is used to solve LMIs (22), (36)–(37). if  sum(checkset(LMIs)<0)=size(checkset(LMIs),1)  then    go to Input adjust given parameters. else    solve $J_{1j}$, $J_2$, $N_{1j}^{-1}$, $N_2^{-1}$, ℏ, and $\Omega$ with LMIs (22), (36)–(37) and substitute them into $K_{1j}=N_{1j}^{-1}{J}_{1j}$, $K_2=N_2^{-1}{J}_2$. end if The gains $K_{1j}$, $K_2$, quantizer parameter ℏ, and ADAETM weighting matrix $\Omega$ are obtained.

4. Simulation Results

4.1. Design Example with PPBTS

By constructing the NCCS shown in Figure 2, the problem of excessive temperature deviation during the operation of the power PPBTS will be solved. ${\mathrm{Sensor}}^1$ measures the steam temperature value of the secondary superheater. After the ADAETM and the influence of the deception attacks, the measurement data are fed back to ${\mathrm{Controller}}^1$. ${\mathrm{Controller}}^1$ compares the measured data with the expected data, and then the output signal of ${\mathrm{Controller}}^1$ is transmitted to ${\mathrm{Controller}}^2$ as the expected data. ${\mathrm{Controller}}^2$ compares the expected data with the quantized steam temperature measurement data at the Desuperheater end, and transmits the control output signal to the Desuperheater spray valve. The Desuperheater spray valve will be attacked during the adjustment of the Desuperheater. Through the proposed controller design strategy, we can ensure the stability and controllability of the steam temperature in the PPBTS under the network environment where the whole system is threatened by deception attacks.

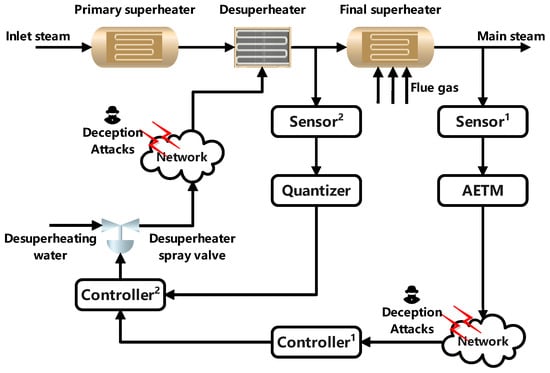
Figure 2. Structure diagram of an NCCS for a nonlinear PPBTS.

The discrete nonlinear networked PPBTS [9] parameters considered in the article are given as follows:

$$\begin{array}{cc}\hfill A_{11}& =\left[\begin{array}{cc}0.6887& -0.0093\\ 0.8356& 0.9951\end{array}\right],B_{11}=\left[\begin{array}{c}0.8356\\ 0.4437\end{array}\right],D_{11}=0.1\hfill \\ \hfill A_{12}& =\left[\begin{array}{cc}0.6908& -0.0093\\ 0.4182& 0.9975\end{array}\right],B_{12}=\left[\begin{array}{c}0.8364\\ 0.2219\end{array}\right],D_{12}=0.1\hfill \\ \hfill C_{11}& =C_{12}=E_{11}=E_{12}=\left[\begin{array}{cc}0& 0.0111\end{array}\right]\hfill \\ \hfill A_{21}& =\left[\begin{array}{ccc}-0.0342& -0.4364& -0.0342\\ 0.3425& 0.6849& -0.0254\\ 0.2542& 0.8762& 0.9899\end{array}\right],B_{21}=\left[\begin{array}{c}0.3425\\ 0.2542\\ 0.1008\end{array}\right]\hfill \\ \hfill A_{22}& =\left[\begin{array}{ccc}-0.0572& -0.5285& -0.1676\\ 0.3352& 0.6468& -0.1262\\ 0.2525& 0.8654& 0.9497\end{array}\right],B_{22}=\left[\begin{array}{c}0.3352\\ 0.2525\\ 0.1005\end{array}\right]\hfill \\ \hfill B_{31}& =\left[\begin{array}{c}-0.0104\\ 0.0483\\ 0.0851\end{array}\right],B_{32}=\left[\begin{array}{c}-0.0185\\ 0.0453\\ 0.0844\end{array}\right],D_{21}=D_{22}=0.2\hfill \\ \hfill C_{21}& =C_{22}=\left[\begin{array}{ccc}0& 0& 0.1\end{array}\right],E_{21}=E_{22}=\left[\begin{array}{ccc}0& 0& 0.2\end{array}\right].\hfill \end{array}$$

Moreover, the MFs are chosen by $d_1\left(x_k^1\right)={\displaystyle \frac{1-{sin}^2\left(x_k^{11}\right)}{2}}$, $d_2\left(x_k^1\right)=1-d_1\left(x_k^1\right)$, $f_1\left(x_k^2\right)={\displaystyle \frac{1-0.5{sin}^2\left(x_k^{21}\right)}{2}}$, and $f_2\left(x_k^2\right)=1-f_1\left(x_k^2\right)$. The initial states of the ${\mathrm{Plant}}^1$ and ${\mathrm{Plant}}^2$ are given as $x_0^1={[-0.51.0]}^T,x_0^2={[0.2-0.1-0.3]}^T$ and the external disturbance is given as follows: ${\omega }_k=0.5e^{-0.05k}\begin{array}{c}\hfill sin\left(0.5k\right)\end{array}$, $12<k\le 45$; otherwise, ${\omega }_k=0$.

Selecting ${\mathfrak{f}}_k^1=0.005tanh\left({\widehat{y}}_k^1\right)$, ${\mathfrak{f}}_k^2=0.005tanh\left(u_k^2\right)$, $\gamma =0.5$, $\underline{\tau }=\underline{\theta }=1.0$, $\overline{\tau }=\overline{\theta }=4$, ${\overline{\alpha }}_1={\overline{\alpha }}_2=0.3$, ${\delta }_1=0.05$, ${\delta }_2=0.02$, ${\delta }_3=0.03$, ${ϵ}_1={ϵ}_3=1$, ${ϵ}_2={ϵ}_4=0.5$, $\Delta =0.001$, $M=1$, and ${\vartheta }_1=0.75<{\vartheta }_2=1.25$. By the design results in Theorem 2, the quantization parameter, security fuzzy controller gains, and the ADAETM weighting matrix are obtained as $\hslash =27.2294$, $K_{11}=0.0069$, $K_{12}=0.0026$, $K_2=-0.5940$, and $\Omega =3.2766\times {10}^8$. The state responses of ${\mathrm{Plant}}^1$ and ${\mathrm{Plant}}^2$ are shown in Figure 3. The change trajectory of control signals $u_k^1$ and ${\overline{u}}_k^2$ are demonstrated on the left in Figure 4. The release instants, the release intervals, and the adaptive law ${\delta }_k$ are shown on the right in Figure 4.

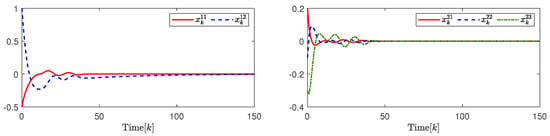
Figure 3. (Left). The response of system state $x_k^1$; (Right). The response of system state $x_k^2$.

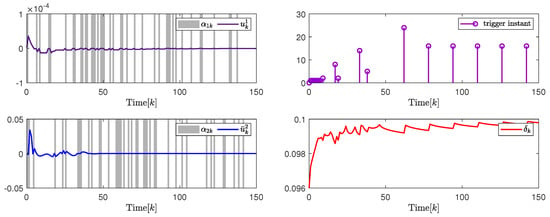
Figure 4. (Left). The control input $u_k^1$ and ${\overline{u}}_k^2$ with ${\overline{\alpha }}_1=0.3$; (Right). The release instants and the release intervals and the adaptive law ${\delta }_k$ with ${\overline{\alpha }}_1=0.3$.

In addition, to further illustrate the impact of the attack probability ${\overline{\alpha }}_1$ on packet transmission rate adjustment and system performance, Figure 5 and Figure 6, and Table 1 give the analysis results under different attack probability ${\overline{\alpha }}_1$. By the design results in Theorem 2, the quantization parameter, security fuzzy controller gains, and the ADAETM weighting matrix are obtained as follows: $\hslash =27.3840$, $K_{11}=0.0098$, $K_{12}=0.0038$, $K_2=-0.3536$, $\Omega =2.2361\times {10}^8$ with ${\overline{\alpha }}_1=0.5$. $\hslash =48.2277$, $K_{11}=0.0158$, $K_{12}=0.0092$, $K_2=-0.3027$, $\Omega =2.2917\times {10}^8$ with ${\overline{\alpha }}_1=0.7$.

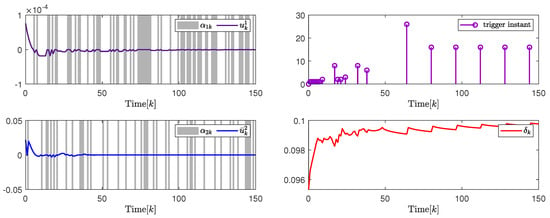
Figure 5. (Left). The control input $u_k^1$ and ${\overline{u}}_k^2$ with ${\overline{\alpha }}_1=0.5$; (Right). The release instants and the release intervals and the adaptive law ${\delta }_k$ with ${\overline{\alpha }}_1=0.5$.

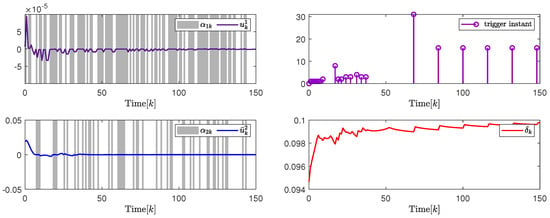
Figure 6. (Left). The control input $u_k^1$ and ${\overline{u}}_k^2$ with ${\overline{\alpha }}_1=0.7$; (Right). The release instants and the release intervals and the adaptive law ${\delta }_k$ with ${\overline{\alpha }}_1=0.7$.

Table 1. Data transmission with different ETMs in Example with PPBTS.

Different ETMs	TN	${\mathit{R}}_{\mathit{e}/\mathit{k}}$	$\mathit{\gamma }$
Triggered mechanism in [27]	47	$31.3\%$	$0.1056$
${\overline{\alpha }}_1=0.3$, ${\delta }_1=0.07$, ${\delta }_2=0.05$, ${\delta }_3=0.03$	20	$13.3\%$	$0.1064$
${\overline{\alpha }}_1=0.5$, ${\delta }_1=0.07$, ${\delta }_2=0.05$, ${\delta }_3=0.03$	22	$14.7\%$	$0.1058$
${\overline{\alpha }}_1=0.7$, ${\delta }_1=0.07$, ${\delta }_2=0.05$, ${\delta }_3=0.03$	24	$16.0\%$	$0.1056$

Based on the above calculation results under different attack probability ${\overline{\alpha }}_1$, Figure 5 on the left and Figure 6 on the left show that the trajectory changes of the control input converge to 0 under ${\overline{\alpha }}_1=0.5$ and ${\overline{\alpha }}_1=0.7$, respectively, and the release instants, and the release intervals, the adaptive law ${\delta }_k$ are shown on the right in Figure 5 and Figure 6, respectively, which indicates the effectiveness of the designed security cascade controller for multi-channel deception attacks. Moreover, to further verify the superiority of the proposed ADAETM, it is compared with the triggered mechanism in [27], and the system performance $\gamma$ under different attack probability ${\overline{\alpha }}_1$ is calculated. Through the transmission number (TN) and transmission rate $R_{e/k}$ in Figure 5 on the right and Figure 6 on the right, and Table 1, it can be seen that the ADAETM designed in this article has great advantages. With the increase in attack probability, the number of triggers will also increase, and the system performance index $\gamma$ will decrease, which explains the rationality of the design of ADAETM to a certain extent. In addition, to further strengthen the demonstration of the superiority of the proposed control design, quantitative performance index analysis under different attack probabilities, such as system convergence time, network channel bandwidth utilization, and optimal $H_{\infty }$ performance index, is presented in Table 2. It can be seen that the increase in attack probability will affect the convergence time of the system and the number of triggered packets to a certain extent, but the design strategy proposed in this article can balance the relationship between attack probability and the number of triggered packets, and maintain the optimal $H_{\infty }$ performance index.

Table 2. Quantitative performance index with different attack probabilities in Example with PPBTS.

Different Attack Probability	System Stability Time	${\mathit{R}}_{\mathit{e}/\mathit{k}}$	$\mathit{\gamma }$
${\overline{\alpha }}_1=0.3$, ${\overline{\alpha }}_2=0.3$	$133/52$	$17.3\%$	$0.1073$
${\overline{\alpha }}_1=0.5$, ${\overline{\alpha }}_2=0.5$	$140/55$	$18.6\%$	$0.1069$
${\overline{\alpha }}_1=0.7$, ${\overline{\alpha }}_2=0.7$	$145/57$	$19.3\%$	$0.1067$

4.2. Comparison Example with PPBPGCS

In order to further verify the superiority of the derived results of Theorem 2, a nonlinear PPBPGCS based on fuzzy model is given. The structure of the NCCS is shown in Figure 7. In the main control loop, ${\mathrm{Sensor}}^1$ is used to measure the output power supply voltage of the power control system. After the influence of ADAETM and deception attacks, the measurement data are fed back to ${\mathrm{Controller}}^1$ and compared with the expected data. The output signal of ${\mathrm{Controller}}^1$ is transmitted to ${\mathrm{Controller}}^2$ as the expected data. In the secondary control loop, ${\mathrm{Controller}}^2$ compares the boiler liquid level data, valve parameters measured by the quantized ${\mathrm{Sensor}}^2$ with the expected data, and transmits the control output signal to the valve that controls the inlet to control the main steam temperature.

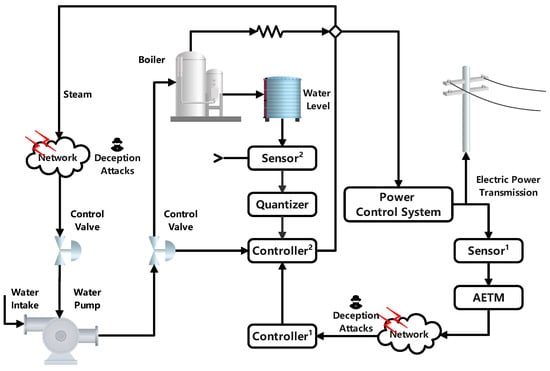
Figure 7. Structure diagram of an NCCS for a nonlinear PPBPGCS.

Suppose that the discrete nonlinear networked PPBPGCS parameters considered in this article are as follows:

$$\begin{array}{cc}\hfill A_{11}& =\left[\begin{array}{cc}0.3443& -0.1768\\ 0.6398& 0.8966\end{array}\right],B_{11}=\left[\begin{array}{c}0.6398\\ 0.3743\end{array}\right]\hfill \\ \hfill A_{12}& =\left[\begin{array}{cc}0.3304& -0.2078\\ 0.6343& 0.8779\end{array}\right],B_{12}=\left[\begin{array}{c}0.6343\\ 0.3278\end{array}\right]\hfill \\ \hfill C_{11}& =C_{12}=\left[\begin{array}{cc}0& 0.45\end{array}\right],D_{11}=D_{12}=0.1\hfill \\ \hfill E_{11}& =E_{12}=\left[\begin{array}{cc}0& 0.45\end{array}\right]\hfill \\ \hfill A_{21}& =\left[\begin{array}{cccc}-0.1474& -0.6879& -0.1888& -0.0165\\ 0.0106& -0.0835& -0.5780& -0.1157\\ 0.0741& 0.4579& 0.6853& -0.0662\\ 0.0424& 0.3300& 0.8977& 0.9781\end{array}\right]\hfill \\ \hfill A_{22}& =\left[\begin{array}{cccc}-0.1465& -0.6812& -0.1733& -0.0144\\ 0.0109& -0.0809& -0.5684& -0.0981\\ 0.0741& 0.4586& 0.6885& -0.0561\\ 0.0424& 0.3301& 0.8985& 0.9814\end{array}\right]\hfill \\ \hfill B_{21}& ={\left[\begin{array}{cccc}0.0106& 0.0741& 0.0424& 0.0140\end{array}\right]}^T\hfill \\ \hfill B_{22}& ={\left[\begin{array}{cccc}0.0109& 0.0741& 0.0424& 0.0140\end{array}\right]}^T\hfill \\ \hfill B_{31}& ={\left[\begin{array}{cccc}-0.1073& 0.0532& 0.0372& 0.0141\end{array}\right]}^T\hfill \\ \hfill B_{32}& ={\left[\begin{array}{cccc}-0.1070& 0.0533& 0.0372& 0.0141\end{array}\right]}^T\hfill \\ \hfill C_{21}& =C_{22}=\left[\begin{array}{cccc}0& 0& 0& 1\end{array}\right],D_{21}=D_{22}=0.1\hfill \\ \hfill E_{21}& =E_{22}=\left[\begin{array}{cccc}0& 0& 0& 1\end{array}\right].\hfill \end{array}$$

Moreover, the MFs are chosen by $d_1\left(x_k^1\right)={cos}^2\left(x_k^{12}\right)$, $d_2\left(x_k^1\right)=1-d_1\left(x_k^1\right)$, $f_1\left(x_k^2\right)=exp\left({\displaystyle \frac{-{\left(x_k^{24}\right)}^2}{3}}\right)$, and $f_2\left(x_k^2\right)=1-f_1\left(x_k^2\right)$. The initial states of the ${\mathrm{Plant}}^1$ and ${\mathrm{Plant}}^2$ are given as $x_0^1={\left[11\right]}^T,x_0^2={\left[1111\right]}^T$ and the external disturbance is given as follows: ${\omega }_k=10e^{-0.01k}{sin}_k$, $0<k\le 15$; Otherwise, ${\omega }_k=0$.

Selecting ${\mathfrak{f}}_k^1=0.1tanh\left({\widehat{y}}_k^1\right)$, ${\mathfrak{f}}_k^2=0.1tanh\left(u_k^2\right)$, $\gamma =1$, $\underline{\tau }=\underline{\theta }=1$, $\overline{\tau }=\overline{\theta }=4$, ${\overline{\alpha }}_1={\overline{\alpha }}_2=0.7$, ${\delta }_1=0.6$, ${\delta }_2=0.4$, ${\delta }_3=0.1$, ${ϵ}_1={ϵ}_3=1$, ${ϵ}_2={ϵ}_4=0.5$, $\Delta =0.1$, $M=10$, and ${\vartheta }_1=0.75<{\vartheta }_2=1.25$. By the design results in Theorem 2, the quantization parameter, security fuzzy controller gains, and the ADAETM weighting matrix are obtained as $\hslash =109.0809$, $K_{11}=0.0025$, $K_{12}=0.0014$, $K_2=0.5201$, and $\Omega =7.1494\times {10}^5$.

The state responses of ${\mathrm{Plant}}^1$ and ${\mathrm{Plant}}^2$ are shown in Figure 8. The change trajectory in the control signals $u_k^1$ and ${\overline{u}}_k^2$ are demonstrated on the left in Figure 9. The release instants, the release intervals, and the adaptive law ${\delta }_k$ are shown on the right in Figure 9.

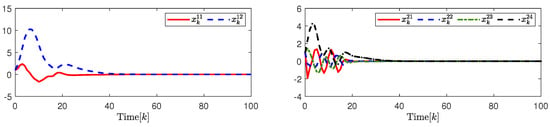
Figure 8. (Left). The response of system state $x_k^1$; (Right). The response of system state $x_k^2$.

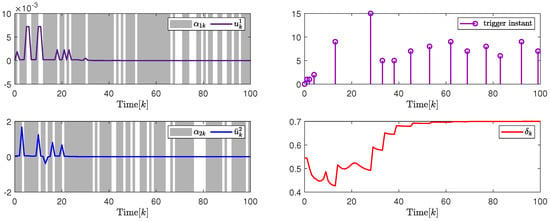
Figure 9. (Left). The control input $u_k^1$ and ${\overline{u}}_k^2$ with ${\overline{\alpha }}_1=0.7$; (Right). The release instants and the release intervals and the adaptive law ${\delta }_k$ with ${\overline{\alpha }}_1=0.7$.

In addition, to further illustrate the impact of the attack probability ${\overline{\alpha }}_1$ on packet transmission rate adjustment and system performance, Figure 10 and Figure 11, and Table 2 give the analysis results under different attack probability ${\overline{\alpha }}_1$. By the design results in Theorem 2, the quantization parameter, security fuzzy controller gains, and the ADAETM weighting matrix are obtained as follows: $\hslash =114.1739$, $K_{11}=0.0022$, $K_{12}=0.0012$, $K_2=0.5048$, $\Omega =7.4453\times {10}^5$ with ${\overline{\alpha }}_1=0.6$. $\hslash =121.9136$, $K_{11}=0.0024$, $K_{12}=0.0013$, $K_2=0.4041$, $\Omega =1.1506\times {10}^6$ with ${\overline{\alpha }}_1=0.8$.

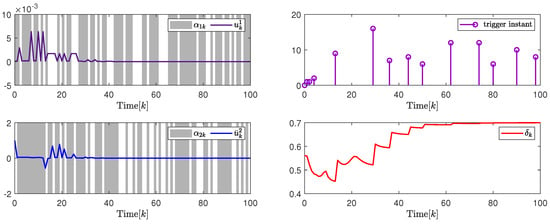
Figure 10. (Left). The control input $u_k^1$ and ${\overline{u}}_k^2$ with ${\overline{\alpha }}_1=0.6$; (Right). The release instants and the release intervals and the adaptive law ${\delta }_k$ with ${\overline{\alpha }}_1=0.6$.

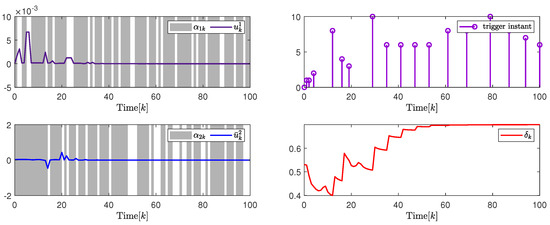
Figure 11. (Left). The control input $u_k^1$ and ${\overline{u}}_k^2$ with ${\overline{\alpha }}_1=0.8$; (Right). The release instants and the release intervals and the adaptive law ${\delta }_k$ with ${\overline{\alpha }}_1=0.8$.

Based on the above calculation results under different attack probability ${\overline{\alpha }}_1$, the left in Figure 10 and Figure 11 are show the trajectory changes of the control input converge to 0 under ${\overline{\alpha }}_1=0.6$ and ${\overline{\alpha }}_1=0.8$, respectively, which indicates the effectiveness of the designed security cascade controller for multi-channel deception attacks. Similar to the analysis of Example with PPBTS, the data in Figure 10 and Figure 11, and Table 3 also show the effectiveness of the designed security cascade controller design algorithm against multi-channel deception attacks. Similar to the analysis results in Section 4.1, Table 4 also gives quantitative performance analysis under different attack probabilities, which further verifies the superiority of the control design.

Table 3. Data transmission with different ETMs in Example with PPBPGCS.

Different ETMs	TN	${\mathit{R}}_{\mathit{e}/\mathit{k}}$	$\mathit{\gamma }$
Triggered mechanism in [27]	37	$37.0\%$	$0.4608$
${\overline{\alpha }}_1=0.6$, ${\delta }_1=0.6$, ${\delta }_2=0.4$, ${\delta }_3=0.1$	15	$15.0\%$	$0.4593$
${\overline{\alpha }}_1=0.7$, ${\delta }_1=0.6$, ${\delta }_2=0.4$, ${\delta }_3=0.1$	17	$17.0\%$	$0.4575$
${\overline{\alpha }}_1=0.8$, ${\delta }_1=0.6$, ${\delta }_2=0.4$, ${\delta }_3=0.1$	19	$19.0\%$	$0.4483$

Table 4. Quantitative performance index with different attack probability in Example with PPBPGCS.

Different Attack Probability	System Stability Time	${\mathit{R}}_{\mathit{e}/\mathit{k}}$	$\mathit{\gamma }$
${\overline{\alpha }}_1=0.6$, ${\overline{\alpha }}_2=0.6$	$55/47$	$29.0\%$	$0.4671$
${\overline{\alpha }}_1=0.7$, ${\overline{\alpha }}_2=0.7$	$57/48$	$31.0\%$	$0.4603$
${\overline{\alpha }}_1=0.8$, ${\overline{\alpha }}_2=0.8$	$60/50$	$35.0\%$	$0.4533$

5. Conclusions

This article mainly explores the SCOFC design problem of nonlinear NCCSs based on ADAETM and dynamic quantization under multi-channel deception attacks interference. The adaptive function of ADAETM can flexibly adjust the triggered threshold according to the state of deception attacks, and further alleviate the impact of deception attacks on system performance and stability. By using Lyapunov–Krasovskii stability theory, matrix decoupling lemma, and relaxation matrix technique, sufficient conditions for the mean square asymptotically stable and prescribed performance of the system are obtained. The criteria for the joint design of event-triggered weight matrix, dynamic quantizer parameters and controller are given in terms of a set of LMIs. Finally, the proposed SCOFC design strategy is verified by simulation of PPBTS and PPBPGCS.

The ADAETM proposed in this article is designed under the assumption that the attack probability is known in advance. Such assumptions inevitably make the design results have certain limitations. In an open network environment, complex, hybrid, and multiple attacks caused by various types of network attacks and a variety of network attack combinations often occur. Therefore, based on the existing work and literature, the future research focus of the security controller design and attack signal observer design problem of NCCSs under multi-channel complex attacks is considered. In addition, the controller design problem of NCCSs affected by internal time-varying delays and other network-induced factors is also a common problem in practical industrial engineering, which also stimulates future research work.