Mathematical Model to Study the Effect of Refuge on Cannibalism in Atractosteus tropicus
Abstract
1. Introduction
2. Equilibrium Points and Their Stability
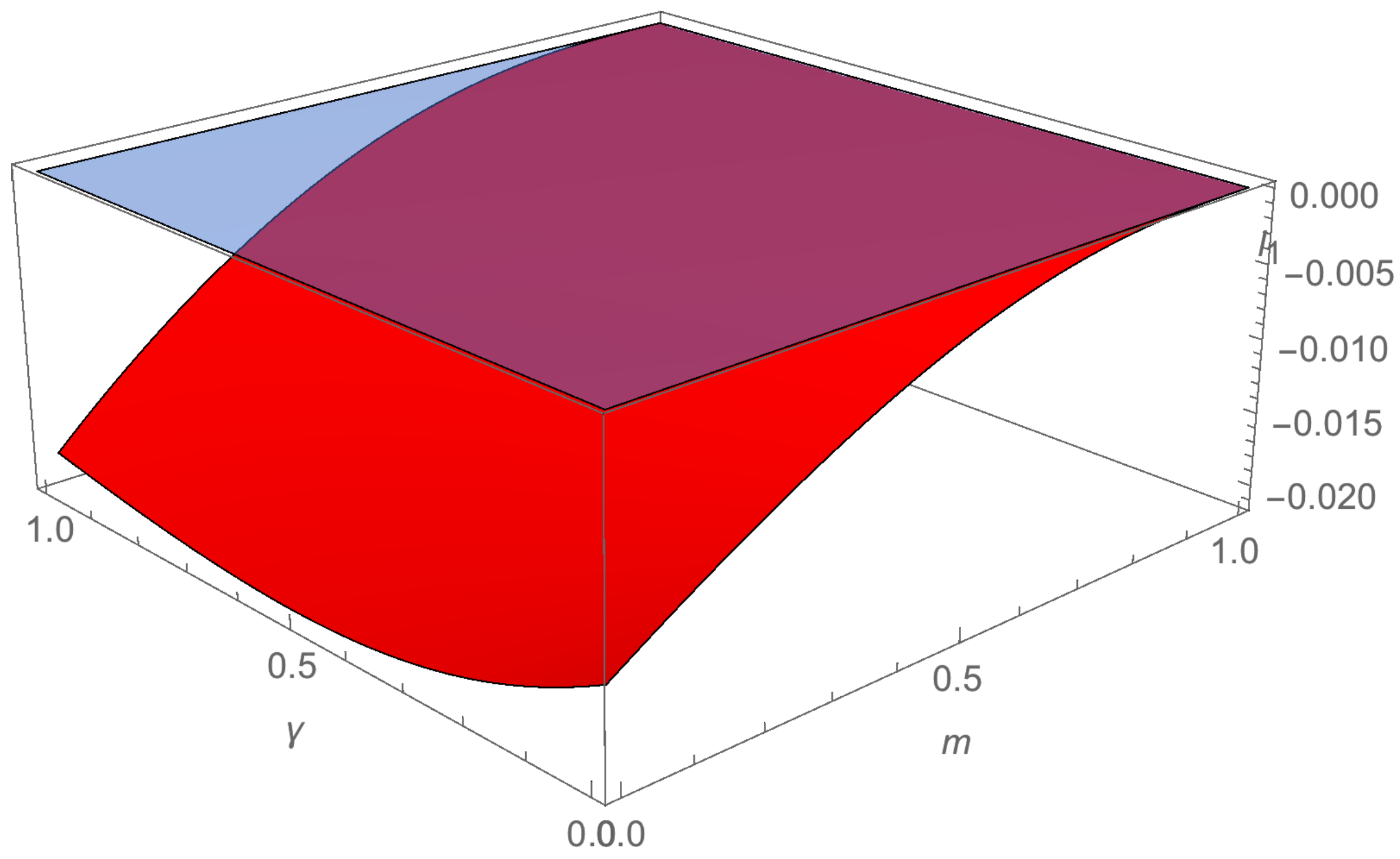
3. Hopf Bifurcation at Equilibrium Point p∗
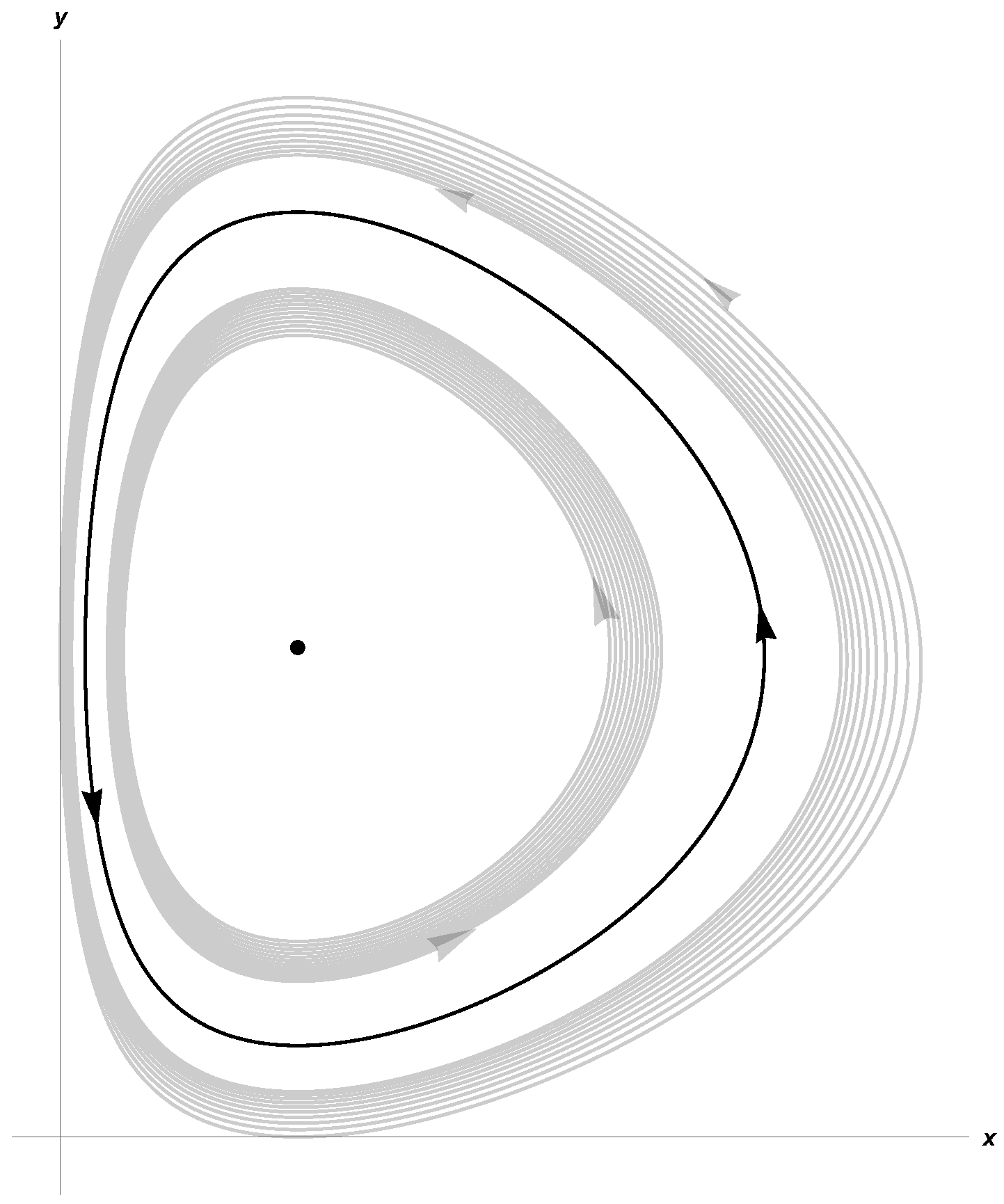
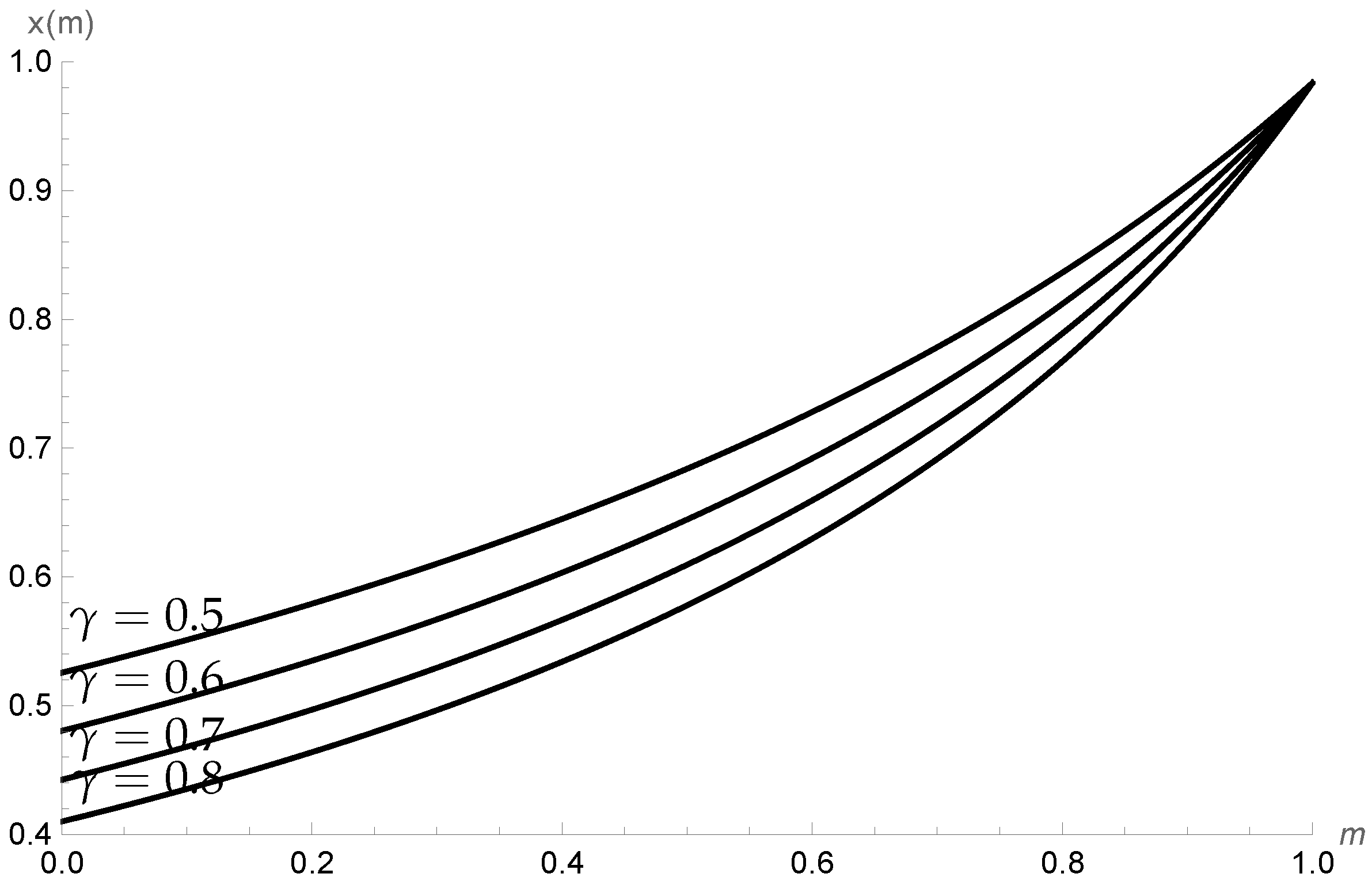
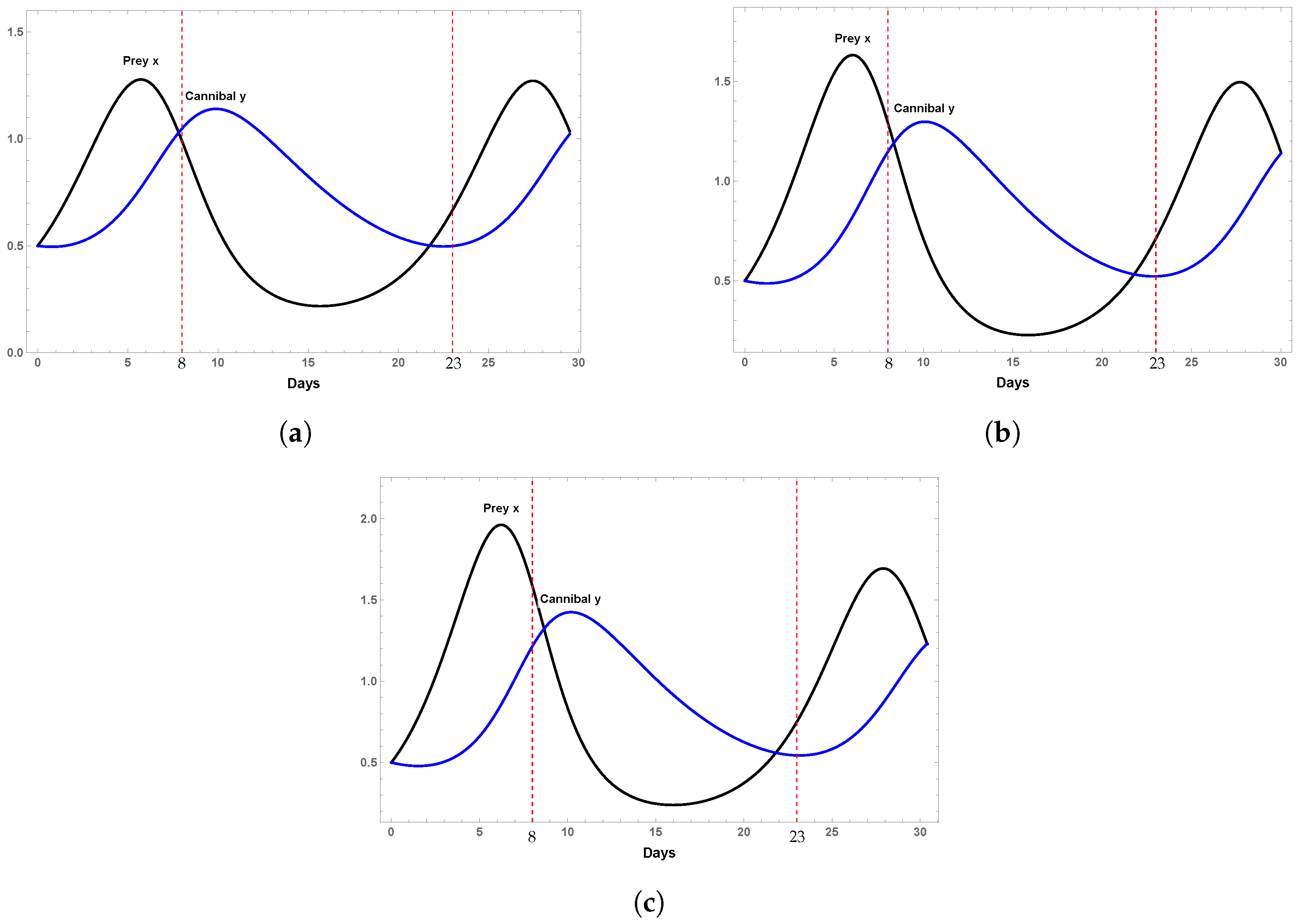
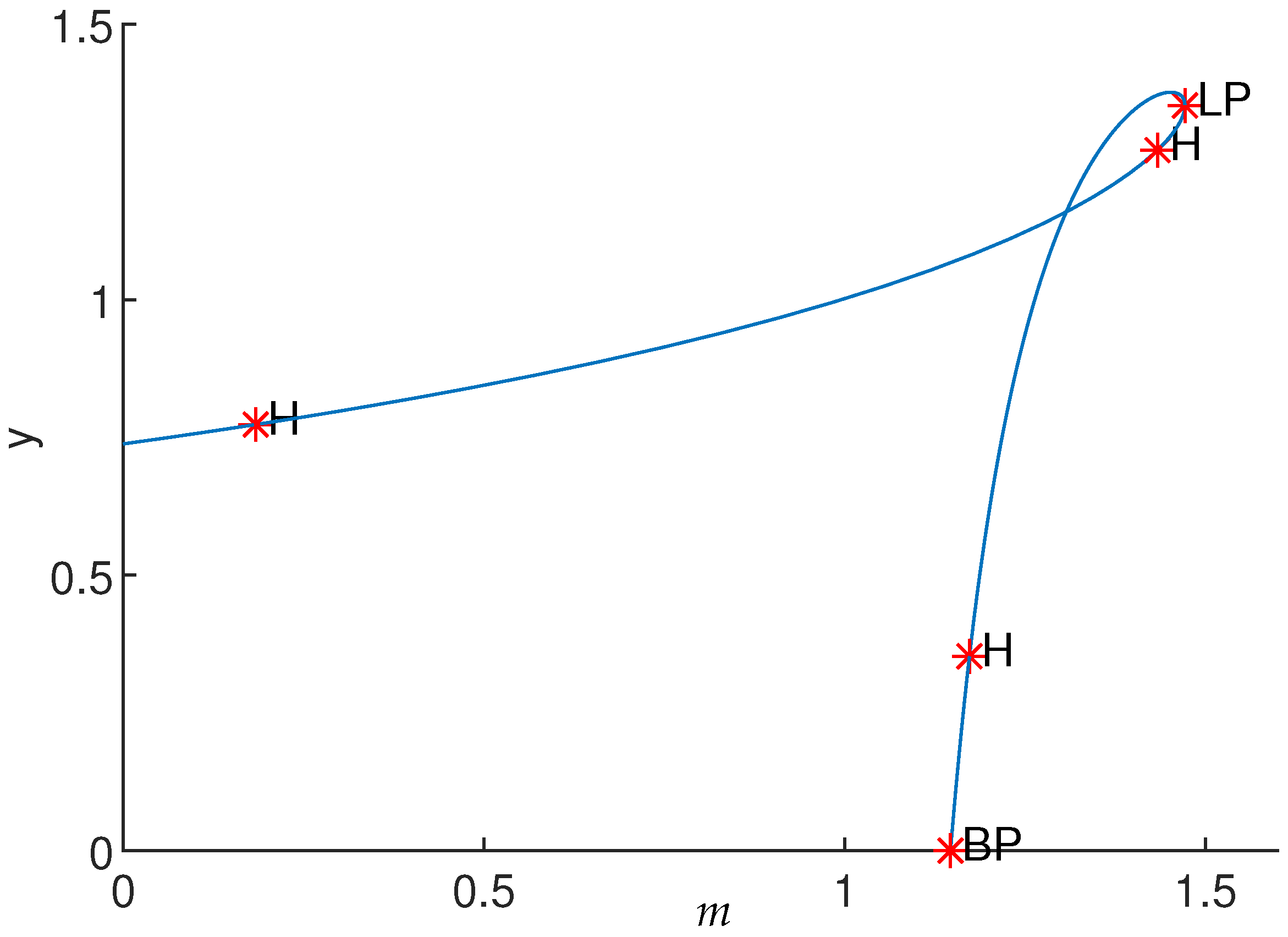
4. Numerical Simulation
4.1. Example 1
4.2. Example 2
4.3. Example 3
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PVC | Polyvinyl chloride |
Appendix A
Appendix A.1. Local Dynamics
Appendix A.2. Proof of Theorem 1
Appendix A.3. Purely Imaginary Eigenvalues
Appendix A.4. Hopf Bifurcation
References
- Ironside, J.E.; Dalgleish, S.T.; Kelly, S.J.; Payne, W. Sex or food? Effects of starvation, size and diet on sexual cannibalism in the amphipod crustacean. Aquat. Ecol. 2019, 53, 1–7. [Google Scholar] [CrossRef]
- Johnson, J.C.; Halpin, R.; Stevens, R., II. Extreme developmental synchrony reduces sibling cannibalism in the black widow spider, Latrodectus hesperus. Anim. Behav. 2016, 120, 61–66. [Google Scholar] [CrossRef]
- Nishimura, K. An interaction-driven cannibalistic reaction norm. Ecol. Evol. 2018, 8, 2305–2319. [Google Scholar] [CrossRef] [PubMed]
- Polis, G.A. The evolution and dynamics of intraspecific predation. Ann. Rev. Ecol. Syst. 1981, 12, 225–251. [Google Scholar] [CrossRef]
- Rosas-Luis, R.; Jiménez-Badillo, M.L.; Montoliu-Elena, L.; Morillo-Velarde, P.S. Food and feeding habits of Octopus insularis in the Veracruz Reef System National Park and confirmation of its presence in the southwest Gulf of Mexico. Mar. Ecol. 2019, 40, e12535. [Google Scholar] [CrossRef]
- Neer, A.V.; Gross, S.; Kesselring, T.; Wohlsein, P.; Leitzen, E.; Siebert, U. Behavioural and pathological insights into a case of active cannibalism by a grey seal. (Halichoerus grypus) on Helgoland, Germany. J. Sea Res. 2019, 148, 12–16. [Google Scholar] [CrossRef]
- Yu, Z.L.; Wang, H.; Song, H.; Bai, Y.C.; Sun, J.C.; Qian, Y.S.; Hu, N.; Yang, M.J.; Zhang, T. Cannibalism by the juveniles of the gastropod Rapana venosa (Muricidae) reared under laboratory conditions. J. Molluscan Stud. 2018, 84, 303–309. [Google Scholar] [CrossRef]
- Pfennig, D.W. Kinship and cannibalism. Bioscience 1997, 47, 667–675. [Google Scholar] [CrossRef]
- Smith, C.; Reay, P. Cannibalism in teleost fishes. Rev. Fish Biol. Fish. 1991, 1, 41–64. [Google Scholar] [CrossRef]
- Pereira, L.S.; Agostinho, A.A.; Winemiller, K.O. Revisiting cannibalism in fishes. Rev. Fish Biol. Fish. 2017, 27, 499–513. [Google Scholar] [CrossRef]
- Baras, E.; Ndao, M.; Maxi, M.Y.Y.; Jeandrain, D.; Thomé, J.P.; Vanadewalle, P.; Melard, C. Sibling cannibalism in dorada under experimental conditions. I. Ontogeny, dynamics, bioenergetics of cannibalism and prey size selectivity. J. Fish Biol. Fish. 2000, 57, 1001–1020. [Google Scholar] [CrossRef]
- Baras, E.; Jobling, M. Dynamics of intracohort cannibalism in cultured fish. Aquac. Res. 2002, 33, 461–479. [Google Scholar] [CrossRef]
- Baras, E. Cannibalism in fish larvae: What have we learned. In Larval Fish Aquaculture; Nova Science Publishers: New York, NY, USA, 2013; pp. 167–199. [Google Scholar]
- Cuff, W.R. Behavioral aspects of cannibalism in larval walleye, Stizostedion vitreum. Can. J. Zool. 1980, 58, 1504–1507. [Google Scholar] [CrossRef] [PubMed]
- Márquez-Couturier, G.; Vázquez-Navarrete, C.J. Estado del arte de la biología y cultivo de pejelagarto (Atractosteus tropicus). Agroproductividad 2015, 8, 44–51. [Google Scholar]
- Nelson, J.S. Fishes of the World; John Wiley Sons: Edmonton, AB, Canada, 2006. [Google Scholar]
- Aguilera, C.; Mendoza, R.; Iracheta, I.; Marquez, G. Digestive enzymatic activity on Tropical gar (Atractosteus tropicus) larvae fed different diets. Fish. Physiol. Biochem. 2012, 38, 679–691. [Google Scholar] [CrossRef]
- Márquez-Couturier, G. Biología y tecnología para el cultivo del pejelagarto Atractosteus tropicus en el sureste de México. Inst. Nac. Pesca 2000, 8, 265–267. [Google Scholar]
- Sepúlveda-Quiroz, C.A.; Alvarez-Villagomez, C.S.; Mendoza-Porras, O.; Peña-Marín, E.S.; Maytorena-Verdugo, C.S.; Pérez-Jiménez, G.M.; Jesus-Contreras, R.; Álvarez-González, C.A.; Martínez-García, R. Attack behavior leading cannibalism in tropical gar (Atractosteus tropicus) larvae under different tank colors and shelter type. Aquaculture 2023, 563, 738991. [Google Scholar] [CrossRef]
- Palma-Cancino, D.J.; Martinez-Garcia, R.; Alvarez-Gonzalez, C.A.; Camarillo-Coop, S.; Peña-Marin, E.S. Esquemas de alimentación para larvicultura de pejelagarto (Atractosteus tropicus Gill): Crecimiento, supervivencia y canibalismo. Ecosist. Recur. Agropec. 2019, 6, 273. [Google Scholar] [CrossRef]
- Márquez-Couturier, G.; Vázquez-Navarrete, C.; Contreras-Sánchez, W.M.; Álvarez-González, C.A. Acuicultura Tropical Sustentable: Una Estrategia Para la Producción y Conservación del Pejelagarto (Atractosteus tropicus) en Tabasco, México; Universidad Juárez Autónoma de Tabasco: Tabasco, México, 2013; pp. 1–223. [Google Scholar]
- Duck, K.; Pajdak, J.; Terech-Majewska, E.; Szarek, J. Intracohort cannibalism and methods for its mitigation in cultured freshwater fish. Rev. Fish Biol. Fish. 2017, 27, 193–208. [Google Scholar] [CrossRef]
- Näslund, J.; Johnsson, J.I. Environmental enrichment for fish in captive environments: Effects of physical structures and substrates. Fish Fish. 2014, 17, 1–30. [Google Scholar] [CrossRef]
- Xi, D.; Zhang, X.; Lü, H.; Zhang, Z. Cannibalism in juvenile black rockfish, Sebastes schlegelii (Hilgendorf, 1880) Reared under controlled conditions. Aquaculture 2017, 479, 682–689. [Google Scholar] [CrossRef]
- Qin, J.G.; Mittiga, L.; Ottolenghi, F. Cannibalism Reduction in Juvenile Barramundi Lates calcarifer by Providing Refuges and Low Light. J. World Aquac. Soc. 2004, 35, 113–118. [Google Scholar] [CrossRef]
- Beay, L.K.; Saija, M. A Stage-Structure Rosenzweig-MacArthur Model with Effect of Prey Refuge. Jambura J. Biomath. 2020, 1, 1–7. [Google Scholar] [CrossRef]
- Kar, T.K. Stability analysis of a prey–predator model incorporating a prey refuge. Commun. Nonlinear Sci. Numer. Simul. 2005, 10, 681–691. [Google Scholar] [CrossRef]
- Nelson, J.S. The Dynamics of Arthropod Predator-Prey Systems; Princeton University Press: Princenton, NJ, USA, 1978. [Google Scholar]
- Nilsson, K.A.; Persson, L. Refuge availability and within-species differences in cannibalism determine population variability and dynamics. Ecosphere 2013, 4, 1–15. [Google Scholar] [CrossRef]
- Hecht, T.; Appelbaum, S. Observations on intraspecific aggression and coeval sibling cannibalism by larval and juvenile Claias gariepinus (Clariidae: Pisces) under controlled conditions. J. Zool. 1998, 214, 21–44. [Google Scholar] [CrossRef]
- Kuznetsov, Y.A. Elements of Applied Bifurcation Theory; Springer: New York, NY, USA, 2004. [Google Scholar]


| Equilibrium Point | Eigenvalues | Local Dynamics |
|---|---|---|
| p1 | Unstable node if . Saddle if . Saddle node if . | |
| p2 | −α, N | Stable node if N < 0. Saddle if N > 0. Saddle node if N = 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sepúlveda-Quiroz, C.A.; Valenzuela, L.M.; Blé, G.; Martínez-García, R.; Álvarez-González, C.A.; López-Molina, A. Mathematical Model to Study the Effect of Refuge on Cannibalism in Atractosteus tropicus. Mathematics 2024, 12, 3380. https://doi.org/10.3390/math12213380
Sepúlveda-Quiroz CA, Valenzuela LM, Blé G, Martínez-García R, Álvarez-González CA, López-Molina A. Mathematical Model to Study the Effect of Refuge on Cannibalism in Atractosteus tropicus. Mathematics. 2024; 12(21):3380. https://doi.org/10.3390/math12213380
Chicago/Turabian StyleSepúlveda-Quiroz, César Antonio, Luis Miguel Valenzuela, Gamaliel Blé, Rafael Martínez-García, Carlos Alfonso Álvarez-González, and Antioco López-Molina. 2024. "Mathematical Model to Study the Effect of Refuge on Cannibalism in Atractosteus tropicus" Mathematics 12, no. 21: 3380. https://doi.org/10.3390/math12213380
APA StyleSepúlveda-Quiroz, C. A., Valenzuela, L. M., Blé, G., Martínez-García, R., Álvarez-González, C. A., & López-Molina, A. (2024). Mathematical Model to Study the Effect of Refuge on Cannibalism in Atractosteus tropicus. Mathematics, 12(21), 3380. https://doi.org/10.3390/math12213380








