Abstract
Accurately estimating the modulation parameters of pseudorandom binary code–pulse amplitude modulation (PRBC–PAM) signals damaged by strong noise poses a significant challenge in emitter identification and countermeasure. Traditionally, weak signal detection methods based on chaos theory can handle situations with low signal-to-noise ratio, but most of them are developed for simple sin/cos waveform and cannot face PRBC–PAM signals commonly used in ultra-low altitude performance equipment. To address the issue, this article proposes a novel adaptive detection and estimation method utilizing the in-depth analysis of the Duffing oscillator’s behaviour and output characteristics. Firstly, the short-time Fourier transform (STFT) is used for chaotic state identification and ternary processing. Then, two novel approaches are proposed, including the adjusting zero value (AZV) method and the chaotic state ratio (CSR) method. The proposed weak signal detection system exhibits unique capability to adaptively modify its internal periodic driving force frequency, thus altering the difference frequency to estimate the signal parameters effectively. Furthermore, the accuracy of the proposed method is substantiated in carrier frequency estimation under varying SNR conditions through extensive experiments, demonstrating that the method maintains high precision in carrier frequency estimation and a low bit error rate in both the pseudorandom sequence and carrier frequency, even at an SNR of −30 dB.
Keywords:
adaptive measurement and parameter estimation; low signal-to-noise ratios (SNRs); pseudorandom sequence estimation; duffing oscillator; chaotic state ratio (CSR) MSC:
93E11; 60G35
1. Introduction
Pseudorandom binary code–pulse amplitude modulation (PRBC–PAM) signals play a pivotal role in proximity sensors and short-range radar due to their remarkable detection precision. The measurement and estimation of PRBC–PAM signal parameters are crucial for further identification and countermeasure. Nevertheless, these processes are considerably challenging, especially in scenarios where the operational range is extended and the signal-to-noise ratio (SNR) is detrimentally low, which is attributable to the limited power output of the sensor [1,2,3]. As depicted in Figure 1, this scenario underscores the significance of accurately measuring and estimating signal parameters under such countermeasure conditions. A lower SNR measured by a reconnaissance system implies the capability to detect and estimate signal parameters from a greater distance relative to the PRBC–PAM sensor. Therefore, studying the measurement and estimation of PRBC–PAM signal parameters is highly important for modern reconnaissance.
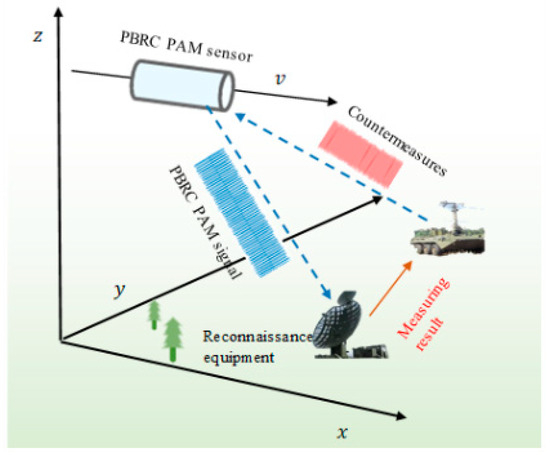
Figure 1.
The measurement and estimation scenario of PRBC–PAM signal.
Although numerous studies on the parameter estimation methods of continuous-wave PRBC signals have been studied, limitations remain, including the general requirement of a known carrier frequency for estimating pseudorandom codes, the low estimation accuracy of the carrier frequency, and poor estimation performance under low SNRs [4,5,6,7]. In contrast, there is not only limited research on pulse PRBC signal parameter estimation methods but also a lack of valuable information. The stochastic resonance (SR) method [8,9] was used to estimate the carrier frequency for an aperiodic signal and PRBC signal; however, the method cannot estimate the PAM pseudorandom sequence. Ref. [10] presented a dual-channel cooperative sub-Nyquist sampling system for linear frequency-modulated BPSK signals. However, the estimation accuracy of the code phase deteriorates rapidly when the SNR is less than 10 dB. The third-order correlation function method in references [11,12] was adopted to estimate PAM pseudorandom sequences, but this method requires a known exact carrier frequency. In addition, none of the studies discussed above obtained effective estimation results at low SNRs. In another realm of the literature, the short-time Fourier transform [13], the smoothed pseudo-Wigner distribution [14], and the fractional Fourier transform [15,16] were used for signal parameter analysis, but the computational cost was large, and the calculation time was high, which made it difficult to fill the real-time demands of signal detection and parameter estimation. By introducing the constant delay, Zheng et al. [17] proposed the parameterized centroid frequency-chirp rate distribution (PCFCRD) technique, which is based on a newly defined correlation function, for noisy multicomponent LFM signal analysis. Antinoise performance and estimation results could be obtained at −12 dB SNR.
The duffing oscillator is a kind of nonlinear system which has a wide application prospect in the area of weak signal detection owing to its sensitivity to weak periodic signals under the critical chaotic state and resistance to noise [18,19,20,21], which can be very helpful for solving the urgent problem in ultra-low signal-to-noise ratio cases. Its abundant nonlinear properties play a vital role in parameter estimation of the continuous-wave PRBC signal [22,23,24,25,26], which is the key support to obtain the carrier frequency and pseudorandom sequence estimation at very low SNRs. However, there are few studies about the PRBC–PAM signal parameter estimation method based on the duffing system. Therefore, further research is urgently needed.
In view of the outstanding properties of the Duffing oscillator system, a weak signal detection system is proposed by us to obtain the exact frequency and PAM sequence estimation of the weak PRBC–PAM signal when faced with low-SNR environments. The main contributions are as follows:
- (1)
- We redesigned the original duffing system by adjusting the frequency of its internal periodic driving force and put forward the adjusting zero value (AZV) method to estimate the carrier frequency of the weak PRBC–PAM signal, which significantly improves the estimation accuracy and stability at very low SNRs.
- (2)
- To obtain a high-accuracy estimation of the pseudorandom sequence of the weak PRBC–PAM signal, the chaotic state ratio (CSR) method is proposed by analyzing the influence of the pulse signal duty ratio on the chaotic states of three-valued signals. The experiment results show a low bit error rate at an SNR of −30 dB, which verifies the estimation accuracy of the chaotic state ratio (CSR) method.
- (3)
- The experiments were conducted under different SNRs, which mainly consists of the prototype of the PRBC–PAM sensor and the signal acquisition system. The estimation results of different methods show that the proposed method is more stable at a higher level under different SNRs. The NRMSE still reaches 0.01 at −30 dB SNR, which is superior to the other methods.
The overall structure of this paper is as follows. Section 2 demonstrates the Duffing oscillator system for weak signal detection, estimated using both the standard sinusoidal signal and the PRBC–PAM signal. Section 3 presents the AZV and CSR methods for estimating the carrier frequency and the pseudorandom sequence of the PRBC–PAM signal. In Section 4, the parameter estimation method described in this paper is simulated and verified under various SNRs. Finally, Section 5 concludes the study and summarizes the key findings.
2. Detection Model and Mechanism
2.1. Traditional Detection System Based on Duffing Equation
The Duffing equation is a typical nonlinear system and has a relatively simple expression and structure. The phase trajectories of this system show distinct characteristics when driven by different types of signals with different parameters, which can be used for weak signal detection. The expression of a traditional Duffing oscillator with a weak signal detection system is as follows:
In a physical sense, x stands for displacement, t represents time, k = 0.5 is the damping coefficient, and −x + x3 is the spring’s nonlinear restoring force. Fcos(ωt) is the internal periodic driving force of the detection system with amplitude F and frequency ω; Acos(ω0t + φ0) is the external input weak periodic signal we are interested in; n(t) is a stochastic disturbance, which we suppose to be a Gaussian white noise with distribution .
In Equation (1), we set |Δω| = |ω0 − ω| as the frequency difference between the oscillator’s internal driving signal and the external input signal. The system has a critical threshold Fc ≈ 0.826, which can be solved by the maximum Lyapunov exponential method. When F < Fc, the system is in a chaotic state, and the phase graph is irregular; when F > Fc, it is in a large-scale periodic state, and the phase trajectories show a stable periodic distribution. At the state transition critical point F = Fc, if the signal to be detected has the same frequency as that of the internal periodic driving force, namely, Δω = 0, the system state will suddenly change to regular large-scale periodic state; while if Δω ≠ 0 and |Δω|/ω ≤ 0.03, the system will be in an intermittent chaotic state, which changes regularly and intermittently between the large-scale periodic state and the chaotic state over time, with a period of T = 2π/|Δω|; if |Δω|/ω > 0.03, the intermittent chaotic state transition will be irregular.
Figure 2 shows the phase graph of a chaotic state and a large-scale periodic state. Figure 3 illustrates the intermittent chaotic state. We set ω0 = 2π × 100 MHz, Δω = 2π × 3 MHz, A = 0.1, φ0 = 0 here.
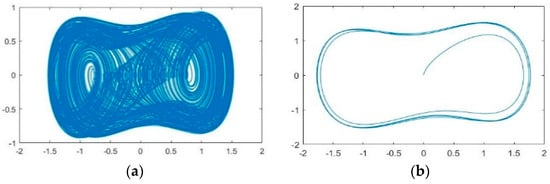
Figure 2.
Phase diagrams of chaotic and large−scale periodic states. (a) Chaotic state, (b) large-scale periodic state, .
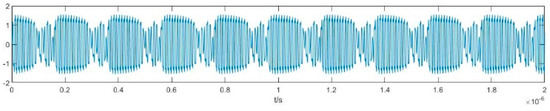
Figure 3.
Time–output diagram of the intermittent chaotic state.
2.2. Detection System Excited by the PRBC–PAM Signal
The signal generation process of the PRBC–PAM signal usually includes directional coupling, pseudorandom code generation, synchronous pulse circuit combination, and phase modulation, as shown in Figure 4.
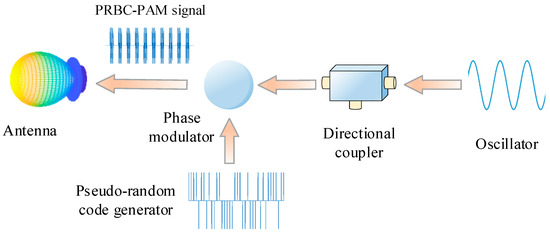
Figure 4.
Generation process of the PRBC–PAM signal.
Equation (2) shows the PRBC signal generated by the m-sequence generator:
where , is the unit pulse with width Tc, P is the pulse number, Tr = PTc is the pseudorandom code repetition period, N is the modulation period number, and Ci = {+1, −1}.
Here, we express the pulse signal as follows:
where Tp is the pulse width, and Tm is the pulse repetition period. In general, the code width of the pseudorandom code in the PRBC–PAM signal is equal to the repetition period of the modulated pulse, namely, Tc = Tm. Hence, the PAM pseudorandom sequence can be expressed as a product of the PRBC signal and the pulse signal as Equation (4):
Figure 5 shows the time-domain graph of the PRBC signal, the high-frequency pulse signal, and the PAM pseudorandom sequence in the case of Tc = Tm.
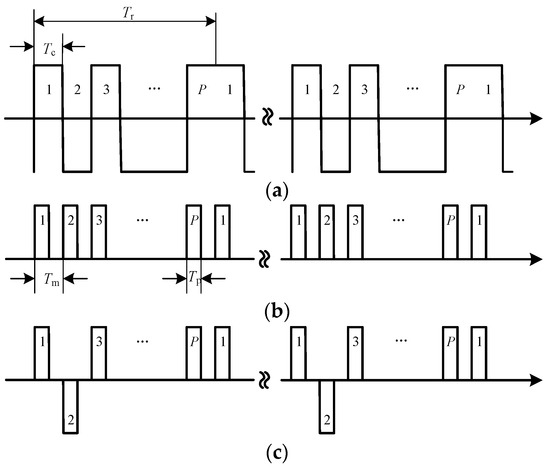
Figure 5.
Waveform evolution process of the PAM pseudorandom sequence: (a) PRBC signal; (b) Pulse signal; (c) PAM pseudorandom sequence.
The transmitted PRBC–PAM signal is obtained by modulating the oscillator signal from the PAM pseudorandom sequence, expressed as Equation (5):
where A is the amplitude of the weak signal, sp(t) is the PAM pseudorandom sequence, u(t) is the pulse signal, ω0 is the carrier frequency, φ0 is the initial phase, and φi is the phase code , where p(t) is the pseudorandom code shown in Equation (2). For simplicity, s(t) is obtained by combining sp(t) with cosine modulation, or u(t) with pseudocode cosine modulation.
When the weak signal detection system is excited by a weak PRBC–PAM signal, i.e., the simple sinusoidal wave to be measured in the original Duffing weak signal detection system is replaced by a PRBC–PAM signal, then we can write the detection model as follows:
Similar to the simple sinusoidal case, set F = Fc, so that the system is in a critical chaotic state. If the noise n(t) is ignored, the total driving force is as follows:
where
where, φ(t) = φ0 + φi, and |Δω| = |ω − ω0|. Next, we analyze the relationship between equivalent amplitude Fe(t) and critical threshold Fc, so as to explore the impact of excitation on the system under different parameter conditions. According to Equation (8), taking Δω = 0 and φ0 = 0 as the simplest example, due to the influence of u(t) and φi, the relationship between the equivalent amplitude Fe(t) and the amplitude of the internal driving signal Fc is constantly changing, as shown in Figure 6. When u(t) = 0, Fe(t) = Fc, the detection system, i.e., Equation (6), will be in a critical chaotic state; when u(t) = 1, if φi = 0, Fe(t) = Fc + A, it will be in a large-scale periodic state; if φi = π, then Fe(t) = |Fc − A|, it will be in a chaotic state. When Δω ≠ 0, φ0 ≠ 0, in the case of u(t) = 1, although Fe(t) is affected by both Δω and φ(t), the cosine value is still within the range of [−1, 1]. Then, Fe(t) also varies within the range of [(|Fc − A|), (Fc + A)], allowing the detection system to switch between chaotic state and large-scale periodic state. Therefore, the phase change pattern of the new weak signal detection system driven by a PRBC–PAM signal is different from that driven by a simple sine signal. Regardless of whether Δω equals zero or not, the detection system’s output will always be in the intermittent chaotic state, which includes the critical chaotic state in addition to the chaotic state and the large-scale periodic state. The Duffing oscillator changes with the values of u(t) and φ(t) in the chaotic state, critical chaotic state and large-scale periodic state, and the PRBC–PAM signal parameters can be estimated according to the variation rules of these three states.
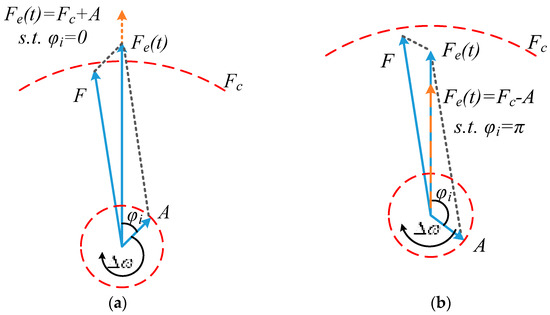
Figure 6.
The magnitude relationship between the equivalent driving force amplitude and the critical threshold of the duffing oscillator system: (a) ; (b) .
3. Parameter Estimation Method for the Weak PRBC–PAM Signal
3.1. System Output Symbolization
Driven by the PRBC–PAM signal, the transition of Equation (6)’s output between three states, namely, chaotic, critical chaotic, and large-scale periodic state, is caused by the gradual variation in the driving force. So, it is natural to infer PRBC–PAM parameters from the information brought by the output sequences using the concept of SSS (Symbol Sequence Statistics) [27,28,29].
According to the basic qualitative analysis of Section 2, it is possible to establish a quantitative relationship between the detection system’s output and input. Inspired by idea of the symbol sequence statistic, the output can be roughened into a new sequence composed of 1, 0, −1 to distinguish chaotic states, critical chaotic states, and large-scale periodic states, to highlight input features, so that the processed output sequence only contains the output state type rather than the real value, highlighting the relationship between the input and output of the detection system, and further obtaining estimated parameters.
The difference between the critical chaotic state and chaotic state is small and hard to distinguish by general signal processing methods. Due to the fact that the three states are in different time positions for the same signal and their frequencies are different, the time–frequency processing technique, short-time Fourier transform (STFT), can be used for state recognition to realize three-valued processing [30,31].
The STFT is a kind of local time–frequency analysis technique. It uses the window function to intercept the signal for a short period and obtains the frequency of the intercepted segment through traditional Fourier transform; then, the time–frequency distribution can be obtained by moving carefully designed window functions along the time axis. The three-dimensional time–frequency distribution of the three states obtained by the STFT is shown in Figure 7, from which it is evident that although the critical chaotic state and the chaotic state are similar, the three states can be effectively distinguished by the STFT method. The amplitude spectrum peaks of the chaotic state fluctuate violently and irregularly, which is relatively chaotic. Although the amplitude spectrum of the critical chaotic state is also messy, the peak value’s distribution basically follows a horizontal line. The amplitude spectral peaks of large-scale periodic states are very clean and flat.

Figure 7.
Three-dimensional time–frequency distribution diagram obtained by the STFT in three states: (a) Chaotic state; (b) Critical chaotic state; (c) Large-scale periodic state.
To further analyze the impact of the internal driving signal’s frequency on the STFT results, time-domain diagrams of three states with different internal driving frequencies are given in Figure 8. For one given state, the time–amplitude curves of the different frequencies vary slightly, but the overall trend stays the same. For these three states, they are obviously different at different frequencies. Firstly, the maximum amplitude of the chaotic state is far from the other two. Secondly, the maximum amplitudes in Figure 8b,c are nearly the same. But in terms of the average value, the mean amplitude in Figure 8b is smaller than in Figure 8c because of the fluctuation in the maximum amplitude curve.
Figure 8.
Time-domain diagram of the STFT in three states: (a) Chaotic state; (b) Critical chaotic state; (c) Large-scale periodic state.
In summary, the time-domain diagram is obtained from the frequency point corresponding to the maximum amplitude in the three-dimensional time–frequency distribution graph obtained by the STFT method, and then, the mean value of the highest amplitude curve is used as the decision parameter of the system state, which is expressed as follows:
where i and j represent the i-th time point and the j-th frequency point, respectively. N is the sequence length, and gHam is the Hamming window function which can significantly sidelobe attenuation that can greatly reduce spectrum leakage. The critical threshold E1 between the chaotic state and the critical chaotic state and E2 between the critical chaotic state and the large-scale periodic state can be obtained through experiments. Then, when Em < E1, the detection system is in a chaotic state; when Em > E2, it is in a large-scale periodic state; and when E1 ≤ Em ≤ E2, it is in a critical chaotic state.
Therefore, excited by a PRBC–PAM signal, the Duffing oscillator output can be processed to obtain a three-valued signal as follows: obtaining the decision parameter Em of the output signal in a certain time interval by the STFT method and then comparing it with E1 and E2 to identify its state; and setting the amplitude value of this period to be −1, 0, and 1 when it is in a chaotic state, critical state, and large-scale periodic state, respectively. Finally, the three-valued signal of the output signal can be obtained after completing the state discrimination for the whole sequence, and it can be represented by Sdf(t):
Taking the measured weak PRBC–PAM signal frequency ω0 as equal to the internal driving signal frequency ω of the Duffing oscillator as an example, when ω0 = ω = 100 MHz, A = 0.6, and Tc = 100 ns, the time-domain diagram of the output signal and the time-domain diagram after three-valued processing of the output signal are shown in Figure 9a,b, respectively. Figure 9 shows that the three-valued Duffing oscillator output signal can be effectively measured by the method based on the STFT.
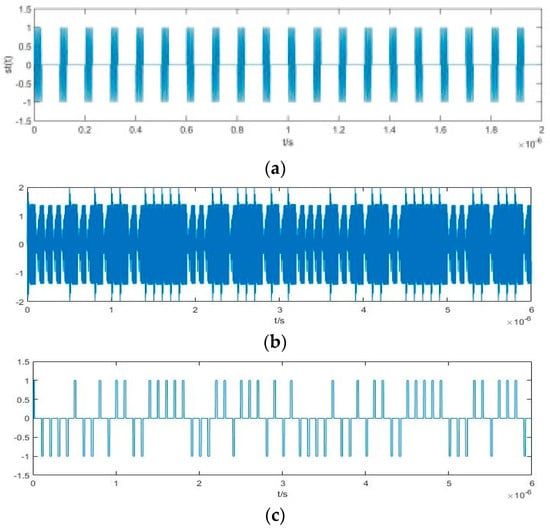
Figure 9.
Time−domain diagrams of the detection system driven by the PRBC-PAM signal: (a) Time-domain diagram of the input PAM’s sequence; (b) Time-domain diagram of the system output; (c) Time-domain diagram of Sdf(t).
3.2. Parameter Estimation
According to Equation (11), the PAM pseudorandom sequence has three values, 1, −1, and 0, and the pseudorandom code has two values, 1 and −1. By comparing the pseudorandom code and the PAM pseudorandom sequence, it is evident that the PAM pseudorandom sequence is the result of adding values of 0 based on the duty cycle characteristics of the pulse signal. Since the duty cycle of the pulse signal is constant, the parameters of the pulse signal can be estimated according to the ratio between the existence times of 1 or −1 and 0 in the PAM pseudorandom sequence.
Figure 10 shows the process for estimating the PRBC–PAM signal parameters based on the AZV and CSR methods of the Duffing oscillator. Firstly, the critical amplitude and frequency of the Duffing oscillator are preset. Secondly, the states of the Duffing oscillator are identified based on STFT; Then, the 0 value of the ternary signal Sdf(t) of the output signal of the Duffing oscillator is adjusted to the nearest non-zero value of the signal p(t), which is a pseudorandom sequence of the pseudo-code pulse Doppler fuze signal. The ratio z1 of the time taken by value 1 in Sdf(t) is the duty cycle of the pulse signal. Next, by averaging the smallest numbers that are close to each other in the duration of 1 or −1 in p(t), the code width Tc of the pseudorandom sequence is obtained, which is also equal to the repetition period Tm of the pulse signal. Finally, the pseudorandom sequence is multiplied by the pulse signal with a known duty cycle, and the PAM pseudorandom sequence is obtained after removing burrs.
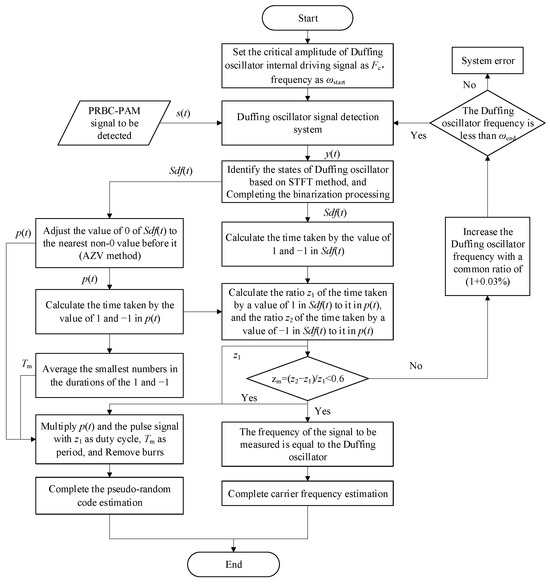
Figure 10.
Flow chart for the PRBC-PAM signal parameter estimation based on the Duffing oscillator.
When the frequency of the to-be-measured PRBC-PAM signal equals the internal driving signal of the Duffing oscillator, i.e., ω0 = ω, the PAM pseudorandom {1,−1,0} code sequence expression of the PRBC-PAM signal totally equals our processed three-valued sequence Sdf(t), as we subtract both of them, and the result is 0. This can be explained by the critical threshold characteristics of the system. The set detection system in the critical chaotic state and ω0 = ω time-domain position of the positive PRBC-PAM pulses will make the equivalent threshold of the system equal to |Fc + A|, the position without pulses will still be in the critical state, and the time-domain position of the negative PRBC-PAM pulses will make the equivalent threshold of the system equal to |Fc − A|. Based on the system state, the further processed Sdf(t) can fully reflect the input PRBC-PAM pulse characteristics. So if we know the frequency, the PAM pseudorandom {1,−1,0} code sequence can be directly estimated by the three-valued Duffing oscillator’s output signal, as can be seen in Figure 9b and Figure 11.
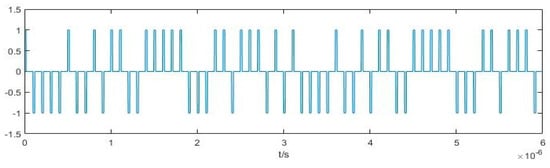
Figure 11.
Time−domain diagram of the PAM pseudorandom sequence.
In addition, the ratio of the time lengths of 1 and −1 of the PAM pseudorandom {1,−1,0} code sequence to the total time length is equal to the duty cycle of the pulse signal. Therefore, the pseudorandom code of the PRBC–PAM signal can be obtained by adjusting the value of 0 of the PAM pseudorandom {1,−1,0} code sequence to the nearest non-zero value before it. In this paper, this method is called adjusting the zero value (AZV) method. Figure 12a shows the pseudorandom code obtained after adjusting the 0 value, and Figure 12b presents the actual pseudorandom code of the signal, which shows that these two figures exhibit a one-to-one correspondence.
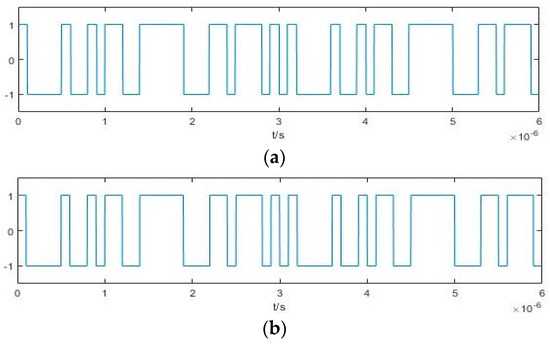
Figure 12.
Pseudo−random code time-domain diagram: (a) Pseudorandom code time-domain diagram obtained by Sdf(t) with the AZV method; (b) Pseudorandom code time-domain diagram of the actual signal.
When the frequency to be measured is not equal to the internal driving signal, i.e., ω0 ≠ ω, there is a significant difference in the time-domain plots of the output Sdf(t) and the PAM pseudorandom sequences. Figure 13a–d shows the detection system’s output signal, its three-valued signal Sdf(t), the estimated pseudorandom code obtained by the AZV method, and the actual PAM pseudorandom sequence when ω = 100 MHz, ω0 = 104 MHz, and the symbol width is p = 100 ns. It is easy to know that the values of 1, −1, and 0 for the PAM pseudorandom sequence and Sdf(t) no longer exhibit a one-to-one correspondence, and the ratio of the existing times of −1 and 0 no longer conforms to the regularity of the duty cycle because of the frequency difference, and the chaotic state and the critical chaotic state only exhibit little difference. According to Equation (8), when Δω = 0, the chaotic state with an equivalent amplitude of |Fc − A| is significantly different from the critical chaotic state with an equivalent amplitude of Fc, which makes it relatively easy to identify the different states of the Duffing oscillator output signal.
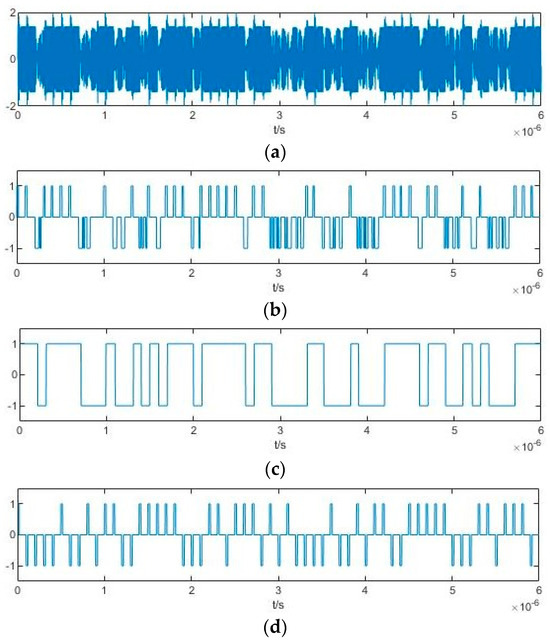
Figure 13.
Time-domain diagram of several signals when Δω ≠ 0: (a) detection system’s output; (b) Sdf(t); (c) Estimated pseudorandom code after the AZV method; (d) Actual PAM pseudorandom sequence.
However, when Δω ≠ 0, the value of cos(Δω + φ(t)) changes with the change in Δω, and the equivalent amplitudes of the chaotic state also change constantly between |Fc − A| and Fc. When the equivalent amplitude of the chaotic state is close to Fc, it is difficult to distinguish between the chaotic state and the critical chaotic state. Although the equivalent amplitude of the large-scale period state also changes between Fc and (Fc + A), due to the sensitivity of the Duffing oscillator for weak signals, as long as the equivalent amplitude Fe is slightly larger than the critical amplitude Fc, the Duffing oscillator system is in a large-scale period state, which means that the change in Δω has little effect on the large-scale period state. Therefore, the time occupied by −1 in Sdf(t) (the existence time of the critical chaotic state) and the time occupied by −1 in the estimated pseudorandom code after AZV are not equal to the duty cycle of the pulse signal, but the time occupied by 1 (the existence time of the large-scale periodic state) is still equal to the duty cycle. The ratio of the time taken by the value of 1 in the actual pseudorandom code to the time taken by the value of 1 in the estimated pseudorandom code after AZV is denoted as , and the ratio of the time taken by the value of −1 in the actual pseudorandom code to the time taken by the value of −1 in the estimated pseudorandom code after the AZV is . Set as the evaluation indicator, which can be expressed as follows:
To find the threshold of zm, the values of zm obtained under different frequency differences Δω are shown in Figure 14 to help determine whether the frequencies are equal. Here, the signal to be detected has a frequency of 100 MHz. With the increase in Δω (the frequency of the Duffing oscillator internal periodic driving force signal changes adaptively), although the value of zm fluctuates to some extent, the overall trend also increases. When zm reaches a certain value (approximately zm = 1.3), it decreases slightly, but it always remains above 0.9. Therefore, a certain threshold can be set when zm is less than the threshold, and the frequency difference is Δω = 0, which means that the carrier frequency of the signal in the test is equal to the internal driving force signal of the Duffing oscillator. When Δω = 0.03 MHz and ω = 100.03 MHz, we can obtain zm = 0.5805. To verify the accuracy of the method and estimate its sensitivity, the parameters of the PRBC–PAM signals at different carrier frequencies are estimated. By adjusting the frequency of the Duffing oscillator’s internal periodic driving signal, the maximum frequency of the Duffing oscillator is taken when zm < 0.6, nearly zm = 0.5805, and the estimated sensitivity can be obtained. Taking the carrier frequency of ω0 = 100 MHz for the PRBC–PAM signal as an example, let the frequency ω of the Duffing oscillator increase continuously and adaptively from 100 MHz; when ω = 100.03 MHz and zm = 0.5805, the estimated sensitivity is rm = (100.03 − 100)/100 × 100% = 0.03%. In addition, simulations are also carried out for the cases of ω0 = 10 kHz, 100 kHz, 10 MHz, 1 GHz, and 10 GHz. The highest frequency of the Duffing oscillator when zm < 0.6, the evaluation indicator zm, and the estimated sensitivity rm are shown in Table 1. In this paper, the carrier frequency estimation method based on the ratio of the time of the critical chaotic state and large-scale periodic state to the corresponding time of the pseudorandom code obtained by the AZV method is referred to as the CSR method.
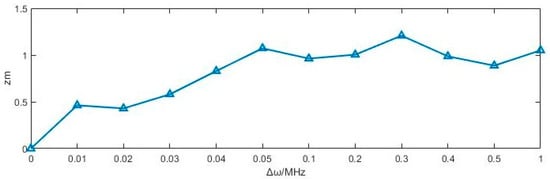
Figure 14.
Relational graph of Δω and zm.

Table 1.
Simulation results at various frequencies.
In practical applications, receivers can roughly measure the signal frequency. Therefore, the carrier frequency range of the PRBC–PAM signal, (ωstart, ωend), can be obtained based on prior knowledge. According to the estimated sensitivity above, the frequency of the internal driving force starts from ωstart and increases adaptively with q = 1 + 0.03%, which is the common ratio. The Duffing oscillator system is run once at each value, and the zm value can be obtained. When zm < 0.6, the PRBC–PAM signal’s carrier frequency is considered equal to the internal driving force signal of the Duffing oscillator.
As described before, when the frequency of the to-be-measured weak signal equals that of the Duffing oscillator’s internal driving force signal, Sdf(t) has a one-to-one correspondence to the PAM pseudorandom sequence, and the pseudorandom code estimated by adjusting Sdf(t) with the AZV method also exhibits one-to-one correspondence with the actual pseudorandom code. However, because the measured carrier frequency is not guaranteed to be the same as the actual carrier frequency and because it is easy for errors to be introduced during three-valued processing, adjusting the zero value can eliminate the influence of burrs or tiny errors, and thus, the estimation result of the pseudorandom code is superior to that of Sdf(t). Therefore, the PAM pseudorandom sequence estimation is completed by obtaining the duty cycle of the pulse signal and the estimated pseudorandom code based on the AZV method rather than directly by Sdf(t). At this time, the signal p(t) obtained by adjusting the value of 0 of Sdf(t) is the pseudorandom code, and the ratio of the time taken by a value of 1 in Sdf(t) to that in p(t) is the duty cycle of the pulse signal, which is called z1. By averaging the smallest numbers in the duration of 1 or −1 in p(t), the code width Tc of the pseudorandom code can be obtained, which is also equal to the repetition period Tm of the pulse signal. Finally, the PAM pseudorandom sequence can be obtained by multiplying the estimated pseudorandom sequence by the pulse signal with a known duty cycle and deburring. Roughly speaking, if the frequency to be estimated is known, the underestimated pseudorandom code of the PRBC-PAM signal can be directly obtained from the ternary result Sdf(t); if the frequency to be estimated is unknown, we should first estimate the frequency to be tested through zm, and then obtain the pseudorandom code of the PRBC-PAM signal as we know the frequency.
4. Experiments and Analysis
To verify the effectiveness of the proposed technology, comprehensive experiments were conducted under different SNRs by adjusting the variance σ2 of Gaussian white noise n(t). The experimental layout and scenario are depicted in Figure 15. The experiment system mainly consists of the prototype of the PRBC–PAM sensor and the signal acquisition system, energized by a direct current (DC)-regulated voltage source, and interfaced with a horn antenna for signal radiation into open space. The apparatus for signal monitoring and analysis encompasses a suite of equipment: a double-ridge waveguide horn antenna, a signal generator, a quad-channel downconverter, a wideband digital receiver, an integrated embedded controller, and a display monitor. Within this system, the signal generator furnishes a downconverted reference signal for the local oscillator. After downconversion, the signal undergoes sampling and analysis by the wideband digital receiver. Furthermore, the embedded controller facilitates parameter configuration for each device in the setup.
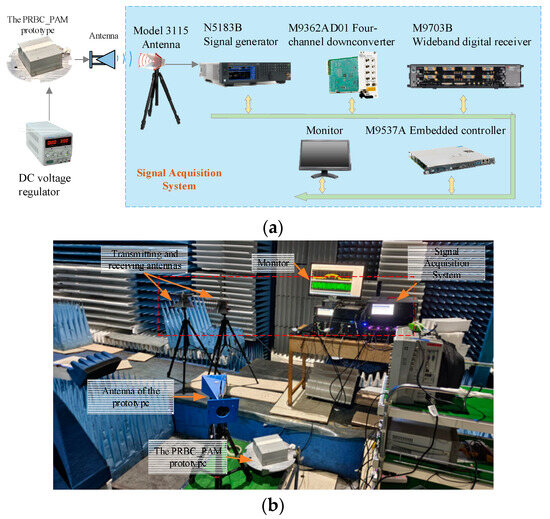
Figure 15.
The experimental layout and scenario: (a) The layout of the experimental setup; (b) The experimental scenario.
We fix the to-be-measured PRBC-PAM signal’s frequency as ω = 100 MHz. The code element width of the pseudorandom code is set to Tc = 100 ns, the repetition period of the pulse signal is fixed as Tm = Tc = 100 ns, and the duty cycle of the pulse signal is set to 20%. A summary of the primary parameters is presented in Table 2.

Table 2.
Summary of main parameters.
4.1. Comparison of Carrier Frequency Estimation Under Different SNRs
Under different levels of SNR, the PRBC–PAM signal’s carrier frequency is estimated according to the AZV and CSR methods based on the Duffing oscillator. The highest frequency of the Duffing oscillator when zm < 0.6, the evaluation indicator zm, and the estimated sensitivity rm are shown in Table 3. The proposed method can achieve an effective estimation of the carrier frequency under different SNRs. When zm < 0.6, rm is generally slightly greater than 0.03%. Therefore, the threshold value of the common ratio of 0.03% can meet the estimation accuracy, and it is still effective under low SNRs. Under an SNR of −30 dB, rm decreases because it is hard to distinguish Duffing’s three-phase states under this situation, and the three-valued processing has a large error. In other words, both the values of 1 and −1 are disordered and cannot meet the requirements of the duty cycle characteristics. The Duffing equation’s output and its three-valued results are shown in Section 4.2.

Table 3.
Carrier frequency estimation results under different SNRs.
To further evaluate the proposed method in carrier frequency estimation of the PRBC–PAM signal, several related state-of-the-art methods are compared with the proposed method, including the SR algorithm in references [8,9], the search algorithm in reference [10], the smoothed pseudo-Wigner–Ville distribution (SPWVD) method proposed in reference [14], the WRFRFT method proposed in reference [15], and the PCFCRD method proposed in reference [17]. The estimated carrier frequency based on the proposed Duffing oscillator and those methods are shown in Figure 13. The normalized root mean square error (NRMSE) results of each method under different SNRs are shown in Figure 16; here, we define the NRMSE as follows [27]:
where x0 is the parameter’s true value, xk is what we estimated, and N represents the number of simulations in a given experiment.
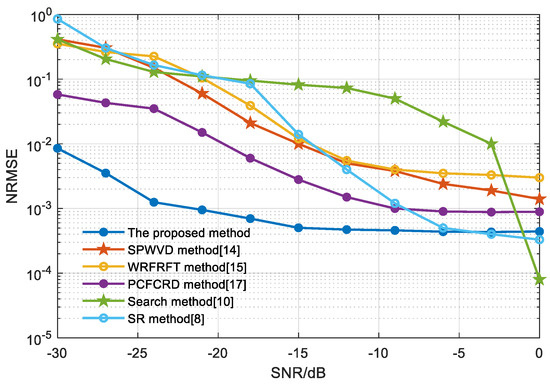
Figure 16.
NRMSE of the carrier frequency estimation of different methods under different SNRs [8,10,14,15,17].
It can be seen from Figure 16 that the carrier frequency estimation results based on the Duffing system proposed in this paper are stable at a higher level under different SNRs. The NRMSE still reaches 0.01 at −30 dB SNR, which is superior to the other methods. Although the NRMSE value of the proposed method is slightly higher when the SNR is 0 dB, its estimation accuracy is sufficiently low, and it has almost no effect on the estimation of the PAM pseudorandom sequence.
4.2. Comparison of PAM Pseudorandom Sequence Estimation Under Different SNRs
As seen in Section 4.1, when the value of zm is less than 0.6 at different SNRs, the values of rm for the carrier frequency are all above 0.03%, so a common ratio of 0.03% can be used to effectively estimate the carrier frequency. To verify that the carrier frequency estimation sensitivity has little influence on the PAM pseudorandom sequence estimation, the analysis is performed on the measured PAM pseudorandom sequence when ω0 = 100.03 MHz. The time-domain diagram of each estimated parameter under different SNRs are shown in Figure 17, Figure 18, Figure 19, Figure 20 and Figure 21. The figures show that with a reduced SNR, the output of the Duffing equation gradually becomes inconsistent, the boundary between the three states gradually blurs, and the difficulty of three-valued processing increases accordingly. Therefore, the deviations between the estimated pseudorandom code or the PAM pseudorandom sequence and the actual signals also increase. When the SNR is −25 dB, the similarity between the estimated results and the actual signals is still very high. However, when the SNR is −30 dB, it is difficult to distinguish the different states of the Duffing equation’s output. Furthermore, the estimation of the pseudorandom code and PAM pseudorandom sequence are also quite different from the actual signals.
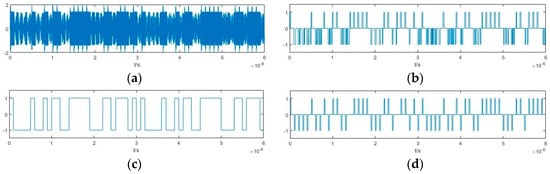
Figure 17.
Time−domain diagram of several signals under an SNR of 0 dB when ω0 = 100.03 MHz: (a) Output signal of the Duffing oscillator y(t); (b) Binarized signal Sdf(t); (c) Estimated pseudorandom code; (d) Estimated PAM pseudorandom sequence.
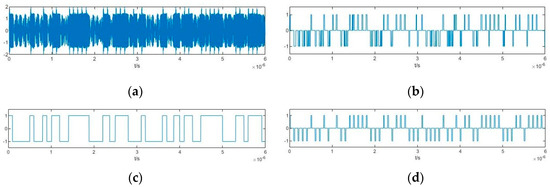
Figure 18.
Time-domain diagram of several signals under an SNR of −10 dB when ω0 = 100.03 MHz: (a) Output signal of the Duffing oscillator y(t); (b) Binarized signal Sdf(t); (c) Estimated pseudorandom code; (d) Estimated PAM pseudorandom sequence.
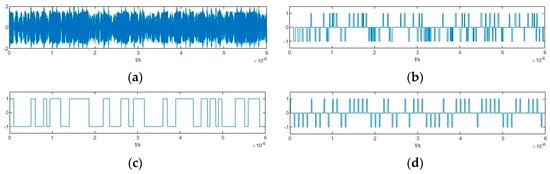
Figure 19.
Time-domain diagram of several signals under an SNR of −20 dB when ω0 = 100.03 MHz: (a) Output signal of the Duffing oscillator y(t); (b) Binarized signal Sdf(t); (c) Estimated pseudorandom code; (d) Estimated PAM pseudorandom sequence.
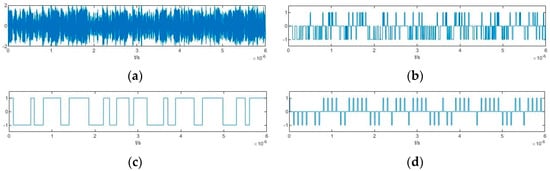
Figure 20.
Time-domain diagram of several signals under an SNR of −25 dB when ω0 = 100.03 MHz: (a) Output signal of the Duffing oscillator y(t); (b) Binarized signal Sdf(t); (c) Estimated pseudorandom code; (d) Estimated PAM pseudorandom sequence.
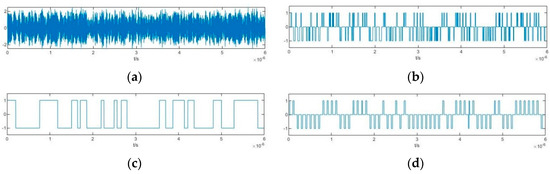
Figure 21.
Time-domain diagram of several signals under an SNR of −30 dB when ω0 = 100.03 MHz: (a) Output signal of the Duffing oscillator y(t); (b) Binarized signal Sdf(t); (c) Estimated pseudorandom code; (d) Estimated PAM pseudorandom sequence.
Under different SNRs, the pulse signal repetition period, duty cycle, and duty cycle evaluation indicator zm are estimated and compared. In addition, the Pearson correlation coefficient is used to compare the estimated pseudorandom code and PAM pseudorandom sequence with the actual signal. The estimated results are shown in Table 4. The Pearson correlation coefficient is defined as follows:
where cov(x, y) is the covariance of variable x and y, and and are the indicator deviations.

Table 4.
Estimation results under different SNRs.
As shown in Table 4, with the reduction in the SNR, the Pearson coefficient between the estimated pseudorandom sequence or PAM pseudorandom sequence and the actual signals gradually decreases, but it can still exceed 0.75 at −25 dB, so there is a high correlation, indicating a good estimation result. Parameters such as the code width, duty cycle, and evaluation indicator zm are found to be similar under different SNRs. However, at −30 dB, the Pearson coefficients decrease substantially, and there is also a large deviation between the values of the estimated and actual duty cycles. The evaluation indicator zm is lower than that of other SNRs because the impact of noise leads to insufficient accuracy in three-valued processing, resulting in a large discrimination error.
In addition, the pseudorandom sequence estimation performance of different related methods is compared to verify the superiority of the proposed method. These methods include the search method in reference [10], the third-order correlation function (TOCF) method in references [11,12], the SPWVD proposed in reference [14], the WRFRFT method proposed in [15], and the PCFCRD method proposed in reference [17]. Figure 18 shows the estimation results of the PAM pseudorandom sequence under different SNRs. Both the Duffing oscillator method and the search method initially estimate the carrier frequency accurately and then estimate the PAM pseudorandom sequence accordingly. From Figure 16 and Figure 22, the precision of the carrier frequency estimation based on the Duffing oscillator method at 0 dB is less than that of the search method, but the PAM pseudorandom sequence estimation precision based on the Duffing method is still substantially greater than that of the search method and the carrier frequency known by the third-order correlation function method as well as the other methods, which has a more obvious advantage under low SNRs. In addition, the bit error rate for the PAM pseudorandom sequence of the proposed method is only 11.67% under an SNR of −30 dB, which is far less than that of the other methods and verifies its effectiveness at a very low SNR.
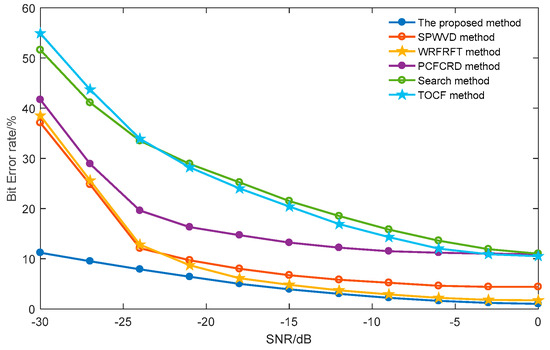
Figure 22.
Bit error rate for the PAM pseudorandom sequence of different method for different SNRs.
In conclusion, the comparison results show that the proposed AZV and CSR methods based on the Duffing oscillator can acquire an estimation precision of 0.03%, and can realize a high-precision estimation of the element width of the pseudorandom code, pseudorandom sequence, duty cycle of the pulse signal, and PAM pseudorandom sequence. At an SNR of −30 dB, the carrier frequency and PAM pseudorandom sequence estimation results still have good performance.
5. Conclusions and Discussion
In this paper, based on the Duffing oscillator weak signal detection system, the AZV and CSR methods are proposed to accurately estimate the carrier frequency and PAM pseudorandom sequence of the PRBC-PAM signal. In the estimation process, the STFT method is used to identify and obtain the three-valued output of the Duffing oscillator driven by a PRBC-PAM signal. The AZV and the CSR method are designed to adaptively estimate the carrier frequency and PAM pseudorandom sequence. Several related methods are compared in the experiment and simulation, which include tests on PAM pseudorandom sequences with maximum common ratio deviation, and the results show that the proposed parameter estimation method can still achieve high estimation accuracy of the PRBC-PAM signal at very low SNR. The NRMSE of its carrier frequency estimation reaches 0.01 at the SNR of −30 dB, while the bit error rate remains at a low level of 11.6%.
Author Contributions
Methodology, M.L., K.W. and J.D.; formal analysis, X.Y. and J.D.; writing—original draft, M.L. and X.H.; funding acquisition, J.D. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to acknowledge the National Natural Science Foundation of China (grant No. 62301051 and No. 61973037).
Data Availability Statement
The data used to support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shi, S.Z.; Zhao, Z.Y.; Liu, J.N. Comparison of radar waveforms combining pseudo-random binary phase coding and chirp modulation for a high-frequency monostatic radar. IET Radar Sonar Navig. 2019, 10, 935–944. [Google Scholar] [CrossRef]
- Zhao, H.C. Design Principle and Method of Radio Fuze; National Defense Industry Press: Beijing, China, 2022. [Google Scholar]
- Zhang, C.; Wang, L.; Jiang, R.; Hu, J.; Xu, S. Radar jamming decision-making in cognitive electronic warfare: A review. IEEE Sens. J. 2023, 20, 11383–11403. [Google Scholar] [CrossRef]
- Hu, G.; Chen, Z.; Zhao, P.; Yang, L. Graph-based confidence verification for BPSK signal analysis under low SNRs. Signal Process. 2023, 20, 1088–1098. [Google Scholar] [CrossRef]
- Wang, J.; Rodriguez, D.; Mishra, A.; Nallabolu, P.R.; Karp, T.; Li, C. 24-GHz impedance-modulated BPSK tags for range tracking and vital signs sensing of multiple targets using an FSK radar. IEEE Trans. Microw. Theory Tech. 2021, 69, 1817–1828. [Google Scholar] [CrossRef]
- Huang, G.; Xiang, Y.; Deng, S.; Zhang, Y.; Wang, J. Sub-Nyquist sampling and parameter measurement of LFM-BPSK hybrid modulated signal. Digit. Signal Process. 2024, 12, 104267–104283. [Google Scholar] [CrossRef]
- Duan, C.; Zhan, Y. The response of a linear monostable system and its application in parameter estimation for PSK signals. Phys. Lett. A 2019, 380, 1358–1362. [Google Scholar] [CrossRef]
- Zhou, Z.; Yu, W.; Wang, J.; Liu, M. A high dimensional stochastic resonance system and its application in signal processing. Chaos Solitons Fractals 2022, 154, 111642–111652. [Google Scholar] [CrossRef]
- Fan, X.; Bai, P.; Liang, X.; Zhang, J.; Liu, B. Detection Algorithm of BPSK Signal of Parameter-adjusted Bistable Stochastic Resonance Model based on Scale Change. IEEE Access 2021, 7, 261–275. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, S.; Zhao, H. Single channel source separation and parameter estimation of multi-component PRBCPM-SFM signal based on generalized period. Digit. Signal Process. 2019, 40, 224–237. [Google Scholar] [CrossRef]
- Adams, E.R.; Gouda, M.; Hill, P.C.J. Detection and characterization of DS/SS signals using higher-order correlation. In Proceedings of the ISSSTA’95 International Symposium on Spread Spectrum Techniques and Applications, Taichung, Taiwan, 17–20 October 2020; Volume 1, pp. 27–31. [Google Scholar]
- Liu, S.K.; Yan, X.P.; Li, P.; Yu, H.H. Design of Jamming Signal on Pseudo-random Code Phase-modulation and Pulse Doppler Combined Fuze Based on Code Reconstruction. Acta Armamentarii 2022, 39, 1088–1094. [Google Scholar]
- Yang, Y.; Peng, Z.; Zhang, W.; Meng, G. Parameterised time-frequency analysis methods and their engineering applications: A review of recent advances. Mech. Syst. Signal Process. 2019, 119, 182–221. [Google Scholar] [CrossRef]
- Hu, Z.; Ma, H. Blind modal estimation using smoothed pseudo Wigner–Ville distribution and density peaks clustering. Meas. Sci. Technol. 2022, 31, 105004–105013. [Google Scholar] [CrossRef]
- Li, X.; Sun, Z.; Zhang, T.; Yi, W.; Cui, G.; Kong, L. WRFRFT-based coherent detection and parameter estimation of radar moving target with unknown entry/departure time. Signal Process. 2023, 16, 107228–107241. [Google Scholar] [CrossRef]
- Akilli, M.; Yilmaz, N. Study of weak periodic signals in the EEG signals and their relationship with postsynaptic potentials. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 26, 1918–1925. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, H.; Liu, Q.H. Parameterized Centroid Frequency-Chirp Rate Distribution for LFM Signal Analysis and Mechanisms of Constant Delay Introduction. IEEE Trans. Signal Process. 2019, 65, 6435–6447. [Google Scholar] [CrossRef]
- Wang, K.; Yan, X.; Yang, Q.; Hao, X.; Wang, J. Weak Signal Detection Based on Strongly Coupled Duffing-Van der Pol Oscillator and Long Short-term Memory. J. Phys. Soc. Jpn. 2020, 89, 14003–14012. [Google Scholar] [CrossRef]
- Wang, Q.B.; Yang, Y.J.; Zhang, X. Weak signal detection based on Mathieu-Duffing oscillator with time-delay feedback and multiplicative noise. Chaos Solitons Fractals 2020, 13, 109832–109843. [Google Scholar] [CrossRef]
- Akilli, M.; Yilmaz, N.; Gediz Akdeniz, K. Automated system for weak periodic signal detection based on Duffing oscillator. IET Signal Process. 2020, 14, 710–716. [Google Scholar] [CrossRef]
- Mao, H.-C.; Feng, Y.-L.; Wang, X.-Q.; Yao, Z.-H. Weak Signal Detection Application Based on Incommensurate Fractional-Order Duffing System. J. Nonlinear Math. Phys. 2024, 31, 33–45. [Google Scholar] [CrossRef]
- Wang, Y.; Cheng, Y.; Wang, L.; Yan, Y.; Zou, S.; Chen, K. Automated weak signal frequency estimation method based on Duffing oscillator and particle swarm optimization. Meas. Sci. Technol. 2022, 34, 15008–15016. [Google Scholar] [CrossRef]
- Yan, S.; Sun, X.; Wang, E.; Song, J.; Cui, Y. Application of weak signal detection based on improved duffing chaotic system. J. Vib. Eng. Technol. 2023, 11, 3057–3068. [Google Scholar] [CrossRef]
- Wang, K.; Yan, X.; Zhu, Z.; Hao, X.; Li, P.; Yang, Q. Blind Estimation Methods for BPSK Signal Based on Duffing Oscillator. Sensors 2020, 20, 6412. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Yan, X.; Li, Z.; Hao, X.; Yu, H. Blind parameter estimation of pseudo-random binary code-linear frequency modulation signal based on Duffing oscillator at low SNR. Chin. Phys. B 2021, 30, 708–724. [Google Scholar] [CrossRef]
- Zhu, Z.; Jia, R.; Yan, X.; Wang, K.; Hou, J. Weak Signal Detection with Duffing Oscillator Based on Circular Boundary Counting Method and STFT State Identification Parameter. In Proceedings of the 2nd International Conference on Electrical and Electronic Engineering (EEE 2019), Hangzhou, China, 26–27 May 2019; Atlantis Press: Paris, France, 2019. [Google Scholar]
- Li, C.; Qu, L. Applications of chaotic oscillator in machinery fault diagnosis. Mech. Syst. Signal Process. 2007, 21, 257–269. [Google Scholar] [CrossRef]
- Tang, X.Z.; Tracy, E.R.; Boozer, A.D.; DeBrauw, A.; Brown, R. Symbol sequence statistics in noisy chaotic signal reconstruction. Physical review. E, Statistical physics, plasmas, fluids, and related interdisciplinary topics. Phys. Rev. E 1995, 51, 3871–3889. [Google Scholar] [CrossRef]
- Hao, B.; Zheng, W. Applied Symbolic Dynamics and Chaos, 2nd ed.; World Scientific Publishing: Singapore, 2018. [Google Scholar]
- Song, I.; Park, P. A normalized least-mean-square algorithm based on variable-step-size recursion with innovative input data. IEEE Signal Process. Lett. 2012, 19, 817–820. [Google Scholar] [CrossRef]
- Lee Rodgers, J.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 2017, 42, 59–66. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).