Fast and Compact Partial Differential Equation (PDE)-Based Dynamic Reconstruction of Extended Position-Based Dynamics (XPBD) Deformation Simulation
Abstract
1. Introduction
- Developing a PDE-based dynamic reconstruction method to recreate deformation models from a series of keyframes with high efficiency, good accuracy, and small data sizes;
- Integrating the PDE-based dynamic reconstruction method with XPBD simulation to reduce keyframes simulated by XPBD and raise the simulation efficiency of deformable objects;
- Constructing a powerful surface representation from elementary functions in closed form solutions to dynamic PDEs to raise the capacity in complicated PDE-based dynamic reconstruction.
2. Related Work
2.1. Shape Deformation Approaches
2.1.1. Geometric Approaches
2.1.2. Physcis-Based Approaches
2.1.3. Data-Driven Approaches
2.1.4. Position-Based Approaches
2.2. Geometric Model Creation Approaches
2.2.1. Geometric Approaches
2.2.2. Physics-Based Approaches
3. Basis of Position-Based Dynamics
3.1. Algorithm Overview
- Prediction: estimating the velocity and position of each vertex at the next time step.
- Correction: applying constraints to rectify the position in solvers.
- Updating: using the corrected position to recompute the relative attributes, including velocities and accelerations.
3.2. The Improvements in XPBD
| Algorithm 1 XPBD algorithm |
1: initialize 2: for j∈ do 3: for all constraints do 4: calculate 5: calculate 6: end for 7: end for 8: 9: |
3.3. XPBD Simulation
4. PDE-Based Dynamic Reconstruction
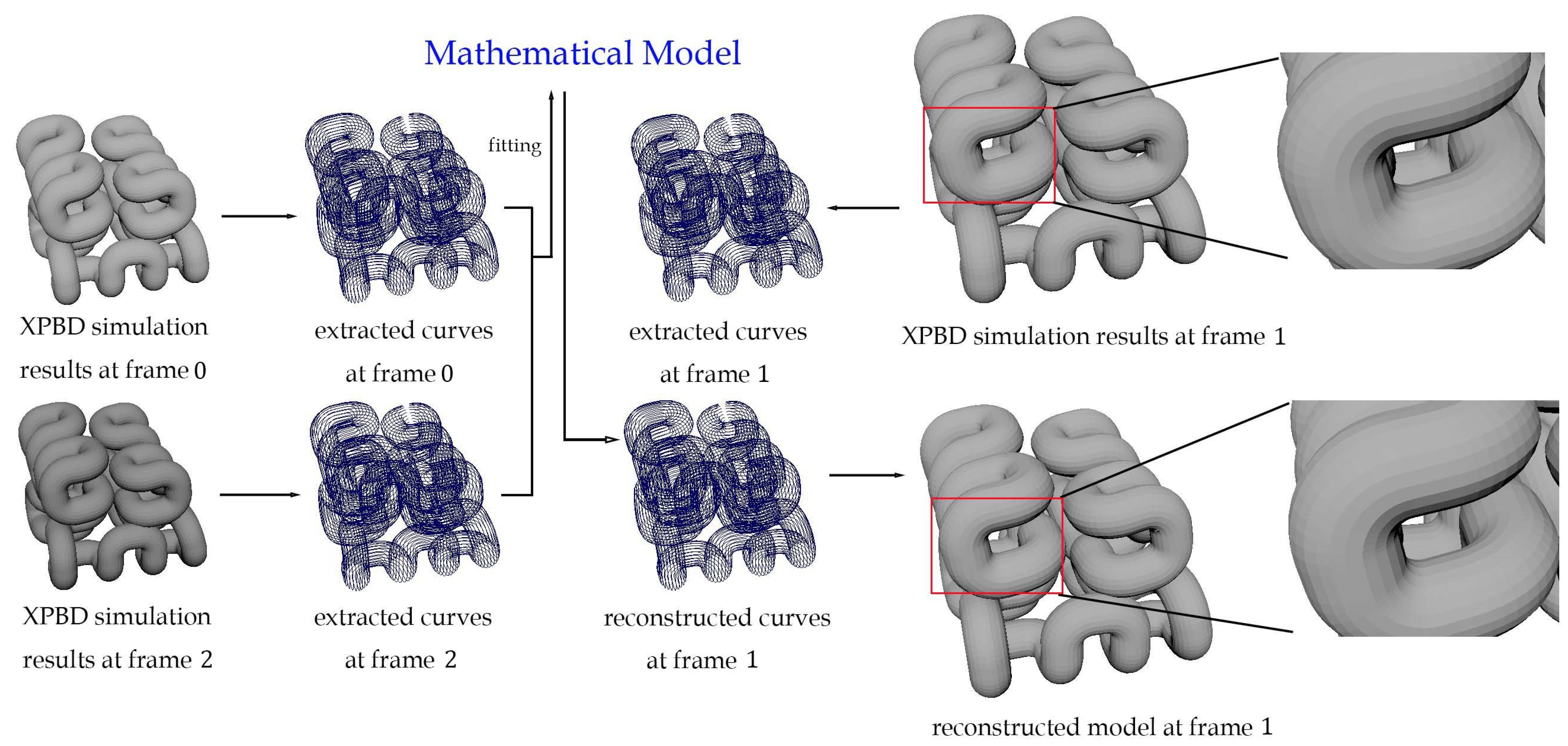
4.1. Mathematical Model
4.2. The Closed-Form Solutions
4.3. Transformation Elimination
4.4. Parametrization
4.5. Unknown Constants Determination
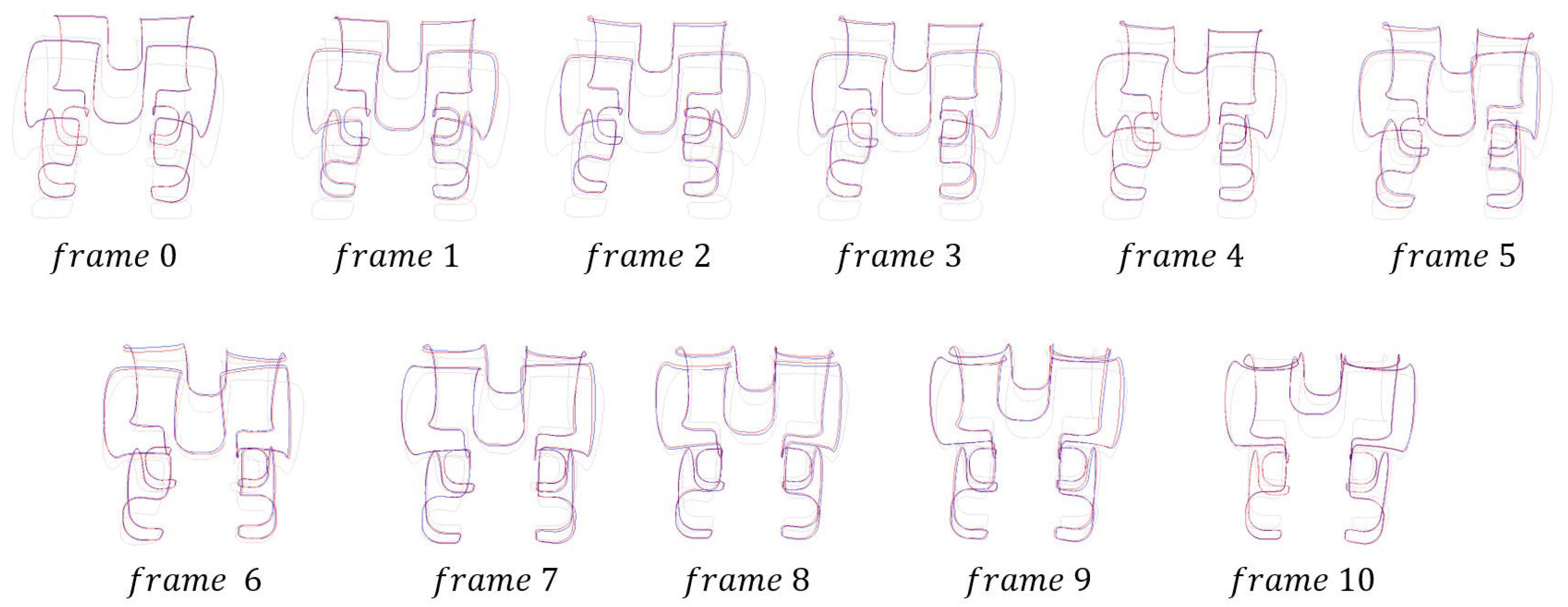
5. Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Daniels, J.; Silva, C.T.; Shepherd, J.; Cohen, E. Quadrilateral mesh simplification. ACM Trans. Graph. (TOG) 2008, 27, 1–9. [Google Scholar] [CrossRef]
- Ebke, H.C.; Campen, M.; Bommes, D.; Kobbelt, L. Level-of-detail quad meshing. ACM Trans. Graph. (TOG) 2014, 33, 1–11. [Google Scholar] [CrossRef]
- Magnenat, T.; Laperrière, R.; Thalmann, D. Joint-Dependent Local Deformations for Hand Animation and Object Grasping; Technical Report; Canadian Information Processing Society: Mississauga, ON, Canada, 1988. [Google Scholar]
- Alexa, M. Linear combination of transformations. ACM Trans. Graph. (TOG) 2002, 21, 380–387. [Google Scholar] [CrossRef]
- Magnenat-Thalmann, N.; Cordier, F.; Seo, H.; Papagianakis, G. Modeling of bodies and clothes for virtual environments. In Proceedings of the 2004 International Conference on Cyberworlds, Tokyo, Japan, 18–20 November 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 201–208. [Google Scholar]
- Kavan, L.; Žára, J. Spherical blend skinning: A real-time deformation of articulated models. In Proceedings of the 2005 Symposium on Interactive 3D Graphics and Games, Washington, DC, USA, 3–5 April 2005; pp. 9–16. [Google Scholar]
- Kavan, L.; Collins, S.; Žára, J.; O’Sullivan, C. Geometric skinning with approximate dual quaternion blending. ACM Trans. Graph. (TOG) 2008, 27, 1–23. [Google Scholar] [CrossRef]
- Mancewicz, J.; Derksen, M.L.; Rijpkema, H.; Wilson, C.A. Delta mush: Smoothing deformations while preserving detail. In Proceedings of the Fourth Symposium on Digital Production, Vancouver, BC, Canada, 9 August 2014; pp. 7–11. [Google Scholar]
- Le, B.H.; Lewis, J. Direct delta mush skinning and variants. ACM Trans. Graph. 2019, 38, 113:1–113:13. [Google Scholar] [CrossRef]
- Sederberg, T.W.; Parry, S.R. Free-form deformation of solid geometric models. In Proceedings of the 13th Annual Conference on Computer Graphics and Interactive Techniques, Dallas, TX, USA, 18–22 August 1986; pp. 151–160. [Google Scholar]
- Coquillart, S. Extended free-form deformation: A sculpturing tool for 3D geometric modeling. In Proceedings of the 17th Annual Conference on Computer Graphics and Interactive Techniques, Dallas, TX, USA, 6–10 August 1990; pp. 187–196. [Google Scholar]
- Coquillart, S.; Jancene, P. Animated free-form deformation: An interactive animation technique. ACM Siggraph Comput. Graph. 1991, 25, 23–26. [Google Scholar] [CrossRef]
- Schein, S.; Elber, G. Discontinuous free form deformations. In Proceedings of the 12th Pacific Conference on Computer Graphics and Applications, 2004, PG 2004, Proceedings, Seoul, Republic of Korea, 6–8 October 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 227–236. [Google Scholar]
- Etzmuss, O.; Gross, J.; Strasser, W. Deriving a particle system from continuum mechanics for the animation of deformable objects. IEEE Trans. Vis. Comput. Graph. 2003, 9, 538–550. [Google Scholar] [CrossRef]
- Desbrun, M.; Schröder, P.; Barr, A. Interactive animation of structured deformable objects. Graph. Interface 1999, 99, 10. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Patidar, K.C. On the use of nonstandard finite difference methods. J. Differ. Equations Appl. 2005, 11, 735–758. [Google Scholar] [CrossRef]
- James, D.L.; Pai, D.K. Artdefo: Accurate real time deformable objects. In Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 8–13 August 1999; pp. 65–72. [Google Scholar]
- Teran, J.; Blemker, S.; Ng-Thow-Hing, V.; Fedkiw, R. Finite volume methods for the simulation of skeletal muscle. In Proceedings of the 2003 ACM SIGGRAPH/Eurographics symposium on Computer Animation, San Diego, CA, USA, 26–27 July 2003; pp. 68–74. [Google Scholar]
- Yousefi, M.; Pervaiz, S. 3D Finite element modeling of wear effects in the punching process. Simul. Model. Pract. Theory 2022, 114, 102415. [Google Scholar] [CrossRef]
- Pressas, I.S.; Papaefthymiou, S.; Manolakos, D.E. Evaluation of the roll elastic deformation and thermal expansion effects on the dimensional precision of flat ring rolling products: A numerical investigation. Simul. Model. Pract. Theory 2022, 117, 102499. [Google Scholar] [CrossRef]
- Allen, B.; Curless, B.; Popović, Z. Articulated body deformation from range scan data. ACM Trans. Graph. (TOG) 2002, 21, 612–619. [Google Scholar] [CrossRef]
- Anguelov, D.; Srinivasan, P.; Koller, D.; Thrun, S.; Rodgers, J.; Davis, J. SCAPE: Shape completion and animation of people. ACM Trans. Graph. 2005, 24, 408–416. [Google Scholar] [CrossRef]
- Der, K.G.; Sumner, R.W.; Popović, J. Inverse kinematics for reduced deformable models. ACM Trans. Graph. (TOG) 2006, 25, 1174–1179. [Google Scholar] [CrossRef]
- Müller, M.; Heidelberger, B.; Hennix, M.; Ratcliff, J. Position based dynamics. J. Vis. Commun. Image Represent. 2007, 18, 109–118. [Google Scholar] [CrossRef]
- Müller, M. Hierarchical Position Based Dynamics. In Proceedings of the 2008 Workshop in Virtual Reality Interactions and Physical Simulation, Grenoble, France, 13–14 November 2008; Volume 8, pp. 1–10. [Google Scholar]
- Müller, M.; Keiser, R.; Nealen, A.; Pauly, M.; Gross, M.; Alexa, M. Point based animation of elastic, plastic and melting objects. In Proceedings of the 2004 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, Grenoble France, 27–29 August 2004; pp. 141–151. [Google Scholar]
- Bouaziz, S.; Martin, S.; Liu, T.; Kavan, L.; Pauly, M. Projective dynamics: Fusing constraint projections for fast simulation. ACM Trans. Graph. (TOG) 2014, 33, 1–11. [Google Scholar] [CrossRef]
- Macklin, M.; Müller, M.; Chentanez, N. XPBD: Position-based simulation of compliant constrained dynamics. In Proceedings of the 9th International Conference on Motion in Games, Burlingame, CA, USA, 10–12 October 2016; pp. 49–54. [Google Scholar]
- Russo, M. Polygonal Modeling: Basic and Advanced Techniques; Jones & Bartlett Learning: Burlington, MA, USA, 2006. [Google Scholar]
- Sohel, F.; Dooley, L.; Karmakar, G. A dynamic Bezier curve model. In Proceedings of the IEEE International Conference on Image Processing, Genova, Italy, 14 September 2005; Volume 2, p. 474. [Google Scholar]
- Maqsood, S.; Abbas, M.; Miura, K.T.; Majeed, A.; Iqbal, A. Geometric modeling and applications of generalized blended trigonometric Bézier curves with shape parameters. Adv. Differ. Equ. 2020, 2020, 550. [Google Scholar] [CrossRef]
- Brakhage, K.H. Analytical investigations for the design of fast approximation methods for fitting curves and surfaces to scattered data. Math. Comput. Simul. 2018, 147, 27–39. [Google Scholar] [CrossRef]
- Bartels, R.H.; Beatty, J.C.; Barsky, B.A. An Introduction to Splines for Use in Computer Graphics and Geometric Modeling; Morgan Kaufmann: Burlington, MA, USA, 1995. [Google Scholar]
- Piegl, L.; Tiller, W. The NURBS book; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Stam, J. Exact evaluation of Catmull-Clark subdivision surfaces at arbitrary parameter values. In Proceedings of the 25th Annual Conference on Computer Graphics and Interactive Techniques, Orlando, FL, USA, 19–24 July 1998; pp. 395–404. [Google Scholar]
- Bouhiri, S.; Lamnii, A.; Lamnii, M.; Zidna, A. A C2 spline quasi-interpolant for fitting 3D data on the sphere and applications. Math. Comput. Simul. 2019, 164, 46–62. [Google Scholar] [CrossRef]
- You, L.; Yang, X.; Pachulski, M.; Zhang, J.J. Boundary constrained swept surfaces for modelling and animation. Comput. Graph. Forum 2007, 26, 313–322. [Google Scholar] [CrossRef]
- You, L.; Ugail, H.; Tang, B.; Jin, X.; You, X.Y.; Zhang, J.J. Blending using ODE swept surfaces with shape control and C1 continuity. Vis. Comput. 2014, 30, 625–636. [Google Scholar] [CrossRef]
- Chaudhry, E.; You, L.; Jin, X.; Yang, X.; Zhang, J.J. Shape modeling for animated characters using ordinary differential equations. Comput. Graph. 2013, 37, 638–644. [Google Scholar] [CrossRef]
- Bloor, M.I.; Wilson, M.J. Using partial differential equations to generate free-form surfaces. Comput.-Aided Des. 1990, 22, 202–212. [Google Scholar] [CrossRef]
- Ugail, H.; Bloor, M.I.; Wilson, M.J. Techniques for interactive design using the PDE method. ACM Trans. Graph. (TOG) 1999, 18, 195–212. [Google Scholar] [CrossRef]
- Zhu, Z.; Zheng, A.; Iglesias, A.; Wang, S.; Xia, Y.; Chaudhry, E.; You, L.; Zhang, J. PDE patch-based surface reconstruction from point clouds. J. Comput. Sci. 2022, 61, 101647. [Google Scholar] [CrossRef]
- Fang, J.; Chaudhry, E.; Iglesias, A.; Macey, J.; You, L.; Zhang, J. Reconstructing Dynamic 3D Models with Small Data by Integrating Position-Based Dynamics and PDE-Based Modelling. Mathematics 2022, 10, 821. [Google Scholar] [CrossRef]
- Bian, S.; Deng, Z.; Chaudhry, E.; You, L.; Yang, X.; Guo, L.; Ugail, H.; Jin, X.; Xiao, Z.; Zhang, J.J. Efficient and realistic character animation through analytical physics-based skin deformation. Graph. Model. 2019, 104, 101035. [Google Scholar] [CrossRef]
- Wang, S.; Xiang, N.; Xia, Y.; You, L.; Zhang, J. Real-time surface manipulation with C 1 continuity through simple and efficient physics-based deformations. Vis. Comput. 2021, 37, 2741–2753. [Google Scholar] [CrossRef]
- Fang, J.; You, L.; Chaudhry, E.; Zhang, J. State-of-the-art improvements and applications of position based dynamics. Comput. Animat. Virtual Worlds 2023, 34, e2143. [Google Scholar] [CrossRef]
- PositionBasedDynamics. Interactive Computer Graphics; Elsevier: Amsterdam, The Netherlands, 2023. [Google Scholar]
- Karimi, A.H.; Naderi, R. Solving Richard’s partial differential equation via Enriched Firefly Algorithm. Asian J. Civ. Eng. 2022, 23, 443–453. [Google Scholar] [CrossRef]
- Jin, T.; Li, F.; Peng, H.; Li, B.; Jiang, D. Uncertain barrier swaption pricing problem based on the fractional differential equation in Caputo sense. Soft Comput. 2023, 27, 11587–11602. [Google Scholar] [CrossRef]
- Cai, P.; Zhang, Y.; Jin, T.; Todo, Y.; Gao, S. Self-adaptive forensic-Based investigation algorithm with dynamic population for solving constraint optimization problems. Int. J. Comput. Intell. Syst. 2024, 17, 15. [Google Scholar] [CrossRef]
- Zhou, Q.; Jacobson, A. Thingi10K: A Dataset of 10,000 3D-Printing Models. arXiv 2016, arXiv:1605.04797. [Google Scholar]
- Prautzsch, H.; Boehm, W.; Paluszny, M. Bézier and B-Spline Techniques; Springer: Berlin/Heidelberg, Germany, 2002; Volume 6. [Google Scholar]



| PDE | B-Spline | |||
|---|---|---|---|---|
| Frame | ||||
| 0 | 0.003035 | 0.005387 | 0.009169 | 0.110480 |
| 1 | 0.007886 | 0.017251 | 0.054134 | 0.187488 |
| 2 | 0.009044 | 0.014629 | 0.090012 | 0.111336 |
| 3 | 0.008655 | 0.019478 | 0.077795 | 0.143668 |
| 4 | 0.005158 | 0.008127 | 0.024759 | 0.2525 |
| 5 | 0.007315 | 0.01675 | 0.062312 | 0.199951 |
| 6 | 0.007807 | 0.018031 | 0.035425 | 0.245637 |
| 7 | 0.006296 | 0.013386 | 0.034231 | 0.106627 |
| 8 | 0.010102 | 0.016598 | 0.037255 | 0.181635 |
| 9 | 0.008118 | 0.016756 | 0.055076 | 0.169511 |
| 10 | 0.003429 | 0.015639 | 0.032914 | 0.270942 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, J.; Xiao, Z.; Zhu, X.; You, L.; Wang, X.; Zhang, J. Fast and Compact Partial Differential Equation (PDE)-Based Dynamic Reconstruction of Extended Position-Based Dynamics (XPBD) Deformation Simulation. Mathematics 2024, 12, 3175. https://doi.org/10.3390/math12203175
Fang J, Xiao Z, Zhu X, You L, Wang X, Zhang J. Fast and Compact Partial Differential Equation (PDE)-Based Dynamic Reconstruction of Extended Position-Based Dynamics (XPBD) Deformation Simulation. Mathematics. 2024; 12(20):3175. https://doi.org/10.3390/math12203175
Chicago/Turabian StyleFang, Junheng, Zhidong Xiao, Xiaoqiang Zhu, Lihua You, Xiaokun Wang, and Jianjun Zhang. 2024. "Fast and Compact Partial Differential Equation (PDE)-Based Dynamic Reconstruction of Extended Position-Based Dynamics (XPBD) Deformation Simulation" Mathematics 12, no. 20: 3175. https://doi.org/10.3390/math12203175
APA StyleFang, J., Xiao, Z., Zhu, X., You, L., Wang, X., & Zhang, J. (2024). Fast and Compact Partial Differential Equation (PDE)-Based Dynamic Reconstruction of Extended Position-Based Dynamics (XPBD) Deformation Simulation. Mathematics, 12(20), 3175. https://doi.org/10.3390/math12203175









