Abstract
In the competitive landscape of online learning, developing robust and effective learning resource recommendation systems is paramount, yet the field faces challenges due to high-dimensional, sparse matrices and intricate user–resource interactions. Our study focuses on geometric matrix completion (GMC) and introduces a novel approach, graph-based truncated norm regularization (GBTNR) for problem solving. GBTNR innovatively incorporates truncated Dirichlet norms for both user and item graphs, enhancing the model’s ability to handle complex data structures. This method synergistically combines the benefits of truncated norm regularization with the insightful analysis of user–user and resource–resource graph relationships, leading to a significant improvement in recommendation performance. Our model’s unique application of truncated Dirichlet norms distinctively positions it to address the inherent complexities in user and item data structures more effectively than existing methods. By bridging the gap between theoretical robustness and practical applicability, the GBTNR approach offers a substantial leap forward in the field of learning resource recommendations. This advancement is particularly critical in the realm of online education, where understanding and adapting to diverse and intricate user–resource interactions is key to developing truly personalized learning experiences. Moreover, our work includes a thorough theoretical analysis, complete with proofs, to establish the convergence property of the GMC-GBTNR model, thus reinforcing its reliability and effectiveness in practical applications. Empirical validation through extensive experiments on diverse real-world datasets affirms the model’s superior performance over existing methods, marking a groundbreaking advancement in personalized education and deepening our understanding of the dynamics in learner–resource interactions.
Keywords:
geometric matrix completion; graph-based truncated norm regularization; learning resource recommendation; intelligent education technology and application MSC:
68T01; 97P80; 15A83
1. Introduction
The digital revolution in education has necessitated the development of intelligent learning resource recommendation systems that can navigate the complex landscape of online learning [1,2,3,4,5]. Central to these systems is the technique of matrix completion, which predicts user preferences by reconstructing a sparsely filled matrix representing user–item interactions [6,7]. While effective, this approach is not without its challenges: the matrices in question are typically high-dimensional and suffer from severe sparsity, which can lead to overfitting and a lack of robustness in the presence of noisy and incomplete data. Furthermore, conventional matrix completion methods often fail to capture the nuanced relationships and patterns inherent in educational data, which are vital for producing meaningful recommendations that can truly enhance the learning experience [8,9].
From the perspective of real-world application, learning resource recommendation systems often grapple with sparse and high-dimensional data, which can impede the accuracy of recommendations. Traditional recommendation techniques may fall short in effectively leveraging the limited user–item interaction data. To overcome these obstacles, researchers have begun exploring the potential of graph-based methods, which introduce a new dimension to the problem by considering the geometric structure of the data [10,11,12,13,14]. By employing a graph-based framework, geometric matrix completion (GMC) can discern the complex and often subtle relationships within the data, offering a nuanced understanding of user preferences and item characteristics. This graph-centric approach is particularly adept at navigating the sparsity of data, enabling the system to make more informed and accurate predictions, thus significantly enhancing the user experience in educational settings. Technically, this kind of methodology acknowledges that user–item interactions are not merely discrete points within a matrix but are instead part of a rich, interconnected graph that represents the complex relationships between users and learning resources. By integrating this graph structure into the matrix completion process, GMC seeks to leverage the additional information to produce more accurate and relevant recommendations [11,15]. The benefits of this method are manifold, including improved recommendation quality in the face of data sparsity and a more profound understanding of the underlying data geometry. It is within this innovative framework that the next generation of learning resource recommendation systems is being developed, promising a more personalized and insightful approach to online learning.
In our study, we introduce a novel model-driven framework for geometric matrix completion (GMC), with a dedicated focus on the task of learning resource recommendation. Central to our methodology (i.e., GMC-GBTNR) is the introduction of graph-based truncated norm regularization (termed GBTNR; see Definitions 2 and 3 in Section 4.1), a novel technique that redefines the GMC problem and offers a fresh perspective on the underlying geometry of user–learning resource interactions. This regularization framework not only captures the complex topological structures within the data but also adeptly handles the inherent noise and sparsity. We propose a new algorithm that operates within this framework, and we provide a rigorous theoretical analysis of its convergence properties, ensuring that our approach is grounded in solid mathematical principles. Through a series of experiments on five real-world learning resource datasets, we validate the effectiveness of our method. Our findings demonstrate a marked improvement over several established matrix completion techniques, showcasing the practical advantages and theoretical soundness of our proposed model-driven framework. We further substantiate the convergence capability of the GMC-GBTNR model with empirical evidence derived from its performance across five distinct datasets.
In summary, our contributions are as follows:
- We introduce the entirely novel concept of graph-based truncated norm regularization (GBTNR), which lays the foundation for a redefined GMC problem statement, enriching the analytical landscape of recommendation systems.
- In response to the optimization challenges presented by the new GMC formulation, we develop an iterative solution algorithm based on the alternating direction method of multipliers (ADMM), tailored to navigate the complexities of the proposed model.
- We present a thorough theoretical proof that underpins the convergence of our model, ensuring its reliability and efficacy.
The remainder of this paper is organized as follows: Section 2 reviews the related studies, encompassing existing methods for both matrix completion and geometric matrix completion. Section 3 introduces the preliminaries, establishing the necessary background and notations. Section 4 details our proposed method and the corresponding theoretical analysis, presenting the novel graph-based truncated norm regularization (GBTNR) approach. Section 5 discusses the experiments conducted to validate the efficacy of our approach, including comparisons with established methods. Finally, Section 6 concludes the paper, summarizing our contributions and suggesting avenues for future research.
2. Related Work
This section provides an in-depth review of the existing literature in the areas of matrix completion and its geometric extensions, highlighting seminal studies and recent advancements.
2.1. Matrix Completion
Matrix completion has emerged as a pivotal technique in the realm of machine learning, particularly for its applications in collaborative filtering and recommendation systems [6,7]. The field gained significant momentum following the influential work of Koren et al. [16], who demonstrated its potent capabilities in the Netflix Prize competition. Their approach addressed the inherent challenge of extremely sparse datasets, characteristic of many real-world scenarios, particularly those involving user–item interactions with millions of dimensions. The essence of matrix completion lies in its ability to predict the missing entries of a partially observed matrix with the assumption that the matrix is of low rank. Candès and Recht [17] provide one of the first theoretical guarantees for matrix completion, showing that under certain conditions, it is possible to perfectly reconstruct low-rank matrices from a sample of their entries. This groundbreaking work laid the mathematical foundation for many subsequent algorithms and applications. Subsequent studies have aimed to improve upon the scalability and accuracy of these methods, with some focusing on the use of auxiliary information [18], and others on algorithmic innovations like singular value decomposition (SVD) for enhancing computational efficiency [16]. For example, Hu et al. [19] propose a fast and accurate approach to matrix completion via truncated nuclear norm regularization. Their method balances computational efficiency with the accuracy of reconstruction, contributing to the practical applicability of matrix completion in large-scale problems. Similarly, Li et al. [20] study the error characteristics of matrix elastic-net regularization algorithms, providing valuable insight into the trade-offs involved in regularization parameter selection. Furthering the development of regularization techniques, Liu et al. [21] introduce a truncated nuclear norm regularization method based on weighted residual error, which enhances the matrix completion process. Their work underscores the importance of developing tailored regularization methods to deal with the nuances of matrix completion. In recent years, the realm of matrix completion has witnessed extensions into more intricate formulations. These include challenging variants such as quaternion matrix completion, which proves valuable in addressing large-scale color image and video inpainting tasks [22]. Additionally, there is the exploration of low-rank high-order tensor completion, particularly relevant in handling complex visual data scenarios [23]. An alternative direction delves into inductive matrix completion, with promising applications in the domain of wireless communications [24].
2.2. Geometric Matrix Completion
Recent strides in matrix completion have been influenced by the integration of geometric structures, which offer a nuanced perspective on user–item interactions. Ma et al. [25] are among the first to suggest the use of manifold learning techniques to exploit the geometric relationships within the data. By borrowing ideas from the field of manifold learning [26,27], Kalofolias et al. [10] extend this by utilizing graph-based approaches to encode similarities, thereby harnessing the inherent structure of the data for improved matrix completion. Rao et al. [28] and Kuang et al. [29] further explored the potential of graph regularization, underscoring the importance of preserving local structures and smoothness in the recommendation process. These contributions are deeply rooted in the field of signal processing on graphs, where Shuman et al. [30] have provided extensive insights into extending classical signal processing techniques to graph-structured data.
The concept of smoothness on graphs has been particularly influential, suggesting that similar users and items (learning resources) are likely to have similar preferences or characteristics. This notion has been operationalized through the development of graph Laplacian regularization techniques, which have been shown to enhance the performance of recommender systems by promoting smoothness over the graph [31,32]. Such techniques have also been instrumental in the formulation of graph convolutional networks [33], which have successfully adapted deep learning methods to data represented on irregular domains. Furthermore, certain research endeavors delve into the matrix completion problem while considering the underlying geometric or topological relationships among rows and/or columns. This is approached from various angles, including spectral viewpoints as explored in the work in [34], a Riemannian manifold perspective as investigated in [35], and the utilization of Plücker coordinates as highlighted in [36].
Summary. Technically, our work represents a distinctive stride in the landscape of matrix completion research, particularly in the realm of geometric matrix completion. We introduce a novel approach, graph-based truncated norm regularization (GBTNR), which combines truncated nuclear norm regularization with graph information. This integration is specifically tailored to address the challenges of learning resource recommendation. GBTNR is designed to adeptly mine and utilize the latent relationships not only between users but also among learning resources themselves. Our methodology transcends traditional limitations of matrix completion techniques, such as their vulnerability to noise and propensity to overestimate the matrix rank. By leveraging the strengths of both graph-based structures and truncated norm regularization, we present a solution that is not only robust and theoretically sound but also uniquely suited to enhance recommendation systems in the e-learning sector. This work, therefore, stands as a significant contribution to the ongoing evolution of matrix completion strategies, particularly in their application to educational technologies.
3. Preliminaries
This section lays the groundwork for understanding the intricacies of matrix completion and geometric matrix completion problems. We delve into the theoretical and methodological preliminaries essential for addressing the challenge of deducing the unknown entries of a matrix from a sparse subset of its observed elements. The ensuing discussion bifurcates into two principal domains: the classical matrix completion framework, which harnesses the power of low-rank matrix assumptions, and the more nuanced geometric matrix completion approach, which incorporates the geometry of the data into the recovery process.
Matrix completion problem. The challenge of inferring the missing elements of a matrix from a subset of its entries necessitates additional mathematical stipulations to define a solvable problem space. A common approach is to posit that the data are restricted to a lower-dimensional subspace, indicative of the matrix’s low rank:
where X represents the matrix under reconstruction, encapsulates the indices of known values, and are the corresponding known values. To accommodate noise and variations, the strict equality can be substituted with a penalization term:
where denotes the indicator matrix, and ∘ signifies the Hadamard product.
Yet, minimizing the rank is an NP-hard problem, rendering it unsolvable for large-scale applications. The most effective convex surrogate for this is:
with denoting the nuclear norm, summing up the singular values of the matrix, as established in the seminal study [17]. Theoretically and empirically, Candès and Recht [17] demonstrate that employing the norm as a relaxation technique in singular value decomposition significantly enhances the likelihood of accurately reconstructing the original matrix with low-rank characteristics.
Geometric matrix completion. An alternative formulation applies a geometric perspective to the rank minimization (see Equation (1)), constraining the solution space to adhere to an inherent geometric structure among the matrix’s rows and columns [10,25,28,37]. The fundamental model is based on the concept of proximity, characterized as an undirected weighted graph for columns, denoted as , which is defined by an adjacency matrix . The elements of this matrix, , are symmetric and only non-zero if an edge exists between nodes i and j within the edge set , representing a connection in the graph. Similarly, the row graph , which encapsulates item similarities, is constructed in a like manner and can be represented by . In the context of recommending learning resources, the row graph can be perceived as analogous to a social network where the edges mirror the relationships between individual students and the affinities they share. Conversely, the column graph represents the intricate web of connections between various learning resources, capturing the similarities or thematic overlaps between them. This dual-graph structure can provide useful auxiliary information for recommendation algorithms, where student–student ties potentially reflect common learning interests and resource–resource links represent curricular similarities.
For both graphs, one can formulate the unnormalized graph Laplacian, a symmetric positive-semidefinite matrix , with D being the degree matrix, calculated as . The Laplacians pertinent to the row and column graphs are symbolized as and , respectively. This allows us to measure the smoothness of the matrix’s columns or rows seen as functions on the respective graphs. This smoothness is quantified by the Dirichlet form: (respecitvely, ).
The geometric matrix completion aims to minimize:
Definition 1.
The singular value decomposition (SVD) of a matrix takes the form (see [38,39]):
where U and V have orthonormal columns, and Σ is diagonal with singular values. For , the singular value shrinkage operator is defined via:
where .
Proposition 1.
Given any and matrix , the singular value shrinkage operator satisfies (see [38,39]):
4. Geometric Matrix Completion via Hybrid Truncated Norm Regularization
4.1. Proposed Method
Basics. Given a matrix , we assume that its geometric information, that is, the row graph and the row graph , are available. Let denote the adjacency matrix of and denote the adjacency matrix of . Their (normalized) graph Laplacian matrices are expressed as and , respectively, where (and ) is the degree matrix of (and ). Based on spectral graph theory [40], we can have their Laplacian eigendecompositions: and , respectively, where denotes the matrix of orthonormal eigenvectors and is the diagonal matrix of the corresponding eigenvalues. (and ) is well-defined due to the positive-semidefiniteness of (and ).
New Definitions. With these notations, we define the truncated Dirichlet norms for the row and column graphs as follows.
Definition 2.
The truncated Dirichlet norm for the row graph is defined as
Definition 3.
The truncated Dirichlet norm for the column graph is defined as
Our proposed GMC-GBTNR. Our proposed method can be formulated as:
where , are regularization parameters.
As shown in Equation (7), our GBTNR approach leverages truncated Dirichlet norms as regularization terms in the optimization problem for matrix completion. Specifically, these norms act on the row and column graphs, incorporating the geometric structure of the data into the learning process. They contribute to the regularization by emphasizing only the significant singular values, as represented by the sum of the squared singular values multiplied by their corresponding truncated eigenvectors, starting from the -th smallest one, as per the truncation parameter .
Theoretically, the truncated Dirichlet norms in the GBTNR approach encapsulate the graph information of users and items, enhancing the model performance. These terms, acting as regularization in the optimization framework, exploit the relational structure inherent in the user–item interactions. This is particularly beneficial in situations with sparse rating data, where traditional collaborative filtering might struggle. By integrating user and item graph information, the GBTNR method can discern underlying patterns and relationships, which are crucial for accurate matrix completion. The technique effectively harnesses these relational data, often leading to more precise recommendations.
Proposition 2.
For any given matrix , any matrices , satisfying (I is the unit matrix of and ), we have (see [19])
Proposition 3.
For any given matrix , any matrix satisfying (I is the unit matrix of and ), we have (see [41])
For simplicity, we denote as a transform matrix induced by row graph and as a transform matrix induced by the column graph . Suppose is the SVD of and is the SVD of with , . Given the SVD of X, i.e, , where , , and , we can take
Based on Propositions 2 and 3, it is easy to verify that
Then the objective function (7) can be reformulated as:
Using the alternative optimization scheme used in [19,42], we can solve the optimization problem (11) via two steps. First, we initialize . In the l-th iteration, we fix and calculate two intermediate matrices and , then conduct SVDs of , , and , respectively, to obtain , , , as formulated in (10). Second, we fix , , , and to update based on the following problem:
Algorithm 1 presents the detailed pseudo-code for these two steps. It should be noted that we assume , are given as inputs for the algorithm implementation, provided that both the row graph and the column graph are known in advance. In practice, it is possible to only consider one transform matrix, i.e., or for the case where only or is available by setting or . The extreme case in which both and are not provided does not fit our problem formulation, which relies on the basis of geometric matrix completion. In the next section, will discuss how to solve the optimization problem (12).
| Algorithm 1 GMC-GBTNR: Geometric Matrix Completion via Graph-Based Truncated Norm Regularization |
|
4.2. Optimization Algorithms
In this subsection, an efficient iterative optimization scheme is created to optimize (12). According to the augmented Lagrangian multiplier method, a common strategy is to approximately minimize the augmented Lagrangian function by adopting an alternating scheme and we use it to solve the model (12). To this end, we introduce the auxiliary variable Z and then (12) is equivalent to the following form:
Note that and are two linear constraints. To handle the two constraints simultaneously, we reformulate the model (13) as follows:
where , : are two linear operators denoted by
and
respectively.
Given a matrix Y with the following block representation,
where (), it is easy to verify that the adjoint operators of and , that is, and , respectively, can be evaluated by (see [19,42])
Then, the augmented Lagrange function of (14) can be written as:
where Y is the Lagrange multiplier matrix and is the penalty parameter. Thus, we can adopt the alternating iteration strategy, i.e., fix some variables and solve the remaining one.
Initially, we compute . We can give the following solution by ignoring the constant term:
Denote a differentiable real function with respect to its matrix argument X as follows:
Then, can be approximated by the Taylor series
where and the first-order gradient can be evaluated by
Therefore, the solution (20) can be refined as:
By Definition 1 and Proposition 1, this could be solved as
Next, we concentrate on calculating .
It is obvious that the objective function of (23) is a quadratic function.
Ultimately, the update of Lagrange multipliers is
To sum up, the full procedure is listed in Algorithm 2.
| Algorithm 2 ADMM for Step 2 of Algorithm 1 |
|
4.3. Convergence Analysis
In this subsection, the convergence of the proposed approach will be discussed. To this end, denote the optimal value of (14) as
and the unaugmented Lagrangian function as
Subsequently, the paper establishes three auxiliary lemmas as foundational results prior to demonstrating the convergence of the proposed method.
Lemma 1.
Assume that is the optimal solution to the unaugmented Lagrangian function (27). Let be the iterative solution to Algorithm 2 and
Then the following inequality holds:
Proof.
Since is the optimal solution to (27), then it follows that
Using , the left-hand side is equal to . In terms of
we can obtain that , i.e., the inequality (28) holds. This completes the proof. □
Actually, implies that is also the optimal solution to the model (14).
Lemma 2.
Let and . Then we have
Proof.
By definition, we know that minimizes . As is closed, convex, and subdifferentiable on X. With the property of subdifferential [43], the optimality condition can be satisfied, namely,
Using , we can rearrange (30) as
This indicates that minimizes
Similarly, minimizes
Accordingly, for the optimal solution , we can obtain
and
Adding both sides of (31) and (32), as well as using , it follows that
where the last equality holds due to . This completes the proof. □
Lemma 3.
Suppose that is the optimal solution to the unaugmented Lagrangian function (27). Denote and define
Then, decreases in each iteration and satisfies the following relationship:
Proof.
Adding the two inequalities in Lemmas 1 and 2 and multiplying through by 2 give that
Using , the first term of (34) can be rewritten as
Due to the fact that , we have
Now, we rewrite the remaining terms, i.e.,
where is taken from (35). Replacing gives
With , this can be converted into
Consequently, (34) is equivalent to
in other words,
Thus, decreases.
Further, in order to obtain (33), it only suffices to verify that the term . In fact, recalling that minimizes and minimizes in Lemma 2, we can add
and
to obtain that
Combining and , we have
This completes the proof. □
Based on the above results, the following convergence theorem is established.
Theorem 1.
Under the conditions of Lemmas 1–3, the iterative solution converges to the optimal solution when k tends to infinity. Namely, as .
Proof.
From Lemma 3, decreases in each iteration and meets
Adding all the terms on both sides and rearranging it, we have
This indicates (as ). Due to the non-negativity of the Frobenius norm, we know and when . By the definition of and , it is easy to find and . Combining Lemmas 1 and 2, it follows that
and
when . That is to say, as . This completes the proof. □
In terms of Theorem 1, it can be seen that the iteration solution to the objective function approximates the optimal value, illuminating the convergence property of the proposed method.
Remark 1.
The GMC-GBTNR model enhances the geometric matrix completion task by incorporating both row-graph and column-graph structures. It advances beyond traditional model-driven methods by integrating structural information with truncated norm details, offering a more comprehensive solution to matrix completion challenges. Unlike the data-driven model, which may lack a solid theoretical underpinning, the GMC-GBTNR stands on a firm theoretical foundation. Its convergence properties, as substantiated in Section 4.3, provide a reliable basis for its effectiveness, making it a robust and theoretically sound approach in the realm of recommendation systems. The GMC-GBTNR framework, while effective, can potentially be elevated by integrating both data-driven and model-driven schemes. Such a hybrid approach may yield even better performance in recommendation tasks due to its comprehensive analysis of data and underlying theoretical models. Nonetheless, crafting a theoretical framework for this hybrid model presents a significant challenge, one that is complex and nuanced, and thus, it remains an area for future research exploration. This endeavor would aim to balance the empirical strengths of data-driven methods with the predictive reliability of model-driven frameworks, carving out new frontiers in the recommendation domain.
5. Experiments
5.1. Datasets
In our experiments, we employ five specialized datasets focusing on learning resources, as meticulously described in reference [44], detailed as follows:
- Ratings dataset (RA) (https://www.kaggle.com/philippsp/book-recommender-collaborative-filtering-shiny, accessed on 1 September 2023): This learning resource dataset encompasses an extensive compilation of book evaluations, featuring approximately 980,000 ratings for 10,000 titles by 53,424 participants. It showcases the application of collaborative filtering techniques, providing an insightful perspective on algorithm-based book recommendations.
- BX-Book-ratings dataset (BBA) (https://www.kaggle.com/ruchi798/bookcrossing-dataset, accessed on on 1 September 2023): This dataset is a comprehensive aggregation of book assessments, comprising 1,149,780 ratings (both explicit and implicit) contributed by 105,283 users for roughly 340,556 books.
- Ratings-Books dataset (RAB) (https://jmcauley.ucsd.edu/data/amazon/, accessed on on 1 September 2023): It includes a vast array of Amazon product evaluations, last updated in 2018. It comprises a detailed collection of data points such as user, item, rating, and timestamp.
- Related-Article Recommendation dataset (RAR) (https://doi.org/10.7910/DVN/AT4MNE, accessed on on 1 September 2023): It originates from a recommender system utilized in the context of digital libraries and reference management software. This dataset is specifically oriented towards literature, featuring 2,663,825 users, 7,224,279 books, and a total of 48,879,167 evaluations.
- LibraryThings dataset (LT) (https://cseweb.ucsd.edu/jmcauley/datasets.html, accessed on on 1 September 2023): It not only provides book ratings but also delves into the social connections among its 70,618 users. It contains 1,387,125 ratings covering 385,251 books. The integration of social interactions and rating correlations in this dataset has yielded optimal results.
These datasets exhibit a high level of sparsity, indicating that many users or learning resources have received only a limited number of ratings. In our experiments, alternative versions of these datasets have been created for comparative analysis. Initially, in each dataset, we selectively focus on users and learning resources that have received a minimum of ten ratings. This approach is strategically implemented to effectively mitigate the significant challenge posed by extensive data sparsity. Then, from the refined version of each dataset, we only choose 3000 users and 3000 items, along with the associated ratings linked to these specific user–item interactions. Table 1 summarizes the statistics of these five real-world datasets with details for the number of users, the number of items, the available graph type, the number of ratings, and the density.

Table 1.
Statistics of datasets for evaluation. For the “Graphs”, “Users/Items" denotes that both user graph and item graph are used.
5.2. Baselines and Experimental Setting
In the experiments, we compare our proposed GMC-GBTNR model to the five existing approaches for matrix completion, detailed as follows:
- IALM [17]: This foundational approach employs the inexact augmented Lagrange multiplier method for precise matrix completion.
- MEN [20]: This strategy incorporates the elastic-net regularization scheme, tailored specifically for matrix recovery.
- TNN [19]: This model is notable for being the first to introduce the truncated nuclear norm method in the realm of matrix completion.
- TNNWRE [21]: Building upon TNN [19], this method enhances it by applying differential weights to the rows of the residual error matrix within an augmented Lagrange function. This modification is designed to expedite the model’s convergence.
- GMC [10]: This advanced approach utilizes a deep learning framework, based on a multi-graph convolutional neural network architecture, for effective matrix completion.
- SMC [34]: The method described is a spectral geometric matrix completion approach, specifically designed to account for the underlying geometric or topological relationships among the rows and/or columns.
- FMC [15]: This method extends and enhances SMC [34], adopting a functional perspective tailored for geometric matrix completion. It employs a reduced basis to represent a function on the product space of two graphs, which inherently provides robust regularization.
Each of these methodologies provides a unique perspective on matrix completion, against which we assess the efficacy of our proposed method. On the other hand, in assessing the models, this study employs the root mean square error (RMSE), a widely recognized metric in the field of recommender systems. This is computed using the formula given as follows:
where represents the actual rating value, is the predicted rating value, and N denotes the total number of missing values/elements in the matrix.
5.3. Results and Discussion
In our experiments, we conduct a performance comparison across five real-world datasets (RA, BBA, RAB, RAR, and LT) using various matrix completion methods. As shown in Table 2, the evaluation encompasses a range of established approaches such as IALM, MEN, TNN, TNNWRE, and GMC, alongside our novel GMC-GBTNR method. The results clearly demonstrate the efficacy of these methods in handling the complexities of different datasets. For instance, in the RA and BBA datasets, while the GMC method shows impressive results with scores of 0.8823 and 3.2578, respectively, our GMC-GBTNR method outshines the rest by recording the lowest and thus the most favorable scores of 0.8252 and 3.1256, respectively. This suggests a significant enhancement in matrix completion capabilities, highlighting the strengths of our approach in these particular datasets. In particular, in the RA and BBA datasets, the method’s superior scores not only demonstrate its effectiveness but also suggest a more nuanced understanding and handling of the inherent complexities within these datasets. This might include better capturing of user–item interactions or more accurately modeling sparse data. In the RAB, RAR, and LT datasets, GMC-GBTNR’s consistent outperformance over other methods like TNNWRE indicates its robust adaptability to different data structures and types. These results could be attributed to the method’s advanced algorithmic structure, which effectively leverages the truncated Dirichlet norms. The truncated Dirichlet norms in the GMC-GBTNR model play a crucial role in enhancing its matrix completion capabilities. These norms function by prioritizing the significant singular values and corresponding eigenvectors in the data, allowing the model to focus on the most impactful features. This selective emphasis is particularly effective in datasets with complex structures or sparse information, as it filters out noise and less relevant details. By homing in on these key elements, GMC-GBTNR can achieve more accurate and robust predictions, as evidenced by its remarkable performance across varied datasets. This approach illustrates the model’s advanced analytical capacity, making it a powerful tool in discerning and leveraging the essential characteristics of data for superior recommendations.

Table 2.
Performance comparison for the five real-world datasets. The performance of our proposed method, GMC-GBTNR, is emphasized with bold text, indicating its superior performance across all datasets compared to the other methods.
Furthermore, the performance metrics in the remaining datasets—RAB, RAR, and LT—reiterate the superior performance of the GMC-GBTNR method. Across these datasets, it consistently surpasses the other methods, marking a notable achievement in the field of matrix completion. In RAR, for example, where the TNNWRE scores 0.0510, our method advances further with a score of 0.0356. Similarly impressive is its performance in the LT dataset, where it achieves a groundbreaking score of 0.8438, significantly ahead of GMC’s 0.8780. These results not only validate the robustness and adaptability of our GMC-GBTNR method but also underscore its potential as a leading solution in matrix completion. By consistently outperforming across a spectrum of datasets, our method establishes a new benchmark in accuracy and efficiency, paving the way for future advancements in this domain.
5.4. Demonstration of Convergence
To illustrate the convergence characteristics of the proposed GMC-GBTNR model, we present the loss curves (of RMSE values) for all five datasets. As depicted in Figure 1, each curve initiates from a specific loss value and exhibits a pronounced decrease, transitioning into a more gradual descent as it nears the 200-epoch mark. This pattern underscores a swift initial improvement during the early covergence phase, followed by a progressive stabilization in convergence rate. Notably, the distinct shapes and levels of the loss curves across the datasets underscore the model’s adaptability and consistent convergence behavior despite varying dataset complexities. This demonstration effectively showcases the effectiveness of the GMC-GBTNR model in achieving convergence. It provides compelling empirical evidence that supports and verifies our theoretical findings regarding the convergence properties of the GMC-GBTNR model, as detailed in Section 4.3. The consistency observed between the theoretical predictions and the practical outcomes underlines the reliability and effectiveness of the GMC-GBTNR model in real-world applications.
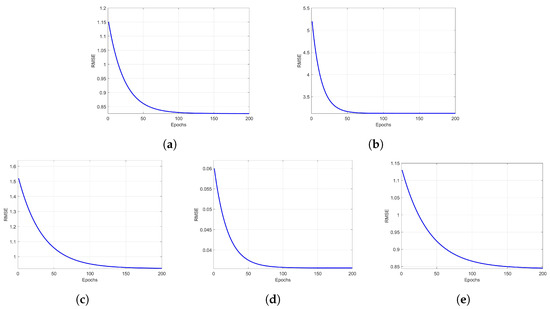
Figure 1.
Demonstration for training loss convergence of GMC-GBTNR on five datasets: (a) RA, (b) BBA, (c) RAB, (d) RAR, (e) LT.
Generally, the convergence property is crucial, as it ensures the stability and reliability of our GMC-GBTNR model. In practical terms, it means that the model will consistently produce accurate and dependable results over time, which is vital for applications in real-world scenarios, as it guarantees that the model’s predictions become more accurate and stable over time, regardless of initial conditions or minor changes in the input data. Theoretically and empirically, this convergence property is key for users who rely on our model for consistent and dependable recommendations, ensuring that the system’s performance remains robust and trustworthy in various scenarios.
5.5. Robustness Analysis
In this section, we investigate empirically the robustness of the proposed GMC-GBTNR model. Specifically, we conduct additional experiments introducing varying levels of white Gaussian noise into the rating matrix . This noise, represented by , was calibrated using , where p varies across a set . This range of p values allowed us to systematically test the model’s performance under different degrees of noise, providing a comprehensive understanding of its resilience to data perturbations.
The experimental results in Table 3 reflect the robustness of the GMC-GBTNR algorithm across five different datasets. Notably, as the noise level increases (with p values ranging from 0.01 to 0.1), the performance of the GMC-GBTNR algorithm exhibits minimal variation, indicating a gradual and stable behavior despite the introduction of noise. This consistent performance across datasets such as RA, BBA, RAB, RAR, and LT suggests that the model maintains its robustness, highlighting its reliability and effectiveness in various conditions. The results are consistent across all datasets, further reinforcing the robust nature of our proposed GMC-GBTNR model.

Table 3.
Evaluation of GMC-GBTNR’s robustness across different levels of noise.
6. Conclusions and Future Work
In this paper, we introduce a novel geometric matrix completion method tailored for learning resource recommendation, incorporating graph-based truncated norm regularization. This approach not only reflects user-to-user and resource-to-resource relationships but also integrates truncated Dirichlet norms for user and item graphs. This combination enhances the model’s capacity to interpret complex data structures and merges the benefits of truncated norm regularization with a thorough analysis of graph relationships. Supported by a comprehensive theoretical analysis and empirical validation across diverse datasets, our GMC-GBTNR model demonstrates reliability and effectiveness in enhancing recommendation systems, thus making a significant contribution to personalized education and enriching our understanding of the dynamics of learner–resource interactions. The GMC-GBTNR model, while effective in certain aspects, faces notable limitations. Its scalability is a primary concern, as the model may struggle with the efficient processing of large datasets, impacting its performance. Additionally, the model’s approach of generating row and column graphs without prior knowledge of the rating distribution can be suboptimal, especially in scenarios where such information is critical. Furthermore, the GMC-GBTNR model encounters challenges in handling extremely sparse rating matrices, which can significantly affect its accuracy and reliability in extracting meaningful insights from such data.
For future work, we aim to tackle the scalability in large educational datasets and integrate domain-specific insights into our model. We also plan to explore the potential of large language models (LLMs) to further refine the GMC-GBTNR model, enhancing its relevance and effectiveness in personalized learning environments. We believe that these future directions promise to extend the impact and applicability of our research in the rapidly evolving field of online education.
Author Contributions
Conceptualization, Y.Y.; Methodology, Y.Y. and S.Y.; Validation, Y.Y., J.S., S.Z. and S.Y.; Formal analysis, Y.Y. and J.S.; Data curation, Y.Y.; Writing—original draft, Y.Y., J.S. and S.Y.; Writing—review & editing, Y.Y., J.S., S.Z. and S.Y.; Visualization, Y.Y. and S.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data will be made available by the authors on request.
Acknowledgments
We would like to thank the three anonymous reviewers for their insightful comments and valuable suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Thai-Nghe, N.; Drumond, L.; Krohn-Grimberghe, A.; Schmidt-Thieme, L. Recommender system for predicting student performance. Procedia Comput. Sci. 2010, 1, 2811–2819. [Google Scholar] [CrossRef]
- Kaklauskas, A.; Zavadskas, E.K.; Seniut, M.; Stankevic, V.; Raistenskis, J.; Simkevičius, C.; Stankevic, T.; Matuliauskaite, A.; Bartkiene, L.; Zemeckyte, L.; et al. Recommender system to analyze student’s academic performance. Expert Syst. Appl. 2013, 40, 6150–6165. [Google Scholar]
- Wu, Z.; Li, M.; Tang, Y.; Liang, Q. Exercise recommendation based on knowledge concept prediction. Knowl.-Based Syst. 2020, 210, 106481. [Google Scholar] [CrossRef]
- Li, M.; Zhang, L.; Cui, L.; Bai, L.; Li, Z.; Wu, X. BLoG: Bootstrapped graph representation learning with local and global regularization for recommendation. Pattern Recognit. 2023, 144, 109874. [Google Scholar] [CrossRef]
- Li, M.; Zhuang, X.; Bai, L.; Ding, W. Multimodal graph learning based on 3D Haar semi-tight framelet for student engagement prediction. Inf. Fusion 2024, 105, 102224. [Google Scholar]
- Ramlatchan, A.; Yang, M.; Liu, Q.; Li, M.; Wang, J.; Li, Y. A survey of matrix completion methods for recommendation systems. Big Data Min. Anal. 2018, 1, 308–323. [Google Scholar]
- Chen, Z.; Wang, S. A review on matrix completion for recommender systems. Knowl. Inf. Syst. 2022, 64, 1–34. [Google Scholar] [CrossRef]
- da Silva, F.L.; Slodkowski, B.K.; da Silva, K.K.A.; Cazella, S.C. A systematic literature review on educational recommender systems for teaching and learning: Research trends, limitations and opportunities. Educ. Inf. Technol. 2023, 28, 3289–3328. [Google Scholar] [CrossRef]
- Dascalu, M.I.; Bodea, C.N.; Mihailescu, M.N.; Tanase, E.A.; Ordoñez de Pablos, P. Educational recommender systems and their application in lifelong learning. Behav. Inf. Technol. 2016, 35, 290–297. [Google Scholar]
- Kalofolias, V.; Bresson, X.; Bronstein, M.; Vandergheynst, P. Matrix completion on graphs. arXiv 2014, arXiv:1408.1717. [Google Scholar]
- Monti, F.; Bronstein, M.; Bresson, X. Geometric matrix completion with recurrent multi-graph neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 3697–3707. [Google Scholar]
- Berg, R.v.d.; Kipf, T.N.; Welling, M. Graph convolutional matrix completion. arXiv 2017, arXiv:1706.02263. [Google Scholar]
- Dong, Y.; Che, H.; Leung, M.F.; Liu, C.; Yan, Z. Centric graph regularized log-norm sparse non-negative matrix factorization for multi-view clustering. Signal Process. 2024, 217, 109341. [Google Scholar] [CrossRef]
- Liu, C.; Wu, S.; Li, R.; Jiang, D.; Wong, H.S. Self-supervised graph completion for incomplete multi-view clustering. IEEE Trans. Knowl. Data Eng. 2023, 35, 9394–9406. [Google Scholar]
- Sharma, A.; Ovsjanikov, M. Geometric matrix completion: A functional view. arXiv 2020, arXiv:2009.14343. [Google Scholar]
- Koren, Y.; Bell, R.; Volinsky, C. Matrix factorization techniques for recommender systems. Computer 2009, 42, 30–37. [Google Scholar] [CrossRef]
- Candès, E.J.; Recht, B. Exact matrix completion via convex optimization. Found. Comput. Math. 2009, 9, 717. [Google Scholar] [CrossRef]
- Srebro, N.; Rennie, J.; Jaakkola, T. Maximum-margin matrix factorization. Adv. Neural Inf. Process. Syst. 2004, 17. [Google Scholar]
- Hu, Y.; Zhang, D.; Ye, J.; Li, X.; He, X. Fast and accurate matrix completion via truncated nuclear norm regularization. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2117–2130. [Google Scholar]
- Li, H.; Chen, N.; Li, L. Error analysis for matrix elastic-net regularization algorithms. IEEE Trans. Neural Netw. Learn. Syst. 2012, 23, 737–748. [Google Scholar]
- Liu, Q.; Lai, Z.; Zhou, Z.; Kuang, F.; Jin, Z. A truncated nuclear norm regularization method based on weighted residual error for matrix completion. IEEE Trans. Image Process. 2016, 25, 316–330. [Google Scholar] [CrossRef]
- Jia, Z.; Jin, Q.; Ng, M.K.; Zhao, X.L. Non-local robust quaternion matrix completion for large-scale color image and video inpainting. IEEE Trans. Image Process. 2022, 31, 3868–3883. [Google Scholar] [PubMed]
- Qin, W.; Wang, H.; Zhang, F.; Wang, J.; Luo, X.; Huang, T. Low-rank high-order tensor completion with applications in visual data. IEEE Trans. Image Process. 2022, 31, 2433–2448. [Google Scholar] [PubMed]
- Masood, K.F.; Tong, J.; Xi, J.; Yuan, J.; Yu, Y. Inductive Matrix Completion and Root-MUSIC-Based Channel Estimation for Intelligent Reflecting Surface (IRS)-Aided Hybrid MIMO Systems. IEEE Trans. Wirel. Commun. 2023, 22, 7917–7931. [Google Scholar]
- Ma, H.; Zhou, D.; Liu, C.; Lyu, M.R.; King, I. Recommender systems with social regularization. In Proceedings of the Fourth ACM International Conference on Web Search and Data Mining, Hong Kong, China, 9–12 February 2011; pp. 287–296. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. Adv. Neural Inf. Process. Syst. 2001, 14, 585–591. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef]
- Rao, N.; Yu, H.F.; Ravikumar, P.K.; Dhillon, I.S. Collaborative filtering with graph information: Consistency and scalable methods. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; pp. 2107–2115. [Google Scholar]
- Kuang, D.; Shi, Z.; Osher, S.; Bertozzi, A. A harmonic extension approach for collaborative ranking. arXiv 2016, arXiv:1602.05127. [Google Scholar]
- Shuman, D.I.; Narang, S.K.; Frossard, P.; Ortega, A.; Vandergheynst, P. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process. Mag. 2013, 30, 83–98. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P.; Sindhwani, V. Manifold regularization: A geometric framework for learning from labeled and unlabeled examples. J. Mach. Learn. Res. 2006, 7, 2399–2434. [Google Scholar]
- Zhou, D.; Schölkopf, B. A regularization framework for learning from graph data. In Proceedings of the ICML 2004 Workshop on Statistical Relational Learning and Its Connections to Other Fields, Banff, AB, Canada, 8 July 2004; pp. 132–137. [Google Scholar]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. arXiv 2013, arXiv:1312.6203. [Google Scholar]
- Boyarski, A.; Vedula, S.; Bronstein, A. Spectral Geometric Matrix Completion. Proc. Math. Sci. Mach. Learn. 2022, 145, 172–196. [Google Scholar]
- Gao, B.; Absil, P.A. A Riemannian rank-adaptive method for low-rank matrix completion. Comput. Optim. Appl. 2022, 81, 67–90. [Google Scholar] [CrossRef]
- Tsakiris, M.C. Low-rank matrix completion theory via Plücker coordinates. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10084–10099. [Google Scholar] [CrossRef] [PubMed]
- Benzi, K.; Kalofolias, V.; Bresson, X.; Vandergheynst, P. Song recommendation with non-negative matrix factorization and graph total variation. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 2439–2443. [Google Scholar]
- Cai, J.F.; Candès, E.J.; Shen, Z. A singular value thresholding algorithm for matrix completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Cao, F.; Chen, J.; Ye, H.; Zhao, J.; Zhou, Z. Recovering low-rank and sparse matrix based on the truncated nuclear norm. Neural Netw. 2017, 85, 10–20. [Google Scholar] [PubMed]
- Chung, F.R.; Graham, F.C. Spectral Graph Theory; American Mathematical Society: Providence, RI, USA, 1997. [Google Scholar]
- Huang, J.; Zhang, F.; Wang, J.; Liu, X.; Jia, J. The perturbation analysis of nonconvex low-rank matrix robust recovery. IEEE Trans. Neural Netw. Learn. Syst. 2023. [Google Scholar] [CrossRef]
- Ye, H.; Li, H.; Cao, F.; Zhang, L. A Hybrid Truncated Norm Regularization Method for Matrix Completion. IEEE Trans. Image Process. 2019, 28, 5171–5186. [Google Scholar] [CrossRef]
- Rockafellar, R.T. Convex Analysis; Princeton University Press: Princeton, NJ, USA, 2015. [Google Scholar]
- Dien, T.T.; Thanh-Hai, N.; Thai-Nghe, N. An approach for learning resource recommendation using deep matrix factorization. J. Inf. Telecommun. 2022, 6, 381–398. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).