1. Introduction
In the approach to physical geometry taken by Mallios and Zafiris [
1], they emphasize the importance of adjoint functors, or adjunctions.
The unifying thread is provided by the ubiquitous notion of adjoint functors in category theory, which characterizes the naturality of the purported approach to physical geometry in functorial terms.
Therefore, it seems appropriate to delve into the history and theory of adjoint functors. Where do they come from mathematically, and how did the concept develop historically? That is the topic of this paper.
Saunders Mac Lane famously said the “Bourbaki just missed” [
2] (
Notes at end of the Adjoints chapter) defining adjunctions in the 1948 Appendix III “On Universal Mappings” to an early version of
Algebre Chapter III on multilinear algebras [
3]. The Appendix was no doubt written by Pierre Samuel who published a very similar paper under his own name during the same year [
4] and was even referenced in the Appendix; therefore, we will “pierce the veil” of Bourbakian anonymity and henceforth refer to Samuel as the author.
A heterodox treatment of adjunctions (Pareigis [
5]; rediscovered and developed in Ellerman [
6]; and thoroughly developed in [
7]) using heteromorphisms shows that Samuel may have been even closer than Mac Lane surmised. The heteromorphic treatment splits an adjunction (as a “molecule”) into two “atoms”, which are representations giving solutions to dual universal mapping problems. Mac Lane shows how to formulate Samuel’s universal mapping property (UMP) in categorical terms, and it is precisely a solution to
one of the universal problems in the heteromorphic treatment. Thus, it only needs to be dualized (turning the mappings around) to arrive at the notion of a solution to the dual universal problem. Putting the two UMP solutions together yields the notion of an adjunction a decade before Kan’s definition [
8] (which does not use heteromorphisms) (The long and somewhat contentious—or at least storied—relationship between Mac Lane and Bourbaki is considered at length in Corry [
9] and the references contained therein. For more about Mac Lane, see McLarty [
10]. For the orthodox homs-only treatment of adjoints, see, in addition to Mac Lane [
2], McLarty [
11], Awodey [
12], or Marquis [
13]).
This heteromorphic treatment of adjoint functors may be helpful in further elucidating the Mallios–Zafiris approach to physical geometry.
2. A Primer on Homs and Hets
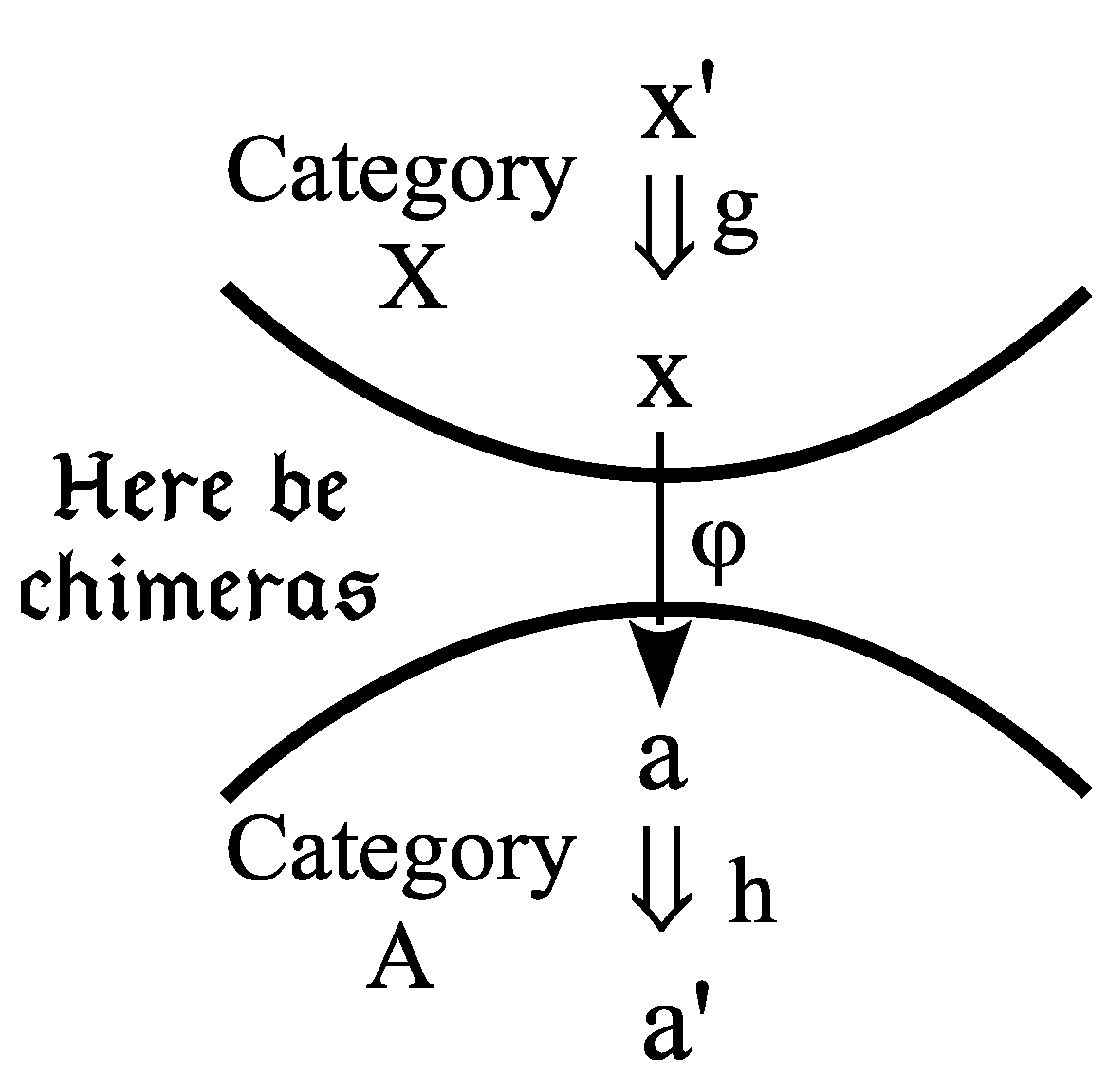
In the conventional approach to category theory, the only object-to-object maps are between objects in the same category, and, thus, they are properly called homomorphisms, or homs for short. The intuitive idea of a heteromorphism (het for short) is an object-to-object morphism between the objects of different categories, such as the injection-of-generators morphism from a set x to the free group generated by x. Since hets have their tail in one category and head in another, they may also be colorfully called chimera morphisms. Hets should not be confused with functors, which map one whole category to another. For instance, the free-group functor from the category of sets to the category of groups has the action on to take a set x to a group , often symbolized by , which is quite distinct from the set-to-group injection-of-generators heteromorphism .
Heteromorphisms between two given categories can be treated using a bifunctor analogous to the way homomorphisms are treated within a category. When one is “given” a category, X, it is then assumed to include the composition of homs within the category, and that is specified rigorously by a hom-bifunctor . Given an X-hom in , then its composition with another X-hom is given by the induced map , where .
Just as one assumes the hom-bifunctor for the morphisms of a category when “given” that category, so, when using heteromorphisms as part of the category-theoretic data, “given” two categories X and A, one would assume not only two hom-bifunctors and but also the two het-bifunctors and .
The analogous way in which het-bifunctors describe the composition of hets and homs is explained in the next section in the context of Mac Lane’s comments about Bourbaki.
3. Mac Lane on Bourbaki and Adjunctions
Consider Mac Lane’s historical comments on Bourbaki and adjoints.
One may also speculate as to why the discovery of adjoint functors was so delayed. …Bourbaki just missed ([1948], Appendix III). His definition of universal construction was clumsy, because it avoided categorical language, but it amounted to studying a bifunctor and asking for a universal element of for each x. This amounts to asking for objects and a natural isomorphism ; it includes the problem of finding a left adjoint F to a functor , with . …Bourbaki’s construction problem emphasized representable functors, and asked “Find so that ”. This formulation lacks the symmetry of the adjunction problem, “Find so that ”—and so missed a basic discovery; this discovery was left to a younger man, perhaps one less beholden to tradition or to fashion.
Mac Lane reviews the book containing that Appendix III in 1949 [
14] but then only mentions, without further comment, the Appendix on the “universal mapping” problem. Appendix III was dropped in the final edition of
Algebre [
15], although some of the content appears (first published in 1957) in the section on Universal Mappings in Bourbaki’s
Elements of Sets [
16].
Mac Lane noted in
Categories for the Working Mathematician (first published in 1971) that Bourbaki’s (i.e., Samuel’s) statement of the universal mapping problem “amounted to” using a bifunctor
and then, for each
x, asking for a representation in
A of the functor
. Bodo Pareigis calls such a bifunctor a
connection [
5] (p. 58) from category
X to category
A; today, such a bifunctor is also called a
-valued
profunctor [
17],
distributor [
18], or
correspondence [
19] (p. 96), depending on the context. The elements of
can be interpreted as heteromorphisms or hets from an object
x in
X to an object
a in
A (The concrete or intuitive interpretation as heteromorphisms of the elements in the values of a “naked” bifunctor
is not available for the bifunctors defined from given functors going one way or another between the categories, such as
or
(including comma categories, e.g., Mac Lane [
2] (p. 45)), since those are clearly hom-sets within a category. However, such bifunctors with hom-set values appear when there is a left or right representation of a naked bifunctor
).
The het-bifunctor gives the rigorous way to handle the composition of a het
in
[thin arrows → and Greek letters for hets] with a homomorphism or hom
in
X [thick Arrows ⟹ and Roman letters for homs] and a hom
in
A. For instance, the composition
is the het that is the image of
under the map:
. Similarly, the composition
is the het that is the image of
under the map:
(The definition of a bifunctor also insures the associativity of composition so that, schematically,
) (
Figure 1).
This is all perfectly analogous to the use of hom-functors to define the composition of homs, and, thus, the bifunctor with the het interpretation of its elements is best termed a het-bifunctor (normal arrows → for all functors).
4. Left and Right Representations of Het-Bifunctors
Given the het-bifunctor Mac Lane referred to as
, the universal mapping problem for each
is: does there exist an object
and a canonical het
such that, given any het
(to any
), there exists a unique hom
such that the following diagram commutes?
If there is a solution for each
, that is equivalent to the het-bifunctor
being represented on the left by a functor
, which means, for each object
, there is an isomorphism natural in
a:
This is said to be a
left representation of the het-
bifunctor or
left representation for short (“
universal solution of the universal problem” in Pareigis [
5] (p. 58)). A left representation is a “universal mapping situation” that gives the functor solution of the het-version of a UMP and often gives half of an adjoint situation (e.g., a semi-adjunction or “half-adjunction” [
6]), in which case the left-representing functor
F is the left adjoint.
Instead of taking
as being independently defined as a het-functor, Mac Lane notes that this would define a left adjoint to a
given functor
if we
defined . Having thus introduced the asymmetry by defining
in this manner while already assuming
G, Mac Lane goes on to say that Bourbaki missed the symmetry of the adjunction equivalence, where
gives a left representation of the bifunctor
. However,
given the (“naked”) het-functor
(i.e., without any
G), the obvious
symmetrical action to perform is to dually define a functor
from the representation of
on the right so that, for each
, there is an isomorphism natural in
x:
which might be called a
right representation of the het-
bifunctor or
right representation for short.
The dual co-universal mapping problem for each
is: does there exist an object
and a canonical het
such that for any het
(from any
), there exists a unique hom
such that the following diagram commutes?
A solution for every
defines the right representing functor
, which gives the right representation.
If the het-bifunctor is represented symmetrically on both the left and right, then we have the natural isomorphisms of an adjunction equivalence:
where
and
are, respectively, the left and right adjoints. The canonical
het unit is obtained by taking
on the left and then taking the image of
in
under the isomorphism. The canonical
het counit is obtained by taking
on the right and then taking the image of
in
under the isomorphism. Then, the adjunction is represented very simply by the adjunctive square diagram.
Given any het
, the left isomorphism gives the unique hom
, so the lower triangle commutes, and the right isomorphism gives the unique hom
, so the upper triangle commutes (There is an interesting side issue: do adjoints
have a “directionality” between the categories
X and
A? This is far from clear in the usual treatment since the functors go both ways and all of the object-to-object morphisms are homs within the two categories. However, in the adjunctive square diagram, all the hets go in the same direction from
X to
A).
All of this is perfectly symmetrical, and it considerably simplifies the convoluted “over-and-back diagrams” for the conventional homs-only treatment of adjoints, where given a hom
in one category, there exists a unique hom
in the other category so that the image hom
back in the original category makes the following diagram commute. (We have used the standard Greek letters
and
for the usual unit and co-unit even though they are homs.)
Contrary to Mac Lane’s remarks, the het treatment is equally as or more symmetric to the conventional homs-only treatment and even simpler. Mac Lane in effect gives Samuel credit for isolating the left representation that solves a universal mapping problem, but the turn-the-arrows-around category-theoretic duality was not clearly understood in 1948, so Samuel did not arrive at the symmetric dual formulation and solution to the co-universal mapping problem, namely a right representation (It is something of a mystery why Mac Lane in 1971 [
2] (Notes at end of Adjoints chaper) did not consider the dual right representation of Samuel’s Het-bifunctor
instead of
starting with a functor
and the resulting bifunctor
and then pointing out that the left representation would yield an adjunction:
). Thus, we might say that Samuel was only a dualization away from defining adjoints in 1948 since adjoints arise as the left and right representing functors for the hets
going from a category
X to a category
A.
5. Pareigis’s “New Characterization” of an Adjunction
Bodo Pareigis’s 1970 text,
Categories and Functors [
5] (translation of the 1969 German edition), is, to our knowledge, the first text and, to this day, the
only category-theory text that in effect uses a het-bifunctor (called a “connection”) to give the heteromorphic “new characterization for pairs of adjoint functors” [
5] (p. 60). Pareigis does not call the elements of
[or in his notation:
[
5] (p. 58) where
and
] heteromorphisms (since he refers to both homs and hets as “morphisms”). Indeed, he quickly defines a new category,
, whose objects are the disjoint union of the objects of the categories
and
, and whose morphisms are of three kinds, the homs of
, the hets from
to
, and the homs of
—all of which are seen as “homs” in
. Pareigis calls it a
directly connected category with the
connection . Given a bifunctor
, this category today might be called the
cograph [
20] or
collage category of the bifunctor and be denoted as
[
19] (p. 96). (If
is the ordered set considered to be a category with
, then Jacob Lurie points out that these categories are in one-to-one correspondence with the functors
for any category
M [
19] (p. 97). Given a bifunctor
, there is the obvious functor
, and, given such a functor
, take
,
, and, for
and
, the het-bifunctor is given by
.)
From the first formalizations of a “universal mapping problem” in 1948 (Samuel [
4]; Bourbaki [
3]), the hets
(for a given
) have been an intrinsic part of the data, since the “solution”
to the universal problem is a (left) representation of those hets by homs
within the codomain category
A [
5] (Lemma 2, p. 58).
For the original universal mapping problem, a solution for each
yields a functor
giving the natural isomorphism:
or in Pareigis’s notation:
The dual co-universal mapping problem (which Samuel did not formulate) starts with the same het-bifunctor data and asks, for a given , for a (right) representation of those hets by homs within the domain category X.
In Pareigis’s (perhaps unnecessarily complicated) presentation of the dual case, he starts with a “connection” going the other way, i.e., a bifunctor
, so that
is the corresponding directly connected category. He also denotes this category as
and calls it an
inversely connected category [
5] (p. 60 where “inversely” is mis-spelled as “universely”). The
co-universal problem is, for a given
(where we have used our different-arrows notation for homs and hets):
Is there an object
and a morphism
such that for each morphism
for all
there is exactly one morphism
, making the diagram
commutative?
A solution for every would again define a representing functor .
Then, Pareigis arrives at his “new characterization” of an adjunction by starting with the connection
so that
is directly connected, and
[note the reversal in the arguments from the previous
] is inversely connected. Then, both of the universal problems have solutions for all
and
if and only if we have a pair of adjoint functors
and
with the natural isomorphisms between the morphism sets [
5] (Theorem 2, pp. 60–61):
Pareigis did not splice the two triangular diagrams for the universal and co-universal problems together at their common hypotenuse, but this would yield the commutative diagram (with our notation for the canonical hets):
Pareigis’s text shows the heteromorphic treatment of adjunctions dates from at least the late 1960s, but it has not “caught on” and is, to our knowledge, not used in any of the more recent texts. Hence, it remains an eccentric or heterodox treatment that is not part of the “official” orthodoxy. In spite of the informal use of hets in mathematical practice, various devices are used in the orthodox formal treatment of universal problems and adjoints so that hets are not explicitly recognized. Contrary to that later orthodoxy, Samuel formally recognized hets in his 1948 statement of the universal problem, but he missed Pareigis’s heteromorphic characterization of adjoints a decade before Kan gave the orthodox treatment since Samuel did not develop the dual co-universal problem.
6. Samuel—With Dualization
Pierre Samuel was explicit about the treatment of homs and hets and denoted them, respectively, with Roman and Greek letters (and we have followed here, for the most part, this Samuel notational convention). He worked with structured sets such as
S-sets and
T-sets so the homs would be the
S-mappings or
T-mappings. He called the hets from an
S-set to a
T-set “
-
-mappings” [
4] (p. 592), and he denoted them with Greek letters to recognize their difference from homs. Samuel also noted that the composition of an
-
-mapping with a
T-mapping would be an
-
-mapping, i.e., hets composed of homs are hets. Samuel ([
3] (Appendix III) and [
4]) used a standard scheme for a solution to a universal problem where, given an
S-set
E, there is a “canonically associated” (old language for a functor)
T-set
and a canonical
-
-mapping
such that for any other
-
-mapping
, there is a uniquely determined
T-mapping
such that the following diagram commutes.
Samuel did not see that this scheme could be dualized as a solution to a co-universal problem as follows. Given a
T-set
F, there is a canonically associated
S-set
and a canonical
-
-mapping
such that for any
-
-mapping
, there is a uniquely determined
S-mapping
such that the following diagram commutes.
Splicing the two triangular diagrams together at the common diagonal het
gives Samuel’s “almost” definition of an adjunction.
7. Chimeras in the Wilds of Mathematical Practice
The homs-only orientation may go back to the original conception of category theory “as a continuation of the Klein Erlanger Programm, in the sense that a geometrical space with its group of transformations is generalized to a category with its algebra of mappings” [
21] (p. 237). While chimeras (such as the injection of the generators into the free group) do not appear in the orthodox “ontological zoo” of category theory, they abound in the wilds of mathematical practice. In spite of the reference to the “Working Mathematician” in the title of Mac Lane’s text [
2], one might seriously doubt that any working mathematician would give, say, the universal mapping property of free groups using the “device” of the underlying set functor
U instead of the traditional description given in the left representation diagram (which does not even mention
U), as can be seen in most any non-category-theoretic text that treats free groups. For instance, consider the following description in Nathan Jacobson’s text [
22] (p. 69).
To summarize: given the set we have obtained a map of X into a group such that if G is any group and , is any map of X into G then we have a unique homomorphism of into G, making the following diagram commutative:
In Jacobson’s diagram, only the
morphism is a group homomorphism and thus would be recognized in homs-only category theory; the vertical and diagonal maps are set-to-group hets so it is the diagram for a left representation (We modified Jacobson’s diagram according to our het–hom convention for the arrows. Other examples from Mac Lane–Birkhoff’s text [
23] are given later).
Indeed, it might be interesting to see how Mac Lane handled the hets naturally involved in a universal mapping property before the development of the homs-only devices used later. To characterize the product within a category
C, a het
from an object
c in the category
C to an object
in the category
is a pair of
C-morphisms
and
, which Mac Lane called a “system” of maps [
24] (p. 264) and was later called a “cone” (a common type of heteromorphism) (Thus, the values of
can be identified with the Cartesian product
). Fixing
, the product
is given by a right representation. That is, there is a universal het
consisting of the cone-het of
C-homs
and
(the projections) such that for any cone-het
and
from an object
c in
C to the object
in the different category
, there is a unique
C-hom
such that the
C-hom followed by the universal het equals the given het. Thus, the
C-hom
is the unique factor map that “transfers” (in this case, “reflects”) the property of “being a cone
” from the universal such cone-het (the projections) to the given such cone
and
(Ellerman [
25]). This is the het statement of the universal mapping property for the product. A het-free description of the product would be as a right adjoint to a diagonal functor
using the homs-only treatment of adjoints.
Diagonal functors and forgetful functors are two “devices” used to give an adjoint characterization of various significant functors without using hets, when there is a simpler characterization available using hets. For instance, Mac Lane [
2] (p. 87) gives a long list of forgetful functors whose left adjoints are significant mathematical constructions. Using the heteromorphic treatment, those significant left adjoints can all be obtained as the left representing functors without mentioning the device of the forgetful functor—as is typical in mathematical practice. Similarly Mac Lane [
2] (pp. 87–88) gives a long list of significant functors that are the left or right adjoints to diagonal functors, but again, in the heteromorphic treatment, the significant functors can be characterized as the left or right representing functors without using the device of a diagonal functor. When not giving “official” statements, category theorists, as working mathematicians, routinely use hets (e.g., cones and cocones) informally and, in some cases,
have to use hets to state the universal mapping characterization of a functor (e.g., the case of tensor products considered below).
8. Hets as “Homs” in a Collage Category
The notion of a homomorphism is so general that hets can always be recast as “homs” in a larger category variously called a
directly connected category [
5] (p. 58) (since Pareigis calls the het-bifunctor a “connection”), a
cograph category [
20], or, more colloquially, a
collage category (since it combines quite different types of objects and morphisms into one category in total disregard of any connection to the Erlangen Program). The
collage category of a het-bifunctor
, denoted
[
19] (p. 96), has as objects the disjoint union of the objects of
X and
A. The
homs of the collage category are defined differently according to the two types of objects. For
x and
objects in
X, the homs
are the elements of
, the hom bifunctor for
X, and, similarly for objects
a and
in
A, the homs
are the elements of
. For the different types of objects, such as
x from
X and
a from
A, the “homs”
are the elements of
, and there are no homs
in the other direction in the collage category.
Does the collage category construction show that “hets” are unnecessary in category theory and that homs suffice? Since all the information given in the het-bifunctor has been repackaged in the collage category, any use of hets can always be repackaged as a use of the “X-to-A homs” in the collage category . In any application, similarly to the previous example of the universal mapping property (UMP) of the free-group functor as a left representation, one must distinguish between the two types of objects and the three types of “homs” in the collage category.
Suppose in Jacobson’s example, one wanted to “avoid” having the different “maps” and group homomorphisms by formulating the left representation in the collage category formed from the category of
, the category of groups
, and the het-bifunctor,
, for set-to-group maps. Since the UMP does not hold for arbitrary objects and homs in the collage category,
, one would have to differentiate between the “set-type objects” in
X and the “group-type objects” in
G, as well as between the “mixed-type homs” in
and the “pure-type homs” in
. Then, the left representation UMP of the free-group functor could be formulated in the het-free collage category
as follows.
For every set-type object x, there is a group-type object and a mixed-type hom such that for any mixed-type hom from the set-type object x to any group-type object G, there is a unique pure-type hom such that .
Thus, the answer to the question “Are hets really necessary?” is “No!”—since one can always use sufficient circumlocutions with the
different types of “homs” in a collage category. Jokes aside, the collage category formulation is essentially only a reformulation of the left representation UMP using clumsy circumlocutions. Working mathematicians use phrases such as “mappings” or “morphisms” to refer to hets in contrast to homomorphisms—and “mixed-type homs” does not seem to be improved phraseology for hets.
In the foundational debates between set theory and category theory, one of the points made by category theorists is that category theory, unlike set theory, reflects the actual practice of working mathematicans. This is actually false when it comes to the abundant hets in the wilds of mathematical practice; the elaborate circumlocutions used in homs-only category theory do not reflect mathematical practice.
9. Heterophobic Devices: Mac Lane’s Universal Arrows
One het-avoidance device is just to avoid the middle term in the adjunction isomorphism:
and to use the elaborate circumlocutions of the homs-only over-and-back adjunction diagrams. While Samuel, Bourbaki, Pareigis, Grothendieck, and other working mathematicians routinely use hets in stating universal mapping properties, Mac Lane went to some lengths to give a het-free definition of a
universal arrow from an object to a functor [
2] (p. 55).
Given the forgetful functor and a graph G, we have constructed (§ II.7) the free category C on G and the morphism of graphs which embeds G in C, and we have shown that this arrow P is “universal” from G to U. A similar universality property holds for the morphisms embedding generators into free algebraic systems of other types, such as groups or rings. Here is the general concept.
Definition 1. If is a functor and c an object of C, a universal arrow from c to S is a pair consisting of an object r of D and an arrow of C, such that to every pair with d an object of D and an arrow of C, there is a unique arrow of D with . In other words, every arrow f to S factors uniquely through the universal arrow u, as in the commutative diagram For example, take
as the set of generators of the free group
and
as the underlying set functor with
d as any other group
G. Then, the universal arrow is
, so for any
,
such that:
Thus, the free-group universal mapping property is stated as a universal arrow from the set of generators to the underlying set functor
U from
to
.
The free-group functor
can be more naturally characterized as the left representing functor for the het-bifunctor
, where the elements in
are all the set-to-group functions
. The simple corresponding diagram for the heteromorphic treatment is that the free-group functor is a left representation diagram for the hets (→) from a fixed set
x to any group
G.
Additionally, the heteromorphic treatment of the UMP of the free group is the one used by working mathematicians, e.g., in ordinary algebra texts.
10. The Tensor Product as an Important Example
In Mac Lane’s remarks about Bourbaki–Samuel, he notes the special case of the tensor product functor.
[Samuel’s universal problem] also includes the problem of finding a tensor product for two modules A and B, with taken to be the set of bilinear functions . Moreover, the tensor product is not in this way an example of a left adjoint (though it is an example of our universal arrows).
The universal mapping property of the tensor product is of interest since it is a case where the heteromorphic treatment is forced since, as Mac Lane notes, the tensor product functor is not a left adjoint (the “nearest” adjunction is the linear version of the Currying adjunction obtained by fixing B: ), and thus the usual device of using the other adjoint (e.g., a forgetful functor) to avoid hets is not available.
For
modules (over some commutative ring
R), one category is the product category
where the objects are ordered pairs
of
R-modules, and the other category is just the category
of
R-modules. The values of the het-bifunctor
are the bilinear functions
. Then, the tensor product functor
given by
gives a left representation:
that characterizes the tensor product. The canonical het
is the image under the isomorphism of the identity hom
obtained by taking
, so we have:
where the single arrows are the bilinear hets and the thick arrow is a module homomorphism within the category
.
Since the tensor product functor is not a left adjoint, Mac Lane defines the notion of a
universal element to give a seemingly het-free treatment.
The idea of universality is sometimes expressed in terms of “universal elements”. If D is a category and a functor, a universal element of the functor H is a pair consisting of an object and an element such that for every pair with there is a unique arrow of D with .
As Mac Lane noted [
2] (p. 58), this can be diagrammed as a universal arrow (from
to
H) using “the” one-element set
and a set function
to pick out an element
, and which involves only homs in
D or
.
Then, Mac Lane notes that the bilinear universal mapping property for the tensor product can be shoe-horned into this homs-only notion of a universal element.
Tensor products provide another example of universal elements. Given two vector spaces V and over the field K, the function H which assigns to each vector space W the set of all bi-linear functions is the object function of a functor , and the usual construction of the tensor product provides both a vector space and a bilinear function , usually written , so that the pair is a universal element for the functor . This applies equally well when the field K is replaced by a commutative ring (and vector spaces by K-modules).
In this example (using
R-modules instead of vector spaces), the het-functor is:
so fixing
,
, and then the above diagram for the universal element is:
which is another convoluted (over-and-back) and seemingly het-free restatement of the simple left representation diagram for the tensor product given above. In the diagram, Mac Lane avoids explicit reference to the hets
by using the het-bifunctor itself explicitly to handle the het-hom composition:
as
, where
is just the het-bifunctor holding
fixed. Thus, the rather jerry-rigged notion of a universal element uses the het-bifunctor
and the set-homs
and
to avoid mentioning the images of *, which are the hets
and
.
In Mac Lane and Birkhoff’s
Algebra textbook [
23], they use hets starting with the special case of a
K-module
A (for a commutative ring
K) and then stating the universal mapping property of the tensor product
using the left representation diagram below—similar to any other working mathematicians. They do not use the homs-only universal element diagram; instead they compose (without comment) the universal bilinear het
with a linear transformation hom
t between
K-modules:
which is equal to the given bilinear het
.
In other words, the arbitrary bilinear function
h is expressed as a composite
with the fixed bilinear function
, as in the commutative diagram
where we have used our notation for the hom
in the diagram.
11. Adjoints vs. Representable Functors: What Is Basic?
There is a growing consensus among category theorists that category theory has foundational importance not simply because it provides the language in which to formulate mathematics (similarly to set theory) but also because it provides the conceptual lens (as set theory does not) to put into focus the important parts of mathematics. Additionally, adjoints are widely perceived as the basic lens (Lawvere [
26]). As Steven Awodey put it:
The notion of adjoint functor applies everything that we have learned up to now to unify and subsume all the different universal mapping properties that we have encountered, from free groups to limits to exponentials, but, more importantly, it also captures an important mathematical phenomenon that is invisible without the lens of category theory. Indeed, I will make the admittedly provocative claim that adjointness is a concept of fundamental logical and mathematical importance that is not captured elsewhere in mathematics.
Other category theorists have given similar testimonials.
To some, including this writer, adjunction is the most important concept in category theory.
The isolation and explication of the notion of adjointness is perhaps the most profound contribution that category theory has made to the history of general mathematical ideas.
(Goldblatt [
28] (p. 438))
Nowadays, every user of category theory agrees that [adjunction] is the concept which justifies the fundamental position of the subject in mathematics.
The Mac Lane–Bourbaki–Samuel episode raises a more basic question: should adjoints be taken as that basic conceptual lens, or should an adjunction be seen as a molecular concept that can be split into the two atoms using the notion of representable functors? (A functor
is
representable if there is a “representing object”
such that
F is naturally isomorphic to
. For instance, given a het bifunctor
, a left representation arises if, for each
, the functor
is representable, which also implies that the representing object is given by a functor
so the isomorphism takes the form:
.) Heteromorphisms seem to be key to that question since, as we have argued, the “natural” or clean formulation of many universal mapping problems is as a heteromorphic representation problem—in contrast, say, to Mac Lane’s convoluted over-and-back homs-only formulations of the universal arrows or universal elements—although ultimately each concept “subsumes” (Mac Lane [
2] (p. 61)) the others.
Given a het-bifunctor
“connection” ([
5] (p. 58)) or “correspondence” (Lurie [
19] (p. 96)) from
X to
A, adjoints arise as the left and right representations of the bifunctor, and, conversely, by the “Adjunction Representation Theorem” [
6] (p. 147):
given any adjunction , heteromorphisms can be defined between (isomorphic copies of) the categories X and A so that (isomorphic copies of) the adjoints arise from the representations on the left and right of the het-bifunctor.
Thus, all adjunctions arise as bi-representations of het-bifunctors, but there can be either a left or right representation without the other (e.g., the tensor product example). Moreover, when one of a pair of adjoints gives the important concept, and the other adjoint functions as an auxiliary device to fill out the het-free notion of an adjunction, then the important left or right representation is routinely used in the literature (along with the necessary hets) without the auxiliary device. These considerations argue that it is the concept of a universal mapping property (which is naturally formulated as a representation of hets) that is the “most important concept in category theory” and that adjunctions arise as the special case of
bi-representations of hets. (See [
7] for an extensive development of this viewpoint.)
Since this treatment of UMPs is based on the notion of a representable functor associated with Alexander Grothendieck ([
30] (representable functors are defined in first section of the first Chapter 0)), it helps to clear up another mystery.
As we can see by looking at his [Grothendieck’s] lectures in the Séminaire Bourbaki from 1957 until 1962, the notion of representable functors became one of the main tools he used…. It is far from clear why Grothendieck decided to use this notion instead of, say, adjoint functors,…. It is also clear from the various seminars that Grothendieck thought in terms of universal “problems”, that is he tried to formulate the problems he was working on in terms of a universal morphism: finding a solution to the given problem amounted to finding a universal morphism in the situation. Grothendieck saw that the latter notion was subsumed under the notion of representable functor.
In short, Grothendieck took as basic the notion of a representable functor (solving a universal problem), and then adjoints arise as the special case of a particularly nice bi-representation. To personalize the “adjoints vs. representable functors” issue, perhaps it is: Mac Lane vs. Grothendieck.
12. Conclusions
We have revisited the heteromorphic approach to adjunctions along with the associated history of these concepts starting with Mac Lane’s famous remarks about how Bourbaki (i.e., Pierre Samuel) “just missed” adjoints, but, after Mac Lane category-theoretically reformulated what Samuel had completed using a Het-bifunctor
, we see that Samuel defined a left representation
. Dualizing yields the notion of a right representation
, so, putting the two isomorphisms together, we have the heteromorphic adjunction equivalence:
which seems to be first developed by Pareigis in the late 1960s. Hence, Samuel did miss adjoints, but (reformulated in categorical terms) he was only a simple dualization away from defining an adjunction a decade before Kan.
These observations prompted analysis of the puzzling reticence in orthodox category theory to formally recognize the object-to-object morphisms for objects in different categories. Some artificiality and various devices are employed to avoid any official use of hets, although hets are commonly used informally by working category theorists, not to mention other working mathematicians. Since hets can be rigorously treated using het-bifunctors [
7] in a way that is quite analogous to the usual hom-bifunctors, the usual heterophobia seems not to be based on any mathematical concerns for rigor. In view of the analogy with the Erlangen Program, the founders only considered homomorphisms, so one rationale may be respect for the founders’ original vision. However, then, reformulating hets as “mixed-type homs” in a collage category completely takes leave of any analogy with the Erlangen Program. The most plausible explanation is simply that the original definitions of category theory lock in, as with the QWERTY keyboard, ref. [
31] in spite of clear shortcomings, such as, in this case, not recognizing the hets of the working mathematician (such as a simple injection of the generators
from a set into the free group on the set).
Finally, we considered the “philosophical” question that lurks in the background about the “most important concept in category theory”: is it the notion of an adjunction or the notion of a representable functor (with many UMPs naturally formulated as an in-category representation of hets between categories)?