Abstract
Chaotic maps are sources of randomness formed by a set of rules and chaotic variables. They have been incorporated into metaheuristics because they improve the balance of exploration and exploitation, and with this, they allow one to obtain better results. In the present work, chaotic maps are used to modify the behavior of the binarization rules that allow continuous metaheuristics to solve binary combinatorial optimization problems. In particular, seven different chaotic maps, three different binarization rules, and three continuous metaheuristics are used, which are the Sine Cosine Algorithm, Grey Wolf Optimizer, and Whale Optimization Algorithm. A classic combinatorial optimization problem is solved: the 0-1 Knapsack Problem. Experimental results indicate that chaotic maps have an impact on the binarization rule, leading to better results. Specifically, experiments incorporating the standard binarization rule and the complement binarization rule performed better than experiments incorporating the elitist binarization rule. The experiment with the best results was STD_TENT, which uses the standard binarization rule and the tent chaotic map.
Keywords:
chaotic maps; binarization schemes; knapsack problem; Sine Cosine Algorithm; Grey Wolf Optimizer; Whale Optimization Algorithm MSC:
90C27
1. Introduction
Optimization problems are increasingly relevant across a wide range of sectors, including mining, energy, telecommunications, and health. A prominent type of these problems is combinatorial optimization problems, where the decision variables are of a categorical nature, such as binary. In these cases, the challenge is to identify the best possible combination of these variables.
The complexity of solving these problems increases exponentially with the number of decision variables. This is because, in a binary combinatorial problem, the search space of these problems is , where n represents the total number of decision variables. This exponential growth of the search space poses significant computational and analytical challenges.
According to the literature [1], methods for addressing complex optimization problems are classified into two main categories: exact methods and approximate methods.
- Exact Methods: These methods focus on ensuring an optimal solution by exhaustively exploring the entire search space. However, their applicability is limited due to scalability issues. As the complexity of the problem increases, the time required to find an optimal solution increases significantly, which can make them impractical for large-scale problems or those with an excessively large search space.
- Approximate Methods: Unlike exact methods, approximate methods do not guarantee the attainment of an optimal solution. However, they are capable of providing high-quality solutions within reasonable computational times, making them very valuable in practice, especially for complex and large-scale problems. Within this category, metaheuristics are particularly notable. These techniques, which include Genetic Algorithms (GA), Particle Swarm Optimization (PSO), and Ant Colony Optimization (ACO), are known for their ability to find efficient solutions to complex problems through intelligent exploration of the search space, avoiding getting trapped in sub-optimal local solutions.
Thus, exact methods are ideal for smaller, manageable problems where precision is required, whereas approximate methods, especially metaheuristics, are the preferred option for larger-scale problems or those with time constraints, where a ”good enough” solution is acceptable and often necessary.
The study of metaheuristics has grown in recent years, with hybridizations emerging as the current trend. There exist hybridizations between metaheuristics such as those proposed in [2,3,4,5], hyperheuristic approaches where a high-level metaheuristic guides another low-level one [6,7,8], approaches where machine learning techniques enhance metaheuristics [9,10,11], and other approaches in which chaos theory is utilized to modify the stochastic behavior of metaheuristics [12,13,14,15].
The integration of chaotic maps into metaheuristics has caught the attention of the scientific community due to its advantages, such as low computational cost and rapid adaptability [16]. Chaotic maps are used as generators of random sequences, contributing to an improvement in the stochastic behavior of metaheuristics. This approach is utilized in various aspects of metaheuristics such as the initialization of solutions [17,18] or in the solution perturbation operators [19,20]. The hybridization of metaheuristics with chaotic maps is significant because it enhances the ability of metaheuristics to avoid getting trapped in local minima and improves global exploration of the search space.
In reviewing the different metaheuristics existing in the literature [21], we can observe that most of them are designed to solve continuous problems; therefore, to solve binary combinatorial problems, it is necessary to binarize them. According to the literature [22], there are different ways to binarize metaheuristics, among which the two-step technique stands out. This binarization process is carried out in two steps: (1) applying a transfer function and (2) applying a binarization rule. In the present work, chaotic maps were used to change the stochastic behavior of the binarization rule to binarize continuous metaheuristics. Specifically, seven chaotic maps were used, which were compared with the original stochastic behavior for binarizing three metaheuristics widely used in the literature.
Among the great variety of metaheuristics that exist in the literature, in the present work we chose the Sine Cosine Algorithm (SCA) [23], Grey Wolf Optimizer (GWO) [24], and Whale Optimization Algorithm (WOA) [25]. These three metaheuristics are population metaheuristics designed to solve continuous optimization problems of great interest to the scientific community. This interest is reflected in the use of these metaheuristics in different works where, for example, SCA was used in [26,27,28,29,30,31], GWO was used in [32,33,34,35,36,37,38,39], and WOA was used in [40,41,42,43,44,45,46].
Given this great interest, the good results obtained in different optimization problems, and the No Free Lunch Theorem [47,48], we are motivated to investigate the behavior of these three metaheuristics in a combinatorial optimization problem, the Knapsack Problem, with the hybridization of chaotic maps.
The main contributions of this work are the following:
- Incorporate chaotic maps into binarization schemes to develop chaotic binarization schemes.
- Use these chaotic binarization schemes in three continuous metaheuristics to solve the 0-1 Knapsack Problem.
- Analyze the results obtained in terms of descriptive statistics, convergence, and non-parametric statistical test.
The following is a brief summary of the structure of this paper: Section 2 provides a comprehensive review of related works that utilize continuous metaheuristics (Section 2.1), defines chaotic maps (Section 2.2), and assesses their application in metaheuristics (Section 2.3). Section 3 examines how continuous metaheuristics can be leveraged to solve binary combinatorial optimization problems. Section 4 outlines our research proposal, which focuses on the implementation of chaotic binarization schemes. Section 5 of this paper details the 0-1 Knapsack Problem (Section 5.1), the experiment configuration (Section 5.2), the results analysis (Section 5.3), the algorithm convergence analysis (Section 5.4), and the non-parametric statistical test analysis (Section 5.5). Finally, Section 6 presents conclusions and future work.
2. Related Work
2.1. Metaheuristics
Metaheuristics are highly flexible and efficient algorithms, capable of delivering quality solutions in manageable computational times [1]. The efficacy of metaheuristics is largely due to their ability to balance two critical phases in the search process, diversification (or exploration) and intensification (or exploitation), using specific operators that vary according to the algorithm in question.
The development of metaheuristics, stimulated by the No Free Lunch Theorem [47,48,49], is based on a variety of sources of inspiration, including human behavior, genetic evolution, social interactions among animals, and physical phenomena. This theorem, fundamental in the field of optimization, states that there is no universal algorithm that is most efficient for solving all optimization problems. The following section will introduce and define the three metaheuristics employed in this research.
2.1.1. Sine Cosine Algorithm
The Sine Cosine Algorithm (SCA) is a metaheuristic proposed by Mirjalili in 2016 [23]. This metaheuristic was designed to solve continuous optimization problems and is inspired by the dual behavior of the trigonometric functions sine and cosine. Algorithm 1 presents the behavior of SCA.
2.1.2. Grey Wolf Optimizer
The Grey Wolf Optimizer [24], proposed by Mirjalili in 2014, is a metaheuristic inspired by the hunting behavior and hierarchical social structure of the grey wolf. The efficacy of this technique is based on the imitation of the dynamics and social interactions observed in a pack of wolves.
In a wolf pack, there are four types of hierarchical roles that are essential in the structure of the GWO.
- Alpha (): These are the wolves that lead the pack. In the context of GWO, they represent the current best solution. The alpha guides the search process and decision making during optimization.
- Beta (): These wolves support the alpha and are considered the second-best solution. In the metaheuristic, they assist in directing the search, providing a secondary perspective in the solution space.
- Delta (): Though strong, delta wolves lack leadership skills. They are the third-best solution in the optimization process and contribute to the diversity of the search, bringing variability and preventing the pack (the algorithm) from becoming stagnant.
- Omega (): These wolves are the lowest in the social hierarchy. They have no leadership power and are dedicated to following and protecting the younger members of the pack. In GWO, they represent the other possible solutions, following the lead of the higher-ranking wolves.
| Algorithm 1 Sine Cosine Algorithm |
Input: The population Output: The updated population and
|
The implementation of these hierarchies in the GWO allows the algorithm to effectively balance exploration (diversification) and exploitation (intensification) of the solution space. The inspiration from the behavior and social structure of grey wolves brings a unique methodology for solving complex optimization problems. Algorithm 2 presents the behavior of GWO.
2.1.3. Whale Optimization Algorithm
The Whale Optimization Algorithm (WOA) is a metaheuristic developed by Mirjalili and Lewis in 2016 [25], inspired by the hunting behavior and social structure of whales. This algorithm mimics the hunting strategy known as “bubble-net feeding”, a sophisticated and coordinated method used by whales to capture their prey. The WOA is characterized by three main phases in its search and optimization process:
- Search for the prey: The whales (search agents) explore the solution space to locate the prey (the best solution). Notably in WOA, unlike other metaheuristics, the position update of each search agent is based on a randomly selected agent, not necessarily the best one found so far. This allows for a broader and more diversified exploration of the solution space.
- Encircling the prey: Once the prey (best solution) is identified, the whales position themselves to encircle it. This stage represents an intensification phase, where the algorithm concentrates on the area around the promising solution identified in the search phase.
- Bubble-net attacking: In the final phase, the whales attack the prey using the bubble-net technique. This phase represents a coordinated and focused effort to refine the search in the selected region and optimize the solution.
| Algorithm 2 Grey Wolf Optimizer |
Input: The population Output: The updated population and
|
The structure of these phases enables the WOA to effectively balance between exploration and exploitation, making it suitable for solving a wide range of complex optimization problems. Algorithm 3 presents the behavior of WOA.
2.2. Chaotic Maps
Dynamic systems, characterized by their lack of linearity and periodicity, exhibit chaos in a way that is both deterministic and seemingly random [50]. Such a characteristic of the dynamic system is recognized as a generator of random behaviors [51]. It is crucial to understand that chaos, although it follows specific patterns and is based on chaotic variables, is not synonymous with absolute randomness [52]. The implementation of chaotic mappings is valued for its ability to minimize computational costs and because it requires only a limited set of initial parameters [16].
Chaotic behavior demonstrates high sensitivity to variations in initial conditions, meaning that any modification of these conditions will influence the resulting sequence [53]. There are numerous chaotic maps referenced in the scientific literature, of which ten are of special relevance [50,52,54]. Equations (1)–(7) shows seven of these chaotic maps, and Figure 1 details the behavior of each of the previously mentioned chaotic maps.
| Algorithm 3 Whale Optimization Algorithm |
Input: The population Output: The updated population and
|
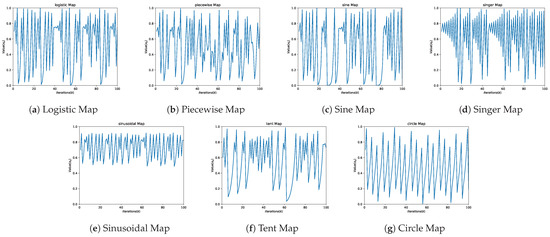
Figure 1.
Chaotic maps.
2.3. Chaotic Maps in Metaheuristics
Hybridization between metaheuristics and chaotic maps can be classified into four categories, which are summarized in Figure 2.
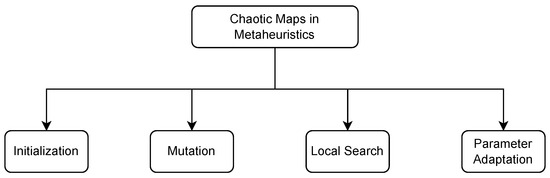
Figure 2.
Chaotic maps in metaheuristics.
- Initialization: The implementation of chaotic maps can be effective in creating initial solutions or populations in metaheuristic techniques, thereby replacing the random generation of these solutions. The nature of chaotic dynamics facilitates the distribution of initial solutions in different areas of the search space, thereby enhancing the exploration phase [13,17,18,55,56,57,58,59].
- Mutation: Chaotic maps can be employed to perturb or mutate solutions. By using the chaotic behavior as a source of randomness, the metaheuristic algorithm can introduce diverse and unpredictable variations in the solutions, aiding in exploration [15,60,61].
- Local Search: Chaotic maps have the potential to effectively steer the local search process within metaheuristic algorithms. By integrating chaotic dynamics into the metaheuristics, the algorithm gains the ability to break free from local optima and delve into various segments of the solution space [14,50,62,63,64,65,66].
- Parameter Adaptation: Chaos maps can be employed to dynamically adapt the parameters of a metaheuristic. The inherent chaotic behavior aids in the real-time adjustment of metaheuristic-specific parameters such as mutation rates and crossover probabilities in a genetic algorithm, thereby enhancing the algorithm’s adaptability throughout the optimization process [12,19,20,67,68,69,70,71,72,73].
3. Continuous Metaheuristics for Solving Combinatorial Problems
The No Free Lunch (NFL) theorem [47,48,49] indicates that there is no optimization algorithm capable of solving all existing optimization problems effectively. This is the primary motivation behind binarizing continuous metaheuristics, as evident in the literature where authors have presented binary versions for the Bat Algorithm [74,75], Particle Swarm Optimization [76], Sine Cosine Algorithm [10,11,77,78], Salp Swarm Algorithm [79,80], Grey Wolf Optimizer [11,81,82], Dragonfly Algorithm [83,84], Whale Optimization Algorithm [11,77,85], and Magnetic Optimization Algorithm [86].
The binarization process aims to transfer continuous solutions from a metaheuristic to the binary domain. In the literature [22], various binarization methods are found, with the two-step technique being a notable one. Researchers use this technique because of its quick implementation and integration into metaheuristics [87,88].
3.1. Two-Step Technique
The two-step technique, as its name suggests, performs the binarization process in two stages. In the first stage, a transfer function is applied, which maps continuous solutions to the real domain . Then, in the second stage, a binarization rule is applied, discretizing the transferred value, thereby completing the binarization process. Figure 3 provides an overview of the two-step technique.
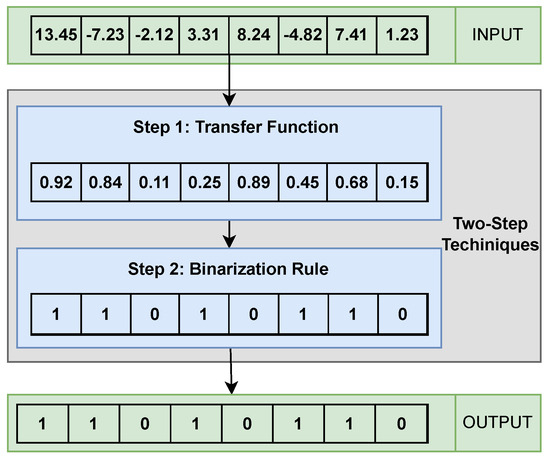
Figure 3.
Two-step technique.
3.1.1. Transfer Function
In 1997, Kennedy et al. [89] introduced transfer functions in the field of optimization. New transfer functions have been introduced over the years [22], and we can observe that there are different types of transfer functions, among which S-Shaped transfer functions [76,90] and V-Shaped transfer functions [91] stand out.
Table 1 and Figure 4 show the S-Shaped transfer functions and V-Shaped transfer functions found in the literature. The notation observed in Table 1 corresponds to the continuous value of the j-th dimension of the i-th individual resulting after the perturbation performed by the continuous metaheuristic.

Table 1.
S-Shaped and V-Shaped transfer functions.
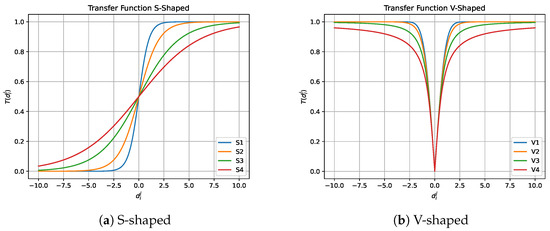
Figure 4.
S-Shaped and V-Shaped transfer functions.
3.1.2. Binarization Rule
The process of binarization involves converting continuous values into binary values, that is, values of 0 or 1. In this context, binarization rules are applied to the probability obtained from the transfer function to obtain a binary value. There are various different rules described in scientific literature [92] that can be utilized for this binarization process. The choice of the binarization rule is crucial since it can vary depending on the context and specific problem needs. It is crucial to consider the appropriate use of the binarization rule to obtain accurate and reliable results. Table 2 shows the five binarization rules found in the literature [87].

Table 2.
Binarization rules.
The notation observed in Table 2 corresponds to the j-th dimension binary value of the i-th current individual, and , observed also in Table 2, corresponds to the j-th dimension binary value of the best solution. Algorithm 4 shows the general scheme of a continuous metaheuristic being binarized. The symbol observed there refers to the perturbation of solutions, which is implemented by each metaheuristic in its own way depending on its inspiration.
| Algorithm 4 General scheme of continuous MHs for solving combinatorial problems |
Input: The population Output: The updated population and
|
4. Proposal: Chaotic Binarization Schemes
Authors who have incorporated chaotic behavior into their metaheuristics indicate that they improve the balance of exploration and exploitation because they obtain better results. On the other hand, Senkerik in [93] shows us a study on chaos dynamics in metaheuristics and tells us the choice of chaotic maps depends closely on the problem to be solved.
As observed in Section 2.3, chaotic maps have been applied to replace the random numbers used in metaheuristics. In this context, we propose using chaotic behavior to carry out the binarization process.
Specifically, we propose replacing the random numbers used in the standard binarization rule, complement binarization rule, and elitist binarization rule with the chaotic numbers generated by the chaotic maps.
As shown in Section 2.2, there are different chaotic maps; some of them can encourage exploration, and others can encourage exploitation. Thus, each original binarization rule will be compared with seven new chaotic variants for each binarization rule; these are detailed in Figure 5.
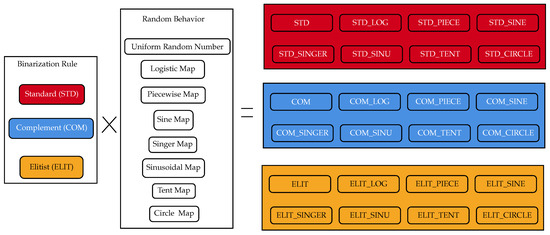
Figure 5.
Chaotic binarization rules.
In other words, our proposal consists of changing the uniform distribution between [0, 1] of the random number existing in the standard binarization rule, complementary binarization rule, and elitist binarization rule by the chaotic distribution of the 7 chaotic maps defined in the present work.
The dimensionality of the chaotic maps will be related to the number of iterations (), population size (), and number of decision variables of the optimization problem (). Thus, the dimensionality of the chaotic maps in the present proposal will be . Suppose we have an optimization problem with 100 decision variables and we use a population of 10 individuals and 500 iterations. In this case, the generated chaotic map will contain values. Algorithm 5 presents a summary of the proposal.
| Algorithm 5 Chaotic binarization schemes |
Input: The population Output: The updated population and
|
5. Experimental Results
To validate our proposal we used the Grey Wolf Optimizer, Sine Cosine Algorithm, and Whale Optimization Algorithm. Each of these continuous metaheuristics was used to solve a set of benchmark instances of the 0-1 Knapsack Problem. The binarization process of each of these metaheuristics is shown in Figure 5. We have 24 different versions of each metaheuristic. To test our proposal, we use benchmark instances widely used in the literature.
5.1. 0-1 Knapsack Problem
The Knapsack Problem is another NP-hard combinatorial optimization problem. Mathematically, it is modeled as follows: Given N objects, where the j-th object has its own weight and profit , and a knapsack that can holds a limited weight capability C, the problem consists of finding the objects that maximize the profit whose sum of weights does not exceed the capacity of the knapsack [94,95,96]. The objective function is as follows:
This is subject to the following restrictions:
where represents the binary decision variables (i.e., whether an element is considered in the knapsack (value 1 in the decision variable) or not considered in the knapsack (value 0 in the decision variable)).
According to the authors in [97], this problem has different practical applications in the real world, such as capital budgeting allocation problems [98], resource allocation problems [99], stock-cutting problems [100], and investment decision making [101].
We use the instances proposed by Pisinger in [102,103] where he presents three sets of benchmark instances that differ due to the correlation between each element. Table 3 shows the details of the benchmark instances of the Knapsack Problem used in this work, where the first column of this table presents the name of the instance, the second column presents the number of items to select, and the third column presents the global optimum of the instance.

Table 3.
Instances of Knapsack Problem.
5.2. Parameter Setting
Regarding the setup of the experiments, each variation of the metaheuristics was run 31 times independently, a population size of 20 individuals was used, and 500 iterations were used. The details of each configuration are detailed in Table 4.

Table 4.
Parameters setting.
Thus, experiments were carried out. Regarding the software and hardware used in the experimentation, we used Python in version 3.10.5 64-bit as the programming language. All the experiments were executed on a machine with Windows 10, an Intel Core i9-10900k 3.70 GHz processor, and 64 GB of RAM.
5.3. Summary of Results
Table 5 shows us the performance of each experiment with the three metaheuristics used in each solved instance. The first column of the table indicates the experiment, while the second and third columns pertain to the solved instance. The second column shows two symbols. The symbol “✓” indicates that the experiment under analysis reached the known global optimum, while the symbol “×” indicates that the experiment under analysis did not reach the known global optimum. Finally, in the third column we will also observe two things. In case the experiment under analysis has reached the known global optimum, this column will indicate in bold and underlined the metaheuristic(s) that reached the global optimum. In case no metaheuristic has reached the optimum, the metaheuristic or metaheuristics that reached the value closest to the optimum will be reported without bold and underlined. This last case applies to instances knapPI_2_100_1000_1, knapPI_2_1000_1000_1, knapPI_1_2000_1000_1, knapPI_2_2000_1000_1, and knapPI_3_2000_1000_1.

Table 5.
Summary of the performance of each experiment in each instance with the three metaheuristics.
By analyzing Table 5 we can observe that the experiments incorporating the standard binarization rule and the complement binarization rule have the best results. In particular, we can highlight the family of experiments incorporating the standard binarization rule since they reach the optimum in instances knapPI_1_500_1000_1, knapPI_2_500_1000_1, knapPI_3_500_1000_1, knapPI_1_1000_1000_1, and knapPI_3_1000_1000_1.
Table 6, Table 7 and Table 8 show the results obtained using GWO, WOA, and SCA, respectively. In these tables, we observe the following: in the first column, we observe the experiment used as defined in Figure 5, and the second, third, and fourth columns are repeated for each solved instance. The first of them indicates the best result obtained, the second of them indicates the average obtained with the 31 runs performed, and the third of them indicates the Relative Percentage Distance (RPD), which is calculated based on Equation (10). The experiments are grouped by base binarization rule, and the best result obtained per family is highlighted in bold and underlined.
where corresponds to the optimum of the instance and corresponds to the best value obtained for the experiment.

Table 6.
Results obtained with GWO for instances (a) knapPI_1_100_1000_1, knapPI_2_100_1000_1, and knapPI_3_100_1000_1; (b) knapPI_1_200_1000_1, knapPI_2_200_1000_1, and knapPI_3_200_1000_1; (c) knapPI_1_500_1000_1, knapPI_2_500_1000_1, and knapPI_3_500_1000_1; (d) knapPI_1_1000_1000_1, knapPI_2_1000_1000_1, and knapPI_3_1000_1000_1; (e) knapPI_1_2000_1000_1, knapPI_2_2000_1000_1, and knapPI_3_2000_1000_1.

Table 7.
Results obtained with WOA for instances (a) knapPI_1_100_1000_1, knapPI_2_100_1000_1, and knapPI_3_100_1000_1; (b) knapPI_1_200_1000_1, knapPI_2_200_1000_1, and knapPI_3_200_1000_1; (c) knapPI_1_500_1000_1, knapPI_2_500_1000_1, and knapPI_3_500_1000_1; (d) knapPI_1_1000_1000_1, knapPI_2_1000_1000_1, and knapPI_3_1000_1000_1; (e) knapPI_1_2000_1000_1, knapPI_2_2000_1000_1, and knapPI_3_2000_1000_1.

Table 8.
Results obtained with SCA for instances (a) knapPI_1_100_1000_1, knapPI_2_100_1000_1, and knapPI_3_100_1000_1; (b) knapPI_1_200_1000_1, knapPI_2_200_1000_1, and knapPI_3_200_1000_1; (c) knapPI_1_500_1000_1, knapPI_2_500_1000_1, and knapPI_3_500_1000_1; (d) knapPI_1_1000_1000_1, knapPI_2_1000_1000_1, and knapPI_3_1000_1000_1; (e) knapPI_1_2000_1000_1, knapPI_2_2000_1000_1, and knapPI_3_2000_1000_1.
When analyzing the results obtained in Table 6, Table 7 and Table 8, we can observe that the best binarization rule is STD_TENT, which reached the optimum with the three metaheuristics in 8 instances out of the 15 solved, and with WOA the optimum was reached in 2 more instances. In addition, with WOA the best result was reached in 1 instance.
This confirms what the authors have previously pointed out: the incorporation of chaotic maps improves performance in metaheuristics.
On the other hand, when we look at the largest instances (i.e., instances knapPI_1_1000_ 1000_1, knapPI_2_1000_1000_1, knapPI_3_1000_1000_1, knapPI_1_2000_1000_1, knapPI_2_ 2000_1000_1, and knapPI_3_2000_1000_1), we can observe that the WOA with the standard binarization rule achieves the best results, reaching the optimum in one and two. This indicates that the perturbation operators used by WOA to move the solutions in the search space are more efficient than the SCA and GWO operators.
5.4. Convergence Analysis
In this section, the convergence speed of the 24 experiments associated with the three metaheuristics will be analyzed by solving the knapPI_1_1000_1000_1 instance. This instance was selected since all the algorithms have similar behaviors in all instances, so the choice was random. For more information, you can consult the GitHub repository associated with this paper so you can see the behavior in the other instances.
Figure 6a, Figure 7a, and Figure 8a show us the behavior of the experiments that include the standard binarization rule in GWO, WOA, and SCA, respectively. In all three metaheuristics, we can observe that the STD_SINGER and STD_SINU experiments exhibit premature stagnation, unlike the others, which demonstrate decent convergence.
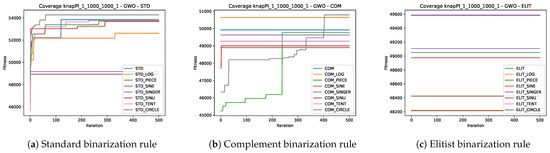
Figure 6.
Convergence graphs of the best execution obtained for the knapPI_1_1000_1000_1 instance using GWO.
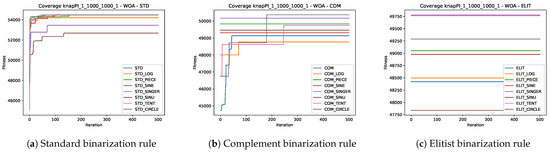
Figure 7.
Convergence graphs of the best execution obtained for the knapPI_1_1000_1000_1 instance using WOA.
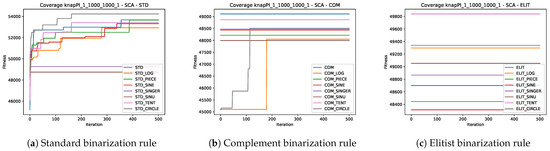
Figure 8.
Convergence graphs of the best execution obtained for the knapPI_1_1000_1000_1 instance using SCA.
On the other hand, in Figure 6b, Figure 7b, and Figure 8b, the behavior of the experiments that include the complement binarization rule in GWO, WOA, and SCA is observed respectively. An unusual behavior is observed where several experiments fail to improve the initial optimum generated by the initial solutions. Furthermore, this behavior is not uniform across the three metaheuristics. For GWO, the experiments COM_PIECE and COM_CIRCLE converge, while for WOA, it is COM, COM_CIRCLE, and COM_TENT, and for SCA, it is COM_TENT and COM_CIRCLE.
Finally, Figure 6c, Figure 7c, and Figure 8c show us the behavior of the experiments that include the elitist binarization rule in GWO, WOA, and SCA, respectively. In this case, it is even more noticeable since all experiments for the three metaheuristics do not improve upon the initial solutions obtained with the generation of initial solutions. This is striking and suggests that when using the elitist binarization rule, the solutions become lost in the search space.
Here again, we can observe two important things. The first is that the binarization rule plays a significant role, and the second is that chaotic maps do have an impact on convergence.
On the other hand, observing the behavior of the experiments that use as a basis the standard binarization rule and complement binarization rule within WOA, we can observe that it has a premature convergence and good results, unlike SCA and GWO, which have a slower convergence. This confirms what we mentioned in Section 5.3: the perturbation operators of WOA solutions are more efficient in exploring and exploiting the search space.
5.5. Statistical Test
In the literature [9,104,105,106], it can be seen that the authors perform a static test to compare the experimental results to determine if there is any significant difference between each experiment. For this type of experimentation, a non-parametric statistical test must be applied. In response to this, we have applied the Wilcoxon–Mann–Whitney test [107,108].
From the Scipy Python library, we can apply this statistical test. The python function is called scipy.stats.mannwhitneyu. One parameter of the above function is “alternative”, which we define as “greater”. We evaluate and contrast two distinct experiments, as previously stated in Figure 5. Thus, we can state the following hypotheses:
If the result of the statistical test is with obtained a p-value < 0.05, we cannot assume that B has worse performance than A, rejecting . This comparison is made because our problem is a maximization problem.
Table 9 shows a summary of the statistical comparisons made. The first column indicates the 24 experiments, the second column indicates how many times the experiment was better than another when we used GWO, the third column indicates how many times the experiment was better than another when we used WOA, the fourth column tells us how many times the experiment was better than the other when we used SCA, and the fifth column tells us how many times one experiment was better than the other when we consider the three metaheuristics. In such a case, metaheuristics compare one experiment against 23 others.

Table 9.
Ranking of best experiments based on statistical tests.
By analyzing Table 9, we can see that the experiments that include the elitist binarization rule are the best in the three metaheuristics. If we check carefully, we can see that ELIT_CIRCLE is statistically worse than the rest of the experiments that include the binarization rule except when we compare with SCA, where only ELIT and ELIT_LOG are statistically better than ELIT_CIRCLE.
After observing all the experiments of the elitist binarization rule family, we can observe the experiments COM_SINU, composed of the complement binarization rule and the capotic sinusoidal map, and STD_SINU, composed of the standard binarization rule and the chaotic sinusoidal map. This is interesting since we can see that the incorporation of the chaotic sinusoidal map contributed to obtaining better results. Although they do not reach optimality in each instance, they are statistically better than the other experiments that include the complement and standard binarization rules.
Another interesting point is that the family of experiments composed by the complement binarization rule obtains statistically better results than those composed of the standard binarization rule with the three metaheuristics used. Finally, the worst experiments are those that include the standard binarization rule, except STD_SINU, since statistically, they fail to beat any other experiment.
Given the experimental results and the statistical tests applied, we can indicate that the binarization rule has a high impact on the binarization process of continuous metaheuristics, as indicated by the authors in [104]. In addition to this, chaotic maps also have an impact on the behavior of metaheuristics, which can be observed in the experimental results, convergence graphs, and statistical tests.
Table 10 shows the results when comparing the 24 experiments applied in GWO, Table 11 shows the results when comparing the 24 experiments applied in WOA, and Table 12 show the results when 24 experiments applied in WOA. These tables are structured as follows: the first column presents the techniques used (Experiment A), and the following columns present the average p-values of the seven instances compared with the version indicated in the column title (Experiment B). The values highlighted in bold and underlined show when the statistical test gives us a value less than 0.05, which is when the null hypothesis () is rejected. Additionally, when we compare the same experiment, it is marked with an “X” symbol.

Table 10.
Average p-value of GWO compared to others experiments.

Table 11.
Average p-value of WOA compared to others experiments.

Table 12.
Average p-value of SCA compared to others experiments.
6. Conclusions
Binary combinatorial problems, such as the Set Covering Problem [9,11,77,104,105], Knapsack Problem [109,110], or Cell Formation Problem [106], are increasingly common in the industry. Given the demand for good results in reasonable times, metaheuristics have begun to gain ground as resolution techniques.
In the literature [21], we can find different continuous metaheuristics, most of which are designed to solve continuous optimization problems. In view of this, it is necessary to apply a binarization process so that they can solve binary combinatorial problems.
Among the best-known binarization processes [22] found is the two-step technique, which uses a transfer function and the binarization rule [87]. Among the binarization rules are the standard binarization rule, the complement binarization rule, and the elitist binarization rule. These three have one factor in common, and that is that they use a random number within the rules.
Our proposal consists of changing the behavior of the random number of the three binarization rules mentioned above by replacing it with chaotic maps. In particular, we use seven different chaotic maps within the three binarization rules mentioned above, thus creating eight experiments, where seven of them use the chaotic maps and the remaining is the original version that uses a random number with a uniform distribution. Regarding the experiments, seven instances and three metaheuristics were widely solved in the literature.
In the present work, it was shown that the incorporation of chaotic maps has a great impact on the behavior of the three metaheuristics considered. This is interesting since it confirms what has been said in the literature, that chaotic maps impact exploration and exploitation and, consequently, obtain better results.
Of all the experiments carried out, we can highlight all those that are based on the standard binarization rule and complement binarization rule since they are statistically better in the three metaheuristics compared to the experiment that is based on the elitist binarization rule.
Given this, we propose a strategy to select the best binarization rule and chaotic map. First, experiment with some instances of the problem using the three binarization rules without modification (i.e., use the standard, complement, and elitist binarization rules) to see which rule is the most suitable. Once the rule is chosen, proceed to experiment with the incorporation of chaotic maps to show which one has more impact during the optimization process. This strategy can be used independently of the binary combinatorial optimization problem to be solved.
As future work, we propose to use this approach in other binary combinatorial optimization problems, such as the Feature Selection Problem or Set Covering Problem, as well as to incorporate these chaotic maps in other binarization rules, such as elitist roulette.
Furthermore, in the literature, there are proposals that use machine learning techniques from the reinforcement learning family to dynamically select binarization schemes during the optimization process [9,10,11,81,85,111]. This work can be extended to use these new binarization schemes as actions to be decided by machine learning techniques to dynamically balance exploration and exploitation.
Author Contributions
Conceptualization, F.C.-C. and B.C.; methodology, F.C.-C. and B.C.; software, F.C.-C.; validation, B.C., R.S., G.G., Á.P. and A.P.F.; formal analysis, F.C.-C.; investigation, F.C.-C., B.C., R.S., G.G., Á.P. and A.P.F.; resources, F.C.-C.; writing—original draft F.C.-C. and B.C.; writing—review and editing, R.S., G.G., Á.P. and A.P.F.; supervision, B.C. and R.S.; funding acquisition, B.C. and R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All the results of this work are available at the GitHub repository (https://github.com/FelipeCisternasCaneo/Chaotic-Binarization-Schemes-for-Solving-Combinatorial-Optimization-Problems.git (accessed on 1 January 2024)) and the database with results (https://drive.google.com/drive/folders/1MpSG6qlQ8d8k-qpalebzJFzbJ-DhFObb?usp=sharing (accessed on 1 January 2024)). GitHub has a limit of 100 MB for a file uploaded to the repository. This is why we have left the database shared on Google Drive. To perform validations, you only need to download the file in the shared Google Drive folder, clone the repository, and incorporate the downloaded file in the “BD” folder of the cloned repository.
Acknowledgments
Broderick Crawford and Ricardo Soto are supported by the grant ANID/FONDECYT/REGULAR/1210810. Felipe Cisternas-Caneo is supported by the National Agency for Research and Development (ANID)/Scholarship Program/DOCTORADO NACIONAL/2023-21230203. Felipe Cisternas-Caneo, Broderick Crawford, Ricardo Soto, Álex Paz, and Alvaro Peña Fritz are supported by grant DI Centenario/VINCI/PUCV/039.368/2023.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Talbi, E.G. Metaheuristics: From Design to Implementation; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Abdel-Basset, M.; Sallam, K.M.; Mohamed, R.; Elgendi, I.; Munasinghe, K.; Elkomy, O.M. An Improved Binary Grey-Wolf Optimizer With Simulated Annealing for Feature Selection. IEEE Access 2021, 9, 139792–139822. [Google Scholar] [CrossRef]
- Zhao, M.; Hou, R.; Li, H.; Ren, M. A hybrid grey wolf optimizer using opposition-based learning, sine cosine algorithm and reinforcement learning for reliable scheduling and resource allocation. J. Syst. Softw. 2023, 205, 111801. [Google Scholar] [CrossRef]
- Ahmed, K.; Salah Kamel, F.J.; Youssef, A.R. Hybrid Whale Optimization Algorithm and Grey Wolf Optimizer Algorithm for Optimal Coordination of Direction Overcurrent Relays. Electr. Power Components Syst. 2019, 47, 644–658. [Google Scholar] [CrossRef]
- Seyyedabbasi, A. WOASCALF: A new hybrid whale optimization algorithm based on sine cosine algorithm and levy flight to solve global optimization problems. Adv. Eng. Softw. 2022, 173, 103272. [Google Scholar] [CrossRef]
- Tapia, D.; Crawford, B.; Soto, R.; Cisternas-Caneo, F.; Lemus-Romani, J.; Castillo, M.; García, J.; Palma, W.; Paredes, F.; Misra, S. A Q-Learning Hyperheuristic Binarization Framework to Balance Exploration and Exploitation. In Proceedings of the International Conference on Applied Informatics, Ota, Nigeria, 29–31 October 2020; Florez, H., Misra, S., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 14–28. [Google Scholar] [CrossRef]
- De Oliveira, S.G.; Silva, L.M. Evolving reordering algorithms using an ant colony hyperheuristic approach for accelerating the convergence of the ICCG method. Eng. Comput. 2020, 36, 1857–1873. [Google Scholar] [CrossRef]
- Gonzaga de Oliveira, S.; Silva, L. An ant colony hyperheuristic approach for matrix bandwidth reduction. Appl. Soft Comput. 2020, 94, 106434. [Google Scholar] [CrossRef]
- Becerra-Rozas, M.; Lemus-Romani, J.; Cisternas-Caneo, F.; Crawford, B.; Soto, R.; García, J. Swarm-Inspired Computing to Solve Binary Optimization Problems: A Backward Q-Learning Binarization Scheme Selector. Mathematics 2022, 10, 4776. [Google Scholar] [CrossRef]
- Cisternas-Caneo, F.; Crawford, B.; Soto, R.; de la Fuente-Mella, H.; Tapia, D.; Lemus-Romani, J.; Castillo, M.; Becerra-Rozas, M.; Paredes, F.; Misra, S. A Data-Driven Dynamic Discretization Framework to Solve Combinatorial Problems Using Continuous Metaheuristics. In Proceedings of the International Conference on Innovations in Bio-Inspired Computing and Applications, Ibica, Spain, 16–18 December 2021; Abraham, A., Sasaki, H., Rios, R., Gandhi, N., Singh, U., Ma, K., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 76–85. [Google Scholar] [CrossRef]
- Lemus-Romani, J.; Becerra-Rozas, M.; Crawford, B.; Soto, R.; Cisternas-Caneo, F.; Vega, E.; Castillo, M.; Tapia, D.; Astorga, G.; Palma, W.; et al. A Novel Learning-Based Binarization Scheme Selector for Swarm Algorithms Solving Combinatorial Problems. Mathematics 2021, 9, 2887. [Google Scholar] [CrossRef]
- Ibrahim, A.M.; Tawhid, M.A. Chaotic electromagnetic field optimization. Artif. Intell. Rev. 2022, 56, 9989–10030. [Google Scholar] [CrossRef]
- Chou, J.S.; Truong, D.N. Multiobjective forensic-based investigation algorithm for solving structural design problems. Autom. Constr. 2022, 134, 104084. [Google Scholar] [CrossRef]
- Gao, S.; Yu, Y.; Wang, Y.; Wang, J.; Cheng, J.; Zhou, M. Chaotic Local Search-Based Differential Evolution Algorithms for Optimization. IEEE Trans. Syst. Man, Cybern. Syst. 2021, 51, 3954–3967. [Google Scholar] [CrossRef]
- Agrawal, P.; Ganesh, T.; Mohamed, A.W. Chaotic gaining sharing knowledge-based optimization algorithm: An improved metaheuristic algorithm for feature selection. Soft Comput. 2021, 25, 9505–9528. [Google Scholar] [CrossRef]
- Naanaa, A. Fast chaotic optimization algorithm based on spatiotemporal maps for global optimization. Appl. Math. Comput. 2015, 269, 402–411. [Google Scholar] [CrossRef]
- Yang, H.; Yu, Y.; Cheng, J.; Lei, Z.; Cai, Z.; Zhang, Z.; Gao, S. An intelligent metaphor-free spatial information sampling algorithm for balancing exploitation and exploration. Knowl.-Based Syst. 2022, 250, 109081. [Google Scholar] [CrossRef]
- Khosravi, H.; Amiri, B.; Yazdanjue, N.; Babaiyan, V. An improved group teaching optimization algorithm based on local search and chaotic map for feature selection in high-dimensional data. Expert Syst. Appl. 2022, 204, 117493. [Google Scholar] [CrossRef]
- Mohmmadzadeh, H.; Gharehchopogh, F.S. An efficient binary chaotic symbiotic organisms search algorithm approaches for feature selection problems. J. Supercomput. 2021, 77, 9102–9144. [Google Scholar] [CrossRef]
- Pichai, S.; Sunat, K.; Chiewchanwattana, S. An asymmetric chaotic competitive swarm optimization algorithm for feature selection in high-dimensional data. Symmetry 2020, 12, 1782. [Google Scholar] [CrossRef]
- Rajwar, K.; Deep, K.; Das, S. An exhaustive review of the metaheuristic algorithms for search and optimization: Taxonomy, applications, and open challenges. Artif. Intell. Rev. 2023, 56, 13187–13257. [Google Scholar] [CrossRef]
- Becerra-Rozas, M.; Lemus-Romani, J.; Cisternas-Caneo, F.; Crawford, B.; Soto, R.; Astorga, G.; Castro, C.; García, J. Continuous Metaheuristics for Binary Optimization Problems: An Updated Systematic Literature Review. Mathematics 2022, 11, 129. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Banerjee, A.; Nabi, M. Re-entry trajectory optimization for space shuttle using sine-cosine algorithm. In Proceedings of the 2017 8th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 19–22 June 2017; pp. 73–77. [Google Scholar] [CrossRef]
- Sindhu, R.; Ngadiran, R.; Yacob, Y.M.; Zahri, N.A.H.; Hariharan, M. Sine–cosine algorithm for feature selection with elitism strategy and new updating mechanism. Neural Comput. Appl. 2017, 28, 2947–2958. [Google Scholar] [CrossRef]
- Mahdad, B.; Srairi, K. A new interactive sine cosine algorithm for loading margin stability improvement under contingency. Electr. Eng. 2018, 100, 913–933. [Google Scholar] [CrossRef]
- Padmanaban, S.; Priyadarshi, N.; Holm-Nielsen, J.B.; Bhaskar, M.S.; Azam, F.; Sharma, A.K.; Hossain, E. A novel modified sine-cosine optimized MPPT algorithm for grid integrated PV system under real operating conditions. IEEE Access 2019, 7, 10467–10477. [Google Scholar] [CrossRef]
- Gonidakis, D.; Vlachos, A. A new sine cosine algorithm for economic and emission dispatch problems with price penalty factors. J. Inf. Optim. Sci. 2019, 40, 679–697. [Google Scholar] [CrossRef]
- Abd Elfattah, M.; Abuelenin, S.; Hassanien, A.E.; Pan, J.S. Handwritten arabic manuscript image binarization using sine cosine optimization algorithm. In Proceedings of the International Conference on Genetic and Evolutionary Computing, Fuzhou, China, 7–9 November 2016; pp. 273–280. [Google Scholar] [CrossRef]
- Emary, E.; Zawbaa, H.M.; Grosan, C.; Hassenian, A.E. Feature subset selection approach by gray-wolf optimization. In Proceedings of the Afro-European Conference for Industrial Advancement, Villejuif, France, 9–11 September 2015; pp. 1–13. [Google Scholar] [CrossRef]
- Kumar, V.; Chhabra, J.K.; Kumar, D. Grey wolf algorithm-based clustering technique. J. Intell. Syst. 2017, 26, 153–168. [Google Scholar] [CrossRef]
- Eswaramoorthy, S.; Sivakumaran, N.; Sekaran, S. Grey wolf optimization based parameter selection for support vector machines. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2016, 35, 1513–1523. [Google Scholar] [CrossRef]
- Li, S.X.; Wang, J.S. Dynamic modeling of steam condenser and design of PI controller based on grey wolf optimizer. Math. Probl. Eng. 2015, 2015, 120975. [Google Scholar] [CrossRef]
- Wong, L.I.; Sulaiman, M.; Mohamed, M.; Hong, M.S. Grey Wolf Optimizer for solving economic dispatch problems. In Proceedings of the 2014 IEEE International Conference on Power and Energy (PECon), Kuching Sarawak, Malaysia, 1–3 December 2014; pp. 150–154. [Google Scholar] [CrossRef]
- Tsai, P.W.; Nguyen, T.T.; Dao, T.K. Robot path planning optimization based on multiobjective grey wolf optimizer. In Proceedings of the International Conference on Genetic and Evolutionary Computing, Fuzhou, China, 7–9 November 2016; pp. 166–173. [Google Scholar] [CrossRef]
- Lu, C.; Gao, L.; Li, X.; Xiao, S. A hybrid multi-objective grey wolf optimizer for dynamic scheduling in a real-world welding industry. Eng. Appl. Artif. Intell. 2017, 57, 61–79. [Google Scholar] [CrossRef]
- Mosavi, M.R.; Khishe, M.; Ghamgosar, A. Classification of sonar data set using neural network trained by gray wolf optimization. Neural Netw. World 2016, 26, 393. [Google Scholar] [CrossRef]
- Bentouati, B.; Chaib, L.; Chettih, S. A hybrid whale algorithm and pattern search technique for optimal power flow problem. In Proceedings of the 2016 8th International Conference on Modelling, Identification and Control (ICMIC), Algiers, Algeria, 15–17 November 2016; pp. 1048–1053. [Google Scholar] [CrossRef]
- Touma, H.J. Study of the economic dispatch problem on IEEE 30-bus system using whale optimization algorithm. Int. J. Eng. Technol. Sci. 2016, 3, 11–18. [Google Scholar] [CrossRef]
- Yin, X.; Cheng, L.; Wang, X.; Lu, J.; Qin, H. Optimization for hydro-photovoltaic-wind power generation system based on modified version of multi-objective whale optimization algorithm. Energy Procedia 2019, 158, 6208–6216. [Google Scholar] [CrossRef]
- Abd El Aziz, M.; Ewees, A.A.; Hassanien, A.E. Whale optimization algorithm and moth-flame optimization for multilevel thresholding image segmentation. Expert Syst. Appl. 2017, 83, 242–256. [Google Scholar] [CrossRef]
- Mafarja, M.M.; Mirjalili, S. Hybrid whale optimization algorithm with simulated annealing for feature selection. Neurocomputing 2017, 260, 302–312. [Google Scholar] [CrossRef]
- Tharwat, A.; Moemen, Y.S.; Hassanien, A.E. Classification of toxicity effects of biotransformed hepatic drugs using whale optimized support vector machines. J. Biomed. Inform. 2017, 68, 132–149. [Google Scholar] [CrossRef]
- Zhao, H.; Guo, S.; Zhao, H. Energy-related CO2 emissions forecasting using an improved LSSVM model optimized by whale optimization algorithm. Energies 2017, 10, 874. [Google Scholar] [CrossRef]
- Igel, C. No Free Lunch Theorems: Limitations and Perspectives of Metaheuristics. In Theory and Principled Methods for the Design of Metaheuristics; Borenstein, Y., Moraglio, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–23. [Google Scholar] [CrossRef]
- Wolpert, D.; Macready, W. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Ho, Y.C.; Pepyne, D.L. Simple explanation of the no-free-lunch theorem and its implications. J. Optim. Theory Appl. 2002, 115, 549–570. [Google Scholar] [CrossRef]
- Li, X.D.; Wang, J.S.; Hao, W.K.; Zhang, M.; Wang, M. Chaotic arithmetic optimization algorithm. Appl. Intell. 2022, 52, 16718–16757. [Google Scholar] [CrossRef]
- Gandomi, A.; Yang, X.S.; Talatahari, S.; Alavi, A. Firefly algorithm with chaos. Commun. Nonlinear Sci. Numer. Simul. 2013, 18, 89–98. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. An improved butterfly optimization algorithm with chaos. J. Intell. Fuzzy Syst. 2017, 32, 1079–1088. [Google Scholar] [CrossRef]
- Lu, H.; Wang, X.; Fei, Z.; Qiu, M. The effects of using chaotic map on improving the performance of multiobjective evolutionary algorithms. Math. Probl. Eng. 2014, 2014, 924652. [Google Scholar] [CrossRef]
- Khennaoui, A.A.; Ouannas, A.; Boulaaras, S.; Pham, V.T.; Taher Azar, A. A fractional map with hidden attractors: Chaos and control. Eur. Phys. J. Spec. Top. 2020, 229, 1083–1093. [Google Scholar] [CrossRef]
- Verma, M.; Sreejeth, M.; Singh, M.; Babu, T.S.; Alhelou, H.H. Chaotic Mapping Based Advanced Aquila Optimizer With Single Stage Evolutionary Algorithm. IEEE Access 2022, 10, 89153–89169. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, H.; Ding, G.; Tu, L. Adaptive chimp optimization algorithm with chaotic map for global numerical optimization problems. J. Supercomput. 2023, 79, 6507–6537. [Google Scholar] [CrossRef]
- Elgamal, Z.; Sabri, A.Q.M.; Tubishat, M.; Tbaishat, D.; Makhadmeh, S.N.; Alomari, O.A. Improved Reptile Search Optimization Algorithm Using Chaotic Map and Simulated Annealing for Feature Selection in Medical Field. IEEE Access 2022, 10, 51428–51446. [Google Scholar] [CrossRef]
- Agrawal, U.; Rohatgi, V.; Katarya, R. Normalized Mutual Information-based equilibrium optimizer with chaotic maps for wrapper-filter feature selection. Expert Syst. Appl. 2022, 207, 118107. [Google Scholar] [CrossRef]
- Wang, L.; Gao, Y.; Li, J.; Wang, X. A feature selection method by using chaotic cuckoo search optimization algorithm with elitist preservation and uniform mutation for data classification. Discret. Dyn. Nat. Soc. 2021, 2021, 7796696. [Google Scholar] [CrossRef]
- Mohd Yusof, N.; Muda, A.K.; Pratama, S.F.; Carbo-Dorca, R.; Abraham, A. Improving Amphetamine-type Stimulants drug classification using chaotic-based time-varying binary whale optimization algorithm. Chemom. Intell. Lab. Syst. 2022, 229, 104635. [Google Scholar] [CrossRef]
- Wang, R.; Hao, K.; Chen, L.; Wang, T.; Jiang, C. A novel hybrid particle swarm optimization using adaptive strategy. Inf. Sci. 2021, 579, 231–250. [Google Scholar] [CrossRef]
- Feizi-Derakhsh, M.R.; Kadhim, E.A. An Improved Binary Cuckoo Search Algorithm For Feature Selection Using Filter Method And Chaotic Map. J. Appl. Sci. Eng. 2022, 26, 897–903. [Google Scholar] [CrossRef]
- Hussien, A.G.; Amin, M. A self-adaptive Harris Hawks optimization algorithm with opposition-based learning and chaotic local search strategy for global optimization and feature selection. Int. J. Mach. Learn. Cybern. 2022, 13, 309–336. [Google Scholar] [CrossRef]
- Hu, J.; Heidari, A.A.; Zhang, L.; Xue, X.; Gui, W.; Chen, H.; Pan, Z. Chaotic diffusion-limited aggregation enhanced grey wolf optimizer: Insights, analysis, binarization, and feature selection. Int. J. Intell. Syst. 2022, 37, 4864–4927. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Zhang, C.; Zhou, C. Multiobjective Harris Hawks Optimization With Associative Learning and Chaotic Local Search for Feature Selection. IEEE Access 2022, 10, 72973–72987. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Y.; Yu, C.; Heidari, A.A.; Li, S.; Chen, H.; Li, C. Gaussian mutational chaotic fruit fly-built optimization and feature selection. Expert Syst. Appl. 2020, 141, 112976. [Google Scholar] [CrossRef]
- Jalali, S.M.J.; Ahmadian, M.; Ahmadian, S.; Hedjam, R.; Khosravi, A.; Nahavandi, S. X-ray image based COVID-19 detection using evolutionary deep learning approach. Expert Syst. Appl. 2022, 201, 116942. [Google Scholar] [CrossRef] [PubMed]
- Joshi, S.K. Chaos embedded opposition based learning for gravitational search algorithm. Appl. Intell. 2023, 53, 5567–5586. [Google Scholar] [CrossRef]
- Too, J.; Abdullah, A.R. Chaotic atom search optimization for feature selection. Arab. J. Sci. Eng. 2020, 45, 6063–6079. [Google Scholar] [CrossRef]
- Sayed, G.I.; Tharwat, A.; Hassanien, A.E. Chaotic dragonfly algorithm: An improved metaheuristic algorithm for feature selection. Appl. Intell. 2019, 49, 188–205. [Google Scholar] [CrossRef]
- Ewees, A.A.; El Aziz, M.A.; Hassanien, A.E. Chaotic multi-verse optimizer-based feature selection. Neural Comput. Appl. 2019, 31, 991–1006. [Google Scholar] [CrossRef]
- Hegazy, A.E.; Makhlouf, M.; El-Tawel, G.S. Feature selection using chaotic salp swarm algorithm for data classification. Arab. J. Sci. Eng. 2019, 44, 3801–3816. [Google Scholar] [CrossRef]
- Sayed, G.I.; Hassanien, A.E.; Azar, A.T. Feature selection via a novel chaotic crow search algorithm. Neural Comput. Appl. 2019, 31, 171–188. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Yang, X.S. Binary bat algorithm. Neural Comput. Appl. 2014, 25, 663–681. [Google Scholar] [CrossRef]
- Rodrigues, D.; Pereira, L.A.; Nakamura, R.Y.; Costa, K.A.; Yang, X.S.; Souza, A.N.; Papa, J.P. A wrapper approach for feature selection based on Bat Algorithm and Optimum-Path Forest. Expert Syst. Appl. 2014, 41, 2250–2258. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. S-shaped versus V-shaped transfer functions for binary particle swarm optimization. Swarm Evol. Comput. 2013, 9, 1–14. [Google Scholar] [CrossRef]
- Crawford, B.; Soto, R.; Lemus-Romani, J.; Becerra-Rozas, M.; Lanza-Gutiérrez, J.M.; Caballé, N.; Castillo, M.; Tapia, D.; Cisternas-Caneo, F.; García, J.; et al. Q-Learnheuristics: Towards Data-Driven Balanced Metaheuristics. Mathematics 2021, 9, 1839. [Google Scholar] [CrossRef]
- Taghian, S.; Nadimi-Shahraki, M. Binary Sine Cosine Algorithms for Feature Selection from Medical Data. arXiv 2019, arXiv:1911.07805. [Google Scholar] [CrossRef]
- Faris, H.; Mafarja, M.M.; Heidari, A.A.; Aljarah, I.; Ala’M, A.Z.; Mirjalili, S.; Fujita, H. An efficient binary salp swarm algorithm with crossover scheme for feature selection problems. Knowl.-Based Syst. 2018, 154, 43–67. [Google Scholar] [CrossRef]
- Tubishat, M.; Ja’afar, S.; Alswaitti, M.; Mirjalili, S.; Idris, N.; Ismail, M.A.; Omar, M.S. Dynamic Salp swarm algorithm for feature selection. Expert Syst. Appl. 2021, 164, 113873. [Google Scholar] [CrossRef]
- Tapia, D.; Crawford, B.; Soto, R.; Palma, W.; Lemus-Romani, J.; Cisternas-Caneo, F.; Castillo, M.; Becerra-Rozas, M.; Paredes, F.; Misra, S. Embedding Q-Learning in the selection of metaheuristic operators: The enhanced binary grey wolf optimizer case. In Proceedings of the 2021 IEEE International Conference on Automation/XXIV Congress of the Chilean Association of Automatic Control (ICA-ACCA), Valparaíso, Chile, 22–26 March 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Sharma, P.; Sundaram, S.; Sharma, M.; Sharma, A.; Gupta, D. Diagnosis of Parkinson’s disease using modified grey wolf optimization. Cogn. Syst. Res. 2019, 54, 100–115. [Google Scholar] [CrossRef]
- Mafarja, M.; Aljarah, I.; Heidari, A.A.; Faris, H.; Fournier-Viger, P.; Li, X.; Mirjalili, S. Binary dragonfly optimization for feature selection using time-varying transfer functions. Knowl.-Based Syst. 2018, 161, 185–204. [Google Scholar] [CrossRef]
- Eluri, R.K.; Devarakonda, N. Binary Golden Eagle Optimizer with Time-Varying Flight Length for feature selection. Knowl.-Based Syst. 2022, 247, 108771. [Google Scholar] [CrossRef]
- Becerra-Rozas, M.; Lemus-Romani, J.; Crawford, B.; Soto, R.; Cisternas-Caneo, F.; Embry, A.T.; Molina, M.A.; Tapia, D.; Castillo, M.; Misra, S.; et al. Reinforcement Learning Based Whale Optimizer. In Proceedings of the International Conference on Computational Science and Its Applications—ICCSA 2021, Cagliari, Italy, 13–16 September 2021; Gervasi, O., Murgante, B., Misra, S., Garau, C., Blečić, I., Taniar, D., Apduhan, B.O., Rocha, A.M.A.C., Tarantino, E., Torre, C.M., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 205–219. [Google Scholar] [CrossRef]
- Mirjalili, S.; Hashim, S.Z.M. BMOA: Binary magnetic optimization algorithm. Int. J. Mach. Learn. Comput. 2012, 2, 204. [Google Scholar] [CrossRef]
- Crawford, B.; Soto, R.; Astorga, G.; García, J.; Castro, C.; Paredes, F. Putting continuous metaheuristics to work in binary search spaces. Complexity 2017, 2017, 8404231. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. How important is a transfer function in discrete heuristic algorithms. Neural Comput. Appl. 2015, 26, 625–640. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. In Proceedings of the 1997 IEEE International Conference on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, 12–15 October 1997; Volume 5, pp. 4104–4108. [Google Scholar] [CrossRef]
- Crawford, B.; Soto, R.; Olivares-Suarez, M.; Palma, W.; Paredes, F.; Olguin, E.; Norero, E. A binary coded firefly algorithm that solves the set covering problem. Rom. J. Inf. Sci. Technol. 2014, 17, 252–264. [Google Scholar]
- Rajalakshmi, N.; Padma Subramanian, D.; Thamizhavel, K. Performance enhancement of radial distributed system with distributed generators by reconfiguration using binary firefly algorithm. J. Inst. Eng. India Ser. B 2015, 96, 91–99. [Google Scholar] [CrossRef]
- Lanza-Gutierrez, J.M.; Crawford, B.; Soto, R.; Berrios, N.; Gomez-Pulido, J.A.; Paredes, F. Analyzing the effects of binarization techniques when solving the set covering problem through swarm optimization. Expert Syst. Appl. 2017, 70, 67–82. [Google Scholar] [CrossRef]
- Senkerik, R. A brief overview of the synergy between metaheuristics and unconventional dynamics. In AETA 2018-Recent Advances in Electrical Engineering and Related Sciences: Theory and Application; Springer: Cham, Switzerland, 2020; pp. 344–356. [Google Scholar] [CrossRef]
- Zou, D.; Gao, L.; Li, S.; Wu, J. Solving 0–1 knapsack problem by a novel global harmony search algorithm. Appl. Soft Comput. 2011, 11, 1556–1564. [Google Scholar] [CrossRef]
- Sahni, S. Approximate Algorithms for the 0/1 Knapsack Problem. J. ACM 1975, 22, 115–124. [Google Scholar] [CrossRef]
- Martello, S.; Pisinger, D.; Toth, P. New trends in exact algorithms for the 0–1 knapsack problem. Eur. J. Oper. Res. 2000, 123, 325–332. [Google Scholar] [CrossRef]
- Zhou, Y.; Shi, Y.; Wei, Y.; Luo, Q.; Tang, Z. Nature-inspired algorithms for 0-1 knapsack problem: A survey. Neurocomputing 2023, 554, 126630. [Google Scholar] [CrossRef]
- Bas, E. A capital budgeting problem for preventing workplace mobbing by using analytic hierarchy process and fuzzy 0–1 bidimensional knapsack model. Expert Syst. Appl. 2011, 38, 12415–12422. [Google Scholar] [CrossRef]
- Reniers, G.L.L.; Sörensen, K. An Approach for Optimal Allocation of Safety Resources: Using the Knapsack Problem to Take Aggregated Cost-Efficient Preventive Measures. Risk Anal. 2013, 33, 2056–2067. [Google Scholar] [CrossRef] [PubMed]
- İbrahim, M.; Sezer, Z. Algorithms for the one-dimensional two-stage cutting stock problem. Eur. J. Oper. Res. 2018, 271, 20–32. [Google Scholar] [CrossRef]
- Peeta, S.; Sibel Salman, F.; Gunnec, D.; Viswanath, K. Pre-disaster investment decisions for strengthening a highway network. Comput. Oper. Res. 2010, 37, 1708–1719. [Google Scholar] [CrossRef]
- Pisinger, D. Where are the hard knapsack problems? Comput. Oper. Res. 2005, 32, 2271–2284. [Google Scholar] [CrossRef]
- Pisinger, D. Instances of 0/1 Knapsack Problem. 2005. Available online: http://artemisa.unicauca.edu.co/~johnyortega/instances_01_KP (accessed on 1 January 2024).
- Lemus-Romani, J.; Crawford, B.; Cisternas-Caneo, F.; Soto, R.; Becerra-Rozas, M. Binarization of Metaheuristics: Is the Transfer Function Really Important? Biomimetics 2023, 8, 400. [Google Scholar] [CrossRef]
- Becerra-Rozas, M.; Cisternas-Caneo, F.; Crawford, B.; Soto, R.; García, J.; Astorga, G.; Palma, W. Embedded Learning Approaches in the Whale Optimizer to Solve Coverage Combinatorial Problems. Mathematics 2022, 10, 4529. [Google Scholar] [CrossRef]
- Figueroa-Torrez, P.; Durán, O.; Crawford, B.; Cisternas-Caneo, F. A Binary Black Widow Optimization Algorithm for Addressing the Cell Formation Problem Involving Alternative Routes and Machine Reliability. Mathematics 2023, 11, 3475. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- García, S.; Molina, D.; Lozano, M.; Herrera, F. A study on the use of non-parametric tests for analyzing the evolutionary algorithms’ behaviour: A case study on the CEC’2005 special session on real parameter optimization. J. Heuristics 2009, 15, 617–644. [Google Scholar] [CrossRef]
- García, J.; Leiva-Araos, A.; Crawford, B.; Soto, R.; Pinto, H. Exploring Initialization Strategies for Metaheuristic Optimization: Case Study of the Set-Union Knapsack Problem. Mathematics 2023, 11, 2695. [Google Scholar] [CrossRef]
- García, J.; Moraga, P.; Crawford, B.; Soto, R.; Pinto, H. Binarization Technique Comparisons of Swarm Intelligence Algorithm: An Application to the Multi-Demand Multidimensional Knapsack Problem. Mathematics 2022, 10, 3183. [Google Scholar] [CrossRef]
- Ábrego-Calderón, P.; Crawford, B.; Soto, R.; Rodriguez-Tello, E.; Cisternas-Caneo, F.; Monfroy, E.; Giachetti, G. Multi-armed Bandit-Based Metaheuristic Operator Selection: The Pendulum Algorithm Binarization Case. In Proceedings of the International Conference on Optimization and Learning, Malaga, Spain, 3–5 May 2023; Dorronsoro, B., Chicano, F., Danoy, G., Talbi, E.G., Eds.; Springer Nature Switzerland: Cham, Switzerland, 2023; pp. 248–259. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).