Abstract
In this study, we introduce the new subclasses, and , of -convex functions associated with sine and cosine functions. First, we obtain the initial coefficient bounds for the first five coefficients of the functions that belong to these classes. Further, we determine the upper bound of the Zalcman functional for the class for the case , proving that the Zalcman conjecture holds for this value of n. Moreover, the problem of the Fekete–Szegő functional estimate for these classes is studied.
Keywords:
analytic functions; subordination; Carathéodory functions; sine function; cosine function; alpha-convex functions; starlike and convex functions; coefficient bounds; Fekete–Szegő functional; Zalcman functional MSC:
30C45; 30C50; 30C55
1. Introduction and Preliminaries
Let be the class consisting of all analytic and normalized functions f, where f has the Taylor expansion of the form
and is the open unit disk; also, the subclass of consisting of univalent functions is denoted by .
Let us consider two analytic functions, and , in . The function is said to be subordinated to , written symbolically as , if there exists an analytic function in , with and for all , such that . In addition, if is an univalent function in , then the following equivalence holds (see [1]):
The family of functions p analytic in satisfying the condition , , and of the form
is denoted by , which represents the well-known Carathéodory function class.
In [2], Mocanu introduced and studied the well-known class of α-convex functions, that is
and the properties of this class of functions were extensively studied during a long period by many researchers (see, for example [3,4,5]). In [6], it was proved that all -convex functions are univalent and starlike, while the subclass is called the class of starlike (normalized) functions in and represents the class of convex (normalized) functions in .
Note that a function is considered starlike in if it is univalent in and maps the open unit disk onto a starlike domain, while it is convex in if it is univalent in and maps the open unit disk onto a convex domain. Therefore, the -convex functions extend both of these two classes, and make a “continuous” transition between these remarkable classes (for details see [2,6]). We would like to emphasize that the notion of subordination plays an important role in Geometric Function Theory because of the above equivalence that deals with the range of the open unit disk by the function Q. Thus, for a function if and only if , and for a function , we have the equivalences
while
Definition 1.
Let us define the new classes, and , with , connected with the sine and cosine functions, respectively, as follows:
Remark 1.
- (i)
- Substituting the value of and in (3), we obtain the following subclasses which were studied in [7,8,9], respectively, that are
- (ii)
- Taking in (4) we obtain the subclass defined in [10], and by taking in (4) we obtain the subclass . An extensive study of the estimations of the first seven coefficients, of some Hankel determinants, of the Zalcman conjecture and of the logarithmic coefficients for these two subclasses was recently given in [11].
- (iii)
- Since the functions Φ and Ψ defined above have real positive parts in , and, moreover, (see the Figure 1a,b, made with MAPLE 2023™ computer software)
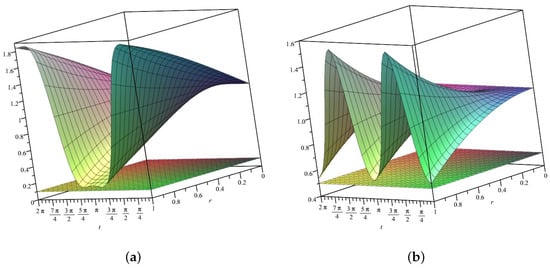 Figure 1. Figures for Remark 1 (iii). (a) The image of , , ; (b) the image of , , .it follows that the classes and are subsets of the class , that is , .
Figure 1. Figures for Remark 1 (iii). (a) The image of , , ; (b) the image of , , .it follows that the classes and are subsets of the class , that is , .
The following lemmas are necessary in the proof of our main results.
Lemma 1.
The inequality (5) is the well-known Carathéodory’s result (see [12,13]), while (6) may be found in [1], and the inequality (7) is from [14] (see also [15] [Lemma 2]).
Lemma 2
2. Initial Coefficient Estimates for the Classes and
In this section, the coefficients of the functions of the classes and are analysed, and the upper bounds for the first five coefficients are obtained.
Theorem 1.
Proof.
If , then there exists a function that is analytic in and satisfies the conditions and for all , such that
Since f is of the form (1), it follows that
From the fact that and for all , if we define the function p by
we obtain that and
According to the above relation, we obtain
and equating the corresponding coefficients of (9) and (10) we obtain
The relation (13) leads to
using triangle inequality we obtain
and according to (7), since , we obtain
The equality (14) leads to
and using the triangle inequality we obtain
From (5) and (6), the above inequality implies that
Now, we will find an upper bound for the each term of the right hand side of the above inequality, as follows.
- (i)
- According to (6), we have
whenever .
- (ii)
- Using, again, the inequality (6), a simple computation shows that
whenever .
- (iii)
- For the sum of the third with the fourth term, using inequality (5), we obtain
- (iv)
Finally, using the upper bounds found for the items (i)–(v), from the inequality (16) we conclude that
□
Remark 2.
A simple computation shows that the upper bounds obtained in the Theorem 1 could be written in the following forms:
and
For and , Theorem 1 reduces to the following corollary:
Remark 3.
The upper bounds given by Theorem 1 are not the best possible, excepting those for the first two coefficients.
- (i)
- Thus, for the case , the function
is the solution of the differential equation , , therefore . For we have
Hence, the estimations given by Theorem 1 are not sharp for and .
- (ii)
- Similarly, for , the function
is the solution of the differential equation , , hence . For this function
Thus, the estimations of Theorem 1 are not sharp for and .
Theorem 2.
If has the form (1), then
Proof.
From (5) and Lemma 2 for the appropriate values , and , the above inequality implies that
and all the estimations are proved. □
For and , Theorem 2 leads us to the following corollary.
Remark 4.
The estimations given by Theorem 2 are not the best possible, excepting those for the first two coefficients.
- (i)
- Thus, for , we have the following result regarding the sharpness of these coefficient inequalities: if , then the inequality is sharp and it is attained for the function that satisfies the differential equation , , that is
- (ii)
- Also, for , we have the next sharpness result: if , then the inequality is sharp being attained for the function , is the solution of the differential equation , and
3. The Fekete–Szegő Inequality for the Classes and
In this section, we determine the upper bounds for the Fekete–Szegő functional for the new defined classes and .
Theorem 3.
If has the form (1), then
For and , the following special is obtained.
Corollary 3.
- (i)
- If , then
- (ii)
- If , then
4. The Zalcman Functional Estimate for Class
Zalcman conjectured in 1960 that the coefficients of the functions , having the form (1), satisfy the inequality
Further, the equality is obtained only for the Koebe function and its rotations. As was shown in [16,17], this implies the Bieberbach conjecture, that is , . It is noteworthy that, for , the above inequality is a well-known consequence of the well-known Area Theorem and can be found in Theorem 1.5 of [1]. In recent years, the Zalcman functional has received special interest from many researchers (see, for example, [18,19,20]).
In the next result, for , we find the Zalcman functional upper bound for the class which allows us to prove that the Zalcman conjecture holds in this case.
Theorem 4.
If has the form (1), then
Proof.
Since
using the result of the Theorem 4, we deduce the following.
Corollary 4.
5. Conclusions
This paper mainly focuses on finding the upper bounds of the first five coefficients for the classes and of -convex functions connected with the sine and cosine function. We also tried to get similar results for the sixth coefficient but the computations became to bulky and we were unable to get any convenient result; therefore, finding an estimate for the general coefficients of these classes seems to be too strong a challenge for us.
Also, we obtained the estimate for the Fekete–Szegő functional for these classes and found the upper bound for the Zalcman functional for these classes for the case ; this allows us to prove that the Zalcman inequality holds for this case.
As we mentioned in Remarks 3 and 4, the upper bounds we get for and for the functions that belong to the classes and are not the best possible; hence, the estimation given in Theorem 4 is not sharp. The problem of finding the best bounds of the above-mentioned coefficients and functionals for these classes remains an interesting open question.
Author Contributions
Conceptualization, K.M., U.J. and T.B.; methodology, K.M., U.J. and T.B.; software, K.M., U.J. and T.B.; validation, K.M., U.J. and T.B.; formal analysis, K.M., U.J. and T.B.; investigation, K.M., U.J. and T.B.; resources, K.M., U.J. and T.B.; data curation, K.M., U.J. and T.B.; writing—original draft preparation, K.M., U.J. and T.B.; writing—review and editing, K.M., U.J. and T.B.; visualization, K.M., U.J. and T.B.; supervision, K.M., U.J. and T.B.; project administration, K.M., U.J. and T.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors are grateful to the reviewers of this article, who gave valuable remarks, comments, and advice on improving the quality of the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pommerenke, C. Univalent Functions; Vandenhoeck & Ruprecht: Göttingen, Germany, 1975. [Google Scholar]
- Mocanu, P.T. Une proprieté de convexité généralisée dans la théorie de la représentation conforme. Mathematica 1969, 11, 127–133. [Google Scholar]
- Acu, M.; Owa, S. On some subclasses of univalent functions. J. Inequal. Pure Appl. Math. 2005, 6, 70. [Google Scholar]
- Dziok, J.; Raina, R.K.; Sokół, J. On α-convex functions related to shell-like functions connected with Fibonacci numbers. Appl. Math. Comput. 2011, 218, 996–1002. [Google Scholar] [CrossRef]
- Singh, G.; Singh, G. Certain subclasses of alpha-convex functions with fixed point. J. Appl. Math. Inform. 2022, 40, 259–266. [Google Scholar]
- Mocanu, P.T.; Reade, M.O. On generalized convexity in conformal mappings. Rev. Roumaine Math. Pures Appl. 1971, 16, 1541–1544. [Google Scholar]
- Arif, M.; Raza, M.; Tang, H.; Hussain, S.; Khan, H. Hankel determinant of order three for familiar subsets of analytic functions related with sine function. Open Math. 2019, 17, 1615–1630. [Google Scholar] [CrossRef]
- Cho, N.E.; Kumar, V.; Kumar, S.; Ravichandran, V. Radius problems for starlike functions associated with the sine function. Bull. Iran. Math. Soc. 2019, 45, 213–232. [Google Scholar] [CrossRef]
- Khan, M.G.; Ahmad, B.; Sokół, J.; Muhammad, Z.; Mashwani, W.K.; Chinram, R.; Petchkaew, P. Coefficient problems in a class of functions with bounded turning associated with Sine function. Eur. J. Pure Appl. Math. 2021, 14, 53–64. [Google Scholar] [CrossRef]
- Bano, K.; Raza, M. Starlike functions associated with cosine functions. Bull. Iran. Math. Soc. 2021, 47, 1513–1532. [Google Scholar] [CrossRef]
- Marimuthu, K.; Jayaraman, U.; Bulboacă, T. Coefficient estimates for starlike and convex functions associated with cosine function. Hacet. J. Math. Stat. 2023, 52, 596–618. [Google Scholar]
- Carathéodory, C. Über den Variabilitätsbereich der Koeffizienten von Potenzreihen, die gegebene Werte nicht annehmen. Math. Ann. 1907, 64, 95–115. [Google Scholar] [CrossRef]
- Carathéodory, C. Über den variabilitätsbereich der fourier’schen konstanten von positiven harmonischen funktionen. Rend. Circ. Mat. Palermo 1911, 32, 193–217. [Google Scholar] [CrossRef]
- Keogh, F.R.; Merkes, E.P. A coefficient inequality for certain classes of analytic functions. Proc. Am. Math. Soc. 1969, 20, 8–12. [Google Scholar] [CrossRef]
- Karthikeyan, K.R.; Lakshmi, S.; Varadharajan, S.; Mohankumar, D.; Umadevi, E. Starlike functions of complex order with respect to symmetric points defined using higher order derivatives. Fractal Fract. 2022, 6, 116. [Google Scholar] [CrossRef]
- Brown, J.E.; Tsao, A. On the Zalcman conjecture for starlike and typically real functions. Math. Z. 1986, 191, 467–474. [Google Scholar] [CrossRef]
- Vasudevarao, A.; Pandey, A. The Zalcman conjecture for certain analytic and univalent functions. J. Math. Anal. Appl. 2020, 492, 124466. [Google Scholar] [CrossRef]
- Bansal, D.; Sokół, J. Zalcman conjecture for some subclass of analytic functions. J. Fract. Calc. Appl. 2017, 8, 1–5. [Google Scholar]
- Ma, W. The Zalcman conjecture for close-to-convex functions. Proc. Am. Math. Soc. 1988, 104, 741–744. [Google Scholar] [CrossRef]
- Khan, M.G.; Ahmad, B.; Murugusundaramoorthy, G.; Mashwani, W.K.; Yalçın, S.; Shaba, T.G.; Salleh, Z. Third Hankel determinant and Zalcman functional for a class of starlike functions with respect to symmetric points related with sine function. J. Math. Comput. Sci. 2022, 25, 29–36. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).