Tight 9-Cycle Decompositions of λ-Fold Complete 3-Uniform Hypergraphs

Abstract

For $2\le t\le m$, let ${\mathbb{Z}}_m$ denote the group of integers modulo m, and let $T{C}_m^{\left(t\right)}$ denote the t-uniform hypergraph with vertex set ${\mathbb{Z}}_m$ and hyperedge set $\{\{i,i+1,i+2,\dots ,i+t-1\}:i\in {\mathbb{Z}}_m\}$. Any hypergraph isomorphic to $T{C}_m^{\left(t\right)}$ is a t-uniform tight m-cycle. In this paper, we consider the existence of tight 9-cycle decompositions of $\lambda$-fold complete 3-uniform hypergraphs. According to the recursive constructions, the required designs of small orders are found. For hypergraphs with large orders, they can be recursively generated using some designs of small orders. Then, we obtain the necessary and sufficient conditions for the existence of $T{C}_9^{\left(3\right)}$-decomposition of $\lambda K_n^{\left(3\right)}$. We show there exists a $T{C}_9^{\left(3\right)}$-decomposition of $\lambda K_n^{\left(3\right)}$ if and only if $\lambda n(n-1)(n-2)\equiv 0(mod54)$, $\lambda (n-1)(n-2)\equiv 0(mod6)$ and $n\ge 9$.

1. Introduction

The problem of cycle decompositions of complete uniform hypergraphs has been studied for a long time. There are several ways of defining an m-cycle in a t-uniform hypergraph. We focus on tight m-cycle, which generalize the Katona–Kierstead [1] definition of a Hamiltonian cycle. The problem of the tight cycle decomposition of $K_n^{\left(3\right)}$ was first investigated by Bailey and Stevens [2]. Hanani obtained the necessary and sufficient conditions for $T{C}_4^{\left(3\right)}$-decomposition of $K_n^{\left(3\right)}$ [3]. More recently, several authors have given partial results on $T{C}_5^{\left(3\right)}$-decomposition of $K_n^{\left(3\right)}$ and $T{C}_7^{\left(3\right)}$-decomposition of $K_n^{\left(3\right)}$ [4,5,6,7,8]. Bunge and Akin et al. solved $T{C}_6^{\left(3\right)}$-decomposition of $K_n^{\left(3\right)}$ and $T{C}_9^{\left(3\right)}$-decomposition of $K_n^{\left(3\right)}$ [9,10]. H. Zhao and J. Wang solved tight 6-cycle decompositions of $\lambda$-fold complete bipartite 3-uniform hypergraphs and tight 6-cycle decompositions of $\lambda$-fold complete 3-uniform hypergraphs [11,12].

There is still much to be discussed about the tight cycle decompositions of complete uniform hypergraphs. In this paper, we will study the tight 9-cycle decompositions of $\lambda$-fold complete 3-uniform hypergraphs.

A hypergraph $H=(V,E)$ consists of a finite nonempty set V of vertices and a set E of nonempty subsets of V, called hyperedges. If for each $e\in E$, we have $\left|e\right|=t$, then H is said to be a t-uniform. In particular, if $t=2$, then H is a graph. If the edge set E contains each t subset of V exactly once, and $\left|V\right|=n$, the hypergraph is called a complete t-uniform hypergraph $K_n^{\left(t\right)}$ of order n.

If a hypergraph does not contain multiple hyperedges (i.e., there are no repeated elements in its hyperedge E), the hypergraph is called a simple hypergraph. When a hypergraph H is simple, we can obtain a $\lambda$-fold hypergraph $\lambda H$ by repeating each hyperedge $\lambda$ times in H. $\lambda K_n^{\left(t\right)}$ is called a $\lambda$-fold complete t-uniform hypergraph.

Let $V_1,V_2$ be pairwise-disjoint sets. The hypergraph with vertex set $V=V_1\cup V_2$ and an edge set consisting of all three subsets having at most two vertices in each of $V_1$ and $V_2$ is denoted by $K_{V_1,V_2}^{\left(3\right)}$. If $\left|V_1\right|=n_1$ and $\left|V_2\right|=n_2$, we use $K_{n_1,n_2}^{\left(3\right)}$ to denote any hypergraph that is isomorphic to $K_{V_1,V_2}^{\left(3\right)}$.

Let $V_1,V_2,V_3$ be pairwise-disjoint sets. The hypergraph with vertex set $V=V_1\cup V_2\cup V_3$ and edge set consisting of all three subsets having exactly one vertex in each of $V_1,V_2,V_3$ is denoted by $K_{V_1,V_2,V_3}^{\left(3\right)}$. If $\left|V_1\right|=n_1,\left|V_2\right|=n_2$, and $\left|V_3\right|=n_3$, we use $K_{n_1,n_2,n_3}^{\left(3\right)}$ to denote any hypergraph that is isomorphic to $K_{V_1,V_2,V_3}^{\left(3\right)}$.

Let $\lambda$ be a positive integer, $\lambda H$ be a t-uniform hypergraph, and $\mathsf{\Gamma }$ be a set of t-uniform hypergraphs. The $\mathsf{\Gamma }$-decomposition of $\lambda H$ is its partitioning into sub-hypergraphs, each of which is isomorphic to a certain hypergraph of $\mathsf{\Gamma }$, which is denoted by $(\lambda H,\mathsf{\Gamma })$-design or $S_{\lambda }(t,\mathsf{\Gamma },H)$. For a $(\lambda K_n^{\left(t\right)},\mathsf{\Gamma })$-design, we denote it as $S_{\lambda }(t,\mathsf{\Gamma },n)$. For a $(\lambda K_{m,n}^{\left(t\right)},\mathsf{\Gamma })$-design, we denote it as $S_{\lambda }(t,\mathsf{\Gamma },m,n)$. If $\mathsf{\Gamma }$ only contains one type of hypergraph J, it is denoted by $S_{\lambda }(t,J,H)$. When $\lambda =1$, $S(t,J,H)$ is replaced with $S_{\lambda }(t,J,H)$.

We use the usual exponential notation for the types of groups divisible $(H,\mathsf{\Gamma })$-designs. Then, type $g_1^{a_1}{g}_2^{a_2}\dots g_s^{a_s}$ denotes that there are $a_i$ groups of size $g_i$, $1\le i\le s$. A group divisible $(H,\mathsf{\Gamma })$-design of type $g_1^{a_1}{g}_2^{a_2}\dots g_s^{a_s}$ can be denoted by $GDD(t,\mathsf{\Gamma },n)$, where $n={\sum }_{i=1}^s{a}_i{g}_i$. For a $(\lambda K_{n_1,n_2,n_3}^{\left(3\right)},\mathsf{\Gamma })$-design, let $n=n_1+n_2+n_3$; we denote it as $GD{D}_{\lambda }(t,\mathsf{\Gamma },n)$ of type $n_1^1{n}_2^1{n}_3^1$.

If $V^{\prime }\subseteq V,E^{\prime }\subseteq E$, then hypergraph $H^{\prime }=(V^{\prime },E^{\prime })$ is called a sub-hypergraph of the hypergraph $H=(V,E)$, and $H\setminus H^{\prime }$ denotes the hypergraph obtained from H by deleting the edges of $H^{\prime }$. For a $(\lambda K_n^{\left(3\right)}\setminus \lambda K_s^{\left(3\right)},\mathsf{\Gamma })$-design, we denote it as $H{S}_{\lambda }(t,\mathsf{\Gamma };n,s)$.

Now, we will give the definition of a tight cycle. For $2\le t\le m$, let ${\mathbb{Z}}_m$ denote the group of integers modulo m, and let $T{C}_m^{\left(t\right)}$ denote the t-uniform hypergraph with vertex set ${\mathbb{Z}}_m$ and hyperedge set $\{\{i,i+1,i+2,\dots ,i+t-1\}:i\in {\mathbb{Z}}_m\}$. Any hypergraph isomorphic to $T{C}_m^{\left(t\right)}$ is a t-uniform tight m-cycle. In this paper, we will use $(a,b,c,d,e,f,g,h,i)$ to denote any hypergraph isomorphic to the $T{C}_9^{\left(3\right)}$ with vertex set $\{a,b,c,d,e,f,g,h,i\}$ and hyperedge set $\left\{\right\{a,b,c\},\{b,c,d\},\{c,d,e\}$, $\{d,e,f\},\{e,f,g\},\{f,g,h\},\{g,h,i\},\{h,i,a\},\{i,a,b\}\}$, as seen in Figure 1. It is worth noting that when ${\infty }_i$ exists in the set of vertices, ${\infty }_i$ is a fixed point, and ${\infty }_i$ remains itself by modulo addition with any number.

2. Recursive Constructions

Construction 1.

Let $k,a,b$ be non-negative integers, and let $\lambda$ be a positive integer. Suppose $n=kb+a$. If there exists an $S_{\lambda }(3,T{C}_9^{\left(3\right)},a)$, an $S_{\lambda }(3,T{C}_9^{\left(3\right)},b+a)$, an $S_{\lambda }(3,T{C}_9^{\left(3\right)},K_{a,b,b}^{\left(3\right)}\cup K_{b,b}^{\left(3\right)})$, an $H{S}_{\lambda }(3,T{C}_9^{\left(3\right)};b+a,a)$, and a $GD{D}_{\lambda }(3,T{C}_9^{\left(3\right)},3b)$ of type $b^3$, then there exists an $S_{\lambda }(3,T{C}_9^{\left(3\right)},n)$.

Proof of Construction 1.

For $k\in \{0,1\}$, the result is vacuously true. For $b=0$ and $a\ge 3$, the result is also vacuously true.

For $k\ge 2$ and $b\ge 1$, let $A,B_1,B_2,\dots ,B_k$ be pairwise-disjoint sets of vertices with $\left|A\right|=a$ and $\left|B_1\right|=\left|B_2\right|=\cdots =\left|B_k\right|=b$, and let $V=A\cup B_1\cup B_2\cup \cdots \cup B_k$. Then, $\lambda K_{kb+a}^{\left(3\right)}$ can be decomposed into the following disjoint union:

$$\lambda \left[K_{A\cup B_1}^{\left(3\right)}\cup \bigcup _{1\le i<j\le k}\left(K_{A,B_i,B_j}^{\left(3\right)}\cup K_{B_i,B_j}^{\left(3\right)}\right)\cup \bigcup _{2\le i\le k}\left(K_{A\cup B_i}^{\left(3\right)}\setminus K_A^{\left(3\right)}\right)\cup \bigcup _{1\le i<j<l\le k}{K}_{B_i,B_j,B_l}^{\left(3\right)}\right]$$

(1)

Therefore, for $a\ge 3$, if there exists an $S_{\lambda }(3,T{C}_9^{\left(3\right)},a)$, an $S_{\lambda }(3,T{C}_9^{\left(3\right)},b+a)$, an $S_{\lambda }(3,T{C}_9^{\left(3\right)},$ $K_{a,b,b}^{\left(3\right)}\cup K_{b,b}^{\left(3\right)})$, an $H{S}_{\lambda }(3,T{C}_9^{\left(3\right)};b+a,a)$, and a $GD{D}_{\lambda }(3,T{C}_9^{\left(3\right)},3b)$ of type $b^3$, then there exists an $S_{\lambda }(3,T{C}_9^{\left(3\right)},n)$. □

Construction 2.

Let $h_1,h_2,h_3,g_1,g_2,g_3$ be positive integers. If there exists a $GD{D}_{\lambda }(3,T{C}_9^{\left(3\right)},g_1+g_2+g_3)$ of type ${g_1}^1{g_2}^1{g_3}^1$, then there exists a $GD{D}_{\lambda }(3,T{C}_9^{\left(3\right)},h_1{g}_1+h_2{g}_2+h_3{g}_3)$ of type ${\left(h_1{g}_1\right)}^1{\left(h_2{g}_2\right)}^1{\left(h_3{g}_3\right)}^1$.

Proof of Construction 2.

Let $A={\bigcup }_{1\le i\le h_1}{A}_i,B={\bigcup }_{1\le j\le h_2}{B}_j$ and $C={\bigcup }_{1\le k\le h_3}{C}_k$, and let $A_i,B_j,C_k$ be pairwise-disjoint sets of vertices with $\left|A_i\right|=g_1,\left|B_j\right|=g_2$ and $\left|C_k\right|=g_3$. For $1\le i\le h_1$, $1\le j\le h_2$, and $1\le k\le h_3$, then

$$\lambda K_{A,B,C}^{\left(3\right)}=\bigcup _{1\le i\le h_1,1\le j\le h_2,1\le k\le h_3}\lambda K_{A_i,B_j,C_k}^{\left(3\right)}.$$

(2)

Therefore, if there exists a $GD{D}_{\lambda }(3,T{C}_9^{\left(3\right)},g_1+g_2+g_3)$ of type ${g_1}^1{g_2}^1{g_3}^1$, then there exists a $GD{D}_{\lambda }(3,T{C}_9^{\left(3\right)},h_1{g}_1+h_2{g}_2+h_3{g}_3)$ of type ${\left(h_1{g}_1\right)}^1{\left(h_2{g}_2\right)}^1{\left(h_3{g}_3\right)}^1$. □

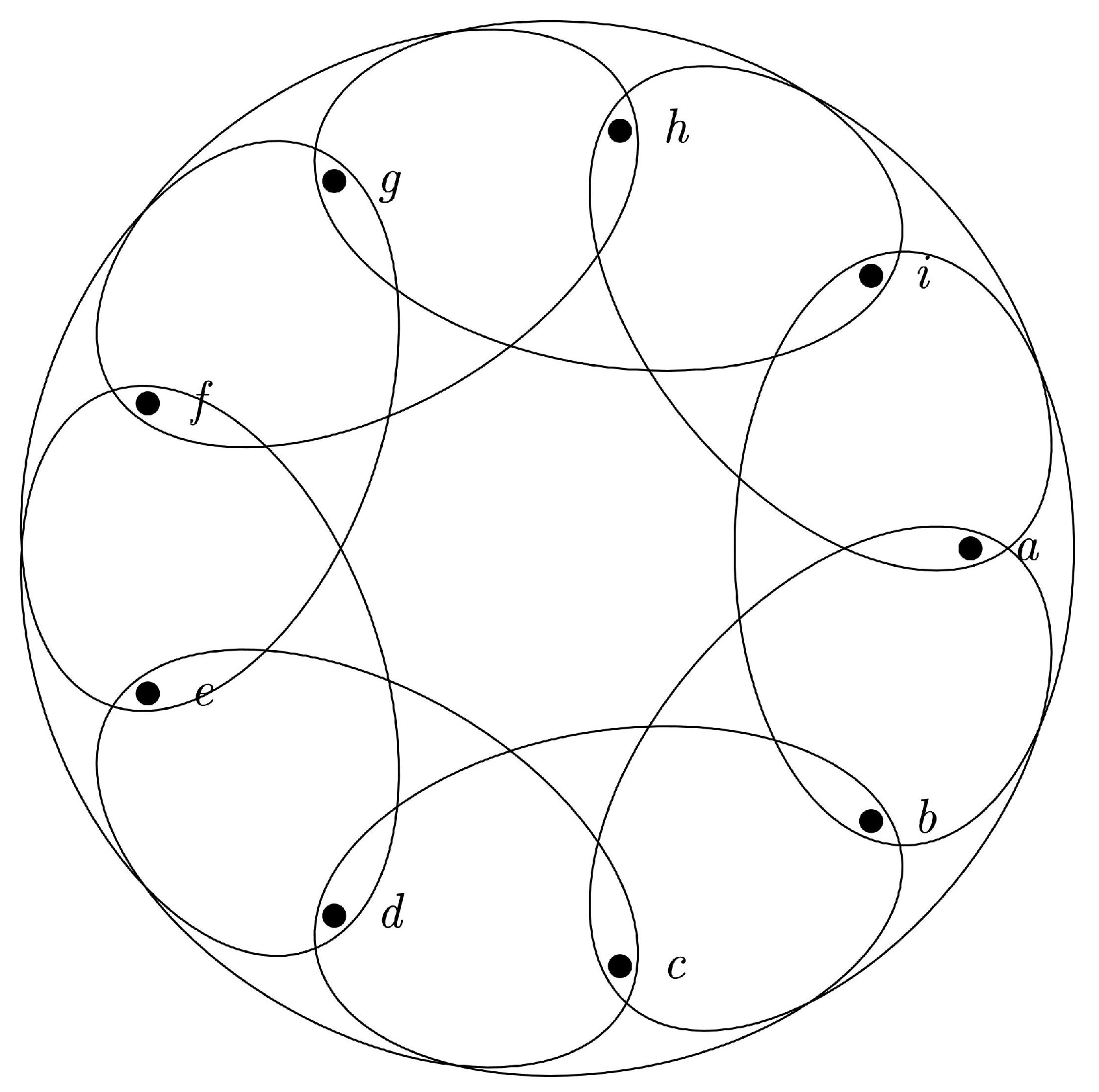
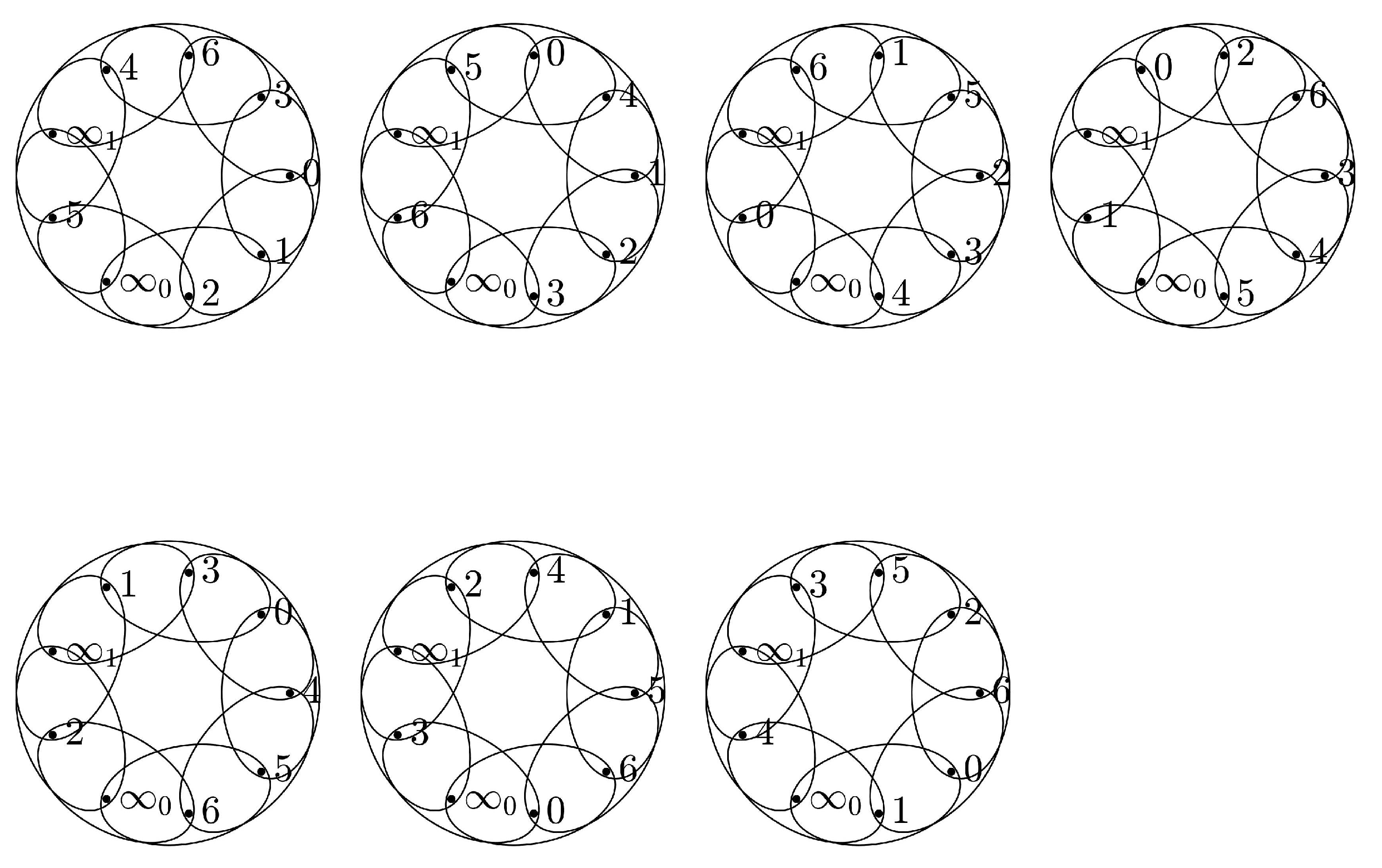
3. Some Small Orders

Lemma 1.

There exists an $S_3(3,T{C}_9^{\left(3\right)},9)$.

Proof of Lemma 1.

Let $V\left(K_9^{\left(3\right)}\right)={\mathbb{Z}}_7\cup \{{\infty }_0,{\infty }_1\}$. Base blocks for this design are given below. All other blocks are obtained by developing these base blocks by +1 modulo 7, where ${\infty }_i+1={\infty }_i$, $i=0,1$.

$$\begin{array}{cc}& \left(0,1,2,{\infty }_0,5,{\infty }_1,4,6,3\right),\left(0,1,5,{\infty }_0,3,{\infty }_1,6,4,2\right),\hfill \\ & \left(3,0,1,{\infty }_0,6,{\infty }_1,5,2,4\right),\left(1,2,{\infty }_0,4,0,6,{\infty }_1,3,5\right).\hfill \end{array}$$

Next, I will briefly explain these base blocks. For $(0,1,2,{\infty }_0,5,{\infty }_1,4,6,3)$, seven blocks can be generated from it by modular addition calculation, as shown in Figure 2. Similarly, the same can be performed using the remaining three base blocks. The 28 blocks generated from all base blocks can contain all 252 hyperedges.

□

Lemma 2.

There exists an $S_9(3,T{C}_9^{\left(3\right)},9)$.

Proof of Lemma 2.

By Lemma 1, there exists an $S_3(3,T{C}_9^{\left(3\right)},9)$. Repeating each block in the $S_3(3,T{C}_9^{\left(3\right)},9)$ three times, we obtain an $S_9(3,T{C}_9^{\left(3\right)},9)$. □

Lemma 3.

There exists an $S_3(3,T{C}_9^{\left(3\right)},10)$.

Proof of Lemma 3.

Let $V\left(K_{10}^{\left(3\right)}\right)={\mathbb{Z}}_{10}$. Base blocks for this design are given below. All other blocks are obtained by developing these base blocks by +1 modulo 10,

$$\begin{array}{cc}& (2,8,4,3,1,5,6,7,9),(7,8,0,1,2,6,3,9,4),\hfill \\ & (7,9,3,2,0,5,6,4,1),(1,3,8,2,6,9,5,7,0).\hfill \end{array}$$

□

Lemma 4.

There exists an $S_3(3,T{C}_9^{\left(3\right)},11)$.

Proof of Lemma 4.

Let $V\left(K_{11}^{\left(3\right)}\right)={\mathbb{Z}}_{11}$. Base blocks for this design are given below. All other blocks are obtained by developing these base blocks by +1 modulo 11,

$$\begin{array}{cc}& (4,7,5,2,6,9,8,10,1),(6,7,3,10,8,2,9,4,1),(9,3,4,7,10,1,0,5,2),\hfill \\ & (3,5,7,8,4,10,0,6,2),(10,1,2,8,7,6,9,5,3).\hfill \end{array}$$

□

Lemma 5.

There exists a $GDD(3,T{C}_9^{\left(3\right)},9)$ of type $3^3$.

Proof of Lemma 5.

Let $V\left(K_{3,3,3}^{\left(3\right)}\right)=\{{\infty }_0,{\infty }_1,{\infty }_2\}\cup \{0,2,4\}\cup \{1,3,5\}$. All other blocks are obtained by developing $({\infty }_0,0,1,{\infty }_1,4,3,{\infty }_2,2,5)$ by +2 modulo 6, where ${\infty }_i+2={\infty }_i,$ $0\le i\le 2$. □

Lemma 6.

There exists a $GD{D}_9(3,T{C}_9^{\left(3\right)},21)$ of type $3^1{9}^2$.

Proof of Lemma 6.

By Lemma 5, there exists a $GDD(3,T{C}_9^{\left(3\right)},9)$ of type $3^3$. Repeating each block in the $GDD(3,T{C}_9^{\left(3\right)},9)$ of type $3^3$ nine times, we obtain a $GD{D}_9(3,T{C}_9^{\left(3\right)},9)$ of type $3^3$. Applying Construction 2, let $\lambda =9,h_1=1,h_2=h_3=3,g_1=g_2=g_3=3$; then, there exists a $GD{D}_9(3,T{C}_9^{\left(3\right)},21)$ of type $3^1{9}^2$. □

Lemma 7.

There exists a $GD{D}_3(3,T{C}_9^{\left(3\right)},27)$ of type $9^3$, and a $GD{D}_9(3,T{C}_9^{\left(3\right)},27)$ of type $9^3$.

Proof of Lemma 7.

By Lemma 5, there exists a $GDD(3,T{C}_9^{\left(3\right)},9)$ of type $3^3$. Repeating each block in the $GDD(3,T{C}_9^{\left(3\right)},9)$ of type $3^3$ three times, we obtain a $GD{D}_3(3,T{C}_9^{\left(3\right)},9)$ of type $3^3$. Applying Construction 2, let $\lambda =3,h_1=h_2=h_3=3,g_1=g_2=g_3=3$; then, there exists a $GD{D}_3(3,T{C}_9^{\left(3\right)},27)$ of type $9^3$.

In a similar way, repeating each block in the $GDD(3,T{C}_9^{\left(3\right)},9)$ of type $3^3$ nine times, we obtain a $GD{D}_9(3,T{C}_9^{\left(3\right)},9)$ of type $3^3$. Applying Construction 2, let $\lambda =9,h_1=h_2=h_3=3,g_1=g_2=g_3=3$; then, there exists a $GD{D}_9(3,T{C}_9^{\left(3\right)},27)$ of type $9^3$. □

Lemma 8.

There exists an $S_3(3,T{C}_9^{\left(3\right)},K_{1,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$, and an $S_9(3,T{C}_9^{\left(3\right)},K_{1,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$.

Proof of Lemma 8.

By [10], there exists an $S(3,T{C}_9^{\left(3\right)},K_{1,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$. Repeating each block in the $S(3,T{C}_9^{\left(3\right)},K_{1,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ three times, we obtain an $S_3(3,T{C}_9^{\left(3\right)},K_{1,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$. Repeating each block in the $S(3,T{C}_9^{\left(3\right)},K_{1,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ nine times, we obtain an $S_9(3,T{C}_9^{\left(3\right)},K_{1,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$. □

Lemma 9.

There exists an $S_3(3,T{C}_9^{\left(3\right)},K_{2,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$, and an $S_9(3,T{C}_9^{\left(3\right)},K_{2,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$.

Proof of Lemma 9.

By [10], there exists an $S(3,T{C}_9^{\left(3\right)},K_{2,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$. Repeating each block in the $S(3,T{C}_9^{\left(3\right)},K_{2,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ three times, we obtain an $S_3(3,T{C}_9^{\left(3\right)},K_{2,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$. Repeating each block in the $S(3,T{C}_9^{\left(3\right)},K_{2,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ nine times, we obtain an $S_9(3,T{C}_9^{\left(3\right)},K_{2,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$. □

Lemma 10.

There exists an $S(3,T{C}_9^{\left(3\right)},9,9)$.

Proof of Lemma 10.

Let $V\left(K_{9,9}^{\left(3\right)}\right)={\mathbb{Z}}_{18}$ with vertex partition $\left\{\{2k:0\le i\le 8\}\right., \left.\{2k+1:0\le i\le 8\}\right\}$. Base blocks for this design are given below. All other blocks are obtained by developing these base blocks by +1 modulo 18,

$$\begin{array}{cc}& (0,1,3,2,7,8,14,5,15),(0,1,11,8,13,16,2,9,14),\hfill \\ & (0,3,15,4,17,1,2,5,14),(2,9,1,12,7,6,16,11,0).\hfill \end{array}$$

□

Lemma 11.

There exists an $S_3(3,T{C}_9^{\left(3\right)},9,9)$, and an $S_9(3,T{C}_9^{\left(3\right)},9,9)$.

Proof of Lemma 11.

By Lemma 10, there exists an $S(3,T{C}_9^{\left(3\right)},9,9)$. Repeating each block in the $S(3,T{C}_9^{\left(3\right)},9,9)$ three times, we obtain an $S_3(3,T{C}_9^{\left(3\right)},9,9)$. Repeating each block in the $S(3,T{C}_9^{\left(3\right)},9,9)$ nine times, we obtain an $S_9(3,T{C}_9^{\left(3\right)},9,9)$. □

Lemma 12.

There exists an $S_9(3,T{C}_9^{\left(3\right)},12)$.

Proof of Lemma 12.

Let $V\left(K_{12}^{\left(3\right)}\right)={\mathbb{Z}}_{11}\cup \left\{{\infty }_0\right\}$. Base blocks for this design are given below. All other blocks are obtained by developing these base blocks by +1 modulo 11, where ${\infty }_0+1={\infty }_0$.

$$\begin{array}{cc}& (0,1,2,4,5,8,9,3,7),(0,1,5,3,8,10,{\infty }_0,9,6),(0,3,6,8,{\infty }_0,4,9,5,7),\hfill \\ & (0,5,{\infty }_0,1,4,7,2,6,9),(0,1,{\infty }_0,4,8,7,5,10,3),(0,1,2,4,5,8,9,{\infty }_0,7),\hfill \\ & (0,1,2,6,4,10,7,9,3),(0,5,{\infty }_0,3,2,8,4,6,9),(0,1,6,{\infty }_0,3,2,7,10,8),\hfill \\ & (0,1,2,8,5,4,9,3,{\infty }_0),(0,3,7,4,8,9,10,1,5),(0,3,7,5,{\infty }_0,1,4,6,10),\hfill \\ & (0,4,{\infty }_0,2,7,1,5,3,8),(0,1,2,9,5,7,8,3,{\infty }_0),(0,1,9,2,4,3,7,{\infty }_0,5),\hfill \\ & (0,3,6,1,7,10,8,9,2),(0,2,6,{\infty }_0,4,3,9,1,7),(0,2,6,3,4,10,7,{\infty }_0,5),\hfill \\ & (0,1,8,4,5,9,{\infty }_0,10,2),(4,5,1,8,3,9,6,0,2).\hfill \end{array}$$

□

Lemma 13.

There exists an $S_9(3,T{C}_9^{\left(3\right)},13)$.

Proof of Lemma 13.

Let $V\left(K_{13}^{\left(3\right)}\right)={\mathbb{Z}}_{13}$. Base blocks for this design are given below. All other blocks are obtained by developing these base blocks by +1 modulo 13,

$$\begin{array}{cc}& (0,1,8,9,7,6,10,3,5),(0,1,7,3,8,5,9,11,6),(0,1,11,8,3,12,6,4,10),\hfill \\ & (0,2,4,5,11,8,3,12,9),(0,2,4,7,3,10,5,9,8),(0,1,3,2,10,11,6,4,7),\hfill \\ & (0,1,8,12,9,10,11,3,7),(0,2,5,10,8,6,12,9,3),(0,3,6,8,12,10,2,5,1),\hfill \\ & (0,4,8,10,9,2,1,6,11),(0,2,7,6,1,8,9,10,3),(0,1,9,7,3,11,10,8,5),\hfill \\ & (0,1,3,6,2,4,12,8,5),(0,3,9,7,5,10,12,11,8),(0,1,10,4,12,3,5,2,8),\hfill \\ & (0,1,4,7,5,11,12,6,10),(0,1,7,3,4,12,10,11,8),(0,2,5,9,7,10,6,1,12),\hfill \\ & (0,1,6,10,8,3,5,9,2),(0,1,6,5,12,9,2,11,10),(0,1,10,9,3,12,4,11,8),\hfill \\ & (11,1,6,12,4,8,5,2,0).\hfill \end{array}$$

□

Lemma 14.

There exists an $S_9(3,T{C}_9^{\left(3\right)},14)$.

Proof of Lemma 14.

Let $V\left(K_{14}^{\left(3\right)}\right)={\mathbb{Z}}_{14}$. Base blocks for this design are given below. All other blocks are obtained by developing these base blocks by +1 modulo 14,

$$\begin{array}{cc}& (0,1,8,2,3,4,6,7,10),(0,1,5,4,13,11,9,3,7),(0,2,5,7,11,3,6,9,1),\hfill \\ & (0,2,9,6,1,10,7,4,8),(0,4,9,11,1,3,12,10,13),(0,3,10,2,11,13,9,8,4),\hfill \\ & (0,1,4,2,6,7,12,9,5),(0,1,3,4,7,9,13,6,5),(0,2,7,9,3,1,12,4,5),\hfill \\ & (0,3,8,11,5,4,6,12,10),(0,1,2,8,13,5,4,7,11),(0,2,9,4,13,12,10,11,5),\hfill \\ & (0,2,6,3,5,10,4,1,8),(0,4,8,5,6,12,10,2,3),(0,4,8,13,1,11,2,5,3),\hfill \\ & (0,3,6,8,4,9,11,1,7),(0,3,6,2,11,10,5,7,1),(0,2,8,11,4,6,5,10,13),\hfill \\ & (0,1,5,8,13,6,9,4,10),(0,1,2,7,11,13,5,6,9),(0,3,6,8,12,10,5,1,2),\hfill \\ & (0,1,12,3,5,7,11,13,2),(0,3,6,10,11,4,13,12,2),(0,2,8,12,1,7,4,11,5),\hfill \\ & (0,1,5,8,10,4,2,11,6),(10,11,7,1,8,2,4,9,5).\hfill \end{array}$$

□

Lemma 15.

There exists an $S_9(3,T{C}_9^{\left(3\right)},15)$.

Proof of Lemma 15.

Let $V\left(K_{15}^{\left(3\right)}\right)={\mathbb{Z}}_{13}\cup \{{\infty }_0,{\infty }_1\}$. Base blocks for this design are given below. All other blocks are obtained by developing these base blocks by +1 modulo 13, where ${\infty }_i+1={\infty }_i$, $i=0,1$.

$$\begin{array}{cc}& (0,1,2,4,5,8,9,3,7),(0,1,5,6,11,8,3,10,12),(0,1,{\infty }_0,3,6,8,4,11,{\infty }_1),\hfill \\ & (0,2,7,11,{\infty }_0,6,12,9,{\infty }_1),(0,5,{\infty }_1,1,{\infty }_0,7,2,11,3),(0,5,{\infty }_1,2,{\infty }_0,6,3,9,1),\hfill \\ & (0,2,7,10,3,{\infty }_1,4,{\infty }_0,6),(0,2,4,11,12,{\infty }_0,10,7,1),(0,1,8,2,11,12,{\infty }_0,3,6),\hfill \\ & (0,1,10,11,5,9,7,6,12),(0,1,3,7,6,{\infty }_1,12,9,5),(0,3,8,1,6,{\infty }_1,2,4,12),\hfill \\ & (0,2,5,4,{\infty }_1,6,10,1,8),(0,5,{\infty }_0,1,2,12,10,7,{\infty }_1),(0,5,{\infty }_0,3,9,11,8,4,6),\hfill \\ & (0,3,8,7,4,1,10,12,{\infty }_0),(0,3,7,6,2,8,5,{\infty }_1,11),(0,3,7,{\infty }_0,1,{\infty }_1,6,2,10),\hfill \\ & (0,3,8,1,6,{\infty }_0,12,{\infty }_1,11),(0,1,3,4,7,12,8,6,{\infty }_0),(0,1,2,8,3,4,7,6,9),\hfill \\ & (0,1,6,{\infty }_0,2,{\infty }_1,3,7,11),(0,1,7,3,6,8,4,11,{\infty }_1),(0,1,2,9,7,5,12,{\infty }_1,4),\hfill \\ & (0,3,{\infty }_1,8,{\infty }_0,5,1,4,10),(0,3,{\infty }_0,8,7,2,9,4,5),(0,3,{\infty }_1,8,{\infty }_0,6,5,4,11),\hfill \\ & (0,2,9,10,12,3,8,11,5),(0,3,8,12,1,11,{\infty }_1,7,6),(0,1,6,4,5,9,10,7,{\infty }_0),\hfill \\ & (0,2,{\infty }_0,7,3,10,8,6,9),(0,1,8,{\infty }_1,6,5,2,9,7),(0,1,4,5,12,{\infty }_1,10,7,2),\hfill \\ & (0,1,4,10,{\infty }_0,12,7,11,3),(9,1,{\infty }_1,5,{\infty }_0,2,11,0,8).\hfill \end{array}$$

□

Lemma 16.

There exists an $S_9(3,T{C}_9^{\left(3\right)},16)$.

Proof of Lemma 16.

Let $V\left(K_{16}^{\left(3\right)}\right)={\mathbb{Z}}_{16}$. Base blocks for this design are given below. All other blocks are obtained by developing these base blocks by +1 modulo 16,

$$\begin{array}{cc}& (0,1,8,2,3,4,6,7,10),(0,1,5,6,14,8,13,10,7),(0,1,13,15,3,5,10,12,4),\hfill \\ & (0,2,9,5,12,1,15,10,7),(0,3,10,14,4,9,12,1,15),(0,3,11,7,1,12,8,15,5),\hfill \\ & (0,4,11,7,13,15,6,5,2),(0,2,6,7,1,4,3,12,11),(0,2,8,5,6,10,11,3,4),\hfill \\ & (0,1,3,9,8,6,12,13,2),(0,2,5,9,11,3,7,14,4),(0,2,9,6,1,13,7,15,11),\hfill \\ & (0,5,10,2,7,14,9,11,1),(0,1,7,12,5,9,15,2,6),(0,1,7,5,14,10,13,2,11),\hfill \\ & (0,1,2,11,10,8,7,4,12),(0,1,9,2,12,15,11,6,5),(0,1,4,7,13,14,6,8,5),\hfill \\ & (0,1,14,5,7,6,13,3,9),(0,2,12,7,9,1,6,13,3),(0,3,12,7,10,5,15,9,1),\hfill \\ & (0,2,4,15,14,5,7,1,8),(0,2,4,3,7,10,14,5,13),(0,1,12,3,14,11,15,7,9),\hfill \\ & (0,2,6,10,9,5,12,7,14),(0,2,6,13,9,10,8,4,3),(0,1,10,11,13,5,2,8,12),\hfill \\ & (0,1,6,11,8,2,15,12,7),(0,4,9,10,15,12,5,2,3),(0,1,11,6,2,12,4,14,5),\hfill \\ & (0,2,12,14,13,1,10,15,7),(0,2,4,15,12,8,5,7,6),(0,3,12,11,15,13,10,4,9),\hfill \\ & (0,2,11,3,9,14,8,6,15),(15,1,4,14,10,2,7,6,11).\hfill \end{array}$$

□

Lemma 17.

There exists an $S_9(3,T{C}_9^{\left(3\right)},17)$.

Proof of Lemma 17.

Let $V\left(K_{17}^{\left(3\right)}\right)={\mathbb{Z}}_{17}$. Base blocks for this design are given below. All other blocks are obtained by developing these base blocks by +1 modulo 17,

$$\begin{array}{cc}& (0,1,8,2,3,4,6,7,10),(0,1,5,6,14,8,15,10,7),(0,1,12,14,10,13,8,15,6),\hfill \\ & (0,2,10,8,4,1,6,9,3),(0,3,11,7,14,1,6,10,12),(0,4,11,16,5,12,9,3,8),\hfill \\ & (0,5,11,15,6,10,3,12,1),(0,5,10,8,3,7,6,15,9),(0,3,6,1,5,16,13,12,11),\hfill \\ & (0,2,9,8,1,6,3,4,11),(0,2,4,1,7,8,15,16,14),(0,2,4,11,16,12,13,9,7),\hfill \\ & (0,1,9,13,6,10,2,5,12),(0,5,11,1,12,16,8,13,10),(0,2,8,6,13,7,3,10,1),\hfill \\ & (0,2,8,13,16,6,15,1,14),(0,4,9,5,3,13,2,16,1),(0,1,9,15,2,3,5,7,8),\hfill \\ & (0,2,12,8,3,7,5,4,10),(0,3,9,4,13,10,7,12,8),(0,3,9,10,1,15,2,13,7),\hfill \\ & (0,2,12,5,3,11,7,14,13),(0,1,7,6,3,16,5,14,2),(0,2,7,4,14,15,9,3,12),\hfill \\ & (0,2,11,15,8,10,13,1,9),(0,2,11,5,7,15,3,16,9),(0,3,6,4,2,5,11,1,10),\hfill \\ & (0,1,6,5,13,3,8,4,2),(0,5,10,9,15,12,14,11,2),(0,4,12,3,7,11,13,1,2),\hfill \\ & (0,3,7,10,1,12,6,5,2),(0,2,12,1,5,4,8,11,13),(0,2,14,4,10,11,5,16,15),\hfill \\ & (0,1,4,12,6,14,10,7,15),(0,2,7,15,6,11,5,8,14),(0,1,3,11,4,16,7,6,12),\hfill \\ & (0,1,13,14,6,11,16,3,9),(0,3,10,14,9,13,1,11,15),(0,3,10,2,12,8,5,6,16),\hfill \\ & (5,7,13,10,14,1,12,3,15).\hfill \end{array}$$

□

Lemma 18.

There exists an $S_9(3,T{C}_9^{\left(3\right)},K_{3,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$.

Proof of Lemma 18.

By Lemma 6 and Lemma 11, there exists a $GD{D}_9(3,T{C}_9^{\left(3\right)},21)$ of type $3^1{9}^2$ and an $S_9(3,T{C}_9^{\left(3\right)},9,9)$. Then, there exists an $S_9(3,T{C}_9^{\left(3\right)},K_{3,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$. □

Lemma 19.

There exists an $S_9(3,T{C}_9^{\left(3\right)},K_{4,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$.

Proof of Lemma 19.

If $A_1,A_2,B,B^{\prime }$ be pairwise-disjoint sets, $A=A_1\cup A_2$, and $\left|A_1\right|=1$, $\left|A_2\right|=3$, $\left|B\right|=9$, $\left|B^{\prime }\right|=9$; then,

$$K_{A,B,B^{\prime }}^{\left(3\right)}\cup K_{B,B^{\prime }}^{\left(3\right)}=(K_{A_1,B,B^{\prime }}^{\left(3\right)}\cup K_{B,B^{\prime }}^{\left(3\right)})\cup K_{A_2,B,B^{\prime }}^{\left(3\right)}.$$

Therefore, $9(K_{4,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})=9(K_{1,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})\cup 9K_{3,9,9}^{\left(3\right)}$. $9(K_{4,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ can be decomposed into $9(K_{1,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ and $9K_{3,9,9}^{\left(3\right)}$. By Lemma 8 and Lemma 6, there exists an $S_9(3,T{C}_9^{\left(3\right)},K_{1,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ and a $GD{D}_9(3,T{C}_9^{\left(3\right)},21)$ of type $3^1{9}^2$. Then, there exists an $S_9(3,T{C}_9^{\left(3\right)},$ $K_{4,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$. □

Lemma 20.

There exists an $S_9(3,T{C}_9^{\left(3\right)},K_{5,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$.

Proof of Lemma 20.

The same as with Lemma 19, $9(K_{5,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})=9(K_{2,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})\cup 9K_{3,9,9}^{\left(3\right)}$. $9(K_{5,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ can be decomposed into $9(K_{2,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ and $9K_{3,9,9}^{\left(3\right)}$. By Lemma 9 and Lemma 6, there exists an $S_9(3,T{C}_9^{\left(3\right)},K_{2,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ and a $GD{D}_9(3,T{C}_9^{\left(3\right)},21)$ of type $3^1{9}^2$. Then, there exists an $S_9(3,T{C}_9^{\left(3\right)},K_{5,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$. □

Lemma 21.

There exists an $S_9(3,T{C}_9^{\left(3\right)},K_{6,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$.

Proof of Lemma 21.

The same as with Lemma 19, $9(K_{6,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})=9(K_{3,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})\cup 9K_{3,9,9}^{\left(3\right)}$. $9(K_{6,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ can be decomposed into $9(K_{3,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ and $9K_{3,9,9}^{\left(3\right)}$. By Lemma 18 and Lemma 6, there exists an $S_9(3,T{C}_9^{\left(3\right)},K_{3,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ and a $GD{D}_9(3,T{C}_9^{\left(3\right)},21)$ of type $3^1{9}^2$. Then, there exists an $S_9(3,T{C}_9^{\left(3\right)},K_{6,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$. □

Lemma 22.

There exists an $S_9(3,T{C}_9^{\left(3\right)},K_{7,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$.

Proof of Lemma 22.

The same as with Lemma 19, $9(K_{7,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})=9(K_{4,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})\cup 9K_{3,9,9}^{\left(3\right)}$. $9(K_{7,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ can be decomposed into $9(K_{4,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ and $9K_{3,9,9}^{\left(3\right)}$. By Lemma 19 and Lemma 6, there exists an $S_9(3,T{C}_9^{\left(3\right)},K_{4,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ and a $GD{D}_9(3,T{C}_9^{\left(3\right)},21)$ of type $3^1{9}^2$. Then, there exists an $S_9(3,T{C}_9^{\left(3\right)},K_{7,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$. □

Lemma 23.

There exists an $S_9(3,T{C}_9^{\left(3\right)},K_{8,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$.

Proof of Lemma 23.

The same as with Lemma 19, $9(K_{8,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})=9(K_{5,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})\cup 9K_{3,9,9}^{\left(3\right)}$. $9(K_{8,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ can be decomposed into $9(K_{5,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ and $9K_{3,9,9}^{\left(3\right)}$. By Lemma 20 and Lemma 6, there exists an $S_9(3,T{C}_9^{\left(3\right)},K_{5,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$ and a $GD{D}_9(3,T{C}_9^{\left(3\right)},21)$ of type $3^1{9}^2$. Then, there exists an $S_9(3,T{C}_9^{\left(3\right)},K_{8,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$. □

Lemma 24.

There exists an $S_9(3,T{C}_9^{\left(3\right)},4,9)$.

Proof of Lemma 24.

Let $V\left(K_{4,9}^{\left(3\right)}\right)=\{{\infty }_0,{\infty }_1,{\infty }_2,{\infty }_3\}\cup {\mathbb{Z}}_9$ with vertex partition $\left\{\{{\infty }_0,{\infty }_1,{\infty }_2,{\infty }_3\},\{0,1,\dots ,8\}\right\}$. Base blocks for this design are given below. All other blocks are obtained by developing these base blocks by +1 modulo 9, where ${\infty }_i+1={\infty }_i,$ $0\le i\le 3$.

$$\begin{array}{cc}& \left(3,6,{\infty }_1,5,7,{\infty }_0,8,4,{\infty }_2\right),\left(3,7,{\infty }_1,5,{\infty }_0,8,{\infty }_2,6,{\infty }_3\right),\left(3,4,{\infty }_3,6,{\infty }_1,1,{\infty }_2,8,{\infty }_0\right),\hfill \\ & \left(3,5,{\infty }_3,4,{\infty }_0,7,{\infty }_1,6,{\infty }_2\right),\left(3,7,{\infty }_3,4,{\infty }_0,6,{\infty }_1,0,{\infty }_2\right),\left(3,4,{\infty }_2,8,{\infty }_3,5,{\infty }_1,6,{\infty }_0\right),\hfill \\ & \left(3,4,{\infty }_2,8,{\infty }_3,7,{\infty }_1,1,{\infty }_0\right),\left(3,7,{\infty }_3,5,{\infty }_0,0,{\infty }_2,1,{\infty }_1\right),\left(3,7,{\infty }_1,5,8,{\infty }_0,4,6,{\infty }_3\right),\hfill \\ & \left(3,4,{\infty }_3,8,{\infty }_0,6,{\infty }_2,0,{\infty }_1\right),\left(3,5,{\infty }_2,8,{\infty }_3,7,{\infty }_1,6,{\infty }_0\right),\left(3,5,{\infty }_2,4,{\infty }_3,7,{\infty }_1,0,{\infty }_0\right),\hfill \\ & \left(3,5,{\infty }_3,8,{\infty }_0,4,{\infty }_2,0,{\infty }_1\right),\left(3,7,{\infty }_1,6,{\infty }_3,4,{\infty }_0,5,{\infty }_2\right),\left(3,4,{\infty }_0,8,{\infty }_2,7,{\infty }_3,6,{\infty }_1\right),\hfill \\ & \left(3,7,{\infty }_1,5,{\infty }_2,8,{\infty }_3,4,{\infty }_0\right),\left(3,7,{\infty }_3,6,4,{\infty }_2,1,0,{\infty }_0\right),\left(3,7,{\infty }_1,5,{\infty }_2,0,{\infty }_3,6,{\infty }_0\right),\hfill \\ & \left(3,6,{\infty }_3,4,5,{\infty }_2,0,7,{\infty }_1\right),\left(3,6,{\infty }_2,4,{\infty }_0,2,{\infty }_1,1,{\infty }_3\right),\left(3,7,{\infty }_3,8,{\infty }_0,2,{\infty }_1,6,{\infty }_2\right),\hfill \\ & \left(2,3,{\infty }_1,0,{\infty }_3,5,{\infty }_2,4,{\infty }_0\right).\hfill \end{array}$$

□

Lemma 25.

There exists an $S_9(3,T{C}_9^{\left(3\right)},5,9)$.

Proof of Lemma 25.

Let $V\left(K_{5,9}^{\left(3\right)}\right)=\{{\infty }_0,{\infty }_1,{\infty }_2,{\infty }_3,{\infty }_4\}\cup {\mathbb{Z}}_9$ with vertex partition $\{\{{\infty }_0,{\infty }_1,{\infty }_2,{\infty }_3,{\infty }_4\}$, $\{0,1,...,8\}\}$. Base blocks for this design are given below. All other blocks are obtained by developing these base blocks by +1 modulo 9, where ${\infty }_i+1={\infty }_i,$ $0\le i\le 4$.

$$\begin{array}{cc}& \left(5,{\infty }_2,{\infty }_3,6,7,{\infty }_4,1,8,{\infty }_1\right),\left(5,8,{\infty }_3,4,2,{\infty }_2,1,6,{\infty }_4\right),\left(5,8,{\infty }_2,{\infty }_4,6,{\infty }_3,{\infty }_1,7,{\infty }_0\right)\hfill \\ & \left(5,6,{\infty }_1,2,{\infty }_4,{\infty }_0,7,3,{\infty }_2\right),\left(5,6,{\infty }_0,{\infty }_3,7,{\infty }_4,{\infty }_1,8,{\infty }_2\right),\left(5,{\infty }_0,{\infty }_2,6,0,{\infty }_3,7,3,{\infty }_1\right)\hfill \\ & \left(5,6,{\infty }_0,2,8,{\infty }_1,7,0,{\infty }_4\right),\left(5,7,{\infty }_0,1,6,{\infty }_4,8,0,{\infty }_3\right),\left(5,6,{\infty }_3,0,{\infty }_4,{\infty }_0,7,3,{\infty }_1\right)\hfill \\ & \left(5,7,{\infty }_0,6,{\infty }_1,0,{\infty }_2,2,{\infty }_4\right),\left(5,{\infty }_0,{\infty }_2,6,2,{\infty }_1,{\infty }_3,7,{\infty }_4\right),\left(5,{\infty }_0,{\infty }_3,6,{\infty }_2,2,{\infty }_4,8,{\infty }_1\right)\hfill \\ & \left(5,{\infty }_2,{\infty }_3,6,0,{\infty }_0,8,1,{\infty }_1\right),\left(5,7,{\infty }_2,1,0,{\infty }_1,{\infty }_0,6,{\infty }_3\right),\left(1,5,{\infty }_3,7,6,{\infty }_1,{\infty }_2,8,{\infty }_4\right)\hfill \\ & \left(1,5,{\infty }_4,{\infty }_1,6,0,{\infty }_2,8,{\infty }_0\right),\left(1,5,{\infty }_3,8,{\infty }_4,2,{\infty }_2,0,{\infty }_0\right),\left(5,8,{\infty }_0,7,0,{\infty }_2,4,3,{\infty }_4\right)\hfill \\ & \left(5,{\infty }_1,{\infty }_3,6,{\infty }_4,7,3,{\infty }_2,2\right),\left(5,8,{\infty }_0,{\infty }_3,6,0,{\infty }_1,1,{\infty }_4\right),\left(1,5,{\infty }_3,6,8,{\infty }_1,4,3,{\infty }_4\right)\hfill \\ & \left(5,{\infty }_2,{\infty }_3,6,8,{\infty }_1,4,{\infty }_0,1\right),\left(5,{\infty }_0,{\infty }_4,6,{\infty }_3,7,3,{\infty }_2,2\right),\left(5,8,{\infty }_3,{\infty }_1,6,{\infty }_2,4,3,{\infty }_0\right)\hfill \\ & \left(5,{\infty }_0,{\infty }_2,6,{\infty }_4,{\infty }_3,7,1,{\infty }_1\right),\left(5,{\infty }_2,{\infty }_4,6,{\infty }_0,8,7,{\infty }_3,3\right),\left(5,{\infty }_1,{\infty }_2,6,0,{\infty }_4,8,{\infty }_0,4\right)\hfill \\ & \left(5,7,{\infty }_1,{\infty }_4,6,0,{\infty }_2,2,{\infty }_3\right),\left(5,{\infty }_0,{\infty }_3,7,2,{\infty }_4,4,3,{\infty }_1\right),\left(0,4,{\infty }_0,2,{\infty }_2,7,{\infty }_3,6,{\infty }_1\right).\hfill \end{array}$$

□

Lemma 26.

There exists an $S_9(3,T{C}_9^{\left(3\right)},6,9)$.

Proof of Lemma 26.

Let $V\left(K_{6.9}^{\left(3\right)}\right)=\{{\infty }_0,{\infty }_1,{\infty }_2,{\infty }_3,{\infty }_4,{\infty }_5\}\cup {\mathbb{Z}}_9$ with vertex partition $\{\{{\infty }_0,{\infty }_1,{\infty }_2,{\infty }_3,{\infty }_4,{\infty }_5\}$, $\{0,1,\dots ,8\}\}$. Base blocks for this design are given below. All other blocks are obtained by developing these base blocks by +1 modulo 9, where ${\infty }_i+1={\infty }_i,$ $0\le i\le 5$.

$$\begin{array}{cc}& \left(0,6,{\infty }_4,4,3,{\infty }_5,5,1,{\infty }_1\right),\left(0,6,{\infty }_5,{\infty }_1,1,8,{\infty }_3,2,{\infty }_2\right),\left(0,1,{\infty }_3,5,{\infty }_5,{\infty }_2,2,6,{\infty }_0\right),\hfill \\ & \left(0,1,{\infty }_2,{\infty }_1,2,{\infty }_3,{\infty }_0,3,{\infty }_5\right),\left(0,7,{\infty }_0,{\infty }_1,1,{\infty }_4,5,4,{\infty }_2\right),\left(0,{\infty }_4,{\infty }_5,1,{\infty }_0,{\infty }_2,2,8,{\infty }_3\right),\hfill \\ & \left(0,{\infty }_2,{\infty }_4,1,{\infty }_0,8,7,{\infty }_1,5\right),\left(0,{\infty }_0,{\infty }_4,1,{\infty }_3,{\infty }_1,2,8,{\infty }_2\right),\left(0,4,{\infty }_4,{\infty }_1,1,7,{\infty }_0,3,{\infty }_5\right),\hfill \\ & \left(0,{\infty }_3,{\infty }_5,1,8,{\infty }_4,2,6,{\infty }_0\right),\left(0,4,{\infty }_3,{\infty }_2,1,{\infty }_4,7,6,{\infty }_1\right),\left(0,7,{\infty }_3,3,{\infty }_4,1,{\infty }_5,8,{\infty }_2\right),\hfill \\ & \left(0,7,{\infty }_3,6,3,{\infty }_4,{\infty }_5,1,{\infty }_1\right),\left(0,4,{\infty }_5,3,{\infty }_1,{\infty }_0,1,2,{\infty }_3\right),\left(0,7,{\infty }_0,6,{\infty }_3,3,{\infty }_4,1,{\infty }_2\right),\hfill \\ & \left(0,{\infty }_1,{\infty }_2,1,{\infty }_5,2,6,{\infty }_0,8\right),\left(0,7,{\infty }_1,3,{\infty }_4,2,{\infty }_0,8,{\infty }_5\right),\left(0,{\infty }_2,{\infty }_3,1,{\infty }_5,7,5,{\infty }_1,8\right),\hfill \\ & \left(0,4,{\infty }_4,{\infty }_0,1,{\infty }_2,7,6,{\infty }_3\right),\left(0,{\infty }_1,{\infty }_3,1,{\infty }_5,7,{\infty }_0,{\infty }_2,2\right),\left(0,4,{\infty }_2,1,{\infty }_5,5,{\infty }_1,2,{\infty }_4\right),\hfill \\ & \left(0,4,{\infty }_2,{\infty }_1,1,5,{\infty }_0,2,{\infty }_3\right),\left(0,1,{\infty }_4,{\infty }_2,2,6,{\infty }_0,4,{\infty }_1\right),\left(0,{\infty }_3,{\infty }_4,1,7,{\infty }_0,{\infty }_1,2,{\infty }_5\right),\hfill \\ & \left(0,6,{\infty }_4,5,1,{\infty }_5,{\infty }_2,2,{\infty }_3\right),\left(0,7,{\infty }_0,{\infty }_3,1,{\infty }_1,{\infty }_4,3,{\infty }_5\right),\left(0,7,{\infty }_4,{\infty }_5,1,{\infty }_0,2,8,{\infty }_2\right),\hfill \\ & \left(0,1,{\infty }_3,{\infty }_1,2,{\infty }_5,3,7,{\infty }_4\right),\left(0,1,{\infty }_5,{\infty }_0,2,3,{\infty }_3,6,{\infty }_2\right),\left(0,7,{\infty }_2,3,{\infty }_4,6,{\infty }_3,4,{\infty }_5\right),\hfill \\ & \left(0,6,{\infty }_5,{\infty }_3,1,5,{\infty }_1,2,{\infty }_2\right),\left(0,7,{\infty }_0,3,{\infty }_2,{\infty }_1,1,4,{\infty }_5\right),\left(0,7,{\infty }_1,3,{\infty }_5,2,{\infty }_2,6,{\infty }_0\right),\hfill \\ & \left(0,{\infty }_0,{\infty }_4,1,{\infty }_3,5,3,{\infty }_1,4\right),\left(0,6,{\infty }_4,{\infty }_2,1,{\infty }_3,7,5,{\infty }_0\right),\left(0,1,{\infty }_3,{\infty }_0,2,3,{\infty }_4,7,{\infty }_1\right),\hfill \\ & \left(0,7,{\infty }_4,3,{\infty }_1,6,{\infty }_5,5,{\infty }_2\right),\left(0,{\infty }_0,{\infty }_1,7,{\infty }_3,2,{\infty }_4,3,{\infty }_5\right),\left(1,7,{\infty }_3,6,{\infty }_2,0,{\infty }_0,8,{\infty }_4\right).\hfill \end{array}$$

□

Lemma 27.

There exists an $S_9(3,T{C}_9^{\left(3\right)},7,9)$.

Proof of Lemma 27.

Let $V\left(K_{7,9}^{\left(3\right)}\right)=\{{\infty }_0,{\infty }_1,{\infty }_2,{\infty }_3,{\infty }_4,{\infty }_5,{\infty }_6\}\cup {\mathbb{Z}}_9$ with vertex partition $\left\{\right\{{\infty }_0,{\infty }_1,{\infty }_2,{\infty }_3$, ${\infty }_4,{\infty }_5,{\infty }_6\}$, $\{0,1,...,8\}\}$. Base blocks for this design are given below. All other blocks are obtained by developing these base blocks by +1 modulo 9, where ${\infty }_i+1={\infty }_i,0\le i\le 6$.

$$\begin{array}{cc}& \left(1,6,{\infty }_3,8,7,{\infty }_4,0,3,{\infty }_2\right),\left(1,6,{\infty }_4,{\infty }_2,7,8,{\infty }_1,3,{\infty }_5\right),\left(6,8,{\infty }_1,2,{\infty }_4,{\infty }_5,7,1,{\infty }_0\right),\hfill \\ & \left(5,6,{\infty }_5,{\infty }_2,7,{\infty }_1,{\infty }_0,8,{\infty }_4\right),\left(5,6,{\infty }_0,{\infty }_2,7,{\infty }_3,1,{\infty }_4,{\infty }_6\right),\left(6,8,{\infty }_6,3,0,{\infty }_3,{\infty }_1,7,{\infty }_2\right),\hfill \\ & \left(6,{\infty }_2,{\infty }_6,7,{\infty }_1,{\infty }_4,8,{\infty }_3,{\infty }_5\right),\left(6,{\infty }_0,{\infty }_5,7,{\infty }_6,{\infty }_3,8,{\infty }_2,3\right),\left(6,{\infty }_0,{\infty }_3,7,8,{\infty }_6,{\infty }_5,0,{\infty }_1\right),\hfill \\ & \left(6,{\infty }_0,{\infty }_6,7,{\infty }_1,0,4,{\infty }_5,3\right),\left(0,6,{\infty }_6,1,8,{\infty }_0,7,{\infty }_4,{\infty }_3\right),\left(1,6,{\infty }_0,{\infty }_4,7,2,{\infty }_3,0,{\infty }_2\right),\hfill \\ & \left(6,8,{\infty }_5,2,1,{\infty }_1,5,{\infty }_6,{\infty }_0\right),\left(6,8,{\infty }_4,3,{\infty }_6,1,5,{\infty }_3,{\infty }_0\right),\left(6,8,{\infty }_4,7,1,{\infty }_6,0,{\infty }_3,{\infty }_5\right),\hfill \\ & \left(5,6,{\infty }_1,8,2,{\infty }_2,{\infty }_6,7,{\infty }_3\right),\left(1,6,{\infty }_0,5,{\infty }_5,0,{\infty }_1,3,{\infty }_2\right),\left(6,{\infty }_1,{\infty }_3,7,8,{\infty }_0,{\infty }_2,0,{\infty }_4\right),\hfill \\ & \left(6,{\infty }_4,{\infty }_5,7,{\infty }_1,{\infty }_2,8,1,{\infty }_3\right),\left(6,{\infty }_2,{\infty }_4,7,8,{\infty }_1,1,{\infty }_6,0\right),\left(1,6,{\infty }_5,{\infty }_0,7,2,{\infty }_6,0,{\infty }_4\right),\hfill \\ & \left(6,8,{\infty }_5,7,1,{\infty }_3,{\infty }_2,0,{\infty }_0\right),\left(6,8,{\infty }_4,3,{\infty }_6,{\infty }_5,7,{\infty }_2,{\infty }_0\right),\left(1,6,{\infty }_1,{\infty }_0,7,4,{\infty }_3,0,{\infty }_6\right),\hfill \\ & \left(5,6,{\infty }_2,{\infty }_5,7,1,{\infty }_6,8,{\infty }_1\right),\left(5,6,{\infty }_2,0,7,{\infty }_4,{\infty }_5,8,{\infty }_1\right),\left(1,6,{\infty }_1,8,{\infty }_4,2,{\infty }_0,7,{\infty }_3\right),\hfill \\ & \left(5,6,{\infty }_5,8,3,{\infty }_2,{\infty }_6,7,{\infty }_0\right),\left(6,8,{\infty }_3,7,{\infty }_1,{\infty }_4,0,{\infty }_0,{\infty }_6\right),\left(6,{\infty }_3,{\infty }_5,7,2,{\infty }_2,0,8,{\infty }_0\right),\hfill \\ & \left(6,{\infty }_1,{\infty }_3,7,8,{\infty }_5,1,4,{\infty }_4\right),\left(6,8,{\infty }_3,{\infty }_6,7,{\infty }_1,0,5,{\infty }_0\right),\left(6,{\infty }_1,{\infty }_5,7,{\infty }_6,1,5,{\infty }_4,4\right),\hfill \\ & \left(0,6,{\infty }_2,{\infty }_3,7,{\infty }_4,{\infty }_6,8,{\infty }_5\right),\left(5,6,{\infty }_6,1,7,{\infty }_0,{\infty }_1,8,{\infty }_2\right),\left(6,{\infty }_0,{\infty }_5,7,0,{\infty }_3,{\infty }_4,8,{\infty }_2\right),\hfill \\ & \left(6,{\infty }_2,{\infty }_4,7,8,{\infty }_6,{\infty }_1,0,{\infty }_0\right),\left(6,{\infty }_1,{\infty }_2,7,2,{\infty }_4,8,{\infty }_0,3\right),\left(1,6,{\infty }_1,5,2,{\infty }_3,3,{\infty }_0,{\infty }_4\right),\hfill \\ & \left(1,6,{\infty }_5,{\infty }_3,7,2,{\infty }_1,3,{\infty }_2\right),\left(6,8,{\infty }_6,{\infty }_2,7,{\infty }_5,{\infty }_4,0,{\infty }_3\right),\left(6,{\infty }_2,{\infty }_5,7,2,{\infty }_3,{\infty }_0,8,{\infty }_6\right),\hfill \\ & \left(5,6,{\infty }_3,{\infty }_2,7,8,{\infty }_6,2,{\infty }_5\right),\left(1,6,{\infty }_0,{\infty }_5,7,0,{\infty }_1,8,{\infty }_3\right),\left(0,6,{\infty }_4,5,{\infty }_6,1,{\infty }_3,2,{\infty }_1\right),\hfill \\ & \left(0,6,{\infty }_2,5,1,{\infty }_6,7,{\infty }_1,{\infty }_5\right),\left(6,8,{\infty }_4,7,{\infty }_6,5,{\infty }_3,2,{\infty }_5\right),\left(4,0,{\infty }_0,8,{\infty }_6,7,{\infty }_5,6,{\infty }_4\right),\hfill \\ & \left(3,0,{\infty }_0,8,{\infty }_1,4,{\infty }_4,1,{\infty }_2\right).\hfill \\ \end{array}$$

□

Lemma 28.

There exists an $S_9(3,T{C}_9^{\left(3\right)},8,9)$.

Proof of Lemma 28

Let $V\left(K_{8,9}^{\left(3\right)}\right)=\{{\infty }_0,{\infty }_1,{\infty }_2,{\infty }_3,{\infty }_4,{\infty }_5,{\infty }_6,{\infty }_7\}\cup {\mathbb{Z}}_9$ with vertex partition $\left\{\right\{{\infty }_0,{\infty }_1,{\infty }_2$, ${\infty }_3,{\infty }_4,{\infty }_5,{\infty }_6,{\infty }_7\}$, $\{0,1,\dots ,8\}\}$. Base blocks for this design are given below. All other blocks are obtained by developing these base blocks by +1 modulo 9, where ${\infty }_i+1={\infty }_i,0\le i\le 7$.

$$\begin{array}{cc}& \left(2,5,{\infty }_1,0,7,{\infty }_0,3,4,{\infty }_3\right),\left(2,5,{\infty }_0,{\infty }_3,3,7,{\infty }_5,0,{\infty }_2\right),\left(2,5,{\infty }_5,4,{\infty }_0,{\infty }_2,3,{\infty }_3,{\infty }_7\right),\hfill \\ & \left(2,6,{\infty }_2,5,{\infty }_7,0,7,{\infty }_6,{\infty }_0\right),\left(2,3,{\infty }_7,{\infty }_0,4,{\infty }_4,8,6,{\infty }_6\right),\left(2,5,{\infty }_6,{\infty }_3,3,{\infty }_5,{\infty }_7,4,{\infty }_4\right),\hfill \\ & \left(2,3,{\infty }_4,{\infty }_3,4,{\infty }_1,5,{\infty }_0,{\infty }_5\right),\left(2,{\infty }_5,{\infty }_6,3,{\infty }_2,{\infty }_4,4,{\infty }_1,{\infty }_7\right),\left(2,{\infty }_4,{\infty }_5,3,{\infty }_1,{\infty }_2,4,{\infty }_6,{\infty }_7\right),\hfill \\ & \left(2,{\infty }_4,{\infty }_6,3,{\infty }_1,{\infty }_5,4,{\infty }_3,{\infty }_2\right),\left(2,{\infty }_1,{\infty }_6,3,6,{\infty }_4,5,0,{\infty }_7\right),\left(2,{\infty }_1,{\infty }_4,3,{\infty }_0,6,5,{\infty }_6,0\right),\hfill \\ & \left(2,{\infty }_0,{\infty }_1,3,4,{\infty }_7,{\infty }_2,5,{\infty }_5\right),\left(2,{\infty }_1,{\infty }_3,3,7,{\infty }_2,6,0,{\infty }_7\right),\left(2,4,{\infty }_2,7,6,{\infty }_3,3,8,{\infty }_5\right),\hfill \\ & \left(2,4,{\infty }_3,7,6,{\infty }_7,3,8,{\infty }_1\right),\left(2,4,{\infty }_0,3,6,{\infty }_1,1,{\infty }_2,{\infty }_5\right),\left(2,4,{\infty }_0,{\infty }_4,3,7,{\infty }_5,6,{\infty }_3\right),\hfill \\ & \left(2,4,{\infty }_2,8,{\infty }_6,3,6,{\infty }_4,{\infty }_7\right),\left(2,3,{\infty }_1,{\infty }_2,4,{\infty }_0,{\infty }_7,5,{\infty }_6\right),\left(2,3,{\infty }_4,{\infty }_6,4,{\infty }_5,{\infty }_3,5,{\infty }_7\right),\hfill \\ & \left(2,{\infty }_4,{\infty }_5,3,{\infty }_6,{\infty }_3,4,{\infty }_0,8\right),\left(2,{\infty }_3,{\infty }_4,3,5,{\infty }_2,{\infty }_0,4,{\infty }_6\right),\left(2,{\infty }_0,{\infty }_6,3,4,{\infty }_4,6,1,{\infty }_2\right),\hfill \\ & \left(2,6,{\infty }_0,{\infty }_3,3,{\infty }_7,{\infty }_6,4,{\infty }_2\right),\left(2,3,{\infty }_1,7,4,{\infty }_3,6,{\infty }_2,{\infty }_7\right),\left(2,6,{\infty }_6,{\infty }_1,3,5,{\infty }_0,4,{\infty }_7\right),\hfill \\ & \left(2,3,{\infty }_5,7,5,{\infty }_0,{\infty }_1,4,{\infty }_3\right),\left(2,5,{\infty }_5,{\infty }_1,3,{\infty }_4,{\infty }_2,4,{\infty }_3\right),\left(2,5,{\infty }_2,{\infty }_6,3,7,{\infty }_5,4,{\infty }_7\right),\hfill \\ & \left(2,{\infty }_5,{\infty }_7,3,7,{\infty }_1,{\infty }_4,4,{\infty }_3\right),\left(2,5,{\infty }_2,4,{\infty }_5,6,7,{\infty }_3,{\infty }_1\right),\left(2,3,{\infty }_0,7,4,{\infty }_4,8,6,{\infty }_1\right),\hfill \\ & \left(2,{\infty }_3,{\infty }_7,3,{\infty }_4,4,{\infty }_5,{\infty }_6,5\right),\left(2,3,{\infty }_6,5,{\infty }_4,{\infty }_0,4,{\infty }_5,{\infty }_2\right),\left(2,6,{\infty }_3,5,{\infty }_4,{\infty }_6,3,1,{\infty }_1\right),\hfill \\ & \left(2,{\infty }_1,{\infty }_7,3,{\infty }_4,{\infty }_5,4,{\infty }_0,7\right),\left(2,6,{\infty }_3,{\infty }_2,3,0,{\infty }_6,8,{\infty }_1\right),\left(2,3,{\infty }_4,5,0,{\infty }_7,6,{\infty }_0,{\infty }_1\right),\hfill \\ & \left(2,5,{\infty }_4,{\infty }_2,3,{\infty }_7,4,{\infty }_6,{\infty }_0\right),\left(2,3,{\infty }_0,5,{\infty }_3,{\infty }_6,4,8,{\infty }_5\right),\left(2,4,{\infty }_5,{\infty }_1,3,{\infty }_2,7,{\infty }_7,{\infty }_6\right),\hfill \\ & \left(2,4,{\infty }_2,8,{\infty }_1,5,{\infty }_6,1,{\infty }_5\right),\left(2,4,{\infty }_2,7,6,{\infty }_0,{\infty }_3,3,{\infty }_4\right),\left(2,5,{\infty }_5,0,{\infty }_0,7,{\infty }_7,6,{\infty }_4\right),\hfill \\ & \left(2,5,{\infty }_7,0,{\infty }_1,7,{\infty }_3,3,{\infty }_5\right),\left(2,3,{\infty }_6,6,{\infty }_2,{\infty }_0,4,8,{\infty }_3\right),\left(2,{\infty }_0,{\infty }_4,3,{\infty }_1,{\infty }_3,4,{\infty }_7,{\infty }_5\right),\hfill \end{array}$$

$$\begin{array}{cc}& \left(2,4,{\infty }_7,{\infty }_3,3,6,{\infty }_6,5,{\infty }_2\right),\left(2,4,{\infty }_7,{\infty }_1,3,{\infty }_4,6,1,{\infty }_0\right),\left(2,3,{\infty }_3,{\infty }_5,4,8,{\infty }_7,5,{\infty }_4\right),\hfill \\ & \left(2,4,{\infty }_1,{\infty }_6,3,{\infty }_5,5,{\infty }_4,{\infty }_3\right),\left(2,3,{\infty }_7,{\infty }_0,4,7,{\infty }_1,6,{\infty }_2\right),\left(2,4,{\infty }_4,{\infty }_2,3,{\infty }_7,6,5,{\infty }_1\right),\hfill \\ & \left(2,6,{\infty }_6,4,{\infty }_3,{\infty }_2,3,{\infty }_1,{\infty }_5\right),\left(2,{\infty }_0,{\infty }_6,3,{\infty }_4,5,{\infty }_5,{\infty }_2,4\right),\left(2,{\infty }_0,{\infty }_1,3,{\infty }_4,4,{\infty }_6,6,{\infty }_2\right),\hfill \\ & \left(3,7,{\infty }_6,8,{\infty }_5,0,{\infty }_0,4,{\infty }_3\right),\left(1,4,{\infty }_5,2,{\infty }_7,0,{\infty }_6,3,{\infty }_3\right),\left(8,0,{\infty }_2,3,{\infty }_7,7,{\infty }_4,2,{\infty }_0\right).\hfill \\ \end{array}$$

□

Lemma 29.

There exists an $H{S}_3(3,T{C}_9^{\left(3\right)};12,3)$.

Proof of Lemma 29.

Let $V\left(K_{3,9}^{\left(3\right)}\right)=\{{\infty }_0,{\infty }_1,{\infty }_2\}\cup {\mathbb{Z}}_9,V\left(K_9^{\left(3\right)}\right)={\mathbb{Z}}_9$. Base blocks for this design are given below. All other blocks are obtained by developing $B_0$ by +1 modulo 9 and $B_1$, where ${\infty }_i+1={\infty }_i,0\le i\le 2$.

$B_0$:

$$\begin{array}{cc}& \left(0,2,{\infty }_2,5,4,{\infty }_1,7,3,{\infty }_0\right),\left(0,2,{\infty }_1,{\infty }_0,3,4,6,7,5\right),\left(2,7,{\infty }_2,{\infty }_1,3,1,6,5,8\right),\hfill \\ & \left(2,{\infty }_0,{\infty }_2,3,8,6,4,7,{\infty }_1\right),\left(0,1,6,4,{\infty }_0,3,8,7,2\right),\left(0,1,6,7,{\infty }_1,2,5,3,{\infty }_2\right),\hfill \\ & \left(2,5,{\infty }_0,6,{\infty }_2,4,0,3,7\right),\left(0,2,{\infty }_1,3,{\infty }_2,6,7,4,{\infty }_0\right).\hfill \end{array}$$

$B_1$:

$$\begin{array}{c}\hfill (0,1,2,3,4,5,6,7,8).\end{array}$$

□

Lemma 30.

There exists an $H{S}_9(3,T{C}_9^{\left(3\right)};12,3)$.

Proof of Lemma 30.

By Lemma 29, there exists an $H{S}_3(3,T{C}_9^{\left(3\right)};12,3)$. Repeating each block in the $H{S}_3(3,T{C}_9^{\left(3\right)};12,3)$ three times, we obtain an $H{S}_9(3,T{C}_9^{\left(3\right)};12,3)$. □

Lemma 31.

There exists an $H{S}_9(3,T{C}_9^{\left(3\right)};13,4)$.

Proof of Lemma 31.

If $V\left(K_{13}^{\left(3\right)}\right)={\mathbb{Z}}_{13}$, $V\left(K_4^{\left(3\right)}\right)={\mathbb{Z}}_4$, $V_1=\{0,1,2,3\}$, $V_2=\{4,5,6,7,8,9,$ $10,11,12\}$, then

$$9K_V^{\left(3\right)}=9K_{V_2}^{\left(3\right)}\cup 9K_{V_1,V_2}^{\left(3\right)}.$$

Therefore, $9(K_{13}^{\left(3\right)}\setminus K_4^{\left(3\right)})$ can be decomposed into $9K_9^{\left(3\right)}$ and $9K_{4,9}^{\left(3\right)}$. By Lemma 2 and Lemma 24, there exists an $S_9(3,T{C}_9^{\left(3\right)},9)$ and an $S_9(3,T{C}_9^{\left(3\right)},4,9)$. Then, there exists an $H{S}_9(3,T{C}_9^{\left(3\right)};13,4)$. □

Lemma 32.

There exists an $H{S}_9(3,T{C}_9^{\left(3\right)};14,5)$.

Proof of Lemma 32.

If $V\left(K_{14}^{\left(3\right)}\right)={\mathbb{Z}}_{14}$, $V\left(K_5^{\left(3\right)}\right)={\mathbb{Z}}_5$, $V_1=\{0,1,2,3,4\}$, $V_2=\{5,6,7,8,9,$ $10,11,12,13\}$, then

$$9K_V^{\left(3\right)}=9K_{V_2}^{\left(3\right)}\cup 9K_{V_1,V_2}^{\left(3\right)}.$$

Therefore, $9(K_{14}^{\left(3\right)}\setminus K_5^{\left(3\right)})$ can be decomposed into $9K_9^{\left(3\right)}$ and $9K_{5,9}^{\left(3\right)}$. By Lemma 2 and Lemma 25, there exists an $S_9(3,T{C}_9^{\left(3\right)},9)$ and an $S_9(3,T{C}_9^{\left(3\right)},5,9)$. Then, there exists an $H{S}_9(3,T{C}_9^{\left(3\right)};14,5)$. □

Lemma 33.

There exists an $H{S}_9(3,T{C}_9^{\left(3\right)};15,6)$.

Proof of Lemma 33.

If $V\left(K_{15}^{\left(3\right)}\right)={\mathbb{Z}}_{15}$, $V\left(K_6^{\left(3\right)}\right)={\mathbb{Z}}_6$, $V_1=\{0,1,2,3,4,5\}$, $V_2=\{6,7,8,9,$ $10,11,12,13,14\}$, then

$$9K_V^{\left(3\right)}=9K_{V_2}^{\left(3\right)}\cup 9K_{V_1,V_2}^{\left(3\right)}.$$

Therefore, $9(K_{15}^{\left(3\right)}\setminus K_6^{\left(3\right)})$ can be decomposed into $9K_9^{\left(3\right)}$ and $9K_{6,9}^{\left(3\right)}$. By Lemma 2 and Lemma 26, there exists an $S_9(3,T{C}_9^{\left(3\right)},9)$ and an $S_9(3,T{C}_9^{\left(3\right)},6,9)$. Then, there exists an $H{S}_9(3,T{C}_9^{\left(3\right)};15,6)$. □

Lemma 34.

There exists an $H{S}_9(3,T{C}_9^{\left(3\right)};16,7)$.

Proof of Lemma 34.

If $V\left(K_{16}^{\left(3\right)}\right)={\mathbb{Z}}_{16}$, $V\left(K_7^{\left(3\right)}\right)={\mathbb{Z}}_7$, $V_1=\{0,1,2,3,4,5,6\}$, $V_2=\{7,8,9,10,11,12,13,14,15\}$, then

$$9K_V^{\left(3\right)}=9K_{V_2}^{\left(3\right)}\cup 9K_{V_1,V_2}^{\left(3\right)}.$$

Therefore, $9(K_{16}^{\left(3\right)}\setminus K_7^{\left(3\right)})$ can be decomposed into $9K_9^{\left(3\right)}$ and $9K_{7,9}^{\left(3\right)}$. By Lemma 2 and Lemma 27, there exists an $S_9(3,T{C}_9^{\left(3\right)},9)$ and an $S_9(3,T{C}_9^{\left(3\right)},7,9)$. Then, there exists an $H{S}_9(3,T{C}_9^{\left(3\right)};16,7)$. □

Lemma 35.

There exists an $H{S}_9(3,T{C}_9^{\left(3\right)};17,8)$.

Proof of Lemma 35.

If $V\left(K_{17}^{\left(3\right)}\right)={\mathbb{Z}}_{17}$, $V\left(K_8^{\left(3\right)}\right)={\mathbb{Z}}_8$, $V_1=\{0,1,2,3,4,5,6,7\}$, $V_2=\{8,9,10,11,12,13,14,15,16\}$, then

$$9K_V^{\left(3\right)}=9K_{V_2}^{\left(3\right)}\cup 9K_{V_1,V_2}^{\left(3\right)}.$$

Therefore, $9(K_{17}^{\left(3\right)}\setminus K_8^{\left(3\right)})$ can be decomposed into $9K_9^{\left(3\right)}$ and $9K_{8,9}^{\left(3\right)}$. By Lemma 2 and Lemma 28, there exists an $S_9(3,T{C}_9^{\left(3\right)},9)$ and an $S_9(3,T{C}_9^{\left(3\right)},8,9)$. Then, there exists an $H{S}_9(3,T{C}_9^{\left(3\right)};17,8)$. □

4. Results

In this part, we obtain the necessary and sufficient conditions for the existence of $T{C}_9^{\left(3\right)}$-decomposition of $\lambda K_n^{\left(3\right)}$.

Theorem 1.

There exists a $T{C}_9^{\left(3\right)}$-decomposition of $\lambda K_n^{\left(3\right)}$ only if $54\mid \lambda n(n-1)(n-2)$, $6\mid \lambda (n-1)(n-2)$ for $n\ge 9$.

Proof of Theorem 1.

Consider that $T{C}_9^{\left(3\right)}$ has size 9 and is 3-regular; whereas $\lambda K_n^{\left(3\right)}$ has size $\lambda C_n^3$ and is $\lambda C_{n-1}^2$-regular. Therefore, for a $T{C}_9^{\left(3\right)}$-decomposition of $\lambda K_n^{\left(3\right)}$ to exist, we must have $3|{\displaystyle \frac{\lambda (n-1)(n-2)}{2}}$, $9|{\displaystyle \frac{\lambda n(n-1)(n-2)}{6}}$ for $n\ge 9$, which is $54\mid \lambda n(n-1)(n-2)$ and $6\mid \lambda (n-1)(n-2)$ for $n\ge 9$. □

Through sorting, the necessary conditions for the existence of $S_{\lambda }(3,T{C}_9^{\left(3\right)},n)$ can be divided into the following three cases:

(1) $n\equiv 1,2(mod27)$ and $n\ge 28$, for $\lambda \equiv 1,2,4,5,7,8(mod9)$;

(2) $n\equiv 0,1,2(mod9)$ and $n\ge 9$, for $\lambda \equiv 3,6(mod9)$;

(3) $n\equiv 3,4,5,6,7,8(mod9)$ and $n\ge 12$, for $\lambda \equiv 0(mod9)$.

Theorem 2.

There exists a $T{C}_9^{\left(3\right)}$-decomposition of $\lambda K_n^{\left(3\right)}$ if $\lambda \equiv 1,2,4,5,7,8(mod9)$, $n\equiv 1,2(mod27)$, and $n\ge 28$.

Proof of Theorem 2.

By [10], there exists an $S(3,T{C}_9^{\left(3\right)},n)$. For any positive integer $\lambda$, repeating each block in the $S(3,T{C}_9^{\left(3\right)},n)$ $\lambda$ times, we obtain an $S_{\lambda }(3,T{C}_9^{\left(3\right)},n)$. □

Theorem 3.

There exists a $T{C}_9^{\left(3\right)}$-decomposition of $\lambda K_n^{\left(3\right)}$ if $\lambda \equiv 3,6(mod9),n\equiv 0,1,2(mod9)$, and $n\ge 9$.

Proof of Theorem 3.

Let k be a positive integer. If $a\le 2$, then $K_{9+a}^{\left(3\right)}\setminus K_a^{\left(3\right)}$ is isomorphic to $K_{9+a}^{\left(3\right)}$. The proof of the existence of $S_{\lambda }(3,T{C}_9^{\left(3\right)},n)$ is discussed in the following three cases:

(1) For $n=9k$. By Lemmas 1, 11, and 7, there exists an $S_3(3,T{C}_9^{\left(3\right)},9)$, an $S_3(3,T{C}_9^{\left(3\right)},9,9)$, and a $GD{D}_3(3,T{C}_9^{\left(3\right)},27)$ of type $9^3$. Applying Construction 1, let $\lambda =3,a=0,b=9$; then, there exists an $S_3(3,T{C}_9^{\left(3\right)},9k)$.

(2) For $n=9k+1$. By Lemmas 3, 8, and 7, there exists an $S_3(3,T{C}_9^{\left(3\right)},10)$, an $S_3(3,T{C}_9^{\left(3\right)},K_{1,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$, and a $GD{D}_3(3,T{C}_9^{\left(3\right)},27)$ of type $9^3$. Applying Construction 1, let $\lambda =3,a=1,b=9$; then, there exists an $S_3(3,T{C}_9^{\left(3\right)},9k+1)$.

(3) For $n=9k+2$. By Lemmas 4, 9, and 7, there exists an $S_3(3,T{C}_9^{\left(3\right)},11)$, an $S_3(3,T{C}_9^{\left(3\right)},K_{2,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$, and a $GD{D}_3(3,T{C}_9^{\left(3\right)},27)$ of type $9^3$. Applying Construction 1, let $\lambda =3,a=2,b=9$; then, there exists an $S_3(3,T{C}_9^{\left(3\right)},9k+2)$.

For any positive integer $\lambda$, repeating each block in the $S(3,T{C}_9^{\left(3\right)},n)$ $\lambda /3$ times, we obtain an $S_{\lambda }(3,T{C}_9^{\left(3\right)},n)$. □

Theorem 4.

There exists a $T{C}_9^{\left(3\right)}$-decomposition of $\lambda K_n^{\left(3\right)}$ if $\lambda \equiv 0(mod9),n\equiv 3,4,5,6,7,8(mod9)$, and $n\ge 12$.

Proof of Theorem 4.

The proof of the existence of $S_{\lambda }(3,T{C}_9^{\left(3\right)},n)$ is discussed in the following six cases.

(1) For $n=9k+3$. By Lemmas 12, 18, 30, and 7, there exists an $S_9(3,T{C}_9^{\left(3\right)},12)$, an $S_9(3,T{C}_9^{\left(3\right)},K_{3,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$, an $H{S}_9(3,T{C}_9^{\left(3\right)};12,3)$, and a $GD{D}_9(3,T{C}_9^{\left(3\right)},27)$ of type $9^3$. Applying Construction 1, let $\lambda =9,a=3,b=9$; then, there exists an $S_9(3,T{C}_9^{\left(3\right)},9k+3)$.

(2) For $n=9k+4$. By Lemmas 13, 19, 31, and 7, there exists an $S_9(3,T{C}_9^{\left(3\right)},13)$, an $S_9(3,T{C}_9^{\left(3\right)},K_{4,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$, an $H{S}_9(3,T{C}_9^{\left(3\right)};13,4)$, and a $GD{D}_9(3,T{C}_9^{\left(3\right)},27)$ of type $9^3$. Applying Construction 1, let $\lambda =9,a=4,b=9$; then, there exists an $S_9(3,T{C}_9^{\left(3\right)},9k+4)$.

(3) For $n=9k+5$. By Lemmas 14, 20, 32, and 7, there exists an $S_9(3,T{C}_9^{\left(3\right)},14)$, an $S_9(3,T{C}_9^{\left(3\right)},K_{5,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$, an $H{S}_9(3,T{C}_9^{\left(3\right)};14,5)$, and a $GD{D}_9(3,T{C}_9^{\left(3\right)},27)$ of type $9^3$. Applying Construction 1, let $\lambda =9,a=5,b=9$; then, there exists an $S_9(3,T{C}_9^{\left(3\right)},9k+5)$.

(4) For $n=9k+6$. By Lemmas 15, 21, 33, and 7, there exists an $S_9(3,T{C}_9^{\left(3\right)},15)$, an $S_9(3,T{C}_9^{\left(3\right)},K_{6,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$, an $H{S}_9(3,T{C}_9^{\left(3\right)};15,6)$, and a $GD{D}_9(3,T{C}_9^{\left(3\right)},27)$ of type $9^3$. Applying Construction 1, let $\lambda =9,a=6,b=9$; then, there exists an $S_9(3,T{C}_9^{\left(3\right)},9k+6)$.

(5) For $n=9k+7$. By Lemmas 16, 22, 34, and 7, there exists an $S_9(3,T{C}_9^{\left(3\right)},16)$, an $S_9(3,T{C}_9^{\left(3\right)},K_{7,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$, an $H{S}_9(3,T{C}_9^{\left(3\right)};16,7)$, and a $GD{D}_9(3,T{C}_9^{\left(3\right)},27)$ of type $9^3$. Applying Construction 1, let $\lambda =9,a=7,b=9$; then, there exists an $S_9(3,T{C}_9^{\left(3\right)},9k+7)$.

(6) For $n=9k+8$. By Lemmas 17, 23, 35, and 7, there exists an $S_9(3,T{C}_9^{\left(3\right)},17)$, an $S_9(3,T{C}_9^{\left(3\right)},K_{8,9,9}^{\left(3\right)}\cup K_{9,9}^{\left(3\right)})$, an $H{S}_9(3,T{C}_9^{\left(3\right)};17,8)$ and a $GD{D}_9(3,T{C}_9^{\left(3\right)},27)$ of type $9^3$. Applying Construction 1, let $\lambda =9,a=8,b=9$; then, there exists an $S_9(3,T{C}_9^{\left(3\right)},9k+8)$.

For any positive integer $\lambda$, repeating each block in the $S(3,T{C}_9^{\left(3\right)},n)$ $\lambda /9$ times, we obtain an $S_{\lambda }(3,T{C}_9^{\left(3\right)},n)$. □

Theorem 5.

There exists a $T{C}_9^{\left(3\right)}$-decomposition of $\lambda K_n^{\left(3\right)}$ if and only if $\lambda n(n-1)(n-2)\equiv 0(mod54),\lambda (n-1)(n-2)\equiv 0(mod6)$, and $n\ge 9$.

Proof of Theorem 5.

According to Theorem 1, we derive the necessary conditions for the existence of $S_{\lambda }(3,T{C}_9^{\left(3\right)},n)$. According to Theorems 2, 3, and 4, we derive the sufficient conditions for the existence of $S_{\lambda }(3,T{C}_9^{\left(3\right)},n)$. Therefore, the conclusion is valid. □

5. Conclusions

In this paper, we considered the existence of tight 9-cycle decompositions of $\lambda$-fold complete 3-uniform hypergraphs. First, we introduced the concepts and definitions used in this paper. Then, according to the recursive constructions, the required designs of small orders were found. Next, we obtained the necessary conditions and sufficient conditions for the existence of $T{C}_9^{\left(3\right)}$-decomposition of $\lambda K_n^{\left(3\right)}$. Finally, we proved that there exists a $T{C}_9^{\left(3\right)}$-decomposition of $\lambda K_n^{\left(3\right)}$ if and only if $\lambda n(n-1)(n-2)\equiv 0(mod54)$, $\lambda (n-1)(n-2)\equiv 0(mod6)$ and $n\ge 9$.

6. Discussion

A hypergraph is one of the basic structures in discrete mathematics, which is an extension of simple graphs. The decomposition of hypergraph has been paid more and more attention by scholars. It has been widely used and important in combinatorial design, graph theory, coding, and other fields. For example, hypergraph decomposition can be used to construct efficient secret sharing schemes. In [13], the application of this technique allows us to obtain secret sharing schemes for several classes of access structures (such as hyperpaths, hypercycles, hyperstars, and acyclic hypergraphs) with improved efficiency over previous results. With continuous research, we believe that the application of hypergraph decomposition will be more extensive.