On Linear Codes over Local Rings of Order p⁴

Abstract

Suppose R is a local ring with invariants $p,n,r,m,k$ and $mr=4,$ that is R of order $p^4.$ Then, $R=R_0+u{R}_0+v{R}_0+w{R}_0$ has maximal ideal $J=u{R}_0+v{R}_0+w{R}_0$ of order $p^{(m-1)r}$ and a residue field F of order $p^r,$ where $R_0=GR(p^n,r)$ is the coefficient subring of $R.$ In this article, the goal is to improve the understanding of linear codes over small-order non-chain rings. In particular, we produce the MacWilliams formulas and generator matrices for linear codes of length N over $R.$ In order to accomplish that, we first list all such rings up to isomorphism for different values of $p,n,r,m,k.$ Furthermore, we fully describe the lattice of ideals in R and their orders. Next, for linear codes C over R, we compute the generator matrices and MacWilliams identities, as shown by numerical examples. Given that non-chain rings are not principal ideals rings, it is crucial to acknowledge the difficulties that arise while studying linear codes over them.

1. Introduction

Linear codes with length N over ring R correspond to R-submodules of $R^N.$ The interest in coding over finite rings began when linear codes over rings and those over fields were linked using Gray maps. Every alphabet ring used in this work is finite, commutative, and contains an identity. If a ring R has one maximal ideal, J (the Jacobson radical), then it is said to be local. Each local ring is associated with specific integer invariants, $p,n,r,m,$ and $k,$ where p is a prime number representing the characteristic of the residue field ${\displaystyle \frac{R}{J}}\cong GF\left(p^r\right)$ of order $p^r,$m satisfies $J^m=0$ with $\mid R\mid =p^{mr},$$p^n$ is the characteristic of R, and k is related to a distinguished basis of $R,$ explained later in Section 2 (see [1,2,3]). The ring R is referred to as a principal ideal ring (PIR) when all of its ideals are principal. When J is principal, it creates a distinguished class known as chain rings [4,5,6]. Codes over local non-chain rings have received less research attention because chain rings are principal ideal rings (PIRs), and many results found for chain rings also hold for PIRs. One of the main reasons that Frobenius rings, defined later, are considered an appropriate class to characterize codes is because they meet both of the MacWilliams theorems [7,8,9]. Frobenius local rings, however, can be decomposed into their primary components. To fully comprehend codes over Frobenius rings, it is necessary, despite difficulties, to consider local non-chain rings. Thus, the primary goal of this work is to produce significant coding results over local non-chain rings in order to advance this field of study. For additional information on this subject, see [10,11,12,13,14] and related references.

The main purpose of this work is to generate important coding results over local non-chain rings to address the significance of these broad discoveries. This paper focuses mainly on codes over local rings with order $p^4$; that is, $mr=4.$ Previous work on these rings was described in [1], where it was emphasized how applicable they are to coding theory and how closely they relate to linear binary codes and ${\mathbb{Z}}_{p^n}$ [15]. In error-correcting theory, we clarify the roles of generator matrices and MacWilliams relations, particularly as they relate to the weight enumerators of a code and its dual code. These methods were taken into consideration by the authors of [16,17] for Frobenius local rings of small order, namely $16.$ In [18], rings of order 32 were used to describe generator matrices and the MacWilliams relations. In an attempt to expand upon earlier discoveries, this paper offers access to more generic rings with higher orders. With $mr=4,$ let $R=R_0+u{R}_0+v{R}_0+w{R}_0,$ where $J=u{R}_0+v{R}_0+w{R}_0$ is the maximum ideal of R and $R_0=GR(p^n,r)$ is its coefficient subring. This paper focuses on two useful tools of coding theory: generator matrices and MacWilliams relations. First, we provide a formula for a generating character $\nu$ associated with R, and we make use of it to generate a matrix $S.$ This matrix is then utilized to obtain the MacWilliams relations between symmetrized weight enumerators for a code C over R and its dual. Next, we investigate generator matrices of linear codes over $R.$ These matrices are extremely useful tools, since they can generate the code and provide the code’s size. There is a well-known canonical form that achieves this for codes over chain rings. However, codes over local non-chain rings do not fit similarly; thus, we give a natural extension of this canonical form (see Theorem 10). We also exhibit several numerical examples to demonstrate why the code’s size cannot always be determined directly from its generator matrix.

Following the basic definitions and information in Section 2, the list of all rings of type $R=R_0+u{R}_0+v{R}_0+w{R}_0$ with invariants $p,n,r,m,k$ such that $mr=4$ are provided in Section 3. A special focus is on supplying all the information required to define the lattice of ideals of rings of order $p^4$ and to describe them. The overall process for creating characters for R when it is Frobenius is given in Section 4. Additionally, an appropriate matrix is also acquired through which MacWilliams relations are deduced. The results for matrices producing linear codes over such rings are given in Section 5.

2. Preliminaries

This section introduces the notations and basic information that will be used later in our discussion. Let J be the maximal ideal of a local ring with identity R. We will rely on the proven results listed below (see [1,2,3,6,8]).

The size of R is $\left|R\right|=p^{mr}$, with $R/J\cong GF\left(p^r\right)=F={\mathbb{F}}_{p^r}.$ The order of J is $p^{(m-1)r}$ if $J^m=0.$ The index of nilpotency of J is denoted by l and defined as $J^l=0$ and $J^{l-1}\ne 0,$ where $l\le m.$ The characteristic of R is expressed as $p^n,$ where $1\le n\le m$. In addition, there is a Galois subring $R_0$ of R with invariants $p,n,r$, written as $R_0=GR(p^n,r).$ This is called a coefficient subring, which is the maximal Galois subring of $R.$ Additionally, there are k and $u_i\in J,$ where $1\le i\le k$ is called the distinguished basis of R over $R_0$, such that:

$$\begin{array}{cc}\hfill & R=R_0+u_1{R}_0+u_2{R}_0+\cdots +u_k{R}_0,\hfill \\ \hfill & J=u_1{R}_0+u_2{R}_0+\cdots +u_k{R}_0.\hfill \end{array}$$

(1)

If J is principal, then R is a chain. In particular, when $J=\left(p\right),$ we have $n=m$ and

$$R=GR(p^n,r)={\mathbb{Z}}_{p^n}\left[\alpha \right]\cong {\displaystyle \frac{{\mathbb{Z}}_{p^n}\left[x\right]}{\left(g\right(x\left)\right)}},$$

where $\alpha$ is a root (primitive element) of a specific polynomial $g\left(x\right)\in {\mathbb{Z}}_{p^n}\left[x\right].$ Let

$$\begin{array}{cc}& \Gamma \left(r\right)=\left(\alpha \right)\cup \left\{0\right\}=\{0,1,\alpha ,{\alpha }^2,\cdots ,{\alpha }^{p^r-2}\};\hfill \\ & {\Gamma }^{*}\left(r\right)=\left(\alpha \right)=\{1,\alpha ,{\alpha }^2,\cdots ,{\alpha }^{p^r-2}\}.\hfill \end{array}$$

Suppose $\gamma \in R,$ so

$$\gamma ={\alpha }_1+p{\alpha }_1+p^2{\alpha }_2+\cdots +p^{n-1}{\alpha }_{n-2}(\mathrm{p}\text{-}\mathrm{adic}\mathrm{expression}).$$

(2)

where ${\alpha }_i\in \Gamma \left(r\right).$ Furthermore, assume that t is the smallest number with the condition of $p^{t}u=0.$ We label $p,n,r,m,k$ and t as the parameters (invariants) of $R.$

In our later discussion, we set $mr=4$ and $t\le n.$ This implies that $R_0$ is ${\mathbb{Z}}_{p^i},$$GR(p^2,2),$$F_{p^2},$ or $F_{p^4}$ depending on r and $n,$ where $i=1,2,3,4.$ In addition, we fix R as follows:

$$\begin{array}{cc}\hfill & R=R_0+u{R}_0+v{R}_0+w{R}_0,\hfill \\ \hfill & J=u{R}_0+v{R}_0+w{R}_0.\hfill \end{array}$$

(3)

This means $1\le k\le 3$ throughout this work; that is, when $k=3,$ we set $u_1=u,u_2=v$ and $u_3=w.$ Thus, R can be expressed as a quotient ring of the form

$$R={\displaystyle \frac{R_0[u,v,w]}{I}},$$

where I is an ideal generated by combinations of $u,v$, and $w.$ As we see later, the structure of I will completely determine $R.$

The total sum of all minimal ideals in R is what we define as the socle of $R,$ also known as soc$\left(R\right).$ Since R is commutative, we have:

$$\begin{array}{cc}& soc\left(R\right)=\{v\in R:v\in \mathrm{ann}(J\left)\right\},\hfill \\ & \mathrm{ann}\left(J\right)=\{a\in R:ay=0,\mathrm{for}\mathrm{all}y\in J\}.\hfill \end{array}$$

We will highlight the definition of Frobenius rings that is most pertinent to our analysis. In [8], we call R Frobenius if

$${\displaystyle \frac{R}{J}}\cong soc\left(R\right).$$

Let ${\mathrm{Hom}}_{\mathbb{Z}}(R,{\mathbb{C}}^{*})$ denote the character group of $(R,+).$ Then, elements of ${\mathrm{Hom}}_{\mathbb{Z}}(R,{\mathbb{C}}^{*})$ are called characters $\nu$ of $(R,+).$ If ker$\left(\nu \right)$ has no non-trivial ideals of $R,$ then $\nu$ is named a generating character.

Theorem 1 

(Honold [8]). The ring R is Frobenius if and only if soc$\left(R\right)$ is cyclic.

A code C of length N over R is a subset of $R^N,$ and it is referred to as linear if it is a R-submodule. Furthermore, by including the inner-product (·) in $R^N$, the dual code $C^{\perp }$ of C is defined as follows:

$$C^{\perp }=\{\mathbf{u}:\mathbf{c}·\mathbf{u}=0,\mathbf{c}\in C\}.$$

(4)

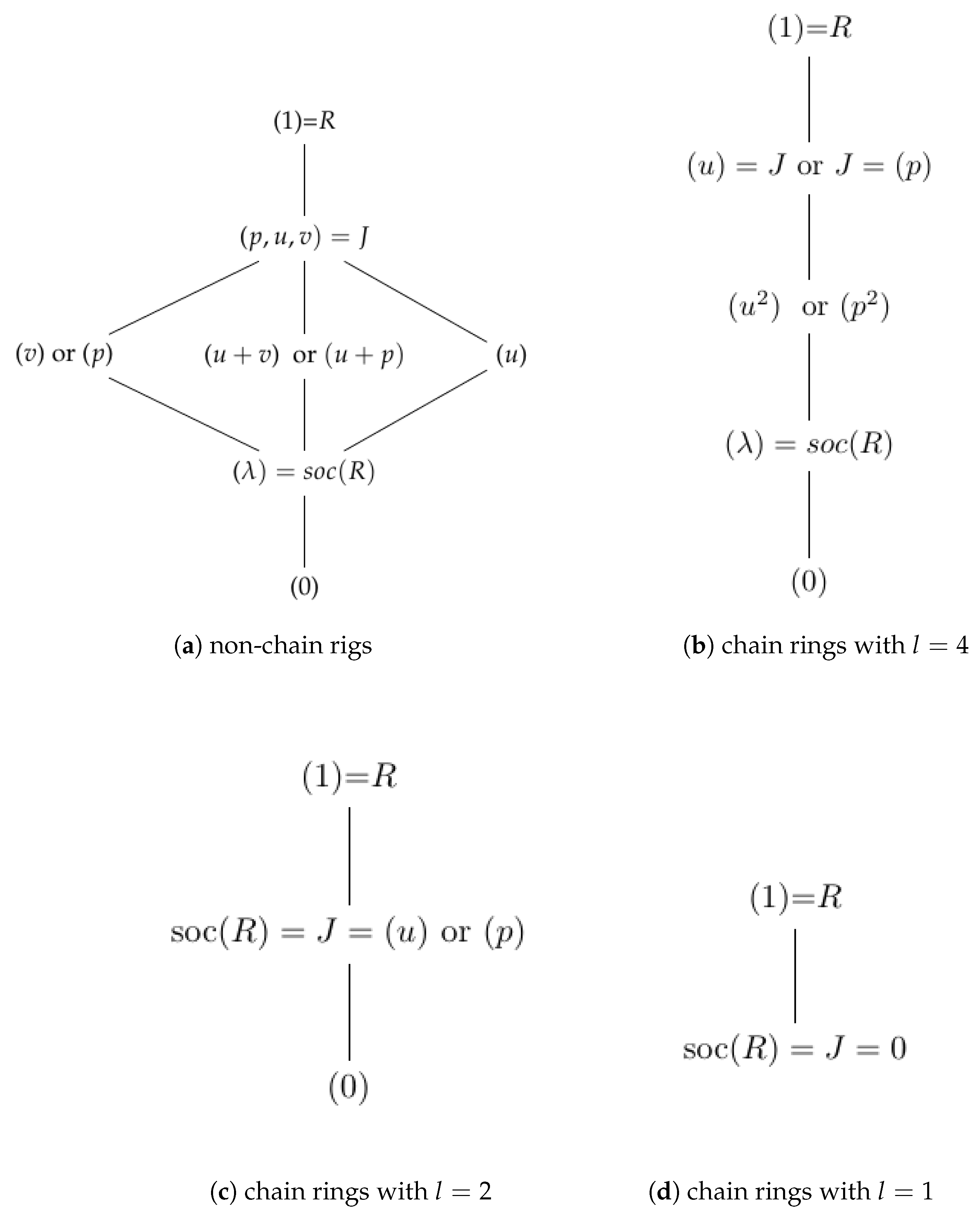
3. Local Rings of Order $p^4$

Take a finite local ring R and its invariants $p,n,r,k,m.$ This section contains the proof of some results on local rings of order $p^4$ and with residue field $F={\mathbb{F}}_{p^r};$ i.e., $mr=4.$ These findings help our discussion that follows in later sections. As $\mid R\mid =p^4,$ then, based on $k,$ we have the following:

$$\left\{\begin{array}{cc}R=R_0+u_1{R}_0,\hfill & \mathrm{if}k=1,\hfill \\ R=R_0+u_1{R}_0+u_2{R}_0,\hfill & \mathrm{if}k=2,\hfill \\ R=R_0+u_1{R}_0+u_2{R}_0+u_3{R}_0,\hfill & \mathrm{if}k=3.\hfill \end{array}\right.$$

Suppose $p^{t_i}$ is the order (additive) of $u_i$ in $R;$ that is, $p^{t_i}{u}_i=0$ for $1\le i\le k.$ Since $\mid R_0\mid =p^{nr},$

$$m=n+t_1+t_2+\cdots +t_k.$$

(5)

Moreover, since $1\le t_i\le n$, for every $i,$

$$\lfloor {\displaystyle \frac{m}{n}}\rfloor -1\le k\le m-n.$$

(6)

If $p\ne 2,$ consider the usual partition on ${\Gamma }^{*}\left(r\right).$

$$\begin{array}{c}\hfill A=\{\beta \in {\Gamma }^{*}\left(r\right):\beta \notin {{\Gamma }^{*}\left(r\right)}^2\};\\ \hfill B=\{\beta \in {\Gamma }^{*}\left(r\right):\beta \in {{\Gamma }^{*}\left(r\right)}^2\}.\end{array}$$

We denote $u_1=u,$$u_2=v$ and $u_3=w$ in our further discussion. Also, we denote $\alpha$ to be a primitive element of $F.$ Because of the order of $R,$ we obtain $rm=4;$ thus, we have many possibilities for r and $m:$ (a) $r=1$ and $m=4;$ (b) $r=m=2;$ (c) $r=4$ and $m=1.$

• Case a: when $r=1.$ Then, we have $m=4$ and $1\le n\le 4.$ Moreover, $F={\mathbb{F}}_p.$ Consider the following subcases depending on the values that n can take.
• Case a1: if $n=1.$ Then, from Equation (6), we have $k=3.$ This explains that there are $u,v,w$ in J, such that:

  $$R={\mathbb{F}}_p+u{\mathbb{F}}_p+v{\mathbb{F}}_p+w{\mathbb{F}}_p.$$

  (7)

In this case, R can be constructed as one of the following:

$$\begin{array}{cc}\hfill & \left(a\right)R_{a1,1}={\displaystyle \frac{{\mathbb{F}}_p[u,v,w]}{{(u,v,w)}^2}};\left(b\right)R_{a1,2}={\displaystyle \frac{{\mathbb{F}}_p[u,v]}{(u^3,v^2,uv)}};\left(c\right)R_{a1,3}={\displaystyle \frac{{\mathbb{F}}_p\left[u\right]}{\left(u^4\right)}}.\hfill \\ \hfill & \left(d\right)R_{a1,4}={\displaystyle \frac{{\mathbb{F}}_2[u,v]}{(u^2,v^2)}};\left(e\right)R_{a1,5}={\displaystyle \frac{{\mathbb{F}}_p[u,v]}{(u^2-\alpha v^2,uv)}};\left(f\right)R_{a1,6}={\displaystyle \frac{{\mathbb{F}}_p[u,v]}{(u^2-v^2,uv)}},\hfill \end{array}$$

(8)

The rings $R_{a1,i}$ listed above are local rings with invarinats $p,1,1,3,4.$ In addition, we imply the following:

$$\mathrm{soc}\left(R_{a1,i}\right)=\left\{\begin{array}{cc}(u_1,u_2,u_3),\hfill & \mathrm{if}i=1,\hfill \\ (u^2,v),\hfill & \mathrm{if}i=2,\hfill \\ \left(u^3\right),\hfill & \mathrm{if}i=3,\hfill \\ \left(uv\right),\hfill & \mathrm{if}i=4,\hfill \\ \left(u^2\right),\hfill & \mathrm{if}i=5,6.\hfill \end{array}\right.$$

(9)

Theorem 2. 

Assume that R is a local ring with $p,1,1,4,3.$ Then, R is isomorphic to a unique ring of $R_{a1,i}$ of Equation (8). Moreover, $R_{a1,i}$ is Frobenius, where $i=3,4,5,6.$

Proof. 

As $k=3,$ then $l\ne 1;$ i.e., $J\ne 0.$ This means that $2\le l\le 4.$ Let $l=2.$ This implies that $J^2=0,$ and hence all multiplications $u^2=uv=v^2=vw=uw=w^2=0.$ Thus, ${(u,v,w)}^2=0,$ and therefore R has the form of $R_{a1,1},$

$$R\cong {\displaystyle \frac{{\mathbb{F}}_p[u,v,w]}{{(u,v,w)}^2}}.$$

We proceed with $l=3.$ In this case, $J^2\ne 0;$ thus, we have exactly three choices of w, which are $u^2,uv$, or $v^2.$ According to a certain choice of $w,$ then we obtain the construction of $R.$ If $w=u^2,$ then $v^2=\beta u^2$ and $uv=\gamma u^2,$ where $\beta ,\gamma \in \Gamma \left(r\right).$ When $\beta =\gamma =0,$ then we have $u^3=0,uv=0=v^2,$ and we obtain $R_{a1,2}.$ Let $\gamma \ne 0,$ then we replace v by $v-\beta u$, which gives $uv=0.$ Now, we obtain $R_{a1,5}$ if $\beta \in A$ and $R_{a1,6}$ if $\beta \in B$ by replacing u with $\delta u,$ where ${\delta }^2=\beta .$ The case $w=v^2$ is similar to that when $w=u^2.$ Suppose $w=uv.$ We only consider the situation $u^2=0$ and $v^2=0.$ When $p\ne 2,$ one can map ${\displaystyle \frac{{\mathbb{F}}_p[u,v]}{(u^2-v^2,uv)}}$ to ${\displaystyle \frac{{\mathbb{F}}_p[u,v]}{(u^2,v^2)}}$ by using $u⟼u+v$ and $v\to u-v;$ thus, we obtain $u^2=-v^2,$ which is isomorphic to $R_{a1,5}$ when $-1\in A$ and isomorphic to $R_{a1,6},$ otherwise. However, this is not true when $p=2.$ Moreover, one can deduce that this is true with the ring ${\displaystyle \frac{{\mathbb{F}}_p[u,v]}{(u^2-uv,v^2)}}.$ All such rings will be represented by ${\displaystyle \frac{{\mathbb{F}}_p[u,v]}{(u^2-v^2,uv)}}.$ In summary, there are 4 rings when $l=3$ of the following form:

$$\begin{array}{cc}& \left\{\begin{array}{cc}& {\displaystyle \frac{{\mathbb{F}}_p[u,v]}{(u^3,v^2,uv)}},\hfill \\ & {\displaystyle \frac{{\mathbb{F}}_p[u,v]}{(u^2-v^2,uv)}},p\ne 2,\hfill \\ & {\displaystyle \frac{{\mathbb{F}}_p[u,v]}{(u^2-\alpha v^2,uv)}},\hfill \end{array}\right.\mathrm{if}w=u^2\hfill \\ & {\displaystyle \frac{{\mathbb{F}}_2[u,v]}{(u^2,v^2)}},\mathrm{if}w=uv.\hfill \end{array}$$

Finally, if $l=4=m,$ then R is a chain with the following form:

$${\displaystyle \frac{{\mathbb{F}}_p\left[u\right]}{\left(u^4\right)}}.$$

The last hypothesis follows directly form Theorem 1 and Equation (9). □

Remark 1. 

When $v=u^2$ and $w=u^3,$ then R is a chain of the form ${\displaystyle \frac{{\mathbb{F}}_p\left[u\right]}{\left(u^4\right)}}.$

• Case a2: if $n=2.$ In this case, $R_0={\mathbb{Z}}_{p^2}.$ Based on Equation (6), $1\le k\le 2,$ i.e., $k=1$ or 2 according to ${\sum }_i{t}_i=2,$ which have the following solutions:

  $$\left\{\begin{array}{cc}& k=1\Rightarrow t_1=t=2;\hfill \\ & k=2\Rightarrow t_1=t_2=1.\hfill \end{array}\right.$$

Theorem 3. 

For rings with invariants $p,2,1,1,4,$ the classes are given as follows:

$$\begin{array}{ccccc}{\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{\left(u^2\right)}},& {\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^2-p)}},& {\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^2-p\alpha )}},& {\displaystyle \frac{{\mathbb{Z}}_4\left[u\right]}{(u^2-2u)}},& {\displaystyle \frac{{\mathbb{Z}}_4\left[u\right]}{(u^2-2-2u)}}.\end{array}$$

(10)

Furthermore, they are all Frobenius.

Proof. 

Since $n=2,$ in this case, $R_0={\mathbb{Z}}_{p^2}.$ Moreover, $k=1,$ and hence, R is a singleton ring of the following form [1]:

$$\begin{array}{c}\hfill R={\mathbb{Z}}_{p^2}+u{\mathbb{Z}}_{p^2}.\end{array}$$

In such case, $u^2\in J=(p,u),$ and thus $u^2=p\beta +p{\beta }_{1}u$ since $pu\ne 0,$ where $\beta ,{\beta }_1\in \Gamma \left(1\right).$

$$\begin{array}{c}\hfill R_{a_2,1}={\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^2-p\beta -p{\beta }_{1}u)}}.\end{array}$$

If ${\beta }_1\ne 0,$ then one can complete the sequare when $p\ne 2;$ hence, we have $u^2=p\beta .$ Now, if $\beta =0,$ then $u^2=0$, and R has the form ${\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{\left(u^2\right)}}.$ In the case where $\beta \ne 0,$ the construction of R depends on whether $\beta \in A$ or $\beta \in B.$ This means that R takes the form of ${\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^2-p)}}$ or ${\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^2-p\alpha )}},$ respectively. Thus, when $p\ne 2,$ we obtain the following non-isomorphic classes of rings:

$$\begin{array}{ccc}{\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{\left(u^2\right)}},& {\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^2-p)}},& {\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^2-p\alpha )}}.\end{array}$$

On the other hand, there are two relations when $p=2;$ namely, $u^2=2u$ and $u^2=2+2u.$ When $\beta ={\beta }_1=0,$ then $u^2=0$, and we return the previous case. Therefore, we acquire exactly three copies of such rings under $p\ne 2$ and four classes, otherwise. Therefore, when $p=2,$ we list them as follows:

$$\begin{array}{cccc}{\displaystyle \frac{{\mathbb{Z}}_4\left[u\right]}{\left(u^2\right)}},& {\displaystyle \frac{{\mathbb{Z}}_4\left[u\right]}{(u^2-2)}}& {\displaystyle \frac{{\mathbb{Z}}_4\left[u\right]}{(u^2-2u)}},& {\displaystyle \frac{{\mathbb{Z}}_4\left[u\right]}{(u^2-2-2u)}}.\end{array}$$

(11)

Moreover, it can be easily shown that

$$soc\left(R\right)=\left(pu\right).$$

This finishes the proof. □

Theorem 4. 

Suppose R is a ring with $p,2,1,2,4$ and $v=u^2.$ Then, R takes the form of only one of the following:

$$\begin{array}{cc}\hfill & R^{*}={\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^3-p\beta ,pu)}},\hfill \\ & R={\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^3,pu)}},\hfill \end{array}$$

where $\beta \in {\Gamma }^{*}\left(1\right).$

Proof. 

Since $k=2,$ we have $t_1=t_2=1;$ i.e., $pu=pv=0.$ The direct sum form of R is as follows:

$$R={\mathbb{Z}}_{p^2}+u{\mathbb{Z}}_{p^2}+v{\mathbb{Z}}_{p^2}.$$

(12)

To classify such rings, we first set $v=u^2.$ Thus, $J=\left(u\right)$, and R is a chain with invariants $p,2,1,4,2$ [6]. As $n=2,$ we must have $p\in J^3,$ and thus $u^3=p\beta ,$ where $\beta \in \Gamma \left(1\right).$ If $\beta =0,$ then we have $u^3=0$ and $pu=0.$ However, if $\beta \in {\Gamma }^{*}\left(1\right),$ we obtain $u^3=p\beta$ and $pu=0.$ Therefore, R can be constructed as follows:

$$\begin{array}{cc}\hfill & R^{*}={\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^3-p\beta ,pu)}},\hfill \\ & R={\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^3,pu)}},\hfill \end{array}$$

where $\beta \in {\Gamma }^{*}\left(1\right).$ Again, based on [6], the number of isomorphic classes $N^{*}$ of $R^{*}$ is already computed, and it depends on the gcd of $p-1$ and $3:$

$$N^{*}=(p-1,3).$$

We conclude that there are $(p-1,3)+1$ of rings under the conditions of Case a2 with $k=2$ and $v=u^2.$ □

Corollary 1. 

There are $(p-1,3)+1$ of rings in Theorem 4. Also, their socle is the ideal $\left(p\right);$ thus, they are Frobenius.

We next go further with $v\ne u^2.$ The construction of R is given as follows:

$$R={\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2-p{\beta }_1,v^2-p{\beta }_2,uv-p{\beta }_3,pu,pv)}},$$

(13)

where ${\beta }_1,{\beta }_2$ and ${\beta }_3\in \Gamma \left(1\right).$

Theorem 5. 

Let R be a local ring with parameters $p,2,1,2,4$ with $v\ne u^2.$ Then, there exist 5 copies of R when $p\ne 2$ and 4 rings if $p=2,$ namely:

$$\left\{\begin{array}{cc}& R_{a2,2,1}={\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2,v^2,uv,pu,pv)}},\hfill \\ & R_{a2,2,2}={\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2-p,v^2,uv,pu,pv)}},\hfill \\ & R_{a2,2,3}={\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2-p,v^2-p,uv,pu,pv)}},\hfill \\ & \left\{\begin{array}{cc}& R_{a2,2,4}={\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2-p,v^2-p\alpha ,uv,pu,pv)}},\hfill \\ & R_{a2,2,5}={\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2-p\alpha ,v^2,uv,pu,pv)}},\hfill \end{array}\right.(p\ne 2)\hfill \\ & R_{a2,2,6}={\displaystyle \frac{{\mathbb{Z}}_{2^2}[u,v]}{(u^2,v^2,uv-2,2u,2v)}}.\hfill \end{array}\right.$$

Proof. 

Observe that $u^2=v^2=uv=0$ if $l=2,$. If $l=3,$ then $u^2,v^2,uv\in J^2.$ Let $v^2=p\delta ,$ $u^2=p\beta ,$ and $uv=p\gamma$ in which $\beta \ne \delta =0$ and $\gamma ,\delta ,\beta \in \Gamma \left(1\right).$ In actuality, $uv=p\gamma$ when $\gamma \ne 0$ implies $uv=p$ through the use of $u^{\prime }={\gamma }^{-1}u.$ Additionally, in the case that $u^2=p\beta$ and $uv=p,$ we obtain $uv=0$ by allowing $v⟼u-\beta v.$ Let $uv=p$ and $\beta =\delta =0$ be assumed. If we replace u by $u+v$ and $u-v$ by $v,$ then $u^2=2p,$$v^2=-2p,$ and $uv=0$ as long as $p\ne 2.$ This means that ${\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2,v^2,uv-p,pu,pv)}}\cong {\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2-2p,v^2+2p,uv,pu,pv)}}.$ Therefore, in the case where $p\ne 2,$ $uv$ can always be selected to be $0.$ Finally, we have the situation where $\delta$ and $\beta$ are in $A.$ Given this, $u^2=\gamma v^2,$ where $\gamma =\beta {\delta }^{-1}$ can be found. This is the same as having $u^2=p$ and $v^2=p\beta$, or having $u^2=p\beta$ and $v^2=p.$ Here,

$${\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2-p\beta ,v^2-p\delta ,uv,pu,pv)}}\cong {\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2-p,v^2-\delta p,uv,pu,pv)}}.$$

This means if $\delta \in B,$ we obtain $R=R_{a2,2,3}$, and when $\delta =\alpha ,$ we have $R=R_{a2,2,4}.$ Furthermore, if either $\beta =0$ or $\delta =0,$ then R has the form ${\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2,v^2-p\delta ,uv,pu,pv)}}$ or ${\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2-p\beta ,v^2,uv,pu,pv)}},$ respectively. If we let $u⟼v$ or $v⟼u,$ then we obtain the following:

$${\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2,v^2-p\delta ,uv,pu,pv)}}\cong {\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2-p\beta ,v^2,uv,pu,pv)}}.$$

Note that if $p\ne 2,$ $\beta$ and $\delta$ can not both be 0; otherwise, $l=2.$ If $p=2,$ we have an extra class which is represented by the ring ${\displaystyle \frac{{\mathbb{Z}}_{2^2}[u,v]}{(u^2,v^2,uv-2,2u,2v)}}.$ Therefore, the results follow. □

Corollary 2. 

Let R be as defined in Theorem 5. Then,

$$\begin{array}{c}\hfill \mathit{soc}\left(R_{a2,2,i}\right)=\left\{\begin{array}{cc}(p,u,v),\hfill & \mathrm{if}i=1,\hfill \\ (p,v),\hfill & \mathrm{if}i=2,\hfill \\ \left(p\right),\hfill & \mathrm{if}i=3,4,\hfill \\ (p,v),\hfill & \mathrm{if}i=5,\hfill \\ \left(2\right),\hfill & \mathrm{if}i=6.\hfill \end{array}\right.\end{array}$$

• Case a3: if $n=3.$ Therefore, based on Equation (6), $k=1.$ This leads to $t=t_1=m-n=1.$ Thus, R has the following forms:

  $$\begin{array}{cc}\hfill & {\displaystyle \frac{{\mathbb{Z}}_{p^3}\left[u\right]}{(u^2,pu)}},\hfill \\ \hfill & {\displaystyle \frac{{\mathbb{Z}}_{p^3}\left[u\right]}{(u^2-p^2\beta ,pu)}},\hfill \end{array}$$

  (14)

  where $\beta \in \Gamma \left(1\right).$ In addition,

  $$\mathrm{soc}\left(R\right)=\left(p^2\right)=\left(u^2\right).$$

  There are three rings of the form of R in Equation (14) if $p\ne 2$ and two when $p=2.$ Furthermore, in all cases, R is Frobenius.
• Case a4: if $n=4.$ Since $n=m=4,$

  $$\begin{array}{cc}\hfill & R={\mathbb{Z}}_{p^4},\hfill \\ \hfill & \mathrm{soc}\left(R\right)=\left(p^3\right).\hfill \end{array}$$

  (15)

  There is only one ring of such R, and it is Frobenius.
• Case b: if $r=2,$ we have $m=2,$ and thus $1\le n\le 2.$ Meanwhile, if $n=2,$ then

  $$R_{b,1}=GR(p^2,2).$$

  (16)

  This ring is unique and Frobenius. Now, assume that $n=1,$ then $k=1,$ and hence

  $$R_{b,2}={\displaystyle \frac{{\mathbb{F}}_{p^2}\left[u\right]}{\left(u^2\right)}}.$$

  (17)

  The ring $R_{b,2}$ is a unique and Frobenius ring with soc$\left(R_{b,2}\right)=\left(u\right).$
• Case c: if $r=4,$ then $m=1.$ Thus, there exists a unique copy of $R,$ which is

  $$R_{c,1}={\mathbb{F}}_{p^4}.$$

  (18)

To end this section, we give the number $N\left(P^4\right)$ of local rings with order $p^4.$ We insert this result into the following theorem, and its proof is deduced from Table 1 and Equation (19) below.

Table 1. Local rings of order $p^4$.

Frobenius Rings
Non-Chain	Chain	Non-Frobenius Rings
$R_1={\displaystyle \frac{{\mathbb{Z}}_4\left[u\right]}{(u^2-2u)}}$	$R_8^{*}={\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^3-p\beta ,pu)}}$	${\displaystyle \frac{{\mathbb{F}}_p[u,v]}{(u^3,v^2,uv)}}$
$R_2^{*}={\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2-p,v^2-p\beta ,uv,pu,pv)}}$	$R_9^{*}={\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^2-p\beta )}}$	${\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2,v^2,uv,pu,pv)}}$
$R_3={\displaystyle \frac{{\mathbb{Z}}_4[u,v]}{(u^2,v^2,uv-2,2u,2v)}}$	$R_{10}={\displaystyle \frac{{\mathbb{F}}_p\left[u\right]}{\left(u^4\right)}}$	$R^{*}={\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2-p\beta ,v^2,uv,pu,pv)}}$
$R_4^{*}={\displaystyle \frac{{\mathbb{Z}}_{p^3}\left[u\right]}{(u^2-p^2\beta ,pu)}}$	$R_{11}={\displaystyle \frac{{\mathbb{F}}_{p^2}\left[u\right]}{\left(u^2\right)}}$	${\displaystyle \frac{{\mathbb{F}}_p[u_1,u_2,u_3]}{{(u_1,u_2,u_3)}^2}}$
$R_5^{*}={\displaystyle \frac{{\mathbb{F}}_p[u,v]}{(u^2-\beta v^2,uv)}}$	$R_{12}={\mathbb{Z}}_{p^4}$	${\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^3,pu)}}$
$R_6={\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{\left(u^2\right)}}$	$R_{13}=GR(p^2,2)$	${\displaystyle \frac{{\mathbb{Z}}_{p^3}\left[u\right]}{(u^2,pu)}}$
$R_7={\displaystyle \frac{{\mathbb{F}}_2[u,v]}{(u^2,v^2)}}$	$R_{14}={\mathbb{F}}_{p^4}$
	$R_{15}={\displaystyle \frac{{\mathbb{Z}}_4\left[u\right]}{(u^2-2-2u)}}$

Theorem 6. 

Suppose that R is a local ring with invaraints $p,n,r,m,k$ and of order $p^4.$ Then,

(i) 

The number $N\left(P^4\right)$ of classes of such rings is as follows:

$$N\left(p^4\right)=\left\{\begin{array}{c}21,\mathit{if}p=2,\hfill \\ \\ \left\{\begin{array}{cc}22,\hfill & \mathit{if}p\equiv 1\left(\mathit{mod}3\right),\hfill \\ \\ 24,\hfill & \mathit{if}p\not\equiv 1\left(\mathit{mod}3\right).\hfill \end{array}\right.(p\ne 2)\hfill \end{array}\right.$$

(ii) 

With respect to Frobenius rings, we have $N_F\left(p^4\right)$ as

$$N_F\left(p^4\right)=\left\{\begin{array}{c}15,\mathit{if}p=2,\hfill \\ \\ \left\{\begin{array}{cc}15,\hfill & \mathit{if}p\equiv 1\left(\mathit{mod}3\right),\hfill \\ \\ 17,\hfill & \mathit{if}p\not\equiv 1\left(\mathit{mod}3\right).\hfill \end{array}\right.(p\ne 2)\hfill \end{array}\right.$$

We conclude this section by listing in Table 1 all local rings of order $p^4$ that were characterized in Theorems 1–5. We place them in two columns: Frobenius rings (chain and non-chain) and non-Frobenius rings, noting that the number of non-isomorphic copies $N\left(R^{*}\right)$ of $R^{*}$ is given as follows:

$$N\left(R^{*}\right)=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}p=2,\hfill \\ 2,\hfill & \mathrm{if}p\ne 2.\hfill \end{array}\right.$$

(19)

Finally, we present the lattices of ideals of all local rings with order $p^4$ in Figure 1. It worth noting that the lattices of ideals of local non-chain rings of order $p^4$ are equivalent, while those of chain rings depends on $l.$

Figure 1. Lattices of ideals.

4. MacWilliams Identities

With $p,n,r,m$ as invariants such as $rm=4$, let R be a Frobenius local ring of order $p^4.$ The MacWilliams identities for various versions of R are now computed. It is actually possible to extend these relations to a larger class of finite rings: the class of all Frobenius rings. These identities are fundamental to the study of coding theory because they introduce a crucial link between a code’s dual and weight enumerator.

Next, we restate the following result, which implements a method to produce a generating character $\nu$ for any such ring. We refer to [18] for the proof. Assume that ${\gamma }_i$ is $p^{n_i}$-root of unity and $a_i\le 4$ for each $i.$

Theorem 7 

([18]). Let $\nu :R\to \mathbb{C}.$ Then, there exists a generating character ν and $q\in {\mathbb{Z}}^{+}$ such that

$$\nu \left(\omega \right)={\gamma }_1^{a_1}{\gamma }_2^{a_2}\cdots {\gamma }_q^{a_q}.$$

(20)

Suppose C is a linear code over R with length N. Let us assume that $n_i\left(\mathbf{c}\right)$ is the number of instances of $a_i$ in c $\in C$. Moreover, assume the elements of R are ordered by $R=\{a_1,a_2,a_3,\cdots a_{p^4}\}.$ The complete weight enumerator is then defined as follows:

$$CWE\left(C\right)=\sum _{c\in }\prod _i{a}_i^{n_i\left(\mathbf{c}\right)}.$$

(21)

$$CW{E}_C(x_{a_1},\cdots ,x_{a_{p^4}})={\displaystyle \frac{1}{\mid C^{\perp }\mid }}CW{E}_{C^{\perp }}(A·x_{a_1},\cdots ,x_{a_{p^4}}),$$

(22)

where $A=\left(a_{ij}\right),$ and $a_{ij}=\nu \left(a_i{a}_j\right).$ We define $wt\left(\mathbf{c}\right)=\mid \{i:c_i\ne 0\}\mid .$ The Hamming weight (HW) enumerator and its MacWilliam identity are given as follows:

$$H{W}_C(a,b)=\sum _{c\in C}{a}^{N-wt\left(\mathbf{c}\right)}{b}^{wt\left(\mathbf{c}\right)},$$

(23)

$$H{W}_C(a,b)={\displaystyle \frac{1}{\mid C^{\perp }\mid }}H{W}_{C^{\perp }}(a+(p^4-1)b,a-b).$$

(24)

Suppose that ∼ is defined on R by $x\sim y$ when there is $\omega \in U\left(R\right)$ such that $x=\omega y.$ This means that the group of units of R acts by translation on (the set) R, and it determines an equivalence relation. Let ${\widehat{s}}_1,\cdots ,{\widehat{s}}_q$ be the equivalence classes, and let $n_i^{\prime }\left(\mathbf{c}\right)$ calculate the number of elements of ${\widehat{b}}_i$ that occurred in the codeword c. Hence, SWE is defined as follows:

$$SW{E}_C(x_{{\widehat{s}}_1},\cdots ,x_{{\widehat{s}}_q})=\sum _{\mathbf{c}\in C}\prod _i{x_{{\widehat{s}}_i}}^{n_i^{\prime }\left(\mathbf{c}\right)}.(\mathrm{symmetrized}\mathrm{weight}\mathrm{enumerator})$$

(25)

We introduce the MacWiliams equation for SWE as follows:

$$SW{E}_C(x_{{\widehat{s}}_1},\cdots ,x_{{\widehat{s}}_q})={\displaystyle \frac{1}{\mid C^{\perp }\mid }}SW{E}_{C^{\perp }}(S·(x_{{\widehat{s}}_1},\cdots ,x_{{\widehat{s}}_q})),$$

(26)

where $S=\left(s_{ij}\right)$ and

$$s_{ij}=\sum _{a\in {\widehat{s}}_j}\nu \left(a_{i}a\right).$$

The formulas of $\nu$ for R are shown in Table 2. As we can notice, once $\nu$ is obtained, it is straightforward to obtain the matrix A in (22). Nonetheless, S in Equation (26) requires the determination of the classes ${\widehat{s}}_i.$ While it takes more work, this procedure is essential to building S if we look at the broader case; that is, R is Frobenius local of order $p^4.$ Note that J in this ring is of order $(p-1)p^3$, with $1\le l\le 4$ as its index of nilpotency, and $soc\left(R\right)$ is cyclic of order $p.$ The following lemma provides a comprehensive scheme for determining $s_{ij}$ in a broader case.

Table 2. $\nu$ for ring R.

Ring	$(\mathit{R},+)$	$\mathit{\nu }$
${\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^3-p\beta ,pu)}}$	${\mathbb{Z}}_{p^2}\times {\mathbb{Z}}_p\times {\mathbb{Z}}_p$	$\nu (a+bu+cv)={\zeta }^a{\left(\gamma \right)}^{b+c}$
${\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2-p,v^2-p\beta ,uv,pu,pv)}}$	${\mathbb{Z}}_{p^2}\times {\mathbb{Z}}_p\times {\mathbb{Z}}_p$	$\nu (a+bu+cv)={\zeta }^a{\left(\gamma \right)}^{b+c}$
${\displaystyle \frac{{\mathbb{Z}}_{2^2}[u,v]}{(u^2,v^2,uv-2,2u,2v)}}$	${\mathbb{Z}}_{2^2}\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2$	$\nu (a+bu+cv)={\zeta }^a{(-1)}^{b+c}$
${\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^2-p\beta )}}$	${\mathbb{Z}}_{p^2}\times {\mathbb{Z}}_{p^2}$	$\nu (a+bu)={\zeta }^{a+b}$
${\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{\left(u^2\right)}}$	${\mathbb{Z}}_{p^2}\times {\mathbb{Z}}_{p^2}$	$\nu (a+bu)={\zeta }^{a+b}$
${\displaystyle \frac{{\mathbb{Z}}_4\left[u\right]}{(u^2-2-2u)}}$	${\mathbb{Z}}_4\times {\mathbb{Z}}_4$	$\nu (a+bu)={\zeta }^{a+b}$
${\displaystyle \frac{{\mathbb{Z}}_4\left[u\right]}{(u^2-2u)}}$	${\mathbb{Z}}_{p^2}\times {\mathbb{Z}}_{p^2}$	$\nu (a+bu)={\zeta }^{a+b}$
$GR(p^2,2)$	${\mathbb{Z}}_{p^2}\times {\mathbb{Z}}_{p^2}$	$\nu (a+bu)={\zeta }^{a+b}$
${\displaystyle \frac{{\mathbb{F}}_p\left[u\right]}{\left(u^4\right)}}$	${\mathbb{Z}}_p\times {\mathbb{Z}}_p\times {\mathbb{Z}}_p\times {\mathbb{Z}}_p$	$\nu (a+bu+c{u}^2+d{u}^3)={\left(\gamma \right)}^{a+b+c+d}$
${\displaystyle \frac{{\mathbb{F}}_{p^2}\left[u\right]}{\left(u^2\right)}}$	${\mathbb{Z}}_p\times {\mathbb{Z}}_p\times {\mathbb{Z}}_p\times {\mathbb{Z}}_p$	$\nu (a+bu+c{u}^2+d{u}^3)={\left(\gamma \right)}^{a+b+c+d}$
${\displaystyle \frac{{\mathbb{F}}_2[u,v]}{(u^2,v^2)}}$	${\mathbb{Z}}_p\times {\mathbb{Z}}_p\times {\mathbb{Z}}_p\times {\mathbb{Z}}_p$	$\nu (a+bu+c{u}^2+d{u}^3)={\left(\gamma \right)}^{a+b+c+d}$
${\displaystyle \frac{{\mathbb{F}}_p[u,v]}{(u^2-\beta v^2,uv)}}$	${\mathbb{Z}}_p\times {\mathbb{Z}}_p\times {\mathbb{Z}}_p\times {\mathbb{Z}}_p$	$\nu (a+bu+c{u}^2+d{u}^3)={\left(\gamma \right)}^{a+b+c+d}$
${\mathbb{F}}_{p^4}$	${\mathbb{Z}}_p\times {\mathbb{Z}}_p\times {\mathbb{Z}}_p\times {\mathbb{Z}}_p$	$\nu (a+bu+c{u}^2+d{u}^3)={\left(\gamma \right)}^{a+b+c+d}$
${\displaystyle \frac{{\mathbb{Z}}_{p^3}\left[u\right]}{(u^2-p^2\beta ,pu)}}$	${\mathbb{Z}}_{p^3}\times {\mathbb{Z}}_p$	$\nu (a+bu)={\xi }^a{\gamma }^b$
${\mathbb{Z}}_{p^4}$	${\mathbb{Z}}_{p^4}$	$\nu \left(a\right)={\delta }^a$

In the table, the symbols $\gamma ,\zeta ,\xi$, and $\delta$ are $p^i$-roots of unity, where $i=1,2,3,4,$ respectively.

Lemma 1. 

Suppose soc$\left(R\right)=\left(\lambda \right),$ where $0\ne \lambda \in R.$ Then, the classes ${\widehat{b}}_i$ for R are given by the following formula:

$$s_{ij}=\left\{\begin{array}{cc}\mid \widehat{s_j}\mid ,\hfill & \mathit{if}{a}_i\widehat{s_j}=\left\{0\right\},\hfill \\ 0,\hfill & \mathit{if}\lambda \notin a_i\widehat{s_j},\hfill \\ (-1){\displaystyle \frac{1}{p^r-1}}\mid \widehat{s_j}\mid ,\hfill & \mathit{if}\lambda \in a_i\widehat{s_j}.\hfill \end{array}\right.$$

(27)

Proof. 

Suppose that $a_i\widehat{s_j}=\left\{0\right\},$ then $s_{ij}={\sum }_{b\in \widehat{s_j}}\nu \left(a_{i}b\right)={\sum }_{b\in \widehat{s_j}}0=\mid \widehat{s_j}\mid$. For the other cases, assume that $a_i\widehat{s_j}\ne \left\{0\right\}.$ First, let $\lambda \in a_i\widehat{s_j}.$ As soc$\left(R\right)=\left(\lambda \right),$ then $\lambda =\beta y,$ where $\beta \in {\Gamma }^{*}\left(r\right)$ and $y\in \widehat{s_j}$ are representative of $\widehat{s_j}.$ Now, suppose also that $x\in a_i\widehat{s_j},$ then $x=a_i{y}^{\prime }$ for some $y^{\prime }$ in $\widehat{s_j}.$ It follows that $x=\gamma \lambda ,$ where $\gamma \in {\Gamma }^{*}\left(r\right).$ This means that all elements of $a_i\widehat{s_j}$ are of the form $\beta \lambda ,$ which can be interpreted as the set $a_i\widehat{s_j}$ being copies of soc$\left(R\right).$ Thus,

$$s_{ij}=N_0\sum _{\beta \in {\Gamma }^{*}\left(1\right)}{e}^{{\displaystyle \frac{\left(2\pi i\right)\beta }{p}}}.$$

However, we have the following formula for complex numbers:

$$1+\sum _{j=1}^{p-1}{e}^{{\displaystyle \frac{\left(2\pi i\right)j}{p}}}=0.$$

(28)

The positive $N_0$ reflects the number of copies of soc$\left(R\right)$, which is precisely $N_0={\displaystyle \frac{1}{p^r-1}}\mid \widehat{s_j}\mid .$ Therefore,

$$s_{ij}=(-1){\displaystyle \frac{1}{p^r-1}}\mid \widehat{s_j}\mid .$$

The last case of the proof can be performed similarly, noting that every element of $a_i\widehat{s_j}$ can be expressed as $x+\beta \lambda ,$ where $\beta \in \Gamma \left(r\right).$ As $\nu (x+\beta \lambda )=\nu \left(x\right)\dot{\nu }\left(\beta \lambda \right),$ then, for a fixed $x,$${\sum }_{\beta \in \Gamma \left(r\right)}\nu \left(x\right)\nu \left(\beta \lambda \right)=\nu \left(x\right){\sum }_{\beta \in \Gamma \left(r\right)}\nu \left(\beta \lambda \right).$ In such case,

$$s_{ij}=\sum _{\beta \in \Gamma \left(r\right)}\sum _x\nu \left(x\right)\nu \left(\beta \lambda \right).$$

Hence, based on Equation (28), ${\sum }_{\beta \in \Gamma \left(r\right)}\nu \left(\beta \lambda \right)=0.$ Thus, we conclude with the result, i.e., $s_{ij}=0.$ □

If R is a chain, then one can obtain the sets of ${\widehat{s}}_i$ as follows.

$$\begin{array}{ccc}\hfill \left\{\begin{array}{cc}& {\widehat{b}}_1=\left\{0\right\},\hfill \\ & {\widehat{b}}_2=U\left(R\right)=F_{p^4}^{*},\hfill \end{array}\right.\mathrm{if}l=1;& \left\{\begin{array}{cc}& {\widehat{b}}_1=\left\{0\right\},\hfill \\ & {\widehat{b}}_2=U\left(R\right),\hfill \\ & {\widehat{b}}_3=J\setminus \left\{0\right\}.\hfill \end{array}\right.\mathrm{if}l=2;\hfill & \hfill \left\{\begin{array}{cc}& {\widehat{b}}_1=\left\{0\right\},\hfill \\ & {\widehat{b}}_2=U\left(R\right),\hfill \\ & {\widehat{b}}_3=J\setminus J^2,\hfill \\ & {\widehat{b}}_4=J^2\setminus J^3,\hfill \\ & {\widehat{b}}_5=\mathrm{soc}\left(R\right)\setminus \left\{0\right\}.\hfill \end{array}\right.\mathrm{if}l=4.\end{array}$$

Theorem 8. 

Suppose that R is a chain of order $p^4.$ Then,

$$S\left(l\right)=\left\{\begin{array}{c}\left(\begin{array}{cc}1& p^4-1\\ 1& -1\end{array}\right),\mathit{if}l=1\\ \left(\begin{array}{ccc}1& (p^2-1)p^2& p^2-1\\ 1& 0& -1\\ 1& -p^2& p^2-1\end{array}\right),\mathit{if}l=2\\ \left(\begin{array}{ccccc}1& (p-1)p^3& (p-1)p^2& (p-1)p& p-1\\ 1& 0& 0& 0& -1\\ 1& 0& 0& -p& p-1\\ 1& 0& -p^2& (p-1)p& p-1\\ 1& -p^3& (p-1)p^2& (p-1)p& p-1\end{array}\right),\mathit{if}l=4.\end{array}\right.$$

Proof. 

For $s_{1j}$ and $s_{j1},$ the values are direct from Lemma 1. As of $l=1,$ soc$\left(R\right)=\left(0\right)$ and $s_{22}=-1$ based on Equation (28). If $l=2,$$\lambda =u$ or $p,$ thus $\lambda \notin a_2{\widehat{s}}_2,$ where $a_2=1.$ Therefore, $s_{22}=0.$ Furthermore, $\lambda \in a_3{\widehat{s}}_2,$ then $s_{32}=-p^2$ using the same lemma, and also $\left\{0\right\}=a_3{\widehat{s}}_3$, which means that $s_{33}=\mid {\widehat{s}}_3\mid .$ Lastly, assume $l=4.$ Note that $\lambda \in a_i\widehat{s_j},$ where $(i,j)=(3,4),(4,3),(5,2).$ Thus, $s_{ij}={\displaystyle \frac{-1}{p-1}}\mid \widehat{s_j}\mid$ from Lemma 1. The other case of $s_{ij}$ is $0,$ where $(i,j)=(2,2),(3,2),(4,2),(2,3)$, and $(3,4)$ because $\lambda \notin a_i\widehat{s_j}.$ Meanwhile, the values of $s_{44},s_{3,5},s_{4,5},s_{5,4}$, and $s_{55}$ are equal to $\mid \widehat{s_j}\mid$, since in all these cases, we have $a_i\widehat{s_j}=0.$ □

When R is not a chain, we list all the equivalence classes ${\widehat{s}}_i.$ The determination of ${\widehat{s}}_i$ relies on the lattices of ideals of R when it is not a chain; please see Figure 1.

1.

When $J=(p,u,v),$

$$\begin{array}{ccc}{\widehat{s}}_1=\left\{0\right\},& {\widehat{s}}_2=U\left(R\right),& {\widehat{s}}_3=\left(u\right)\setminus \mathrm{soc}\left(R\right),\\ \mid {\widehat{s}}_1\mid =1& \mid {\widehat{s}}_2\mid =(p-1)p^3& \mid {\widehat{s}}_3\mid =(p-1)p\\ {\widehat{s}}_4=\left(v\right)\setminus \mathrm{soc}\left(R\right),& {\widehat{s}}_5=(u+v)\setminus \mathrm{soc}\left(R\right),& {\widehat{s}}_6=\mathrm{soc}\left(R\right)\setminus \left\{0\right\}\\ \mid {\widehat{s}}_4\mid =(p-1)p& \mid {\widehat{s}}_5\mid =(p-1)p& \mid {\widehat{s}}_6\mid =p-1.\end{array}$$

(29)

2.

When $J=(p,u),$

$$\begin{array}{ccc}{\widehat{s}}_1=\left\{0\right\},& {\widehat{s}}_2=U\left(R\right),& {\widehat{s}}_3=\left(u\right)\setminus \mathrm{soc}\left(R\right),\\ \mid {\widehat{s}}_1\mid =1& \mid {\widehat{s}}_2\mid =(p-1)p^3& \mid {\widehat{s}}_3\mid =(p-1)p\\ {\widehat{s}}_4=\left(p\right)\setminus \mathrm{soc}\left(R\right),& {\widehat{s}}_5=(u+p)\setminus \mathrm{soc}\left(R\right),& {\widehat{s}}_6=\mathrm{soc}\left(R\right)\setminus \left\{0\right\}\\ \mid {\widehat{s}}_4\mid =(p-1)p& \mid {\widehat{s}}_5\mid =(p-1)p& \mid {\widehat{s}}_6\mid =p-1.\end{array}$$

(30)

For simplicity, we denote $S_1$ and $S_2$ as follows:

$$\begin{array}{cc}& S_1=\left(\begin{array}{cccccc}1& (p-1)p^3& (p-1)p& (p-1)p& (p-1)p& p-1\\ 1& 0& 0& 0& 0& -1\\ 1& 0& ϵ& -p& -p& p-1\\ 1& 0& -p& (p-1)p& -p& p-1\\ 1& 0& -p& -p& {ϵ}_{\beta }& p-1\\ 1& -p^3& (p-1)p& (p-1)p& (p-1)p& p-1\end{array}\right),\hfill \\ \hfill \mathrm{where}\\ & \begin{array}{cc}\hfill ϵ=\left\{\begin{array}{cc}-p,\hfill & \mathrm{if}p=2,\hfill \\ p(p-1),\hfill & \mathrm{if}p\ne 2\hfill \end{array}\right.,& {ϵ}_{\beta }=\left\{\begin{array}{cc}-p,\hfill & \mathrm{if}\beta \ne -1,\hfill \\ p(p-1),\hfill & \mathrm{if}\beta =-1.\hfill \end{array}\right.\hfill \end{array}\hfill \\ \\ & S_2=\left(\begin{array}{cccccc}1& (p-1)p^3& (p-1)p& (p-1)p& (p-1)p& p-1\\ 1& 0& 0& 0& 0& -1\\ 1& 0& -p& (p-1)p& -p& p-1\\ 1& 0& (p-1)p& -p& -p& p-1\\ 1& 0& -p& -p& {ϵ}_{\beta }& p-1\\ 1& -p^3& (p-1)p& (p-1)p& (p-1)p& p-1\end{array}\right).\hfill \end{array}$$

Note that the entries of $S_1$ and $S_2$ are obtained from Equation (27) in Lemma 1 and $\mid {\widehat{s}}_i\mid$ given above in Equations (29) and (30).

Theorem 9. 

Suppose that R is non-chain Frobenius of order $p^4.$ Then, S takes the from of $S_1$ or $S_2.$

Proof. 

The proof depends heavily on Lemma 1, which means in order to obtain the entries $s_{ij}$ of the matrix $S,$ it is enough to investigate the subsets $a_i{\widehat{s}}_j:$ Either $0\in a_i{\widehat{s}}_j,$$\lambda \in a_i{\widehat{s}}_j$ or $\lambda \notin a_i{\widehat{s}}_j\ne \left\{0\right\}.$ Let us first consider the classes ${\widehat{s}}_j$ and their sizes $\mid {\widehat{s}}_j\mid$ as mentioned above. Suppose also soc$\left(R\right)=\left(\lambda \right),$ $a_1=0, a_2=1, a_3=u, a_4=p\mathrm{or}v, a_5=u+p\mathrm{or}u+v, a_6=\lambda .$ For all $i,$ we have $a_i{\widehat{s}}_1=\left\{0\right\}$. Then, $s_{i1}=1.$ Next, observe the following:

$$\left\{\begin{array}{cc}0\in a_1{\widehat{s}}_i,\hfill & \mathrm{if}1\le i\le 6,\hfill \\ 0\in a_6{\widehat{s}}_i,\hfill & \mathrm{if}3\le i\le 6,\hfill \\ 0\in a_i{\widehat{s}}_6,\hfill & \mathrm{if}2\le i\le 5.\hfill \end{array}\right.$$

Thus, all elements of such subsets are $0,$ and based on Lemma 1, we obtain

$$s_{1i}=s_{6i}=s_{i6}=\mid {\widehat{s}}_i\mid .$$

On the other hand, one can see that $\lambda \notin a_2\widehat{s_i}\cup a_i\widehat{s_2},$ where $2\le i\le 5.$ Thus, for the same values of the index $i,$ we obtain

$$s_{2i}=0=s_{i2}$$

with regard to the remaining cases $a_i{\widehat{s}}_j,$ where $3\le i,j\le 5.$ First, note that $\lambda$ is in all $a_5{\widehat{s}}_3,a_5{\widehat{s}}_4,a_3{\widehat{s}}_5$, and $a_4{\widehat{s}}_5.$ Hence, based on the same lemma,

$$s_{ij}={\displaystyle \frac{-1}{p-1}}\left(p(p-1)\right)=-p.$$

The value of $s_{55}$ depends on $\beta .$ We know that $a_5=(u+v)$ or $a_5=(u+p)$ and ${\widehat{s}}_5=(u+v)\setminus \mathrm{soc}\left(R\right)$ or ${\widehat{s}}_5=(u+p)\setminus \mathrm{soc}\left(R\right).$ Then, in any case of R (non-chain ring), we have $\lambda (\beta +1)\in a_5{\widehat{s}}_5.$ If $\beta =-1,$ then $0\in a_5{\widehat{s}}_5,$ and thus $s_{55}=p(p-1),$ while if $\beta \ne -1,$ then $\lambda \in a_5{\widehat{s}}_5;$ hence, $s_{55}=-p.$ In other words,

$$s_{55}={ϵ}_{\beta },$$

where ${ϵ}_{\beta }$ is defined above. We notice that $s_{33}=s_{44}$ because $\left(u^2\right)=\left(v^2\right)$ or $\left(u^2\right)=\left(p^2\right)$, except for ${\displaystyle \frac{{\mathbb{Z}}_4}{(u^2-2u)}},$ where $s_{33}=-2$ and $s_{44}=2.$ Furthermore, $s_{34}=s_{43}$ for all rings, since $a_3{\widehat{s}}_4=a_4{\widehat{s}}_3.$ To conclude, we have two different submatrices of size $3\times 3$ of the following form:

$$\begin{array}{cc}\hfill \left(\begin{array}{ccc}ϵ& -p& -p\\ -p& p(p-1)& -p\\ -p& -p& {ϵ}_{\beta }\end{array}\right),& \left(\begin{array}{ccc}-p& p(p-1)& -p\\ p(p-1)& -p& -p\\ -p& -p& {ϵ}_{\beta }\end{array}\right).\hfill \end{array}$$

Therefore, we obtain $S_1$ and $S_2$ for each R non-chain Frobenius ring of order $p^4$ as desired. □

Before ending this section, we introduce Table 3 to present all matrices S and ${\widehat{s}}_i$ corresponding to rings $R.$ For clarification, we then move on to a numerical demonstration of these computations and their steps, for example, of a ring with order $3^4=81;$ i.e., $p=3.$ We will first concentrate on comprehending $\widehat{s_i}$ under ∼ before building $S.$

Table 3. S and ${\widehat{s}}_i$ for Frobenius local rings of order $p^4$.

Ring	soc$\left(\mathit{R}\right)$	$\mathit{S}$	${\widehat{\mathit{s}}}_{\mathit{i}}$
${\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^3-p\beta ,pu)}}$	$\left(p\right)$	$S\left(4\right)$	$\left(0\right),U\left(R\right),J\setminus J^2,J^2\setminus J^3,\mathrm{soc}\left(R\right)\setminus \left\{0\right\}$
${\displaystyle \frac{{\mathbb{Z}}_{p^2}[u,v]}{(u^2-p,v^2-p\beta ,uv,pu,pv)}}$	$\left(p\right)$	$S_2$	$\left(0\right),U\left(R\right),\left(u\right)\setminus \mathrm{soc}\left(R\right),\left(v\right)\setminus \mathrm{soc}\left(R\right),(u+v)\setminus \mathrm{soc}\left(R\right),\mathrm{soc}\left(R\right)\setminus \left\{0\right\}$
${\displaystyle \frac{{\mathbb{Z}}_{2^2}[u,v]}{(u^2,v^2,uv-2,2u,2v)}}$	$\left(2\right)$	$S_1$	$\left(0\right),U\left(R\right),\left(u\right)\setminus \mathrm{soc}\left(R\right),\left(v\right)\setminus \mathrm{soc}\left(R\right),(u+v)\setminus \mathrm{soc}\left(R\right),\mathrm{soc}\left(R\right)\setminus \left\{0\right\}$
${\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{(u^2-p\beta )}}$	$\left(u^3\right)$	$S\left(4\right)$	$\left(0\right),U\left(R\right),J\setminus J^2,J^2\setminus J^3,\mathrm{soc}\left(R\right)\setminus \left\{0\right\}$
${\displaystyle \frac{{\mathbb{Z}}_{p^2}\left[u\right]}{\left(u^2\right)}}$	$\left(pu\right)$	$S_1$	$\left(0\right),U\left(R\right),\left(u\right)\setminus \mathrm{soc}\left(R\right),\left(p\right)\setminus \mathrm{soc}\left(R\right),(u+p)\setminus \mathrm{soc}\left(R\right),\mathrm{soc}\left(R\right)\setminus \left\{0\right\}$
${\displaystyle \frac{{\mathbb{Z}}_4\left[u\right]}{(u^2-2-2u)}}$	$\left(u^3\right)$	$S\left(4\right)$	$\left(0\right),U\left(R\right),J\setminus J^2,J^2\setminus J^3,\mathrm{soc}\left(R\right)\setminus \left\{0\right\}$
${\displaystyle \frac{{\mathbb{Z}}_4\left[u\right]}{(u^2-2u)}}$	$\left(u^2\right)$	$S_2$	$\left(0\right),U\left(R\right),\left(u\right)\setminus \mathrm{soc}\left(R\right),\left(p\right)\setminus \mathrm{soc}\left(R\right),(u+p)\setminus \mathrm{soc}\left(R\right),\mathrm{soc}\left(R\right)\setminus \left\{0\right\}$
$GR(p^2,2)$	$\left(p\right)$	$S\left(2\right)$	$\left(0\right),U\left(R\right),J\setminus \left\{0\right\}$
${\displaystyle \frac{{\mathbb{F}}_p\left[u\right]}{\left(u^4\right)}}$	$\left(u^3\right)$	$S\left(4\right)$	$\left(0\right),U\left(R\right),J\setminus J^2,J^2\setminus J^3,\mathrm{soc}\left(R\right)\setminus \left\{0\right\}$
${\displaystyle \frac{{\mathbb{F}}_{p^2}\left[u\right]}{\left(u^2\right)}}$	$\left(u\right)$	$S\left(2\right)$	$\left(0\right),U\left(R\right),J\setminus \left\{0\right\}$
${\displaystyle \frac{{\mathbb{F}}_2[u,v]}{(u^2,v^2)}}$	$\left(uv\right)$	$S_1$	$\left(0\right),U\left(R\right),\left(u\right)\setminus \mathrm{soc}\left(R\right),\left(v\right)\setminus \mathrm{soc}\left(R\right),(u+v)\setminus \mathrm{soc}\left(R\right),\mathrm{soc}\left(R\right)\setminus \left\{0\right\}$
${\displaystyle \frac{{\mathbb{F}}_p[u,v]}{(u^2-\beta v^2,uv)}}$	$\left(u^2\right)$	$S_2$	$\left(0\right),U\left(R\right),\left(u\right)\setminus \mathrm{soc}\left(R\right),\left(v\right)\setminus \mathrm{soc}\left(R\right),(u+v)\setminus \mathrm{soc}\left(R\right),\mathrm{soc}\left(R\right)\setminus \left\{0\right\}$
${\mathbb{F}}_{p^4}$	$\left(0\right)$	$S\left(1\right)$	$\left(0\right),U\left(R\right)$
${\displaystyle \frac{{\mathbb{Z}}_{p^3}\left[u\right]}{(u^2-p^2\beta ,pu)}}$	$\left(p^2\right)$	$S_2$	$\left(0\right),U\left(R\right),\left(u\right)\setminus \mathrm{soc}\left(R\right),\left(p\right)\setminus \mathrm{soc}\left(R\right),(u+p)\setminus \mathrm{soc}\left(R\right),\mathrm{soc}\left(R\right)\setminus \left\{0\right\}$
${\mathbb{Z}}_{p^4}$	$\left(p^3\right)$	$S\left(4\right)$	$\left(0\right),U\left(R\right),J\setminus J^2,J^2\setminus J^3,\mathrm{soc}\left(R\right)\setminus \left\{0\right\}$

Example 1. 

We now construct S for $R={\displaystyle \frac{{\mathbb{Z}}_{27}\left[u\right]}{(u^2-9,3u)}}.$ Let us assume that the elements of R are ordered as follows: if $i,j\in {\mathbb{Z}}_{27},$ then i comes before j if $i<j$ as an integer, and $i+u$ comes before $j+u$ if i precedes $j.$ The equivalence classes are therefore as follows:

$$\left\{\begin{array}{cc}& \widehat{s_1}=\left\{0\right\}{a}_1=0,\hfill \\ & {\widehat{s}}_2=U\left(R\right)=\{i,i+ju:(i,3)=1\},a_2=1,\hfill \\ & \widehat{s_3}=\left(u\right)\setminus \left(9\right),a_3=u,\hfill \\ & \widehat{s_4}=\left(3\right)\setminus \left(9\right),a_4=3,\hfill \\ & \widehat{s_5}=(u+3)\setminus \left(p^2\right),a_5=u+3,\hfill \\ & \widehat{s_6}=soc\left(R\right)\setminus \left\{0\right\}=J^2\setminus \left\{0\right\}=\left(9\right),a_6=9.\hfill \end{array}\right.$$

Note that $I=(u^2-9,3u)$ which means that R is not a chain. Moreover, $\beta =1$, and since $p=3,$ then $\beta \ne -1.$ Thus, ${ϵ}_{\beta }=-p=-3.$ Therefore, by using Theorem 9, and after making the necessary computations, S takes the following form:

$$S_2=\left(\begin{array}{cccccc}1& 54& 6& 6& 6& 2\\ 1& 0& 0& 0& 0& -1\\ 1& 0& -3& 6& -3& 1\\ 1& 0& 6& -3& -3& 1\\ 1& 0& -3& -3& -3& 1\\ 1& -27& 6& 6& 6& 1\end{array}\right).$$

Remark 2. 

The matrix S can be obtained for R when $\mid R\mid >p^4,$ but the computations will be tedious.

Remark 3. 

Based on the above discussion, the matrices S for chain rings that have same l are equivalent.

5. Generator Matrices

This section finds matrices G that produce linear codes over $R.$ Generating a standard form generator matrix for a code is a fundamental method in coding theory. The process of creating a generator matrix, a minimal set of generators from which the code size can be computed, is simple when dealing with codes over chain rings. It is much more difficult to find a minimal set of generators for codes over local rings that are not chain rings. It is always possible to find such a minimal set of generators, but unlike in the case of chain rings, this does not always make it easy to determine the code size from such a generator matrix. In this regard, little work have been done. The Frobenius local rings that have been investigated are those of order 16 and $32;$ that is, when $p=2.$ The generator matrices of linear codes over rings of order 16 are considered in [16], while the ring ${\displaystyle \frac{{\mathbb{Z}}_4\left[u\right]}{(u^2-p^3\beta ,pu)}}$ is thoroughly studied in [18].

If R is any chain rings with index $l=1,2$ or $4,$ then $G_1,G_2$ or $G_3,$ respectively, are given as follows:

$$\begin{array}{cc}& G_1=\left(\begin{array}{cc}{I}_{t_0}& H_{0,1}\end{array}\right),\hfill \\ & G_2=\left(\begin{array}{ccc}{I}_{t_0}& H_{0,1}& H_{0,2}\\ 0& u{I}_{t_1}& u{H}_{1,2}\end{array}\right),\hfill \\ & G_3=\left(\begin{array}{ccccc}{I}_{t_0}& H_{0,1}& H_{0,2}& H_{0,3}& H_{0,4}\\ 0& u{I}_{t_1}& u{H}_{1,2}& u{H}_{1,3}& u{H}_{1,4}\\ 0& 0& u^2{I}_{t_2}& u^2{H}_{2,2}& u^2{H}_{2,3}\\ 0& 0& 0& u^3{I}_{t_3}& u^3{H}_{3,2}\end{array}\right),\hfill \end{array}$$

where $H_{ij}$s are matrices over R with different sizes. A code with a generator matrix of this form is said to have type $\left\{t_0,t_1,...,t_{l-1}\right\},$ where $t_i$s are the sizes of the matrices $I_{t_i}.$ A code C with such generator matrix has an immediate size as follows:

$$\mid C\mid ={\left(p^r\right)}^{{\sum }_{i=0}^{l-1}(l-i)t_i}.$$

(31)

Now, R will denote Frobenius non-chain rings. First, we provide a precise definition of a generator matrix in this context. Keep in mind that the classical case of codes over fields is being generalized here. To demonstrate the challenges of creating a matrix and the limitations of this kind of matrix, we have concluded this work for a practical canonical form for codes over local Frobenius rings, and eventually, for Frobenius rings.

Definition 1. 

If the vectors with coefficients from J cannot be combined linearly in a nontrivial way to equal the zero vector, we refer to the vectors ${\mathbf{v}}_1,\cdots ,{\mathbf{v}}_e$ as modularly independent. When the rows of G independently produce the code C, then G is a generator matrix over the ring R.

Figure 1 above illustrates lattices of ideals of $R.$ As $\mid J\mid =p^{(m-1)r},$$\mid \left(p\right)\mid =\mid \left(v\right)\mid =\mid \left(u\right)\mid =\mid (u+p)\mid =\mid (v+u)\mid =p^{(m-2)r}$, and $\mid \mathrm{soc}\left(R\right)\mid =p.$ Therefore, the goal of this section is to produce a collection of independent modular vectors that function as a code’s generator matrix’s rows. A complete description of the structure of G is given by the following theorem.

Theorem 10. 

Let C be a linear code with length N over $R.$ Thus,

where $T_{ij}$ are matrices of various sizes and $w=v$ or $p.$

Proof. 

Let G be a matrix such that the row $r_i$s of the matrix produce C as an R-module. Every column containing a unit is moved to the left of $G.$ We obtain a matrix of the following form via row reduction on those columns:

$$G=\left(\begin{array}{cc}{I}_{t_0}& *\\ 0& T\end{array}\right)$$

Now, not every element in T is a unit. To transform the matrix into the next form, we shift all columns containing elements of $J=(w,u)$ to the left once more and apply the primary row operations.

$$G=\left(\begin{array}{ccc}{I}_{t_0}& *& *\\ 0& u& *\\ 0& w& *\\ 0& 0& T_1\end{array}\right).$$

We continue with this algorithm, making sure that the matrix $T_1$ is created by placing elements in columns such that they form a pair $(w,u).$ We keep doing this until the matrix takes on the form that we want.

Only one of (w), (u), or (w + u) is represented by the elements of the matrix T₂’s columns. We will now move over to the matrix T₂. The three ideals are (u), (w), and (w + u). We choose a particular ordering for each ideal to produce one expression of the matrix. The matrix will be constructed using this selected order consistently. Assuming α is a unit of R, we proceed as follows: columns with entries of the form uβ, columns with elements of the form (w)v, and finally, we address columns that take the form (u + w)v. We carry out row reduction in the standard way in each step. Observe that both (w) and (u + w) contain the socle ideal. Consequently, we redo similar process with soc(R) = (λ), since the remaining column entries will come from (λ).

Finally, every component of $T_3$ originates from the ideal that $\lambda$ generates. We obtain a matrix that precisely corresponds to the desired form by removing any rows that contain only zeros and completing one last row reduction round. □

We present an example showing the steps of our earlier algorithm described in Theorem 10.

Example 2. 

Suppose that C is a linear code with length $N=3$ over $R={\displaystyle \frac{{\mathbb{F}}_p[u,v]}{(u^2-v^2,uv)}}$ and generated by the vectors $(0,\beta ,u),(0,u,v),(0,v,u)$ and $(0,0,v);$ i.e., $C=⟨(0,\beta ,u),(0,u,v),(0,v,u),(0,0,v)⟩,$ where β is a unit of $R.$ Let $G_0$ be a matrix constructed by the vectors generating C as its rows. Therefore,

$$G_0=\left(\begin{array}{ccc}u& \beta & 0\\ 0& u& v\\ 0& v& u\\ 0& 0& v\end{array}\right).$$

Step 1. Move column 2, $c_2$, to the left:

$$\left(\begin{array}{ccc}\beta & u& 0\\ u& 0& v\\ v& 0& u\\ 0& 0& v\end{array}\right).$$

Step 2. Carry out row reductions as ${\beta }^{-1}u{r}_1-r_2$ and ${\beta }^{-1}v{r}_1-r_3.$ Since $uv=0,$

$$\left(\begin{array}{ccc}\beta & u& 0\\ 0& {\beta }^{-1}{u}^2& v\\ 0& 0& u\\ 0& 0& v\end{array}\right).$$

Step 3. Move $c_3$ to the left:

$$\left(\begin{array}{ccc}\beta & 0& u\\ 0& v& {\beta }^{-1}{u}^2\\ 0& u& 0\\ 0& v& 0\end{array}\right).$$

Step 4. Apply the row reduction by $r_2-r_4,$ noting that $u^2=v^2.$ Therefore:

$$G=\left(\begin{array}{ccc}\beta & 0& u\\ 0& v& {\beta }^{-1}{u}^2\\ 0& u& 0\\ 0& 0& {\beta }^{-1}{u}^2\end{array}\right).$$

Then, G is the desired matrix with $t_0=t_1=t_2=t_3=1.$ The size of G is $4\times 3.$ Note that $t_0+2t_1+t_3=4$ is the number of rows, and $t_0+t_1+t_3=3$ is the number of columns.

Remark 4. 

The size of G in Theorem 10 is $f\times e,$ where $f=t_0+2t_1+\cdots +t_5$ and $e=t_0+t_1+\cdots +t_5+e_1$, and $e_1$ is the number of columns of the matrix $T_{57}.$

Example 3 shows that a minimal set of generators may not exist for C over a (non-chain) Frobenius singleton local, which makes the code more complicated. Stated differently, it highlights the differences in coding over chain rings and non-chain rings.

Example 3. 

If G is a matrix of C over $R={\displaystyle \frac{{\mathbb{Z}}_8\left[u\right]}{(u^2-4,2u)}}$ of the following form:

$$\left(\begin{array}{cc}2& u\\ u& 0\\ 0& 2\end{array}\right).$$

Assuming that $M_1$ is the R-submodule produced by rows $r_1$ and $r_2$ of $G,$ and $M_2$ is the R-submodule generated by $r_3$ of $G,$

$$M_1\cap M_2\ne \varphi .$$

Noting that $u^2=4$ and $2u=0$ in R, then $(0,4)\in M_1\cap M_2$ since $(0,4)=u(2,u)+u(u,0)$, and also, $(0,4)=2(0,2).$ This indicates that the R-submodule C cannot be reduced.

Example 4. 

To have C over $R={\displaystyle \frac{{\mathbb{Z}}_8\left[u\right]}{(u^2-4,2u)}}$ of order $16,$ set $N=1$ with $C=(2,u).$ Then, $\mid C\mid =16.$ Meanwhile, to construct C with size $32,$ suppose $C=(\mathit{w},\mathit{d})$ with $N=2,$$\mathit{w}=(2,u)$, and $\mathit{d}=(u,2).$ This implies that $\mid C\mid =32.$ Take $N=4,$ $\mathit{w}=(2,0,u,2)$, and $\mathit{d}=(u,2,0,0).$ Hence, $\mid C\mid =2^8.$ Therefore,

$$C\cong \left(\mathit{w}\right)\oplus \left(\mathit{d}\right).$$

Example 5. 

Suppose that G for C with length $N=2$ over ${\displaystyle \frac{{\mathbb{F}}_p[u,v]}{(u^2-v^2,uv)}}$ has the following form:

$$\left(\begin{array}{cc}u& 0\\ v& v\\ 0& u\end{array}\right).$$

Note that $t_0=0$ and $t_1=t_2=1.$ Consider the submodules $⟨(u,0),(v,v)⟩$ and $⟨0,u⟩$ which have non-trivial intersections. Thus, the size of C might not be easily obtained from G. However, if we add $r_1$ to $r_3,$ we obtain the following:

$$\left(\begin{array}{cc}u& u\\ v& v\\ 0& u\end{array}\right).$$

In such $G,$$⟨(u,0),(v,v)⟩\cap ⟨0,u⟩=\varphi .$ Therefore,

$$\mid C\mid =\mid ⟨(u,0),(v,v)⟩\mid \times \mid ⟨0,u⟩\mid =8\times 4=32.$$

6. Conclusions

We conclude that, up to isomorphism, all local rings of the form $R=R_0+u{R}_0+v{R}_0+w{R}_0$ and $\mid R\mid =p^4$ have been successfully classified in terms of $p,n,r,m,k.$ Furthermore, generator matrices and MacWilliams relations for linear codes over such rings have been discovered. These are popular and effective tools for encoding data over chain rings; codes over local non-chain rings may not be able to achieve such a case. The challenge is in identifying a smallest number of generators and counting the code size because non-chain local rings are not PIRs. This restriction suggests that in order to effectively handle this issue, different approaches or strategies are needed.