Liftable Point-Line Configurations: Defining Equations and Irreducibility of Associated Matroid and Circuit Varieties
Abstract
1. Introduction
- a.
- Four of degree 3, deduced directly from the collinearities in the point-line configuration.
- b.
- Ten of degree 6, in 18 variables, each consisting of 14 or 16 terms.
- c.
- 16 of degree 3, each deduced from collinearities in the point-line configuration.
- d.
- 28 of degree 12 in 36 variables, each consisting of around 250 terms.
- The matroid variety is irreducible. (Theorem 4)
- If is liftable, then and (Theorem 5)
- If is connected quasi-liftable, then and (Theorem 1)where is the matroid variety whose associated configuration is a line with n marked points. Furthermore, the decompositions are, respectively, irreducible and prime.
2. Preliminaries
2.1. Matroids and Matroid Varieties
- the independent sets are subsets of the bases;
- the dependent sets of M are the nonindependent sets;
- the circuits of M are the minimal dependent sets;
- defined by is the rank function of M. By the basis exchange axiom, each basis has the same cardinality, which is equal to and we call this value the rank of the matroid M denoted ;
- the flats of M;
- The closure operator of M is defined as . The closure of a subset of E is the smallest flat containing the subset.
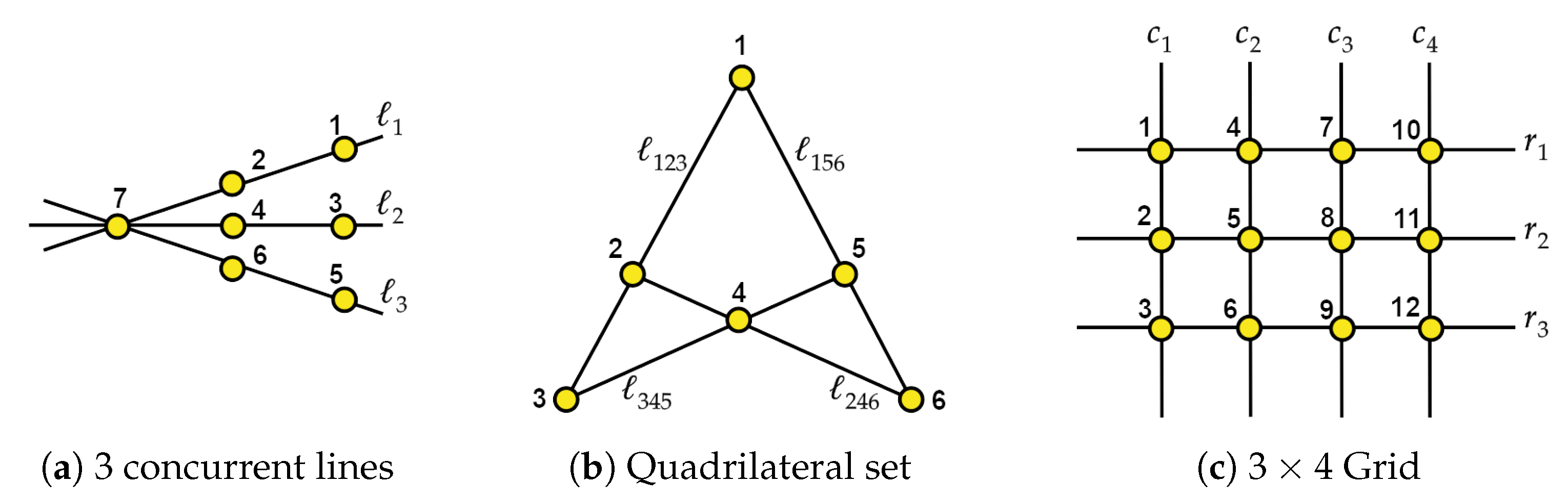
2.2. Point-Line Configurations
- Singletons in are all the rank-one flats of M and correspond to points of ;
- Rank-two flats of M of cardinality at least 3 correspond to lines in .
- ,
- , and
- .
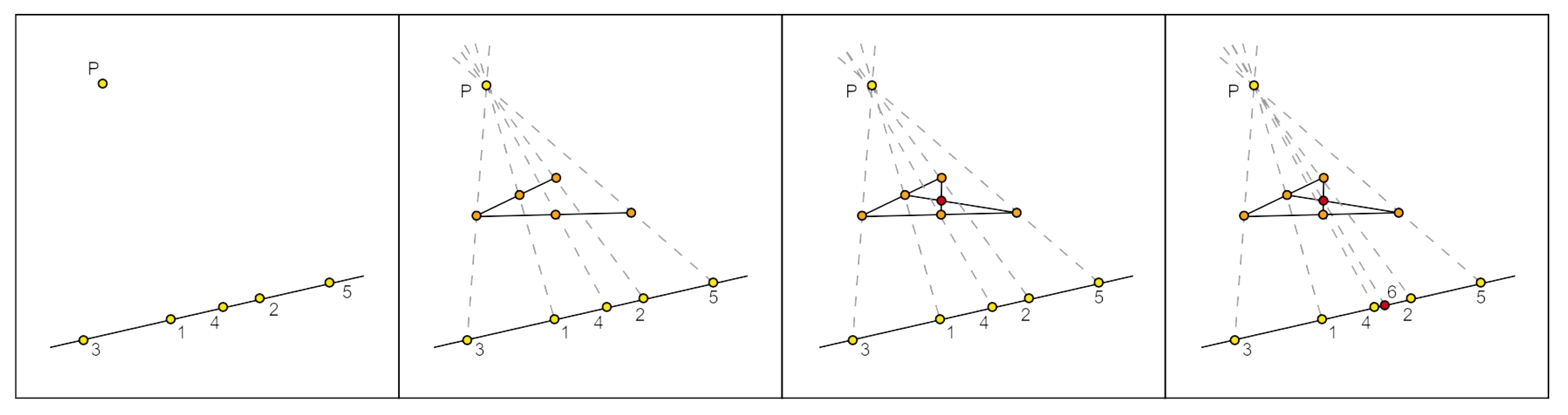
3. (Quasi-)Liftable Configurations
3.1. Realization Space of Liftable Configurations
- All the collinearities (i.e., triplets of collinear points) of are collinearities of ;
- The points of do not lie on a single line.
- •
- The configuration is strictly liftable.
- •
- The linear system , where Λ is the collinearity matrix of , has solution space of dimension at least , or equivalently .
- is strictly liftable over , or
- has the property ∗ in .
3.2. Irreducible Decomposition of Varieties of (Quasi-)Liftable Configurations
- Either their linear span is 2-dimensional, in which case is uniquely determined;
- The linear span has dimension strictly less than 2, in which case we choose generically such that it contains .
- S1.
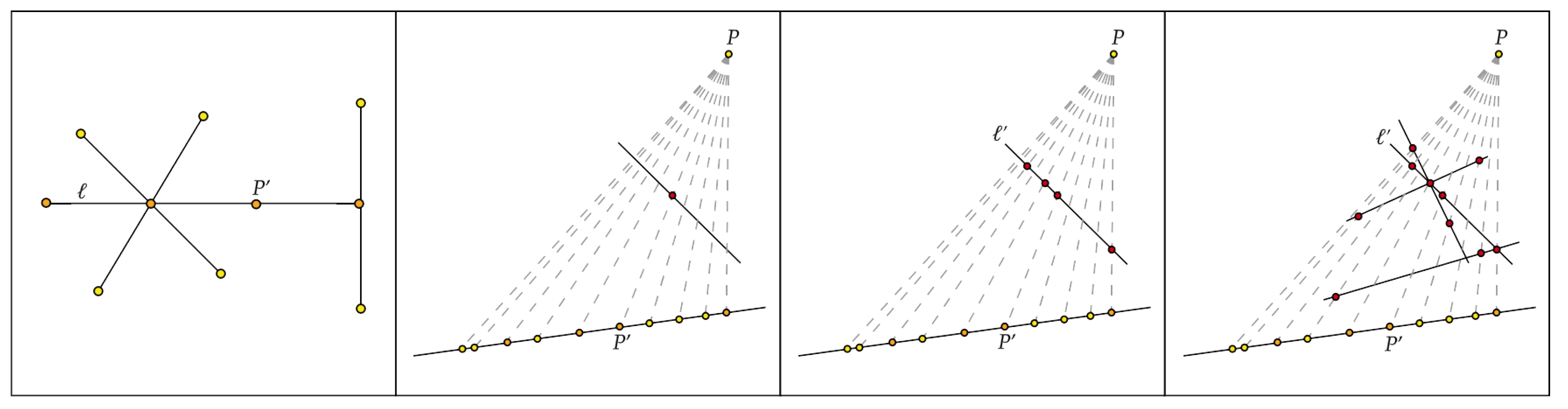
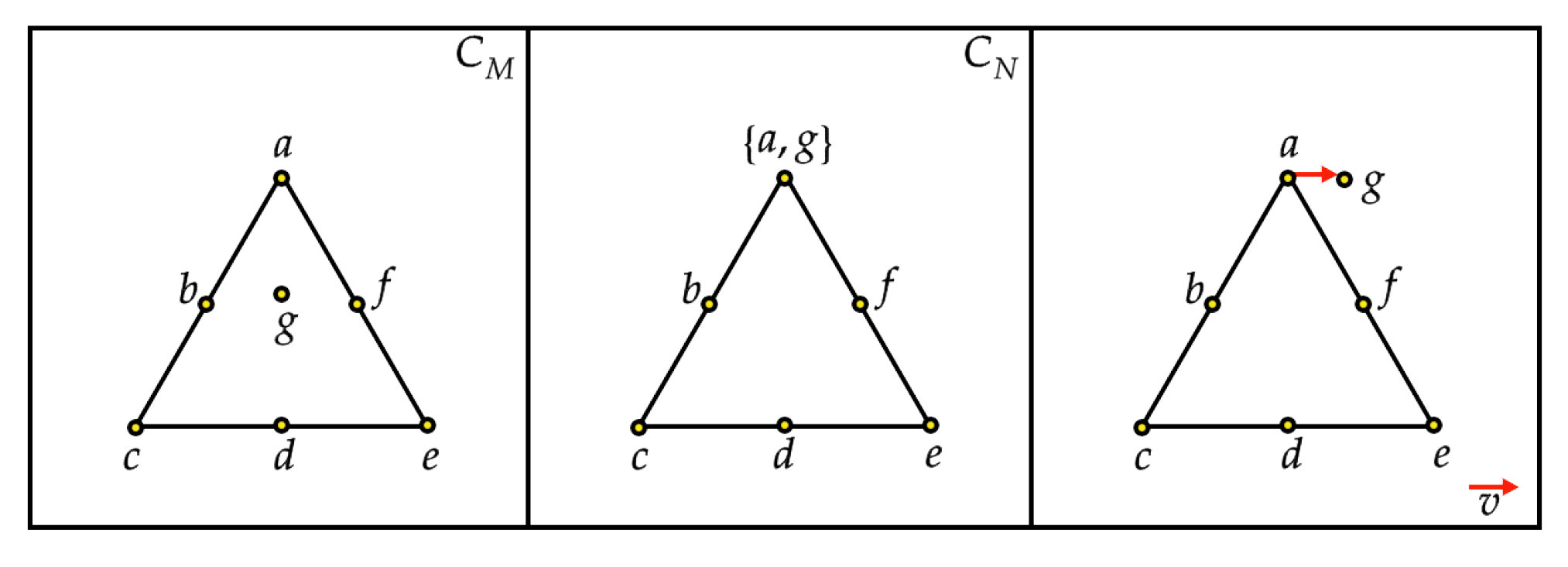
- For any index and for any , if the point does not belong to any line in , then it can be translated along any direction. In other words, we perturb the column by adding to it a vector , where v has unitary norm (see Figure 6 for an example). In turn, we can assume that for any , all points in lie at least on a line in .
- S2.
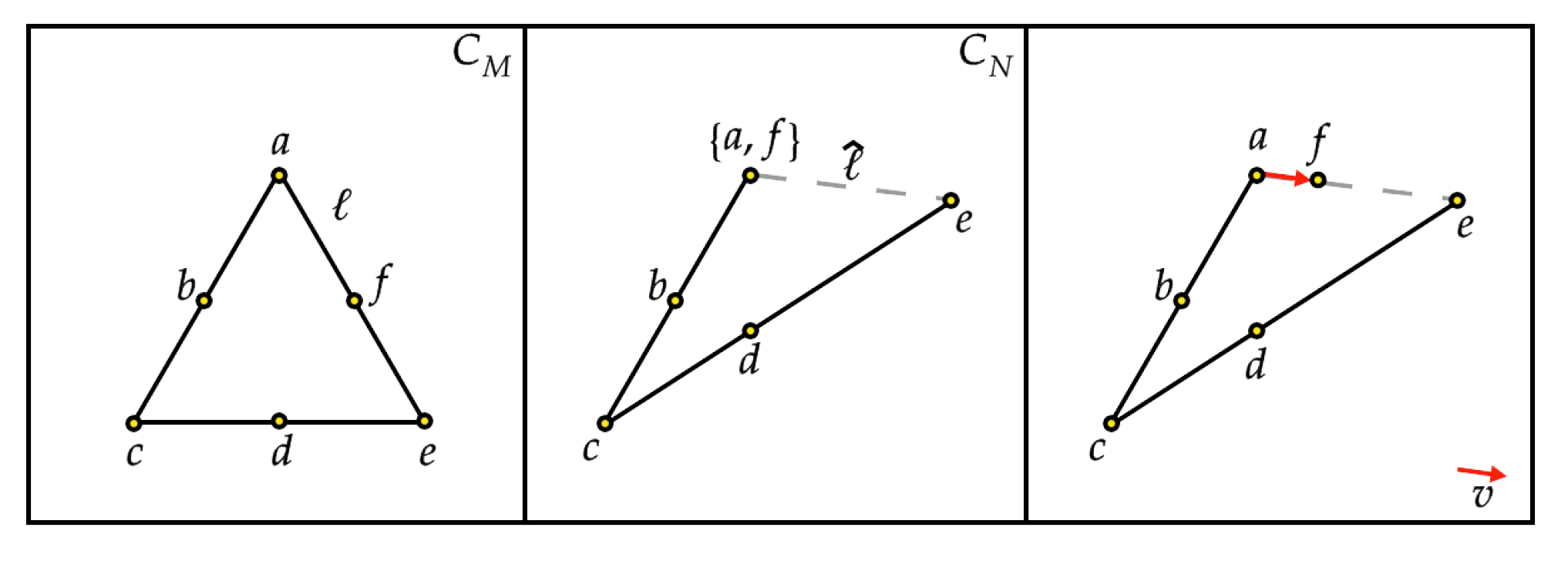
- For any and for any , we check whether the point belongs to a single line ℓ in . If this is the case, the point can be realized by translating the corresponding column along the ghost line , as in Figure 7. Thus, we can further assume that for any , all points in lie at the intersection of two lines in .
- S3.
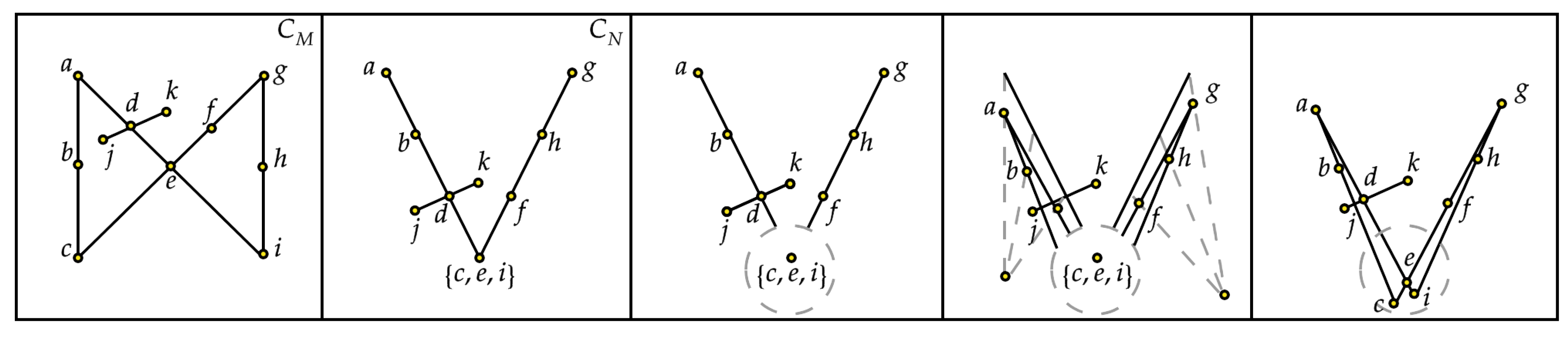
- For any k, if all the (ghost) lines through coincide on a unique (ghost) line ℓ, then we perturb all points of along ℓ. Figure 8 illustrates that this operation might not lead to a full realization of , as it does not take the independence relations into account. However, it generates all required collinearities, leading to a dependent matroid for M. Any remaining multiple point now lies at the intersection of the realization of at least two nonoverlapping lines.
- S4.
- We now remove all remaining multiple points from the configuration, and we consider the multiple lines L that are incident to them. We resolve the multiple lines using a lifting procedure, which can be followed graphically from Figure 9. We consider the following two steps:
- S4.1.
- In view of the liftability property of and the induction hypothesis, we can perform a lifting of the subconfiguration of N that involves only the remaining points on L and the (ghost) lines that coincide with L. Here, we pick our projection point in general position, away from all lines generated by points of . It follows from the proof of Lemma 4 that the distance between C and the lifted configuration can be bounded by .
- S4.2.
- If a lifted point i was the intersection of L with another (ghost) line , prior to the lifting, then we need to further perturb it. In , the point i lies at the intersection of two lines ℓ and . In , coincides with the line L. After the lifting, we have that is lifted and intersects at a unique point. We redefine i to be this unique intersection point, whose distance from the previous lifted point is a continuous function of .
For any lifted (ghost) line resulting from this operation and containing a point in one of the multiple points through ℓ, we can assume, without loss of generality, that it is still arbitrarily close to the concerned multiple points. This can be explained considering that if the multiple points had not been removed from the configuration, the lifting could still have been performed. In particular, any such lifted line intersects all the other lines incident to the multiple point in a neighborhood of the multiple point itself. - S5.
- For any multiple point , we consider the lines through excluded from step S4. Namely, those corresponding to rank-two flats of N that do not contain more than a rank-two flat of M. Let be the number of such lines. If , we have to perturb of them so that they are not all concurrent on the same point in the projective plane. This can be performed considering that none of these lines is a multiple line, and for any such line ℓ, we perform the following two steps, depicted in Figure 10:
- S5.1.
- We pick a generic direction . Our goal is moving all points on ℓ in the direction of v.
- S5.2.
- We select a basis B for the (ghost) line ℓ. Then, fixing a unitary vector v, we consider the linear subspace . For each point i lying on ℓ, we perturb i as follows. By assumption, i belongs to exactly one or two lines of . If i belongs to two lines ℓ and , then we move i to the closest point in the intersection of the ghost line and . Otherwise, if i belongs uniquely to the line ℓ, we move i to the closest point of .
The total distance that points have moved is a continuous function in . - S6.
- For any k, after having performed steps 4 and 5, all lines incident to now intersect in points whose coordinates can be obtained by adding a vector to the coordinates of (v is supposed to have unit norm). Therefore, we can finally resolve all multiple points by taking the intersection of the corresponding lines, as in the right-most representations of Figure 9 and Figure 10.
3.3. The Ideal of Quasi-Liftable Configurations
- The collinearity conditions of ;
- The extensions of the minors of the collinearity matrix .
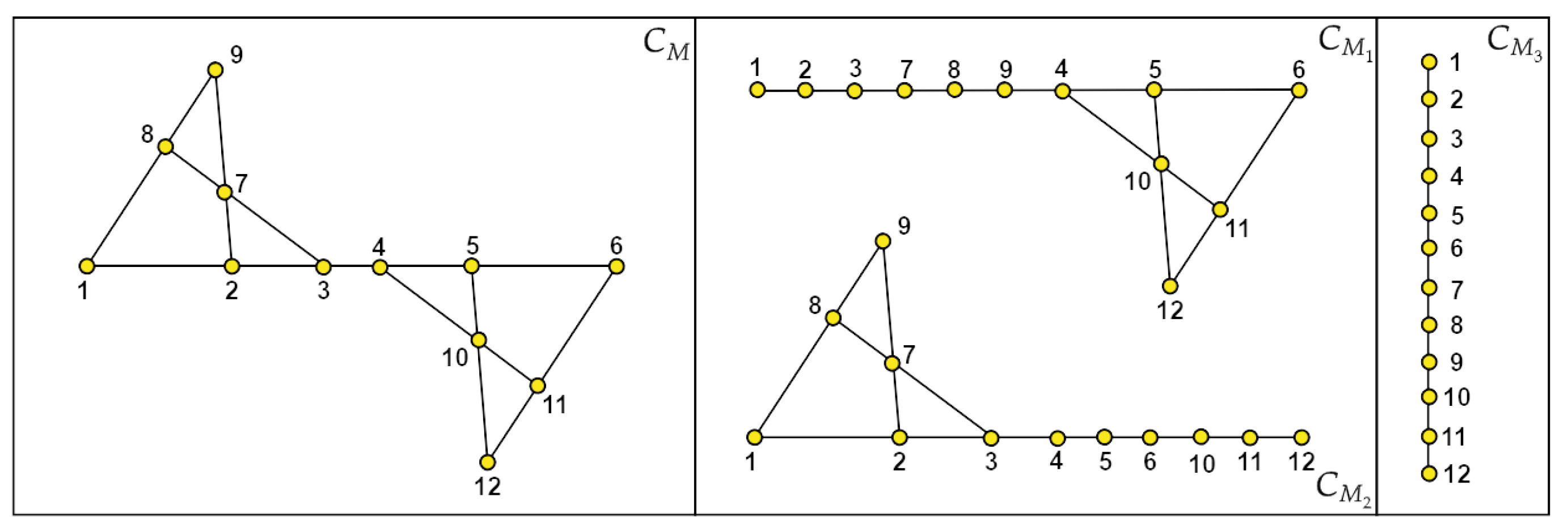
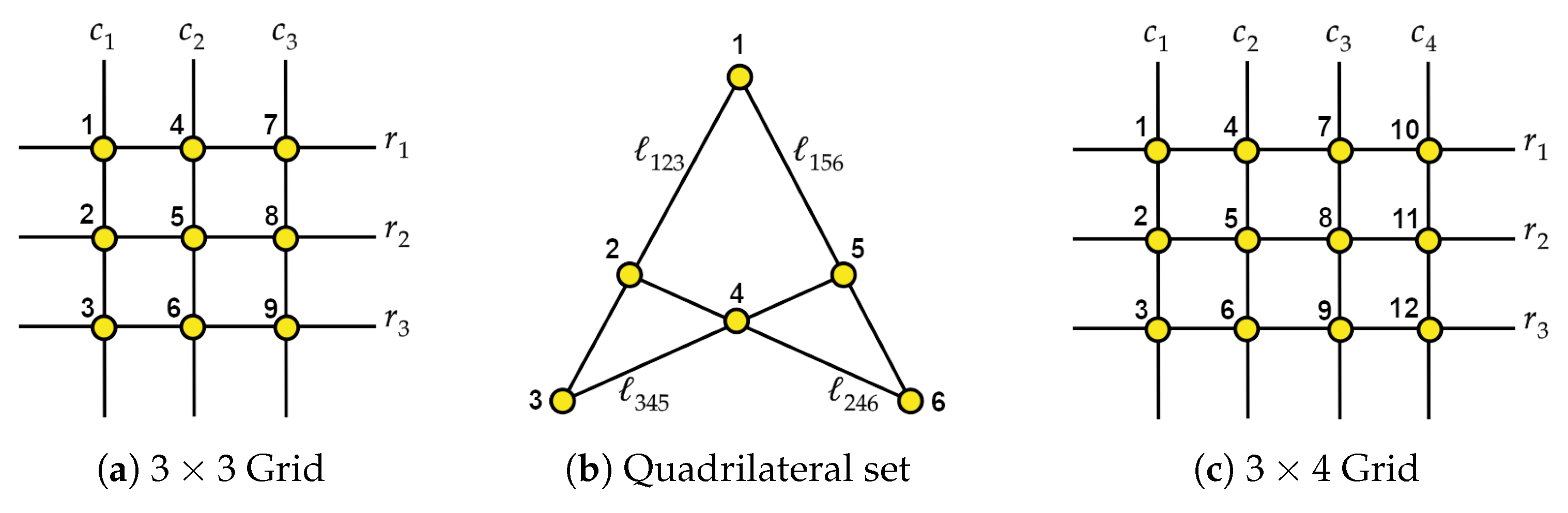
4. The Quadrilateral Set
- The letter multidegree , where , , and are, respectively, the numbers of x, y, and z variables.
- The point multidegree where is the number of variables corresponding to coordinates of the point for any .
- i.
- The points are the projective image of a quadrilateral set.
- ii.
- The polynomials vanish for any and any .
- iii.
- The polynomials vanish for any and any .
- iv.
- The polynomials vanish for any .
- v.
- The polynomials vanish for any with .
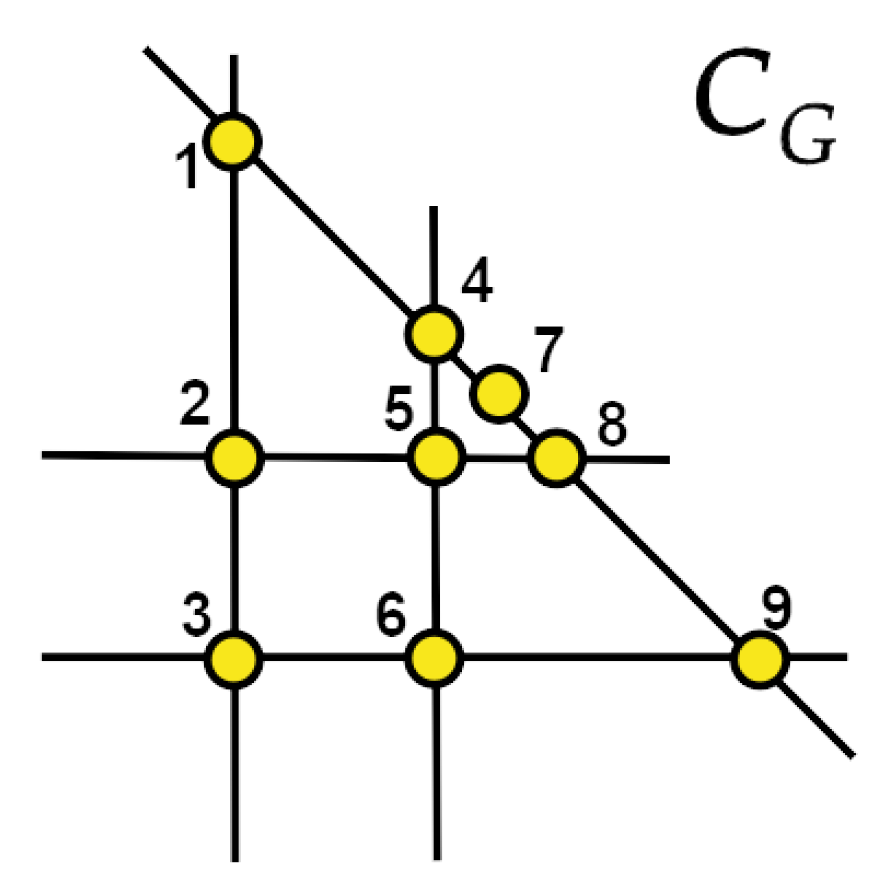
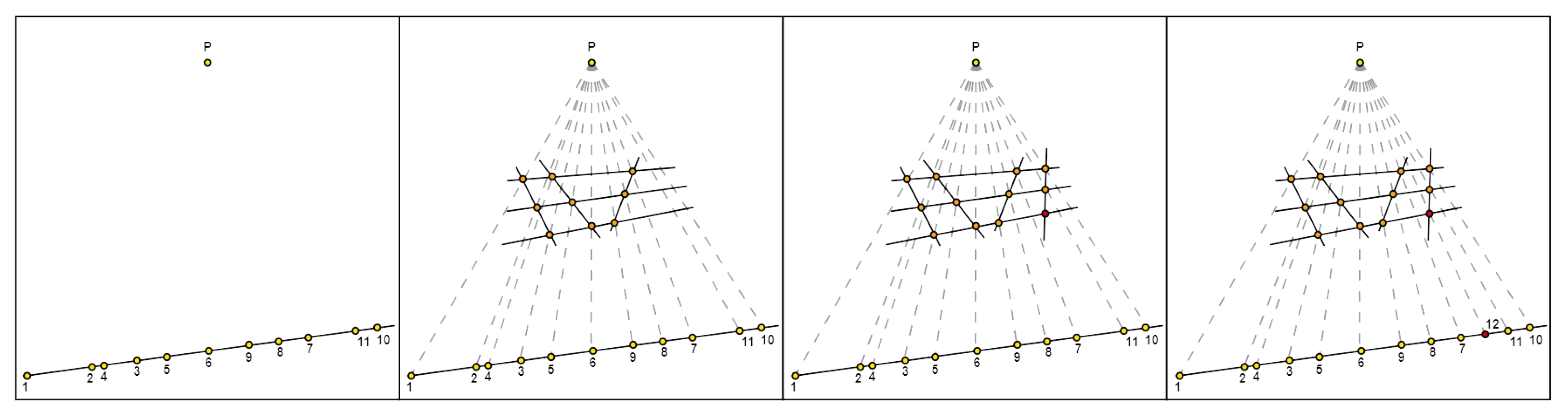
5. The Grid Matroid
- Let be a column in , whose points are and , where the upper index labels the row. Then, the points in are in natural bijection with a 3 × 3 matrix.
- Let Σ be the set of permutation matrices σ over three elements. For , we denote as the nonzero entry of the th row and as the corresponding point in .
- For , each column has a single point paired with a nonzero entry of σ. We label and the points in which belong to . In particular, is the point with the lowest index.
- Let be six points in , not necessarily distinct. We introduce the polynomials:
- is a basis for the projective line . Thus, there exists a unique choice of such that: (i) and () .
- is a basis for the projective line . Thus, there exists a unique choice of such that: () and () .
- is a basis for the projective line . Thus, there exists a unique choice of such that: (v) and () .
- is a basis for the projective line . Thus, there exists a unique choice of such that: () .
- is a basis for the projective line . Thus, there exists a unique choice of such that: () .
- is a basis for the projective line . Thus, there exists a unique choice of such that: () .
- i.
- The points are projective image of a grid.
- ii.
- The polynomials vanish for any and any .
- iii.
- The polynomials vanish for any and any .
- iv.
- The polynomials vanish for any .
- v.
- The polynomials vanish for any with .
- Rows correspond to the columns of the grid.
- Rows correspond to the first row of the grid.
- Rows correspond to the second row of the grid.
- Rows correspond to the third row of the grid.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Whitney, H. On the abstract properties of linear dependence. In Hassler Whitney Collected Papers; Springer: Berlin/Heidelberg, Germany, 1992; pp. 147–171. [Google Scholar]
- MacLane, S. Some interpretations of abstract linear dependence in terms of projective geometry. Am. J. Math. 1936, 58, 236–240. [Google Scholar] [CrossRef]
- White, N. A tutorial on Grassmann-Cayley algebra. In Invariant Methods in Discrete and Computational Geometry; Springer: Berlin/Heidelberg, Germany, 1995; pp. 93–106. [Google Scholar]
- White, N. Geometric applications of the Grassmann-Cayley algebra. In Handbook of Discrete and Computational Geometry; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017; pp. 1581–1592. [Google Scholar]
- Oxley, J. Matroid Theory; Oxford University Press: Oxford, NY, USA, 2006; Volume 3. [Google Scholar]
- Gelfand, I.; Goresky, R.; MacPherson, R.; Serganova, V. Combinatorial geometries, convex polyhedra, and Schubert cells. Adv. Math. 1987, 63, 301–316. [Google Scholar] [CrossRef]
- Sidman, J.; Traves, W.; Wheeler, A. Geometric equations for matroid varieties. J. Comb. Theory Ser. A 2021, 178, 105360. [Google Scholar] [CrossRef]
- Bruns, W.; Schwänzl, R. The number of equations defining a determinantal variety. Bull. Lond. Math. Soc. 1990, 22, 439–445. [Google Scholar] [CrossRef]
- Bruns, W.; Conca, A. Gröbner Bases and Determinantal Ideals. In Proceedings of the Commutative Algebra, Singularities and Computer Algebra, Sinaia, Romania, 17–22 September 2003; Springer: Dordrecht, The Netherlands, 2003; pp. 9–66. [Google Scholar]
- Sturmfels, B. Gröbner bases and Stanley decompositions of determinantal rings. Math. Z. 1990, 205, 137–144. [Google Scholar] [CrossRef]
- Ene, V.; Herzog, J.; Hibi, T.; Mohammadi, F. Determinantal facet ideals. Mich. Math. J. 2013, 62, 39–57. [Google Scholar] [CrossRef]
- Mohammadi, F.; Rauh, J. Prime splittings of determinantal ideals. Commun. Algebra 2018, 46, 2278–2296. [Google Scholar] [CrossRef]
- Lee, S.; Vakil, R. Mnëv-Sturmfels universality for schemes. In A Celebration of Algebraic Geometry; AMS: Providence, RI, USA; Clay Mathematics Institute: Cambridge, MA, USA, 2013; Volume 18, pp. 457–468. [Google Scholar]
- Mnëv, N. The universality theorems on the classification problem of configuration varieties and convex polytopes varieties. In Proceedings of the Topology and Geometry—Rohlin Seminar; Springer: Berlin/Heidelberg, Germany, 2006; pp. 527–543. [Google Scholar]
- Sturmfels, B. On the matroid stratification of Grassmann varieties, specialization of coordinates, and a problem of N. White. Adv. Math. 1989, 75, 202–211. [Google Scholar] [CrossRef][Green Version]
- Bokowski, J.; Sturmfels, B. Computational synthetic geometry. Lect. Notes Math. 1989, 1355, 1–166. [Google Scholar]
- Drton, M.; Sturmfels, B.; Sullivant, S. Lectures on Algebraic Statistics; Springer Science & Business Media: New York, NY, USA, 2008; Volume 39. [Google Scholar]
- Clarke, O.; Grace, K.; Mohammadi, F.; Motwani, H. Matroid stratifications of hypergraph varieties, their realization spaces, and discrete conditional independence models. Int. Math. Res. Not. 2023, 2023, 18958–19019. [Google Scholar] [CrossRef]
- Clarke, O.; Mohammadi, F.; Motwani, H. Conditional probabilities via line arrangements and point configurations. Linear Multilinear Algebra 2022, 70, 5268–5300. [Google Scholar] [CrossRef]
- Caines, P.; Mohammadi, F.; Sáenz-de Cabezón, E.; Wynn, H. Lattice conditional independence models and Hibi ideals. Trans. Lond. Math. Soc. 2022, 9, 1–19. [Google Scholar] [CrossRef]
- Clarke, O.; Mohammadi, F.; Rauh, J. Conditional independence ideals with hidden variables. Adv. Appl. Math. 2020, 117, 102029. [Google Scholar] [CrossRef]
- Sturmfels, B. Computational algebraic geometry of projective configurations. J. Symb. Comput. 1991, 11, 595–618. [Google Scholar] [CrossRef][Green Version]
- Grayson, D.; Stillman, M. Macaulay2, a Software System for Research in Algebraic Geometry. Available online: http://www2.macaulay2.com (accessed on 10 February 2024).
- Pfister, G.; Steenpass, A. On the primary decomposition of some determinantal hyperedge ideal. J. Symb. Comput. 2021, 103, 14–21. [Google Scholar] [CrossRef]
- Richter-Gebert, J. Perspectives on Projective Geometry: A Guided Tour through Real and Complex Geometry; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Sturmfels, B. Algorithms in Invariant Theory; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar]
- Sitharam, M.; John, A.S.; Sidman, J. Handbook of Geometric Constraint Systems Principles, 1st ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Cox, D.; Little, J.; O’shea, D.; Sweedler, M. Ideals, Varieties, and Algorithms; Springer: Berlin/Heidelberg, Germany, 1997; Volume 3. [Google Scholar]
- Matsumura, H. Commutative Ring Theory; Number 8; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Milne, J. Algebraic Geometry (v6.02). 2017. Available online: www.jmilne.org/math/ (accessed on 10 February 2024).
- Knutson, A.; Lam, T.; Speyer, D.E. Positroid varieties: Juggling and geometry. Compos. Math. 2013, 149, 1710–1752. [Google Scholar] [CrossRef]
- Postnikov, A. Total positivity, Grassmannians, and networks. arXiv 2006, arXiv:math/0609764. [Google Scholar]
- Mohammadi, F.; Zaffalon, F. Combinatorics of essential sets for positroids. J. Algebra 2024, 657, 456–481. [Google Scholar] [CrossRef]
- Mohammadi, F.; Monin, L.; Parisi, M. Triangulations and canonical forms of amplituhedra: A fiber-based approach beyond polytopes. Commun. Math. Phys. 2021, 387, 927–972. [Google Scholar] [CrossRef]
- Liwski, E.; Mohammadi, F. Solvable and nilpotent matroids: Realizability and irreducible decomposition of their associated varieties. arXiv 2024, arXiv:2408.12784. [Google Scholar]
- Liwski, E.; Mohammadi, F. Paving matroids: Defining equations and associated varieties. arXiv 2024, arXiv:2403.13718. [Google Scholar]


| Gener. | Coeff. of | Coeff. of | Coeff. of | Coeff. of | |
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | |||||
| - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clarke, O.; Masiero, G.; Mohammadi, F. Liftable Point-Line Configurations: Defining Equations and Irreducibility of Associated Matroid and Circuit Varieties. Mathematics 2024, 12, 3041. https://doi.org/10.3390/math12193041
Clarke O, Masiero G, Mohammadi F. Liftable Point-Line Configurations: Defining Equations and Irreducibility of Associated Matroid and Circuit Varieties. Mathematics. 2024; 12(19):3041. https://doi.org/10.3390/math12193041
Chicago/Turabian StyleClarke, Oliver, Giacomo Masiero, and Fatemeh Mohammadi. 2024. "Liftable Point-Line Configurations: Defining Equations and Irreducibility of Associated Matroid and Circuit Varieties" Mathematics 12, no. 19: 3041. https://doi.org/10.3390/math12193041
APA StyleClarke, O., Masiero, G., & Mohammadi, F. (2024). Liftable Point-Line Configurations: Defining Equations and Irreducibility of Associated Matroid and Circuit Varieties. Mathematics, 12(19), 3041. https://doi.org/10.3390/math12193041






