Approximate Analytic Frequency of Strong Nonlinear Oscillator
Abstract
1. Introduction
2. Exact and Approximate Frequency of the Truly Nonlinear Oscillator
2.1. Transformation of the Truly Nonlinear Oscillator into the Linear One
2.2. Example of a Truly Non-Integer Order Nonlinear Oscillator
3. Approximate Frequency of Vibration of the Harmonic Any-Order Nonlinear Oscillator
3.1. Approximate Frequency Based on the Approximate Frequency of the Truly Nonlinear Oscillator
3.2. Example of a Harmoni–Non-Integer Order Nonlinear Oscillator
4. Frequency and Period of Oscillator with Sum of Nonlinearities of the Polynomial Type
5. Conclusions
- The method of transformation of the oscillator with a strong polynomial nonlinearity of integer or non-integer orders into a linear oscillator, based on the equality or almost equality of periods of vibration, gives a result which is suitable for practical application in technics.
- The frequency of vibration of the truly strong nonlinear oscillator is approximately equivalent to (, where c1 is the coefficient of nonlinearity, A is the amplitude of vibration and is the order of nonlinearity. The error of the approximate frequency is up to 4% in comparison to the exact one. The difference between the exact and suggested frequency is higher if the order of nonlinearity is lower and the amplitude of vibration is higher than one. Otherwise, the difference is negligible for higher orders of nonlinearity and amplitudes smaller than one.
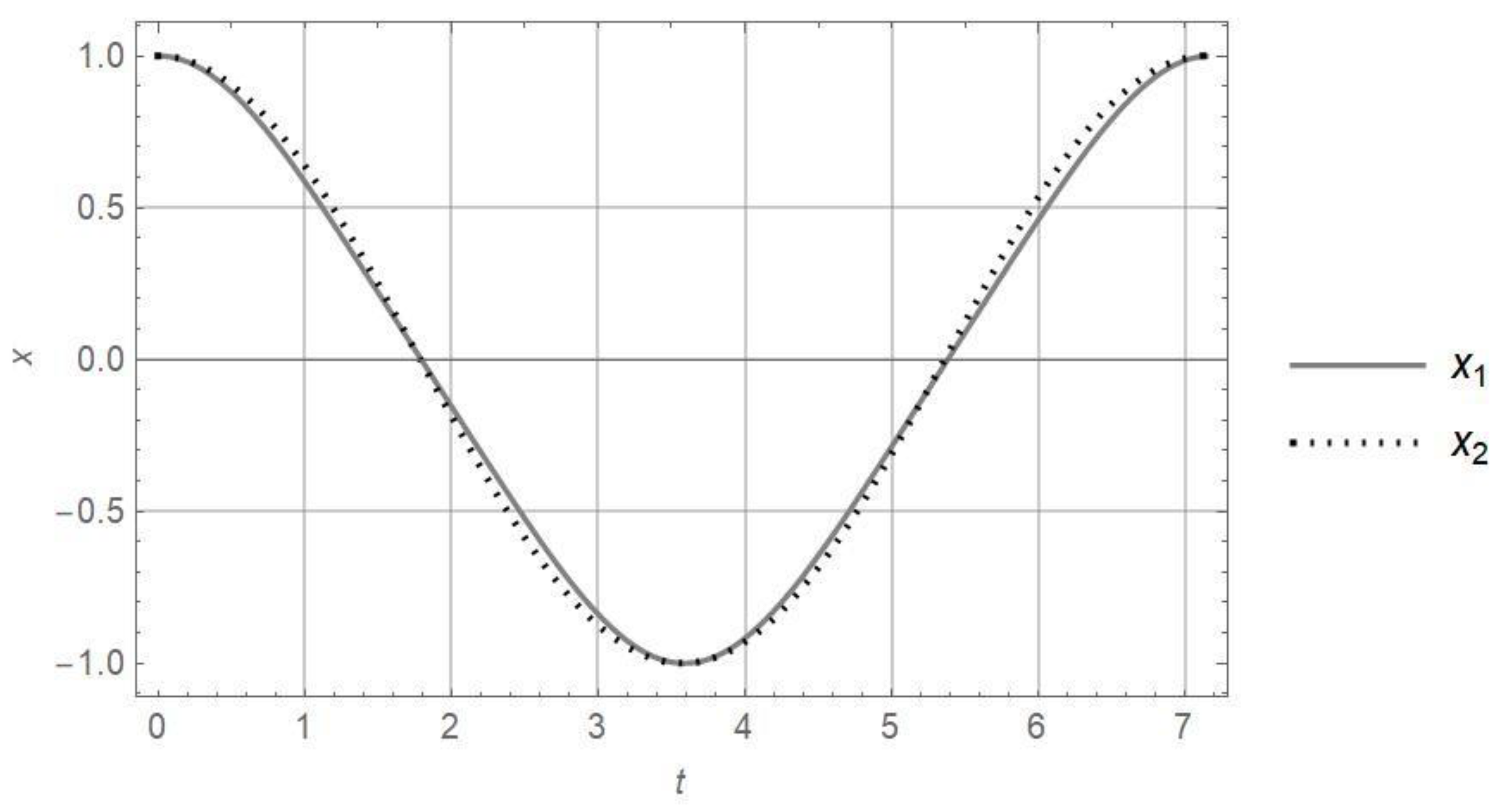
- The recently developed approximate frequency of the harmonic any-order oscillator is the function of frequencies of the harmonic and the truly nonlinear oscillator. The test of the approximate expression for cubic nonlinearity shows good agreement with the exact frequency for the Duffing oscillator. For other orders of nonlinearity, the difference between approximate and exact periods of vibration of the nonlinear oscillator depends on the relation between the linear and nonlinear terms. However, when the linear term is 10 or more times higher than the nonlinear one, the period of vibration is negligible.
- The advantage of the suggested frequency expression is that it is useful for frequency computation for any non-integer order nonlinear oscillator. The analytic formulation is of the algebraic type and suitable for application by engineers and technicians.
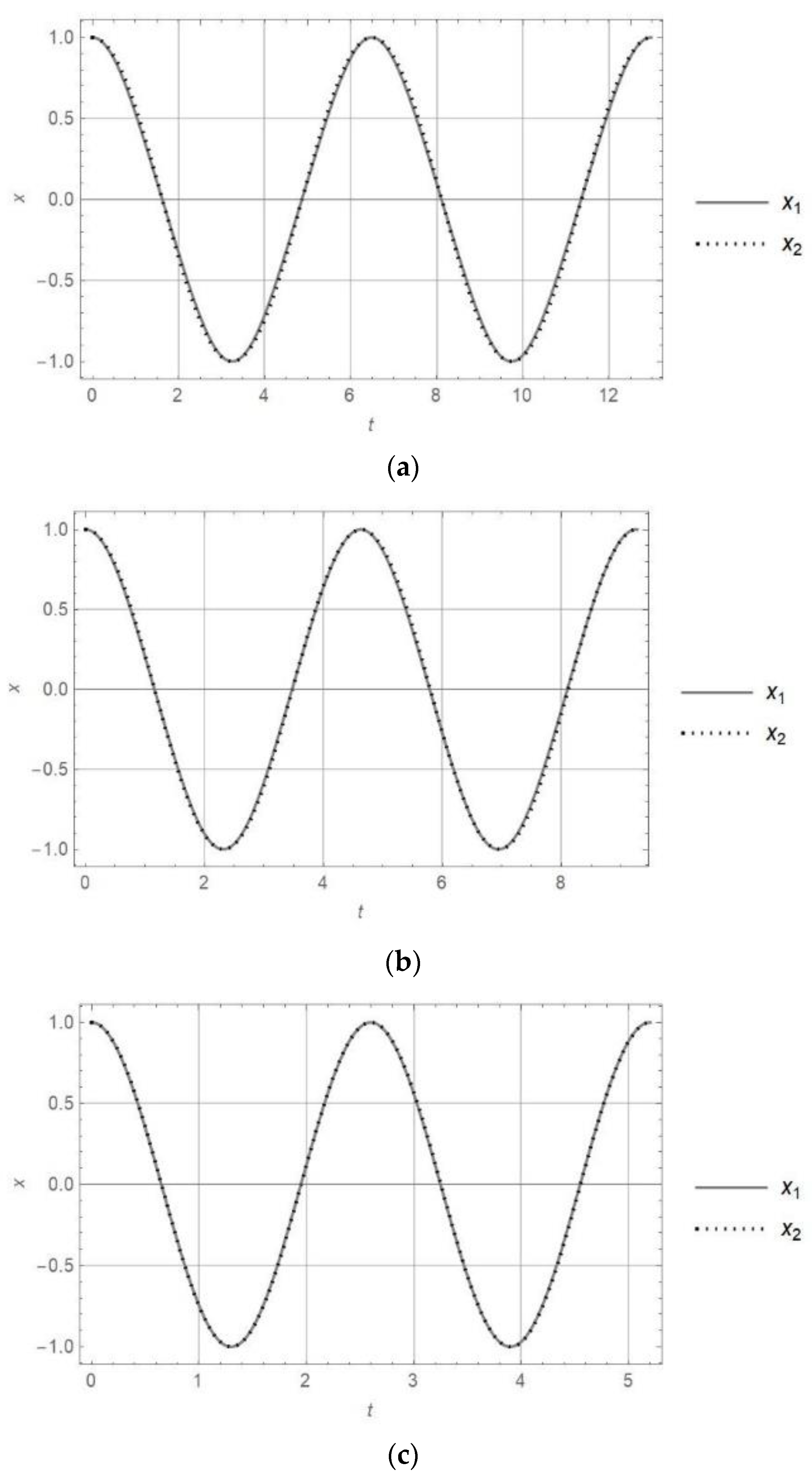
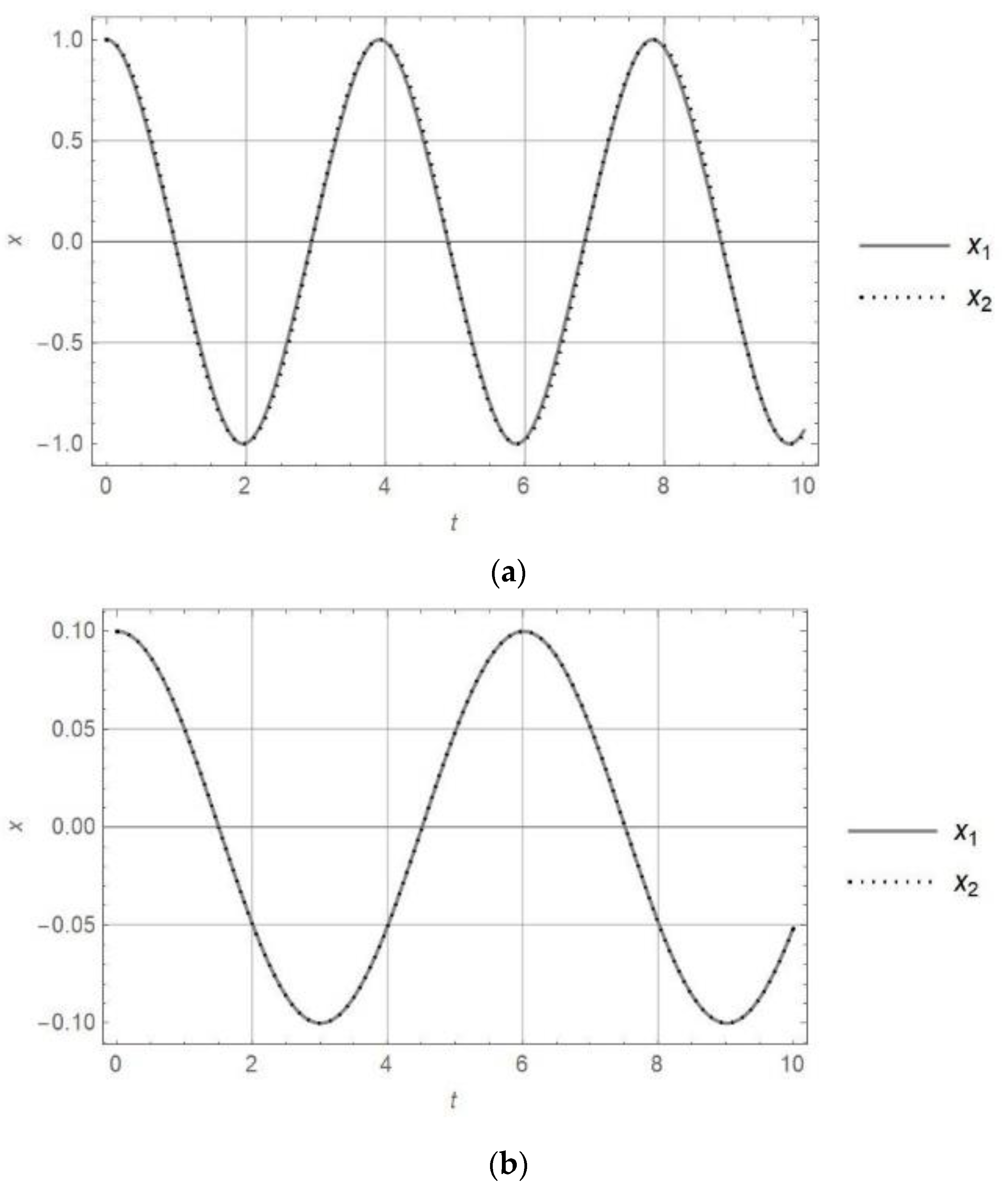
- The equivalent transformation of the nonlinear oscillator into the linear one, based on the equality of the period of vibration, shows that the responses for these oscillators are almost of the same form. It is valid for orders of nonlinearity up to four.
- Finally, in this paper it is suggested to apply the approximate linear oscillator obtained with equivalent transformation instead of the original complex nonlinear oscillator. The quantitative difference in the response and period of vibration is smaller than 5%, while the amplitude of vibration is equal.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bogolubov, N.N.; Mitropolskij, Y.A. Asymptotic Methods in the Theory of Non-Linear Vibrations; Nauka: Moscow, Russian, 1968. (In Russian) [Google Scholar]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; Wiley: New York, NY, USA, 1979. [Google Scholar]
- Duffing, G. Erzwungene Schwingungen bei Veranderlicher Eigenfrequenz und ihre Technische Bedeutung; Vieweg & Sohn: Braunschweig, Germany, 1918. [Google Scholar]
- Sathyaseelan, D.; Hariharan, G. Wavelet-based approximation algorithms for some nonlinear oscillator equations arising in engineering. J. Inst. Eng. Ser. C 2020, 101, 185–192. [Google Scholar] [CrossRef]
- Anjum, N.; Suleman, M.; Lu, D.; He, J.H.; Ramzan, M. Numerical iteration for nonlinear oscillators by Elzaki transform. J. Low Freq. Noise Vib. Act. Control. 2020, 39, 879–884. [Google Scholar] [CrossRef]
- He, W.; Kong, H.; Qin, Y.M. Modified variational iteration method for analytical solutions of nonlinear oscillators. J. Low Freq. Noise Vib. Act. Control. 2019, 38, 1178–1183. [Google Scholar] [CrossRef]
- Tahir, M.; Shah, N.A.; Tag, S.M.; Imran, M. An application to formable transform: Novel numerical approach to study the nonlinear oscillator. J. Low Freq. Noise Vib. Act. Control. 2024, 43, 729–743. [Google Scholar]
- Gamal, M.I.; Alwaleed, K.; Abdulaziz, A. Approximate analytical solutions to nonlinear oscillations via semi-analytical method. Alex. Eng. J. 2024, 98, 97–102. [Google Scholar]
- Yeasmin, I.A.; Sharif, N.; Rahman, M.S.; Alam, M.S. Analytical technique for solving the quadratic nonlinear oscillator. Results Phys. 2020, 18, 103303. [Google Scholar] [CrossRef]
- Sierra-Porta, D. Analytic approximations to Liénard nonlinear oscillators with modified energy balance method. J. Vib. Eng. Technol. 2020, 8, 713–720. [Google Scholar] [CrossRef]
- Yu, D.N.; He, J.H.; Garcıa, A.G. Homotopy perturbation method with an auxiliary parameter for nonlinear oscillators. J. Low Freq. Noise Vib. Act. Control. 2019, 38, 1540–1554. [Google Scholar] [CrossRef]
- Pasha, S.A.; Nawaz, Y.; Arif, M.S. The modified homotopy perturbation method with an auxiliary term for the nonlinear oscillator with discontinuity. J. Low Freq. Noise Vib. Act. Control. 2019, 38, 1363–1373. [Google Scholar] [CrossRef]
- Manimegalai, K.; Zephania CF, S.; Bera, P.K.; Bera, P.; Das, S.K.; Sil, T. Study of strongly nonlinear oscillators using the Aboodh transform and the homotopy perturbation method. Eur. Phys. J. Plus 2019, 134, 264. [Google Scholar] [CrossRef]
- Lashkarboluki, A.; Hosseini, H.; Ganji, D.D. Investigating the solutions of two classical nonlinear oscillators by the AG method. Int. J. Appl. Comput. Math. 2021, 7, 1–16. [Google Scholar] [CrossRef]
- Ismail, G.M.; Mahmoud, A.E.; Mohra, Z.; Hijaz, A.; Maha, E.M. Highly accurate analytical solution for free vibrations of strongly nonlinear Duffing oscillator. J. Low Freq. Noise Vib. Act. Control. 2022, 41, 223–229. [Google Scholar] [CrossRef]
- Song, P.; Shao, L.; Zhang, W. Residue-regulating homotopy method for strongly nonlinear oscillators. Nonlinear Dyn. 2022, 109, 1905–1921. [Google Scholar] [CrossRef]
- Ismail, G.M.; El-Moshneb, M.M.; Zayed, M. A modified global error minimization method for solving nonlinear Duffing-harmonic oscillators. AIMS Math. 2023, 8, 484–500. [Google Scholar] [CrossRef]
- Moatimid, G.M.; Amer, T.S.; Galal, A.A. Studying highly nonlinear oscillators using the non-perturbative methodology. Sci. Rep. 2023, 13, 20288. [Google Scholar] [CrossRef]
- Kovacic, I.; Brennan, J.M. (Eds.) The Duffing Equation—Nonlinear Oscillators and Their Behaviour; Wiley: Chichester, UK, 2011. [Google Scholar]
- He, J.H. The simplest approach to nonlinear oscillators. Results Phys. 2019, 15, 102546. [Google Scholar] [CrossRef]
- He, J.H. The simpler, the better: Analytical methods for nonlinear oscillators and fractional oscillators. J. Low Freq. Noise Vib. Act. Control. 2019, 38, 1252–1260. [Google Scholar] [CrossRef]
- He, J.H.; Hou, W.F.; Qie, N.; Gepreel, K.A.; Shirazi, A.H.; Hamid, M.S. Hamiltonian-base frequency-amplitude formulation for nonlinear oscillators. Facta Univ. Ser. Mech. Eng. 2021, 19, 199–208. [Google Scholar]
- Kontomaris, S.V.; Chliveros, G.; Malamou, A. Approximate solutions for undamped nonlinear oscillations using He’s formulation. J. Multidiscip. Sci. J. 2023, 6, 140–151. [Google Scholar] [CrossRef]
- El-Dib, Y.O. Insightful and comprehensive formularization of frequency–amplitude formula for strong or singular nonlinear oscillators. J. Low Freq. Noise Vib. Act. Control. 2023, 42, 89–109. [Google Scholar] [CrossRef]
- Basit, M.A.; Huq, M.A.; Hasan, M.K.; Alam, M.S. An approximation technique for solving nonlinear oscillators. J. Low Freq. Noise Vib. Act. Control. 2024, 43, 239–249. [Google Scholar]
- Mickens, E.R. Truly Nonlinear Oscillations; World Scientific: Hackensack, NJ, USA, 2010. [Google Scholar]
- Yuste, S.B. Quasi-pure-cubic oscillators studied using a Krylov-Bogolubov method. J. Sound Vib. 1992, 158, 267–275. [Google Scholar] [CrossRef]
- Cveticanin, L. Homotopy-perturbation method for pure non-linear differential equation. Chaos Solitons Fractals 2006, 30, 1221–1230. [Google Scholar] [CrossRef]
- Cveticanin, L.; Pogany, L. Oscillator with sum of non-integer order non-linearities. J. Appl. Math. 2012, 2012, 649050. [Google Scholar] [CrossRef]
- Rosenberg, R.M. The Ateb(h)-functions and their properties. Q. Appl. Math. 1963, 21, 37–47. [Google Scholar] [CrossRef]
- Droniuk, I.; Nazarkevich, M. Modeling nonlinear oscillatory system under disturbance by means of Ateb-functions. In Proceeding of the Sixth International/Working Conference on Performance Modeling and Evaluation of Heterogenous Networks HET-NETs 2010, Zakopane, Poland, 14–16 January 2010; pp. 325–334. [Google Scholar]
- Cveticanin, L. Oscillator with fraction order restoring force. J. Sound Vib. 2009, 320, 1064–1077. [Google Scholar] [CrossRef]
- Cveticanin, L. Strong Nonlinear Oscillators, Analytical Solutions, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Hieu, D.V. A new approximate solution for a generalized nonlinear oscillator. Int. J. Appl. Comput. Math. 2019, 5, 126–136. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables; Nauka: Moscow, Russian, 1972. [Google Scholar]
- Gradstein, I.S.; Rjizhik, I.M. Table of Integrals, Series and Products; Nauka: Moscow, Russian, 1971. (In Russian) [Google Scholar]
- Liu, Y.; Qin, Z.; Chu, F. Nonlinear forced vibrations of FGM sandwich cylindrical shells with porosities on an elastic substrate. Nonlinear Dyn. 2021, 104, 1007–1021. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Z.; Chu, F. Nonlinear vibrations of auxetic honeycomb thin plates based on the modified Gibson functions. Thin-Walled Struct. 2023, 193, 111259. [Google Scholar] [CrossRef]
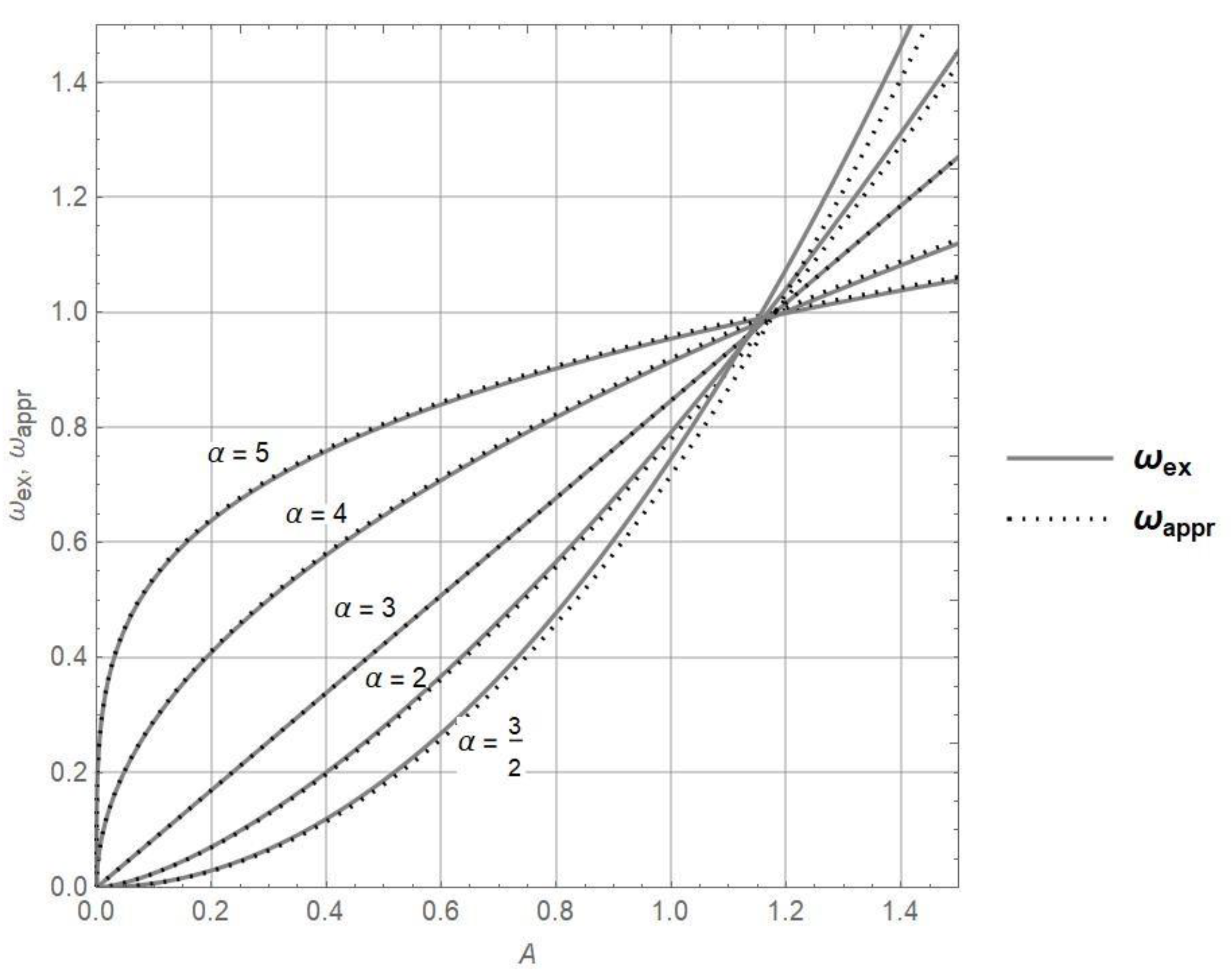

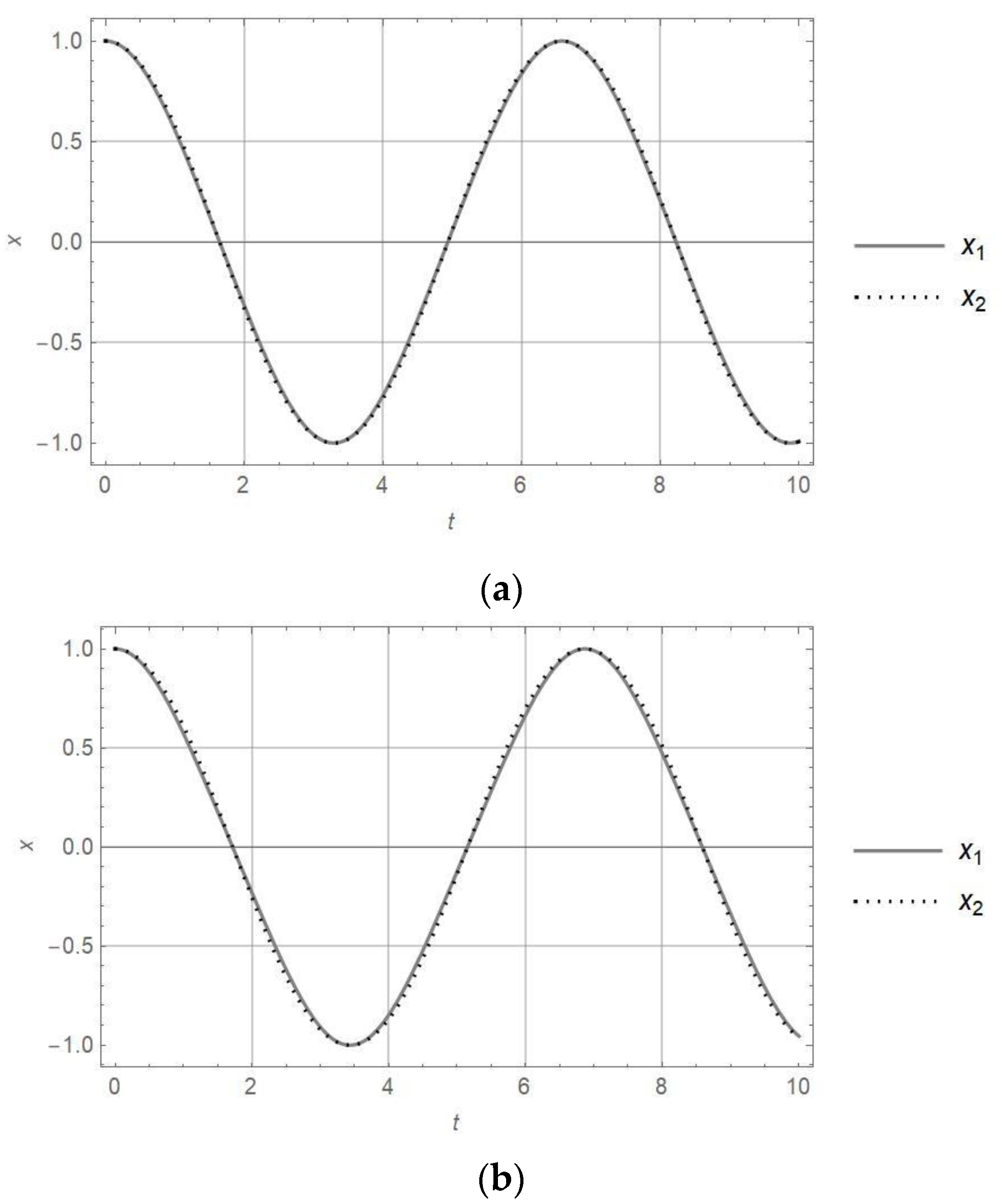
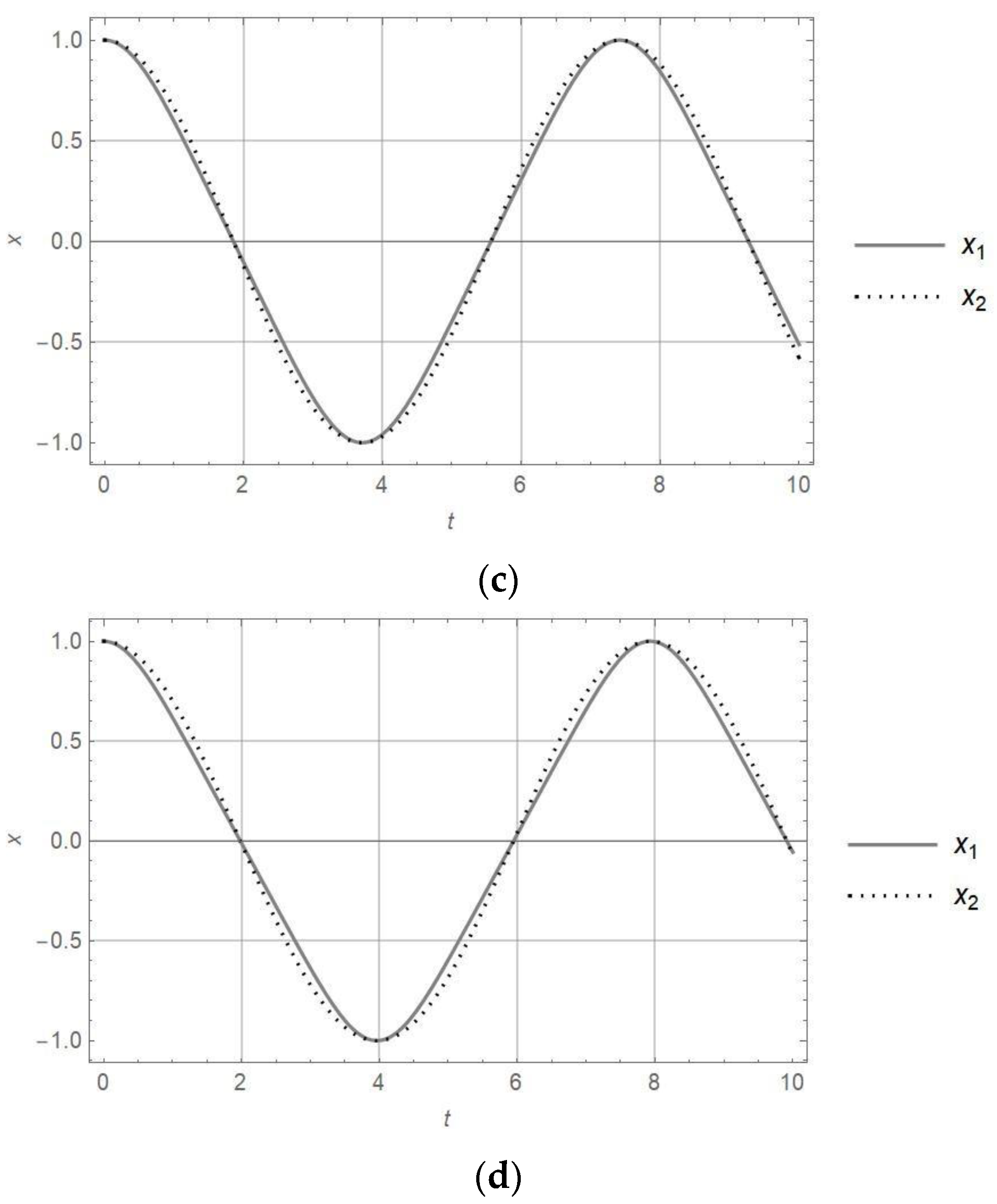


| 3/2 | 7.89 | 0.51 | |||
| 2 | 9.32 | 0.63 | |||
| 3 | 2.22 | 0 | |||
| 4 | 10.7 | 1.58 | |||
| 5 | 25.1 | 3.89 |
| 1 | 3/2 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| AS | any | 1.20429 | 1.19526 | 1.18034 | 1.16780 | 1.15714 |
| 0 | 0.1 | 0.5 | 1 | 5 | 10 | |
|---|---|---|---|---|---|---|
| Tex (34) | 7.41628 | 6.93312 | 5.66276 | 4.78227 | 2.6188 | 1.91641 |
| T (36) | 7.41628 | 6.93459 | 5.66872 | 4.78957 | 2.61931 | 1.91826 |
| 0 | 0.06540 | 0.09634 | 0.09448 | 0.08693 | 0.09678 |
| 0 | 0.1 | 0.5 | 1 | 5 | 10 | |
|---|---|---|---|---|---|---|
| 6.28320 | 5.98774 | 5.12760 | 4.44063 | 2.56380 | 1.89349 | |
| 6.57874 | 6.24500 | 5.28639 | 4.54257 | 2.582976 | 1.90118 | |
| 6.86579 | 6.48893 | 5.43191 | 4.63391 | 2.59943 | 1.90771 | |
| 7.92930 | 7.36451 | 5.91625 | 4.92450 | 2.64853 | 1.92731 | |
| 8.40887 | 7.74333 | 6.10616 | 5.03165 | 2.66385 | 1.93274 |
| A | |||||
|---|---|---|---|---|---|
| 0 | 6.28320 | 6.28320 | 6.28320 | 6.28320 | 6.28320 |
| 0.1 | 5.53318 | 6.03271 | 6.25758 | 6.27803 | 6.27825 |
| 0.5 | 4.89737 | 5.43191 | 5.78258 | 6.04717 | 6.17332 |
| 1 | 4.54257 | 4.63391 | 4.79158 | 4.92205 | 5.03165 |
| AS (Table 2) | 4.4429 (AS = 1.2043) | 4.4429 (AS = 1.1953) | 4.4429 (AS = 1.1803) | 4.4429 (AS = 1.1678) | 4.4429 (AS = 1.1571) |
| 2 | 4.15113 | 3.84094 | 3.19187 | 2.55886 | 1.74517 |
| 3 | 3.60325 | 2.75842 | 1.33345 | 0.62784 | 0.33587 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cveticanin, L.; Zukovic, M.; Cveticanin, D. Approximate Analytic Frequency of Strong Nonlinear Oscillator. Mathematics 2024, 12, 3040. https://doi.org/10.3390/math12193040
Cveticanin L, Zukovic M, Cveticanin D. Approximate Analytic Frequency of Strong Nonlinear Oscillator. Mathematics. 2024; 12(19):3040. https://doi.org/10.3390/math12193040
Chicago/Turabian StyleCveticanin, Livija, Miodrag Zukovic, and Dragan Cveticanin. 2024. "Approximate Analytic Frequency of Strong Nonlinear Oscillator" Mathematics 12, no. 19: 3040. https://doi.org/10.3390/math12193040
APA StyleCveticanin, L., Zukovic, M., & Cveticanin, D. (2024). Approximate Analytic Frequency of Strong Nonlinear Oscillator. Mathematics, 12(19), 3040. https://doi.org/10.3390/math12193040






