Abstract
In order to improve quality assurance in wafer manufacturing, there are strict process requirements. Besides the well-known residency time constraints (RTCs), a dual-arm cluster tool also requires each robot arm to execute a specific set of tasks. We call such a tool an arm task-constrained dual-arm cluster tool (ATC-DACT). To do this, one of the arms is identified as the dirty one and the other as the clean one. The dirty one can deal with raw wafers, while the clean one can deal with processed wafers. This requirement raises a new problem for scheduling a cluster tool. This paper discusses the scheduling problem of ATC-DACTs with RTCs. Due to the arm task constraints, the proven, effective swap strategy is no longer applicable to ATC-DACTs, making the scheduling problem difficult. To address this problem, we explicitly describe the robot waiting as an event and build a Petri net (PN) model. Then, we propose a hybrid task sequence (HTS) as an operation strategy by combining the swap and backward strategies. Based on the HTS, the necessary and sufficient conditions for schedulability are established; also, a linear programming model is developed. We then develop an algorithm using these results to optimally schedule the system. Industrial case studies demonstrate the application of this method.
MSC:
90C27; 93C65
1. Introduction
As a kind of complex wafer fabrication system that integrates various fabrication processes and robot operations in semiconductor manufacturing, cluster tools are crucial. Optimizing the operation of cluster tools is essential for enhancing the overall performance and efficiency of semiconductor production lines [1,2]. As shown in Figure 1, cluster tools comprise several process modules (PMs), a single-arm or dual-arm robot, and two loadlocks (LLs) for cassette loading and unloading. Single-wafer processing technology is employed in PMs, allowing each PM to process only one wafer at a time. Typically, 25 wafers with the same recipe are held in a cassette [3]. The robot follows a predetermined recipe to deliver wafers from a cassette to PMs for processing. Once all the operations are finished, a wafer is returned to its original position in the cassette.
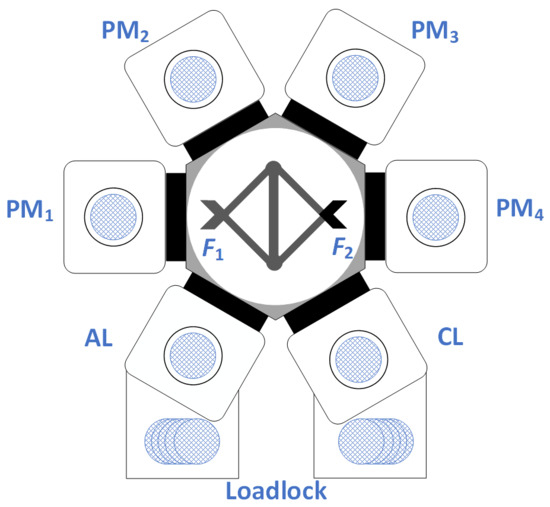
Figure 1.
A dual-arm cluster tool.
In this article, the addressed cluster tool is equipped with a dual-arm robot; thus, it is named a dual-arm cluster tool. The two arms are closely coupled in its structure, allowing only one arm to load or unload a wafer into or from a PM at a time. Therefore, when one arm performs an unloading or loading task at a PM or LL, the arm should enter the PM or LL to pick up or place a wafer. Additionally, with several LLs, it ensures that raw wafers can enter the tool for processing in time. Thus, LLs are not the bottleneck in terms of a tool’s throughput.
Preventing wafer contamination is crucial for wafer quality and production efficiency, and it is the key factor in ensuring high-quality and sustainable manufacturing. For this purpose, one of the requirements is to impose strict wafer residency time constraints (RTCs) on the tool operation [4,5]. With RTCs, once a wafer is processed in a PM, it needs to be taken out from the PM within a limited time; if not, the chemical gas and high temperature would contaminate or damage the wafer. Notice that there may be dust on raw wafers, which are called dirty wafers in semiconductor fabs. After a dirty wafer visits a processing step, it is cleaned such that a processed wafer is called a clean wafer. Thus, if once a robot arm grasps a raw wafer, the arm may be contaminated. Then, if this arm is used to deliver a processed wafer, it may contaminate it. Thus, in wafer fabrication practice, an arm task constraint (ATC) is imposed to further ensure the wafer fabrication quality to avoid the mutual contamination of wafers via robot arms. Such a constraint is typically employed for chemical vapor deposition processes. By this constraint, the robot arms are classified into two types: dirty and clean ones. The dirty arm can perform tasks for grasping raw wafers (dirty wafers) only, while the clean arm should be dedicated to grasping processed wafers (clean wafers). As shown in Figure 1, we use F1 and F2 to denote the dirty and clean arms, respectively. Thereafter, we call this cluster tool an arm task-constrained dual-arm cluster tool (ATC-DACT in short).
The structure of this article is outlined below. After the related work is reviewed in the subsequent section, Section 3 then presents the scheduling strategy and develops the colored PN model for the system of an ATC-DACT under the scheduling strategy. In Section 4, we analyze the temporal properties and analytically derive the necessary and sufficient conditions for obtaining a feasible schedule. With these conditions, we propose an integrated scheduling algorithm that combines linear programming to achieve an optimal cycle time. In Section 5, the practical applicability of the proposed method is demonstrated through experiments. This demonstrates how the proposed method can be effectively applied and validated. Finally, Section 6 summarizes the findings and identifies further avenues for research directions, to address the remaining problems.
2. Literature Review
In recent years, great attention has been paid to the scheduling of dual-arm cluster tools in semiconductor manufacturing [4,6,7,8,9,10,11,12,13]. However, to the best of the authors’ knowledge, all of them are conducted under the assumption that both robot arms can perform any robot task, which is different from the problem addressed in this paper. As a result, the findings from these studies cannot be applied to the case here. Thus, we conduct this study on scheduling an ATC-DACT to respond to the demand of practical applications.
To increase productivity and ensure product consistency and production stability, a cluster tool typically operates under a steady state for most of the time. If the robot remains constantly busy and its task time dominates the cycle time, under such a state, the tool is said to be transport-bound. Conversely, under most real production environments, wafer processing in a PM takes significantly more time than robot tasks, making a tool be process-bound. For process-bound situations, productivity can be maximized if a backward strategy is employed for single-arm cluster tools [14,15] and a swap strategy is applied for dual-arm cluster tools [16]. These research results are obtained for tools without RTCs being imposed. Although an ATC-DACT is a dual-arm cluster tool, a traditional swap strategy cannot be used, since the strategy cannot be performed for some of the steps. For these steps, the tool can just act as a single-arm one. Thus, for ATC-DACTs, the scheduling strategy should be a hybrid one by combining the backward and swap strategies. With this observation, we study the scheduling problem of ATC-DACTs.
With RTCs, the authors in [4,7,17] propose several methods to devise feasible and optimal periodic schedules for cluster tools equipped with a dual-arm robot. Moreover, Wu et al. [3,8] develop a type of method from the control theory perspective for scheduling cluster tools for robots with either single or dual arms, aiming at the effective optimization and viability of schedules. Lim et al. [18] address the challenge of unbalanced processing parameters among the steps to enhance the effectiveness in meeting RTCs by introducing a novel category of robot task sequences. Ko et al. [9] address the concurrent handling of multiple wafer types by proposing a method for cluster tools with a dual-arm robot. Their method focuses on meeting RTCs and achieving the shortest cycle time by determining the optimal release sequence for different wafer types. Lim et al. [19] propose a flexible method to improve the stability of schedules for cluster tools with RTCs and processing time variations. The management of robot waiting time has been identified as a critical factor in scheduling single- and dual-arm cluster tools, while adhering to RTCs. Consequently, researchers have introduced a method referred to as the robot waiting time method, which is discussed in [11,15]. By utilizing this method, cluster tools with both RTCs and activity time variations can be effectively scheduled [1,19,20,21,22,23,24]. The above discussion is summarized in Table 1.

Table 1.
System characteristics and scheduling methods of cluster tools.
It follows from the above discussion that the existing studies are conducted under the assumption that there is no restriction on performing tasks for a robot arm. Thus, the robot task sequence for an ATC-DACT differs from both the backward and swap strategies that are employed in the existing methods. Hence, properly determining the robot task sequence is of utmost importance in analyzing the addressed problem. Also, we need to identify the robot’s two arms so that the tasks can be correctly performed. Thus, the existing techniques are not applicable to the addressed problem, and this work attempts to cope with it. To accurately describe the dynamic behavior of the system, we construct a PN model. In the developed model, we associate different colors with the two arms, ensuring the correct representation of their behavior. It is worth noting that this approach differs from the model presented in [25]. This model is highly compact, easily extendable, and capable of eliminating all infeasible states independently. Consequently, we can search for an optimal schedule within a feasible space, significantly simplifying the scheduling complexity. Based on this, proper robot task sequences are proposed, and an efficient scheduling method is derived. In summary, this work makes the following contributions: (1) proposing a scheduling strategy that can be applied to ATC-DACTs; (2) with a PN model built, necessary and sufficient schedulability conditions are derived; (3) an efficient scheduling algorithm is proposed to obtain a feasible and optimal schedule; and (4) industrial examples are given to show the applications of the proposed method.
3. System Modeling
The effectiveness of PNs in modeling discrete event systems, particularly in semiconductor manufacturing, has been demonstrated in many studies [22,23,27,28]. These studies emphasize the application of PNs to accurately model and analyze the behavior of cluster tools in semiconductor manufacturing. The efficient scheduling of cluster tools with both single-arm and dual-arm robots, while considering RTCs, has been achieved by analyzing the robot waiting based on PN models [3,8]. Since an ATC-DACT can neither operate as a single-arm cluster tool nor a dual-arm one, the PN models and scheduling methods in [3,8] are not applicable. A colored Petri net (CPN) model is presented for the discussed cluster tools under a hybrid operational strategy that combines the backward and swap strategies in this work. This model accurately represents the behavior of ATC-DACTs and allows for efficient analysis and scheduling optimization.
3.1. Steady-State Process
Starting from its idle state, a cluster tool undergoes an initial transient process to be transferred into a steady state. Suppose that there are n processing steps for a specific wafer type and Step i is configured with mi PMs. During the initial transient process, wafers are delivered to the PMs from LLs for processing. As the system evolves, when every PM is processing a wafer, i.e., there are wafers being processed, the system enters a steady state and operates periodically. When a cluster tool is to be terminated, the wafers in the system are completed one by one and returned to LLs without delivering raw wafers to the system. After completing them, the tool returns to the idle state. The primary focus of this research is the analysis of scheduling for the steady-state process in question.
There are extensive research reports that focus on modeling and evaluating the performance of scheduling cluster tools under a steady state [8,26,29]. According to Shin et al. [30], robot tasks are subsequently followed by process activities. Therefore, scheduling robot tasks is crucial for cluster tools. It is recognized that each robot task takes a constant time that is significantly shorter than that for wafer processing in PMs [7].
In wafer fabrication, wafers within a cassette are processed following a sequence of process steps guided by a recipe. Also, it is possible to configure a specific number of PMs for each step to achieve a proper workload distribution among the n steps [11], which is represented by the wafer flow pattern (m1, m2, m3, …, mn), where mi indicates the number of PMs for Step i. Throughout this entire article, we discuss the scenarios where n ≥ 2. At the beginning, raw wafers are retrieved from an LL, while completed wafers are returned to the LL. Upon unloading the last wafer from the LL, the ATC-DACT processes wafers from cassettes in the other LLs. The tool continuously repeats a stable cycle through this pipeline-style processing until it has completed the processing of all the wafers that are required.
3.2. Finite Capacity PN
Scheduling an ATC-DACT involves dynamically assigning finite resources to its activities. Given that modeling resource allocation can be effectively achieved using a finite capacity PN, we propose a PN model for the ATC-DACT utilizing the concept of a finite capacity PN. This study derives the PN concept from the work introduced in [31,32]. A finite capacity PN refers to a specific type of directed graph that consists of transitions and places. Let N = {0, 1, 2, …} and Nn = {1, 2, 3, …, n}. Denote PN = (P, T, I, O, M, K), where (1) the finite set of places is denoted as P = {p1, p2, …, pm}; (2) the finite set of transitions is denoted as T = {t1, t2, …, tn}, satisfying P ∩ T = ∅ and P ∪ T ≠ ∅; (3) the input function is denoted as I: P × T → N; (4) the output function is denoted as O: P × T → N; (5) M: P → N is a marking that counts the tokens in places, and the initial marking is given as M0; and (6) K: P → Nn is a capacity function, and K(p) gives p’s capacity.
The set of all input places to transition t is referred to as its preset, denoted as λt = {p: p ∈ P and I (p, t) > 0}; and the set of all output places from t is known as its postset, denoted as tλ = {p: p ∈ P and O(p, t) > 0}. Likewise, the preset of p is expressed as λp = {t ∈ T: O(p, t) > 0}, and its postset is expressed as pλ = {t ∈ T: I(p, t) > 0}.
Definition 1.
For a transition t ∈ T in a finite capacity PN, it is considered enabled if both Conditions (1) and (2) are satisfied for ∀p ∈ P.
and
A transition is firable when it is enabled. The firing of a firable transition t results in a making evolution at marking M according to (3).
M(p) ≥ I(p, t)
K(p) ≥ M(p) − I(p, t) + O(p, t)
M(p) = M(p) − I(p, t) + O(p, t)
As for Definition 1, for a transition t to be firable, it requires that any place in λt should have adequate tokens, while any place in tλ should have sufficient free space. Accordingly, t is referred to as process-enabled when Condition (1) is satisfied, while it is referred to as resource-enabled when Condition (2) is satisfied. Hence, it should be both process- and resource-enabled when t is enabled. A series of transition firings leads to a series of markings. A transition in a PN is considered live if it can fire at least once again in some firing sequence for every marking M reachable from M0. We say that M is reachable from M0 if there exists a series of transition firings that transform M0 into M. Let R(M0) denote the set comprising all markings that can be reached from M0. A PN is deemed live when every t ∈ T is live. The property of liveness in a PN ensures the occurrence of all events and activities represented in the model.
3.3. PN Modeling for ATC-DACT
We number the processing steps as Steps 1 to n. To ensure brevity in the presentation, we assume that both Steps 0 and n + 1 are for LLs that are treated as resources for this processing step. As a result, with n steps, the system comprises a total of n + 1 steps. The mi PMs configured for Step i, i ∈ Nn, are modeled by a timed place pi with K(pi) = mi; while LLs (Steps 0 and n + 1) can be modeled by p0 with K (p0) = ∞, implying that they can store all the raw and completed wafers. In the model, we describe the robot using place r; we have K(r) = 2, indicating its capacity for holding two wafers simultaneously. Different colors are used to identify the two arms modeled by the two tokens. Then, we present how to model each processing step. For Step 1, a swap operation can be applied, and each robot arm can hold a wafer, allowing the robot to accommodate a total of two wafers. To schedule a cluster tool, at Step 1, the robot may wait before, after, or during swapping. Thus, for Step 1, besides p1, we add timed places q12 and q13 with K(q12) = K(q13) = 1, meaning that the robot waits during a swap operation while holding a wafer. For Step i, i ∈ Nn, the presence of place qi with K(qi) = 1 represents the robot’s waiting before unloading a completed wafer from pi. For cases with n > 2, from Steps 2 to n, only arm F2 is allowed to be used and the robot acts as a single-arm one; thus, it follows the backward strategy. Hence, to operate an ATC-DACT, the robot follows a hybrid task strategy (HTS), i.e., a swap operation is adopted at both Steps 1 and 0, or Step 1 only, while a backward operation is employed in the subsequent steps.
Based on the HTS, the PN model that describes the dynamical behavior of an ATC-DACT is illustrated in Figure 2, where, pictorially, circles ( ) represent places, bold black bars (
) represent places, bold black bars ( ) represent transitions, and black and gray dots (● and ●) are used to denote the tokens for F2 and F1, respectively. Connections between transitions and places are depicted using directed arcs.
) represent transitions, and black and gray dots (● and ●) are used to denote the tokens for F2 and F1, respectively. Connections between transitions and places are depicted using directed arcs.
 ) represent places, bold black bars (
) represent places, bold black bars ( ) represent transitions, and black and gray dots (● and ●) are used to denote the tokens for F2 and F1, respectively. Connections between transitions and places are depicted using directed arcs.
) represent transitions, and black and gray dots (● and ●) are used to denote the tokens for F2 and F1, respectively. Connections between transitions and places are depicted using directed arcs.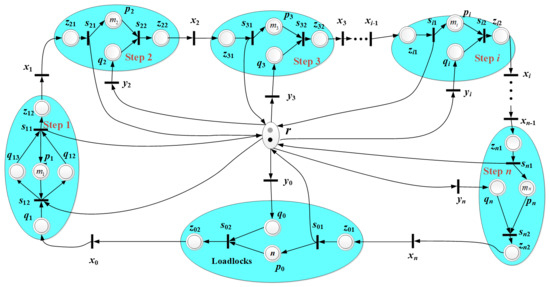
Figure 2.
A PN Model for an ATC-DACT (n > 2).
When n = 2, we can derive the PN depicted in Figure 3. In this case, the robot executes swap operations at Steps 1 and 0. Additionally, F1 and F2 can be utilized at LLs (Step 0).
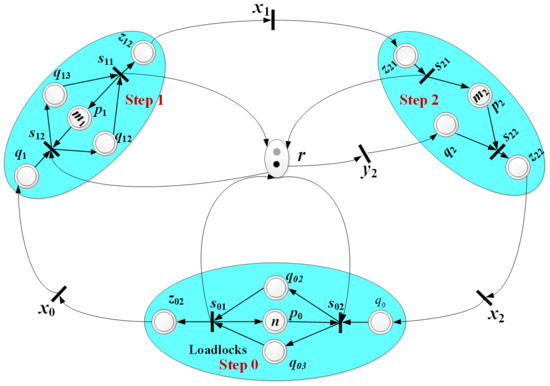
Figure 3.
A PN Model for an ATC-DACT (n = 2).
After being released into the system via LLs, wafers proceed to the PMs following a predetermined order. The robot is responsible for wafer transportation, thereby engaging in various tasks, including unloading a wafer from a PM/LL and loading a wafer into a PM/LL, moving between PMs/LLs, and performing swaps. Each task consumes time and is captured and represented using timed transitions within the PN model. According to Figure 2, the transitions denoted as xi in the model represent the robot’s movements between PMs/LLs while carrying a wafer. Transitions s11 and s12 represent the swapping process at p1, symbolizing the unloading and loading of a wafer from and into p1, respectively. The robot loading/unloading a wafer into/from Step i is denoted by transition si1 and si2, i ∈ Nn\N1. To model the robot tasks associated with unloading a wafer from an LL, aligning it, and loading a wafer into an LL, the timed transitions s01 and s02 are employed. When n > 2, according to Figure 2, timed transition yi represents the robot’s movement from Steps i + 2 to i. Similarly, yi−1 represents the robot’s movement from Step 0 to n − 1, y0 depicts the robot’s movement from Step 3 to 0, and yn depicts the robot’s movement from Step 2 to n. When n = 2 in Figure 3, timed transition y2 is used for the robot waiting at Step 2. For the nontimed places, transitions xi−1 and si1 are connected by place zi1, transitions si2 and xi, are connected by zi2, the connection between s02 and x0 is facilitated by z02, and the connection between s01 and xn is facilitated by z01.
Due to that, dirty and clean arms should be distinguished. The model is enhanced by incorporating colors into the PN model to address this issue. We use f1 and f2 to denote the two tokens for F1 and F2 in place r, and they have colors c1 and c2, respectively. Only the token with color c1 can enable transitions s02 and s11, and tokens with color c2 trigger all other transitions. Then, to determine which transition should be triggered at a given moment, the colors for transitions should be defined.
Definition 2.
In the developed model, the color of s02 and s11 is defined as C(s02) = C(s11) = c1; and the color of sij is defined as C(sij) = c2, {(i, j)|i ∈ Nn, j ∈ {1, 2}}\{(0,2), (1,1)}. In this way, if q ∈ λsij and a token in q enables sij, then this token has the same color c1 as that of s02 or s11, and color c2 is same as the color of sij, {(i, j)|i ∈ Nn, j ∈ {1, 2}}\{(0,2), (1,1)}.
Notice that, according to Definition 2, if a token has color c1, it indicates that f1 enables s02 or s11, and when a token has color c2, f2 enables sij, {(i, j)|i ∈ Nn, j ∈ {1, 2}}\{(0,2), (1,1)}. The token f1 in z02 implies that it enables s02; then token f1 triggers x0; so, the color of transition x0 is C(x0) = c1. All other transitions xi are initiated by f2; thus, the colors of transitions xi’s are defined as C(xi) = c2, i ∈ Nn. Nevertheless, it should be noted that the model is only applicable for analyzing qualitative properties [33].
Theoretically, M0 should depict the system’s startup state, i.e., an idle condition where all PMs are free. However, considering the objective of achieving an optimal steady-state cyclic scheduling, all PMs are engaged in processing at the steady state. To tackle this issue, we can think that the system is initially processing virtual wafers, denoted as W0. M0(pi) represents the number of tokens in pi, disregarding the color of the tokens at M0. Thus, M0 can be described as M0(pi) = K(pi) and M0(q12) = M0(q13) = M0(qi) = 0, i ∈ Nn. During the evolution of the PN model, virtual wafers are sequentially removed, while actual wafers are loaded into the system sequentially. The system enters a steady state once all virtual wafers have been removed. By definition, M(pi) represents the number of tokens in pi at M, disregarding the tokens’ color; M(p0, c1) is the number of tokens with color c1 in p0 at M; M(pi, c2) the number of tokens with color c2 in pi at M; M(r) the number of tokens in r, disregarding the tokens’ color at M; M(r, c1) the counts of tokens with color c1 in r at M; and M(r, c2) the counts of tokens with color c2 in r at M. This study presents a transition control policy formulated as follows to avoid deadlock for the PN model.
Definition 3.
At marking M, for the PN model of an ATC-DACT with n > 2, transition yi, i ∈ Nn\N1, is said to be control-enabled if M(pi+1, c2) = mi+1 − 1; and transition yn is said to be control-enabled if M(pi, c2) = mi, i ∈ Nn; transition y0 is said to be control-enabled if M(pi, c2) = mi, i ∈ Nn\{2}, and M(p2, c2) = m2 − 1.
The control policy specified in Definition 3 is presumed to govern the PN model. According to Definition 3, at marking M0, the only enabled transition is yn. When yn fires, it is succeeded by sn2, xn, and s01 to reach M1, at which only yn−1 is enabled. The firing of yn−1 is succeeded by s(n−1)2, xn−1, and sn1 to reach Mk, at which only yn−k is enabled. Then, the firing of yn−k is followed by s(n−k)2, xn−k, and s(n−k+1)1, resulting in the attainment of marking Mn−2 such that only y0 is enabled. By firing y0 and then s02, x0, and s12, the system reaches Mn, at which only y0 is enabled, resulting in the firing of y0, sn2, xn, and s01. Notice that markings M0 and Mn are identical, implying a completed cycle.
Definition 4.
For the PN model of an ATC-DACT with n = 2, at marking M, transition s02 is considered to be control-enabled if M(p0, c1) = K(p0), M(r, c1) = 1, and M(q0, c2) = K(q0); s12 is considered to be control-enabled if M(p1, c2) = K(p1), M(r, c2) = 1, and M(q1, c1) = K(q1); and s22 is considered to be control-enabled if M(p2, c2) = m2, M(r, c1) = 1, and M(q2, c2) = K(q2); and s21 is considered to be control-enabled if M(p1, c2) = m1 and M(p2, c2) = m2 − 1.
Notice that if f1 is in r and f2 is in q0, transition s02 is firable; if f2 is in r and f1 is in q1, s12 is firable; if f1 is in r and f2 is in q2, s22 is firable. Triggering s21 results in only one token with color c2 in z21. Hence, by Definitions 3 and 4, it can be readily verified that the PN model accurately represents the behavior of the steady-state process of an ATC-DACT.
With the above modeling, we provide the model structure, the state of the system (i.e., marking), rules for transition enabling and firing, and the logic governing the behavior of the system. Meanwhile, by controlling y0 and yi, i ∈ Nn\N1, as stated in Definition 3, it ensures that the PN model is deadlock-free.
While the model can guarantee the deadlock-freeness in the system, it does not necessarily imply the liveness of the PN model. This is due to time delay constraints associated with certain activities, if we treat the violation of wafer RTCs as non-liveness. In contrast, it can be easily verified that if an unrestricted token residency time is permitted for every pi, then the PN must exhibit its liveness. In other words, it is the RTCs that make the system non-live. To describe this, let τi represent the sojourn time of a wafer in a PM at Step i, i ∈ Nn. To meet the RTCs, once a wafer completes its processing at a step, it is required to depart from the PM within a limited time window. Let δi denote such a limited time at Step i, i ∈ Nn. Further, let αi, i ∈ Nn, represent the required processing time of a wafer in a PM at Step i. Then, di = τi − αi presents the wafer delay time of a wafer in a PM at Step i, i ∈ Nn. The liveness property of the PN allows us to derive the following proposition.
Proposition 1.
Given the permissive wafer sojourn time window [αi, αi + δi] for Step i, i ∈ Nn, and the PN of an ATC-DACT being determined to be live when si2 is enabled at any reachable marking M, we can ensure the satisfaction of Constraint (4).
αi ≤ τi ≤ αi + δi
Within the context of the model illustrated in Figure 2, each place or transition symbolizes a specific task that consumes time. Consequently, it is imperative to assign temporal values to these elements. The time needed to fire transition xi is expressed by μ, that is, the time duration for the robot to rotate between PMs/LLs; β signifies the firing time of transitions si1 and si2 (where i ≠ 0), indicating the time required for the robot to execute wafer unloading/loading operations, with β0 representing the firing time of transition s02, which represents the temporal duration necessary for the robot to unload and align wafers from an LL. If the robot does not wait during a swap operation at p1, the time for firing transitions s12 and s11 together forms the duration of a swap operation, calculated as λ = 2β + μ, encompassing the time of unloading, rotation, and loading operations. To optimize the schedule of an ATC-DACT, the robot may intentionally wait some time; it can wait during a swap operation and before unloading a wafer for both a swap operation and non-swap operation. Let ωis represent the robot waiting time during a swap operation at pi, and ωi1 the robot waiting time before unloading a wafer at pi; both of them are the decision variables for the scheduling problem of an ATC-DACT. Table 2 provides the definitions of places and transitions in the PN model and the corresponding time requirements.

Table 2.
Time durations for places and transitions.
Based on the established PN model and analysis, this work regards scheduling an ATC-DACT as a control strategy to investigate the schedulability of the system and obtain an effective scheduling method.
4. Schedulability Analysis and Scheduling Method
4.1. Temporal Properties
Due to the adoption of the swap operation at Step 1 and/or Step 0 and the employment of the backward operation in the subsequent steps of the task sequence, the number of steps involved affects how to schedule the system. Thus, we investigate the scheduling problem with two cases of n = 2 and n > 2, respectively.
For the first case with n = 2, let θ1 represent the time taken for Step 1 to complete a wafer. At Step 1, the robot acts as a dual-arm system and uses both F1 and F2 to perform a swap operation. Under the steady state with the robot waiting time ω1s during a swap operation, to complete a wafer, task sequence σ1 = ⟨firing s11 and s12 (λ + ω1s) → wafer processing (α1)⟩ is performed. Hence, with m1 PMs for Step 1, the time required for the completion of a wafer can be calculated using Equation (5).
θ1 = (α1 + δ1 + λ + ω1s)/m1 = (α1 + δ1 + 2β + μ + ω1s)/m1
Let θ2 be the required time for the completion of a wafer at Step 2. With Steps 1 and 2 being examined together, the robot acts as neither a single-arm nor a dual-arm one, since the robot performs a backward operation at Step 2 using F2 only, while it performs a swap operation at both Steps 0 and 1 using both F1 and F2. The time for swapping at Step 0 is λ0 = β + μ + β0. Under the steady state, with the consideration of robot waiting, task sequence σ2 = ⟨firing s22 (β) → firing x2 (μ) → robot waiting in q0 (ω01) → firing s02 and s01 (λ0 + ω0s) → firing x0 (μ) → robot waiting in q1 (ω11) → firing s11 and s12 (λ + ω1s) → firing x1 (μ) → firing s21 (β) → wafer processing (α2) → the wafer remains in the PM after processed (i.e., the delay time) (d2)⟩ is performed for the completion of a wafer at Step 2. Thus, with m2 PMs for Step 2, θ2 can be calculated using Equation (6).
Under steady state, with the robot waiting activities being considered, the sequence of robot tasks within a cycle can be rewritten as σ2 = ⟨firing s22 (β) → firing x2 (μ) → robot waiting in q0 (ω01) → firing s02 and s01 (λ0 + ω0s) → firing x0 (μ) → robot waiting in q1 (ω11) → firing s11 and s12 (λ + ω1s) → firing x1 (μ) → firing s21 (β) → robot waiting in q2 (ω21)⟩. We use ψ to denote the robot cycle time, and we can obtain
where ψ = ψ1 + ψ2, with ψ1 = 5β + β0 + 5μ being the robot task time and ψ2 = + being the robot waiting time.
The key to determining the feasibility of a solution lies in whether Constraint (4) can be met or not for each Step i, i ∈ Nn. To do so, an analysis of the wafer sojourn time in each PM is essential. The robot completes a wafer by performing the operations in σ1 or σ2. Therefore, the wafer sojourn time in p1 and p2 can be obtained by Equations (8) and (9), respectively.
τ1 = m1 × ψ − (2β + μ + ω1s)
For the case with n > 2, the robot executes a swap operation at Steps 1 and 0 with both F1 and F2, respectively. From Steps 2 to n, F2 performs the backward operation. Under the steady state, with the robot waiting activities being considered, the task sequence is the same as σ1. With m1 PMs for Step 1, according to σ1, θ1 can be calculated according to Equation (5).
From Steps 2 to n, F2 performs the backward operation. Under the steady state, taking into account the robot waiting activities, task sequence σ3 = ⟨firing s22 (β) → firing x2 (μ) → firing s31 (β) → firing y0 (μ) → robot waiting in q0 (ω01) → firing s02 (β0) → firing x0 (μ) → robot waiting in q1 (ω11) → firing s11 and s12 (λ + ω1s) → firing x1 (μ) → firing s21 (β) → wafer processing (α2) → the wafer remains in the PM after processed (i.e., the delay time) (d2)⟩ is performed for the completion of a wafer. With m2 PMs for Step 2, according to σ3, θ2 is given by Equation (10).
Let θi be the completion time of a wafer at Step i, i ∈ Nn\N2. Under the steady state, taking into account the robot waiting activities, task sequence σ4 = ⟨firing si2 (β) → firing xi (μ) → firing s(i+1)1 (β) → firing yi−1 (μ) → robot waiting in qi−1 (ω(i−1)1) → firing s(i−1)2 (β) → firing xi−1 (μ) → firing si1 (β) → wafer processing (αi) → the wafer remains in the PM after processed (i.e., the delay time) (di)⟩ is performed to process a wafer. With mi PMs for Step i, according to σ4, θi can be determined using Equation (11).
θi = (αi + di + 4β + 3μ + ω(i−1)1)/mi
For the satisfaction of Constraint (4), τi should be computed, and it relies on the cycle time of the robot. Therefore, it is necessary to analyze the periodic motion of the robot to determine its cycle time. The robot task sequence can be written as σ5 = ⟨firing sn2 (β) → firing xn (μ) → firing s01 (β) → firing yn−1 (μ) → robot waiting in qn−1 (ω(n−1)1) → firing s(n−1)2 (β) → firing xn−1 (μ) → firing sn1 (β) → firing yn−2 (μ) → firing y2 (μ) → robot waiting in q2 (ω21) → firing s22 (β) → firing x2 (μ) → firing s31 (β) → firing y0 (μ) → robot waiting in q0 (ω01) → firing s02 (β0) → firing x0 (μ) → robot waiting in q1 (ω11) → firing s11 and s12 (λ + ω1s) → firing x1 (μ) → firing s21 (β) → firing yn (μ) → robot waiting in qn (ωn1) → firing sn2 again⟩, and a cycle completes. Then, we can obtain the time taken for a robot task cycle as given by Equation (12).
where ψ = ψ1 + ψ2, with ψ1 = (2n + 1)β + β0 + (2n + 2)μ being the robot task time and ψ2 = ω1s + being the robot waiting time.
A wafer is completed by performing the operations in σ1, σ3, σ4, or σ5. Therefore, the τ1 is the same as that obtained by (8), and τ2 and τi are obtained by Equations (13) and (14), respectively.
τi = mi × ψ − (4β + 3μ + ω(i−1)1)
4.2. Schedulability Conditions and Linear Programs for Solution
With the PN model and timeliness analysis described above, we can now discuss the existence of feasible solutions. Let Θ represent the cycle time. The following result can be derived.
Proposition 2.
For an ATC-DACT, if the HTS operates under the steady state, the robot cycle time should equal the time required to complete a wafer at each step and the cycle time of the entire system, i.e., Equations (15) and (16) hold.
where θ1 with n ≥ 2, θ2 with n = 2, θ2 with n > 2, and θi, i ∈ Nn\N2 and n > 2, are obtained by (5), (6), (10) and (11), respectively.
Θ = ψ = θ1 = θ2, n ≥ 2
Θ = ψ = θi, i ∈ Nn\N2 and n > 2
Under the conditions outlined in Proposition 2, we can adjust the waiting time of the robot to ensure that each PM takes the same time to complete a wafer. Therefore, the scheduling problem here is to optimally regulate the waiting time of the robot to maximize productivity and satisfy the RTCs as well. To make the PN model for an ATC-DACT live by finding a feasible schedule, the θi for Step i should be within a specific range. The upper and lower bounds of θi are denoted as Φiu and Φil, respectively, and they are determined as follows.
and
and
Φ1u = (α1 + δ1 + 2β + μ)/m1, n ≥ 2
Φ1l = (α1 + 2β + μ)/m1, n ≥ 2
Φ2u = (α2 + δ2 + 5β + β0 + 5μ)/m2, n ≥ 2
Φ2l = (α2 + 5β + β0 + 5μ)/m2, n ≥ 2
Φiu = (αi +δi + 4β + 3μ)/mi, i ∈ Nn\N2, n > 2
Φil = (αi + 4β + 3μ)/mi, i ∈ Nn\N2, n > 2
Given a schedule, if it makes θi ∈ [Φil, Φiu] and ∀i ∈ Nn and the PN for the system is live, then the schedule is feasible. Next, for n = 2, we discuss how to schedule the system by examining cases with different steps as the bottlenecks; while for n > 2, i ∈ Nn\N2, we drive a linear programming model to schedule the system. Let Φlmax = max{Φil, i ∈ Nn}; the following lemmas can be developed.
Lemma 1.
Under a steady-state process, if ψ1 ≤ Φlmax ≤ Φiu, ∀i ∈ Nn, an ATC-DACT with RTCs is schedulable via the HTS strategy.
Proof.
From Φlmax ≤ Φiu, it can be seen that [Φ1l, Φ1u] ∩ [Φ2l, Φ2u] ∩ [Φ3l, Φ3u] ∩…∩ [Φnl, Φnu] ≠ ∅ holds, meaning that we can set Θ = Φlmax = ψ. Let ψ2 = ψ − ψ1 = Φlmax − ψ1. When n = 2, set ω0s = ω1s = 0 and ω01 = ω11 = 0; we can obtain ψ2 = ω21. According to (8) and (17), τ1 = m1 ×ψ − (2β + μ) = m1 × Φlmax − (2β + μ) ≥ m1 × (α1 + 2β + μ)/m1 − (2β + μ) = α1, and τ1 = m1 ×ψ − (2β + μ) = m1 ×Φlmax − (2β + μ) ≤ m1 × (α1 + δ1 + 2β + μ)/m1 − (2β + μ) = α1 + δ1. Then, from (3.5) and (3.14), τ2 = m2 ×ψ − (5β + β0 + 5μ) = m2 × Φlmax − (5β + β0 + 5μ) ≥ m2 × (α2 + 5β + β0 + 5μ)/m2 − (5β + β0 + 5μ) = a2, and τ2 = m2 ×ψ − (5β + β0 + 5μ) = m2 × Φlmax − (5β + β0 + 5μ) ≤ m2 × (α2 + δ2 + 5β + β0 + 5μ)/m2 − (5β + β0 + 5μ) = α2 + δ2. Setting ω0s = 0 in Equation (13) is equivalent to setting ω0s = ω1s = 0 in (9). In this case, (13) also conforms to Constraint (4). This makes the RTCs satisfied. If n > 2 and i ∈ Nn\N2, set ω1s = 0 and ωi1 = 0, i ∈ {0, 1, 2, …, n − 1}, by (14), τi = mi × ψ − (4β + 3μ + ω(i−1)1) = mi × Φlmax − (4β + 3μ) ≥ mi × (αi + 4β + 3μ)/mi − (4β + 3μ) = αi, and τi = mi × ψ − (4β + 3μ + ω(i−1)1) = mi × Φlmax − (4β + 3μ) ≤ mi × (αi + δi + 4β + 3μ)/mi − (4β + 3μ) = αi + δi, satisfying the RTCs. Therefore, the lemma holds and the tool is process-bound. □
Lemma 2.
Under a steady-state process, if Φlmax ≤ ψ1 ≤ Φiu, ∀i ∈ Nn, an ATC-DACT with RTCs is schedulable via the HTS strategy in all cases except the case that n = 2 and the bottleneck is Step 2 with m2 = 1.
Proof.
From Φlmax ≤ Φiu, it can be seen that [Φ1l, Φ1u] ∩ [Φ2l, Φ2u] ∩ [Φ3l, Φ3u] ∩…∩ [Φnl, Φnu] ≠ ∅ holds, meaning that Θ ∈ [Φlmax, Φumin] exists such that the robot does not wait anywhere, making (15) and (16) valid. In this case, we just let = 0 and = 0, ψ = ψ1 + ψ2 = ψ1 = Θ. If n ≥ 2, according to (8) and (17), τ1 = m1 × ψ − (2β + μ) = m1 × ψ1 − (2β + μ) ≥ m1 × (a1 + 2β + μ)/m1 − (2β + μ) = α1, and τ1 = m1 × ψ − (2β + μ) = m1 × ψ1 − (2β + μ) ≤ m1 × (α1 + δ1 + 2β + μ)/m1 − (2β + μ) = α1 + δ1. The requirements of the RTCs are met for Step 1. When Φlmax ≤ ψ1 ≤ Φiu, ∀i ∈ Nn\N1, apart from the case that n = 2 and the bottleneck is Step 2 with m2 > 1, it can be derived from Equations (9) and (18) that τ2 = m2 ×ψ − (5β + β0 + 5μ) = m2 × ψ1 − (5β + β0 + 5μ) ≥ m2 × (α2 + 5β + β0 + 5μ)/m2 − (5β + β0 + 5μ) = α2, and τ2 = m2 × ψ − (5β + β0 + 5μ) = m2 × ψ1 − (5β + β0 + 5μ) ≤ m2 × (α2 + δ2 + 5β + β0 + 5μ)/m2 − (5β + β0 + 5μ) = α2 + δ2. Setting ω0s = 0 in Equation (13) is equivalent to setting ω0s = ω1s = 0 in (9). In this case, Equation (13) also conforms to Constraint (4). The system satisfies the RTCs. If n > 2 and i ∈ Nn\N2, according to (14) and (19), τi = mi × ψ − (4β + 3μ + ω(i−1)1) = mi × ψ1 − (4β + 3μ + ω(i−1)1) ≥ mi × (αi + 4β + 3μ)/mi − (4β + 3μ) = αi, and τi = mi × ψ − (4β + 3μ + ω(i−1)1) = mi × ψ1 − (4β + 3μ + ω(i−1)1) ≤ mi × (αi +δi + 4β + 3μ)/mi = αi + δi. The system also satisfies the RTCs. We will show in the following that when Φlmax ≤ ψ1 ≤ Φiu, ∀i∈Nn, if n = 2 and the bottleneck is Step 2 with m2 = 1, an ATC–DACT with RTCs is not schedulable. Hence, the lemma holds. □
In Lemma 2, we excluded the situation where n = 2 and the bottleneck is Step 2 with m2 = 1 without giving proof. We present the proof for that by giving a corollary in the following.
Corollary 1.
Under a steady-state process, if Φlmax ≤ ψ1 ≤ Φiu, ∀i ∈ Nn, n = 2, and the bottleneck is Step 2 with m2 = 1, an ATC-DACT with RTCs is unschedulable via the HTS strategy.
Proof.
With Φlmax ≤ ψ1 ≤ Φiu, ∀i ∈ Nn, if n = 2 and the bottleneck is Step 2, we have ψ1 = 5β + β0 + 5μ and Φlmax = Φ2l = (α2 + 5β + β0 + 5μ)/m2, leading to (α2 + 5β + β0 + 5μ)/m2 ≤ 5β + β0 + 5μ, i.e., α2 ≤ (m2 − 1)(5β + β0 + 5μ) must hold. If m2 = 1, to make this result hold, α2 = 0 must hold, this is meaningless and the corollary is proved. □
Both Lemmas 1 and 2 discuss the cases that [Φ1l, Φ1u] ∩ [Φ2l, Φ2u] ∩ [Φ3l, Φ3u] ∩…∩ [Φnl, Φnu] ≠ ∅. Nevertheless, [Φ1l, Φ1u] ∩ [Φ2l, Φ2u] ∩ [Φ3l, Φ3u] ∩…∩ [Φnl, Φnu] = ∅ may occur, implying that, for some steps, Φlmax > Φiu may hold. In this case, let E = {i|Φlmax > Φiu, i ∈ Nn}, F ∈ Nn\E. Then, the robot waiting times ωi1, ω0s, and ω1s, for ∀i ∈ N2, can be set as follows.
ω1s = 0, i = 1, i ∈ F, n ≥ 2
ω1s = m1 × (Θ − Φ1u), i = 1, i ∈ E, n ≥ 2
For the case of [Φ1l, Φ1u] ∩ [Φ2l, Φ2u] = ∅, we then present the following results.
Lemma 3.
Under a steady-state process, for an ATC-DACT with RTCs, when n = 2 and Step 2 is the bottleneck, assume that [Φ1l, Φ1u] ∩ [Φ2l, Φ2u] = ∅ and ψ1 < Φlmax. Let Φlmax + ΔΦ = ψ = Θ, ΔΦ ≥ 0. In this case, if m1 ≥ m2, an ATC-DACT with RTCs is unschedulable.
Proof.
It will be included in the proof of Lemma 4 presented in the following. □
Lemma 4.
Under a steady-state process, for an ATC-DACT with RTCs, when n = 2 and Step 2 is the bottleneck, if [Φ1l, Φ1u] ∩ [Φ2l, Φ2u] = ∅ and + ≤ Θ − ψ1, let Φlmax + ΔΦ = ψ = Θ, ΔΦ ≥ 0. Then, if there exist ω1s > 0, m1 < m2 and [m1 × (α2 + 5β + β0 + 5μ)/m2 − (α1 + δ1 + 2β + μ) + + ω0s]/(m2 − m1) ≤ ΔΦ ≤ [m1 × (α2 + 5β + β0 + 5μ)/m2 − (α1 + δ1 + 2β + μ) + δ2 + + ω0s]/(m2 − m1), the system is schedulable and the minimum cycle is Θmin = α2/(m2 − 1).
Proof.
When n = 2 and Step 2 is the bottleneck, we have Φlmax = Φ2l > Φ1u. Let Φlmax + ΔΦ = ψ = Θ. By Equation (8) and Φ2l > Φ1u, we have τ1 = m1 × ψ − (2β + μ + ω1s) = m1 × (Φ2l + ΔΦ) − (2β + μ + ω1s) > m1 × (Φ1u + ΔΦ) − (2β + μ + ω1s) = α1 + δ1 + 2β + μ + m1 × ΔΦ − (2β + μ + ω1s) = α1 + δ1 + m1 × ΔΦ − ω1s. For a feasible schedule, τ1 ≤ α1 + δ1 and ΔΦ ≥ 0 must hold. We can make τ1 ≤ α1 + δ1 and ΔΦ ≥ 0 satisfied by simply setting ω1s > 0. By Proposition 2 and Constraint (4), under a steady state, we have θ2 = Φlmax + ΔΦ = (τ2 + 5β + β0 + 5μ + + )/m2 = (α2 + 5β + β0 + 5μ)/m2 + ΔΦ, and α2 ≤ τ2 = α2 + m2 × ΔΦ − ≤ α2 + δ2, leading to the following Equation (24).
By Proposition 2, we have θ1 = Φlmax + ΔΦ = (τ1 + 2β + μ + ω1s)/m1 = (α2 + 5β + β0 + 5μ)/m2 + ΔΦ, τ1 = m1 × (α2 + 5β + β0 + 5μ)/m2 + m1 × ΔΦ − (2β + μ + ω1s). Based on Equation (24), one can obtain τ1 = m1 × (α2 + 5β + β0 + 5μ)/m2 + m1 × ΔΦ − (2β + μ + ω1s) ≥ m1 × (α2 + 5β + β0 + 5μ)/m2 + m1 × ΔΦ − (2β + μ + m2 × ΔΦ) = m1 × Φ2l + (m1 − m2) × ΔΦ − (2β + μ) > m1 × Φ1u + (m1 − m2) × ΔΦ − (2β + μ) = α1 + δ1 + (m1 − m2) × ΔΦ. Then, if m1 ≥ m2, leading to τ1 > α1 + δ1, Constraint (4) is violated and it is the case of Lemma 3, i.e., we present the proof of Lemma 3. On the contrary, if m1 < m2, by Equations (5) and (22), we have τ1 = α1 + δ1. In this case, for a feasible schedule, α2 ≤ τ2 ≤ α2 + δ2 should hold. By Equation (8), α2 ≤ τ2 ≤ α2 + δ2 and ω1s = m1 × (Φlmax + ΔΦ − Φ1u), we can obtain the following Equation (25).
Let = 0, ΔΦmin = [m1 × (α2 + 5β + β0 + 5μ)/m2 − (α1 + δ1 + 2β + μ) + ω0s]/(m2 − m1). Based on Equation (21), ΔΦmin = [m1 × (α2 + 5β + β0 + 5μ)/m2 − (α1 + δ1 + 2β + μ) + α1 + δ1 + (1 − m1) Θ − 3β − β0 − 4μ]/(m2 − m1) = [(α2 + 5β + β0 + 5μ) − m2 × (5β + β0 + 5μ)]/[m2 × (m2 − 1)].
Hence, we can find a feasible schedule by setting the cycle time as Θmin = Φlmax + ΔΦ = Φ2l + ΔΦmin = α2/(m2 − 1), which is the shortest one. Thus, Lemma 4 is proven. □
Lemma 5.
Under a steady-state, for an ATC-DACT with RTCs, when n = 2 and Step 1 is the bottleneck, suppose that [Φ1l, Φ1u] ∩ [Φ2l, Φ2u] = ∅ and Φlmax − ψ1 ≥ + . Then, the system is schedulable.
Proof.
When n = 2 and Step 1 is the bottleneck, we have Φlmax = Φ1l > Φ2u. It follows from Φlmax − ψ1 ≥ + that ω21 = ψ2 − ( + ) = Φlmax − ψ1 − ( + ) ≥ 0. Therefore, we have ψ = Φlmax. For Step 1 ∈ F, by Equation (8), τ1 = m1 × ψ − (2β + μ + ω1s) = m1 × Φ1l − (2β + μ)= m1 × (α1 + 2β + μ)/m1 − (2β + μ) = α1. For Step 2 ∈ E, by Equations (9) and (21), setting = 0, τ2 = m2 × ψ − (5β + β0 + 5μ + ω0s) = m2 × Φlmax − [5β + β0 + 5μ + m2 × (Φlmax − Φ2u)] = α2 + δ2. Because E ∪ F = N2 and E ∩ F = ∅, the RTCs are satisfied for both steps. Therefore, it is schedulable. □
Lemmas 4 and 5 provide the necessary and sufficient conditions for the system to be schedulable under [Φ1l, Φ1u] ∩ [Φ2l, Φ2u] = ∅ and ψ1 < Φlmax when n = 2 without discussing the case for n > 2. Based on Equations (5), (10) and (11), when i > 2, the robot waiting time to be considered by Step i has no correlation with that of Steps 1 and 2. Unlike Steps 1 and 2, the correlation can be generated by ω1s. Hence, it becomes significantly more challenging to determine the robot waiting time that satisfies the RTCs while minimizing the cycle time. In this case, deriving the necessary and sufficient conditions for optimally scheduling the system is very difficult. To solve this problem, we can use the analysis’s insights to express the problem as a linear program. This formulation enables us to identify a feasible and optimal schedule efficiently.
Linear Programming Model (LPM).
Under a steady-state process, for an ATC-DACT with RTCs, when n > 2, suppose that [Φ1l, Φ1u] ∩ [Φ2l, Φ2u] ∩ [Φ3l, Φ3u] ∩…∩ [Φnl, Φnu] = ∅ and ψ1 < Φlmax. Let Φlmax + ΔΦ = ψ = Θ, ΔΦ ≥ 0. A linear program is established to obtain a schedule as follows.
Minimize Θ
αi ≤ τi ≤ αi + δi
τ1 = m1 × ψ − (2β + μ + ω1s)
τi = mi × ψ − (4β + 3μ + ω(i−1)1)
Θ = ψ = θ1 = θ2, n ≥ 2
Θ = ψ = θi, i ∈ Nn\N2 and n > 2
Φlmax + ΔΦ = Θ, ΔΦ ≥ 0
Φlmax = max{Φil, i ∈ Nn}
In the LPM, Constraint (4) guarantees that the wafer sojourn time is within the permissible time windows. Then, Equation (12) obtains the robot cycle time. Constraints (8), (13) and (14) determine the sojourn time under the HTS. Constraints (15) and (16) come from Proposition 2. These two equations combined with Equations (26) and (27) are used to calculate ωis, ωi1, and Θ. By the LPM, if a feasible schedule is found, the system is schedulable; otherwise, it is unschedulable.
With [Φ1l, Φ1u] ∩ [Φ2l, Φ2u] ∩ [Φ3l, Φ3u] ∩…∩ [Φnl, Φnu] ≠ ∅, we present Lemmas 1 and 2, where it is assumed that ψ1 ≤ Φiu, ∀i ∈ Nn. However, with [Φ1l, Φ1u] ∩ [Φ2l, Φ2u] ∩ [Φ3l, Φ3u] ∩…∩ [Φnl, Φnu] ≠ ∅, there may be a Step k ∈ Nn such that ψ1 > Φku. As stated by Lemma 6 below, the system is not schedulable in this case.
Lemma 6.
Under a steady-state process, for an ATC-DACT with RTCs, if Φlmax ≤ Φiu, ∀i ∈ Nn, and there exists Step k such that ψ1 > Φku, then the tool is not schedulable via the HTS strategy.
Proof.
If k = 1 and n ≥ 2, by Equations (8) and (17), and ψ1 > Φ1u, τ1 = m1 × ψ − (2β + μ + ω1s) = m1 × (ψ1 + ψ2) − (2β + μ + ω1s) > m1 × Φ1u − (2β + μ + ω1s) = α1 + δ1 − ω1s. Due to Φlmax ≤ Φ1u, we can obtain ω1s = 0, so that τ1 > α1 + δ1, violating the RTC. If k = 2 and n = 2, by Equations (9) and (18), and ψ1 > Φ2u, τ2 = m2 × ψ − (5β + β0 + 5μ + + ) = m2 × (ψ1 + ψ2) − (5β + β0 + 5μ + + ) > m2 × (Φ2u+ ψ2) − (5β + β0 + 5μ + + ) = α2 + δ2 + m2 × ω21 + (m2 − 1)( + ). Based on Equation (21), m2 × ω21 + (m2 − 1)( + ) ≥ 0. Then, we have τ2 > α2 + δ2; the lemma holds. If k = 2 and n > 2, by Equations (13) and (18), and ψ1 > Φ2u, τ2 = m2 × ψ − (5β + β0 + 5μ + + ω1s) = m2 × (ψ1 + ψ2) − (5β + β0 + 5μ + + ω1s) > m2 × (Φ2u + ψ2) − (5β + β0 + 5μ + + ω1s) = α2 + δ2 + m2 × ω21 + (m2 − 1)(ω1s + ). Again, we obtain m2 × ω21 + (m2 − 1)(ω1s + ) ≥ 0. Then, we have τ2 > α2 + δ2, violating Constraint (4); the lemma holds. If k > 2 and n > 2, by Equations (14) and (19), and ψ1 > Φku, τk = mk × ψ − (4β + 3μ + ω(k−1)1) = mk × (ψ1 + ψ2) − (4β + 3μ + ω(k−1)1) > mk × (Φku + ψ2) − (4β + 3μ + ω(k−1)1) = αk + δk + mk × ω1s + (mk × − ω(k−1)1). We can obviously obtain mk × ω1s + (mk × − ω(k−1)1) ≥ 0. Then, we have τk > αk + δk, violating Constraint (4); it is not schedulable either in this case. □
In the above discussion, we build the necessary and sufficient conditions for ATC-DACTs with RTCs to be schedulable under a steady state. Next, with the above results, Algorithm 1 is given to optimally schedule the system by calculating ωis, i ∈ {0,1}and ωi1, i ∈ {0} ∪ Nn.
| Algorithm 1. If an ATC-DACT is schedulable, find a schedule by setting the robot waiting time | ||
| Input: αi, β, β0, μ, mi, i ∈ Nn | ||
| Output: ωis, i ∈ {0,1} and ωi1, i ∈ {0} ∪ Nn, Θ | ||
| (1) | Calculate Φil, i ∈ Nn, and ψ1 by (7), (12) and (17)–(19) | |
| (2) | If the conditions stated in Lemma 1 are met | |
| (2.1) | ωis = 0, i ∈ {0, 1}; | |
| (2.2) | ωi1 = 0, ∀i ∈ Nn−1; | |
| (2.3) | ωn1 = Φlmax − ψ1; | |
| (2.4) | Θ = ψ = Φlmax. | |
| (3) | If the conditions stated in Lemma 2 are met | |
| (3.1) | ωi1 = 0, ∀i ∈ {0} ∪ Nn; | |
| (3.2) | ωis = 0, i ∈ {0, 1}; | |
| (3.3) | Θ = ψ = ψ1. | |
| (4) | If the conditions stated in Lemma 4 are met | |
| (4.1) | For Step 1 ∈ E, ω1s = m1 × (Θ − Φ1u); | |
| (4.2) | For Step 2 ∈ F, ω0s = (m2 − m1) Θ + α1 + δ1 − (α2 + 3β + β0 + 4μ) and = 0; | |
| (4.3) | ωn1 = Θ − ψ1 − ; | |
| (4.4) | Θmin = Φ2l + ΔΦmin = α2/(m2 − 1). | |
| (5) | If the conditions stated in Lemma 5 are met | |
| (5.1) | For Step 1 ∈ F, ω1s = 0; | |
| (5.2) | For Step 2 ∈ E, ω0s = m2 × (Φlmax − Φ2u) and = 0; | |
| (5.3) | Θ = Φlmax = Φ1l. | |
| (6) | Else | |
| Call LPM. | ||
Through Algorithm 1, under the HTS strategy, if an ATC-DACT is checked to be schedulable according to Lemmas 1, 2, 4, and 5, a feasible schedule can be achieved by simply setting the robot waiting time. Also, by the LPM, a feasible schedule can be efficiently found if it exists. The primary concern is whether the resulting schedule is optimal, which is addressed by the following theorem.
Theorem 1.
If an ATC-DACT is schedulable by the HTS strategy checked by Lemmas 1, 2, 4, and 5, then a schedule obtained through Algorithm 1 is deemed optimal.
Proof.
By Algorithm 1, for Lemmas 1 and 5, the system’s cycle time Θ = Φlmax. Suppose a steady-state schedule exists under the HTS strategy with Θ < Φlmax. Without loss of generality, suppose that Step k is the bottleneck step represented as Φlmax = Φkl. When n ≥ 2, k = 1, by (8), we can obtain τ1 = m1 × ψ − (2β + μ + ω1s) = m1 × Θ − (2β + μ + ω1s) < m1 × Φlmax − (2β + μ + ω1s) = m1 × Φ1l − (2β + μ + ω1s). Then, by (17), we have τ1 < α1 − ω1s. Because ω1s = 0, τ1 < α1, violating the RTCs. Hence, in this case, there is no feasible schedule if Θ < Φlmax. When n = 2, k = 2, by (9), we can obtain τ2 = m2 × ψ − (5β + β0 + 5μ + + ) = m2 × Θ − (5β + β0 + 5μ + + ) < m2 × Φ2l − (5β + β0 + 5μ + + ). Then, by (18), we have τ2 < α2 − ( + . Because + ≥ 0, τ2 < α2, there is no feasible schedule if Θ < Φlmax. When n > 2, k = 2, by (13), we can obtain τ2 = m2 × ψ − (5β + β0 + 5μ + + ω1s) = m2 × Θ − (5β + β0 + 5μ + + ω1s) < m2 × Φ2l − (5β + β0 + 5μ + + ω1s). Then, by (18), we have τ2 < α2 − ( + ω1s), implying no feasible schedule in this case if Θ < Φlmax. When n > 2, k ∈ Nn\N2, by (14), we can obtain τk = mk × ψ − (4β + 3μ + ω(k−1)1) < mk × Φkl − (4β + 3μ + ω(k−1)1). Then, by (19), we have τk < α2 − ω(k−1)1; it is not possible to find a feasible schedule if Θ < Φlmax. For Lemma 2, by Algorithm 1, the resulting schedule is considered unfeasible when the system is scheduled with Θ = ψ < ψ1. For Lemma 4, by Algorithm 1, the system’s minimum cycle time Θmin = Φ2l + ΔΦmin = α2/(m2 − 1). Suppose a steady-state schedule exists under the HTS strategy with the condition that ΔΦ1 < ΔΦmin. That is, ΔΦ1 < [(α2 + 5β + β0 + 5μ) − m2 × (5β + β0 + 5μ)]/[m2 × (m2 − 1)]. By Proposition 2 and Constraint (4), under a steady state, we have θ2 = Φlmax + ΔΦ1 = (τ2 + 5β + β0 + 5μ + + )/m2 = (α2 + 5β + β0 + 5μ)/m2 + ΔΦ1, and α2 ≤ τ2 = α2 + m2 × ΔΦ1 − . Then, we have ΔΦ1 ≥ ( + )/m2. Let = 0, by Equations (21) and (22), we have ΔΦ1 ≥ [(α2 + 5β + β0 + 5μ) − m2 × (5β + β0 + 5μ)]/[m2 × (m2 − 1)]. This conflicts with the assumption that ΔΦ1 < [(α2 + 5β + β0 + 5μ) − m2 × (5β + β0 + 5μ)]/[m2 × (m2 − 1)]. Hence, there is no ΔΦ1 smaller than ΔΦmin for a feasible solution. Finally, linear programming can reliably produce an optimal solution for a given problem, so the cycle time obtained using the LPM is minimized. □
So far, we have established necessary and sufficient conditions for the schedulability of ATC-DACTs and presented the corresponding algorithm to obtain a feasible and optimal schedule, if one exists. Next, we present cases to demonstrate the practical application of the methods outlined in this paper.
Cluster tools are widely applied to wafer fabrication for various processes in semiconductor manufacturing fabs. The vendor of cluster tools should govern the fabrication of wafers that require these processes and fabs provide just the fabrication parameters. Thus, if a cluster tool is developed for some processes, scheduling algorithms dedicated to these processes are necessary. Then, controller should be developed by the vendor for this cluster tool such that relevant scheduling algorithms can be embedded into the controller. Then, in operating this cluster tool, the operator in fabs needs to input the relevant parameters only to complete the fabrication for a given process. Thus, the proposed algorithm here is for the development of controllers for cluster tools in semiconductor manufacturing.
5. Demonstrative Examples
To show how the to apply the proposed method and demonstrate its efficiency and effectiveness, some industrial examples are presented in this section. The research group of this paper is working with some semiconductor-manufacturing equipment venders and semiconductor-manufacturing fabs. The data for the presented examples are obtained from them. In the dataset, the time unit is seconds and omitted in the following cases. The algorithm is coded using the Gurobi Python interface (gurobipy) on a personal computer equipped with Intel Core i3-10100 CPUs running at 3.60 GHz and 16.0 of RAM.
Example 1.
The WFP of this example is (1, 1, 1). Steps 1, 2, and 3 are served by PM1, PM2, and PM3, respectively, and we discuss four cases.
Case 1: The processing time is α1 = 160.0, α2 = 100.0, α3 = 138.0; the RTCs are given as δ1 = 30.0, δ2 = 20.0, and δ3 = 30.0; the robot task time is β = 10.0, β0 = 15.0, and μ = 2.0. This case’s PN model is as in Figure 2 with n = 3. We can obtain Φ1l = 182.0, Φ1u = 212.0, Φ2l = 175.0, Φ2u = 195.0, Φ3l = 186.0, Φ3u = 216.0, and ψ1 = 101.0. Thus, Φlmax = Φ3l = 186.0 > ψ1 and Φlmax < Φ2u < Φ1u; the conditions stated in Lemma 1 are met, i.e., a feasible schedule exists. Based on Algorithm 1, we have Θ = ψ = Φlmax = 186.0, ψ2 = ψ − ψ1 = 186.0 − 101.0 = 85.0. Also, by Algorithm 1, ω1s = ω01 = ω11 = ω21 = 0.0 and ω31 = 85.0 are set; we obtain a feasible and optimal schedule.
Case 2: The processing time is α1 = 90.0, α2 = 37.0, α3 = 78.0; the RTCs are given as δ1 = 32.0, δ2 = 20.0, and δ3 = 25.0; β = 15.0, β0 = 20.0, and μ = 3.0. This case’s PN model is as in Figure 2 with n = 3. We can obtain Φ1l = 123.0, Φ1u = 155.0, Φ2l = 147.0, Φ2u = 167.0, Φ3l = 139.0, Φ3u = 164.0, and ψ1 = 149.0. Thus, Φlmax < ψ1 < Φumin; the conditions in Lemma 2 are satisfied, implying the existence of a feasible schedule. By Algorithm 1, we have Θ = ψ1 = 149.0, so ψ = ψ1 = 149.0. Then, a feasible and optimal schedule is obtained by simply setting ω1s = ω01 = ω11 = ω21 = ω31 = 0.0 via Algorithm 1.
Case 3: In Case 2, the permissive delay time at Step 1 is changed to δ1 = 25.0, with the other parameters being unchanged. This case’s PN model is as in Figure 2, with n = 3. We can obtain Φ1l = 123.0, Φ1u = 148.0, Φ2l = 147.0, Φ2u = 167.0, Φ3l = 139.0, Φ3u = 164.0, and ψ1 = 149.0. Thus, Φlmax = 147.0 < Φ1u <Φ3u and ψ1 > Φ1u, the conditions stated in Lemma 6 are met, and it is evident that scheduling is not feasible.
Case 4: The processing time is α1 = 90.0, α2 = 67.0, α3 = 78.0; the RTCs are given as δ1 = 15.0, δ2 = 20.0, and δ3 = 25.0; β = 15.0, β0 = 20.0, and μ = 3.0. This case’s PN model is as in Figure 2, with n = 3. We can obtain Φ1l = 123.0, Φ1u = 138.0, Φ2l = 177.0, Φ2u = 197.0, Φ3l = 139.0, Φ3u = 164.0, and ψ1 = 149.0. Thus, [Φ1l, Φ1u] ∩ [Φ2l, Φ2u] ∩ [Φ3l, Φ3u] = ∅ and ψ1 < Φlmax. By applying the LPM, it shows that no feasible schedule can be found.
Example 2.
The WFP of this example is (1, 2); PM1 serves for Step 1, and PM2 and PM3 serve for Step 2. There are five cases.
Case 1: The wafer processing time is α1 = 100.0 and α2 = 180.0; the RTCs are given as δ1 = 25.0 and δ2 = 25.0; β = 6.0, β0 = 10.0, and μ = 3.0. This case’s PN model is as in Figure 3, with n = 2. We can obtain Φ1l = 115.0, Φ1u = 140.0, Φ2l = 117.5, Φ2u = 130.0, and ψ1 = 55.0. Thus, Φlmax = Φ2l = 117.5 > ψ1 and Φlmax < Φ2u < Φ1u; the conditions stated in Lemma 1 are met. In this case, it is schedulable. By Algorithm 1, we have Θ = ψ = Φlmax = 117.5, so ψ2 = ψ − ψ1 = 117.5 − 55.0 = 62.5. By setting ω0s = ω1s = ω01 = ω11 = 0.0 and ω21 = 62.5 via Algorithm 1, we obtain a feasible and optimal schedule.
Case 2: The processing time is α1 = 70.0 and α2 = 105.0; the RTCs are given as δ1 = 20.0 and δ2 = 15.0; the robot task time is β = 15.0, β0 = 20.0, and μ = 3.0. This case’s PN model is as in Figure 3, with n = 2. We can obtain Φ1l = 103.0, Φ1u = 123.0, Φ2l = 107.5, Φ2u = 122.5, and ψ1 = 110.0. Thus, Φlmax = Φ2l = 107.5 < ψ1 = 110.0, Φlmax < ψ1 < Φ2u < Φ1u and m2 = 2; the conditions stated in Lemma 2 are met, i.e., it is schedulable. By Algorithm 1, we set Θ = ψ = ψ1 = 107.5, and ω0s = ω1s = ω01 = ω11 = ω21 = 0.0 to achieve a schedule that is feasible and optimal.
Case 3: In Case 2, the processing time at Step 1 is changed to α1 = 50.0, the permissive delay time at Step 1 is changed to δ1 = 25.0, and the other parameters are unchanged. This case’s PN model is as in Figure 3, with n = 2. We can obtain Φ1l = 83.0, Φ1u = 108.0, Φ2l = 107.5, Φ2u = 122.5, and ψ1 = 110.0. Thus, Φlmax = Φ2l = 107.5 < Φ1u < Φ2u and ψ1 > Φ1u; the conditions stated in Lemma 6 are met. In this case, it shows that no feasible schedule can be found.
Case 4: In Case 3, the processing time at Step 2 is changed to α2 = 120.0, the permissive delay time at Step 1 is changed to δ1 = 30.0, and the other parameters are unchanged. This case’s PN model is as in Figure 3 with n = 2. We can obtain Φ1l = 83.0, Φ1u = 113.0, Φ2l = 115.0, Φ2u = 122.5, and ψ1 = 110.0. Thus, [Φ1l, Φ1u] ∩ [Φ2l, Φ2u] = ∅, ψ1 < Φlmax. and m1 < m2. It is checked that the conditions stated in Lemma 4 are met, showing that a feasible schedule can be found. In this case, Θmin = α2/(m2 − 1) = 120.0. Based on Algorithm 1, let = 0.0, we have ω0s = (m2 − m1) Θmin + α1 + δ1 − (α2 + 3β + β0 + 4μ) = 3.0, ω1s = m1 × (Θmin − Φ1u) = 120.0 − 113.0 = 7.0. Hence, ω21 = Θ − ψ1 − = 120.0 − 110.0 − 3.0 − 7.0 = 0.0.
Case 5: In Case 2, the processing time at Step 1 is changed to α1 = 90.0, and the other parameters are unchanged. This case’s PN model is as in Figure 3, with n = 2. We can obtain Φ1l = 123.0, Φ1u = 143.0, Φ2l = 107.5, Φ2u = 122.5, and ψ1 = 110.0. Thus, Φlmax = Φ1l = 123.0 > Φ2u and ψ1 < Φlmax. By (20) and (23); let = 0.0, we have ω1s = 0.0 and ω0s = m2 × (Φlmax − Φ2u) = 1.0, and + = 1.0 < Φlmax − ψ1 = 13.0. The conditions stated in Lemma 5 are met. Therefore, based on Algorithm 1, by setting ω1s = 0.0, ω0s = 1.0 and ω21 = 13.0 − 1.0 = 12.0, a schedule that is feasible and optimal is successfully found.
As discussed above, there may exist unscheduled cases. The results of the experiments can be clearly seen in Table 3. If such a case is detected by the proposed method, this provides process engineers with a message, and engineers can redesign the process to cope with the problem.

Table 3.
Summary of experimental results for industrial examples.
6. Conclusions
Within this study, we explore the scheduling optimization problem under steady state for arm task-constrained dual-arm cluster tools (ATC-DACTs) with RTCs using a PN model. With the configuration properties, we find that when the two arms of a dual-arm robot should be distinguished as dirty and clean ones, meeting the RTCs is more challenging in scheduling such a cluster tool. Thus, finding an optimal and feasible schedule for such tools is a critical issue, and the existing methods are not applicable.
To address this issue, this work builds a colored PN model for it. The PN model explicitly describes when the robot should wait, and the robot waiting is modeled explicitly as an event, thereby revealing the relationship between the wafer sojourn time in a PM and the system cycle time. The PN model uses colors to distinguish the dirty and clean arms. Based on the model, a hybrid task strategy (HTS) for the robot is proposed as a scheduling strategy by combining the swap and backward strategies. We then present necessary and sufficient conditions for the schedulability of an ATC-DACT with RTCs. It is shown that the presence of a feasible schedule is contingent upon both the number of fabrication process steps and the identification of the bottleneck step. We discuss different situations in establishing the schedulability conditions in the case of n = 2. For n > 2, i ∈ Nn\N2, an LPM is established. Then, by summarizing the obtained results, we give an algorithm that can efficiently find a schedule that is both feasible and optimal, if one exists. Finally, this article validates these findings through various case studies.
While this work makes significant strides in addressing the steady-state scheduling problem for ATC-DACTs with RTCs, there are still avenues for further research. First, the current study focuses solely on the steady-state behavior of the system, neglecting the transient processes that occur during system starting or following changes in the production plan. Optimizing these transient processes could further enhance the overall throughput and efficiency of ATC-DACTs. Second, the built model assumes perfect knowledge of all system parameters and does not account for potential uncertainties or disruptions, such as machine breakdowns or wafer defects. Incorporating robust scheduling strategies that can adapt to such uncertainties represents an important direction for future work.
Author Contributions
Conceptualization, L.G. and N.W.; methodology, L.G.; software, S.Z.; validation, T.L.; formal analysis, L.G.; investigation, W.W.; resources, T.L.; data curation, S.Z.; writing—original draft preparation, L.G.; writing—review and editing, L.G.; visualization, W.W.; supervision, N.W. and S.Z.; project administration, S.Z.; funding acquisition, N.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Development Fund (FDCT), Macau SAR (File Nos. 0018/2021/A1, 0083/2021/A2 and 0011/2023/RIA1).
Data Availability Statement
All data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| LL | Loadlock. |
| PM | Process module. |
| PN | Petri net. |
| ATC-DACT | Arm task-constrained dual-arm cluster tool. |
| RTC | Residency time constraint. |
| HTS | Hybrid task sequence. |
| Nn | = {1, 2, 3, …, n}. |
| N | = {0, 1, 2, …}. |
| n | The number of processing steps in a cluster tool. |
| mi | The number of PMs configured for Step i, i ∈ Nn. |
| PMi | The ith PM in a cluster tool. |
| WFP | = (m1, m2, …, mn) defined as wafer flow pattern. |
| K | Capacity function in a PN. |
| M | Marking for a PN. |
| P | Set of places in a PN and P = {p1, p2, …, pm }. |
| T | Set of transitions and T = {t1, t2, …, tn}. |
| I | Input function. |
| O | Output function. |
| ai | The processing time in a PM at Step i, i ∈ Nn. |
| δi | The longest time for a wafer to stay in a PM at Step i after it is processed, i ∈ Nn. |
| di | The wafer delay time of a wafer in a PM at Step i, i ∈ Nn. |
| τi | The sojourn time of a wafer in a PM at Step i, i ∈ Nn. |
| θi | The completion time of a wafer at Step i, i ∈ Nn. |
| μ | The time taken for the robot to rotate between PMs/LLs. |
| β | The time required for the robot to execute wafer unloading/loading operations. |
| β0 | The time required for the robot to unload and align wafers from an LL. |
| λ | The time taken for unloading, rotation, and loading operations. |
| ωis | The robot waiting time during a swap operation at pi, i ∈ {0,1}. |
| ωi1 | The robot waiting time before unloading a wafer at pi, i ∈ Nn ∩ {0}. |
| ψ | The robot cycle time. |
| ψ1 | The robot task time in a cycle. |
| ψ2 | The robot waiting time in a cycle. |
| Θ | The cycle time. |
| Φiu and Φil | The upper and lower bounds of the cycle time for the system. |
References
- Pan, C.R.; Qiao, Y.; Wu, N.Q.; Zhou, M.C. A novel algorithm for wafer sojourn time analysis of single-arm cluster tools with wafer residency time constraints and activity time variation. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 805–818. [Google Scholar]
- Bader, M.E.; Hall, R.P.; Strasser, G. Integrated processing equipment. Solid State Technol. 1990, 33, 149–154. [Google Scholar]
- Wu, N.Q.; Chu, C.B.; Chu, F.; Zhou, M.C. A Petri net method for schedulability and scheduling problems in single-arm cluster tools with wafer residency time constraints. IEEE Trans. Semicond. Manuf. 2008, 21, 224–237. [Google Scholar] [CrossRef]
- Rostami, S.; Hamidzadeh, B.; Camporese, D. An optimal periodic scheduler for dual-arm robots in cluster tools with residency constraints. IEEE Trans. Robot. Autom. 2001, 17, 609–618. [Google Scholar] [CrossRef]
- Lee, T.-E.; Park, S.-H. An extended event graph with negative places and tokens for time window constraints. IEEE Trans. Autom. Sci. Eng. 2005, 2, 319–332. [Google Scholar] [CrossRef]
- Kim, H.-J.; Lee, J.-H. Closed-form expressions on lot completion time for dual-armed cluster tools with parallel processing modules. IEEE Trans. Autom. Sci. Eng. 2019, 16, 898–907. [Google Scholar] [CrossRef]
- Kim, J.-H.; Lee, T.-E.; Lee, H.-Y.; Park, D.-B. Scheduling analysis of time-constrained dual-armed cluster tools. IEEE Trans. Semicond. Manuf. 2003, 16, 521–534. [Google Scholar] [CrossRef]
- Wu, N.Q.; Zhou, M.C. A closed-form solution for schedulability and optimal scheduling of dual-arm cluster tools with wafer residency time constraint based on steady schedule analysis. IEEE Trans. Autom. Sci. Eng. 2010, 7, 303–315. [Google Scholar]
- Ko, S.-G.; Yu, T.-S.; Lee, T.-E. Wafer delay analysis and workload balancing of parallel chambers for dual-armed cluster tools with multiple wafer types. IEEE Trans. Autom. Sci. Eng. 2021, 18, 1516–1526. [Google Scholar] [CrossRef]
- Lee, T.-G.; Yu, T.-S.; Lee, T.-E. Cleaning plan optimization for dual-armed cluster tools with general chamber cleaning periods. IEEE Trans. Autom. Sci. Eng. 2023, 20, 1890–1906. [Google Scholar] [CrossRef]
- Nishi, T.; Matsumoto, I. Petri net decomposition approach to deadlock-free and non-cyclic scheduling of dual-armed cluster tools. IEEE Trans. Autom. Sci. Eng. 2015, 12, 281–294. [Google Scholar] [CrossRef]
- Qiao, Y.; Wu, N.Q.; Zhou, M.C. Schedulability and scheduling analysis of dual-arm cluster tools with wafer revisiting and residency time constraints based on a novel schedule. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 472–484. [Google Scholar] [CrossRef]
- Wang, J.; Liu, C.; Zhou, M.; Leng, T.; Albeshri, A. Optimal Cyclic Scheduling of Wafer-Residency-Time-Constrained Dual-Arm Cluster Tools by Configuring Processing Modules and Robot Waiting Time. IEEE Trans. Semicond. Manuf. 2023, 36, 251–259. [Google Scholar] [CrossRef]
- Lopez, M.J.; Wood, S.C. Systems of multiple cluster tools: Configuration, reliability, and performance. IEEE Trans. Semicond. Manuf. 2003, 16, 170–178. [Google Scholar] [CrossRef]
- Lee, T.-E.; Lee, H.-Y.; Shin, Y.-H. Workload balancing and scheduling of a single-armed cluster tool. In Proceedings of the 5th APIEMS Conferences, Gold Coast, Australia, 12–15 December 2004; pp. 1–6. [Google Scholar]
- Venkatesh, S.; Davenport, R.; Foxhoven, P.; Nulman, J. A steady state throughput analysis of cluster tools: Dual-blade versus single-blade robots. IEEE Trans. Semicond. Manuf. 1997, 10, 418–424. [Google Scholar] [CrossRef]
- Lee, J.-H.; Kim, H.-J.; Lee, T.-E. Scheduling lot switching operations for cluster tools. IEEE Trans. Semicond. Manuf. 2013, 26, 592–601. [Google Scholar] [CrossRef]
- Lim, Y.; Yu, T.-S.; Lee, T.-E. A new class of sequences without interferences for cluster tools with tight wafer delay constraints. IEEE Trans. Autom. Sci. Eng. 2019, 16, 392–405. [Google Scholar] [CrossRef]
- Lim, Y.; Yu, T.-S.; Lee, T.-E. Adaptive scheduling of cluster tools with wafer delay constraints and process time variation. IEEE Trans. Autom. Sci. Eng. 2020, 17, 375–388. [Google Scholar] [CrossRef]
- Yang, F.J.; Wu, N.Q.; Qiao, Y.; Su, R.; Zhang, C.J. (Digital twin) wafer sojourn time fluctuation analysis for time-constrained dual-arm multi-cluster tools with activity time variation. Int. J. Comput. Integr.Manuf. 2020, 34, 734–751. [Google Scholar] [CrossRef]
- Kim, H.-J.; Lee, J.-H.; Lee, T.-E. Schedulability Analysis for Noncyclic Operation of Time-Constrained Cluster Tools with Time Variation. IEEE Trans. Autom. Sci. Eng. 2016, 13, 1409–1414. [Google Scholar] [CrossRef]
- Guo, X.W.; Liu, S.X.; Zhou, M.C.; Tian, G.D. Disassembly sequence optimization for large-scale products with multiresource constraints using scatter search and Petri Nets. IEEE Trans. Syst. Man Cybern. Syst 2016, 46, 2435–2446. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.F.; Li, Z.W.; Al-Ahmari, A. Nonpure Petri net supervisors for optimal deadlock control of flexible manufacturing systems. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 252–265. [Google Scholar] [CrossRef]
- Kim, J.-H.; Lee, T.-E. Schedulability Analysis of Time-Constrained Cluster Tools with Bounded Time Variation by an Extended Petri Net. IEEE Trans. Autom. Sci. Eng. 2008, 5, 490–503. [Google Scholar] [CrossRef]
- Wu, N.Q.; Chu, F.; Chu, C.B.; Zhou, M.C. Petri Net-based scheduling of single-arm cluster tools with reentrant atomic layer deposition processes. IEEE Trans. Autom. Sci. Eng. 2011, 8, 42–55. [Google Scholar] [CrossRef]
- Yi, J.G.; Ding, S.W.; Song, D.Z.; Zhang, M.T. Steady-state throughput and scheduling analysis of multicluster tools: A decomposition approach. IEEE Trans. Autom. Sci. Eng. 2008, 5, 321–336. [Google Scholar]
- Huang, B.; Zhou, M.C.; Huang, Y.S.; Yang, Y.W. Supervisor synthesis for FMS based on critical activity places. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 881–890. [Google Scholar] [CrossRef]
- Huang, B.; Zhou, M.C.; Zhang, P.Y.; Yang, J. Speedup techniques for multiobjective integer programs in designing optimal and structurally simple supervisors of AMS. IEEE Trans. Syst. Man Cybern. Syst 2018, 48, 77–88. [Google Scholar] [CrossRef]
- Kim, W.; Yu, T.-S.; Lee, T.-E. Integrated scheduling of a dual-armed cluster tool for maximizing steady schedule patterns. IEEE Trans. Syst. Man. Cybern. Syst. 2021, 51, 7282–7294. [Google Scholar] [CrossRef]
- Shin, Y.-H.; Lee, T.-E.; Kim, J.-H.; Lee, H.-Y. Modeling and implementing a real-time scheduler for dual-armed cluster tools. Comput. Ind. 2001, 45, 13–27. [Google Scholar] [CrossRef]
- Zhou, M.C.; Venkatesh, K. Modeling, Simulation and Control of Flexible Manufacturing Systems: A Petri Net Approach; World Scientific: Singapore, 1998. [Google Scholar]
- Zhou, M.C.; Jeng, M.D. Modeling, analysis; simulation; scheduling, and control of semiconductor manufacturing systems: A Petri net approach. IEEE Trans. Semicond. Manuf. 1998, 11, 333–357. [Google Scholar] [CrossRef]
- Wu, N.Q.; Zhou, M.C. Colored timed Petri nets for modeling and analysis of cluster tools. Asian J. Control 2010, 12, 253–266. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).