Abstract
In this paper, we express as a linear combination of alternating multiple zeta values, where and , with and being harmonic and alternating harmonic numbers, respectively. These sums include Subbarao and Sitaramachandrarao’s alternating analogues of Tornheim’s double series as a special case. Our method is based on employing two different techniques to evaluate the specific integral associated with a 3-poset Hasse diagram.
Keywords:
alternating multiple zeta values; generalized alternating harmonic numbers; Mordell–Tornheim series; alternating Tornheim-type double series; 3-poset integral MSC:
11M32; 40B05
1. Introduction
Given as a sequence of positive integers and with , and , an alternating multiple zeta value (AMZV) is defined as [1,2,3]
We usually put a bar on top of if . For example, . The numbers and r are called the weight and depth of , respectively. In particular, if for all , then
is the multiple zeta values [4,5]. We let denote k repetitions of a. For example, and .
The generalized harmonic numbers and the generalized alternating harmonic numbers are defined as
where s and n are positive integers. In particular, is the classical harmonic number, and is the alternating harmonic number. The well-known formula for integers ,
was systematically developed by Nielsen [6]. This formula was originally discovered by Euler and later rediscovered by Ramanujan. Another famous formula
was proved by Sitaramachandrarao [6,7]. Harmonic numbers are encountered in Feynman diagram calculations [8], appear in equilibrium analyses [9], and are also applied to the quicksort algorithm [10], among others. Moreover, series involving harmonic numbers have applications across various mathematical disciplines and related fields (see [11,12,13,14,15,16]).
For an r-tuple of positive integers, the Mordell–Tornheim multiple zeta values are defined as
The examination of the special values of this function, specifically for at positive integer points, was first undertaken by Tornheim [17] and independently by Mordell [18], particularly in the case where . These values were later rediscovered by Witten [19] in his work on the volume formula for certain moduli spaces pertinent to theoretical physics. Therefore, we usually refer to this double series as a Tornheim–Witten double series, a Mordell–Tornheim double series, or simply a Tornheim double series.
Bradley and Zhou [20] demonstrated that this value can be expressed as a linear combination of multiple zeta values. Recently, the author of [21] gave an explicit formula for the Mordell–Tornheim multiple zeta values:
where , is the symmetric group of n objects, and represents the permutations induced by on the nonnegative integer set .
Subbarao and Sitaramachandrarao [22] introduced the alternating analogues of Mordell–Tornheim series, which were defined as
They posed the problem to evaluate and for any positive integer r. Tsumura [23,24] provided evaluation formulas for and for any positive odd integer r. He [25,26] also provided evaluation formulas for and for positive integers when is odd. Zhao [27] expressed them as a linear combination of alternating double zeta values.
Kuba [28] studied two general Tornheim series:
which are generalizations of Tornheim’s double series. Inspired by these insights, in this paper, we aim to study the following generalized form and express it as a linear combination of alternating multiple zeta values:
where and . This general form includes both R-series and T-series as concrete examples. For example, we obtain the formula
This paper is organized as follows. In Section 2, we introduce the algebraic structure for alternating multiple zeta values [29,30,31] and present a combinatorial generalization of the iterated integral associated with a 3-poset, represented by a Hasse diagram.
In Section 3, we use the 3-poset integrals to express these two alternating Mordell–Tornheim series as a linear combination of alternating double zeta values, which are the same as the expressions given by Zhao [27].
In Section 4, we decompose A-series as a linear combination of S-series (see Equation (15) for the exact definition), which are power-series expansions of some integrals associated with a 3-poset Hasse diagram. This leads to the calculation of 21 different types of S-series. We provide details of the evaluations of these S-series in Section 5 and Section 6.
In Section 7, we integrate the S-series expressions from the previous two sections with the results from Section 3, compiling all the A-series we plan to evaluate.
In the final section, we showcase the practical implications of our findings through examples like
This paper introduces a method for evaluating a specific 3-poset integral in two different ways: one approach uses the shuffle relations and their associated Lyndon words, and the other uses the corresponding infinite-series expansions. Indeed, this method can be applied not only to double series but also extended to triple series or any finite number of infinite-series sums. An explanation is provided in the concluding remarks section.
2. Algebraic Settings and Integrals Associated with 3-Posets
Let be the -algebra of polynomials in three non-commutative variables, graded by degree, where x, y, and z are each assigned a degree of 1. The algebra is identified with the graded -vector space , which is spanned by the monomials in the variables x, y, and z (see [29,30,31,32]).
Let be the subalgebra of generated by words not beginning with y and not ending with x. The words in are called “admissible words”.
In other words, the subalgebra is generated by admissible words. Let be the -linear map that assigns to each word in , where , the multiple integral
Here, , , and . As the word is in , we always have and , so the integral converges.
Let us define the bilinear product ⧢ (the shuffle product) on by the rules
for any word w, and
for any words , , any letters , y, or z (), and then extend the above rules to the whole algebra by linearity. It is known that each of the above products is commutative and associative [33,34]. We denote the algebras by . By the standard shuffle product identity of iterated integrals, the evaluation map Z is again an algebra homomorphism for the multiplication ⧢ (see [34]):
We introduce a combinatorial generalization of the iterated integral, the integral associated with a 3-poset. We review the definitions and basic properties of 3-labeled posets (we call them 3-posets for short in this paper) and the associated integrals (see [35]).
Definition 1.
A 3-poset is a pair , where is a finite partially ordered set (poset for short) and is a map from X to . We often omit and simply say “a 3-poset X”. The is called the label map of X.
A 3-poset is called admissible if for all maximal elements and for all minimal elements .
A 3-poset X is depicted as a Hasse diagram in which an element x with , , is represented by ∘, •, ⊚, respectively. For example, the diagram
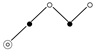 represents the 3-poset with order and label . For convenience, we use
represents the 3-poset with order and label . For convenience, we use  to represent a circles arranged in a chain.
to represent a circles arranged in a chain.
 represents the 3-poset with order and label . For convenience, we use
represents the 3-poset with order and label . For convenience, we use  to represent a circles arranged in a chain.
to represent a circles arranged in a chain.Definition 2.
For an admissible 3-poset X, we define the associated integral
where
Note that the admissibility of a 3-poset corresponds to the convergence of the associated integral. We also recall an algebraic setup for 3-posets. Let be the -algebra generated by the isomorphism classes of 3-posets, whose multiplication is given by the disjoint union of 3-posets. Then, the integral (6) defines a -algebra homomorphism from the subalgebra of generated by the classes of admissible 3-posets. We refer to this type of integral as a 3-poset integral.
There is a -linear map that transforms a 3-poset into a finite sum of words in x, y, and z. This transformation is characterized by the following two conditions: the first condition states that for a totally ordered , , and the second condition asserts that if a and b are non-comparable in X, then can be expressed as , where represents the 3-poset obtained from X by adjoining a new relation . This W sends onto and satisfies
It is known that 2-posets are special cases of 3-posets (see [35,36]).
Let . We list some useful identities for the algebra : For any nonnegative integers , and d, we have
Note that the variables in the summand are assumed to be nonnegative integers throughout this paper. For example, we use the notation to indicate .
In particular, when or z, i.e., are the same elements, the shuffle relations are simplified as follows [21,32]:
3. The Formulas for Alternating Mordell–Tornheim Series
In this section, we utilize the 3-poset integrals to represent two alternating Mordell–Tornheim series, the R-series and T-series, as a linear combination of alternating double zeta values, consistent with the expressions provided by Zhao [27].
Proposition 1.
Given three nonnegative integers a, b, and s, we have
Proof.
Let us consider the following 3-poset integral:
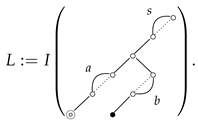 This integral L can be written as
where
Convert and into forms that represent infinite series:
Then, the 3-poset integral L can be rewritten as
This is exactly the representation of . On the other hand, using Equation (7), where and W sends onto , we have
By applying Equation (8), we obtain
By applying the Z map to the above shuffle relation, we have
Therefore, we conclude our result. □
This integral L can be written as
where
Convert and into forms that represent infinite series:
Then, the 3-poset integral L can be rewritten as
This is exactly the representation of . On the other hand, using Equation (7), where and W sends onto , we have
By applying Equation (8), we obtain
By applying the Z map to the above shuffle relation, we have
Therefore, we conclude our result. □
 This integral L can be written as
This integral L can be written as
Next, we apply similar methods to handle the T-series. Therefore, we explain only the important parts and appropriately reduce some of the detailed explanations.
Proposition 2.
For any three nonnegative integers a, b, and s, we have
Proof.
Let us consider the following 3-poset integral:
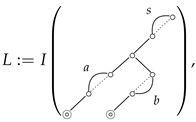 which has the following infinite-series expansion:
This is exactly the representation of . On the other hand, using the W map to transform this 3-poset diagram into , we have
By applying Equation (11) and using the Z mapping, we obtain
Combining the infinite-series expansion of L, we obtain the desired result. □
which has the following infinite-series expansion:
This is exactly the representation of . On the other hand, using the W map to transform this 3-poset diagram into , we have
By applying Equation (11) and using the Z mapping, we obtain
Combining the infinite-series expansion of L, we obtain the desired result. □
 which has the following infinite-series expansion:
which has the following infinite-series expansion:
4. The Decomposition Relation of the -Series
Given of positive integers and with , we define
where . We simplify the notations according to the following rules: when , we place a bar on top of , denoted as ; if , we place a bar on top of , denoted as . For example,
In order to compute the series, we transform these series into a linear combination of the series defined below.
We define
where . An additional condition for simplifying the notation is that if , we set to 0. For example,
It is evident that both the A-series and S-series exhibit symmetric properties:
Since and , we have
Using the same technique, we can transform all the evaluations of into the evaluations of . We list them as follows:
By organizing the above equations and considering their symmetry, we only need to explore the following 21 types of series to fully represent all possible series:
and the following three forms:
The first ten S-series are discussed in the next section, and the subsequent eight S-series are studied in Section 6. For the last three S-series, it should be noted that
This series is . We apply Equation (1) and obtain (see Equation (11) in [21])
Also,
which corresponds to . Its expression is determined by Proposition 1. Similarly, the series
is determined by Proposition 2.
5. The First Ten -Series
First, we calculate the first ten types of the S-series. We demonstrate our method using as an example. The basic calculation principles for the remaining nine types follow a similar approach to the one demonstrated.
Theorem 1.
Given five nonnegative integers , and s, we have
Proof.
Let
where
Then, we can express the following 3-poset integral as an iterated integral:
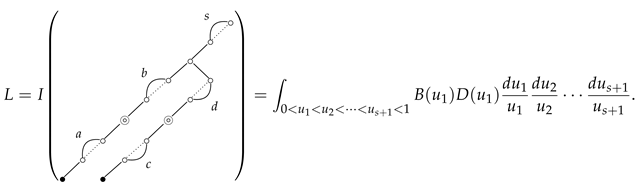 Transform and into representations as infinite series:
Substituting this form of into , we have
Similarly, we rewrite as
The 3-poset integral L becomes
Applying Equation (7), where and W maps onto , we have
By Equation (10), we obtain
Using the Z map to transform the above shuffle relation, we have
Transform and into representations as infinite series:
Substituting this form of into , we have
Similarly, we rewrite as
The 3-poset integral L becomes
Applying Equation (7), where and W maps onto , we have
By Equation (10), we obtain
Using the Z map to transform the above shuffle relation, we have
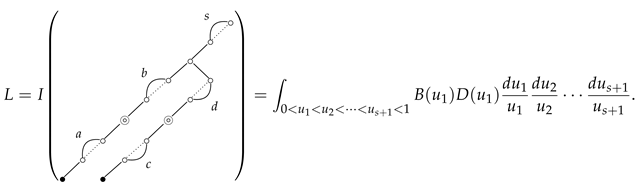 Transform and into representations as infinite series:
Transform and into representations as infinite series:
This is the representation of . □
For the remaining nine types, we omit the derivation process due to the similarity in methods and only provide the results. Two of these types use a 3-poset Hasse diagram that is actually a 2-poset Hasse diagram. Thus, we can use Equation (13) to simplify their expressions. We discuss these two types at the end of this section.
The remaining two S-series are
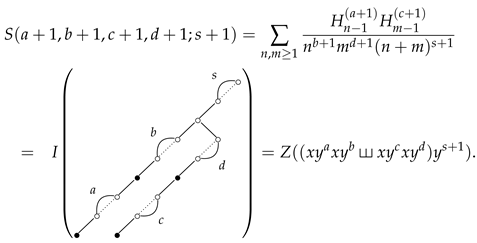 and
and
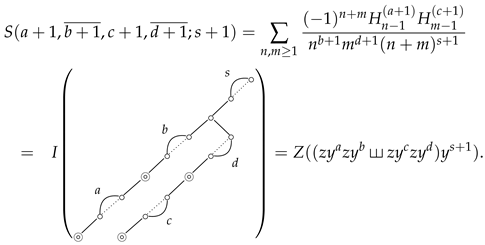 Using Equation (13) rather than Equation (10) simplifies their expressions.
Using Equation (13) rather than Equation (10) simplifies their expressions.
 and
and
 Using Equation (13) rather than Equation (10) simplifies their expressions.
Using Equation (13) rather than Equation (10) simplifies their expressions.
In fact, Equation (34) has been proved in Theorem 5 in [21].
6. The Following Eight -Series
To illustrate the derivation process for the last eight types of the S-series, we start with . The basic steps for deriving the remaining seven types are similar.
Theorem 2.
Given four nonnegative integers , and s, we have
Proof.
Let
and
We have
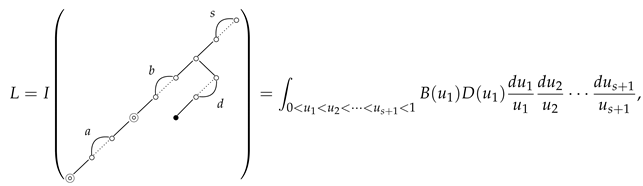 where
Transform and into representations as infinite series:
Substituting this form of into , we have
The 3-poset integral L becomes
Applying Equation (7), where and W maps onto , we have
By Equation (9), we obtain
Using the Z map to transform the above shuffle relation, we have
where
Transform and into representations as infinite series:
Substituting this form of into , we have
The 3-poset integral L becomes
Applying Equation (7), where and W maps onto , we have
By Equation (9), we obtain
Using the Z map to transform the above shuffle relation, we have
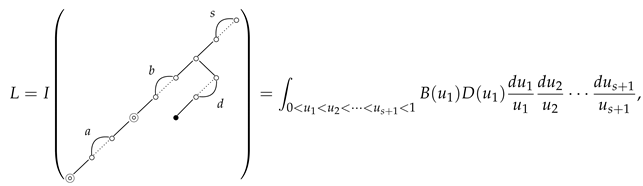 where
where
This is the representation of . □
We use a similar method to express the remaining seven types of as a linear combination of alternating multiple zeta values:
In fact, we can apply Equation (12) to Equations (36) and (38), but the resulting expressions will not be significantly simplified. Therefore, we leave this to interested readers (see Theorem 6 in [21]).
7. The Expressions of -Series
By combining the results from the previous two sections and using Equations (16) through (25), we can list the expressions for all the A-series. For example, consider
Applying Equation (18), we find that
There are four S-series in the expression. For the first S-series, , we use Equation (27) and obtain
To address the second S-series, , Equation (37) is employed. By substituting d with in Equation (37) while keeping the other parameters unchanged, the expression for the second S-series can be derived as follows:
We apply Theorem 2 to the third S-series, . The S-series mentioned in Theorem 2 is written as . Due to symmetry, this S-series can also be written as . To find the expression for the S-series we need, we can replace the parameters in Theorem 2: change a to c, b to d, and d to . This results in the required S-series being expressed as follows:
Now, w apply the results from Proposition 1 to the fourth S-series. The S-series in Proposition 1 is . Utilizing symmetry, this S-series can be represented as . Therefore, by replacing parameter a with and parameter b with in Proposition 1, we obtain the desired , which is expressed as follows:
By combining the expressions of the four S-series mentioned above, we arrive at the final representation of .
Building upon the demonstrated example, we proceed to transform the required A-series into four S-series using Equations (16)–(25). Leveraging the representation outcomes from the preceding two sections and Propositions 1 and 2, with suitable substitutions for the respective parameters, we derive a representation that converts the four desired S-series into a linear combination of alternating multiple zeta values. Since the methods are similar, we no longer demonstrate each step individually. Below, we list the expressions for all A-series.
Because and rely on 2-poset Hasse diagrams, their expressions are relatively simple. The expression for is available in Equation (26) in [21]. Consequently, we only provide the expression for here.
8. Examples and Concluding Remarks
Here, we substitute into the formulas for the A-series from the previous section and list the results for reference. We have numerically verified these equations using Mathematica 13.
Since the number of corresponding terms for multiple zeta values increases significantly when the parameters are greater than zero, we provide only one additional example here.
In this paper, we present a method by evaluating a particular 3-poset integral using two distinct techniques: one employs the shuffle relations with their corresponding Lyndon words, and the other utilizes the corresponding infinite-series expansions. For example,
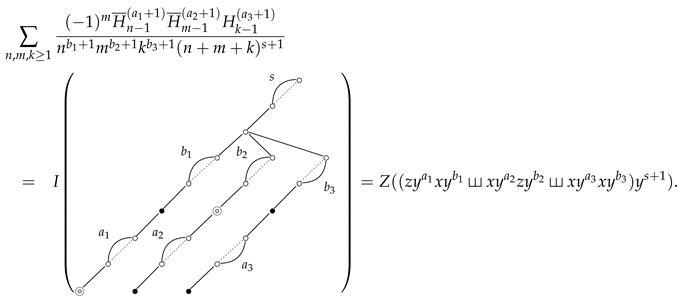

When we express the shuffle relation of the above equation as a sum of Lyndon words ([29,32]) and then convert it to alternating multiple zeta values using the Z function, the relationship becomes complex. For example, the above shuffle equation can be expressed as a sum of 15 different Lyndon words. The coefficient of each Lyndon word is made up of a sum of finite products of binomial coefficients. However, once the shuffle relations are determined, the expressions of alternating multiple zeta values can be easily obtained.
Using our method, it becomes straightforward to derive the desired representation of the infinite-series sum as a linear combination of alternating multiple zeta values.
Funding
This research was funded by the National Science and Technology Council, Taiwan, R. O. C., under grant NSTC 112-2115-M-845-001.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Borwein, D.; Borwein, J.; Bradley, D. Parametric Euler sum identities. J. Math. Anal. Appl. 2006, 316, 328–338. [Google Scholar] [CrossRef]
- Zhao, J. On a conjecture of Borwein, Bradley and Broadhurst. J. Reine Angew. Math. 2010, 639, 223–233. [Google Scholar] [CrossRef]
- Xu, C. Explicit formulas of some mixed Euler sums via alternating multiple zeta values. Bull. Malays. Math. Sci. Soc. 2020, 43, 3809–3827. [Google Scholar] [CrossRef]
- Hoffman, M.E. Multiple harmonic series. Pac. J. Math. 1992, 152, 275–290. [Google Scholar] [CrossRef]
- Eie, M. The Theory of Multiple Zeta Values with Applications in Combinatorics; Monographs in Number Theory; World Scientific: Singapore, 2013; Volume 7. [Google Scholar]
- Sitaramachandra Rao, R. A formula of S. Ramanujan. J. Number Theory 1987, 25, 1–19. [Google Scholar] [CrossRef]
- Flajolet, P.; Salvy, B. Euler sums and contour integral representations. Exp. Math. 1998, 7, 15–35. [Google Scholar] [CrossRef]
- Vermaseren, J.A.M. Harmonic sums, Mellin transforms and integrals. Int. J. Mod. Phys. 1999, 14, 2037–2076. [Google Scholar] [CrossRef]
- Powers, B.R. N-Player final-offer arbitration: Harmonic numbers in equilibrium. Am. Math. Mon. 2023, 130, 559–576. [Google Scholar] [CrossRef]
- Harris, P.E.; Kretschmann, J.; Mori, J.C.M. Lucky cars and the quicksort algorithm. Am. Math. Mon. 2024, 131, 417–423. [Google Scholar] [CrossRef]
- Blümlein, J.; Kurth, S. Harmonic sums and Mellin transforms up to two loop order. Phys. Rev. D 1999, 60, 014018. [Google Scholar] [CrossRef]
- Campbell, J.M.; Chen, K.-W. Explicit identities for infinite families of series involving squared binomial coefficients. J. Math. Anal. Appl. 2022, 513, 126219. [Google Scholar] [CrossRef]
- Chen, K.-W. Generalized harmonic number sums and quasisymmetric functions. Rocky Mt. J. Math. 2020, 50, 1253–1275. [Google Scholar] [CrossRef]
- Chen, K.-W.; Chen, Y.-H. Infinite series containing generalized harmonic functions. Notes Number Theory Discret. Math. 2020, 26, 85–104. [Google Scholar] [CrossRef]
- Chen, K.-W.; Yang, F.-Y. Infinite series involving harmonic numbers and reciprocal of binomial coefficients. AIMS Math. 2024, 9, 16885–16900. [Google Scholar] [CrossRef]
- Sofo, A.; Nimbran, A.S. Euler sums and integral connections. Mathematics 2019, 7, 833. [Google Scholar] [CrossRef]
- Tornheim, L. Harmonic double series. Am. J. Math. 1950, 72, 303–314. [Google Scholar] [CrossRef]
- Mordell, L.J. On the evaluation of some multiple series. J. Lond. Math. Soc. 1958, 33, 368–371. [Google Scholar] [CrossRef]
- Witten, E. On quantum gauge theories in two dimensions. Commun. Math. Phys. 1991, 141, 153–209. [Google Scholar] [CrossRef]
- Bradley, D.M.; Zhou, X. On Mordell-Tornheim sums and multiple zeta values. Ann. Sci. Math. 2010, 34, 15–23. [Google Scholar]
- Chen, K.-W. On some general Tornheim type series. Mathematics 2024, 12, 1867. [Google Scholar] [CrossRef]
- Subbarao, M.V.; Sitaramachandra Rao, R. On some infinite series of L. J. Mordell and their analogues. Pac. J. Math. 1985, 119, 245–255. [Google Scholar] [CrossRef]
- Tsumura, H. On some combinatorial relations for Tornheim’s double series. Acta Arith. 2002, 105, 239–252. [Google Scholar] [CrossRef]
- Tsumura, H. On alternating analogues of Tornheim’s double series. Proc. Am. Math. Soc. 2003, 131, 3633–3641. [Google Scholar] [CrossRef][Green Version]
- Tsumura, H. Evaluation formulas for Tornheim’s type of alternating double series. Math. Comput. 2004, 73, 251–258. [Google Scholar] [CrossRef]
- Tsumura, H. On alternating analogues of Tornheim’s double series II. Ramanujan J. 2009, 19, 81–90. [Google Scholar] [CrossRef]
- Zhao, J. A note on colored Tornheim’s double series. Integers 2010, 10, 879–882. [Google Scholar] [CrossRef][Green Version]
- Kuba, M. On evaluations of infinite double sums and Tornheim’s double series. Sém. Lothar. Combin. 2008, 58, 11. [Google Scholar]
- Chen, K.-W. Sum relations from shuffle products of alternating multiple zeta values. Mediterr. J. Math. 2022, 19, 206. [Google Scholar] [CrossRef]
- Hoffman, M.E. The algebra of multiple harmonic series. J. Algebra 1997, 194, 477–495. [Google Scholar] [CrossRef]
- Minh, H.N.; Petitot, M. Lyndon words, polylogarithms and the Riemann ζ function. Discret. Math. 2000, 217, 273–292. [Google Scholar] [CrossRef]
- Li, Z.; Qin, C. Shuffle product formulas of multiple zeta values. J. Number Theory 2017, 171, 79–111. [Google Scholar] [CrossRef]
- Bigotte, M.; Jacob, G.; Oussous, N.E.; Petitot, M. Lyndon words and shuffle algebras for generating the coloured multiple zeta values relations tables. Theor. Comput. Sci. 2002, 273, 271–282. [Google Scholar] [CrossRef]
- Ihara, K.; Kaneko, M.; Zagier, D. Derivation and double shuffle relations for multiple zeta values. Compos. Math. 2006, 142, 307–338. [Google Scholar] [CrossRef]
- Yamamoto, S. Multiple zeta-star values and multiple integrals. RIMS Kôkyûroku Bessatsu 2017, 68, 3–14. [Google Scholar]
- Yamamoto, S. Integrals associated with 2-posets and applications to multiple zeta values. RIMS Kôkyûroku Bessatsu 2020, 83, 27–46. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).