Single-Machine Scheduling with Simultaneous Learning Effects and Delivery Times

Abstract

This paper studies the single-machine scheduling problem with truncated learning effect, time-dependent processing time, and past-sequence-dependent delivery time. The delivery time is the time that the job is delivered to the customer after processing is complete. The goal is to determine an optimal job schedule to minimize the total weighted completion time and maximum tardiness. In order to solve the general situation of the problem, we propose a branch-and-bound algorithm and other heuristic algorithms. Computational experiments also prove the effectiveness of the given algorithms.

1. Introduction

A common assumption when solving traditional scheduling problems in the field of operations and production management is that the processing time required for each job remains a fixed, predetermined constant. However, this simplistic view often fails to align with the intricate and dynamic processing environments of the real world. Essentially, the assumption of constant processing time ignores a fundamental aspect of the production process: the learning effect, which refers to the phenomenon that, as workers or machines repeatedly perform a job, their proficiency and familiarity with the task gradually increase. Therefore, when constructing a scheduling strategy, in-depth consideration of the impact of the learning effect is key to ensuring that the strategy is both accurate and adaptable to the ever-changing production environment.

In addition to extensive research on the learning effect in scheduling problems, it is also important to include the time when the job is delivered to the customer, which is the delivery time. Delivery time is one of the key metrics for measuring the efficiency of a company’s operations, supply chain management, and customer satisfaction. A shorter delivery time usually means that an enterprise can respond faster to market demand, improve customer satisfaction, and potentially increase market competitiveness. Therefore, many enterprises are committed to optimizing production processes, increasing productivity, improving logistics management, and using other measures to shorten delivery time.

However, the learning effect will not continue indefinitely and, when it reaches a certain level, learning efficiency will no longer increase significantly but may even remain unchanged or decline slightly. For example, after reaching a certain level of proficiency or optimization of the workers or machines, it faces the limitations of other factors, such as physiological fatigue, machine wear, and so on.

2. Related Work

The learning effect scheduling problem has been widely investigated by many studies during the last few decades (see Wu et al. [1], Azzouz et al. [2], Sun et al. [3], Lv and Wang [4], Zhao [5], Wang and Wang [6], Paredes-Astudillo et al. [7]). Recent studies include Ma et al. [8], who investigated a regular single-machine online scheduling problem based on the positional learning effect. Mor et al. [9] explored the application of the learning effect to flow shop scheduling to minimize the makespan, total completion time, and total load. Chen et al. [10] developed a polynomial time algorithm to optimize the total cost, including penalty and investment costs related to the due-window. Zhang et al. [11] considered single-machine resource allocation scheduling with exponential time-dependent learning effects. Lv and Wang  [12] considered two-machine flow shop scheduling with a truncated learning effect. For the total completion time minimization subject to release dates, they proposed some heuristic and branch-and-bound algorithms. In addition, the widespread application of learning effects in scheduling problems also includes the combination of learning and the deterioration effect (Lin [13]), as well as the simultaneous study of the learning effect and setup time (Zhu et al. [14] and Jiang et al. [15]), the relationship between position-dependent weights (Wang et al. [16]) and machine maintenance (Wu et al. [17]), and other production applications.

The importance of delivery time as a key factor in scheduling problems cannot be overstated. For example, Wang et al. [18] investigated the single-machine scheduling problems with past-sequence-dependent delivery time. Ji et al. [19] simultaneously considered the single-machine scheduling problem with controllable processing time and due-window assignment, in which the processing time of the job is a function of the learning effect and resource allocation. In addition, there are many studies exploring the combination of delivery time and due-date or due-window assignment, such as Ahmadizar and Farhadi [20], Zhang et al. [21], and Pan et al. [22]. At the same time, the simultaneous study of delivery time and deterioration effect includes Qian and Han [23], who studied the delivery time scheduling problem with the deterioration effect, and who introduced the corresponding polynomial time algorithm for the proposed problem. Furthermore, this direction also includes Mao et al. [24,25], Zhao et al. [26], and Lu et al. [27]. Research on the relationship between delivery time and the learning effect includes Ren et al. [28], Wang et al. [29], and Qian et al. [30]. Toksari et al. [31] validated that the single-machine scheduling problems with exponential past-sequence-dependent delivery time and the learning effect have polynomial time algorithms for minimizing makespan, total completion time, weighted total completion time, and maximum tardiness.

The truncated learning effect has also attracted significant attention from scholars. Wang et al. [32] conducted research on single-machine scheduling problems with a truncated learning effect and resource allocation. Li et al. [33] considered flow shop scheduling with general truncated learning effects. For makespan minimization, they proposed a branch-and-bound algorithm and some heuristics. Ren et al. [34], on the other hand, considered both the truncated learning effect and delivery time. Wang and Zhang [35] explored the single-machine scheduling problems with a truncated learning effect and $psd$ times and provided the worst-case ratio of total weighted completion time and maximum tardiness.

Based on Wang and Zhang [35], in this paper, a specific non-increasing convex function, i.e., ${\displaystyle \frac{1}{t+1}}$, with respect to the start time t is introduced in the processing time model, and heuristic, branch-and-bound, Tabu search, and simulated annealing algorithms are proposed to find the optimal solution to the problem. The structure of this article is as follows: Section 3 describes the studied problem. Section 4 provides the required optimal properties and lower bounds for two problems. Section 5 provides upper bounds for two problems. Section 6 introduces several other common heuristic algorithms. Section 7 conducts data simulations. The last section contains some conclusions.

3. Problem Statement

There are n independent and non-preempted jobs available for processing on a single-machine, and all the jobs are available at time zero. Let ${\tilde{p}}_{jr}^A$ denote the actual processing time of job $J_j$ scheduled at position r; that is:

$${\tilde{p}}_{jr}^A\left(t\right)={\tilde{p}}_j\widehat{\iota }\left(t\right)\max \{r^{\delta },\eta \},$$

(1)

where r is the position of job $J_j$ in the processing sequence, t is the starting time of job $J_j$, ${\tilde{p}}_j$ is the basic processing time (i.e., the job processing time without the learning effect) of job $J_j$, $\widehat{\iota }\left(t\right)$ is a non-increasing convex function of the starting time t, $\widehat{\iota }\left(t\right)$ satisfies $0<\widehat{\iota }\left(t\right)\le 1$, $\widehat{\iota }\left(0\right)=1$, ${\widehat{\iota }}^{\prime }\left(t\right)<0$$({\widehat{\iota }}^{\prime }\left(t\right)$ is the derivative of $\widehat{\iota }\left(t\right))$, $\delta$ ($\delta <0$) is the learning effect, $\eta$ is a given parameter, and $0<\eta <1$. Let ${\tilde{q}}_j$ denote the past-sequence-dependent delivery time of job $J_j$, which can be denoted by $q_{psd}$. As in Koulamas et al. [36], ${\tilde{q}}_j$ is:

$${\tilde{q}}_j=\theta {\displaystyle \sum _{l=1}^{j-1}}{\tilde{p}}_l,$$

(2)

where $\theta \ge 0$. The goal is to find an optimal schedule such that the total weighted completion time (i.e., ${\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$, where ${\tilde{w}}_j$ (resp. ${\tilde{C}}_j$) is the weight (resp. completion time) of job $J_j$) and the maximum tardiness ${\tilde{T}}_{\max }\left(={\max }_{j=1,\dots ,n}\left\{\max \left(0,{\tilde{C}}_j-{\tilde{d}}_j\right)\right\}\right)$ are to be minimized. Using the three-field notation, this problem can be denoted as follows:

$$1|{\tilde{p}}_{jr}^A\left(t\right)={\tilde{p}}_j\widehat{\iota }\left(t\right)\max \{r^{\delta },\eta \},q_{psd}|G,$$

(3)

where $G\in \left\{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j,{\tilde{T}}_{\max }\right\}$. In this paper, we only consider $\widehat{\iota }\left(t\right)$ to be a special function, i.e., $\widehat{\iota }\left(t\right)={\displaystyle \frac{1}{t+1}}$.

4. Lower Bounds

4.1. Optimal Properties

This paper can provide the following properties under the condition of anti-consistency.

Lemma 1 

(Wang and Zhang [35]). For the problem $1|{\tilde{p}}_{jr}^A\left(t\right)={\tilde{p}}_j\widehat{\iota }\left(t\right)\max \{r^{\delta },\eta \},q_{psd}|\sum {\tilde{w}}_j{\tilde{C}}_j$, if ${\tilde{p}}_k\le {\tilde{p}}_h$ implies ${\tilde{w}}_k\ge {\tilde{w}}_h$, the optimal job sequence ${\pi }^{*}$ can be obtained by non-decreasing order of ${\displaystyle \frac{{\tilde{p}}_k}{{\tilde{w}}_k}}$ (WSPT rule).

Lemma 2 

(Wang and Zhang [35]). For the problem $1|{\tilde{p}}_{jr}^A\left(t\right)={\tilde{p}}_j\widehat{\iota }\left(t\right)\max \{r^{\delta },\eta \},q_{psd}|{\tilde{T}}_{\max }$, if ${\tilde{p}}_k\le {\tilde{p}}_h$ implies ${\tilde{d}}_k\le {\tilde{d}}_h$, the optimal job sequence ${\pi }^{*}$ can be obtained by non-decreasing order of ${\tilde{d}}_k$ (i.e., the EDD rule).

4.2. Criterion ${\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$

Let $\lambda =\left({\tilde{\lambda }}_s,{\tilde{\lambda }}_u\right)$ be the sequence in which ${\tilde{\lambda }}_s$ is the scheduled part and ${\tilde{\lambda }}_u$ is the unscheduled part. Assuming that there are s jobs in the scheduled part, the remaining $(n-s)$ jobs are all in ${\tilde{\lambda }}_u$. The objective function can be divided into known and unknown parts, which can be written as follows:

$$\begin{array}{cc}\hfill W=& {\displaystyle \sum _{j=1}^s}{\tilde{w}}_j{\tilde{C}}_j+{\displaystyle \sum _{j=s+1}^n}{\tilde{w}}_{\left[j\right]}[{\displaystyle \sum _{l=1}^s}{\displaystyle {\tilde{p}}_l^A}+{\displaystyle \sum _{l=s+1}^n}{\tilde{p}}_{\left[l\right]}{\displaystyle \frac{1}{{\displaystyle {\sum }_{l=1}^s}{\displaystyle {\tilde{p}}_l^A}+{\displaystyle {\sum }_{m=s+1}^{l-1}}{\displaystyle {\tilde{p}}_{\left[m\right]}^A}+1}}\max \{l^{\delta },\eta \}\hfill \\ & +\theta \left({\displaystyle \sum _{l=1}^s}{\tilde{p}}_l+{\displaystyle \sum _{l=s+1}^{j-1}}{\tilde{p}}_{\left[l\right]}\right)].\hfill \end{array}$$

It can be known that ${\displaystyle {\sum }_{j=1}^s}{\tilde{w}}_j{\tilde{C}}_j$ and ${\displaystyle {\sum }_{l=1}^s}{\displaystyle {\tilde{p}}_l^A}$ are fixed constants, so it follows that:

$$\begin{array}{cc}\hfill W\ge & {\displaystyle \sum _{j=1}^s}{\tilde{w}}_j{\tilde{C}}_j+{\displaystyle \sum _{j=s+1}^n}{\tilde{w}}_{\min }[{\displaystyle \sum _{l=1}^s}{\displaystyle {\tilde{p}}_l^A}+{\displaystyle \sum _{l=s+1}^n}{\tilde{p}}_{\left[l\right]}{\displaystyle \frac{1}{{\displaystyle {\sum }_{l=1}^s}{\displaystyle {\tilde{p}}_l^A}+{\displaystyle {\sum }_{m=s+1}^{l-1}}{\displaystyle {\tilde{p}}_{\left[m\right]}^A}+1}}\max \{l^{\delta },\eta \}\hfill \\ & +\theta \left({\displaystyle \sum _{l=1}^s}{\tilde{p}}_l+{\displaystyle \sum _{l=s+1}^{j-1}}{\tilde{p}}_{\left[l\right]}\right)],\hfill \end{array}$$

where ${\tilde{w}}_{\min }=\min \{{\tilde{w}}_{s+1},{\tilde{w}}_{s+2},\dots ,{\tilde{w}}_n\}$. Then, the first lower bound can be calculated as:

$$\begin{array}{cc}\hfill & L{\displaystyle B_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^1}\hfill \\ \hfill =& {\displaystyle \sum _{j=1}^s}{\tilde{w}}_j{\tilde{C}}_j+{\displaystyle \sum _{j=s+1}^n}{\tilde{w}}_{\left(j\right)}[{\displaystyle \sum _{l=1}^s}{\displaystyle {\tilde{p}}_l^A}+{\displaystyle \sum _{l=s+1}^n}{\tilde{p}}_{<l>}{\displaystyle \frac{1}{{\displaystyle {\sum }_{l=1}^s}{\displaystyle {\tilde{p}}_l^A}+{\displaystyle {\sum }_{m=s+1}^{l-1}}{\displaystyle {\tilde{p}}_{<m>}^A}+1}}\max \{l^{\delta },\eta \}\hfill \\ \hfill & +\theta \left({\displaystyle \sum _{l=1}^s}{\tilde{p}}_l+{\displaystyle \sum _{l=s+1}^{j-1}}{\tilde{p}}_{<l>}\right)],\hfill \end{array}$$

(4)

in which ${\tilde{p}}_{<s+1>}\le {\tilde{p}}_{<s+2>}\le \dots \le {\tilde{p}}_{<n>}$, and ${\displaystyle {\tilde{p}}_{<m>}^A}$ ($m=s+1,s+2,\dots ,n$) is the actual processing time of the mth position by the order of ${\tilde{p}}_{<s+1>}\le {\tilde{p}}_{<s+2>}\le \dots \le {\tilde{p}}_{<n>}$.

Let ${\tilde{p}}_{\min }=\min \{{\tilde{p}}_{s+1},{\tilde{p}}_{s+2},\dots ,{\tilde{p}}_n\}$; then, the second lower bound can be obtained similarly to the first as follows:

$$\begin{array}{cc}\hfill & L{\displaystyle B_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^2}\hfill \\ \hfill =& {\displaystyle \sum _{j=1}^s}{\tilde{w}}_j{\tilde{C}}_j+{\displaystyle \sum _{j=s+1}^n}{\tilde{w}}_{\left(j\right)}[{\displaystyle \sum _{l=1}^s}{\displaystyle {\tilde{p}}_l^A}+{\displaystyle \sum _{l=s+1}^n}{\tilde{p}}_{\min }{\displaystyle \frac{1}{{\displaystyle {\sum }_{l=1}^s}{\displaystyle {\tilde{p}}_l^A}+{\displaystyle {\sum }_{m=s+1}^{l-1}}{\displaystyle {\tilde{p}}_{\min }^A}+1}}\max \{l^{\delta },\eta \}\hfill \\ \hfill & +\theta \left({\displaystyle \sum _{l=1}^s}{\tilde{p}}_l+{\displaystyle \sum _{l=s+1}^{j-1}}{\tilde{p}}_{\min }\right)],\hfill \end{array}$$

(5)

where ${\tilde{w}}_{(s+1)}\ge {\tilde{w}}_{(s+2)}\ge \dots \ge {\tilde{w}}_{\left(n\right)}$ according to Lemma 1.

The third lower bound is

$$\begin{array}{cc}\hfill & L{B}_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^3\hfill \\ \hfill =& {\displaystyle \sum _{j=1}^s}{\tilde{w}}_j{\tilde{C}}_j+{\displaystyle \sum _{j=s+1}^n}{\tilde{w}}_{\left(j\right)}[{\displaystyle \sum _{l=1}^s}{\displaystyle {\tilde{p}}_l^A}+{\displaystyle \sum _{l=s+1}^n}{\tilde{p}}_{<l>}{\displaystyle \frac{1}{{\sum }_{l=1}^s{\tilde{p}}_l^A+{\sum }_{m=s+1}^{l-1}{\tilde{p}}_{<m>}^A+1}}\max \{l^{\delta },\eta \}\hfill \\ \hfill & +\theta \left({\displaystyle \sum _{l=1}^s}{\tilde{p}}_l+{\displaystyle \sum _{l=s+1}^{j-1}}{\tilde{p}}_{<l>}\right)],\hfill \end{array}$$

(6)

where ${\tilde{w}}_{(s+1)}\ge {\tilde{w}}_{(s+2)}\ge \dots \ge {\tilde{w}}_{\left(n\right)}$ and ${\tilde{p}}_{<s+1>}\le {\tilde{p}}_{<s+2>}\le \dots \le {\tilde{p}}_{<n>}$, and where ${\tilde{p}}_{<m>}^A$ is the actual processing time of the mth position by the order of ${\tilde{p}}_{<s+1>}\le {\tilde{p}}_{<s+2>}\le \dots \le {\tilde{p}}_{<n>}$. Note that ${\tilde{w}}_{\left(k\right)}$ and ${\tilde{p}}_{<k>}$ may not necessarily correspond to the same job.

To make the lower bound tighter, select the largest of Equations (4)–(6) as the lower bound; that is:

$$L{B}_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}=\max \left\{L{B}_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^1,L{B}_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^2,L{B}_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^3\right\}.$$

(7)

4.3. Criterion ${\tilde{T}}_{\max }$

Similar to criterion ${\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$, it follows that

$$\begin{array}{ccc}\hfill {\tilde{T}}_{[s+1]}& =& \max \left\{0,{\tilde{C}}_s+{\tilde{p}}_{[s+1]}{\displaystyle \frac{1}{{\sum }_{l=1}^{s-1}{\tilde{p}}_l^A+{\tilde{p}}_s^A+1}}\max \{{(s+1)}^{\delta },\eta \}+\theta {\tilde{p}}_s-d_{[s+1]}\right\};\hfill \end{array}$$

that is,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\tilde{T}}_{[s+j]}=\max \{& 0,{\tilde{C}}_s+{\displaystyle \sum _{l=1}^j}{\tilde{p}}_{[s+l]}{\displaystyle \frac{1}{{\sum }_{l=1}^{s-1}{\tilde{p}}_l^A+{\sum }_{m=s}^{s+j-1}{\tilde{p}}_{\left[m\right]}^A+1}}\max \{{(s+l)}^{\delta },\eta \}+\theta {\displaystyle \sum _{m=s}^{s+j-1}}{\tilde{p}}_{\left[m\right]}\hfill \\ & -d_{[s+j]}\}.\hfill \end{array}\end{array}$$

Thus, the following lower bound can be obtained by defining ${\tilde{d}}_{\max }=\max \{{\tilde{d}}_{s+1},{\tilde{d}}_{s+2},\dots ,{\tilde{d}}_n\}$ as:

$$\begin{array}{cc}\hfill & L{B}_{{\tilde{T}}_{\max }}^1\hfill \\ \hfill =& \underset{j=1,\dots ,n-s}{\max }\left\{\begin{array}{c}\max \{0,{\tilde{C}}_1-{\tilde{d}}_1\},\dots ,\max \{0,{\tilde{C}}_s-{\tilde{d}}_s\},\hfill \\ \max \{0,{\tilde{C}}_s+{\displaystyle {\sum }_{l=1}^{n-s}}{\tilde{p}}_{<s+l>}{\displaystyle \frac{1}{{\sum }_{l=1}^{s-1}{\tilde{p}}_l^A+{\sum }_{m=s}^{n-1}{\tilde{p}}_{\left[m\right]}^A+1}}\max \{{(s+l)}^{\delta },\eta \}\hfill \\ +\theta {\displaystyle {\sum }_{m=s}^{j-1}}{\tilde{p}}_{\left[m\right]}-{\tilde{d}}_{\max }\}\hfill \end{array}\right\},\hfill \end{array}$$

(8)

where ${\tilde{p}}_{<s+1>}\le {\tilde{p}}_{<s+2>}\le \dots \le {\tilde{p}}_{<n>}$ can be obtained by Lemma 2, and ${\tilde{p}}_{<m>}^A$ ($m=s+1,s+2,\dots ,n$) is the actual processing time of the mth position by the order of ${\tilde{p}}_{<s+1>}\le {\tilde{p}}_{<s+2>}\le \dots \le {\tilde{p}}_{<n>}$.

The second lower bound can also be calculated as follows:

$$\begin{array}{cc}\hfill & L{B}_{{\tilde{T}}_{\max }}^2\hfill \\ \hfill =& \underset{j=1,\dots ,n-s}{\max }\left\{\begin{array}{c}\max \{0,{\tilde{C}}_1-{\tilde{d}}_1\},\dots ,\max \{0,{\tilde{C}}_s-{\tilde{d}}_s\},\hfill \\ \max \{0,{\tilde{C}}_s+{\displaystyle {\sum }_{l=1}^{n-s}}{\tilde{p}}_{<s+l>}{\displaystyle \frac{1}{{\sum }_{l=1}^{s-1}{\tilde{p}}_l^A+{\sum }_{m=s}^{n-1}{\tilde{p}}_{\left[m\right]}^A+1}}\max \{{(s+l)}^{\delta },\eta \}\hfill \\ +\theta {\displaystyle {\sum }_{m=s}^{j-1}}{\tilde{p}}_{\left[m\right]}-{\tilde{d}}_{(s+j)}\}\hfill \end{array}\right\},\hfill \end{array}$$

(9)

where ${\tilde{p}}_{<s+1>}\le {\tilde{p}}_{<s+2>}\le \dots \le {\tilde{p}}_{<n>}$, ${\tilde{d}}_{(s+1)}\le {\tilde{d}}_{(s+2)}\le \dots \le {\tilde{d}}_{\left(n\right)}$, and ${\tilde{p}}_{<m>}^A$ is the actual processing time of the mth position by the order of ${\tilde{p}}_{<s+1>}\le {\tilde{p}}_{<s+2>}\le \dots \le {\tilde{p}}_{<n>}$. Note that ${\tilde{p}}_{<k>}$ and ${\tilde{d}}_{\left(k\right)}$ may not correspond to the same job.

To make the lower bound tighter, select the largest of Equations (8) and (9) as the lower bound, which can be denoted as follows:

$$L{B}_{{\tilde{T}}_{\max }}=\max \left\{L{B}_{{\tilde{T}}_{\max }}^1,L{B}_{{\tilde{T}}_{\max }}^2\right\}.$$

(10)

5. Upper Bounds

The following methods are given to calculate the upper bounds to correct the given lower bounds.

5.1. Criterion ${\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$

Firstly, the upper bound (UB) calculation method for ${\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$ is given through Lemma 1 as follows (Algorithm 1).

Algorithm 1: Upper Bound for ${\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$

Step 1. Obtain the sequence ${\pi }_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^1$ by non-decreasing of ${\tilde{p}}_k$ ($k=1,2,\dots ,n$); Step 2. Obtain the sequence ${\pi }_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^2$ by non-increasing of ${\tilde{w}}_k$ ($k=1,2,\dots ,n$); Step 3. Obtain the sequence ${\pi }_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^3$ by non-decreasing of ${\displaystyle \frac{{\tilde{p}}_k}{{\tilde{w}}_k}}$ ($k=1,2,\dots ,n$); Step 4. From Steps 1–3, calculate and select the smallest object function value ${\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$ as the initial sequence ${\pi }_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^0$; Step 5. Set $s=2$. Select the first two jobs from ${\pi }_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^0$, and select the better one of the two possible sequences; Step 6. Set $s=s+1$. Insert the sth job in sequence ${\pi }_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^0$ into s possible positions to obtain the best partial sequence. Next, determine all possible sequences by interchanging jobs in positions k and j of the above partial sequence for $k,j$ ($1\le k<s,k<j\le n$). Select the best $s(s-1)/2$ partial sequence that has the minimum value ${\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$; Step 7. If $s=n$, then Stop; otherwise, return to Step 6.

5.2. Criterion ${\tilde{T}}_{\max }$

The upper bound (UB) of ${\tilde{T}}_{\max }$ is calculated in the same way, and the following algorithm (Algorithm 2) can be obtained based on Lemma 2:

Algorithm 2: Upper Bound for ${\tilde{T}}_{\max }$

Step 1. Obtain the sequence ${\pi }_{{\tilde{T}}_{\max }}^1$ by non-decreasing of ${\tilde{p}}_k$ ($k=1,2,\dots ,n$); Step 2. Obtain the sequence ${\pi }_{{\tilde{T}}_{\max }}^2$ by non-decreasing of ${\tilde{d}}_k$ ($k=1,2,\dots ,n$); Step 3. From Steps 1–2, calculate and select the smallest object function value ${\tilde{T}}_{\max }$ as the initial sequence ${\pi }_{{\tilde{T}}_{\max }}^0$; Step 4. Set $s=2$. Select the first two jobs from ${\pi }_{{\tilde{T}}_{\max }}^0$, and select the better one of the two possible sequences; Step 5. Set $s=s+1$. Insert the sth job in sequence ${\pi }_{{\tilde{T}}_{\max }}^0$ into s possible positions to obtain the best partial sequence. Next, determine all possible sequences by interchanging jobs in positions k and j of the above partial sequence for $k,j$ ($1\le k<s,k<j\le n$). Select the best $s(s-1)/2$ partial sequence that has the minimum value ${\tilde{T}}_{\max }$; Step 6. If $s=n$, then Stop; otherwise, return to Step 5.

5.3. Branch-and-Bound Algorithm

Based on the above-mentioned lower and upper bounds, the branch-and-bound (B&B) algorithm with enumeration as the central idea is proposed. This algorithm follows a depth-first strategy, assigning jobs in a forward manner starting from the first job position (assign a job to a node). This enumeration algorithm can be used as an optimal program to solve the problem posed in this study in the steps described below (i.e., Algorithm 3).

Algorithm 3: Branch-and-Bound

Step 1. (Upper bound) Calculate the initial sequence with the upper bound by Algorithm 1 for ${\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$ (Algorithm 2 for ${\tilde{T}}_{\max }$); Step 2. (Bounding) Calculate the lower bounds $L{B}_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}$, $L{B}_{{\tilde{T}}_{\max }}$ (see Equations (7) and (10)) for the node. If the lower bound of a node exceeds the calculated upper bound, all subsequent nodes including it are deleted. Otherwise, replace it as the new solution; Step 3. (Termination) Continue until all nodes have been explored.

6. Other Heuristic Algorithms

In addition to the algorithms mentioned above, this study will also use the following heuristic algorithms that are widely used in scheduling problems.

6.1. Tabu Search

In this subsection, a Tabu search (TS) algorithm is used to find a near-optimal solution. Tabu search is a search element algorithm used to jump out of local optima, where the initial sequence used in the TS algorithm is chosen from Algorithm 1, and the maximum number of iterations for the TS algorithm is set at 100n, where n is the number of jobs. As in Wu et al. [37] and Lv et al. [38], the implementation of the TS algorithm is given below (Algorithm 4):

Algorithm 4: Tabu Search

Step 1. Let the tabu list be empty and the iteration number be 0; Step 2. Let the sequence obtained from Algorithm 1 for ${\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$ (Algorithm 2 for ${\tilde{T}}_{\max }$) be the initial sequence that records the value of the objective function ${\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$ (${\tilde{T}}_{\max }$). Set the current schedule as the best solution ${\pi }_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^{*}$ (${\pi }_{{\tilde{T}}_{\max }}^{*}$); Step 3. Search the associated neighborhood of the current schedule and resolve if there is a schedule ${\pi }_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^{**}$ (${\pi }_{{\tilde{T}}_{\max }}^{**}$) with the smallest objective function value in associated neighborhoods and if it is not in the tabu list; Step 4. If ${\pi }_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^{**}$ (${\pi }_{{\tilde{T}}_{\max }}^{**}$) is better than ${\pi }_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^{*}$ (${\pi }_{{\tilde{T}}_{\max }}^{*}$), set ${\pi }_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^{*}={\pi }_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}^{**}$ (${\pi }_{{\tilde{T}}_{\max }}^{*}={\pi }_{{\tilde{T}}_{\max }}^{**}$). Update the tabu list and the number of iterations; Step 5. If there is not a schedule in associated neighborhoods and it is not in the tabu list or if the maximum number of iterations is reached, then output the local optimal sequence ${\pi }_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}$ (${\pi }_{{\tilde{T}}_{\max }}$) and the corresponding function value. Otherwise, update the tabu list and turn to Step 3.

6.2. Simulated Annealing

Simulated annealing (SA) can also obtain the initial sequence according to Algorithm 1 (resp. Algorithm 2) for ${\pi }_{{\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j}$ (resp. ${\pi }_{{\tilde{T}}_{\max }}$), which is another type of heuristic algorithm that can jump out of the local optimal solution. The specific problem-solving steps are as follows (Algorithm 5):

Algorithm 5: Simulated Annealing

Step 1. The initial sequence can be calculated by Algorithm 1 for ${\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$ (Algorithm 2 for ${\tilde{T}}_{\max }$); Step 2. Use the pairwise exchange neighborhood generation method to obtain other solutions; Step 3. (Acceptance probability) If the objective function value of the new schedule is smaller than that of the original schedule, it is automatically accepted. However, if the new schedule objective value is larger, it may still be accepted with a decreasing probability as the process progresses. The acceptance probability is determined by the following exponential distribution function: $$P\left(accept\right)=exp(-a\times \Delta {\displaystyle \sum _{j=1}^n}{\tilde{w}}_j{\tilde{C}}_j)(orP\left(accept\right)=exp(-a\times \Delta {\tilde{T}}_{\max })),$$ where a is a control parameter, and $\Delta {\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$ ($\Delta {\tilde{T}}_{\max }$) is the change in the value of the objective function. In addition, the method was adopted to change a in the lth iteration as follows: $$a={\displaystyle \frac{l}{\vartheta }},$$ where $\vartheta$ is an experimental constant. In this experiment, let $\vartheta =1$. If the function ${\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$ (${\tilde{T}}_{\max }$) increases as a result of a random pairwise interchange, the new sequence is accepted when $P\left(accept\right)>\epsilon$, in which $\epsilon$ is randomly sampled from the uniform distribution. Step 4. (Stopping condition) Our preliminary trials indicated that the quality of the sequence is stable after 300n iterations (see Wu et al. [37]).

7. Computational Experiments

To show the efficiency of each algorithm, we assume that $\widehat{\iota }\left(t\right)={\displaystyle \frac{1}{t+1}}$, and the computational experiments were performed. The procedures were coded in Visual Studio 2022 v17.1.0 software and run on a HUAWEI (Shenzhen, China) personal computer with an Intel^® Core™ i5-7200U @ 2.50 2.70 GHz CPU, 4.00 GB RAM, and the Windows 10 operating system. By systematically varying the parameter values and observing their effect on the data output, we gradually narrowed down the feasible range of parameters until we found the parameter intervals that produced stable, reliable, and expected data results (see Table 1).

Table 1. Numerical parameters.

Serial Number	Parameter	Value
1	$\delta$	−0.05, −0.15, −0.25, −0.35, −0.45
2	$\eta$	$(0.5,1)$
3	$\theta$	$[1,5]$
4	${\tilde{p}}_k$	$[1,50]$, $[1,100]$
5	${\tilde{w}}_k$	$[1,50]$, $[1,100]$
6	${\tilde{d}}_k$	$[1,C_{\max }]$

Note: $C_{\max }$ is the makespan base on the non-decreasing order of ${\tilde{p}}_k$ (i.e., SPT rule, Wang and Zhang [27]).

Based on the given data, we conducted data simulations on a small scale. The results are summarized in Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9, where Table 2, Table 3, Table 4 and Table 5 reflect the mean and maximum values of CPU time (in milliseconds) as well as the node number of the B&B and the relative error, and Table 6, Table 7, Table 8 and Table 9 reflect their p99 values, in which P99 denotes the data point at the 99th percentile position after the data set is sorted in ascending order. The error of the solution by UB (TS, SA) is calculated as follows:

$${\displaystyle \frac{\tilde{Q}\left(X\right)-{\tilde{Q}}^{*}}{{\tilde{Q}}^{*}}}\times 100\%,$$

where $\tilde{Q}\left(X\right)$ is the objective function value generated by Algorithm X, $X\in \{UB,TS,SA\}$, and ${\tilde{Q}}^{*}$ is the optimal value generated by the B&B Algorithm.

Table 2. Results of $\tilde{Q}={\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$ for ${\tilde{p}}_k,{\tilde{w}}_k\in [1,50]$.

		$\mathit{BB}\sim$ CPU		$\mathit{UB}\sim$ CPU		$\mathit{TS}\sim$ CPU		$\mathit{SA}\sim$ CPU		$\frac{\tilde{\mathit{Q}}\left(\mathit{UB}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$		$\frac{\tilde{\mathit{Q}}\left(\mathit{TS}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$		$\frac{\tilde{\mathit{Q}}\left(\mathit{SA}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$
$\mathit{n}$	$\mathit{\delta }$	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max
10	−0.05	619.20	1861.00	2.20	4.00	6046.00	6469.00	28.90	34.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.15	263.90	521.00	2.30	4.00	6194.00	6497.00	29.20	34.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.25	753.70	2113.00	2.20	4.00	6506.40	7065.00	30.00	34.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.35	536.90	1248.00	2.40	3.00	6401.50	6601.00	30.10	36.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.45	522.80	2327.00	2.30	3.00	6211.90	6599.00	30.00	36.00	0.00	0.00	0.00	0.00	0.00	0.00
11	−0.05	2529.40	5997.00	3.00	4.00	10,315.50	10,639.00	35.00	42.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.15	4240.50	10,626.00	2.60	4.00	9490.30	9616.00	33.10	36.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.25	2350.10	7252.00	2.60	3.00	9533.70	9655.00	34.10	41.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.35	2862.90	6677.00	2.50	3.00	9494.90	9608.00	33.00	38.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.45	2840.10	6384.00	2.50	3.00	9554.90	9781.00	34.80	39.00	0.00	0.00	0.00	0.00	0.00	0.00
12	−0.05	11,829.70	34,021.00	3.00	4.00	13,648.40	13,981.00	38.50	43.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.15	20,299.50	51,703.00	3.20	4.00	13,871.60	14,202.00	38.10	43.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.25	35,064.80	72,411.00	3.20	5.00	13,926.70	14,377.00	40.60	47.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.35	17,803.20	37,647.00	3.30	4.00	14,608.00	14,781.00	38.90	42.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.45	22,831.10	80,466.00	3.10	4.00	14,471.10	15,071.00	38.30	41.00	0.00	0.00	0.00	0.00	0.00	0.00
13	−0.05	265,656.90	923,120.00	3.50	4.00	20,448.90	20,785.00	46.90	61.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.15	249,231.90	1,473,884.00	3.40	4.00	20,387.90	21,140.00	44.00	55.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.25	112,572.70	302,798.00	3.20	5.00	19,454.30	20,821.00	42.90	53.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.35	268,053.80	946,366.00	3.00	4.00	18,161.90	19,484.00	40.60	43.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.45	160,286.90	745,930.00	3.20	4.00	20,307.30	20,550.00	46.10	52.00	0.00	0.00	0.00	0.00	0.00	0.00
14	−0.05	1,172,122.50	7,567,940.00	3.90	5.00	28,585.20	30,211.00	48.50	54.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.15	1,424,138.70	4,481,564.00	4.00	5.00	28,565.70	29,477.00	64.10	70.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.25	929,375.40	2,344,144.00	3.70	4.00	28,179.60	28,865.00	49.60	53.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.35	833,666.90	1,431,689.00	3.80	5.00	26,882.00	28,400.00	47.00	51.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.45	736,525.30	1,193,341.00	3.90	5.00	27,906.00	29,114.00	48.50	54.00	0.00	0.00	0.00	0.00	0.00	0.00

Table 3. Results of $\tilde{Q}={\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$ for ${\tilde{p}}_k,{\tilde{w}}_k\in [1,100]$.

		$\mathit{BB}\sim$ CPU		$\mathit{UB}\sim$ CPU		$\mathit{TS}\sim$ CPU		$\mathit{SA}\sim$ CPU		$\frac{\tilde{\mathit{Q}}\left(\mathit{UB}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$		$\frac{\tilde{\mathit{Q}}\left(\mathit{TS}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$		$\frac{\tilde{\mathit{Q}}\left(\mathit{SA}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$
$\mathit{n}$	$\mathit{\delta }$	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max
10	−0.05	841.80	1846.00	2.50	3.00	6338.80	6439.00	29.50	32.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.15	349.40	1058.00	2.30	3.00	6381.50	6447.00	29.00	31.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.25	289.70	559.00	2.50	3.00	6300.20	6468.00	29.60	33.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.35	369.40	681.00	2.50	4.00	6392.40	6497.00	28.90	33.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.45	326.30	1137.00	2.70	4.00	6393.20	6583.00	29.90	35.00	0.00	0.00	0.00	0.00	0.00	0.00
11	−0.05	2277.50	7576.00	2.80	4.00	9555.20	10,574.00	32.90	40.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.15	3059.00	7235.00	2.60	4.00	9623.40	10,245.00	35.10	40.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.25	2820.40	7941.00	2.90	4.00	9622.40	10,029.00	35.00	41.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.35	1825.00	4495.00	3.00	4.00	9438.90	9636.00	34.60	39.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.45	3975.40	8359.00	3.10	4.00	9510.50	9574.00	32.40	37.00	0.00	0.00	0.00	0.00	0.00	0.00
12	−0.05	43,663.80	249,222.00	3.00	4.00	13,429.20	13,721.00	37.90	42.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.15	15,348.60	48,956.00	3.00	3.00	13,489.70	13,579.00	38.50	43.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.25	11,382.60	31,237.00	3.00	4.00	13,531.00	13,761.00	37.40	41.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.35	15,998.20	41,520.00	3.20	4.00	13,551.90	13,629.00	36.80	40.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.45	11,888.50	23,289.00	2.90	4.00	13,488.40	13,764.00	36.60	40.00	0.00	0.00	0.00	0.00	0.00	0.00
13	−0.05	109,898.30	275,375.00	3.20	5.00	19,035.90	19,623.00	41.10	45.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.15	105,751.30	351,782.00	3.20	4.00	20,933.70	21,178.00	58.40	67.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.25	154,626.70	558,105.00	3.50	5.00	20,908.20	21,192.00	44.70	50.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.35	126,965.30	388,984.00	3.60	5.00	21,161.30	21,623.00	45.40	56.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.45	86,593.80	179,924.00	3.20	4.00	20,846.10	21,103.00	45.80	50.00	0.00	0.00	0.00	0.00	0.00	0.00
14	−0.05	1,975,604.70	6,520,424.00	4.00	5.00	28,643.70	29,639.00	50.40	61.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.15	627,934.70	1,950,400.00	3.80	5.00	28,375.90	29,788.00	50.70	57.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.25	1,348,825.50	5,293,208.00	3.70	5.00	27,533.80	28,386.00	50.40	57.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.35	1,584,079.50	3,760,187.00	3.80	4.00	27,597.90	28,497.00	47.50	52.00	0.00	0.00	0.00	0.00	0.00	0.00
	−0.45	525,962.40	2,133,680.00	3.60	5.00	27,711.00	28,777.00	50.80	57.00	0.00	0.00	0.00	0.00	0.00	0.00

Table 4. Results of $\tilde{Q}={\tilde{T}}_{\max }$ for ${\tilde{p}}_k,{\tilde{w}}_k\in [1,50]$.

		$\mathit{BB}\sim$ CPU		$\mathit{UB}\sim$ CPU		$\mathit{TS}\sim$ CPU		$\mathit{SA}\sim$ CPU		$\frac{\tilde{\mathit{Q}}\left(\mathit{UB}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$		$\frac{\tilde{\mathit{Q}}\left(\mathit{TS}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$		$\frac{\tilde{\mathit{Q}}\left(\mathit{SA}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$
$\mathit{n}$	$\mathit{\delta }$	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max
10	−0.05	10,305.20	36,694.00	0.50	1.00	6015.20	6323.00	28.20	31.00	0.04218	0.39472	0.03749	0.34789	0.00283	0.02818
	−0.15	10,480.30	34,742.00	0.80	1.00	6166.50	6907.00	28.80	31.00	0.08256	0.43024	0.03495	0.15143	0.02095	0.15143
	−0.25	9196.60	32,804.00	0.60	1.00	6415.30	7057.00	29.90	33.00	0.07226	0.55399	0.00010	0.00044	0.00005	0.00027
	−0.35	4954.30	11,796.00	0.50	1.00	6459.70	6808.00	28.50	31.00	0.18064	0.87068	0.16134	0.80792	0.06763	0.54899
	−0.45	4865.40	22,349.00	0.60	1.00	6241.00	6538.00	28.90	32.00	0.18803	1.50585	0.06177	0.43674	0.07752	0.43663
11	−0.05	91,394.00	622,506.00	0.80	1.00	10,001.10	10,646.00	34.00	37.00	0.25495	2.30240	0.14385	1.27138	0.13366	1.30486
	−0.15	56,224.40	204,366.00	0.60	1.00	9461.60	9772.00	34.70	43.00	0.06988	0.23636	0.01290	0.08721	0.00456	0.03986
	−0.25	12,090.70	38,411.00	0.90	1.00	9562.80	9686.00	35.40	38.00	0.09294	0.69462	0.08318	0.69308	0.06598	0.42501
	−0.35	13,685.00	31,216.00	0.80	1.00	9459.70	9690.00	33.00	39.00	0.02092	0.20837	0.00825	0.08166	0.01607	0.15985
	−0.45	18,151.40	38,034.00	0.60	1.00	4864.90	9833.00	33.30	37.00	0.11889	0.91132	0.07830	0.78286	0.10588	0.91320
12	−0.05	157,757.60	810,455.00	0.90	3.00	13,496.00	14,138.00	37.90	40.00	0.04467	0.36133	0.00726	0.07235	0.04465	0.36133
	−0.15	127,675.80	1,065,652.00	0.70	1.00	13,645.70	14,137.00	40.60	47.00	0.06921	0.53511	0.05355	0.53497	0.02415	0.14151
	−0.25	296,353.00	2,182,038.00	0.80	1.00	13,741.40	14,244.00	40.30	42.00	0.09690	0.39529	0.06874	0.32601	0.05331	0.39529
	−0.35	88,240.90	538,187.00	0.90	1.00	14,561.60	14,750.00	40.30	51.00	0.20473	1.21564	0.10062	0.45672	0.10604	0.45672
	−0.45	413,334.20	1,836,635.00	1.00	2.00	14,099.60	15,139.00	38.90	45.00	0.08252	0.41016	0.02552	0.24349	0.01177	0.09664
13	−0.05	1,029,283.60	7,508,050.00	1.50	4.00	20,240.20	20,774.00	44.00	48.00	0.03795	0.22730	0.00474	0.02579	0.03795	0.22730
	−0.15	683,977.20	3,227,291.00	1.10	2.00	19,994.40	20,716.00	47.30	53.00	0.10531	0.62497	0.06028	0.42515	0.09941	0.62497
	−0.25	628,087.20	2,123,450.00	1.40	2.00	18,789.50	20,336.00	43.90	51.00	0.05224	0.40890	0.02712	0.17042	0.01294	0.10057
	−0.35	2,514,477.00	16,455,978.00	0.90	1.00	17,355.60	18,137.00	40.90	45.00	0.07098	0.36171	0.02734	0.12875	0.07098	0.36171
	−0.45	614,653.20	2,136,786.00	0.90	2.00	19,857.20	20,682.00	46.60	55.00	0.12851	0.44154	0.03852	0.22742	0.04689	0.22950
14	−0.05	4,243,698.70	16,271,598.00	1.40	3.00	27,734.50	30,028.00	50.80	54.00	0.00384	0.03828	0.00000	0.00001	0.00384	0.03828
	−0.15	2,984,049.70	20,082,425.00	1.20	2.00	27,863.80	29,586.00	50.80	55.00	0.16317	1.04992	0.02443	0.13516	0.16317	1.04992
	−0.25	7,974,330.60	38,573,838.00	1.40	2.00	27,222.70	29,202.00	51.50	64.00	0.08036	0.79983	0.03371	0.33332	0.08036	0.79983
	−0.35	4,460,957.40	37,780,840.00	1.10	2.00	26,115.40	28,408.00	50.00	67.00	0.09733	0.46055	0.01941	0.19361	0.09733	0.46055
	−0.45	1,992,466.30	7,281,374.00	1.20	2.00	27,364.00	29,196.00	51.40	61.00	0.22166	1.66465	0.18160	1.54309	0.20138	1.66465

Table 5. Results of $\tilde{Q}={\tilde{T}}_{\max }$ for ${\tilde{p}}_k,{\tilde{w}}_k\in [1,100]$.

		$\mathit{BB}\sim$ CPU		$\mathit{UB}\sim$ CPU		$\mathit{TS}\sim$ CPU		$\mathit{SA}\sim$ CPU		$\frac{\tilde{\mathit{Q}}\left(\mathit{UB}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$		$\frac{\tilde{\mathit{Q}}\left(\mathit{TS}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$		$\frac{\tilde{\mathit{Q}}\left(\mathit{SA}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$
$\mathit{n}$	$\mathit{\delta }$	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max	Mean	Max
10	−0.05	11,898.80	57,335.00	0.60	1.00	6197.00	6556.00	29.60	35.00	0.09524	0.83987	0.08399	0.83987	0.08420	0.83987
	−0.15	10,861.50	28,751.00	0.40	1.00	6283.70	6477.00	31.60	37.00	0.05090	0.50884	0.03943	0.39433	0.00000	0.00000
	−0.25	13,352.90	72,680.00	0.50	1.00	6161.80	6561.00	29.60	34.00	0.05048	0.24549	0.00818	0.08170	0.00000	0.00000
	−0.35	7534.20	46,164.00	0.70	1.00	6379.10	6586.00	30.00	33.00	0.07483	0.36011	0.05767	0.35996	0.02587	0.13494
	−0.45	3355.30	15,258.00	0.60	1.00	6582.30	7616.00	30.00	33.00	0.23372	2.33720	0.13830	1.38300	0.00000	0.00000
11	−0.05	11,727.30	27,595.00	0.50	1.00	9158.10	9709.00	33.20	38.00	0.05618	0.21427	0.03154	0.17124	0.01724	0.17150
	−0.15	49,113.70	122,708.00	0.80	1.00	9471.50	9669.00	33.50	36.00	0.06573	0.44529	0.06012	0.41753	0.00284	0.02826
	−0.25	25,227.10	147,330.00	0.50	1.00	9627.00	10,188.00	35.70	42.00	0.12450	1.02758	0.08730	0.87293	0.00004	0.00024
	−0.35	36,752.00	275,376.00	0.60	1.00	9292.10	9659.00	33.50	39.00	0.05718	0.31665	0.03415	0.19332	0.03172	0.31665
	−0.45	4012.80	12,740.00	0.60	2.00	9527.90	9687.00	34.40	38.00	0.09081	0.66967	0.04638	0.23765	0.04376	0.19914
12	−0.05	228,804.40	1,216,417.00	1.00	1.00	13,300.50	13,812.00	38.70	43.00	0.04202	0.23287	0.01873	0.18729	0.04202	0.23287
	−0.15	163,787.10	895,682.00	1.00	1.00	13,050.80	13,526.00	39.50	44.00	0.00922	0.06557	0.00001	0.00004	0.00000	0.00002
	−0.25	155,448.80	790,989.00	1.00	1.00	13,125.80	13,624.00	38.70	43.00	0.10681	0.51907	0.06011	0.38198	0.09175	0.46834
	−0.35	316,255.90	2,364,817.00	0.90	1.00	13,364.60	13,898.00	38.10	42.00	0.11751	0.54056	0.02235	0.22345	0.00147	0.01435
	−0.45	496,839.00	2,609,338.00	1.00	2.00	13,124.00	13,872.00	38.40	44.00	0.04466	0.23933	0.02020	0.20190	0.03430	0.23933
13	−0.05	393,103.50	2,633,680.00	1.00	2.00	18,654.40	19,578.00	44.20	48.00	0.09319	0.73525	0.02453	0.16912	0.06215	0.42484
	−0.15	1,614,567.50	7,339,914.00	1.10	2.00	20,351.20	21,565.00	46.50	48.00	0.29944	1.28499	0.07542	0.41595	0.17030	1.28499
	−0.25	1,028,580.60	5,506,700.00	1.10	2.00	20,091.00	21,060.00	48.10	53.00	0.04309	0.19368	0.00735	0.07347	0.00857	0.08571
	−0.35	649,025.30	3,329,984.00	1.20	2.00	20,733.00	22,232.00	45.60	54.00	0.09363	0.45811	0.05546	0.45640	0.03537	0.17480
	−0.45	986,772.90	4,045,625.00	0.90	1.00	20,052.60	21,235.00	45.60	58.00	0.00000	0.00003	0.00000	0.00001	0.00000	0.00003
14	−0.05	1,396,713.10	4,382,671.00	1.40	2.00	27,991.30	29,138.00	52.50	62.00	0.03093	0.13401	0.01705	0.13049	0.03093	0.13401
	−0.15	2,599,787.50	10,633,928.00	1.00	1.00	27,803.70	29,593.00	52.90	65.00	0.02042	0.20398	0.01966	0.19642	0.01966	0.19642
	−0.25	3,708,771.50	20,829,998.00	1.50	2.00	27,054.60	28,450.00	50.10	53.00	0.32720	2.78410	0.09193	0.91912	0.30721	2.78481
	−0.35	1,896,808.60	9,928,279.00	1.50	2.00	26,980.30	28,288.00	49.90	60.00	0.12860	0.60568	0.04617	0.24369	0.08606	0.36122
	−0.45	740,966.10	3,267,537.00	1.50	2.00	27,695.10	29,096.00	48.70	56.00	0.02891	0.12388	0.00038	0.00326	0.02623	0.11463

Table 6. The p99 values of $\tilde{Q}={\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$ for ${\tilde{p}}_k,{\tilde{w}}_k\in [1,50]$.

n	$\mathit{\delta }$	$\mathit{BB}\sim$ CPU	$\mathit{UB}\sim$ CPU	$\mathit{TS}\sim$ CPU	$\mathit{SA}\sim$ CPU	$\frac{\tilde{\mathit{Q}}\left(\mathit{UB}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$	$\frac{\tilde{\mathit{Q}}\left(\mathit{TS}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$	$\frac{\tilde{\mathit{Q}}\left(\mathit{SA}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$
10	−0.05	1779.64	3.91	6453.79	33.82	0.00	0.00	0.00
	−0.15	511.82	3.91	6484.40	34.00	0.00	0.00	0.00
	−0.25	2088.97	3.82	7051.41	33.82	0.00	0.00	0.00
	−0.35	1192.92	3.00	6597.76	35.91	0.00	0.00	0.00
	−0.45	2167.61	3.00	6584.69	35.73	0.00	0.00	0.00
11	−0.05	5947.50	3.91	10,635.04	41.55	0.00	0.00	0.00
	−0.15	10,449.60	3.91	9614.38	35.82	0.00	0.00	0.00
	−0.25	7076.59	3.00	9648.97	40.64	0.00	0.00	0.00
	−0.35	6598.16	3.00	9607.01	37.73	0.00	0.00	0.00
	−0.45	6278.25	3.00	9780.46	38.82	0.00	0.00	0.00
12	−0.05	32,919.31	3.91	13,972.90	42.91	0.00	0.00	0.00
	−0.15	51,645.49	4.00	14,191.74	42.91	0.00	0.00	0.00
	−0.25	72,109.32	4.91	14,365.03	46.73	0.00	0.00	0.00
	−0.35	37,495.17	4.00	14,773.35	41.82	0.00	0.00	0.00
	−0.45	78,260.73	4.00	15,051.20	41.00	0.00	0.00	0.00
13	−0.05	884,032.91	4.00	20,776.09	60.28	0.00	0.00	0.00
	−0.15	1,391,338.25	4.00	21,100.76	54.55	0.00	0.00	0.00
	−0.25	294,466.97	4.91	20,785.18	52.37	0.00	0.00	0.00
	−0.35	913,411.51	3.91	19,462.94	43.00	0.00	0.00	0.00
	−0.45	695,887.03	4.00	20,539.02	52.00	0.00	0.00	0.00
14	−0.05	7,023,622.79	4.91	30,137.74	53.91	0.00	0.00	0.00
	−0.15	4,427,725.64	4.91	29,468.18	69.82	0.00	0.00	0.00
	−0.25	2,335,338.31	4.00	28,844.84	53.00	0.00	0.00	0.00
	−0.35	1,422,758.39	4.91	28,392.26	50.82	0.00	0.00	0.00
	−0.45	1,190,194.87	4.91	29,046.14	53.73	0.00	0.00	0.00

Table 7. The p99 values of $\tilde{Q}={\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$ for ${\tilde{p}}_k,{\tilde{w}}_k\in [1,100]$.

n	$\mathit{\delta }$	$\mathit{BB}\sim$ CPU	$\mathit{UB}\sim$ CPU	$\mathit{TS}\sim$ CPU	$\mathit{SA}\sim$ CPU	$\frac{\tilde{\mathit{Q}}\left(\mathit{UB}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$	$\frac{\tilde{\mathit{Q}}\left(\mathit{TS}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$	$\frac{\tilde{\mathit{Q}}\left(\mathit{SA}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$
10	−0.05	1.00	36,582.04	6322.55	31.00	0.36	0.32	0.03
	−0.15	1.00	32,939.03	6852.55	30.91	0.41	0.15	0.14
	−0.25	1.00	31,930.10	7045.39	33.00	0.52	0.00	0.00
	−0.35	1.00	11,768.73	6800.17	30.91	0.86	0.80	0.51
	−0.45	1.00	21,185.84	6527.83	32.00	1.40	0.41	0.43
11	−0.05	1.00	577,820.91	10,637.54	37.00	2.11	1.17	1.19
	−0.15	1.00	195,931.92	9759.13	42.64	0.23	0.08	0.04
	−0.25	1.00	37,683.62	9683.48	38.00	0.65	0.64	0.40
	−0.35	1.00	31,184.32	9688.47	38.73	0.19	0.07	0.15
	−0.45	1.00	37,845.27	9832.91	36.91	0.84	0.71	0.84
12	−0.05	2.82	766,120.01	14,102.90	40.00	0.34	0.07	0.34
	−0.15	1.00	975,232.51	14,136.91	46.91	0.50	0.49	0.14
	−0.25	1.00	2,034,697.47	14,243.64	42.00	0.39	0.32	0.37
	−0.35	1.00	500,028.35	14,749.82	50.55	1.14	0.44	0.44
	−0.45	1.91	1,828,255.73	15,127.21	44.64	0.41	0.22	0.09
13	−0.05	3.82	6,949,396.78	20,755.73	48.00	0.22	0.03	0.22
	−0.15	1.91	3,105,394.01	20,709.07	52.82	0.60	0.40	0.60
	−0.25	2.00	2,088,152.09	20,256.08	50.64	0.38	0.16	0.09
	−0.35	1.00	15,534,130.68	18,127.91	44.64	0.35	0.13	0.35
	−0.45	1.91	2,028,775.74	20,673.90	54.46	0.44	0.22	0.22
14	−0.05	2.91	16,002,957.72	29,994.79	54.00	0.03	0.00	0.03
	−0.15	2.00	18,625,896.32	29,536.95	55.00	0.98	0.13	0.98
	−0.25	2.00	36,543,648.06	29,187.33	63.01	0.73	0.30	0.73
	−0.35	1.91	34,893,804.61	28,402.06	66.01	0.46	0.18	0.46
	−0.45	2.00	7,111,942.52	29,151.18	60.28	1.54	1.42	1.54

Table 8. The p99 values of $\tilde{Q}={\tilde{T}}_{\max }$ for ${\tilde{p}}_k,{\tilde{w}}_k\in [1,50]$.

n	$\mathit{\delta }$	$\mathit{BB}\sim$ CPU	$\mathit{UB}\sim$ CPU	$\mathit{TS}\sim$ CPU	$\mathit{SA}\sim$ CPU	$\frac{\tilde{\mathit{Q}}\left(\mathit{UB}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$	$\frac{\tilde{\mathit{Q}}\left(\mathit{TS}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$	$\frac{\tilde{\mathit{Q}}\left(\mathit{SA}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$
10	−0.05	1779.64	3.91	6453.79	33.82	0.00	0.00	0.00
	−0.15	511.82	3.91	6484.40	34.00	0.00	0.00	0.00
	−0.25	2088.97	3.82	7051.41	33.82	0.00	0.00	0.00
	−0.35	1192.92	3.00	6597.76	35.91	0.00	0.00	0.00
	−0.45	2167.61	3.00	6584.69	35.73	0.00	0.00	0.00
11	−0.05	5947.50	3.91	10,635.04	41.55	0.00	0.00	0.00
	−0.15	10,449.60	3.91	9614.38	35.82	0.00	0.00	0.00
	−0.25	7076.59	3.00	9648.97	40.64	0.00	0.00	0.00
	−0.35	6598.16	3.00	9607.01	37.73	0.00	0.00	0.00
	−0.45	6278.25	3.00	9780.46	38.82	0.00	0.00	0.00
12	−0.05	32,919.31	3.91	13,972.90	42.91	0.00	0.00	0.00
	−0.15	51,645.49	4.00	14,191.74	42.91	0.00	0.00	0.00
	−0.25	72,109.32	4.91	14,365.03	46.73	0.00	0.00	0.00
	−0.35	37,495.17	4.00	14,773.35	41.82	0.00	0.00	0.00
	−0.45	78,260.73	4.00	15,051.20	41.00	0.00	0.00	0.00
13	−0.05	884,032.91	4.00	20,776.09	60.28	0.00	0.00	0.00
	−0.15	1,391,338.25	4.00	21,100.76	54.55	0.00	0.00	0.00
	−0.25	294,466.97	4.91	20,785.18	52.37	0.00	0.00	0.00
	−0.35	913,411.51	3.91	19,462.94	43.00	0.00	0.00	0.00
	−0.45	695,887.03	4.00	20,539.02	52.00	0.00	0.00	0.00
14	−0.05	7,023,622.79	4.91	30,137.74	53.91	0.00	0.00	0.00
	−0.15	4,427,725.64	4.91	29,468.18	69.82	0.00	0.00	0.00
	−0.25	2,335,338.31	4.00	28,844.84	53.00	0.00	0.00	0.00
	−0.35	1,422,758.39	4.91	28,392.26	50.82	0.00	0.00	0.00
	−0.45	1,190,194.87	4.91	29,046.14	53.73	0.00	0.00	0.00

Table 9. The p99 values of $\tilde{Q}={\tilde{T}}_{\max }$ for ${\tilde{p}}_k,{\tilde{w}}_k\in [1,100]$.

n	$\mathit{\delta }$	$\mathit{BB}\sim$ CPU	$\mathit{UB}\sim$ CPU	$\mathit{TS}\sim$ CPU	$\mathit{SA}\sim$ CPU	$\frac{\tilde{\mathit{Q}}\left(\mathit{UB}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$	$\frac{\tilde{\mathit{Q}}\left(\mathit{TS}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$	$\frac{\tilde{\mathit{Q}}\left(\mathit{SA}\right)-\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}{\tilde{\mathit{Q}}\left(\mathit{Opt}\right)}$
10	−0.05	1.00	54,600.71	6552.04	34.82	0.77	0.76	0.76
	−0.15	1.00	28,288.04	6474.21	36.82	0.46	0.36	0.00
	−0.25	1.00	68,076.05	6559.65	33.82	0.24	0.07	0.00
	−0.35	1.00	42,965.58	6583.21	32.91	0.35	0.34	0.13
	−0.45	1.00	14,337.84	7547.78	32.91	2.13	1.26	0.00
11	−0.05	1.00	27,395.02	9704.86	37.91	0.21	0.17	0.16
	−0.15	1.00	119,386.46	9665.94	36.00	0.42	0.40	0.03
	−0.25	1.00	140,723.82	10,179.72	41.73	0.95	0.79	0.00
	−0.35	1.00	253,145.91	9658.82	38.91	0.31	0.19	0.29
	−0.45	1.91	12,473.06	9679.62	37.91	0.63	0.23	0.20
12	−0.05	1.00	1,168,389.31	13,804.71	42.91	0.23	0.17	0.23
	−0.15	1.00	843,280.49	13,525.73	43.91	0.06	0.00	0.00
	−0.25	1.00	748,983.66	13,607.80	42.82	0.50	0.36	0.45
	−0.35	1.00	2,185,049.74	13,887.38	41.91	0.53	0.20	0.01
	−0.45	1.91	2,564,437.00	13,865.61	43.91	0.22	0.18	0.22
13	−0.05	1.91	2,436,347.89	19,569.36	47.91	0.68	0.16	0.40
	−0.15	1.91	6,954,946.38	21,516.94	48.00	1.27	0.40	1.19
	−0.25	1.91	5,214,892.01	21,056.49	52.91	0.19	0.07	0.08
	−0.35	2.00	3,150,038.27	22,156.76	53.64	0.44	0.42	0.17
	−0.45	1.00	3,882,834.17	21,227.35	57.28	0.00	0.00	0.00
14	−0.05	2.00	4,372,111.75	29,095.25	61.46	0.13	0.12	0.13
	−0.15	1.00	10,141,020.50	29,550.43	64.10	0.19	0.18	0.18
	−0.25	2.00	19,428,368.78	28,446.40	53.00	2.57	0.84	2.56
	−0.35	2.00	9,678,404.17	28,284.49	59.46	0.58	0.24	0.35
	−0.45	2.00	3,203,748.33	29,062.16	56.00	0.12	0.00	0.11

From Table 2 and Table 3, for ${\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j$, the CPU time grows with the increase in n, and the UB and SA algorithms are substantially shorter than the B&B and TS algorithms. Specifically, for job numbers 10–11, the TS algorithm exhibits a longer CPU time compared to the B&B algorithm, whereas for job numbers ranging from 12 to 14, the TS algorithm outperforms the B&B algorithm in terms of CPU time. Additionally, the UB, TS, and SA algorithms perform very well in terms of the error (all 0%). Based on these observations, it can be inferred that, when the value range of ${\tilde{p}}_k,{\tilde{w}}_k\in [1,50]/[1,100]$, the algorithms (UB, TS, and SA) perform remarkably well.

From Table 4 and Table 5, for ${\tilde{T}}_{\max }$, the CPU time of the UB, SA, and TS algorithms is much shorter than that of the B&B algorithm. By comparing tables, it is easy to find that the maximum error of the UB (TS, SA) algorithm is less than 2.8% (1.55%, 2.78%). It can be concluded that, when the value range of ${\tilde{T}}_{\max }\in [1,50]/[1,100]$, the algorithm (i.e., UB, TS, and SA) performs better.

Based on these observations, it can be inferred that, when the ranges of ${\tilde{p}}_k,{\tilde{w}}_k\left({\tilde{T}}_{\max }\right)$$\in [1,50]/[1,100]$, the algorithms (UB, TS, and SA) perform remarkably well. Moreover, the computational results also show that the UB algorithm has a shorter CPU time than the TS and SA algorithms, but its error performance is not better than that of the TS and SA algorithms.

Based on the data obtained above, the different algorithms of CPU time (see Figure 1) for $\tilde{Q}={\tilde{T}}_{\max }\left({\sum }_{j=1}^n{\tilde{w}}_j{\tilde{C}}_j\right)$, where ${\tilde{p}}_k,{\tilde{w}}_k\in (1,50)/(1,100)$. It is clear that the UB algorithm stands out with the shortest running time, which takes no more than 5 ms. In addition, the SA algorithm also has a relatively short running time, with its maximum runtime being only 70 ms, and it performs well in terms of errors. Among them, the TS algorithm has the longest CPU time, which reaches 30,211 ms.

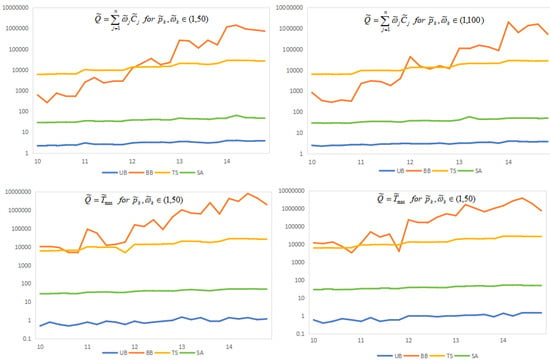
Figure 1. Numerical parameters.

For further investigation of the performance of the UB, SA, and TS algorithms, statistical test results are presented in Table 10. As the results in Table 4 and Table 5 show that SA and TS potentially outrun UB, statistical hypothesis tests are implemented to compare the effectiveness of SA, TS, and UB. As an example, the instances where ${\tilde{T}}_{\max }\in [1,100]$ for jobs 11–14 are considered. The t-test is used for the tests: $t_1={\displaystyle \frac{\overline{X_{UB}}-\overline{X_{SA}}}{S_w\sqrt{1/m_{UB}+1/m_{SA}}}}$, $t_2={\displaystyle \frac{\overline{X_{UB}}-\overline{X_{TS}}}{S_w\sqrt{1/m_{UB}+1/m_{TS}}}}$, where $S_w^2={\displaystyle \frac{(m_{UB}-1)S_{UB}^2+(m_{SA\left(TS\right)}-1)S_{SA\left(TS\right)}^2}{m_{UB}+m_{UB}-2}}$, and $\overline{X}$ denotes the mean error. The corresponding statistical hypothesis test is configured as $H_0:{\mu }_{UB}>{\mu }_{SA},H_1:{\mu }_{SA}\le {\mu }_{UB}$;$H_3:{\mu }_{UB}>{\mu }_{TS},H_4:{\mu }_{UB}\le {\mu }_{TS}$. A type I error of $1\%$ is used, and $t_{critical}=2.5$. Experiment results in Table 4 show that the hypothesis that $H_0:{\mu }_{Case2}>{\mu }_{Case1}$ and $H_3:{\mu }_{UB}>{\mu }_{TS}$ with a type I error of $1\%$ cannot be rejected statistically.

Table 10. Calculated t values for the hypothesis tests.

n	$\mathit{\delta }$	${\mathit{t}}_1$	${\mathit{t}}_2$
11	−0.05	2.565	2.619
	−0.15	2.597	2.909
	−0.25	2.569	2.813
	−0.35	2.618	2.877
	−0.45	2.583	2.867
12	−0.05	2.562	2.814
	−0.15	2.648	2.956
	−0.25	2.639	2.946
	−0.35	2.578	2.916
	−0.45	2.618	2.879
13	−0.05	2.618	2.965
	−0.15	2.642	3.014
	−0.25	2.561	2.829
	−0.35	2.631	3.009
	−0.45	2.634	2.967
14	−0.05	2.650	3.047
	−0.15	2.617	2.999
	−0.25	2.561	2.933
	−0.35	2.564	2.813
	−0.45	2.627	2.914

8. Conclusions

This article investigates the learning effect scheduling problem with past-sequence-dependent delivery time, where the processing time of the job is a non-increasing convex function related to the learning effect. The aim is to find the optimal job sequence while minimizing the total weighted completion time and maximum tardiness. After analysis, both of these problems are NP-hard. The corresponding lower bounds are given through the proposed optimal properties, and heuristic algorithms are provided to calculate the upper bounds to correct them. The branch-and-bound algorithm and two other commonly used metaheuristic algorithms for solving scheduling problems are used under the given two bounds, and the effectiveness of the proposed algorithms are verified based on the results of data simulations. Future research directions can extend it to flow shop scheduling (see Rossit et al. [39], Panwalkar and Koulamas [40], Koulamas and Kyparisis [41], Khatami et al. [42], and Lv and Wang [43]) and other optimization problems with deteriorating jobs (see Huang [44], Liu et al. [45], and Sun et al. [46]).