Robust Invariance Conditions of Uncertain Linear Discrete Time Systems Based on Semidefinite Programming Duality
Abstract
1. Introduction
2. Preliminaries
3. Results
3.1. Robust Invariant Set with Symmetric Constraints
3.2. Robust Invariant Set under Saturated Controller
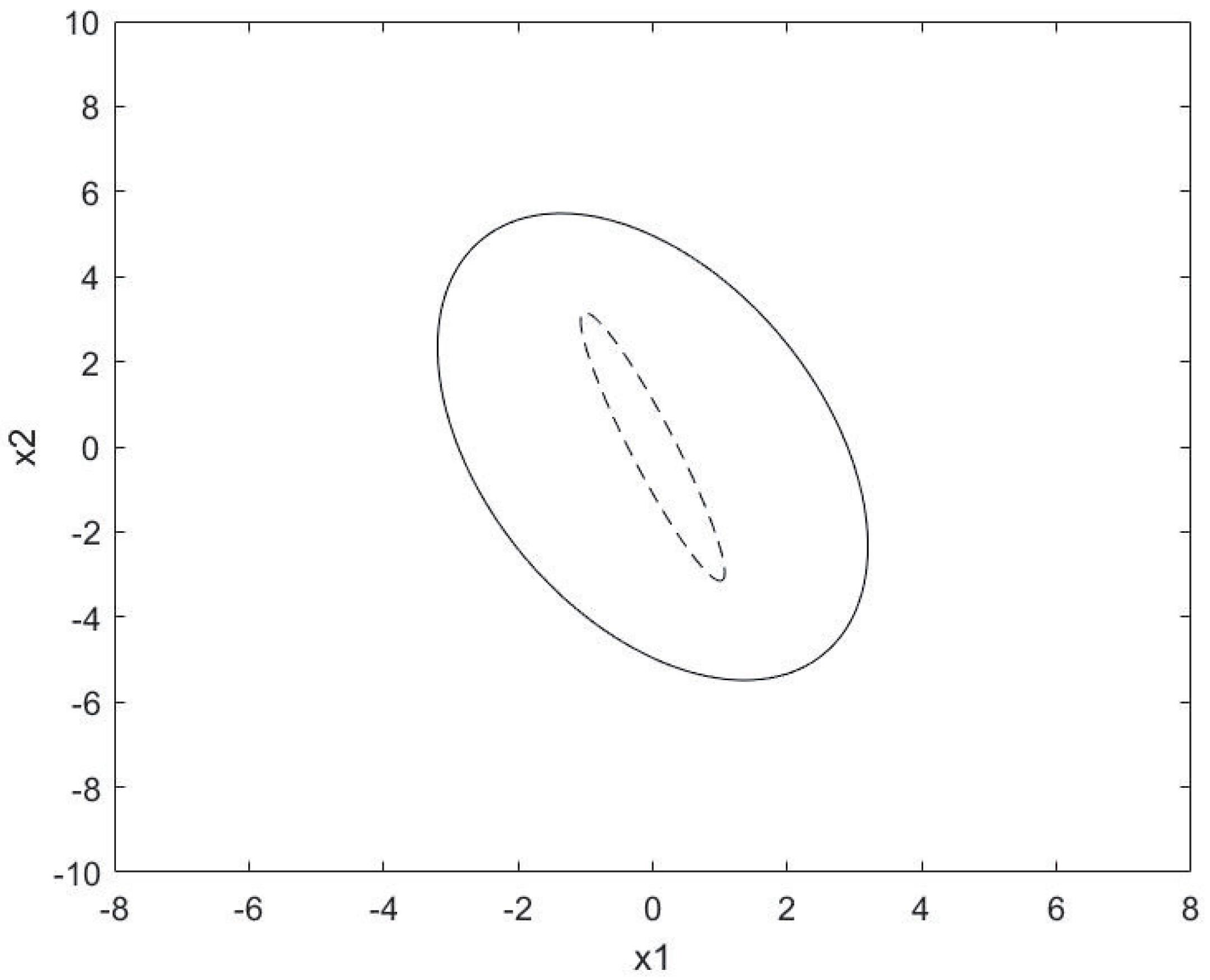
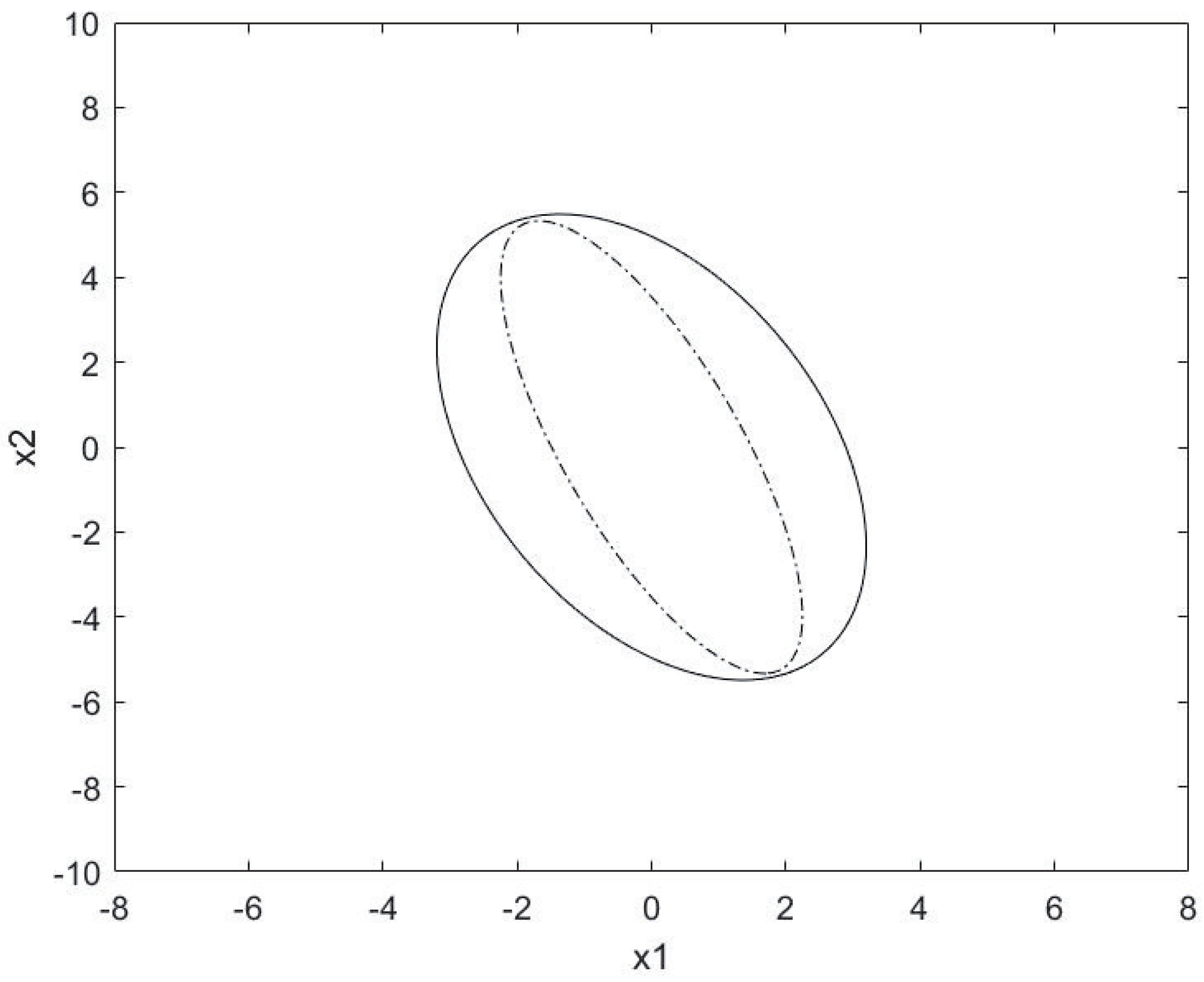
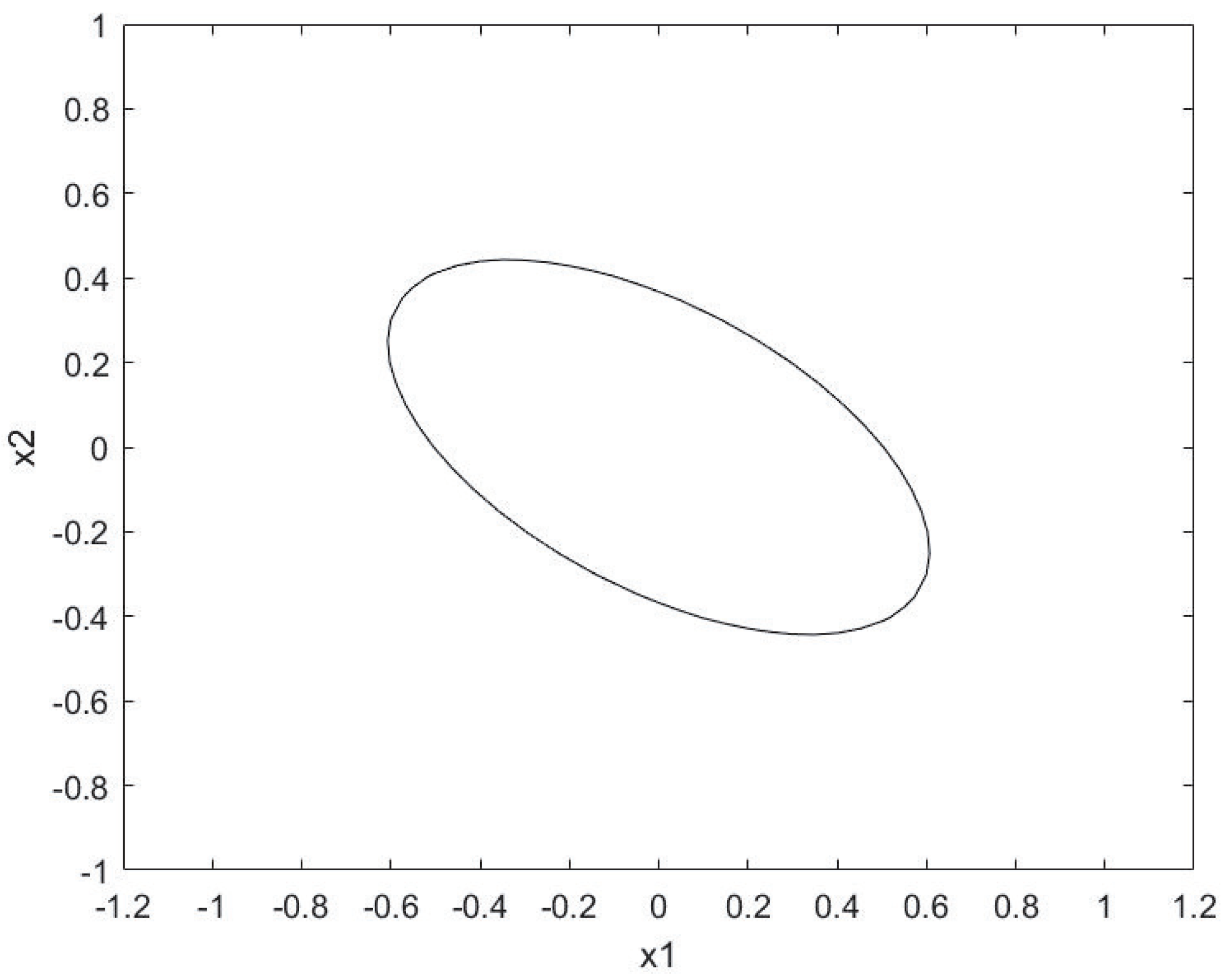
4. Numerical Examples
Validity of Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LMI | Linear Matrix Inequality |
| SDP | Semi-definite Programming |
| SDSIP | semi-definite and semi-infinite programming problems |
References
- Athanasopoulos, N.; Smpoukis, K.; Jungers, R.M. Invariant sets analysis for constrained switching systems. IEEE Control Syst. Lett. 2017, 1, 256–261. [Google Scholar] [CrossRef]
- Hu, T.; Lin, Z.; Chen, B.M. An analysis and design method for linear systems subject to actuator saturation and disturbance. Automatica 2002, 38, 351–359. [Google Scholar] [CrossRef]
- Kerrigan, E.C.; Maciejowski, J.M. Invariant sets for constrained nonlinear discrete-time systems with application to feasibility in model predictive control. In Proceedings of the 39th IEEE Conference on Decision and Control (Cat. No. 00CH37187), Sydney, NSW, Australia, 12 December 2000; Volume 5, pp. 4951–4956. [Google Scholar]
- Fiacchini, M.; Alamo, T. Probabilistic reachable and invariant sets for linear systems with correlated disturbance. Automatica 2021, 132, 109808. [Google Scholar] [CrossRef]
- Bravo, J.M.; Limón, D.; Alamo, T.; Camacho, E.F. On the computation of invariant sets for constrained nonlinear systems: An interval arithmetic approach. Automatica 2005, 41, 1583–1589. [Google Scholar] [CrossRef]
- Colaru, S.; De Doná, J.A.; Seron, M.M.; Stoican, F. Positive invariant sets for fault tolerant multisensor control schemes. Int. J. Control 2010, 83, 2622–2640. [Google Scholar]
- Tahir, F.; Jaimoukha, I.M. Robust positively invariant sets for linear systems subject to model-uncertainty and disturbances. IFAC Proc. Vol. 2012, 45, 213–217. [Google Scholar] [CrossRef]
- Korda, M.; Henrion, D.; Jones, C.N. Convex computation of the maximum controlled invariant set for polynomial control systems. SIAM J. Control Optim. 2014, 52, 2944–2969. [Google Scholar] [CrossRef]
- Wang, C.; Yang, H.; Ivanov, I.G. Controlled Invariant Sets of Discrete-Time Linear Systems with Bounded Disturbances. Mathematics 2023, 11, 3421. [Google Scholar] [CrossRef]
- Chen, Y.; Peng, H.; Grizzle, J.; Ozay, N. Data-driven computation of minimal robust control invariant set. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami, FL, USA, 17–19 December 2018; pp. 4052–4058. [Google Scholar]
- Trodden, P. A one-step approach to computing a polytopic robust positively invariant set. IEEE Trans. Autom. Control 2016, 61, 4100–4105. [Google Scholar] [CrossRef]
- Wang, C.; Yang, H. On positively invariant polyhedrons for discrete-time positive linear systems. Adv. Contin. Discret. Model. 2023, 34, 1–25. [Google Scholar] [CrossRef]
- Balakrishnan, V.; Vandenberghe, L. Semidefinite programming duality and linear time-invariant systems. IEEE Trans. Autom. Control 2003, 48, 30–41. [Google Scholar] [CrossRef]
- Li, S.J.; Yang, X.Q.; Teo, K.L. Duality for semi-definite and semi-infinite programming. Optimization 2003, 52, 507–528. [Google Scholar] [CrossRef][Green Version]
- Lei, Y.; Yang, H. Dual optimization approach to set invariance conditions for discrete-time dynamic systems. Optim. Eng. 2023, 24, 2727–2744. [Google Scholar] [CrossRef]
- Klep, I.; Schweighofer, M. An exact duality theory for semidefinite programming based on sums of squares. Math. Oper. Res. 2013, 38, 569–590. [Google Scholar] [CrossRef]
- Yiping, C. A Proof of the Discrete-Time KYP Lemma Using Semidefinite Programming Duality. In Proceedings of the 2007 Chinese Control Conference, Zhangjiajie, China, 26 July 2007; pp. 156–160. [Google Scholar]
- Xue, B.; Wang, Q.; Zhan, N.; Fränzle, M. Robust invariant sets generation for state-constrained perturbed polynomial systems. In Proceedings of the 22nd ACM International Conference on Hybrid Systems: Computation and Control, Montreal, QC, Canada, 16–18 April 2019; pp. 128–137. [Google Scholar]
- Nguyen, H.-N. Constrained Control of Uncertain, Time-Varying, Discrete-Time Systems; Series: Lecture Notes in Control and Infomration Sciences, N 451; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Hu, T.; Lin, Z.; Chen, B.M. Analysis and design for discrete-time linear systems subject to actuator saturation. Syst. Control Lett. 2002, 45, 97–112. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Wang, C.; Bi, X.; Ivanov, I.G. Robust Invariance Conditions of Uncertain Linear Discrete Time Systems Based on Semidefinite Programming Duality. Mathematics 2024, 12, 2512. https://doi.org/10.3390/math12162512
Yang H, Wang C, Bi X, Ivanov IG. Robust Invariance Conditions of Uncertain Linear Discrete Time Systems Based on Semidefinite Programming Duality. Mathematics. 2024; 12(16):2512. https://doi.org/10.3390/math12162512
Chicago/Turabian StyleYang, Hongli, Chengdan Wang, Xiao Bi, and Ivan Ganchev Ivanov. 2024. "Robust Invariance Conditions of Uncertain Linear Discrete Time Systems Based on Semidefinite Programming Duality" Mathematics 12, no. 16: 2512. https://doi.org/10.3390/math12162512
APA StyleYang, H., Wang, C., Bi, X., & Ivanov, I. G. (2024). Robust Invariance Conditions of Uncertain Linear Discrete Time Systems Based on Semidefinite Programming Duality. Mathematics, 12(16), 2512. https://doi.org/10.3390/math12162512