Transverse Compression of a Thin Inhomogeneous Elastic Layer
Abstract
1. Introduction
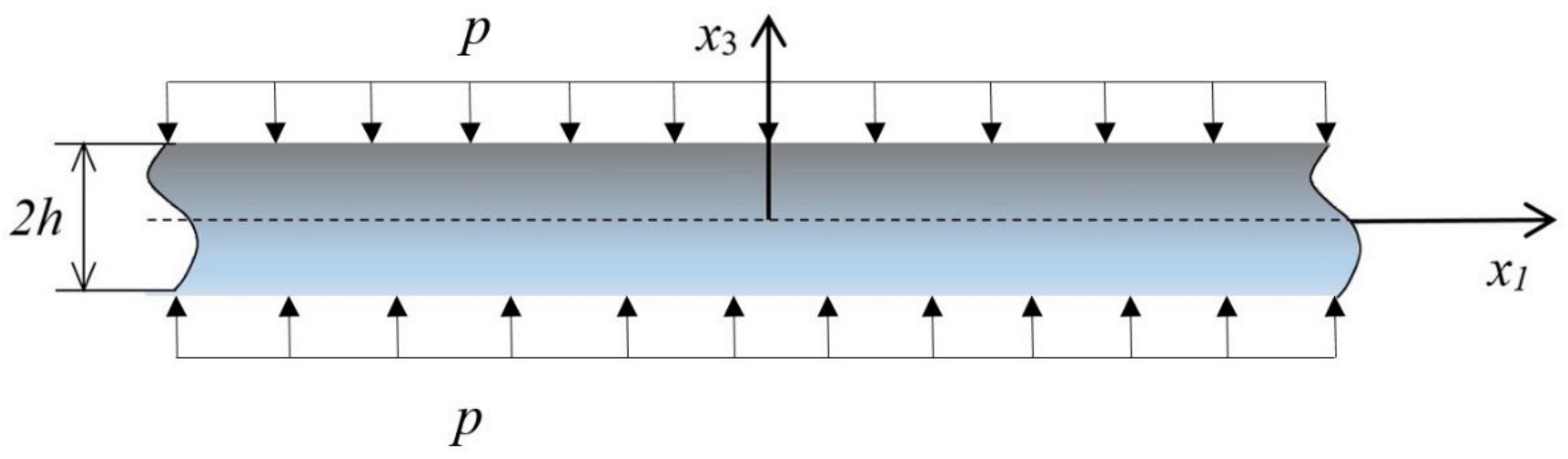
2. Statement of the Problem
3. Asymptotic Solution
4. Particular Cases
5. Prescribed Transverse Displacements
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chalhoub, M.S.; Kelly, J.M. Effect of bulk compressibility on the stiffness of cylindrical base isolation bearings. Int. J. Solids Struct. 1990, 26, 743–760. [Google Scholar] [CrossRef]
- Gent, A.; Lindley, P. The compression of bonded rubber blocks. Proc. Inst. Mech. Eng. 1959, 173, 111–122. [Google Scholar] [CrossRef]
- Koh, C.G.; Lim, H.L. Analytical solution for compression stiffness of bonded rectangular layers. Int. J. Solids Struct. 2001, 38, 445–455. [Google Scholar] [CrossRef]
- Pinarbasi, S.; Akyuz, U.; Mengi, Y. A new formulation for the analysis of elastic layers bonded to rigid surfaces. Int. J. Solids Struct. 2006, 43, 4271–4296. [Google Scholar] [CrossRef]
- Pinarbasi, S.; Mengi, Y.; Akyuz, U. Compression of solid and annular circular discs bonded to rigid surfaces. Int. J. Solids Struct. 2008, 45, 4543–4561. [Google Scholar] [CrossRef]
- Tsai, H.C.; Lee, C.C. Compressive stiffness of elastic layers bonded between rigid plates. Int. J. Solids Struct. 1998, 35, 3053–3069. [Google Scholar] [CrossRef]
- Tsai, H.C. Compression behavior of annular elastic layers bonded between rigid plates. J. Mech. 2012, 1, 1–7. [Google Scholar] [CrossRef]
- Brady, B.T. An exact solution to the radially end-constrained circular cylinder under triaxial loading. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1971, 8, 165–178. [Google Scholar] [CrossRef]
- Qiao, S.; Lu, N. Analytical solutions for bonded elastically compressible layers. Int. J. Solids Struct. 2015, 58, 353–365. [Google Scholar] [CrossRef]
- Alzaidi, A.S.M.; Kaplunov, J.; Nikonov, A.; Zupančič, B. Transverse compression of a thin elastic disc. Z. Angew. Math. Phys. 2024, 75, 116. [Google Scholar] [CrossRef]
- Miyamoto, Y.; Kaysser, W.A.; Rabin, B.H.; Kawasaki, A.; Ford, R.G. (Eds.) Functionally Graded Materials: Design, Processing and Applications; Springer Science+Business Media: New York, NY, USA, 2013. [Google Scholar]
- Gupta, A.; Talha, M. Recent development in modeling and analysis of functionally graded materials and structures. Prog. Aerosp. Sci. 2015, 79, 1–14. [Google Scholar] [CrossRef]
- Adıyaman, G.; Öner, E.; Yaylacı, M.; Birinci, A. A study on the contact problem of a layer consisting of functionally graded material (FGM) in the presence of body force. J. Mech. Mater. Struct. 2023, 18, 125–141. [Google Scholar] [CrossRef]
- Ege, N.; Erbaş, B.; Kaplunov, J.; Noori, N. Low-frequency vibrations of a thin-walled functionally graded cylinder (plane strain problem). Mech. Adv. Mater. Struct. 2023, 30, 1172–1180. [Google Scholar] [CrossRef]
- Kaplunov, J.; Erbaş, B.; Ege, N. Asymptotic derivation of 2D dynamic equations of motion for transversely inhomogeneous elastic plates. Int. J. Eng. Sci. 2022, 178, 103723. [Google Scholar] [CrossRef]
- Le, K.C. An asymptotically exact first-order shear deformation theory for functionally graded plates. Int. J. Eng. Sci. 2023, 190, 103875. [Google Scholar] [CrossRef]
- Akhmedov, N.K.; Sofiyev, A.H. Asymptotic analysis of three-dimensional problem of elasticity theory for radially inhomogeneous transversally-isotropic thin hollow spheres. Thin-Walled Struct. 2019, 139, 232–241. [Google Scholar] [CrossRef]
- Huang, Q.; Gao, Y.; Hua, F.; Fu, W.; You, Q.; Gao, J.; Zhou, X. Free vibration analysis of carbon-fiber plain woven reinforced composite conical-cylindrical shell under thermal environment with general boundary conditions. Compos. Struct. 2023, 322, 117340. [Google Scholar] [CrossRef]
- Akhmedov, N.K.; Gasanova, N.S. Asymptotic behavior of the solution of an axisymmetric problem of elasticity theory for a sphere with variable elasticity modules. Math. Mech. Solids. 2020, 25, 2231–2251. [Google Scholar] [CrossRef]
- Argatov, I.; Mishuris, G. (Eds.) Contact Mechanics of Articular Cartilage Layers: Asymptotic Models; Springer: Cham, Switzerland, 2015; 335p. [Google Scholar]
- Goldenveizer, A.L. Algorithms for the asymptotic construction of a linear two-dimensional theory of thin shells and the Saint-Venant principle. PMM J. Appl. Math. Mech. 1994, 58, 1039–1050. [Google Scholar] [CrossRef]
- Gregory, R.D.; Wan, F.Y.M. On plate theories and Saint-Venant’s principle. Int. J. Solids Struct. 1985, 21, 1005–1024. [Google Scholar] [CrossRef]
- Aghalovyan, L.A. Asymptotic Theory of Anisotropic Plates and Shells; World Scientific: Singapore, 2015. [Google Scholar]
- Goldenveizer, A.L. Theory of Thin Elastic Shells; Nauka: Moscow, Russia, 1976. [Google Scholar]
- Goldenveizer, A.L. The general theory of elastic bodies (shells, coatings and linings). Mech. Solids 1992, 3, 3–17. [Google Scholar]
- Kaplunov, J.D.; Kossovich, L.J.; Nolde, E.V. Dynamics of Thin Walled Elastic Bodies; Academic Press: San Diego, CA, USA, 1998. [Google Scholar]
- Erbaş, B.; Kaplunov, J.; Rajagopal, K.R. Elastic bending and transverse compression of a thin plate with density-dependent Young’s modulus. Int. J. Non-Linear Mech. 2024, 160, 104651. [Google Scholar] [CrossRef]
- Arumugam, J.; Alagappan, P.; Bird, J.; Moreno, M.; Rajagopal, K.R. A new constitutive relation to describe the response of bones. Int. J. Non-Linear Mech. 2024, 161, 104664. [Google Scholar] [CrossRef]
- Abd Aziz, A.U.; Ammarullah, M.I.; Ng, B.W.; Gan, H.S.; Abdul Kadir, M.R.; Ramlee, M.H. Unilateral external fixator and its biomechanical effects in treating different types of femoral fracture: A finite element study with experimental validated model. Heliyon 2024, 10, e26660. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alzaidi, A.S.M.; Kaplunov, J.; Zupančič, B.; Nikonov, A. Transverse Compression of a Thin Inhomogeneous Elastic Layer. Mathematics 2024, 12, 2502. https://doi.org/10.3390/math12162502
Alzaidi ASM, Kaplunov J, Zupančič B, Nikonov A. Transverse Compression of a Thin Inhomogeneous Elastic Layer. Mathematics. 2024; 12(16):2502. https://doi.org/10.3390/math12162502
Chicago/Turabian StyleAlzaidi, Ahmed S. M., Julius Kaplunov, Barbara Zupančič, and Anatolij Nikonov. 2024. "Transverse Compression of a Thin Inhomogeneous Elastic Layer" Mathematics 12, no. 16: 2502. https://doi.org/10.3390/math12162502
APA StyleAlzaidi, A. S. M., Kaplunov, J., Zupančič, B., & Nikonov, A. (2024). Transverse Compression of a Thin Inhomogeneous Elastic Layer. Mathematics, 12(16), 2502. https://doi.org/10.3390/math12162502







