Abstract
The multifaceted nature of online rumors poses challenges to their identification and control. Current approaches to online rumor governance are evolving from fragmented management to collaborative efforts, emphasizing the proactive management of rumor propagation processes. This transformation considers diverse rumor types, the response behaviors of self-media and netizens, and the capabilities of regulatory bodies. This study proposes a multi-agent intervention model rooted in uncertainty theory to mitigate online rumor dissemination. Its empirical validation includes comparing three rumor categories and testing it against a single-agent model, highlighting the efficacy of collaborative governance. Quantitative assessments underscore the model’s utility in providing regulatory authorities with a robust theoretical framework for adaptive decision-making and strategy adjustments based on real-world conditions.
Keywords:
uncertainty theory; multi-agent intervention model; timing of intervention; decision making; online rumor MSC:
90-10
1. Introduction
The emergence and evolution of the Internet have revolutionized information dissemination, enhancing global communication while also fostering an environment prone to online rumors. This phenomenon is exacerbated during major emergencies, posing significant threats to cybersecurity. The sudden onset of the COVID-19 pandemic in early 2020 exemplified this issue, triggering a surge in unsubstantiated claims propagated through digital media amid widespread panic. Such activities not only destabilized social harmony but also strained regulatory authorities.
As of December 2023, China’s internet user base reached 1.092 billion, marking a 24.8 million increase from the previous year, with an internet penetration rate of 77.5%. Notably, the popularity of short-video platforms highlights the predominance of self-media among netizens. This shift has diversified the landscape of online rumors, presenting new challenges for regulatory oversight. Effectively managing online rumors has thus become a critical imperative in the era of self-media.
The 20th National Congress of the Communist Party of China emphasized the necessity of ‘enhancing comprehensive internet governance and fostering a favorable online environment’, aligning with principles that prioritize public benefit. Similarly, the ‘Opinions on Accelerating the Establishment of a Comprehensive Online Governance System’, adopted during the 9th meeting of the Central Committee for Comprehensively Deepening Reform in July 2019, underscore a strategic shift towards proactive and collaborative governance in information dissemination.
Given these policy imperatives and practical challenges, the study of online rumor governance assumes critical importance for ensuring social stability and public safety. Central to this endeavor is identifying the optimal timing for intervening in rumors, a key determinant of effective rumor management. Zhao et al. [1], in their comprehensive analysis of the scientific literature on rumor governance, identified significant gaps, particularly in addressing the prevention, monitoring, and governance stages of rumors, and the uncertainties inherent in intervening in online rumor propagation. Moreover, existing studies predominantly focus on regulatory authorities as decision-makers, neglecting other influential actors in the process.
Therefore, this paper aims to address the following research questions:
1. How can regulators determine the optimal timing for intervention to maximize the effectiveness of rumor control while minimizing intervention costs?
2. To what extent do the attitudes of self-media platforms and netizens influence the timing of interventions in managing online rumors?
3. How can appropriate mathematical theories be leveraged to address uncertainties in the process of online rumor intervention?
By addressing these questions, this study aims to contribute to the development of effective strategies for managing online rumors within the complexities of modern digital communication environments. This paper introduces a multi-agent intervention model for online rumor propagation. The model includes the roles of self-media and netizens and examines the optimal time for regulatory authorities to intervene. The primary contributions of this research are structured as follows: Section 2 introduces the technical roadmap of this study. Section 3 provides a comprehensive literature review. Section 4 defines the research questions and outlines our hypotheses. Section 5 develops the model, establishing pertinent objectives and constraint functions, followed by model transformations. Section 6 illustrates the model’s application and offers insights. Finally, Section 7 summarizes this study’s findings.
2. Literature Review
The rapid proliferation of online rumors poses significant risks to social stability and national security, threatening public trust and undermining governmental credibility. Effectively managing these rumors is crucial to protecting national interests and maintaining a healthy online environment, making it a persistent focal point of social concern. Internet rumors, diverse and derivative in nature, necessitate regulatory authorities implementing timely and targeted measures for their identification and control. The implementation and timing of interventions are critical to their effectiveness in mitigating the impact of online rumors.
Disseminating information to counter rumors proves to be an effective intervention strategy. Several scholars have explored various approaches to intervening in the dissemination of online rumors, focusing on rumor refutation as a key method to inhibit their spread. Jung, Ross, and Stieglitz [2] conducted a study analyzing Twitter posts during the 2017 G20 summit, categorizing tweets into rumors, debunking messages, uncertainty about rumors, and uncertainty about the debunking news. They concluded that timely and authoritative debunking by official sources is the most effective in halting rumors. Jiang, Gao, and Zhuang [3] view the propagation of rumors and counter-rumors as a dynamic, reciprocal process. Their research delves into the interaction between false rumors and debunking efforts, identifying effective rumor debunking as a crucial tool against widespread digital misinformation. They proposed a Rumor Propagation–Debunking (RSD) model using ordinary differential equations (ODEs) to explore this dynamic relationship. In a different approach, Zhang et al. [4] used explainable machine learning methods and information theory to assess the effectiveness of social media rumor debunking and its influencing factors. Analyzing 10,150 COVID-19 debunking posts on Sina Weibo, they concluded that the benefits of rumor refutation outweigh any drawbacks. They also noted significant variations in the effectiveness of debunking across different rumor types, themes, and levels of engagement. Additionally, Gao et al. [5] analyzed 501 validated anti-rumor posts and comments from 80 government accounts on Sina Weibo between 18 January and 29 February 2020. They evaluated the efficacy of rumor refutation based on the public sentiment expressed in comments, concluding that fact-checking, a comprehensive response approach, and the clear presentation of information can enhance the effectiveness of debunking rumors to some extent.
Beyond interventions like rumor refutation, determining the optimal timing of an intervention is also a critical area of study. Renowned scholars have identified viable strategies for intervening to mitigate the spread of online rumors. To design effective rumor control strategies, Qin, Zhang, and Hu [6] introduced a ternary interaction evolutionary game model on social networking platforms involving the media, government, and netizens. Their experiments suggest that the government can promote truthful reporting by the media and alleviate the pressures of rumor regulation through a balanced approach of lenient regulation complemented by a strict yet reasonable reward and punishment mechanism. Similarly, Huo and Ma [7] explored a dynamic model featuring two time delays to illustrate the interactions between public opinion and official sectors during networked group events. Their findings propose an optimal timing for government interventions that can effectively manage large-scale online incidents.
Furthermore, Wang et al. [8] developed a SCIR public opinion propagation model and proposed a direct immunity strategy for public opinion control. They emphasized that the timing and intensity of interventions are crucial factors in suppressing public opinions effectively. Xu et al. [9] constructed an information diffusion model based on complex networks to analyze the effects of governmental actions on information spread. Their findings confirm that the timing of interventions, government information platforms, network connectivity, and the public’s willingness to communicate significantly influence intervention outcomes.
Considering the effects of expert involvement and delays in government response, Jain et al. [10] proposed a mathematical model of the dynamics of malicious news in homogeneous social networks. Their study reveals that delays in expert responses and a lack of proactive engagement in understanding new developments can hinder accurate assessments of social network opinions on specific events, adversely affecting rumor control and emergency responses. Li and Wang [11] introduced a cross-network propagation model of public opinion in a two-layer OSN and discussed public opinion control strategies, particularly the timing and intensity of interventions. They argue that regulators should prioritize the timing of interventions, aiming to act in the early stages of public opinion dissemination.
Fu et al. [12] conducted research on COVID-19 rumors and proposed targeted rumor management policies. Moreover, scholars have quantified the timing of interventions. Gao and Feng [13] modeled the network rumor control system as a stochastic system with two correlated Bernoulli-distributed random variables, aiming to achieve lower costs in terms of overhead, time, and energy consumption. From a topology control perspective, Yuan and Sun [14] proposed an intervention algorithm based on subgraph partition by adopting a reverse intervention strategy to suppress the spread of malicious information at minimal cost.
Li and Guo [15] proposed a comprehensive rumor propagation model that incorporates background detection, public education, official debunking, and legal punishment interventions. By applying optimal control theory, they derived the expression of the optimal control pair and conducted numerical experiments to simulate optimal control under 11 different strategies. Wan et al. [16] introduced a new competitive information coupling diffusion model to describe the information diffusion process in online social networks. Taking into account realistic constraints, they established an optimization problem with constraints to achieve the optimal allocation of intervention strategies over time and minimize the overall loss.
After reviewing the literature on interventions in online rumor propagation both domestically and internationally, several observations emerge.
Firstly, existing research methods for intervening in online rumor propagation primarily revolve around dynamic models akin to infectious diseases, system dynamics models, and game-theoretic models. However, there is notably scarce research applying uncertainty programming models to the management of online rumors.
Secondly, within the current literature, the timing of interventions into online rumor propagation typically employ probability theory, machine learning [17], and optimal control theory [18]. Few studies, however, utilize uncertainty theory to tackle this issue.
Optimizing the timing of interventions to control the spread of online rumors presents inherent uncertainties. While probability theory is instrumental in studying uncertainty problems, it relies on frequency-based analyses and necessitates sufficient data to establish probability distributions. In practice, historical data often inadequately predict future trends, making specific probability distributions challenging to ascertain, thereby limiting the efficacy of probability theory in this context.
Conversely, uncertainty theory proves advantageous in managing subjective uncertainties stemming from insufficient or unreliable data. Hence, this paper adopts uncertainty theory to explore optimal timing strategies for intervening in online rumor propagation.
3. Technical Process
Our technical roadmap comprises the following six steps:
- Step 1:
- Literature Review and Issue Identification
- Collect and analyze the relevant literature and research results on online rumor management.
- Identify key issues and challenges within the current research landscape.
- Step 2:
- Problem Definition and Hypothesis Formulation
- Define the primary research question and establish corresponding hypotheses.
- Outline the research framework and develop an analytical model as the foundation.
- Step 3:
- Model Development and Objective Setting
- Create a multi-agent intervention model that includes self-media and netizens.
- Determine the optimal intervention time and its influencing factors.
- Establish relevant objective functions and constraints.
- Step 4:
- Model Formalization and Mathematical Approaches
- Formalize and transform the intervention model using mathematical techniques.
- Explore mathematical theories suitable for addressing uncertainties.
- Step 5:
- Model Application and Insights
- Apply the model to real-world cases and evaluate its effectiveness.
- Provide comprehensive insights and analyze factors affecting intervention timing.
- Step 6:
- Conclusion and Future Directions
- Summarize the key findings and conclusions drawn from the study.
- Discuss study limitations and propose directions for future research.
As shown in Figure 1, this roadmap guides our research on how to effectively manage online rumors, using rigorous analysis and modeling to inform practical interventions.
Figure 1.
A flowchart of the technical process.
4. Problem Description
In order to enhance the realism of managing online rumors, it is crucial to consider not only the decision-making processes of regulatory authorities but also the involvement of relevant entities such as self-media and netizens. Here, self-media and netizens refer to individuals or groups other than regulatory authorities who are distinct from the members of these authorities.
When intervening in the spread of online rumors, regulatory authorities typically assess both the effectiveness of an intervention and the minimization of the associated costs. This study measures the effectiveness of online rumor intervention by analyzing the rate of rumor dissemination.
The cost of regulatory interventions can be divided into three parts. Firstly, different types of online rumors may elicit varied responses from self-media and netizens. Regulatory decisions to reward such entities based on their responses contribute to the cost of intervention. Secondly, variable costs are influenced by the duration of the rumor’s circulation. Lastly, fixed costs are incurred regardless of the intervention’s duration. The degree of intervention cost serves as a metric to quantify the expenses associated with intervening in online rumor propagation.
In summary, regulatory authorities aim to minimize total intervention costs and reduce the rate at which rumors spread when determining the optimal timing for an intervention.
Aligned with the research context, the following hypotheses are proposed:
Hypothesis 1 (H1).
The level of attention people pay to online rumors correlates exponentially with the duration of the rumors’ circulation and the proportion of users forwarding real information. Attention decreases with prolonged rumor duration and the increased retweeting of factual information. The spread rate of online rumors positively correlates with public attention due to the exponential decay of attention over time [19].
Hypothesis 2 (H2).
Regulatory personnel exhibit bounded rationality. Their interventions in online rumor propagation consider their own interests.
Hypothesis 3 (H3).
Variable costs for regulatory authorities positively correlate with the duration of an online rumor’s circulation. Longer rumor durations increase intervention costs due to reduced timeliness [20].
Hypothesis 4 (H4).
During the spread of online rumors, non-regulatory participants react in two ways: forwarding real information or refraining from doing so. Regulatory authorities may reward participants based on their responses. The proportion of users forwarding real information positively correlates with the rewards received.
Hypothesis 5 (H5).
Participant reactions are categorized as positive or negative based on the proportion of users forwarding real information. A proportion greater than 0.5 indicates a positive response, while less than 0.5 indicates a negative response.
5. Model Building
The aim of this study is to determine how regulatory authorities can optimally time their intervention in the spread of online rumors across various types, considering the responses of self-media and netizens. The goal is to achieve the most effective intervention outcomes while minimizing costs.
In addressing the intervention timing across n categories of online rumors, involving participation from m entities, regulatory authorities are positioned as decision-makers. The timing of their intervention is treated as a key decision variable. The primary objective for regulatory authorities is to minimize both the total intervention costs and the spread rate of online rumors. To accomplish this, this paper develops a model of intervention timing in the context of multiple agents participating in the spread of online rumors. The effectiveness of the proposed model and algorithm is validated through numerical examples.
5.1. Parameter Introduction
In order to more clearly describe the multi-agent participation model of online rumor propagation intervention timing, we use the following symbolic variables:
| indicates the timing of the regulatory intervention, ; | |
| indicates the time when the online rumor began to be published, ; | |
| indicates the proportional coefficient of the spread rate of online rumors to the attention of online rumors, ; | |
| indicates the highest threshold for the spread rate of online rumors; | |
| indicates the proportional coefficient of the variable intervention cost to the regulatory authority and the duration of the online rumor’s publication, ; | |
| indicates the proportion of users who forwarded true information related to category i online rumors by category k entities, , ; | |
| indicates the correlation coefficient between the bonuses of the subject of category k and the proportion of users who retweet true information related to the online rumors in category i, , ; | |
| indicates the degree of consumption of the fixed intervention costs for the regulatory authorities; | |
| indicates the highest threshold value for the total cost consumption of the regulatory authority. |
5.2. Multi-Objective Functions
The regulatory authorities serve as decision-makers regarding the timing of an intervention in the spread of online rumors. Their objective is to minimize both the propagation rate of online rumors and the total intervention cost while meeting specified constraints.
The timing of an intervention in category i online rumors by regulatory authorities is denoted by , with representing the start time of publication of category i online rumors. Therefore, the time since the beginning of the publication of category i online rumors can be expressed as , which can be normalized to .
5.2.1. Minimize the Spread Rate of Online Rumors
According to Hypothesis 1, the attention people pay to online rumors is exponentially related to the duration of their publication and the proportion of users who share authentic information. Furthermore, attention decreases as the duration of the online rumor’s publication and the proportion of users sharing authentic information increase. Therefore, the attention paid to category i online rumors can be expressed as .
Since the spread rate of online rumors is positively correlated with attention, and represents the proportion coefficient relating the spread rate to attention, the expression of the propagation rate of online rumors in category i is . Thus, the sum of propagation rates across six types of online rumors is given by
The objective of a regulatory intervention in online rumor propagation is to reduce the overall rate of its spread. Before making decisions, regulatory authorities have expectations regarding the effectiveness of interventions (where the effectiveness is represented by the propagation rate of online rumors). They aim to minimize the expected propagation rate, expressed as
5.2.2. Minimize the Total Cost of the Intervention
According to Hypothesis 3, the variable cost incurred by the regulatory authority correlates positively with the duration of online rumor dissemination. Here, represents the proportional coefficient linking the variable intervention cost to the regulatory authority to the duration of online rumor publication. Hence, the variable intervention cost of category i online rumors can be expressed as .
Additionally, according to Hypothesis 4, there exists a positive correlation between the incentives received by participants and the proportion of users who share authentic information. denotes the correlation coefficient between the incentives provided to category k entities and the proportion of users who retweet accurate information related to category i online rumors. Therefore, the incentive given by regulatory authorities to category k entities when managing category i online rumors can be expressed as .
Incorporating the participation of category k entities, the expression of the total cost of regulating interventions across n categories of online rumors is
According to Hypothesis 2, regulatory personnel are bounded rational agents. The cost of an intervention is also considered when intervening in the spread of online rumors. Regulators will have certain expectations of the degree of consumption of the total cost of the intervention before making a decision and want to minimize the expected degree of consumption of the total cost of the intervention; i.e.,
5.3. Opportunity Constraints and Multi-Objective Models
5.3.1. Opportunity Constraints on the Propagation Rate of Online Rumors
In an uncertain environment, the spread rate of online rumors fluctuates continuously. This propagation rate is positively correlated with the public’s attention to online rumors, with uncertain proportional coefficients linking the two. Consequently, the rate of online rumor propagation itself becomes uncertain. Regulators are looking for the probability that the spread rate of n categories of online rumors remains below a maximum threshold to exceed a specified level of confidence. Therefore, when managing the propagation rate of online rumors using an opportunity constraint, the expression of the constraint can be formulated as
Within this constraint, M is the uncertainty measure, is the highest threshold value of the propagation rate of each type of online rumor, and is the confidence level.
5.3.2. Constraints on the Opportunity to Intervene in the Degree of Total Cost Consumption
In an uncertain environment, the degree of the total cost consumption of a regulatory intervention is always changing. The variable intervention cost is positively correlated with the publication time of online rumors, and the proportional coefficient of the two is an uncertain variable; thus, the variable intervention cost is also an uncertain variable, and, as such, the total intervention cost is also an uncertain variable. The regulator expects that the probability that the total cost of intervening in n categories of online rumors is lower than the maximum threshold and higher than a certain probability, so the opportunity constraint is used to manage the total cost consumption of a government intervention, and the expression of the constraint of the total cost of an intervention by a regulatory authority is
Among these variables, M denotes the uncertainty measure, represents the maximum threshold value for the total cost consumption incurred by the regulatory authority for each type of online rumor, and stands for the confidence level.
5.3.3. Timing Constraints on Interventions
The timing of a regulatory intervention in combating online rumors must coincide with their spread. Let denote the time at which online rumors of category i cease spreading. Therefore, the timing constraint for the regulatory intervention can be formulated as
5.3.4. Multi-Objective Model
In order to obtain the optimal decision for the timing of an intervention in online rumor propagation with the participation of netizens and self-media, an intervention timing model of online rumor propagation with multi-agent participation is constructed as follows:
Here,
- is the constraint on the propagation rate of online rumors;
- is the constraint on the degree of consumption of the total cost of the intervention.
5.4. An Equivalent Form of the Model
Model (8) represents a general framework for multi-agent involvement in the intervention timing model of online rumor propagation, characterized as an uncertain planning model. To streamline the model’s solution, this paper presents its equivalent form, grounded in the principles of uncertainty theory. This specific equivalent form and the proof process are detailed in Theorem 1.
Theorem 1.
Let be a set of independent normal indeterminate variables, hence , . Thus, possesses an uncertain distribution function that monotonically increases. Similarly, let be a set of independent normal uncertain variables, . Therefore, has an uncertain distribution function that continuously increases monotonically. Assume is a set of independent normal uncertain variables, . In this case, has an uncertain distribution function that continuously increases monotonically. The model can be rewritten as Model (9)
Proof.
According to Definition A4 and Theorem A3 in Appendix A, is a normal uncertain variable: . Therefore,
Similarly, and are also normal uncertain variables: and . Hence,
Thus, we have proven the two objective functions in Model (9).
According to Theorem A2 in Appendix A, the inverse function of at is
The inverse function of at is
Therefore, using Theorems A1 and A3 from Appendix A, constraint (I) in Model (8) can be written as
which simplifies to
Therefore, the two-constraint expression of Model (9) is proven.
Thus, Theorem 1 is proven. □
6. Comparative Experiments
In order to enable regulatory authorities to better apply the multi-agent participation model of online rumor propagation intervention timing, we conducted numerical experiments with examples [21] to elaborate on the application of the model.
6.1. Parameter Settings
As we all know, in addition to the regulatory authorities, the participants in the process of intervening in the spread of online rumors also include self-media and netizens. Considering these two types of participants, self-media, i.e., and netizens, i.e., , is critical to analyzing the impact of their regulatory attitudes on the optimal intervention time decision for regulatory authorities.
Due to the correlation coefficients involving the spread rate and attention paid to online rumors, the variable costs to regulatory authorities and the duration of rumor publishing, as well as the bonuses for category k entities and the proportion of users forwarding true information related to category i rumors, are factors influenced by numerous variables. Future conditions may diverge from historical patterns, cautioning against reliance solely on past data. Hence, this study employs uncertainty theory to estimate the relationships between rumor spread rate and attention, the variable costs of intervention to authorities, and rumor duration. Expert empirical methods are used to predict their uncertainty distributions, with the parameter values detailed in Table 1, while other parameters are specified in Table 2.

Table 1.
Parameter values for uncertain distributions.

Table 2.
Values of other parameters.
6.2. Solve and Analyze
If the regulatory authorities use Model (9) to determine the optimal intervention time for the above three types of online rumor propagation during an epidemic, Model (9) can be converted into Model (10) according to the value of the relevant parameters.
The fmincon function in MATLAB 2019 is employed to determine the optimal timing of a regulatory intervention in three distinct types of online rumor propagation. Initially, multi-objective programming is streamlined into a single-objective format for resolution. Subsequently, this study analyzes the optimal intervention timing across various types of online rumors, considering different attitudes and participant weights.
6.2.1. Analysis of Results Obtained When the Participants Have the Same Weight
This section analyzes the influence of self-media and netizens’ participation in supervision and attitudes on the optimal time for regulatory intervention, respectively. Assuming that the weight of the propagation rate of online rumors and the degree of the cost consumption of regulatory authorities is the same, that is, , the proportion of users who forward real information on self-media and among netizens is shown in Table 3.

Table 3.
Examples of different attitudes of self-media and netizens.
Table 3 shows the regulatory attitudes of self-media and netizens, that is, the value of . Next, the models of self-media and netizens are solved separately, and the results for non-self-media and netizen participation are compared and analyzed for a greater understanding. The five situations of a positive media response, negative media response, positive response of netizens, negative response of netizens, and no self-media or netizen participation are recorded as examples 1, 2, 3, 4, and 5, respectively.
As shown in Figure 2, as the proportion of black increases, the spread of rumors is getting closer to its end. Therefore, we can intuitively see from Figure 1 that, under the same-weight scenario, the optimal intervention times are only during the birth and extinction periods, and there is no diffusion period. Specifically, see Table 4.

Figure 2.
The proportion of the optimal timing of intervention to the whole rumor propagation cycle.

Table 4.
Optimal timing of intervention with participants having the same weight.
From Table 4, we can conclude that the impacts of self-media and public participation on the timing of an intervention are as follows:
- a.
- The Role of Self-Media
Our findings, as illustrated in Table 4, reveal that the presence of self-media significantly alters the optimal timing for intervening in online rumors. Notably: For international hot spots, intervention should shift from the initial outbreak (birth period) to when the rumor starts to decline (extinction period). For anecdotal rumors, the best time to intervene has moved from when these rumors are almost over (extinction period) to their emergence (birth period). In matters concerning people’s livelihoods, a slight adjustment is recommended from the mid-birth period to the early birth phase.
- b.
- Impact of Passive Media Response
When the media responds passively, the intervention in international hot spots rumors should again shift from the birth to the extinction period, mirroring the effect seen with self-media participation. The timing for addressing rumors about people’s livelihoods changes marginally from the middle to the early birth period. For anecdotal rumors, the optimal time for intervention moves from the late extinction period to the early stage of extinction.
- c.
- Influence of Netizen Participation
The involvement of netizens, whether active or passive, also impacts the timing of interventions. Similar to the self-media scenario, the timing for intervening in international hot spot rumors shifts to the extinction period. Livelihood-related rumors should be addressed earlier, moving from the middle to the early birth period. For anecdotal rumors, active responses by netizens necessitate earlier interventions, shifting from the end to the early extinction period. Passive reactions suggest a shift to the middle of the extinction period.
Strategic Insights and Recommendations:
- International Hot Spots: In the absence of external influences, regulators should act during the birth period for optimal impact and cost-effectiveness. Once self-media and netizens engage, intervention should be delayed until the rumor’s decline (extinction period).
- Livelihood-Related Rumors: Independent of external participation, early intervention during the rumor’s birth is advised. With the involvement of self-media and netizens, an even earlier intervention is preferable.
- Anecdotal Rumors: When self-media actively disseminates true information, intervention should occur at the rumor’s inception. If self-media is passive but netizens are active, regulators should act during the rumor’s decline. Specifically, if self-media is negatively responsive while netizens are positively engaged, an early extinction-period intervention is ideal. Conversely, with passive netizen reactions, the middle extinction period is recommended.
6.2.2. Analysis of Results Obtained When Participants Have Different Weights
In order to obtain the influence of the regulatory authorities’ focus on the governance effect and low costs on optimal intervention timings, different weights were assigned to the two objective functions. The results are shown in Table 5.

Table 5.
Examples of different weights.
The five situations of an active media response, negative media response, the positive response of netizens, the negative response of netizens, and no self-media or netizen participation are recorded as examples 1, 2, 3, 4, and 5, respectively. Table 6 shows the results when the regulator focuses on the effect of governance, and Table 7 when the regulator focuses on low cost. Figure 3 and Figure 4 show the data distributions in Table 6 and Table 7, respectively.

Table 6.
The optimal timing of interventions focusing on the governance effect.

Table 7.
The optimal timing of interventions focusing on low costs.
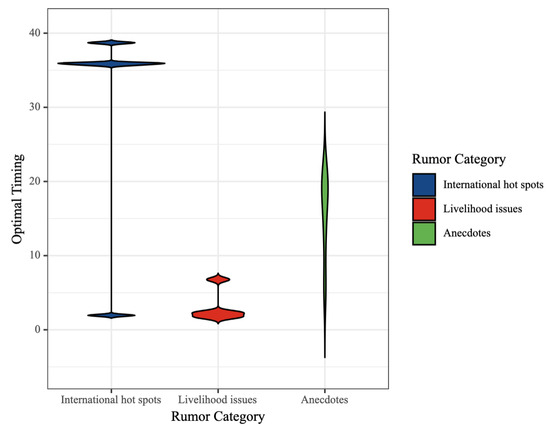
Figure 3.
Distribution of optimal timing of interventions focused on governance effect.
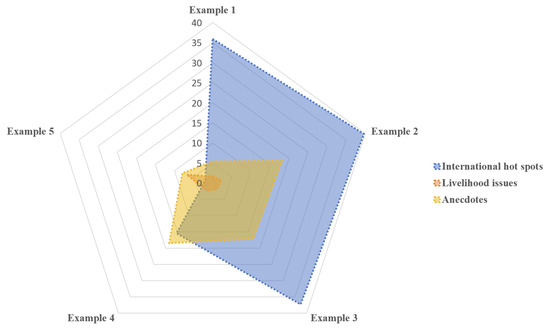
Figure 4.
Distribution of optimal timing of interventions focused on low cost.
- a.
- Influence of Negative Responses from Self-Media and Netizens
As detailed in Table 6, the timing for intervening in online rumors undergoes significant shifts depending on the type of response from self-media and netizens. Specifically, with international hot spot rumors, when self-media and netizens respond negatively, the optimal intervention time moves from the initial outbreak (birth period) to the phase of decline (extinction period). For livelihood-related rumors, there is a slight adjustment in intervention timing from the middle to the early birth period. For anecdotal rumors, the timing of the intervention remains unchanged, indicating that these rumors are less influenced by the nature of the responses from self-media and netizens.
- b.
- Impact of Active Responses from Self-Media and Netizens
In scenarios where self-media and netizens actively engage with the content, international hot spot rumors, similar to negative responses, experience a shift in the optimal intervention time from the birth to the extinction period. With livelihood-related rumors, a minor adjustment is again noted, with the intervention timing moving from the middle to the early birth period. For anecdotal rumors, as with negative responses, there is no notable change in the timing of interventions, suggesting a consistent pattern regardless of the type of active engagement.
These findings underscore the significant impact that the nature of the response from self-media and netizens has on the timing of interventions for different types of online rumors. For international hot spots, whether the response is negative or positive, a delayed intervention during the extinction period is advised for maximum effectiveness. Conversely, livelihood-related rumors require a quicker response early in their life cycle, irrespective of the response type. The consistency in intervention timing for anecdotal rumors regardless of the response type suggests that these may be inherently less susceptible to public sentiment shifts. These insights guide strategic planning for regulatory actions, emphasizing the need for tailored intervention approaches based on the type of rumor and the nature of public engagement.
The data presented in Table 7 reveal significant changes in the optimal times for intervening in online rumors, influenced by the involvement of self-media and netizens. This section discusses these changes across different categories of online rumors.
- International Hot Spot Online Rumors: The optimal intervention time for international hot spot online rumors shifts from the birth period to the extinction period. This change suggests that interventions become more effective later in the rumor’s life cycle, when self-media responds negatively and netizen participation is high.
- Anecdotal Online Rumors: Similarly, the best timing for intervening in anecdotal online rumors moves from the diffusion period to the extinction period. This indicates that delaying an intervention until the later stages could be more beneficial when these actors are engaged.
- Online Rumors Related to People’s Livelihoods: The intervention timing for rumors concerning people’s livelihoods has seen a slight adjustment, shifting from the middle to the early birth period. Although this shift is less dramatic compared to the other types of rumors, it underscores the importance of early intervention in such cases.
The observed changes underscore the dynamic nature of rumor management in the digital age, highlighting how the behavior of self-media and netizens can significantly alter intervention strategies.
Based on the results presented, we can derive several key insights regarding the timing of regulatory interventions in the context of managing online rumors about international hot spots and people’s livelihood issues. These findings can be summarized into two main categories: intervention timings based on the involvement of entities other than regulatory authorities and based on a focus on governance effectiveness or cost-efficiency.
- a.
- Intervention without Other Entities’ Involvement
General Strategy: to achieve optimal governance effectiveness and minimal costs, regulatory authorities should intervene during the early stages, known as the birth period, of the rumor cycle. Specific Cases: For rumors affecting people’s livelihoods, the ideal moment for intervention is during the middle of the birth period. For international hot topics, once self-media and netizens begin participating, authorities should aim to intervene during the extinction phase of the rumors.
- b.
- Decision Making Based on the Focus of the Intervention
Governance Effectiveness: if the priority is the effectiveness of governance, regulatory authorities should intervene during the extinction period of the rumor cycle. Cost Efficiency: if minimizing costs is the priority, intervention should occur during the diffusion phase of the rumor.
- c.
- Role of Self-Media and Netizen Involvement
When netizens are involved and the self-media response is passive, intervention should take place during the extinction period of the rumor, regardless of whether the focus is on governance effectiveness or cost reduction. If self-media actively engages, the recommended time for intervention is during the birth period of the rumor. This structured approach underscores the necessity of regulatory authorities adapting their strategies based on the involvement of other entities and their specific intent in managing online rumors. This enables more effective and cost-efficient interventions tailored to the dynamics of rumor spread and participant involvement.
6.3. Effectiveness of Models
When the parameters are set according to Table 1, the iterative convergence of the objective function value is recorded at 0.581694. Comparing this result with the findings of scholar Jin [20], we observe a notable improvement in the optimal solution when considering the participation of media and netizens. Originally, the value of the objective function was 0.741646, which has been optimized to 0.581649 after adjustments. The reduction in the objective function value signifies that active participation from the media and netizens positively enhances the intervention’s impact. This cooperative approach between the media, netizens, and regulatory authorities increases the overall effectiveness of online rumor governance. The model’s effectiveness is thus confirmed.
6.4. Revelation and Analysis
The analysis of the experimental results provides several insights:
- The Impact of Self-Media and Netizens: The involvement of self-media and netizens significantly influences the optimal timing for interventions. For international hot spot rumors, the optimal intervention period shifts from the birth period to the extinction period. In contrast, for rumors concerning people’s livelihoods, this shift is less pronounced, moving from the middle to the early birth period. Notably, self-media’s active engagement drastically changes the best intervention timing of anecdotal rumors from the extinction to the birth period.
- Optimal Timing with Self-Media and Netizens’ Involvement: Regardless of whether regulatory authorities prioritize governance effectiveness or cost-efficiency, the presence of self-media and netizens dictates that the best time to intervene in international hot spot rumors is during their extinction period. For rumors related to people’s livelihoods, early intervention, right at the beginning of their emergence, proves most effective.
- Anecdotal Rumors Without External Participation: When anecdotal rumors circulate without the participation of self-media or netizens, the regulatory focus—whether on governance effectiveness or cost reduction—significantly affects the optimal intervention timing. Focusing on governance leads to an intervention during the extinction period, whereas prioritizing cost reduction shifts this to the diffusion period.
Overall, the involvement of self-media and netizens delays the optimal intervention time for international hot spots but advances it for rumors related to people’s livelihoods and anecdotal issues. The specific intervention strategy—whether proactive or reactive—tends to influence the timing less for livelihood-related rumors than for anecdotal ones, where an active self-media response accelerates the optimal timing of the intervention.
7. Conclusions
This paper has investigated the impact of the attitudes of netizens and self-media on interventions in online rumors, set against the backdrop of three distinct types of rumors. It has also considered the incentive mechanisms provided by regulatory authorities. To tackle the inherent uncertainties in rumor intervention, we constructed a multi-agent programming model aimed at optimally timing interventions during the spread of online rumors. This model was solved by deriving its equivalent form. Comparative experiments were carried out among the three types of rumors and compared against a single-agent model. The results reveal that the optimal timing of an intervention varies across different types of rumors. Furthermore, the active involvement of self-media and netizens significantly enhances the effectiveness of these interventions. This underscores the crucial role of the incentive mechanisms employed by regulatory authorities in effectively managing online rumors. It also highlights the collective importance of efforts from the media, netizens, and regulatory bodies in maintaining a healthy online environment.
Online rumor intervention remains a vital area of research. Prior to this study, our team had engaged in preliminary research and published several related papers. Our investigations have evolved from focusing on interventions made by regulatory authorities alone to include coordinated efforts involving regulatory authorities, netizens, and self-media. This evolution has enriched our understanding and brought our research closer to addressing real-world scenarios. Moving forward, we aim to refine our understanding of online rumor intervention by incorporating additional uncertain factors, such as the ambiguity of rumors and the influence of self-media, which will make our models more realistic.
One limitation of this study is its reliance on specific assumptions of the uncertainty theory, which may not fully capture the complex dynamics of real-world rumor propagation. Future research could benefit from integrating more diverse theoretical frameworks with empirical data to enhance the model’s applicability and accuracy.
Author Contributions
Conceptualization, Y.N.; methodology, D.L.; validation, F.L.; data curation, Y.G.; writing—original draft preparation, M.J.; writing—review and editing, M.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the National Social Science Foundation of China (21BGL001), the Shandong Natural Science Foundation (ZR2020MG003), and the Special Project for Internet Development of Social Science Planning Special Program of Shandong Province (17CHLJ23).
Data Availability Statement
The data presented in this study is available on request from the corresponding authors, and the dataset was jointly completed by the team, so the data is not publicly available.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
This section presents the key definitions and theorems integral to uncertainty theory, an axiomatic mathematical framework distinct from probability theory. This theory has found extensive applications in various fields such as uncertain statistics [22,23,24,25], programming [26,27,28], gaming [29,30], and differential equations [31,32,33].
Consider , a nonempty universal set, and L, a -algebra over . In uncertainty theory, each element in L is an event, assigned a belief measure which indicates the likelihood of occurring. The measure M, adhering to certain mathematical properties, quantifies this belief. Based on Liu’s foundational work [34], we adhere to three axioms:
Axiom 1 (Normality): .
Axiom 2 (Duality): for any .
Axiom 3 (Subadditivity): for any countable collection of events ,
Definition A1
(Liu [34]). The set function M qualifies as an uncertain measure if it fulfills the normality, duality, and subadditivity axioms.
Axiom 4 (Product Axiom): In uncertainty spaces , for , the produced uncertain measure M is defined by
where each is an event from .
Definition A2
(Liu [34]). An uncertain variable ξ maps from an uncertainty space to real numbers, such that for any Borel set B of real numbers, the event is a subset of Γ;
Analogous to probability theory, where random variables are defined by probability distributions, uncertain variables in uncertainty theory are characterized by uncertain distribution functions.
Definition A3
(Liu [34]). The uncertain distribution function of an uncertain variable ξ is
where x is a real number.
Definition A4
(Liu [34]). A normal uncertain variable ξ is defined by the uncertainty distribution
denoted as , where e and σ are parameters and .
If for , then the linear combination
remains a normal uncertain variable, given for all i, where
Theorem A1
(Liu [34]). For an uncertain variable ξ with an inverse uncertainty distribution , the inequality
holds if and only if
where and c is a constant.
Theorem A2
(Liu [34]). Given the independent uncertain variables , each with a standard uncertainty distribution , and a function that is continuous and strictly increasing for and decreasing for , the function
yields an uncertain variable with an inverse distribution
Theorem A3
(Liu [34]). The expected value of an uncertain variable ξ obeying the distribution Φ is given by
The inverse distribution of a normal uncertain variable is specifically
Theorem A4
(Liu [34]). For two independent uncertain variables, and , with defined expected values, and any real constants and , the expected value of their linear combination is
References
- Zhao, J.; Liu, H.; Dong, H.; Zhang, W.; Xin, J.; Zhou, X.; Wang, Z.; Zhang, X.; Ren, X.; Zhang, S. A synergistic study of policy and literature on rumor governance. Heliyon 2024, 10, e29995. [Google Scholar] [CrossRef] [PubMed]
- Jung, A.-K.; Ross, B.; Stieglitz, S. Caution: Rumors ahead—A case study on the debunking of false information on Twitter. Big Data Soc. 2020, 7, 2053951720980127. [Google Scholar] [CrossRef]
- Jiang, M.; Gao, Q.; Zhuang, J. Reciprocal spreading and debunking processes of online misinformation: A new rumor spreading—Debunking model with a case study. Phys. A Stat. Mech. Its Appl. 2021, 565, 125572. [Google Scholar] [CrossRef]
- Zhang, S.; Hou, J.; Zhang, Y.; Yao, Z.; Zhang, Z. Detecting Social Media Rumor Debunking Effectiveness During Public Health Emergencies: An Interpretable Machine Learning Approach. Sci. Commun. 2024, 5, 125–141. [Google Scholar] [CrossRef]
- Gao, H.; Guo, D.; Yin, H.; Wu, J.; Cao, Z.; Li, L. Strategies and effectiveness of the Chinese government debunking COVID-19 rumors on Sina Weibo: Evaluating from emotions. J. Appl. Commun. Res. 2022, 50, 632–654. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, M.; Hu, H. Ternary interaction evolutionary game of rumor and anti-rumor propagation under government reward and punishment mechanism. Data Anal. Knowl. Discov. 2023, 111, 21409–21439. [Google Scholar] [CrossRef]
- Huo, L.; Ma, C. The interaction evolution model of mass incidents with delay in a social network. Phys. A Stat. Mech. Its Appl. 2017, 484, 440–452. [Google Scholar] [CrossRef]
- Wang, Y.M.; Guo, T.Y.; Li, W.D.; Chen, B. Direct immune-SCIR public-opinion propagation model based on real-time online users. Chin. Phys. B 2020, 29, 100204. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, L.; Xu, B.; Jiang, W.; Deng, C.; Ji, F.; Xu, X. An information integration and transmission model of multi-source data for product quality and safety. Inf. Syst. Front. 2019, 21, 191–212. [Google Scholar] [CrossRef]
- Jain, A.; Dhar, J.; Gupta, V. Rumor model on homogeneous social network incorporating delay in expert intervention and government action. Commun. Nonlinear Sci. Numer. Simul. 2020, 84, 105189. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J. Cross-network propagation model of public opinion information and its control in coupled double-layer online social networks. Aslib J. Inf. Manag. 2022, 74, 354–376. [Google Scholar] [CrossRef]
- Fu, C.; Liao, L.; Xie, H.; Zhou, X. How can we implement targeted policies of rumor governance? An empirical study based on survey experiment of COVID-19. Chin. Public Adm. Rev. 2023, 14, 120–131. [Google Scholar] [CrossRef]
- Gao, M.z.; Feng, D.q. Stochastic stability analysis of networked control systems with random cryptographic protection under random zero-measurement attacks. Front. Inf. Technol. Electron. Eng. 2018, 19, 1098–1111. [Google Scholar] [CrossRef]
- Yuan, D.; Sun, H. Reverse Intervention for Dealing with Malicious Information in Online Social Networks. Comput. Inform. 2020, 39, 156–173. [Google Scholar] [CrossRef]
- Li, T.; Guo, Y. Nonlinear dynamical analysis and optimal control strategies for a new rumor spreading model with comprehensive interventions. Qual. Theory Dyn. Syst. 2021, 20, 84. [Google Scholar] [CrossRef] [PubMed]
- Wan, P.; Wang, X.; Wang, X.; Wang, L.; Lin, Y.; Zhao, W. Intervening Coupling Diffusion of Competitive Information in Online Social Networks. IEEE Trans. Knowl. Data Eng. 2021, 33, 2548–2559. [Google Scholar] [CrossRef]
- Sangwan, S.R.; Bhatia, M. D-BullyRumbler: A safety rumble strip to resolve online denigration bullying using a hybrid filter-wrapper approach. Multimed. Syst. 2022, 28, 1987–2003. [Google Scholar] [CrossRef]
- Huo, L.; Ma, C. Optimal Control of Rumor Spreading Model with Consideration of Psychological Factors and Time Delay. Discret. Dyn. Nat. Soc. 2018, 2018, 9314907. [Google Scholar] [CrossRef]
- Bodaghi, A.; Goliaei, S.; Salehi, M. The number of followings as an influential factor in rumor spreading. Appl. Math. Comput. 2019, 357, 167–184. [Google Scholar] [CrossRef]
- Cui, J.; Chen, S.; Li, C. An Empirical Study on the Ways to Quit Multi-types of Internet Rumors Based on Big Data: Take “Rumors during the Novel Coronavirus Pneumonia Epidemic” as an Example. Inf. Stud. Theory Appl. 2021, 44, 67–73. (In Chinese) [Google Scholar]
- Jin, M.; Liu, F.; Ning, Y.; Zhou, J. Governing Online Rumor: An Uncertain Intervention Timing Model for Online Rumor Propagation from the Perspective of Government. J. Uncertain Syst. 2024, 17, 2350011. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, B. A modified uncertain maximum likelihood estimation with applications in uncertain statistics. Commun. Stat.-Theory Methods 2023, 12, 1–22. [Google Scholar] [CrossRef]
- Lio, W. Uncertain statistics and COVID-19 spread in China. J. Uncertain Syst. 2021, 14, 2150008. [Google Scholar] [CrossRef]
- Yao, K. Uncertain statistical inference models with imprecise observations. IEEE Trans. Fuzzy Syst. 2017, 26, 409–415. [Google Scholar] [CrossRef]
- Ye, T.; Liu, B. Uncertain hypothesis test with application to uncertain regression analysis. Fuzzy Optim. Decis. Mak. 2022, 21, 157–174. [Google Scholar] [CrossRef]
- Jin, M.; Ning, Y.; Liu, F.; Zhao, F.; Gao, Y.; Li, D. An Evaluation Model for the Influence of KOLs in Short Video Advertising Based on Uncertainty Theory. Symmetry 2023, 15, 1594. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Guo, H.; Ma, W. Multi-water resources optimal allocation based on multi-objective uncertain chance-constrained programming model. Water Resour. Manag. 2020, 34, 4881–4899. [Google Scholar] [CrossRef]
- Li, B.; Huang, Y. Uncertain random portfolio selection with different mental accounts based on mixed data. Chaos Solitons Fractals 2023, 168, 113198. [Google Scholar] [CrossRef]
- Yang, X.; Gao, J.; Luo, S.; Loia, V. A concept of nucleolus for uncertain coalitional game with application to profit allocation. Inf. Sci. 2022, 597, 244–252. [Google Scholar] [CrossRef]
- Gao, J.; Cui, Z.; Li, H.; Jia, R. Optimization and Coordination of the Fresh Agricultural Product Supply Chain Considering the Freshness-Keeping Effort and Information Sharing. Mathematics 2023, 11, 1922. [Google Scholar] [CrossRef]
- Ye, T.; Liu, B. Uncertain hypothesis test for uncertain differential equations. Fuzzy Optim. Decis. Mak. 2023, 22, 195–211. [Google Scholar] [CrossRef]
- Liu, Z. Generalized moment estimation for uncertain differential equations. Appl. Math. Comput. 2021, 392, 125724. [Google Scholar] [CrossRef]
- Yang, X.; Liu, Y.; Park, G.K. Parameter estimation of uncertain differential equation with application to financial market. Chaos Solitons Fractals 2020, 139, 110026. [Google Scholar] [CrossRef]
- Liu, B. Uncertainty Theory; Springer: Berlin, Germany, 2007. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).